1.
Introduction
Nowadays online collective actions, such as rumors spreading on the Internet, become pervasive worldwide, especially on social media Apps, such as Facebook, Twitter, Weibo and WeChat [1−8]. Information attractiveness, rumor propagation, individual judgments, social trust on media, and spreading probability may induce people or agents to believe and spread rumors in cyberspace [4,6,9,10−12]. Rumor spreading has a long story since the beginning of human society [13−18]. For ancient world, rumor spreading strategies have been widely applied to launch protesting, social crisis, natural disasters, or uprisings [19−21]. As an important social phenomenon, rumor spreading can undermine or attack opponents and lead to social panic and destabilization [19,22−24]. The effect of a second rumor counteracting the original rumor also complicates the rumor spreading phenomenon and the mathematical model [25]. Therefore, it is important and necessary to explore the spreading mechanism of rumors or information. For now, more attention has been paid to reasons of online cases, but less has been paid to speading curves, and here we focus the curve shapes of online rumor spreading, for various scenarios.
As a typical category, rumor spreading can be investigated under the perspective of collective actions, which have been explored by social sciences [2−4,9,10,26,27], natural sciences [1,28−32] and other interdisciplinary fields [11,33−37]. For the mechanism of rumor spreading, there are a lot of related models [1−6,8,12,18,38,39−66], and the SIR model is probably the most fundamental and widely used. This model refers to dynamic process of susceptible-infected-removed for individuals [6−8,17,35,39], which was initially applied in epidemics [44−46,48,49,52,54,65]. Then, expanded SIR models are proposed, such as SIS [7], 2SI2R [67], ICSAR [12], SIHR [39], BBV [42], SEIR [44], SIRaRu [45], SICR [46], SSIC [48], DSIR, C-DSIR [57] and ISR [58], etc. They adjust SIR models according to different situations [7,12,39,42,43,45,57,67]. Besides of related SIR models, other methods of ANFIS model [68], Markov chain [31], Lyapunov model [11], machine learning [66], random differential equation (RDE) [35], theory analysis [3,26,37,38,67,69], game theory [11,13,47,66], agent-based modeling [1,9,11,17,29,32,27,33−35,38] and social networks [22,26−29,32,34,35,39,53,55,58,64−67] are also applied and combined to explore the mechanism.
Besides of the spreading mechanism, evolutionary curves (trends) of online collective actions have become critical and remains unsolved [1,3,6,10,15,19,21,24,27,28,37,63,66]. Here, we try to find and verify the mechanisms that generate different curve shapes. As indicated, the common curve shape of collective behaviors (rumor spreading or cooperative actions) is the S-shape [4,6,10,15,19,21,24,27,28,37]. With specific rules and regulations, this is an ideal shape [70−74]. The most ideal type is standard S-shape curve, which is close to accumulative probability curve of the normal distributions [72,74,75], and its density function can be obtained across the whole range. If the function of S-shape curves can be obtained, we are able to predict the whole spreading process of online rumors, in advance. Hence, it is feasible to use it to solve and predict dynamics of spreading curves. In this work, we apply the method of agent-based modeling [1,4,9,11,15,17,21,24,29,32,33,34,35,76], to explore spreading mechanisms of online rumors. Under big data dissemination, mechanism design is critical in determining, investigating, and predicting evolutionary dynamics of online rumors spreading [4,5,7,8,13,26,48,58]. For all the agents, attributions of internal (subjective) thresholds and external social trust thresholds are proposed. According to real cases observed, both internal and external factors are heterogeneities. To explore different spreading curves of simulations, local neighborhood interactions between agents and their neighbors will be modeled and simulated repeatedly. Based on agent-based modeling, we explore factors and mechanmisms of the rumor spreading process [11,12,18,29,30,33,34,56] or curve shapes [62,66,67,70,71,73−76]. Besides, the rumor spreading is heavily investigated in complex networks [77−94], but little studied applying deterministic models [25].
In the real world, we have different variables or factors that lead to distinct spreading curves. Different parameter settings produce different spreading shapes or curves[1,3,6,17,18,69]. So, we explore the laws and regularities of spreading curves under different conditions. We try to find the best parameter combination, which best fits and explains the spreading curves observed. This paper has five sections. After the introduction section, we propose the modeling and parameter settings in the second section. Then, we report different shapes of curves and dynamic trends. The spreading duration is also observed, and we compare durations under different conditions and situations.
2.
Materials and methods
Agent-based modeling and related simulations have become the mainstream modeling pathway to explore the spreading mechanism of information [1,3,6,9,11,12,17,27,29,32−35,38]. For all agents, they should automatically makes decisions by themselves, under specific and dynamic situations or environments. Their actions or behaviors are determined or shaped by certain action rules and individual attributions [3,6,9,11−13,17,27,32,35,36,41,43]. When hearing the rumors, each agent has 3 scoring mechanisms, whose overall thresholds should be satisfied by the times heard.
(a) Internal scoring threshold. Facing the rumors, people online are subjective to internal factors. They will judge or evaluate this information, and decide whether to spread them or not. The internal scoring threshold (Internali) refers to the subjective judgement or scoring when hearing the rumors. According to the threshold theory [76], action will happen as long as the threshold can be satisfied or overcome. This internal threshold implies that information (rumor) should satisfy this condition, before it can be spread further. Therefore, the internal threshold denotes the propensity to cut the spreading of rumors. Hence, a higher value of Internali leads to a lower probability of spreading, within minds of agents. This internal scoring threshold is within the mind of individuals, and it is therefore heterogeneous within individuals. This can be also deemed as subjective judgments or attitudes of individuals [9,27]. For instance, thinking the rumor (information) should be known to more, the current agents may tend to spread it, and their internal scoring threshold is much lower. The negative values of Internali implies that the agent will spread romors when first heard them, this is equivalent to the effect of Internali=0.
(b) External scoring threshold. Under certain societies, the external scoring threshold (Externali) refers to general environment (social trust level) that shapes the propensity of spreading for agents. It reflects the macro-level social trust within the society, where agents are interacting with each other and make decisions on spreading. In reality, people are heterogeneous and we apply heterogeneity settings in the Agent-based Modeling [2,3,7,9,11,26,27,30,37]. The mean(Externali) measure the general or aggregate level of social trust. Social trust mechanism [5,9,12,27,28,37,39,43,44,60,61,65−67,95] greatly shapes the spreading pattern of online rumors. For a society with a low trust level, the rumor spreading can be very fast, and Externali should be very lower. Under a totalitarian and repressive regimes, information is controlled and stratified, and rumors spread pervasively [10,37,96,97]. In a society where we have higher social trust levels, it is difficult to spread rumors and Externali should be larger. When social trust level is lower, the rumor is more likely to be spread. Negative value of Externali implies that the society is running without social trust, this is equivalent to the effect of Externali=0.
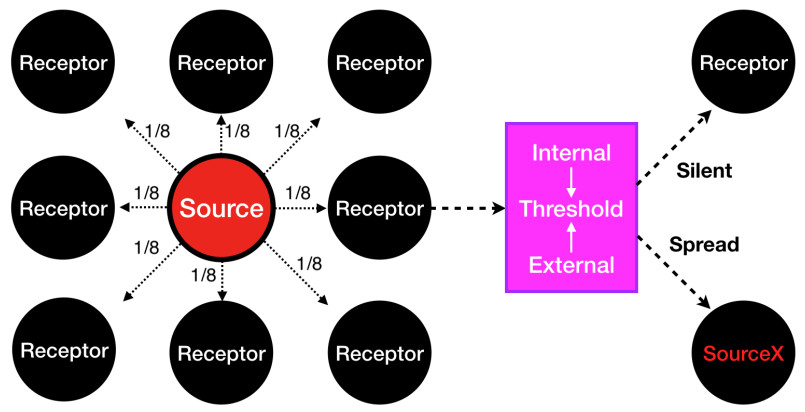
(c) Spreading distances and the combined threshold. The mechanism of threshold and rumor or information spreading can be illustrated in Figure 1, where the Source (in the center) is the initial agent that is spreading the rumors to neighbors. The coordinate of the initial Source is (0,0), and the coordinate of each agent i is (x,y). For other agent (x,y), the distance to Source is calculate as √(x−0)2+(y−0)2=√x2+y2. The Distancei refers to total length of the spreading chains, and this length influences agents on whether to spread rumors or not. Besides, the Distancei also indicates the social distance between the Source to agents. For instance, if the distance is longer, the spreading of rumor (information) becomes weaker, because the rumor has been spread many times before it reaches this agent. If the distance is shorter, the information (rumor) keeps more of original states and seems to be more trustable.
(d) The hearing times should satisfy combined threshold. In Eq (2.1), the combined threshold (Thresholdi) of each agent (i) is the product of three single or separate threshold mechanisms, such as Internali, Externali and Distancei to the initial Source. Agents may not spread the rumor when first heardring it, but they may do so after hearing the rumor repeatedly. Hence, we apply the parameter Times.Heardi(t) to record how many times the agent has heard the rumor. As in Eq (2.2), it is increased by either one (hearing) or zero (not hearing), at each time. For each agent, the Times.Heardi(t) should overcome the (Thresholdi), so that the agent can overcome it and spread the rumor. If not, the agent just hears this rumor, remains silent, and will not spread it. Once the agent i who hears the rumor and decides to spread, its category shifts from the "Receptor" to the "SourceX", which is used to distinguish the initial "Source" in Figure 1.
(e) Rumor spreading process. Figure 1 depicts the model settings and the spreading process of the rumors, and all agents will interact and spread the rumor on a square lattice. Initially, the original source (in the center) spread the rumors to neighbors randomly. In total, we have two classes of agents (Source or Receptor). For the source, he or she spread the rumors when it begins; for the receptors, they hear (receive) the rumors but merely spread them as their thresholds have been satisfied [6,7,18,27−29,32,39,41,42,45,55,61]. The initial "Source" is set on the center of the world (0, 0), it is the orginal source of the rumor. It spread the rumor randomly to eight neighbors, which implies that each neighbor (receptor) has a 1/8 probability to hear the rumor. For other agents (receptor), the time of hearing the rumor tends to increases, and the spreading threshold of receptors will be overcome gradually. If the threshold of the agent (receptor) is satisfied, it will become a "SourceX", and decide to spread the rumor. We run the simulations and record instant spreading percentage and other observations at each time t. This spreading process goes on until all the agents hear the rumor, i.e., the spreading percentage reaches 100%.
(f) Parameters Settings. All agents stand on the square lattice (size = 51 × 51). Therefore, the center is (0, 0) and the maximal coordinate of corner agents is (± 25, ± 25). Each agent has eight neighbors to interact with. Considering the heterogeneity of agents, the Internali are subjective and heterogeneous [3,4,5,7,9,11,12,27,32,33,38,39,44]. Both extremely high and low individuals are in a small proportion of the population, and most are in the middle range. Therefore, the distribution of Internali is assumed to be normal distribution. If Internali=1, the internal scoring does not affect the rumor spreading. Similarly, the external scoring threshold (Externali) is assumed to be normally distributed as well. If Externali=1, it has little influence on the spreading. To reflect these situations, we set their mean values of Internali and Externali to be one, i.e., mean(Internali)=mean(Externali)=1. As we plan to compare the effects of threshold, so we also have mean(Internali)=mean(Externali)=0. For both Internali and Externali, the heterogeneity is determined by SD (standard deviations), sd1 and sd2. To explore full-scale effects of heterogeneities (sd1 and sd2), the serial number of {0, 0.5, 1, 2, 3} is applied in simulations. The sd1=sd2=0 refers to the complete homogeneity; sd1=sd2=1 means weak heterogeneity; sd1=sd2=2 is strong heterogeneity and sd1=sd2=3 refers to extreme heterogeneity. For some simulations, we run them 100 to 300 times, and take the mean (average) values as the stable or reliable outcomes.
3.
Results
We use the software NetLogo 6.1.1 under MacOS system to run model simulations. Netlogo is an multi-agent programming software for simulating complex networks and social phenomena. It is one of the most widely used software for agent-based modeling[98]. Netlogo is especially suitable for modeling complex systems evolving over time [99]. Rumor propagation is a sequential process, so we use netlogo software as our simulation tool. We simulate evolutionary dynamics (curves) of online collective actions, based on variant means and heterogeneities (sd1 & sd2) and other parameter settings. Hence, the distribution of key variables and curve shapes can be obtained. The exploration ranges from simple situations to complex situations, which aims to better understand and reflect the reality. Here, S-shape curves typically contains three-stages, such as early-stage (slow-growing), middle-stage (fast-growing), and late-stage (slow-growing). For standard S-shape curves, we can see normal distributions of observations. For other S-shape curves that are not standard S-curves, we define them as quasi-S-shape curves, because no normal distributions have been observed.
3.1. Homogeneous zero thresholds
We first explore the simplest situation where there are no thresholds, which are deemed as "homogeneous zero thresholds". The threshold is zero for all agents, i.e., mean and SD of both heterogeneities are zero. For each agent, they will spread the rumor at (t+1), as long as they hear it in t. Under this case, we obtain the standard S-shape curves. For each rumor spreading process, we observe and record the whole process, in terms of key indicators (variables), such as steps (duration) and the curves. We simulate the model for 300 times, so that we can get their distributions. In Figure 2A, the distribution of steps (durations) can be visualized (N = 300). It seems that it follows the normal distribution as the density line in blue is symmetric and bell-shaped. The longest duration is 54 steps, and the shortest is about 42 steps. The average duration is 46.87 steps and SD is 2.214 steps. We use Q-Q normal plot to check its normal distribution in Figure 2B, and it indicates that most values are normally distributed. In Figure 2C, the 300 curves of rumor spread processes are visualized, and most of them present standard S-shape curves that are symmetric. Each one is similar to the others, and they outbreak and vanish at the same time. For each curve, the spreading percentage grows from zero to 100%. As the 300 spreading curves are generated from the same set of parameters, the average curve of 300 curves is produced to reflect the setting of parameters better than each one of 300 curves. In Figure 2D, the average (overall) curve represents the 300 curves under the homogeneous zero thresholds. Although simple, it provides the baseline of the ideal state where agents spread the rumor as long as they hear or receive it, without difficulties or obstacles (thresholds). Based on this ideal state, we add more real settings or considerations into simulations to explore real-state curves.
3.2. Heterogeneous zero thresholds
Under the "homogeneous zero thresholds" scenario where sd1=sd2=0, all thresholds are zero, and there is no obstacles or costs (threshold) for agents to spread rumors. However, under the "heterogeneous zero thresholds" scenario, the mean of thresholds is zero but the SD is non-zero, which means the thresholds for individuals are not zero (sd1=sd2>0). Similarly, we run each simulation 300 times to obtain 300 curves under the same set of parameter levels or values. Given the mean is zero, we vary both internal and external heterogeneities to explore the effects of individual heterogeneity (sd1) and social heterogeneity (sd2).
(a) For sd1=sd2=0.5, we repeatedly run the simulation and obtain the 300 spreading curves, and then visualize the distribution of durations (N = 300). In Figure 3A, the spreading processes under sd1=sd2=0.5 are close to the standard S-curves as well. However, it takes a longer time for the spreading percentage to reach the 100% level because the mean duration is 72.34 steps that is larger than 46.87 under sd1=sd2=0 (the ideal state). Under sd1=sd2=0.5, the SD of duration is about 4.23. The distribution of durations is close to the normal distribution as well, because the density line in blue is symmetric.
(b) For sd1=sd2=1, the degree of heterogeneities grows further. It seems that the S-shape curves are obvious as well. The distribution of duration is also close to the normal distribution, as the density line is smooth and symmetric. Comparing sd1=sd2=0.5 and sd1=sd2=1, the curves are more diverse and the spreading duration increases further in Figure 3B. As the heterogeneity grows, it takes longer to achieve the spreading rate of 100%. The average duration is about 102.98 steps, larger than 72.34 steps. The SD is 7.437, larger than 4.23. Besides, the curve starts to have a longer tail under sd1=sd2=1.
(c) For sd1=sd2=2, the heterogeneities become much stronger. It seems that standard S-shape curves disappear, but we see quasi-S-shape curves. For each curve, it takes on an S-shape curve first and then with a long straight line. The right tail is more obvious, and it, therefore, takes more time to achieve the 100% spreading percentage. The mean is 152.5, which is much larger than 102.98. For these 300 curves, the tail (if any) usually lasts for 100 steps. This is mainly caused by the increase in heterogeneity. For the distribution in Figure 3C, it does not follow the normal distribution anymore, as the density line in blue is not symmetric or bell-curved. Indeed, the distribution is rather skewed.
(d) Under sd1=sd2=3, the heterogeneities are extremely strong. As well, the S-shape curves disappear, and curves are with longer right tails. Their right tails are much more obvious under sd1=sd2=3, and it takes a much longer time to achieve 100%. For instance, the average duration is 220.1 steps, which is much larger than 152.5 steps. For these curves, it usually lasts for over 100 steps, which is mainly caused by the growing heterogeneity. The distribution in Figure 3D does not follow the normal distribution anymore, as the density line in blue is not symmetric or bell-curved. The distribution is rather more skewed than sd1=sd2=2. The SD is 63.49 steps, which means that curves are much more diverse.
3.3. Curves under thresholds with homogeneity
Under thresholds with homogeneity, agents have the same thresholds, i.e., mean(Internali)=mean(Externali)=1 and sd1=sd2=0. The spreading duration in Figure 4 is relatively time-consuming and it takes over 1600 steps to achieve 100%. Besides, it combines linear and nonlinear stages into a whole process: (a) as t = 107, the spreading curve is linear and grows slowly because the spreading of rumors just begins. The percentage in Figure 4A is about 10%; (b) as t = 312, the spreading curve in Figure 4B is linear as well, and it is around 30%; (c) while t = 746, the curve in Figure 4C is also linear, but the dynamics shift from linear to nonlinear stage. The percentage is about 80%; (d) as t = 1678, the spreading process ends and 100% has been achieved. The duration is therefore 1678. The whole curve in Figure 4D has explicit linear and nonlinear stages. In the rapid spreading stage (linear stage), the percentage rate is about 80%; then, it takes a much longer time to reach 100%, in the slowly spreading stage (nonlinear stage).
As it takes a longer time for the spreading to achieve 100%, we merely run it 50 times and obtain 50 spreading curves. Figure 5 visualizes these 50 curves, and they share the same common trends as parameter setting is the same. The common trend (black curve) is calculated as the mean of 50 curves. The turning point D (purple point) can be seen when t=900. The long period of spreading is caused by homogeneity (equal probability). Under homogeneity with threshold, each agent has to accumulate Times.Heardi to overcome Thresholdi. As the probability is 1/8, it is time-consuming for it to spread. The turning point D is mainly caused by the limitation of the available neighborhood. In the earlier period, the number of available neighbors is plenty. However, we have no enough neighbors after the D point. The spreading curves, under thresholds with homogeneity, can explain the reality. For the spreading of breaking news, a much higher spread percentage (for example 80%) can be achieved quickly, at the beginning or outbreak stage. After that, the spreading process slows down. It usually takes a much longer time for it to be known by the whole population. It is even impossible for the 100% spreading percentage can be reached, i.e. the duration of rumor spreading will be definitely long.
3.4. Curves under thresholds with heterogeneity
Figures 4 and 5 visualize the spreading curves under thresholds with homogeneity. It indicates that it is not S-curve but a combination of linear and nonlinear stages. Besides, the spreading process is time-consuming. To compare with "thresholds with homogeneity", here we introduce the "thresholds with heterogeneity" scenario where sd1=sd2>0. The agents may have variant thresholds, which are closer to reality. We explore the spreading curves from two aspects: (a) the shape of curves. The spreading curve is more like S-shaped curve. For some cases (breaking news), we also have two-stage curves in Figure 5. There are also observed spreading curves that can be linear combination of the S-shape in Figure 3A, B and two-stage curves in Figure 5; (b) the duration of spreading. The span or duration is another critical indicator. For some cases, the spreading process is completed within a short time; for others, this process takes a long time. Based on previous figures, the heterogeneity may have significant effects on the duration or span. Under thresholds with heterogeneity, it takes a longer time and each simulation is run 100 times.
(a) Under sd1=sd2=0.5, heterogeneity increases slightly from 0 to 0.5. Figure 6A visualizes evolutionary dynamics curves and distributive traits of durations (N = 100). These spreading curves do not vary a great deal, and they also have two stages, which are similar to Figure 5. The distribution of duration is depicted in Figure 6A, and the distribution is asymmetric but closer to normal distribution. The average duration is slightly reduced as well. The mean is around 1096 steps, less than 1678 in Figure 4. The main reason is that the heterogeneity does not change a lot from homogeneity (sd1=sd2=0) and heterogeneity is still weak. Under the weak heterogeneity, the effects are weak as well and the changes are not so obvious.
(b) Under sd1=sd2=1. The degree of heterogeneity increases slightly from 0.5 to 1 (middle heterogeneity). There is an obvious variance in spreading curves (N = 100). First, the common trend is stable, and these spreading curves are generally two-staged. It is not enough for this heterogeneity degree to produce the shift of spreading curves. However, the 100 spreading curves are getting more diverse than in Figure 6A, which is mainly caused by the increment of heterogeneity; Meanwhile, the duration of rumor spreading has been largely reduced. Under middle heterogeneity, the mean is 419 steps, much larger than weak heterogeneity (1096 steps), and this is a substantial decrease. It seems that the duration follows the normal distribution, as the density line in blue is smooth and symmetric (bell-curved).
(c) Under sd1=sd2=2. The degree of heterogeneity increases from 1 to 2, which is deemed the strong heterogeneity. Some obvious changes can be seen, and the curve shape has been changed, from two-stage curves to S-shape curves. However, this is not the standard S-curve in Figure 3A, B, but the S-curves with longer tails. The strong heterogeneity produces transitions of curves' shape. As well, the 100 spreading curves are getting as diverse as Figure 6B, which is mainly caused by the increment of heterogeneity; Meanwhile, the rumor spreading duration has been reduced further. Under middle heterogeneity, the mean is 419 steps, but it is merely 268 steps under the strong heterogeneity, which is a substantial decline. The duration does not follow normal distribution, as it is obviously skewed.
(d) Under sd1=sd2=3, the heterogeneity grows from 2 to 3, which is the extreme heterogeneity. This extreme heterogeneity produces significant changes in terms of the curves' shape (N = 100). Under extreme heterogeneity, it is neither two-staged nor S-shaped, but the S-shape curve with a long tail. They are getting more diverse as well, which is mainly caused by the growing heterogeneity. It has been indicated in Figure 6A-C that heterogeneity reduces the duration of spreading. However, the duration increases slightly under extreme heterogeneity. Under strong heterogeneity, the mean is 268, but 322 steps under extreme heterogeneity. The duration does not follow normal distribution as well, as the density line is obviously skewed. However, heterogeneity generally reduces the duration and facilitates the spreading, which holds true especially within the normal range.
4.
Exploring the duration of spreading
Besides spreading curves, we explore the spreading duration. In general, we have two scenarios which are under no thresholds where mean(Internali)=mean(Externali)=0, and under thresholds where mean(Internali)=mean(Externali)=1. For two situations, each heterogeneity (sd1 or sd2) takes 21 values from {0, 0.05, 0.1, 0.015, …, 2.95, 3) and we run simulations to obtain outcome observations, and investigate the relationship between durations and heterogeneities. Eqs (4.1)−(4.3) explore the effects of single heterogeneity (sd1 or sd2) and the total heterogeneity SD. As in Figure 6, the effects of heterogeneities may be nonlinear, so we add nonlinear terms SD2, sd21 and sd22 into Eqs (4.4)−(4.6) to explore quadratic effects. For each, β0 refers to the constant and ϵ is the residual. We have two advantages to evaluate the factors and durations of rumor spreading. The first one is that we can back-calculate and predict the trend in advance by doing this. The second is that we can accurately know the effects of related possible factors
4.1. Under zero thresholds
First, we explore the durations under the scenario of zero thresholds. Models 1−6 are correspondence to Eqs (4.1)−(4.6). In model 1, we add the intercept β0, and it seems that both sd1 and sd2 have significant and negative effects on the duration of collective actions. However, the explanatory power (adjusted R2) is as low as 17.54%. Hence, we drop the intercept β0 in models 2 to 6. Model 2 suggests that both sd1 and sd2 have positive effects on durations, which means that heterogeneity enlarges the spreading duration (process). In model 3, we focus on the aggregate heterogeneity of S D =sd1+sd2. It indicates that SD has positive effects on spreading durations as well. The linear effects of heterogeneity can be evaluated by models 1−3. As there exist the nonlinear effects of heterogeneity as well in Figures 5 and 6. We introduce quadratic forms of sd1, sd2 and SD to explore linear and nonlinear effects in models 4−6. We estimate the nonlinear effects of SD in model 4 and this nonlinear effect is statistically significant. There is a peak point as the nonlinear effect (quadratic form) is negative. The adjusted R2 is about 53.19%, larger than the linear effect in model 3 (45%). In model 5, we investigate nonlinear effect of sd1 and the pattern of sd1 is similar to SD. The coefficient of the quadratic form sd21 is negative, and the coefficient of sd1 is positive. Hence, there should be a certain sd1 level that achieves the peak or highest spreading duration. The adjusted R2 in model 5 is higher than the merely linear effect in model 2 (53.56% > 52.38%). We explore nonlinear effect of sd2 in model 6, and the nonlinear effect of sd22 is negative as well. The heterogeneity postpones the complete (100%) spreading of rumors under zero thresholds.
In Figure 7, we check the distribution of residuals for models 1−6. It suggests that the means of six residuals (blue vertical lines in the subfigures) are close to zero for most models, although some diverse values can be observed.
4.2. Under thresholds
Then, we explore durations under thresholds where mean(Internali)=mean(Externali)=1 and sd1/sd2∈(0,0.05,0.1,…2.95,3). As well, models 7−12 correspond to Eqs (4.1)−(4.6), respectively. In model 7, we add the intercept term β0, and it has no significant effects. Both sd1 and sd2 have significant and positive effects on spreading duration, which implies that heterogeneity increases spreading duration under thresholds. The explanatory power (adjusted R2) is 60.06%. We drop the intercept β0 and a much higher adjusted R2 can be achieved in models 8 to 12. Model 8 indicates that both sd1 and sd2 have positive effects, which means that heterogeneity enlarges the spreading process. The adjusted R2 jumps into 89.59% from 60.06%. We focus on SD=sd1+sd2 in model 9, and SD also has positive effects on spreading duration. However, the adjusted R2 is 77.14%. The outcomes of linear effects of heterogeneity can be visualized in models 7−9. Nevertheless, there exist nonlinear effects of heterogeneity as well. In models 10−12, we introduce quadratic forms of sd1, sd2 and SD, to explore linear and nonlinear effects. In model 10, we estimate linear and nonlinear effects of SD, and the nonlinear effect is statistically significant. There seems to be a peak point as the nonlinear effect of the quadratic form is negative. The adjusted R2 is about 80.35%, larger than the linear effect in model 10 (77.14%). We explore nonlinear effect of sd1 in model 11, and its pattern is similar to the aggregate heterogeneity SD. The coefficient of the quadratic form sd21 is negative, which means that there is a certain level of sd1 that can achieve the highest spreading duration. The adjusted R2 in model 11 is also higher than merely the linear effect in model 7 (80.54% > 60.06%). We explore nonlinear effect of the sd2, and the nonlinear effect of sd22 is also negative. Under non-zero thresholds, it also postpones the duration of 100% spreading.
In Figure 8, we check the distribution of residuals for models 1−6. It suggests that the means of six residuals (blue vertical lines in the subfigures) are close to zero for most models, although some diverse values can be observed.
5.
Discussions and conclusions
For the previous researches, more attention is paid to the whole process or dynamic curves [7,12,39,42,44−46,48,49,52,54,57,58,65,67], but we focus on different curves shapes. Based on specific mechanism that we found, we can better understand and predict the spreading process, according to the real target cases. Besides of two advantages, we also have two limitations. The first one is our model and setting are also ideal or simple, however real cases are also complex. The second is that some parameters and attributions of agents (netizens) are still hard to measure and calculate.
5.1. Threshold-mean effects on spreading durations
As we compare scenarios under the zero (mean) thresholds and non-zero thresholds, the effects vary with or without thresholds. Individual thresholds generally postpone the spreading process and therefore enlarge the durations. It includes: (a) As there is no threshold or the mean is zero, i.e., mean(Internali)=mean(Externali)=0, the spreading process is much faster. In Figure 2, the mean of spreading duration is about 46.87 steps (sd1=sd2=0). In Figure 3, the means are 72.34 steps (sd1=sd2=0.5), 102.98 steps (sd1=sd2=1), 152.5 steps (sd1=sd2=2) and 220.1 steps (sd1=sd2=3); (b) However, the spreading duration under non-zero thresholds, mean(Internali)=mean(Externali)=1, is much larger. For instances, the average duration is 1678 steps in figure 4 (sd1=sd2=0), 1096 steps in Figure 6A (sd1=sd2=0.5), 418 steps in Figure 6B (sd1=sd2=1), 267 steps in Figure 6C (sd1=sd2=2), and 327 in Figure 6D (sd1=sd2=3). The effect of thresholds refers to the mean of thresholds, and it plays a positive role in the spreading duration. In other words, it delays the process of rumors or information spreading. The possible reason is that thresholds mean difficulties that individuals should overcome before they spread rumors (information) to others (neighbors).
5.2. Threshold-heterogeneity (SD) effects on spreading durations
For investigating mechanisms of collective actions, the heterogeneity is the key variable, because people or agents are variant [1,3,4,7,9,13,15,27,52,70,73,74,76,100,101]. It seems that heterogeneity of individuals enhances collective behaviors [52,67,73,74,76,100−103]. However, we find that it delays or undermines the spreading process and enlarges the spreading duration. We run each simulation 300 times to compare the mean of spreading durations. In Figures 2 and 3 where the mean of threshold is zero, the heterogeneity delays the process of rumor spreading as it increases, i.e., 220.1 steps (sd1=sd2=3) > 152.5 steps (sd1=sd2=2) > 102.98 steps (sd1=sd2=1) > 72.34 steps (sd1=sd2=0.5) > 46.87 steps (sd1=sd2=0). For zero mean threshold, Figure 9A-D shows nonlinear trends when the heterogeneity grows. Joint effects of sd1 and sd2 can be visualized in Figure 9D.
In Figure 6 where we have substantial thresholds, the spreading duration varies as the heterogeneity changes. It is similar that heterogeneity increases the duration and postpones the complete (100%) spreading of rumors. For instances, a weaker heterogeneity in general has shorter spreading duration in Figure 5 (homogeneity) and Figure 6 (heterogeneity), i.e., 1200 + steps (sd1=sd2=0) > 1096 steps (sd1=sd2=0.5) > 419 steps (sd1=sd2=1) > 322 steps (sd1=sd2=3) > 268 steps (sd1=sd2=2). Therefore, heterogeneity leads to a longer spreading duration. Combining that heterogeneity improves the occurrence of collective action, it seems that heterogeneity felicitates the emergence of collective actions but results in longer durations of collective behaviors, including rumor/information spreading. For non-zero threshold, Figure 9E-H shows linear trends of spreading durations when the heterogeneity grows. The joint effects of sd1 and sd2 can be visualized in Figure 9H. Comparing linear trends in Figure 9E-H and nonlinear trends in Figure 9A-D, it concludes that real heterogeneity results in longer spreading durations.
5.3. Spreading curve shapes under heterogeneity
Real rumor spreading process often take on S-shape curves [6,7,13,17,18,21,24,29,36,37,39,54,55,76]. As one of the ideal types of evolutionary processes [70,71,72,73,76], we also see S-curves here: (a) Under zero thresholds. In Figure 2, standard S-shape curves are obtained under homogeneous zero threshold. The S-shape curves is the accumulative probability curves (CDF) of spreading percentage. For standard S-shape curves, these curves should be quite close to the CDF of normal distributions. As the CDF curve of normal distribution is given, the S-shape curve can be used to explore evolutionary dynamics or rumor spreading. Therefore, we obtain standard or ideal S-shape curves when each one has zero thresholds. As heterogeneity grows, S-shape curves have longer and longer tails. In Figure 3A (sd1=sd2=0.5), the S-shape is almost the same as Figure 2; however, the S-shape curves in Figure 3B (sd1=sd2=1) begin to have right tails with a tail length of about 25 steps; as the heterogeneity increases further, the length of tail is around 150 steps in Figure 3C (sd1=sd2=2); this trend continues and the tail length is over 300 steps when sd1=sd2=3. Given right tails removed, we also obtain typical S-shape curves; (b) Under non-zero thresholds. For homogeneity (sd1=sd2=0), the curve is two-staged divided by point D. As the heterogeneity grows slightly (sd1=sd2=0.5), the two-stage trend remains stable. However, two-stage trends become S-shape curves as heterogeneity increases further (sd1=sd2≥1). For instance, the curves are normal in S-shape in Figure 6B (sd1=sd2=1). As it becomes stronger (sd1=sd2≥2), S-shape curves also have longer right tails. For sd1=sd2=2 the tail length is about 250 steps; for sd1=sd2=3, it is over 300 steps. For under zero thresholds and under non-zero thresholds, the curves were getting more diverse under same parameter settings, as heterogeneity provides more randomness and uncertainty to the spreading process. Comparing these two situations, the S-curves can be seen when heterogeneity exists and even gets stronger. In reality, heterogeneity is inevitable [1,3,4,7,9,13,15,27,52,70,73,74,76]. Therefore, S-shape curve is the commonly-seen trends of rumor spreading. Based on the crowd detection and censoring technology [104,105], we can predict the (online) collective actions. The SIR models can also have accumulative S-shape trend [17,45,49,57,88,106], and the big difference is the mechanism. SIR models are calculated by differential equations and mathematical models not by behavior-based. To improve the investigations and predictions of online rumor-spreading, both agent-based modeling and SIR models should be combined and cross-validated. Our model can also be extended to other networks, such as complex scale-free networks. Although the intermediate process of rumor propagation in basic networks and complex scale-free networks may be different, its propagation rules and algorithm are consistent. According to specific data and network cases, we can use we can use other networks including complex scale-free networks.
Acknowledgments
This work was supported by the National Social Science Foundation of China (Grant No. 17ZDA117, 19ZDA143 & 0ASH005).
Conflict of interest
The authors declare there is no conflflict of interest.









 DownLoad:
DownLoad:




















