Fractional transportation problem under interval-valued Fermatean fuzzy sets

1.   Introduction

The idea of generalization of a commutative semigroup was first introduced by Kazim and Naseeruddin in $1972$ ^[11]. They named it as a left almost semigroup $($LA-semigroup$)$. It is also called an Abel-Grassmann's groupoid (AG-groupoid) ^[18]. An AG-groupoid is a non-associative and non-commutative algebraic structure mid way between a groupoid and a commutative semigroup ^[15]. An AG-groupoid with left identity is called an AG-group if it has inverses ^[10]$.$ An AG-groupoid is a groupoid $S$ whose elements satisfy the left invertive law $(ab)c = (cb)a$ for all $a, b, c\in S$. In ^[11]$,$ it was shown that an AG-groupoid $S$ is medial$,$ that is$,$ $(ab)(cd) = (ac)(bd)$ holds for all $a, b, c, d\in S.$ A left identity may or may not exist in an AG-groupoid$.$ The left identity of an AG-groupoid allows the inverses of elements$.$ If an AG-groupoid has a left identity$,$ then it is unique ^[15]$.$ The paramedial law $(ab)(cd) = (dc)(ba)$ holds for all $a, b, c, d\in S$ in an AG-groupoid $S$ with left identity$.$ We can get $a(bc) = b(ac)$ for all $a, b, c\in S$ by applying medial law with left identity$.$ An AG-groupoid $(S, \cdot)$ together with a partial order $\leq$ on $S$ that is compatible with an AG-groupoid operation, meaning that for $x, y, z\in S,$ $x\leq y\Rightarrow zx\leq zy$ and $xz\leq yz,$ is called an ordered AG-groupoid ^[12]. Different classes of an ordered AG-groupoid such as left regular, right regular and completely regular ordered AG-groupoids have been characterized by using several ideals for example fuzzy interior ideals, fuzzy left (right) ideals and soft ideals in ^{[1,24,25,26,27,28]}.

The algebraic structures described above are usually considered as theoretical tools with merely no real application. In other words, to deal with real-world uncertain and ambiguous problems$,$ the strategies commonly used in classical mathematics are not always useful. To utilize these tools their connection with fuzzy set theory is required. To fimiliarize the reader with fuzzy set theory we now review the brief history of fuzzy sets and their extensions.

In $1965,$ Zadeh ^[30] proposed the concept of fuzzy sets as an extension of the classical notion of sets$.$ In traditional set theory$,$ an element is either in or out of the set$.$ Fuzzy set theory$,$ on the other hand$,$ allows for a gradual determination of the membership of elements in a set$,$ which is represented using a membership function having a value in the real unit interval $[0, 1].$ Since the membership functions of fuzzy sets constrained to values $0$ or $1$ are special cases of the characteristic functions of classical sets$,$ this shows that the fuzzy sets generalize the classical sets$.$ In many cases$,$ however$,$ because the membership function is a single-valued function$,$ it cannot be used to represent both support and objection evidences$.$ The intuitionistic fuzzy set$,$ which is a generalization of Zadeh's fuzzy set$,$ was introduced by Atanassov ^[2]$.$ It has both a membership and a non-membership function$,$ allowing it to better express the fuzzy character of data than Zadeh's fuzzy set$,$ which only has a membership function$.$ The values of the membership function and the non-membership function in an IFS are some times difficult to describe as exact numbers in real-world decision problems. Instead, the ranges of their values are frequently provided. In such instances, Atanassov and Gargov generalized the idea of intuitionistic fuzzy set to interval-valued intuitionistic fuzzy set (IVIFS) ^[3]. In view of above information from the literature, the motivation of this paper is based upon the following points:

● To develop a connection between AG-groupoids and fuzzy set theory by developing a technique for ranking fuzzy numbers.

● The main difference between IFS and IVIFS is that the membership and non-membership functions in IFS are represented by numbers while in IVIFS they are represented as intervals. If in IVIFS the intervals of zero length (same end points) are considered they become IFS, hence they generalize the idea of IFS. So the motivation is to develop results based upon IVIFS therefore they also hold for IFS at the same time.

This paper consist of six sections. In Section 1, the introduction to literature regarding AG-groupoids and fuzzy set theory is given. Section 2 covers the necessary background required to develop understanding for the upcoming sections. IVIF-score left (right) ideals are defined and supported with examples and visualization in Section 3. Sections 4 and 5 consist of structural properties of different IVIF-score ideals and their practical applications respectively. main findings and future research direction is given in Section 6.

2.   Preliminaries

A fuzzy set ^[30] $f$ on a non-empty set $S$ is an object, with grades of membership $\mu_f(s):S\rightarrow [0, 1]$ having the form

The membership function $\mu_f(s)$ assigns each element $s$ of $f$ a single number form $[0, 1]$. However, as the membership function is only a single-valued function, which cannot be used to express the membership and non-membership evidences in many practical scenarios.

An intuitionistic fuzzy set $($IFS$)$ ^[2] $F$ of a non empty set $S$ is an object having the form

The functions $\mu _{F}:S\longrightarrow \lbrack 0, 1]$ and $\upsilon _{F}:S\longrightarrow \lbrack 0, 1]$ denote the degree of membership and the degree of non-membership of $x$ in $F$ respectively such that for all $x\in S,$ we have

An interval-valued intuitionistic fuzzy set $($IVIFS$)$ ^[3] $I$ of a non empty set $S$ is an object having the form

where

with the condition

Clearly, if

then the IVIFS reduces to IFS ^[2].

According to the above definition, the basic component of an IVIFS is an ordered pair with an interval-valued membership degree and an interval-valued nonmembership degree of $x$ in $I.$ An interval-valued intuitionistic fuzzy number (IVIFN) is the term given to this ordered pair ^[20]. For simplicity, an IVIFN is usually stated as

where

Xu also proposes a score function and an accuracy function for IVIFNs in ^[20] and uses them to develop an approach to multi-attribute decision making problems.

In order to rank the IVIFNs$,$ we now introduce the unit-valued score function, (uv-score function) as follows$:$

Definition 1. Let $\mathcal{I}$ be the set of all IVIFNs$.$ A uv-score function on $\mathcal{I}$ can be defined by the mapping

where $\overset{\ast }{\xi } = ([a, b], [c, d]),$ $\Theta _{(\overset{\ast }{\mu }, \overset{\ast }{\upsilon })}$ is the uv-score function, $\mathit{\ }$ and $\Theta _{(\overset{\ast }{ \mu }, \overset{\ast }{\upsilon })}(\overset{\ast }{\xi })$ is the uv-score of $\overset{\ast }{\xi }.$

In particular$,$

if $\Theta _{(\overset{\ast }{\mu }, \overset{\ast }{ \upsilon })}(\overset{\ast }{\xi }) = 1,$ then the IVIFN $\overset{\ast }{\xi }$ takes the largest value $\overset{\ast }{\xi }_{+} = ([1, 1], [0, 0]).$

If $\Theta _{(\overset{\ast }{\mu }, \overset{\ast }{\upsilon })}(\overset{\ast }{ \xi }) = 0,$ then the IVIFN $\overset{\ast }{\xi }$ takes the smallest value $\overset{\ast }{\xi }_{-} = ([0, 0], [1, 1]).$ Clearly, the greater the $\Theta _{(\overset{\ast }{\mu }, \overset{\ast }{\upsilon })}(\overset{\ast }{\xi }),$ the larger the $\overset{\ast }{\xi }.$

Let

be the two IVIFNs$.$ Then the uv -scores of $\overset{\ast }{\xi }_{1}$ and $\overset{\ast }{\xi }_{2}$ are as follows$:$

Since, the uv-score of an IVIFN $\overset{\ast }{\xi }_{2}$ is higher than that of an IVIFN $\overset{\ast }{\xi }_{1}.$ So

However$,$ if we take

then

In this case, the uv-score function cannot distinguish between the IVIFNs $\overset{\ast }{\xi }_{1}$ and $\overset{\ast }{\xi } _{2}.$ To address this issue, consider the following definition of a uv-accuracy function.

Definition 2. ^[20] Let $\mathcal{I}$ be the set of all IVIFNs$.$ A uv-accuracy function on $\mathcal{I}$ is a mapping

where $\overset{\ast }{\xi } = ([a, b], [c, d]),$ $\Phi _{(\overset{\ast }{\mu }, \overset{\ast }{\upsilon })}$ is the uv-accuracy function of $\overset{\ast }{\xi },$ and $\Phi _{(\overset{\ast }{\mu }, \overset{\ast }{\upsilon })}(\overset{\ast }{ \xi })$ is the uv-accuracy degree of $\overset{\ast }{\xi }.$

From above IVIFNs

the uv-accuracy degrees of $\overset{\ast }{\xi }_{1}$ and $\overset{\ast }{\xi }_{2}$ are as follows$:$

Since, the uv-accuracy degree of an IVIFN $\overset{\ast }{\xi }_{1}$ is higher than that of an IVIFN, so

The hesitancy degree of IVIFNs can be defined by the following formula ^[20]

The relationship between the score function and the accuracy function has been established to be similar to the relationship between the mean and variance in statistics ^[6]$.$ In statistics$,$ an efficient estimator is described as a measure of the variance of an estimate's sampling distribution; the lower the variance$,$ the better the estimator's performance$.$ On this basis$,$ it is reasonable and appropriate to say that the higher an IVIFN's uv-accuracy degree$,$ the better the IVIFN$.$

In $2007,$ a technique ^[20] was developed for comparing and rating two IVIFNs based on the score function and the accuracy function$,$ which was motivated by the aforementioned study$.$ We can now compare and rate two IVIFNs in the same way using the uv-score function and uv -accuracy function$,$ as shown below$.$

Definition 3. Let $\overset{\ast }{\xi } _{1} = ([a_{1}, b_{1}], [c_{1}, d_{1}])$ and $\overset{\ast }{\xi } _{2} = ([a_{2}, b_{2}], [c_{2}, d_{2}])$ be the two IVIFNs$,$ $\Theta _{(\overset{ \ast }{\mu }, \overset{\ast }{\upsilon })}(\overset{\ast }{\xi }_{1})$ and $\Theta _{(\overset{\ast }{\mu }, \overset{\ast }{\upsilon })}(\overset{\ast }{ \xi }_{2})$ be the uv-scores of the IVIFNs $\overset{\ast }{\xi }_{1}$ and $\overset{\ast }{\xi }_{2}$ respectively$,$ also $\Phi _{(\overset{\ast }{\mu }, \overset{\ast }{\upsilon })}(\overset{\ast }{\xi }_{1})$ and $\Phi _{(\overset{\ast }{\mu }, \overset{\ast }{\upsilon })}(\overset{\ast }{\xi } _{2})$ be the uv-accuracy degrees of the IVIFNs $\overset{\ast }{\xi }_{1}$ and $\overset{\ast }{\xi }_{2}$ respectively$.$ Then

● If $\Theta _{(\overset{\ast }{\mu }, \overset{\ast }{ \upsilon })}(\overset{\ast }{\xi }_{1}) < \Theta _{(\overset{\ast }{\mu }, \overset{\ast }{\upsilon })}(\overset{\ast }{\xi }_{2}),$ then $\overset{\ast }{\xi }_{1} < \overset{\ast }{\xi }_{2}.$

● If $\Theta _{(\overset{\ast }{\mu }, \overset{\ast }{ \upsilon })}(\overset{\ast }{\xi }_{1}) = \Theta _{(\overset{\ast }{\mu }, \overset{\ast }{\upsilon })}(\overset{\ast }{\xi }_{2}),$ then

i) If $\Phi _{(\overset{\ast }{\mu }, \overset{\ast }{\upsilon })}(\overset{\ast }{\xi }_{1}) < \Phi _{(\overset{\ast }{\mu }, \overset{\ast }{ \upsilon })}(\overset{\ast }{\xi }_{2}),$ then $\overset{\ast }{ \xi }_{1} < \overset{\ast }{\xi }_{2}.$

ii) If $\Phi _{(\overset{\ast }{\mu }, \overset{\ast }{\upsilon })}(\overset{\ast }{\xi }_{1}) = \Phi _{(\overset{\ast }{\mu }, \overset{\ast }{ \upsilon })}(\overset{\ast }{\xi }_{2}),$ then $\overset{\ast }{ \xi }_{1} = \overset{\ast }{\xi }_{2}.$

3.   IVIF-score left (right) ideals of ordered AG-groupoids

In this section, we have explored the notions and examples of IVIF- score left $($right$)$ ideals and IVIF-score $($0, 2$)$-ideals in an ordered AG-groupoid.

Definition 4. Let $\Theta _{(\overset{\ast }{\mu }, \overset{\ast }{\upsilon })}$ be a uv-score function of an ordered AG-groupoid $S$ and $x, y\in S.$ Then $\Theta _{(\overset{\ast }{\mu }, \overset{\ast }{\upsilon })}$ is called an IVIF -score left $($right$)$ ideal of $S,$ if the following conditions are satisfied.

i) $\Theta _{(\overset{\ast }{\mu }, \overset{\ast }{\upsilon })}(xy)\geq \Theta _{(\overset{\ast }{\mu }, \overset{\ast }{\upsilon })}(y)$ $\left(\Theta _{(\overset{\ast }{\mu }, \overset{\ast }{\upsilon })}(xy)\geq \Theta _{(\overset{\ast }{\mu }, \overset{\ast }{\upsilon })}(x)\right);$

ii) $x\leq y\implies \Theta _{(\overset{\ast }{\mu }, \overset{\ast }{\upsilon })}(x)\geq \Theta _{(\overset{\ast }{\mu }, \overset{\ast }{\upsilon })}(y).$

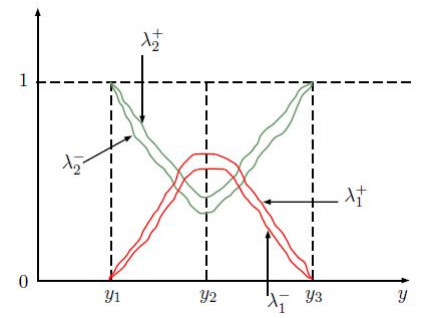
Example 1. Let us consider the following collection of IVIFS $\mathcal{I} = \{ \overset{ \ast }{\xi }_{j} = ($$\overset{\ast }{\mu }$$_{\xi _{j}},$$\overset{\ast }{ \upsilon }$$_{\xi _{j}});$ $j = 1, 2, 3, 4, 5, 6\}$ on an ordered AG-groupoid $S_1 = \{a, b, c, d, e, f\}$ with the binary operation and order defined as follows (see Tables 1 and 2):

It is now a trivial matter to check that

is the IVIF-score left and IVIF-score right ideal of $S.$

The following graph Figure 1 demonstrates the ranking comparison of each $x\in S$ while generating $\Theta _{(\overset{\ast }{\mu }, \overset{\ast }{\upsilon })}.$

Remark 1. Every IVIF-score right ideal of an ordered AG-groupoid $S$ is an IVIF-score left ideal of $S$ but the converse is not true in general which can be seen from the following example.

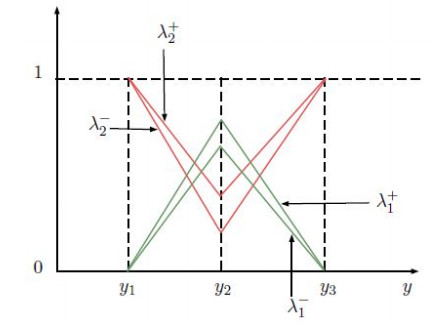
Example 2. Consider the following collection of IVIFS $\mathcal{I} = \{ \overset{\ast }{ \xi }_{j} = ($$\overset{\ast }{\mu }$$_{\xi _{j}},$$\overset{\ast }{ \upsilon }$$_{\xi _{j}});$ $j = 1, 2, 3, 4, 5\}$ on an ordered AG-groupoid $S_2 = \{a, b, c, d, , e\}$ with the binary operation and order defined as follows (see Tables 3 and 4):

One can see that

is an IVIF-score left ideal of $S$. Note that $\Theta _{(\overset{\ast }{\mu }, \overset{\ast }{\upsilon })}(bd)\ngeq \Theta _{(\overset{\ast }{\mu }, \overset{\ast }{\upsilon })}(b)$ implying that $\Theta _{(\overset{\ast }{ \mu }, \overset{\ast }{\upsilon })}$ is not an IVIF-score right ideal of $S$.

Following is a graphical representation of the ranking comparison of each $x\in S$ during the construction of $\Theta _{(\overset{\ast }{\mu }, \overset{ \ast }{\upsilon })}$ (see Figure 2).

4.   On characterization problems of intra-regular ordered AG-groupoids

The aim of this section is to investigate the concept of a uv-score $($uv-accuracy$)$ function in order to develop the notions of IVIF-score left $($right$)$ ideals and IVIF-score $(0, 2)$-ideals in an ordered AG-groupoid. We also study some important characterization problems in an ordered AG-groupoid using these newly developed IVIF-score ideals$.$ In this regard$,$ we intend to respond to a question about the relationship between an IVIF-idempotent subsets of an ordered AG-groupoid $S$ and its IVIF-score $(0, 2)$-ideals, especially when an IVIF-idempotent subset of $S$ will be an IVIF-score $(0, 2)$-ideal in terms of an IVIF-score right ideal and an IVIF-score left ideal of $S$. In addition$,$ we also use IVIF-score left $($right$)$ ideals to characterize an intra-regular ordered AG-groupoid (AG-group) which is a semilattice of left simple AG-groupoids$.$

As an extension of the findings in ^[13,23], it should be noted that the results of this section may be followed easily for a case of fuzzy sets in an AG-groupoid without order.

If $S$ is an AG-groupoid with product $\cdot :S\times S\longrightarrow S,$ then

both will denote the product

Similarly

will denote the product

Definition 5. For $\emptyset \neq A\subseteq S,$ we define

For $A = \{a\},$ we usually written as $\left(a\right].$

The following statements are true for an ordered AG-groupoid $S$ ^[27], and will be used frequently without mention in the sequel$.$

$i)$ $A\subseteq \left(A\right]$ $\forall \; A\subseteq S;$

$ii)$ if $A\subseteq B\subseteq S,$ then $\left(A\right] \subseteq \left(B \right];$

$iii)$ $\left(A\right] \left(B\right] \subseteq \left(AB\right]$ $\forall$ $A, B\subseteq S;$

$iv)$ $\left(A\right] = \left(\left(A\right] \right]$ $\forall$ $A\subseteq S;$

$vi)$ $\left(\left(A\right] \left(B\right] \right] = \left(AB\right]$ $\forall$ $A, B\subseteq S;$

$vii)$ $A = \left(A\right]$ if $A$ is any type of ideal$.$

Definition 6. A non-empty subset $A$ of an ordered AG-groupoid $S$ is called a left $($resp. right$)$ ideal of $S,$ if

$i)$ $SA\subseteq A$ $($resp. $AS\subseteq A);$

$ii)$ if $a\in A$ and $b\in S$ such that $b\leq a,$ then $b\in A,$ that is if $(A] = A.$

Equivalently$,$ if $(SA]\subseteq A$ $($resp. $(AS]\subseteq A).$

Definition 7. Let $S$ be an ordered AG-groupoid$.$ Then $S$ is left simple if it does not properly contain any left ideal$.$

Definition 8. An AG-subgroupoid $F$ of an an ordered AG-groupoid $S$ is called a filter of $S$ if

$a)$ $x, y\in S,$ $xy\in F\implies x\in F$ and $y\in F.$

$b)$ $x\in F,$ $S\ni z\leq x\implies z\in F.$

We denote by $N(x)$ the filter of $S$ generated by $s$ $(s\in S)$. Let $\mathcal{N}$ be the equivalence relation on $S$ defined by

Definition 9. Let $S$ be an ordered AG-groupoid$.$ An equivalence relation $\rho$ on $S$ is called congruence if

A congruence $\rho$ on $S$ is called semilattice congruence if

Let $\rho$ is a semilattice congruence on an ordered AG-groupoid $S.$ Then $(s)_{\rho }$ is an AG-subgroupoid of $S$ for every $s\in S.$ Indeed, $\emptyset \neq (s)_{\rho }\subseteq S.$

Let $x, y\in S.$ Since $x\rho s$ and $y\rho s,$ we have $xy\rho s^{2}.$ As $s^{2}\rho s,$ we have $xy\rho s,$ that is, $xy\in (s)_{\rho }.$

Let $\rho$ is a congruence on an ordered AG-groupoid $S.$ Then the multiplication "$\cdot$" on the set

is defined by

and $(S/\rho, \cdot)$ is an AG-subgroupoid.

Definition 10. Let $S$ be an ordered AG-groupoid$.$ Then $S$ is a semilattice of left simple AG-groupoids if and only if there exists a semilattice $Y$ and a family

of left simple AG-subgroupoids of $S$ such that

$a)$ $S_{k}\cap S_{l} = \emptyset$ for every $k, l\in Y,$ $k\neq l.$

$b)$ $S = \underset{l\in Y}{\cup }S_{l}.$

$c)$ $S_{k}S_{l}\subseteq S_{kl}$ for every $k, l\in Y.$

Equivalently$,$ $S$ is a semilattice of left simple AG-groupoids if there exists a semilattice congruence $\rho$ on $S$ such that the $\rho$ -class $(x)_{\rho }$ of $S$ containing $x$ is a simple AG-subgroupoid of $S$ for every $x\in S.$

In ^[17], T. Saito has shown that a semigroup $S$ is a semilattice of left simple semigroups if and only if the set of left ideals of $S$ is a semilattice under the multiplication of subsets, which is similar to say that $S$ is left regular and every left ideal of $S$ is two-sided. In addition, S. Lajos ^[14] has shown that a semigroup $S$ is left regular and its left ideals are two-sided if and only if $P_{1}\cap P_{2} = P_{1}P_{2}$ for any two left ideals $P_{1}, P_{2}$ of $S$. We are now considering these results in the context of an ordered AG-groupoid, which will provide more comprehensive and generalized findings.

Definition 11. ^[25] An ordered AG-groupoid $S$ is intra-regular if for each $a\in S,$ there exists $x, y\in S,$ such that $a\leq xa^{2}\cdot y.$ Equivalently$,$ if $a\in (Sa^{2}\cdot S]$ for every $a\in S$ or $A\subseteq (SA^{2}\cdot S]$ for every $A\subseteq S.$

Theorem 1. For an ordered AG-groupoid $S$ with left identity$,$ the following conditions are equivalent$:$

$i)$ $S$ is a semilattice of left simple AG-groupoids$;$

$ii)$ $S$ is intra-regular and every left ideal of $S$ is two-sided$;$

$iii)$ the set of all left ideals of $S$ is a semilattice under the multiplication of subsets$;$

$iv)$ if $P_{1}$ and $P_{2}$ are left ideals of $S,$ then

$v)$ if $P_{1},$ $P_{2}$ and $P$ are left ideals of $S,$ then

Proof. $i)\Rightarrow v):$ Let $P_{1}, P_{2}$ be the left ideals of $S.$ Then by given assumption$,$

Let $z\in (P_{1}P_{2}].$ Then

As

for some $m\in Y,$ therefore $ab, ba\in S_{m}.$

Since $S_{m}$ is left simple$,$ then it is easy to see that, there exists $x\in S_{m}$ such that $ab\leq x\cdot ba.$

Thus we have

which implies $z\in (P_{1}P_{2}].$

Similarly we can show that

Hence

for any left ideals $P_{1}$ and $P_{2}$ of $S.$

Now let $P$ be left ideal of $S$ and let $z\in P = S_{k}$ for some $k\in Y.$ Since $z\in P$ and $S_{k}$ is an AG-subgroupoids of $S,$ we have $z^{2}\in P.$

Since $z, z^{2}\in S_{k},$ then it is easy to see that, there exists $x\in S_{k}$ such that

we have $z\in (P^{2}].$ On the other hand, we have

implies

$v)\Rightarrow iv):$ If $P_{1}, P_{2}$ are the left ideals of $S,$ then

Therefore by given condition,

Thus we have

Since $(P_{1}P_{2}]\neq \emptyset,$ we have $P_{1}\cap P_{2}\neq \emptyset.$ Therefore $P_{1}\cap P_{2}$ is a left ideal of $S$, and by given condition,

Thus we get

$iv)\Rightarrow ii):$ Let $a\in S.$ Then, $(Sa]$ is a left ideal of $S,$ and clearly $a\in (Sa].$ By using given assumption,

which implies that $a\leq xa^{2}\cdot y$ for some $x, y\in S.$

Now let $P$ be a left ideal of $S.$ Then

Indeed, if $a\in P,$ $s\in S,$ then

$ii)\Rightarrow i):$ Let $S$ be intra-regular. Then by using given condition, it is easy to show that $(s)_{\mathcal{N}}$ is a left simple AG-subgroupoid of $S$ for every $s\in S.$

Hence $S$ is a semilattice of left simple AG-groupoids.

$i)\Rightarrow iii):$ Let $\rho$ be a semilattice congruence on $S$ such that $(s)_{\rho }$ is a left simple AG-subgroupoid of $S$ for every $s\in S$ and let $P_{1},$ $P_{2}$ and $P$ be left ideals of $S.$ We endow $S$ with equality relation

Then $S$ is an ordered AG-groupoid, $\rho$ is a semilattice congruence on $S$ and $(s)_{\rho }$ is a left simple AG-subgroupoid of $S$ for every $s\in S.$

By $i)\Rightarrow v),$ we have

implies

Indeed, if $a\in (P_{1}P_{2}],$ then $a\leq bc$ for some $b\in P_{1}$ and $c\in P_{2}.$

Since $(a, bc)\in \leq,$ we have $a = bc,$ which implies $a\in P_{1}P_{2}.$

Similarly, we have

which is what we set out to prove.

$iii)\Rightarrow iv):$ Straightforward.

Definition 12. The product of any uv-score functions $\Omega _{(\overset{\ast }{ \mu }, \overset{\ast }{\upsilon })}$ and $\Upsilon _{(\overset{\ast }{\mu }, \overset{\ast }{\upsilon })}$ of $S$ is defined by

where

for any $x\in S.$

The proof of the following four lemmas are same as in ^[25,26].

Lemma 1. Let $S$ be an ordered AG-groupoid. For $\emptyset \neq A, B\subseteq S,$ the following holds.

$i)$ $\mathbb{C} _{A}\cap \mathbb{C} _{B} = \mathbb{C} _{A\cap B}.$

$ii)$ $\mathbb{C} _{A}\circ \mathbb{C} _{B} = \mathbb{C} _{(AB]}.$

Lemma 2. If $\Omega _{(\overset{\ast }{\mu }, \overset{\ast }{\upsilon })}$ is any uv-score function of an ordered AG-groupoid $S,$ then $\Omega _{(\overset{\ast }{\mu }, \overset{\ast }{\upsilon })}$ is an IVIF-score right $($left$)$ ideal of $S$ if and only if

Lemma 3. Let $S$ be an ordered AG-groupoid and $\emptyset \neq A\subseteq S.$ Then $A$ is a right $($left$)$ ideal of $S$ if and only if $\mathbb{C} _{A}$ is an IVIF-score right $($left$)$ ideal of $S.$

Lemma 4. If $S$ is an intra-rgular ordered AG-groupoid with left identity and $\Omega _{(\overset{\ast }{\mu }, \overset{\ast }{\upsilon })}$ is an IVIF-score left $($right$)$ ideal of $S,$ then

Theorem 2. Let $S$ be an ordered AG-groupoid. Then every left ideal of $S$ is two-sided if and only if every IVIF-score left ideal of $S$ is two-sided$.$

Proof. It is simple$.$

Theorem 3. For an ordered AG-groupoid $S$ with left identity$,$ the following conditions are equivalent$:$

$i)$ $S$ is a semilattice of left simple AG-groupoids$;$

$ii)$ $S$ is intra-regular and every IVIF-score left ideal of $S$ is an IVIF-score ideal$;$

$iii)$ for every IVIF-score left ideal $\Theta _{(\overset{\ast }{\mu }, \overset{\ast }{\upsilon })}$ and $\Psi _{(\overset{\ast }{\mu }, \overset{\ast }{\upsilon })}$ of $S;$

$iv)$ the set of all IVIF-score left ideals of $S$ forms a semilattice under the composition of IVIFSs$;$

$v)$ the set of all left ideals of $S$ forms a semilattice under the composition of subsets$.$

Proof. $i)\Rightarrow ii):$ It can be followed from Theorems 1 and 2.

$ii)\Rightarrow iii):$ Let $\Theta _{(\overset{\ast }{\mu }, \overset{\ast }{ \upsilon })}$ and $\Psi _{(\overset{\ast }{\mu }, \overset{\ast }{\upsilon })}$ be any IVIF-score left ideals of $S$ with left identity $e,$ and $a\in S.$ Since $S$ is intra-regular, there exist some $x, y\in S$ for which

Consequently

Thus

Similarly

As a result,

for every IVIF-score left ideal $\Theta _{(\overset{\ast }{\mu }, \overset{ \ast }{\upsilon })}$ and $\Psi _{(\overset{\ast }{\mu }, \overset{\ast }{ \upsilon })}$ of $S.$

$iii)\Rightarrow iv):$ It is simple$.$

$iv)\Rightarrow v):$ Let $P_{1}$ and $P_{2}$ be any left ideals of $S$, then by given assumption, it is easy to see that $P_{1}P_{2}$ $(P_{2}P_{1})$ is a left ideal of $S,$ and thus

Let $x\in (P_{1}P_{2}].$ Using Lemmas 1 and 3, and the given assumption$,$ we have

This indicates that

Thus

Similarly, we can show that

Therefore

Now to prove that every left ideal $P_{1}$ of $S$ is idempotent$,$ let $x\in P_{1}.$ Then by the given assumption$,$ we have

which shows that

Hence

for every left ideal $P_{1}$ of $S.$

$v)\Rightarrow i):$ Let $a\in S.$ Since $(Sa]$ is the left ideal of $S$ and $a\in (Sa],$ so by given assumption

which shows that $a\leq xa^{2}\cdot y$ for some $x, y\in S.$ Hence $S$ is intra-regular$.$ Using Theorem 1, $S$ is a semilattice of left simple AG-groupoids$.$

Theorem 4. Let $S$ be an ordered AG-group$.$ Then the following conditions are equivalent$:$

$i)$ $S$ is a semilattice of left simple AG-groupoids$;$

$ii)$ $S$ is intra-regular and every IVIF-score left ideal of $S$ is an IVIF-score ideal$;$

$iii)$ for every IVIF-score left ideal $\Theta _{(\overset{\ast }{\mu }, \overset{\ast }{\upsilon })}$ and $\Psi _{(\overset{\ast }{\mu }, \overset{\ast }{\upsilon })}$ of $S;$

$iv)$ the set of all IVIF-score left ideals of $S$ forms a semilattice under the composition of IVIFSs$;$

$v)$ the set of all left ideals of $S$ forms a semilattice under the composition of subsets$;$

$vi)$ let $R$ and $P$ be any left and right ideals of $S$ respectively$.$

Proof. $(i)\implies (ii)\implies (iii)\implies (iv)\implies (v)$ can be followed from Theorem 3.

$(v)\implies (vi):$ Let $R$ and $P$ be any left and right ideals of $S$ respectively$,$ then it is easy to see that

Let $a\in R\cap P^{2},$ then

Let $e$ be the left identity of $S,$ then for $a\in S$ there exists $a^{^{\prime }}\in S$ such that

Therefore

implies

$(vi)\implies (i):$ Since $(Sa^{2}]$ and $(Sa]$ are the right and left ideals of $S$ respectively$\ $such that

and

therefore by using given assumption$,$ we have

which implies

for some $x, y\in S.$ Thus

Hence $S$ is intra-regular$.$ Using Theorem 1, $S$ is a semilattice of left simple AG-groupoids$.$

Remark 2. Assume $S$ is an ordered AG-groupoid with left identity and $a\in S.$ The smallest left ideal of $S$ containing $a$ is thus $P_{a} = (Sa],$ and the smallest right ideal of $S$ containing $a^{2}$ is $R_{a^{2}} = (Sa^{2}].$

Theorem 5. Let $S$ be an ordered AG-groupoid with left identity. Then the following conditions are equivalent$:$

$i)$ $S$ is intra-regular$.$

$ii)$ Let $P_{a}$ be the smallest left ideal of $S$ containing $a,$ then:

$iii)$ Let $P_{1}$ and $P_{2}$ be any left ideals of $S,$ then:

$iv)$ Let $\Omega _{(\overset{\ast }{\mu }, \overset{\ast }{\upsilon })}$ and $\Upsilon _{(\overset{\ast }{\mu }, \overset{\ast }{\upsilon })}$ are any IVIF-score left ideals of $S,$ then:

Proof. $i)\implies iv):$ Let $\Omega _{(\overset{\ast }{\mu }, \overset{\ast }{ \upsilon })}$ and $\Upsilon _{(\overset{\ast }{\mu }, \overset{\ast }{ \upsilon })}$ be the IVIF-score left ideals of an intra-regular $S$ with left identity $e$ for all $a\in S$. Now, for $a\in S,$ there exists some $x, y\in S$ such that

Thus

This suggests that

It is clear that

by applying Lemmas 2 and 4. As a result,

$iv)\implies iii):$ Let $P_{1}$ and $P_{2}$ be any left ideals of $S$. Then, according to Lemma 3, $\mathbb{C} _{P_{1}}$ and $\mathbb{C} _{P_{2}}$ are the IVIF-score left ideals of $S.$ If we take $x\in P_{1}\cap P_{2}$ and apply Lemma 1, we get

This implies

and, as a result,

It is obvious

Hence

$iii)\implies ii):$ It is obvious.

$ii)\implies i):$ Since $(Sa]$ is the smallest left ideal of $S$ that contains $a.$ Using Theorem 3 $v)\Rightarrow i),$ $S$ is intra-regular.

Theorem 6. Assume $S$ is an ordered AG-group. Then the following conditions are equivalent$:$

$i)$ $S$ is intra-regular$;$

$ii)$ Let $R_{a^{2}}$ is the smallest right ideal of $S$ containing $a^{2},$ then;

$iii)$ Let $R_{1}$ and $R_{2}$ be any right ideals of $S,$ then;

$iv)$ Let $\Omega _{(\overset{\ast }{\mu }, \overset{\ast }{\upsilon })}$ and $\Upsilon _{(\overset{\ast }{\mu }, \overset{\ast }{\upsilon })}$ be any IVIF-score right ideals of $S,$ then;

Proof. $i)\implies iv):$ Let $\Omega _{(\overset{\ast }{\mu }, \overset{\ast }{ \upsilon })}$ and $\Upsilon _{(\overset{\ast }{\mu }, \overset{\ast }{ \upsilon })}$ be both IVIF-score right ideals of $S$ with left identity $e$ and $\mathcal{V}(a)\neq \emptyset$ for all $a\in S$. Now for $a\in S,$ there exists some $x, y\in S$ such that

Thus

Thus by using Lemmas 2 and 4, we get

$iv)\implies iii):$ Let $R_{1}$ and $R_{2}$ be any right ideals of $S$. Then by Lemma 3, $\mathbb{C} _{R_{1}}$ and $\mathbb{C} _{R_{2}}$ are IVIF-score right ideals of $S.$ Let $x\in R_{1}\cap R_{2}.$ Then by using Lemma 1, we have

which implies that

and therefore

It is easy to see that

and therefore

$iii)\implies ii):$ It is obvious.

$ii)\implies i):$ Since $(Sa^{2}]$ is the smallest right ideal of $S$ containing $a^{2}$. Therefore

Using Theorem 4 $vi)\Rightarrow i),$ $S$ is intra-regular.

Definition 13. A non-empty subset $A$ of an ordered AG-groupoid $S$ is called a $(0, 2)$ -ideal of $S,$ if

$i)$ $SA^{2}\subseteq A;$

$ii)$ if $a\in A$ and $b\in S$ such that $b\leq a,$ then $b\in A,$ that is if $(A] = A.$

Equivalently$,$ if $(SA^{2}]\subseteq A.$

Definition 14. Let $\Theta _{(\overset{\ast }{\mu }, \overset{\ast }{\upsilon })}$ be a uv-score function of an ordered AG-groupoid $S$ and $x, y, z\in S.$ Then $\Theta _{(\overset{\ast }{\mu }, \overset{\ast }{\upsilon })}$ is called an IVIF-score $(0, 2)$-ideal of $S,$ if the following conditions are satisfied.

$i)$ $\Theta _{(\overset{\ast }{\mu }, \overset{\ast }{\upsilon })}(x\cdot yz)\geq \Theta _{(\overset{\ast }{\mu }, \overset{\ast }{\upsilon })}(y)\wedge \Theta _{(\overset{\ast }{\mu }, \overset{\ast }{\upsilon })}(z);$

$ii)$ $x\leq y\implies \Theta _{(\overset{\ast }{\mu }, \overset{\ast }{\upsilon })}(x)\geq \Theta _{(\overset{\ast }{\mu }, \overset{\ast }{\upsilon })}(y).$

The next two lemmas are straightforward, hence their proofs are omitted.

Lemma 5. If $\Theta$ is any uv-score function of an ordered AG-groupoid $S,$ then $\Theta$ is an IVIF-score $(0, 2)$-ideal of $S$ if and only if $S\circ \Theta ^{2}\subseteq \Theta.$

Theorem 7. Let $\Theta$ be an IVIF-idempotent subset of an ordered AG-groupoid $S$ with left identity. Then the following conditions are equivalent$:$

$(i)$ Let $\Omega _{(\overset{\ast }{\mu }, \overset{\ast }{\upsilon })}$ be an IVIF-score right ideal and $\Upsilon _{(\overset{\ast }{\mu }, \overset{ \ast }{\upsilon })}$ be an IVIF-score left ideal of $S,$ then

$(ii)$ $\Theta$ is an IVIF-score $(0, 2)$-ideal of $S.$

Proof. $(i)\implies (ii):$ We can obtain the following by using Lemma 2.

As a result of Lemma 5, $\Theta$ is an IVIF-score $(0, 2)$-ideal of $S.$

$(ii)\implies (i):$ Setting $\Upsilon _{(\overset{\ast }{\mu }, \overset{\ast }{\upsilon })} = S\circ \Theta$ and $\Omega _{(\overset{\ast }{\mu }, \overset{ \ast }{\upsilon })} = S\circ \Theta ^{2}$, then using Lemma 5, we obtain

This is what we set out to show.

5.   Applications of IVIF-score (0, 2)-ideals

Many researchers have studied several real world problems in an interval-valued intuitionistic fuzzy environment by developing various decision-making techniques. For example, Yue and Jia ^[29] presented a soft computing model for group decision problems. Chen et al. ^[5] established a method for dealing with group decision problems in the context of IVIFSs. Further to that, Cai and Han ^[4] applied IVIFSs to a data mining-based decision-making problem by providing an example of selecting an ERP system, which validated the developed approach. Moreover, Xu and Shen ^[19] suggested a new outranking choice method and illustrated it with a practical supplier selection example.

We now devise a technique to see which alternative is a good choice for further analysis on the basis of IVIF-score (0, 2)-ideals. The steps are broken down as follows$:$

$i)$ Take the collection of alternatives $X = \{x_{i}:i = 1, 2, 3..., n\}.$

$ii)$ Construct an ordered AG-groupoid on collection $X$ under a combination rule "$\cdot$" and order "$\leq$".

$iii)$ Define an IVIFS on $X$ that creates an IVIF-score $(0, 2)$-ideal of $(X, \cdot, \leq)$.

$iv)$ Rank all the IVIFNs by using uv-score function (use uv -accuracy function if uv-scores are equal).

To take a decision that will rank the available alternatives according to the requirements, we utilize an IVIF-score $(0, 2)$-ideal of an ordered AG-groupoid.

Selection of warehouse distributors

A warehouse is made up of a variety of components, including shelves and containers for storage, air conditioning systems for temperature-sensitive products, storage management software and inventory control software to keep the two in sync, picking equipment to transport goods from one location to another, and so on. While, a distribution centre is distinct from a warehouse in that it includes components for picking, packaging, and shipping, as well as storage. However, virtually all warehouses nowadays are built to include distribution centre functionality. As a result of these overlapping goals, warehousing has come to play a significant part in the supply management process. Planning, information collecting, product procurement, inventory management, transportation, delivery, and return of items are all part of the e-commerce supply management process. A warehouse can help you handle most of these procedures smoothly and optimize your business for optimum returns. Warehousing is a critical component of the supply chain operation. Even though this is not a customer-facing activity and your consumers may never be aware of it, their purchasing experience will be impeded without it.

Shipping a truckload of products from multiple warehouses to different marketplaces varies due to different modes of transportation and distances involved. An international corporation has five warehouses, designated by $x_{1},$ $x_{2},$ $x_{3},$ $x_{4}$ and $x_{5},$ with locations as follows:

$x_{1}:City\text{ }Centre$: It is located in the city centre, which is the economic, social, cultural, political, and geological soul of a metropolis.

$x_{2}:Downtown$: It is situated in downtown, which is the busiest section of a city, with the most merchants, cafés, skyscrapers, and passengers.

$x_{3}:Suburb$: It is in a suburb where citizens reside away from the middle of a major metropolitan area.

$x_{4}:Slum$: It is located in a slum, which is a tightly packed metropolitan residential area made up of low-quality dwelling units.

$x_{5}:Midtown$: It is the part of a city near the centre.

The rankings of the IVIFNs associated with each warehouse in the collection $X = \{x_{1}, x_{2}, x_{3}, x_{4}, x_{5}\}$ will decide the rankings.

Let consider the collection of warehouses $X = \{x_{1}, x_{2}, x_{3}, x_{4}, x_{5} \}$. Let the combination rule be the time taken to pick an item form warehouse and bringing it to the selling point, e.g. time taken to picking first item from warehouse $x_1$ then second item from $x_4$ is same as time taken to pick a single item from $x_5$, similarly time taken to pick two items from $x_1$ ($x_1$ to $x_1$) is same as time required for picking a single item from $x_4$. All the possible combinations are listed in table below (see Table 5):

It is easy to see that $(X, \cdot, \leq)$ is an ordered AG-groupoid$.$

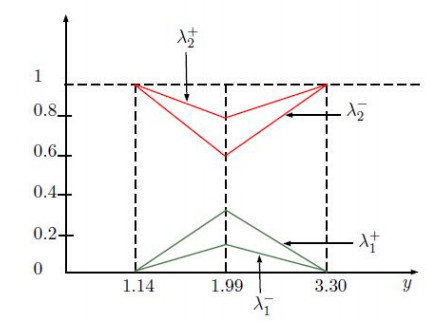
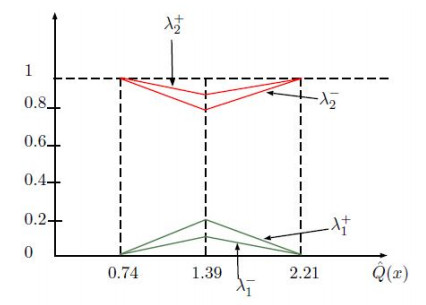
Consider the following collection of IVIFS $\mathcal{I} = \{ \overset{\ast }{ \xi }_{j} = ($$\overset{\ast }{\mu }$$_{\xi _{j}},$$\overset{\ast }{ \upsilon }$$_{\xi _{j}});$ $j = 1, 2, 3, 4, 5\}$ on $X$ as follows (see Table 6):

The above table shows that $\Theta _{(\overset{\ast }{\mu }, \overset{\ast }{ \upsilon })}(\mathcal{I})$ is an IVIF-score $(0, 2)$-ideal of $(X, \cdot, \leq)$.

Sort all of the alternatives according to their respective uv-scores. If two uv-scores (Definition 1) are equal, the uv-accuracy function (Definition 2) can be used to sort the alternatives (see Figure 3).

The preferences of the alternatives based on an IVIF-score $(0, 2)$-ideal on $(X, \cdot, \leq)$ can be seen from the following Table 7:

6.   Conclusions

We developed some novel characterization results for an intra-regular ordered AG-groupoid. We used the notions of uv-score and uv -accuracy functions under interval-valued intuitionistic fuzzy environment to provide a method that satisfies a decision maker while making the decision by incorporating the concept of IVIF-score $(0, 2)$-ideals in an ordered AG-groupoid. The results of this paper are developed for ordered AG-groupoids but they also hold for un-ordered AG-groupoids, so these results could be considered as extended results. They also generalize the results already developed on the structure of AG-groupoids and ordered groupoids by considering various versions of fuzzy sets. The work carried out in this paper is in the most generalized form and is capable of extending the existing theory of AG-groupoids

Based on our proposed concept, more applications for future research work can be found in a variety of directions. Among them are the following$:$

● Using the concepts of a Pythagorean fuzzy set (PFS) ^[21] and interval valued picture hesitant fuzzy set (IVPHF) ^[7], one can investigate an ordered AG-groupoid in detail.

● To characterize an ordered AG-groupoid using the notion of a q-rung orthopair fuzzy set (Cq-ROFS) ^[22].

● To investigate the concept of a linear Diophantine fuzzy set (LDFS) ^[16], their algebraic structures ^[9] and complex linear Diophantine fuzzy set (CLDFS) ^[8] in the framework of an ordered AG-groupoid.

Acknowledgments

The authors extend their appreciation to the Deanship of Scientific Research at King Khalid University, KSA for funding this work through General Research Project under grant number R.G.P.1/277/43$.$

Conflict of interest

The authors declare no conflict of interest.