1.
Introduction
Over the past three decades, there have been expanded attempts to develop more flexible distributions for modeling data in different applied sciences including economics, engineering, biological studies, environmental sciences, medical sciences, and finance. One such attempt is to add one or more parameters to the baseline model to construct a new extended distribution.
Some well-known families are the Marshall-Olkin-G [1], beta-G [2], transmuted-G [3], Kumaraswamy-G [4], Weibull-G [5], transmuted exponentiated generalized-G [6], Kumaraswamy transmuted-G family [7], generalized transmuted-G [8], generalized odd log-logistic-G [9], log-logistic tan-G [10], Marshall-Olkin-Weibull-H [11], and modified generalized-G families [12], among others.
Recently, Kavya and Manoharan [13] introduced a new transformation called the Kavya-Manoharan-G (KM-G) class. Many extended forms of classical distributions have been proposed based on the KM-G family. For example, the KM inverse length biased exponential [14], KM Kumaraswamy exponential [15], KM log-logistic [16], KM power-Lomax [17], KM Burr X [18], and KM Kumaraswamy distributions [19].
In this paper, we propose a new family of distributions by adding one extra shape parameter in the KM-G class to construct the so-called generalized Kavya-Manoharan-G (GKM-G) family, which provides greater flexibility to the generated models. The GKM-G family is constructed based on the exponentiated-H (exp-H) family [20] as one of the most widely used generalization techniques. Using this technique, the cumulative distribution function (CDF) of the exp-H class takes the form
where H(x;φ) is the baseline CDF, which depends on the parameter vector φ.
The GKM-G family can be considered as a proportional reversed hazard (PRH) family. The PRH models are very important in reliability theory and survival analysis, especially in the analysis of left censored lifetime data and in the study of parallel systems [21]. More information about the PRH models can be explored in [22] and [23].
In fact, the technique for generating exp-H models can be traced back to Lehmann [20]. This generalization method received a great deal of attention in the last three decades, and more than fifty exp-H distributions have already been published. Some notable exponentiated distributions include the exponentiated Weibull [24], exponentiated Weibull-Pareto [25], and exponentiated Weibull family [26], among others. It has been illustrated that the exp-H distributions provide greater flexibility and have useful applications in many applied fields such as biomedical sciences, environmental studies, and reliability analysis. Since the exponentiated distribution is more appealing than its baseline counterpart, we provide the same approach for a family of distributions studied by [13].
We study a comprehensive description of some of its mathematical properties. The new family may attract wider applications in reliability, engineering, environmental, and medicine fields due to its simple analytical forms and its flexibility. The special sub-models of the GKM-G family can provide right-skewed, reversed-J shaped, and unimodal densities, as well as increasing, bathtub, decreasing, unimodal, and modified bathtub hazard rate (HR) shapes. These flexible shapes are important for modeling several real-life data encountered in many applied fields.
A special sub-model based on the exponential (E) distribution called the generalized Kavya-Manoharan exponential (GKME) is studied. The GKME distribution provides greater flexibility for modeling real-life data in several applied fields such as reliability, environmental, and medicine, as illustrated in Section 8. Five real data applications show that the GKME distribution provides consistently better fits as compared to other competing extended forms of the E model, namely, the generalized exponential (GE) [27], generalized inverted exponential (GIE) [28], Marshall-Olkin exponential (MOE) [1], alpha-power exponential (APE) [29], generalized Dinesh-Umesh-Sanjay exponential (GDUSE) [30], Kavya-Manoharan exponential (KME) [13], and E distributions.
Additionally, the behavior of the unknown parameters of the GKME distribution for several sample sizes and parameter combinations is investigated using eight different estimation procedures. A guideline for selecting the optimum estimation method to estimate the GKME parameters is developed, which we believe applied statisticians and reliability engineers would find useful. Also, comprehensive simulations are performed to evaluate and compare the performance of various estimators.
The rest of the paper is organized as follows. In Section 2, the GKM-G family is defined. Four special sub-models of the GKM-G family are presented in Section 3. In Section 4, some mathematical properties of the GKM-G class are obtained. In Section 5, we derive the rth moment of the GKME distribution and present some numerical results for it. Estimation methods of the GKME parameters are presented in Section 6. In Section 7, we provide a detailed simulation study. Section 8 provides five real-life data applications to show empirically the flexibility of the GKME distribution. Finally, some remarks and future perspectives are presented in Section 9.
2.
Construction of the GKM-G family
Let G(x;φ) and g(x;φ) denote the CDF and probability density function (PDF) of a baseline model with parameter vector φ, then the CDF of the KM family [13] is defined as
The corresponding PDF of (2.1) is defined by
The HR function (HRF) reduces to
By inserting (2.1) in Eq (1.1), the CDF of the GKM-G family is defined by
The PDF of the GKM-G family reduces to
The HRF of the GKM-G family follows as
The extra shape parameter α may allow us to study the tail behavior of the PDF (2.3) with more flexibility. Additionally, the GKM-G family is considered an important class for modeling different real-life data due to its flexibility in accommodating all important forms of the HRF. A random variable X having the PDF (2.3) is denoted by X∼GKM-G (α,φ). Simply, the proposed GKM-G family reduces to the KM-G family [13] when α=1.
3.
Four special sub-models
In this section, we provide four special sub-models of the GKM-G family, namely, the GKME, GKM-Burr X (GKMBX), GKM-Burr XII (GKMBXII), and GKM-log logistic (GKMLL) distributions. These sub-models are capable of modeling monotone and non-monotone failure rates including increasing, reversed J shaped, decreasing, bathtub, modified bathtub, and upside-down bathtub. They also can have right-skewed, symmetrical, and reversed-J shaped densities. Figures 1–4 display all these shapes.
3.1. The GKME distribution
The CDF and PDF of the E distribution are defined, respectively, by G(x)=1−e−λx and g(x)=λe−λx, where x>0,λ>0. By inserting the CDF of the E distribution in (2.2), the CDF of the GKME distribution follows as
The corresponding PDF of the GKME distribution reduces to
Therefore, the random variable with PDF (3.2) is denoted by X∼GKME(α,λ). The GKME distribution reduces to the KME distribution [13] for α=1.
The HRF of the GKME distribution is given by
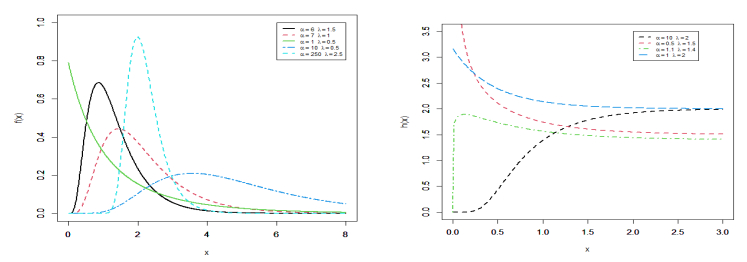
Figure 1 displays some possible shapes of the PDF and HRF of the GKME distribution.
3.2. The GKMBX distribution
The CDF of the Burr-X (BX) distribution is G(x)=[1−e−(λx)2]β, where x>0,λ,β>0. By inserting the CDF of the BX distribution in (2.2), the CDF of the GKMBX distribution follows as
The corresponding PDF follows as
The GKMBX distribution reduces to the KMBX distribution for α=1. The GKM-Rayleigh distribution follows as a special case for β=1. The KM-Rayleigh distribution follows for α=β=1. Figure 2 displays some possible shapes of the PDF and HRF of the GKMBX distribution.
3.3. The GKMBXII distribution
The CDF of the BXII distribution is G(x)=1−(1+xλ)−β, where x>0,β,λ>0. By inserting the CDF of the BXII distribution in (2.2), the CDF of the GKMBXII distribution is obtained as
The PDF of the GKMBXII distribution reduces to
Figure 3 shows some possible shapes of the PDF and HRF of the GKMBXII distribution.
3.4. The GKMLL distribution
Consider the CDF of the log-logistic (LL) distribution, say, G(x)=1−[1+(xλ)β]−1, where x>0,β,λ>0, then the CDF of the GKMLL distribution takes the form
The corresponding PDF of the GKMLL distribution reduces to
Figure 4 displays some possible shapes of the PDF and HRF of the GKMLL distribution.
4.
Properties of GKM-G family
This section provides some mathematical properties of the GKM-G family.
4.1. Linear representation
In this section, we provide a useful representation of the CDF and PDF of the GKM-G family in terms of exp-G density. Consider the following generalized binomial series
Applying (4.1) to (2.2), we obtain
Using the exponential series, we can write
Substituting (4.2) and (4.3) in (2.2), the CDF of the GKM-G takes the form
Hence, the CDF of the GKM-G family can be expressed as
where
and Hk(x)=G(x)k is the CDF of the exp-G family with power parameter k>0. By differentiating the above equation, the PDF of the GKM-G family follows as
where hk(x)=kg(x)G(x)k−1 is the exp-G density with power parameter k. Thus, several mathematical properties of the GKM-G family can be obtained simply from those properties of the exp-G family.
4.2. Quantile function and moments
The quantile function (QF) of X, say, Q(u)=F−1(x), can be obtained by inverting (2.2), then the QF of the GKM-G family follows as
where φ=e/(e−1) and QG(u)=G−1(u) is the QF of the baseline G distribution and u∈(0,1).
Henceforth, Tk denotes the exp-G random variable with power parameter k. The rth moment of X follows from (4.5) as
The moment generating function (MGF), MX(t)=E(etX), of X can be derived from (4.5) in two different formulas. The first one is given by
where Mk(t) is the MGF of Tk(x). Hence, MX(t) can be determined from the exp-G generating function.
The second formula for MX(t) follows from (4.5) as
where τ(t,k−1)=∫10exp[tQG(u)]uk−1du.
4.3. Incomplete moments
The sth incomplete moment of X can be expressed from (4.5) as
The first incomplete moment follows from (4.7) when s=1. It can be applied to construct Bonferroni and Lorenz curves, which are defined, for a given probability π, by B(π)=φ1(q)/(πμ'1) and L(π)=φ1(q)/μ'1, respectively, where μ'1 is given by (4.6) with r=1 and q=Q(π) is the QF of X at π. These curves are very useful in economics, reliability, demography, insurance, and medicine.
Now, φ1(t) can be determined in two expressions. The first expression for φ1(t) is derived from (4.7) as
Where lk(t)=∫t−∞xhk(x)dx is the first incomplete moment of the exp-G family. A second expression for φ1(t) takes the form
where υk(t)=k∫G(t)0QG(u)uk−1du, which can be computed numerically, and QG(u) is the QF corresponding to G(x), i.e., QG(u)=G−1(u).
The mean deviations about the mean [δ1=E(|X−μ'1|)] and about the median [δ2=E(|X−M|)] of X are given by δ1=2μ'1F(μ'1)−2φ1(μ'1) and δ2=μ'1−2φ1(M), respectively, where μ'1=E(X),M=Q(0.5) is the median. F(μ'1) is easily evaluated from (2.2).
4.4. Mean residual life and mean inactivity time
The mean residual life (MRL) represents the expected additional life length for a unit, which is alive at age t, and it is defined by MRLx(t)=E(X−t|X>t), for t>0. The MRL of X is
where S(t) is the survival function (SF) of the GKM-G family. Inserting (4.8) in (4.9), we obtain
The mean inactivity time (MIT) represents the waiting time elapsed since the failure of an item, on condition that this failure occurred in (0,t). The MIT is defined by MITX(t)=E(t−X|X≤t), for t>0. The MIT of X reduces to
Combining Eqs (4.8) and (4.10), the MIT of X follows as
4.5. Entropies
The Rényi entropy of a random variable X represents a measure of variation of the uncertainty. The Rényi entropy is defined by
Using the GKM-G density (2.3), we can write
where φ=e/(e−1). Applying the power series (4.2) to the last term, we obtain
Hence,
Applying the exponential series, we obtain
Thus, f(x)θ reduces to
where
The Rényi entropy of the GKM-G family reduces to
The Shannon entropy (SI) follows as a special case of the Rényi entropy when θ tends to 1.
4.6. Order statistics
Let X1,…,Xn be a random sample from the GKM-G family. The PDF of Xi:n can be written as
where B(.,.) is the beta function. Using (2.2) and (2.3), we can write
Applying the generalized binomial series to (4.12), we have
Inserting (4.13) in Eq (4.11), the PDF of Xi:n reduces to
where hk+1(x)=(k+1)g(x)G(x)k is the exp-G density with power parameter k+1 and
Hence, the PDF of the GKM-G order statistics is a linear combination of exp-G densities. Based on (4.15), we can derive the properties of Xi:n from those properties of Tk+1. For example, the qth moment of Xi:n is given by
4.7. Probability weighted moments
The probability weighted moments (PWMs) are proposed by Greenwood et al. [31] as a special class of moments. This class is used to derive estimates of the parameters and quantiles of distributions, which can be expressed in inverse form. They also have moderate biases, low variance, and comparable with the maximum likelihood (ML) estimators. Let X be a random variable with PDF f(x) and CDF F(x), then the (j,i)th PWM of X, denoted by ρj,i, is defined by
where jand i are nonnegative integers.
Using the CDF and PDF of the GKM-G family and Eq (4.14), we can write
The last equation can be expressed as
where
Thus, the PWM of X is given by
5.
Moments of the GKME distribution
In this section, we derive a simple formula for the rth moment of the GKME distribution. Based on Eq (4.5), the PDF of the GKME distribution can be expressed as follows:
Applying binomial expansion to (1−e−λx)k−1, the last equation follows as
The GKME PDF reduces to
where
andgm+1(x)=(m+1)λexp(−(m+1)λx) denotes the E density with rate parameter (m+1)λ. Equation (5.1) means that the GKME density is expressed as a single linear combination of E densities.
Hence, the rth moment of GKME distribution follows from (5.1) as
Clearly, the mean of the GKME distribution, say, μ'1=μX, follows from the above equation when r=1. It is given by
Table 1 lists the numerical integration and the summation (SUM) formula of μX for different values of λ and α at truncated L terms. These numerical values are computed by R statistical software. Table 1 shows that the summation (5.2) converges to the numerical integral (NUI) of μX for different values of λ and α when L becomes very large, where L is the truncated terms from this summation.
Furthermore, the μX, variance (σ2X), skewness (ψ1), and kurtosis (ψ2) of the GKME distribution are computed numerically for some values of α and λ using the R software. The numerical values of the four measures are displayed in Table 2. This table indicates that μX and σ2X are increasing functions of α, whereas ψ1 and ψ2 are decreasing functions of α. It is also noted that ψ1 can range in the interval (1.2643, 3.1841). The spread of ψ2 is much larger, ranging from 5.7854 to 18.1205.
The QF of the GKME distribution is given by
The QF can be used to study the relationships between the parameters (λ, α) and the skewness and kurtosis, and the Galton´s skewness and Moors´ kurtosis depend on the QF. Figure 5 displays the Galton´s skewness and the Moors´ kurtosis for the GKME distribution for some parametric values of λ and α.
6.
Estimation methods for the GKME parameters
In this section, we use eight methods to estimate the GKME parameters, namely: the maximum likelihood estimators (MLEs), least-squares estimators (LSEs), weighted least-squares estimators (WLSEs), maximum product of spacing estimators (MPSEs), percentiles estimators (PCEs), Cramér-von Mises estimators (CVMEs), Anderson-Darling estimators (ADEs), and right-tail Anderson-Darling estimators (RTADEs).
6.1. Maximum likelihood
Let x1,…,xn be a random sample from the GKME distribution with parameters α and λ. Let x1:n<x2:n<⋯<xn:n be the associated order statistics, then, the log-likelihood function has the form
where ki=e−ee−λxi. The MLEs of α and λ can be obtained by maximizing the last equation with respect to α and λ, or by solving the following nonlinear equations:
and
The MLEs can also be obtained by using different programs such as R (optim function), Mathematica, and SAS (PROC NLMIXED).
6.2. Least-squares and weighted least-squares
The LS and WLS methods are used to estimate the parameters of the beta distribution [32]. The LSEs and WLSEs of the GKME parameters α and λ can be obtained by minimizing
with respect to α and λ, where υi=1 in case of the LS approach and υi=(n+1)2(n+2)/[i(n−i+1)] in case of the WLS approach. Furthermore, the LSEs and WLSEs follow by solving the nonlinear equations
where
and
6.3. Maximum product of spacings
The MPS method is used to estimate the parameters of continuous univariate models as an alternative to the ML method [33,34]. The uniform spacings of a random sample of size n from the GKME distribution can be defined by
where Di denotes the uniform spacings, where F(x0:n⎸α,λ)=0,F(xn+1:n⎸α,λ)=1, and ∑n+1i=1Di(α,λ)=1. The MPSEs of the GKME parameters can be obtained by maximizing
with respect to α and λ. Further, the MPSEs of the GKME parameters can also be obtained by solving
where Δs(xi:n⎸α,λ)=0 are defined in (5.1) and (5.2) for s=1,2.
6.4. Percentile method
The percentile method [35] is used to estimate the unknown parameters of the GKME distribution by equating the sample percentile points with the population percentile points. Let ui=i/(n+1) be an unbiased estimator of F(xi:n⎸α,λ), then the PCEs of the GKME parameters are obtained by minimizing the following function:
with respect to α and λ.
6.5. Cramér-von Mises method
The CVMEs [36,37] can be obtained based on the difference between the estimates of the CDF and the empirical CDF. The CVMEs of the GKME parameters are obtained by minimizing the following function
Further, the CVMEs follow by solving the nonlinear equations
where Δs(xi:n⎸α,λ)=0are defined in (5.1) and (5.2) for s=1,2.
6.6. Anderson-Darling and right-tail Anderson-Darling
The ADEs are another type of minimum distance estimators. The ADEs of the GKME parameters are obtained by minimizing
with respect to α and λ. The ADEs can also be determined by solving the nonlinear equations
The RTADEs of the GKME parameters α and λ are obtained by minimizing the following function, with respect to α and λ,
7.
Simulation analysis
In this section, we assess the performance of all estimation methods of the GKME parameters using a simulation study. We generate 2000 samples from the GKME distribution for different sample sizes of n={20,50,100,250} and different parametric values of α=(0.5,0.75,1.5,2) and λ=(0.5,1.3,1.5). We obtain the average values of the estimates (AEs) and mean square errors (MSEs) for each estimate.
The performance of different estimators is evaluated in terms of MSEs, i.e., the most efficient estimation method will be the one whose MSEs values decay toward zero as the sample size increases. Tables 3–6 show the AEs and MSEs (in parentheses) of the MLEs, LSEs, WLSEs, MPSEs, PCEs, CVMEs, ADEs, and RTADEs. It is noted that, as the sample size increases, the AEs tend to the true parameter values. Furthermore, the values of the MSEs decay toward zero, indicating that all estimators are asymptotically unbiased. According to the values in these tables, all eight estimation methods perform very well in terms of MSEs.
8.
Data analysis in different applied fields
In this section, we present five applications of real-life data from medicine, environmental, and reliability fields to illustrate the flexibility of the GKME model. The ML method is used to estimate the parameters of each model and R statistical software is used for computations. We compare the fitting performance of the GKME with other competing E models, namely: The GE [27], GIE [28], MOE [1], APE [29], GDUSE [30], KME [13], and E distributions.
To compare the competing distributions with the proposed GKME model, we calculate some goodness-of-fit statistics, including the Cramér-von Mises (W∗), Anderson-Darling (A∗), and Kolmogorov-Smirnov (KS) statistics with its p-value.
8.1. Modeling reliability data
The first set of data is studied by Murthy et al. [38], and it represents the time between failures for a repairable item. The data observations are: 1.43, 0.11, 0.71, 0.77, 2.63, 1.49, 3.46, 2.46, 0.59, 0.74, 1.23, 0.94, 4.36, 0.40, 1.74, 4.73, 2.23, 0.45, 0.70, 1.06, 1.46, 0.30, 1.82, 2.37, 0.63, 1.23, 1.24, 1.97, 1.86, 1.17.
8.2. Modeling environmental data
The second set of data represents the waiting times (in minutes) before the service of 100 bank customers. This data set is previously studied by Ghitany et al. [39]. The data observations are: 0.8, 0.8, 3.2, 3.3, 4.6, 4.7, 6.2, 6.2, 7.7, 8, 9.7, 9.8, 12.5, 12.9, 17.3, 18.1, 27, 31.6, 1.3, 3.5, 4.7, 6.2, 8.2, 10.7, 13, 18.2, 33.1, 1.5, 1.8, 1.9, 3.6, 4, 4.1, 4.8, 4.9, 4.9, 6.3, 6.7, 6.9, 8.6, 8.6, 8.6, 10.9, 11, 11, 13, 13.3, 13.6, 18.4, 18.9, 19, 38.5, 1.9, 2.1, 2.6, 4.2, 4.2, 4.3, 5, 5.3, 5.5, 7.1, 7.1, 7.1, 8.8, 8.8, 8.9, 11.1, 11.2, 11.2, 13.7, 13.9, 14.1, 19.9, 20.6, 21.3, 2.7, 2.9, 3.1, 4.3, 4.4, 4.4, 5.7, 5.7, 6.1, 7.1, 7.4, 7.6, 8.9, 9.5, 9.6, 11.5, 11.9, 12.4, 15.4, 15.4, 17.3, 21.4, 21.9, 23.
The third set of data is studied by Dumonceaux and Antle [40] and it consists of annual maximum flood levels (in millions of cubic feet per second) over a 20-year period of the Susquehanna River at Harrisburg, Pennsylvania. The data observations are: 0.654, 0.613, 0.315, 0.449, 0.297, 0.402, 0.379, 0.423, 0.379, 0.324, 0.269, 0.740, 0.418, 0.412, 0.494, 0.416, 0.338, 0.392, 0.484, 0.265.
8.3. Modeling medicine data
The fourth set of the data is analyzed by Mann [41], and it represents the number of vehicle fatalities for 39 counties in South Carolina in 2012. The data observations are: 22, 26, 17, 4, 48, 9, 9, 31, 27, 20, 12, 6, 5, 14, 9, 16, 3, 33, 9, 20, 68, 13, 51, 13, 2, 4, 17, 16, 6, 52, 50, 48, 23, 12, 13, 10, 15, 8, 1.
The fifth set of data is given by Lee and Wang [42], and it represents the remission times (in months) of a random sample of 128 bladder cancer patients. The data observations are: 0.08, 2.09, 3.48, 4.87, 6.94, 8.66, 13.11, 23.63, 0.20, 2.23, 3.52, 4.98, 6.97, 9.02, 13.29, 0.40, 2.26, 3.57, 5.06, 7.09, 9.22, 13.80, 25.74, 0.50, 2.46, 3.64, 5.09, 7.26, 9.47, 14.24, 25.82, 0.51, 2.54, 3.70, 5.17, 7.28, 9.74, 14.76, 26.31, 0.81, 2.62, 3.82, 5.32, 7.32, 10.06, 14.77, 32.15, 2.64, 3.88, 5.32, 7.39, 10.34, 14.83, 34.26, 0.90, 2.69, 4.18, 5.34, 7.59, 10.66, 15.96, 36.66, 1.05, 2.69, 4.23, 5.41, 7.62, 10.75, 16.62, 43.01, 1.19, 2.75, 4.26, 5.41, 7.63, 17.12, 46.12, 1.26, 2.83, 4.33, 5.49, 7.66, 11.25, 17.14, 79.05, 1.35, 2.87, 5.62, 7.87, 11.64, 17.36, 1.40, 3.02, 4.34, 5.71, 7.93, 11.79, 18.10, 1.46, 4.40, 5.85, 8.26, 11.98, 19.13, 1.76, 3.25, 4.50, 6.25, 8.37, 12.02, 2.02, 3.31, 4.51, 6.54, 8.53, 12.03, 20.28, 2.02, 3.36, 6.76, 12.07, 21.73, 2.07, 3.36, 6.93, 8.65, 12.63, 22.69.
8.4. Findings from the five datasets
Tables 7–11 provide the values of W∗, A∗, KS, and the KS p-value of the fitted models for the five datasets, respectively. Further, Tables 7–11 display the MLEs and standard errors (SEs) (appear in parentheses) of the parameters of the GKME, GE, GDUSE, MOE, APE, GIE, E, and KME models. The values in these tables indicate that the GKME distribution has the lowest values of W∗, A∗, and KS statistics and largest p-value, among all fitted models. The fitted functions of the GKME model including the fitted PDF, CDF, SF, and probability-probability (PP) plots for all datasets are displayed in Figures 6–8, respectively.
9.
Conclusions
We proposed a new class of continuous distributions called the GKM-G family. The GKM-G family generalizes the KM family and provides greater flexibility. Some special models of the GKM-G family are provided. Some of its basic properties are studied. Eight methods are used for estimating the parameters of the GKME distribution. The performance of the estimators is assessed by simulation studies for small and large samples. Our study shows that all considered estimation approaches are consistent. Five real-life data applications from medicine, environment, and reliability fields are analyzed to illustrate the flexibility of the GKME distribution. These applications indicate that the GKME distribution provides a better fit as compared to other existing exponential distributions.
For a possible direction of future works, the research in this article can be extended in some ways. For example, construction of autoregressive processes based on the special sub-models of the GKM-G family, constructing regression models by exploiting the flexibility of the GKME distribution, and a discrete version of the GKME distribution may be established. Furthermore, considering the works of Alsadat et al. [43] and Tolba et al. [44], the parameters of the GKME distribution can be explored using the Bayesian approach under complete and censored samples. Additionally, considering the work of Chinedu et al. [45], the GKME distribution and other special models of the family may have some applications to the single acceptance sampling plan under different scenarios of failure rates. Also, the detailed study of theoretical statistical properties that distinguishes the GKME distribution and makes it distinct from some corresponding distributions such as the skewness and kurtosis can be addressed according to the works of Barakat [46] and Barakat and Khaled [47].
Use of AI tools declaration
The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.
Acknowledgments
The authors extend their appreciation to the Deputyship for Research and Innovation, Ministry of Education in Saudi Arabia for funding this research work through project number 445-9-854.
The authors also would like to thank the Editor and the reviewers for their constructive comments and suggestions, which greatly improved the paper.
Conflict of interest
The authors declare no conflict of interest.









 DownLoad:
DownLoad:










