Stationary distribution and extinction of a stochastic SEIQ epidemic model with a general incidence function and temporary immunity

1.   Introduction

Since the middle of 1960, Europe has a history of concrete paving block (CPB) as a road pavement material, which subsequently developed in Central America, South America, and South Africa. Then in 1970, it was known in England, Canada, Australia, New Zealand, and Japan. Which eventually spread in the Middle East and Asia. Initially, they used CPB for courtyards, sidewalks, parks, and footpaths. However, at present, it is widely used in container terminals, airports, class Ⅰ traffic, and so on. The change from lightweight to heavy load is the reason for the increase in CPB compressive strength more than 300 kg/cm² becomes a necessity. It was encouraging more research that leads to an increase in compressive strength effectively.

According to Brian Shackel 2003, in the period 1980 to 2003, there were 500 papers at international conferences that discussed CPB an overview of the technology. Broadly, the technology can split into four areas. These are paver manufacture, quality control, evaluating of paving through direct testing, and design of pavements ^[1]. Dry concrete or CPB needs exclusive technology in the compaction process to achieve maximum compressive strength. The intended technology is mixing with mixed materials, handling of controlled agammaegates, placing of CPB, and several compacting techniques ^[2], as compaction is on soil compaction.

For mixed materials technology, the researchers had previously researched CPB mixture added materials to find the right proportion to replace sand or cement with waste material. Ceramic waste material can replace 20% cement and 30% fine agammaegate with compressive strength reaching 50 MPa ^[3,4]. We replaced cement with fly ash 0% to 30% content, which will reduce the compressive strength of CPB ^[5]. The following added material is the utilization of marble waste as CPB added an element. After conducting physical and mechanical tests of CPB production results, the type of cement turned out to show a significant factor. Mechanical strength decreases with increasing marble content during melting-freeze resistance and improved wear resistance. Marble waste is better than ordinary agammaegate in the production of concrete paving blocks ^[6]. Then the use of plastic waste as CPB added material. The authors recommend that paving blocks made from recycled plastic waste should be used in non-traffic areas such as sidewalks, sidewalks, pedestrian plazas, landscapes, monument sites, and in standing water areas due to their low water absorption properties and relative compressive strength low. Compared to the global specification threshold of 5–25% and low density to concrete strength of 0.69–17.24 N/mm^{2 [7]}, respectively. The use of CPB for asphalt pavement replacement facilities is increasing at this time, causing many researchers to develop CPB research ranging from CPB mixture materials to manufacturing technology. One of them is that the CPB mixture in the form of mud was found the requirements of slippage resistance and is, therefore, suitable only for use in the construction of pedestrian walkways and house yards ^[8]. The addition of kaolin to increase thermodynamic, optical, fluorescence, compressive strength, and abrasion resistance of concrete paving blocks increased by 10% has the highest potential to be applied to construction. Metakaolin is an inorganic material whose essential ingredients formed from compounds of silicon dioxide (SiO₂) and aluminum oxide (Al₂O₃) ^[9].

The next CPB compaction research is handling of controlled agammaegate then research on the use of several agammaegate maximum sizes, each of which is 19 mm, which has a compressive strength of 25.6 MPa at a maximum grain size of 38 mm compressive strength of 24.80 MPa and 76 mm max agammaegate has a compressive strength of 18.90 MPa. In contrast to the compressive strength data, the particular group has an increased density to increase the agammaegate size of 2390, 2420, and 2480 kg/m³, respectively, where the reverse trendline can be related to the order of compressive strength ^[10]. The next CPB compaction research technology is changing the composition of the essential ingredients of CPB. Laboratory experiments compare and investigate the effect of 12% and 15% cement content in concrete mixtures at five different w/c ratios. In total, 60 concrete mixes were thrown and tested to determine dry density, compressive strength, and slip resistance of concrete paving block samples. Design strength levels ranging from 20 to 33 MPa and 31 to 42 MPa are achieved using a w/c ratio from 0.50 to 0.70 for 12% cement content and 0.45 to 0.65 for 15% cement content ^[11]. Characteristic compressive strength (cylinder strength for the ACI method and cube strength for the DoE method), from 15 to 50 N/mm². Based on the estimated proportions, the experimental mixture was thrown and tested for compression at 7 and 28 d. When paving blocks are proportional to the ACI mixed design method, the compressive strength achieved is higher than the Sri Lanka Standard compressive strength requirements for paving blocks ^[12]. The next study was CPB with a ratio between agammaegate and cement; the results showed that the higher the rate, the higher the compressive strength produced for all types of mixtures ^[13]. Old research processed waste tea ash (PWTA) as a substitute for cement paving blocks at doses of 10%, 20%, 30%, 40%, and 60% by weight of cement was investigated for the first time. The results showed the density of PWTA paving blocks decreased because the percentage of cement replacement increased because PWTA had a lower density than cement. Increased PWTA content reduces the quality of paving blocks in terms of compressive strength, flexural strength, water absorption, and acid resistance due to increased cavities in paving blocks ^[14].

Then compaction technology is pressing in the CPB manufacturing process, the same as in the soil compaction. During the production process applying pressing methods to increase the compressive strength of dry concrete or CPB. The characteristics of the mixture affect the working ability of bare cement. DC-B has a coarser mix than DC-A, and therefore requires a higher compression pressure during production to achieve a significant increase in the percentage of compression strength ^[15]. However, this method is challenging to implement on CPB because of the durability of mold, and if pressing on the CPB manufacturing process is forced, it will damage the shell. Seventy years ago, many researchers applied soil compaction technology and CPB in combination with a vibrating press (vibropressing). In the event of vibration, the grain material consolidation by regulating the particles into motion, thereby eliminating internal friction. L’Hermite and Tournon (1948) explain that the internal resistance in fresh concrete during vibration is 0.15 psi (0.001 MPa), while the internal frictionless vibrational conditions are around three psi (0.02 MPa). Thus, internal friction during wave is reducing about 5 percent from the rest ^[16]. With a wave, the process of forming the characteristics of perlite, sound absorption board with mold vibration technology so that it has a more uniform density and is better for the sound absorption effect ^[17]. Vibration for compacting concrete must enough, not excessive, and not less. Vibration can cause problems with the equipment while operated for excessive time. It is more likely to cause issues with the mixture being disproportionate because the amount of water added is excessive, conversely if less concrete vibration can cause severe defects to the durability of the concrete surface ^[18]. So, the duration of shakes in the concrete will depend on the amount of volume, grain size, frequency, amplitude, and so on.

From all the research reviews above, there are fundamental things that have not thought about CPB compaction technology. The compaction technology is conventional, pressing technology, and vibropressing technology. In the vibropressing technology are time, frequency, and a pushing. In all the above studies, the added ingredients for CPB will produce different compressive strengths if treated with incredible treatment. In studies that vary the composition of the essential components of a mixture of CPB will also experience different compressive strength characteristics if done with different compaction method. Even the paving machine that already uses the technique of vibropressing with the system combining the duration, frequency, and pressing will produce a different compressive strength.

For this reason, this research will test mixtures with the same composition but different time vibrations and the frequency at 75 kg/cm² pressing treatments. This research aims to measure the level of compressive strength of CPB, which is done by conventional technology, pushing technology, and vibropressing, as well as proving that the increase in CPB compressive strength is very dependent on the technology, vibration and forcing compaction used.

2.   Materials and methods

2.1.   Three tools for CPB production

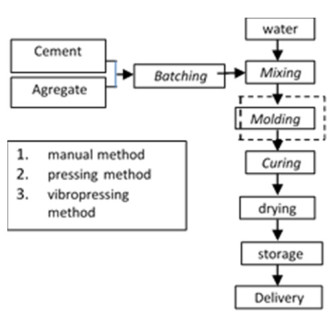
In this research, using three types of CPB production equipment, each using manual power through a punch, a press machine that uses a hydraulic press, and the third uses a vibrating and pressing combination (see Figure 1) and production procedure as Figure 2.

2.2.   Three methods of CPB production

In this research, there are three ways to produce CPB, including manual method, hydraulic pressing method, and vibropressing method. The difference in the three ways production occurs in the treatment of molding.

To reach research accurately, it is making test specimens with three methods, including the conventional way (see Figure 3), the hydraulic pressing method (see Figure 4), and the vibropressing method. (see Figure 5). For the conventional way, it only uses 1 unit of traditional equipment. For the pressing technique, it uses 1 unit of pressing machine and mold with 3 Hp of electrical energy to drive the hydraulics. Especially, for the vibropressing treatment, the concrete mixture is compacted with two kinds of a dynamo, one dynamo for hydraulic pressing energy and other for vibration. The second method and third method pressed in the style of 75 kg/cm².

2.3.   Characteristics of cement and aggregates

In Indonesia Nasional Standard (03-0691-1996) about a concrete paving block (CPB), there are no specific requirements regarding materials for CPB materials but only explain about the reference, classification, quality requirements, how to take samples, test methods and needs to pass the test (see Figure 6). So, this study concludes that the material criteria for CPB are identical to standard concrete ^[19]. This SNI (Standard National Indonesia) regulation only explains about characteristics of the material. In more detail, the description of the sand material test methods is in Table 1 for agammaegates properties and Table 2 for sieve analysis.

2.4.   Regulators for the third method (vibropressing)

All energy load on the CPB producing process by vibropressing way must always be measured carefully, to get a good CPB. The tools included:

1. A timer, or a vibration timer, is a device mounted with a panel box that functions to regulate the connection of the motor dynamo with electricity for a specified duration of time.

2. Pressing regulator, which measures the amount of CPB machine pressing at the time of production. It is essential because to know the capacity of the mat when pressing.

3. Inventor, this tool is used to adjusting the number of dynamo vibrations in each minute—the amount of rotation per minute that is set ranges from 30 to 60 rpm.

4. Accelerometer application, this tool is used to record the acceleration of vibrations as a result of adjusting the amount of rotation of the dynamo used to vibrate the mat table.

2.5.   Mix design

The strength of the plan based on the ACI method with the proportion of volume = cement: fine agammaegates: stone crush ash = 1:4:4 with 0.6 water-cement ratio an average compressive strength target of CPB of 18.3 N/mm^{2 [1]}. Coarse agammaegates are taken from stone crusher processing with grain sizes from 0 to 9.5 mm. The water used is well water that is fit for drinking, and there are no additional ingredients other than those above. The size of paving is 6 × 10.5 × 21 mm, with a total of 10 pcs with one mold for a method (3) while for ways (1) and (2) once for product 1 pcs.

2.6.   Treatment of making test sample

There are several sample treatments from three compaction methods, which include:

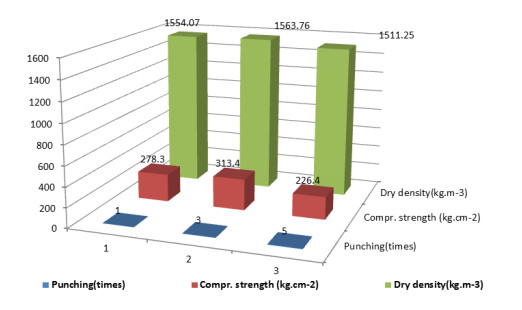
1. The first method is a conventional way, which is doing a punch with a hand beater, each of which is three times a punch, five times a punch, and seven blows.

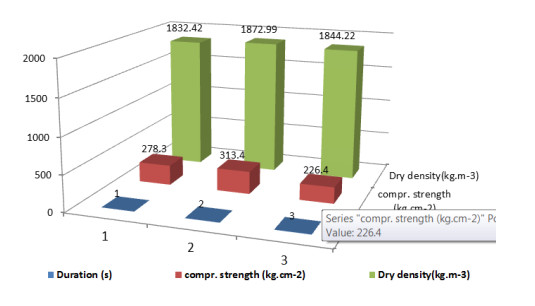
2. The second method is pressing way, which is pushing the sample with at 75 kg/cm² and the duration of press 1, 2, and 3 s, respectively.

3. The third method is vibropressing compaction, which is compaction with a combination of vibropressing on each sample in the form of vibrating acceleration, vibration duration and pressure of 75 kg/cm² at the time of production with 12 specimens for each treatment (see Table 3).

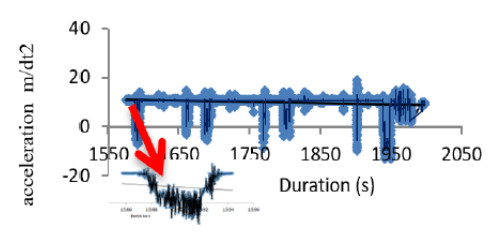
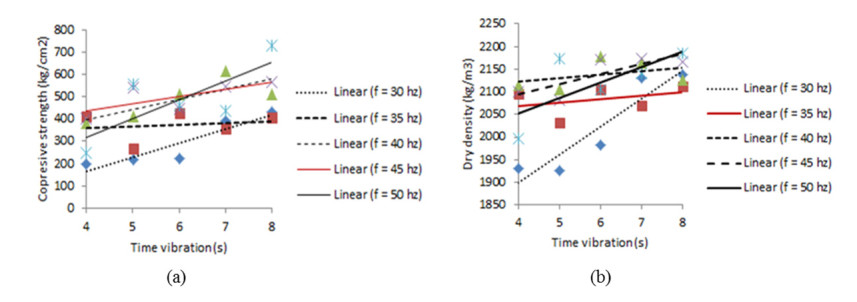
The sample treatment above accord to the capacity of the machine in producing CPB. The relationship between a device in Figure 6 to the sample treatment is a timer device (see Figure 7a) to set the time as shown in Table 3 column 4, pressing regulator (see Figure 7b) is used to set the compressive strength of the sample as listed in Table 3 column 2, inventor (see Figure 6c) to set the frequency as shown in Table 3 column 3 and accelerometer application (see Figure 6d) which is useful for recording vibrations (see Figure 8). Energy is the primary source in the process of making CPB test specimens by vibropressing. So that all activities in the CPB manufacturing process must be measured. In making CPB with vibropressing method, it is a pressing 75 kg/cm² with a frequency between 30–50 Hz and a vibrating time of 4–8 s, producing a graph of vibration acceleration between −5 to 10 m/s² (see Figure 8).

The vibration in the data recording image above is sample specimens 1–15, according to Table 3 about sample treatment, The graph gives an explanation of the CPB production of one treatment, which means that when producing is vibrated twice with the intention of the first vibrations is mixed smoothing, and the second vibration is compaction. Treatment data in Table 3 is the duration of a wave at compaction and written 4 to 8 s. After making test specimens according to the proportion and mix design of strength characteristic 300 kg/cm² at the age of 28 d, then this research carried out the process of measuring dimensions, weighing and calculating each unit of specimens and recording them in the test form (see Figure 9). The compressive strength by the following Eq 1:

where: P = compressive load (kg) and A = area of press (cm²).

3.   Results and discussions

3.1.   Effect of conventional compaction on CPB compressive strength

The blow in the conventional manufacturing process does not seem to provide significant changes, both from the compressive strength and weight of the CPB properties (see Figure 10). Because there is no preparation of granules that can fill the cavities of the agammaegates mixture, then occurs the compression of total grains only. So, optimum agammaegates compression equals the maximum compressive strength of CPB. If the compaction punch is more, there will be a decrease in compressive strength and volume weight because, in this mix design, the dimensions of 6 cm × 10 cm × 21 cm only require a maximum punch 3×. In contrast, more than that will change the composition of the agammaegate that is already solid. This compaction is identical to soil compaction at the time to get the optimum moisture content.

3.2.   Effect of pressing compaction on CPB compressive strength

For the compaction method with pressing (see Figure 11), there is a trend of increasing dry density, although not significant. At the same time, compressive strength occurs at the peak of 2 s duration and decreases after 2 s. But in general, both dry density and compressive strength in this method are relatively fixed or not much change despite the compressive time extension. As in previous studies, it has been stated that the absence of vibration in compaction causes extraordinary friction between the agammaegate grains. It cause of optimal compressive strength challenging to achieve.

3.3.   Vibropressing CPB compacting

The method of increasing compaction repetition with the same amount of energy in a manual way and pressing method does not show a significant increase in compressive strength dry density tests. They are different if repetitive compacting with higher power will increase the density compressive strength significantly. The higher the concrete density, the higher the compressive force that occurs ^[20]. Vibropressed compaction method gives treatment at 75 kg/cm² pressure. The duration of test specimens, the machine requires a range between 4–8 s because the device must produce large amounts of CPB in every second while the frequency of CPB machines uses test samples with rates ranging from 30 to 50 Hz.

At the constant pressing, the addition of the great shakes and significant frequency, there was a marked increase in compressive strength from the compressive strength of 200 to reach 600 kg/cm². So, this describes that the increase in energy has more impact when compared to the repetition of the same power. As mentioned above, the process of compaction of dry concrete approaches the similarity with the process of compaction in the soil. Optimal compaction frequency also provides uniform density distribution across layers. At higher rates, the underside of the segment is denser while the top is loosened. Avoiding loosening of the topsoil can limit the need for compaction in the upper layer ^[21]. In general, the maximum increase in compressive strength and surface hardness is when vibrations occur again at the initial setting time of 2 h. The average increase in the compressive strength of concrete with re-vibration ranges from 3.5% to 21.8% ^[22]. In other studies, also found, the optimal vibration time for standard concrete is 60 s. Longer vibration time or less than 60 seconds reduces the compressive strength. Even the compressive strength of the sample is about 36% lower, which is 240 s of vibration time than 60 s of vibration time. The need for vibration time is very dependent on the ratio W/C ratio ^[23]. Besides W/C, the rate also depends on the volume of the concrete vibration. The higher the amount of compacted concrete, the more extended the wave needed, or in other words, the higher the size, the higher the vibrational energy required (see Figure 12). The sharp effect of frequency on compressive strength and density of CPB reinforces the results of past studies that the influence of rate on compressive strength reaches 42% ^[24].

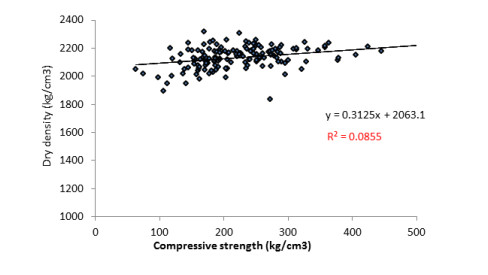
3.4.   Compressive strength vs dry density relation for vibropressing test

The relationship between compressive strength and dry density CPB is still identical to standard concrete properties. Namely, the higher the compressive strength, the higher the dry density ^[19]. But what distinguishes between concrete and CPB is the issue of compressive strength uniformity. In standard concrete has a more uniform compressive strength for each test object compared to CPB. Provisional estimates occur because of the manufacturing process and the different sample sizes of the test specimens (see Figure 13).

4.   Conclusions

The series of studies above show that compaction technology has a significant role in the compaction process and increases the compressive strength of CPB. For the manual method and the method of pressing, the compressive strength with the same composition only produces changes in the increase in compressive strength that is relatively small, with a range of 5%. Vibropressing technology provides compressive strength increases in the field of 200–300%. There are several causes which include:

● The punch and pressing method do not significantly increase the compressive strength and density of the CPB due to the position of the granules which are vulnerable to very high friction, so that even if there is an increase in the energy for the punch and pressing it cannot increase the compressive strength and density significantly.

●The vibration method reduces friction between the grains by up to 5% as mentioned in previous studies is true, so that the grain arrangement occurs entirely in the agammaegate shaking process, which makes the mixture tight and able to reduce pores in a large scale.

●Vibropressing method is the best way to get CPB with the highest strength and density.

●With pressures of 75 kg/cm², the time vibrations of 4–8 s and with a maximum frequency of 50 Hz still produces compressive strength and density whose graphics are again rising, this explains that the more frequency rate and time vibrating needed can always have the opportunity to increase the compressive strength and density up to optimal conditions.

●The nature of the compressive strength and dry density relationship is identical to standard concrete, but the uniformity of compressive strength and dry density in CPB is a big challenge in the manufacturing process. Researchers need evaluation on the process of taking sample material, the process of making samples, and the curing process on each sample.

Acknowledgments

This research project was supported by the home industry and the Structural and Construction Laboratory at The University of Jember.

Conflict of interests

This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.