In this paper, we study the existence of ground state sign-changing solutions for following p-Laplacian Kirchhoff-type problem with logarithmic nonlinearity
{−(a+b∫Ω|∇u|pdx)Δpu=|u|q−2ulnu2, x∈Ωu=0, x∈∂Ω,
where Ω⊂RN is a smooth bounded domain, a,b>0 are constant, 4≤2p<q<p∗ and N>p. By using constraint variational method, topological degree theory and the quantitative deformation lemma, we prove the existence of ground state sign-changing solutions with precisely two nodal domains.
1.
Introduction
In experiential life testing, it is preferable to stop the trial before all of the elements fail due to funding and time constraints. The observations that result from that condition are known as censored samples, and there is a variety of censoring procedures. If the test is conducted at a predefined censoring time it is called type Ⅰ (T-Ⅰ) censoring. The test is accomplished after a specified number of failures in type Ⅱ (T-Ⅱ). The hybrid censoring scheme (HCS) combines T-Ⅰ and T-Ⅱ censoring techniques with the following characteristics: In a life-testing situation, suppose there are n items that are alike. Suppose that they have independent and identical lifetime distributions. The ordered failure times of these objects will be X1:n,X2:n,...,Xn:n. The test is completed when a predetermined number of elements, 1≤r≤n, r fail, or when a predetermined duration T∈(0,∞) ends. HCS types Ⅰ and Ⅱ are the two types of hybrid censorship proposed in [1].
The T-Ⅰ HCS completes the life-testing experiment at a random time T∗1=min(xr:n,T). The T-Ⅰ HCS has the drawback of having extremely few failures until the specified time T∗1. To overcome this problem, Childs et al. [2] proposed the T-Ⅱ HCS, which guarantees an established failure rate and a completion time of T∗2=max(xr:n,T). Nevertheless, the T-Ⅱ HCS guarantees a certain number of failures, but identifying and conducting them may take some time for the life test, which is a drawback. Chandrasekar et al. [3] extended these techniques by investigating two extensions of this type, known as generalized type-Ⅰ HCS (GT-Ⅰ HCS) and generalized type-Ⅱ HCS (GT-Ⅱ HCS). Our interest here in the GT-Ⅰ HCS can be described below.
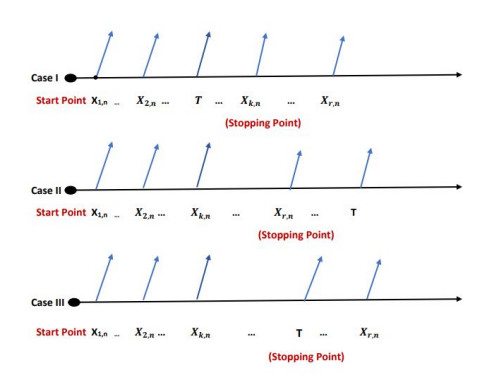
In the GT-Ⅰ HCS, one specifies k,r∈(1,2,...,n) and time (0<T<∞), where k<r. When the kth failure is observed after the time T, in this position, T∗=xk:n. When the kth failure is observed before the time T, in this situation, T∗=min(xr:n,T). Consequently, the GT-Ⅰ HCS improves the T-Ⅰ HCS by enabling the experiment to proceed after T if there have been very few failures up to that point (see Figure 1):
From Figure 1, we summarized the GT-Ⅰ HCS as follows:
Ⅰ: If x1:n<x2:n<...<T<...<xk:n, in this situation, T∗=xk:n.
Ⅱ: If x1:n<...<xk:n<...<xr:n<..<T, in this situation, T∗=xr:n.
Ⅲ: If x1:n<...<xk:n<...<T<...<xr:n, in this situation, T∗=T.
Assume that X is a non-negative random variable with the probability density function (pdf) f(x). Shannon [4] defined entropy as follows to measure the uncertainty contained in X:
where f(x) is the pdf of a random variable X. Estimation studies for Shannon entropy with various censoring and distribution strategies can be found in [5,6,7,8]. Ahmadini et al. [9] examined a Bayesian estimate (BE) of dynamic cumulative residual entropy based on the Pareto Ⅱ distribution. Dynamic cumulative residual Renyi entropy estimators for Lomax distribution were considered in [10]. References [11,12] used the record value data to investigate a Bayesian entropy estimator for Lomax and generalized inverse exponential distributions, respectively. Almarashi et al. [13] looked at the Bayesian estimator of dynamic cumulative residual entropy for the Lindley distribution. Hassan et al. [14] studied the statistical inference of information measures for a power-function model in the presence of outliers. Helmy et al. [15] proposed Shannon entropy for the Lomax model in the context of unified hybrid censored samples. In the paper by Hassan et al. [16], estimation of differential entropy for Pareto distribution in the presence of outliers was considered. The logical entropy was suggested in [17] as a new information measure. Ellerman [17] also defined logical mutual information and logical conditional entropy and discussed the relation of logical entropy to Shannon's entropy. For more details about logical entropy and its application to quantum states and fuzzy probability spaces see [17,18,19].
Despite Shannon's entropy's enormous success, it has certain flaws and might not always be appropriate. Extropy, a different measure of uncertainty that expands on Shannon's entropy, has been suggested as a way to fix these flaws. In the paper by Lad et al. [20], extropy was discussed as an alternate measure of uncertainty and as the complementary dual of entropy. The extropy is provided via
The scoring of forecasting distributions is one statistical application of extropy. A forecasting distribution's predicted score, for example, is equal to the negative sum of its entropy and extropy under the total log scoring rule [21]. Extropy has been widely studied in commercial and scientific fields, such as astronomical studies of heat distributions in galaxies [22]. Qiu [23] investigated some characterization results, monotone qualities, lower bounds of extropy of order statistics and record values. Residual extropy was introduced in [24] to assess the residual uncertainty of a non-negative random variable, as follows:
where ¯F(.) is the survival function. Since 2015, important properties of the extropy measure have been studied in the literature. References [23,24], for example, looked at qualities such as residual extropy, ordered statistics extropy and record value extropy. Raqab and Qiu [25] recently investigated several properties of the extropy measure under ranked set sampling. In contrast, some authors have lately studied the problem of estimating extropy depending on a complete sample [26]. Based on progressive T-Ⅱ censoring, Hazeb et al. [27] investigated non-parametric estimation of the extropy and entropy measures. Hassan et al. [28] discussed estimating the extropy and cumulative residual extropy of the Pareto distribution in the presence of outliers.
The most often used model for examining skewed data and hydrological processes is the gamma distribution. The exponentiated gamma distribution (EGD) is one of the crucial families of distributions in lifetime testing. Both monotonic and nonmonotonic failure rates may be accommodated by this model thanks to its adaptability. On the other hand, the idea of extropy has found use in a variety of domains. It should be emphasized that the literature has paid little attention to the parametric estimation problem of extropy and associated residuals. To the best of the authors' knowledge, and considering the significance of the EGD and extropy measures, the Bayesian and non-Bayesian estimators of these measures are not presented. Additionally, this issue becomes quite significant when the data are censored. In the current study, we use the GT-Ⅰ HCS, which is an approach that improves the T-Ⅰ HCS. Therefore, the main motivation behind this may be summarized as follows:
● Extropy and residual extropy of the EGD are examined using the maximum likelihood (ML) and Bayesian estimation methods.
● The Bayesian estimators for the extropy and residual extropy measures are created using some balanced loss functions (BLOFs).
● Lindley's approximation is used to calculate the Bayesian estimators of extropy and residual extropy under a BLOF.
● Both the simulation problem and application to actual data are discussed.
The rest of the paper is organized as follows. The extropy and residual extropy expressions of the EGD are developed in Section 2. The ML estimators of extropy and residual extropy based on the GT-Ⅰ HCS are discussed in Section 3. The Lindley method for calculating Bayesian estimators of extropy measures under different BLOFs is discussed in Section 4. The simulation issue and its application to real data are analyzed in Sections 5 and 6 respectively. Eventually, we conclude the paper in Section 7.
2.
The EGD
A number of distributions have been proposed for monotonic failure rates, but the Weibull and gamma distributions are the most commonly employed. The survival function of the gamma distribution cannot be written in nice closed forms, which makes it difficult to make further mathematical modifications. For such a distribution, the survival and hazard functions are often computed numerically. This is one of the main reasons why the gamma distribution is less popular than the Weibull distribution. Although the Weibull distribution offers a good closed form for the hazard and survival functions, it does have some disadvantages. The EGD was investigated in [29] as an alternative to gamma and Weibull distributions, which has a cumulative distribution function (cdf) F(x) and pdf f(x) of the following respective forms:
and
where ξ is the shape parameter and γ is the scale parameter. The EGD has received a lot of attention. Shawky and Bakoban [30] offered Bayesian and non-Bayesian estimators for this distribution's parameters and some features for the EGD under record values. Shawky and Bakoban [31] also reported inference on this model's order statistics and developed improved goodness-of-fit tests for the EGD. Feroze and Aslam [32] introduced Bayesian analysis of the EGD for T-Ⅱ censored samples. Singh et al. [33] investigated Bayesian estimation of the EGD under progressive T-Ⅱ censoring by utilizing various approximation techniques. Mahmoud et al. [34,35] studied Bayesian estimation and prediction of the EGD under the unified hyper-censoring scheme.
Substituting Eq (2.2) into Eq (1.2) will give the extropy of the EGD:
from the binomial theorem,
then, Eq (2.3) becomes
then,
To find the residual extropy of the EGD, substituting Eq (2.2) into Eq (1.3), we get
and
Employing the binomial theory more than one time, we get
where ∫∞tx2+ve−(2+j)γxdx is the upper incomplete gamma function and is provided via Γ(v+3,tγ(2+j))(2γ+jγ)v+3; then,
and the residual extropy of the EGD is calculated below:
It can be noted that Eqs (2.5) and (2.10) are each a function of parameters ξ and γ, which constitute the needed formulations of ψ(x) and ψt(x) of the EGD.
3.
ML estimation
Here, the ML estimators for the GED are provided via the GT-Ⅰ HCS. Assume that, in a life-testing study, there are n similar elements; let X1:n,X2:n,...,Xn:n indicate the sorted failure times for these elements, with fixed values of r,k∈1,2,...,n, k<r<n and time T∈(0,∞). The likelihood function of ξ and γ is given by
where D is the experiment's total number of failures until time c, and its values are represented by
where d denotes the number of failures that occurred until time T. Substituting Eqs (2.1) and (2.2) into Eq (3.1), we get
where xi is written instead of xi:n for simplified form. Taking the two sides' logarithms, say, l, we get
If we take derivatives of Eq (3.4) with regard to ξ and γ, we can obtain
and
Set Eqs (3.5) and (3.6) equal to zero and solve them to determine the ML estimator of ξ and γ:
and
The explicit forms for these equations seem to be quite difficult to get; thus, we may use an appropriate numerical approach to obtain these estimators. Then, the ML estimators of ψ(x), ψt(x), say, ˆψ(x),ˆψt(x), are respectively as follows:
and
4.
Bayesian estimation
Using different types of BLOFs, we can find Bayesian estimators for ξ, γ, ψ(x) and ψt(x). We assume that ξ and γ are distributed separately as gamma (a1,b1) and gamma (a2,b2) priors, respectively, since the gamma distribution is utilized as a conjugate prior for some distributions and, at the same time, it is a conjugate prior for the EGD (see [32]). Then, the prior of ξ and γ is given by
and,
where a1,a2,b1 and b2>0 are considered to be constant and known hyperparameters. The joint prior density of ξ and γ is calculated as follows:
The posterior distribution is calculated as follows:
The joint posterior density function is calculated from Eqs (3.3) and (4.1) as follows:
E1 is the normalizing constant, which is equal to
4.1. BLOF
BLOFs are interesting because they include the proximity of a specified estimator δ to both a target estimator δo and the unknown parameter θ that has been estimated, as stated by Zellner's formula (see [36]):
where 0≤ω≤1, ρ(θ,δ) is any loss function that can be used, ρ(δ,δo) is an unbalanced loss function for the likelihood function and δo is a chosen θ prior estimator.
Given the balanced squared error (BSEL) loss function ρ(θ,δ)=(δ−θ)2, then Eq (4.5) becomes
In this situation, the BE of θ is given by
where θ=(ξ,γ,ψ(x) and ψt(x)). Hence,
If we choose
where q≠0, we get the balanced linear exponential (BLN) loss function, and the BE of θ in this situation is
If we choose
when q≠0, we can get the balanced general entropy (BGE) loss function, and the BE of θ in this situation is
From Eqs (4.7)–(4.9), it should be observed that all Bayesian estimators are expressed as a ratio of two integrals, which cannot be simplified or directly computed. As a result, we compute the estimates using the Lindley method.
4.2. Lindley method
Lindley [37] proposed this method to approximate the ratio of two integrals, which approaches the ratio of the integrals as a whole and yields a single numerical value. The approximate BEs of ξ,γ,ψ(x) and ψt(x) are computed using the Lindley method in this subsection. The Lindley method can be expressed in general cases as follows:
where (i,j,k,l)=1,2,...,m and ˆξ and ˆγ are the ML estimators of ξ and γ, respectively.
Also, ui(ξ)=∂u∂ξ; uij(ξ,γ)=∂2u∂ξ∂γ; lijk(ξ,γ,γ)=∂3u(ξ,γ)∂ξ∂γ∂γ;
ρ=logπ(ξ,γ) is the logarithm of the joint prior density function ρj(ξ,γ)=∂ρ∂γ;
(σij)N×N=−(∂2l∂ξ∂γ)−1, where l is the likelihood function. Note that σij=(i,j)th elements of the Fisher information matrix −(∂2l∂ξ∂γ)−1.
For the two-parameter case, the Lindley method is given by
where, u1=∂u∂ξ; u12=∂2u∂ξ∂γ; l122=∂3u∂ξ∂γ∂γ; ρ2=∂ρ∂γ; σ12 is the (1,2)th element of the inverse of the Fisher information matrix. The details and derivative can be found in Appendix A.
5.
Numerical outcomes
In this part, we look into the efficiency of the ML estimates (MLEs) and BEs of ξ, γ, ψ(x) and ψt(x) for the EGD in terms of the mean squared error (MSE) under different BLOFs.
● For given hyperparameters a1,b1,a2 and b2, generate random values of ξ and γ.
● Making use of ξ and γ obtained in the previous step, we generate a sample of upper-ordered values from an EGD of size n.
● The MLE of ξ,γ,ψ(x) and ψt(x) has been computed for different values of r, k and T, according to Section 3.
● The BE of ξ,γ,ψ(x) and ψt(x), based on the BSEL, BLN, and BGE loss functions using the Lindley method, has been provided, respectively, for different values of r, k and T, according to Section 4.
● The MSE over N samples is provided by Eq (5.1), if ˆθ is an estimate of θ.
where ˆθ=(ˆξ,ˆγ,ˆψ(x) and ^ψt(x)).
● The steps that came before are repeated N=1000 times to generate a sample from the EGD with the hyperparameters (a1=2,b1=4,a2=1.5), ω=0.5 and t=0.4.
● The shape parameter q is selected as q=(−0.6,0.6), and the performance of the BLN and BGE loss functions varies depending on the value of q.
● The true selected values of the parameters are ξ=0.7 and γ=2.3, and the true values of ψ(x)=−0.283279 and ψt(x)=−0.274054.
● The MLEs and BEs of ξ,γ, ψ(x) and ψt(x) were studied under the following conditions:
1- Values of n,r,k are taken as (n=250,r=230,k=150) and (n=150,r=120,k=80) at different values of T, where T=(0.8,1.5,3) (see Table 1).
2- Values of n,r,T are taken as (n=150,r=120,T=3) at different values of k, where k=(60,80,100) (see Table 2).
3- Values of n,r,T are taken as (n=250,r=230,T=3) at different values of k, where k=(150,180,210) (see Table 2).
4- Values of n,k,T are taken as (n=150,k=80,T=3) for different values of r, where r=(90,110,130) (see Table 3).
5- Values of n,k,T are taken as (n=250,k=100,T=3) for different values of r, where r=(150,180,230) (see Table 3).
6- The simulation results are listed in Tables 1–3 and illustrated in Figures 2–7.
Here are some observations on the MLEs and BEs of the extropy and residual extropy results displayed in Tables 1–3.
● The MSEs of the MLEs and BEs decrease when n increases.
● MSEs of the MLEs and BEs of extropy and residual extropy decrease as r increases with fixed n,k,T (Figures 2 and 3).
● The BE of ψBLN(x) at q=−0.6 and ψ(t)BLN at q=0.6 is favored over the others in terms of having the lowest MSE for different values of T, resulting in reduced variability.
● MSEs of the MLEs and BEs of extropy and residual extropy decrease as k increases with fixed n,r,T (Figures 4 and 5).
● The MSE values show that, in most cases, the BEs of extropy are best under the BGE loss function, whereas the BEs of residual extropy are best under the BLN loss function.
● The BEs of extropy increase by increasing the number of failures r or k. Additionally, as demonstrated in Figures 6 and 7, the BEs of residual extropy decrease as the number of failures r or k increases.
● The BE of extropy and its residual yields a smaller value than the MLE.
● The BEs of ψ(x) and ψt(x), viz., the BLN loss function at q=0.6, have a lot of information and the BEs using the BGE loss function at q=−0.6 have a lot of information since they have a low level of uncertainty.
6.
Analysis of data
These data were used in [38], and they represented the daily average wind speeds from January 1,2009 to October 4,2009 for Cairo city. The National Climatic Data Center in Asheville, NC, United States of America produced this information and recorded it as follows:
The Kolmogorov-Smirnov (K-S) test was used to determine if the data distribution is an EGD or not. The calculated value of the K-S distance is 0.0808528, and the P-value is 0.504649. Figure 8 shows the estimated pdf and cdf.
Now, let us examine what occurs if the data set is censored. Using the uncensored data set, we produce three artificial GT-Ⅰ HCS sets in the ways described below (see Table 4):
Case Ⅰ: T=9,k=85,r=95; therefore, D=85,c=xk=10.
Case Ⅱ: T=13,k=85,r=95; therefore, D=95,c=xr=12.5.
Case Ⅲ: T=11,k=85,r=95; therefore, D=92,c=T=11.
We employed ML and Bayesian estimation of extropy and residual extropy in these cases. Using BLOFs (BSEL, BLN, BGE) with ω=0.5 and q=(−0.6,0.6), we employed the Lindley method. We employed a non-informative prior to calculate the BEs because we have no knowledge of the priors; thus, we chose a1=0,b1=0,a2=0 and b2=0.
We note from the study of this application that the BE of extropy and its residual yields a smaller value than the MLE. The BE of extropy and its residual via BLN and BGE loss functions at q=0.6 takes a large value compared to their values at q=−0.6. Finally, we reach the conclusion that the simulated research is supported by real data.
7.
Conclusions
We have investigated extropy as a supplementary dual of entropy and an alternative measure of uncertainty in this paper, as well as investigating residual extropy as a measure of residual uncertainty of a non-negative random variable for the EGD. The maximum likelihood and Bayesian estimation of the parameters, extropy and residual extropy for the EGD under the GT-Ⅰ HCS are discussed in this paper. The BE of extropy and residual extropy for the EGD is derived based on BLOFs (BSEL, BLN, BGE). In terms of their MSE, the Lindley method is used to determine the BEs of extropy and residual extropy with BSEL, BLN, and BGE loss functions. Application to real-world data is available.
In general, the MSE values decrease as the number of failures rises, according to the results of the study. When compared to different estimates, the BE of residual extropy under the BLN loss function performed well, and the extropy under the BGE loss function performed well in the majority of situations. By increasing the number of failures r or k, the BEs of extropy are raised. Additionally, increasing the number of failures r or k decreases the BEs of residual extropy. From the application result for a positive value of q, the BE values for extropy and its residual using the BLN and BGE loss functions are larger than the opposite for a negative value of q. Finally, we have highlighted that data outputs and simulations are significant.
Use of AI tools declaration
The authors declare that they have not used artificial intelligence tools in the creation of this article.
Acknowledgments
This research work was funded by Institutional Fund Projects under grant no. (IFPIP: 549-150-1443). The authors gratefully acknowledge the technical and financial support provided by the Ministry of Education and King Abdulaziz University, DSR, Jeddah, Saudi Arabia.
Conflict of interest
The authors declare no conflict of interest.
Appendix A
The Fisher information matrix is presented here as follows:
(σij)N×N=−(∂2l∂ξ∂γ)−1, where l is the likelihood function and this matrix is given by
using Eqs (3.5) and (3.6), we have
and









 DownLoad:
DownLoad:










