A new computational for approximate analytical solutions of nonlinear time-fractional wave-like equations with variable coefficients

1.   Introduction

Fractional calculus is a branch of mathematical analysis, which studies the generalization of integrals and derivatives of integer order to arbitrary order, that can be real or complex. In recent years, many scientists and researchers have been interested in the topic of fractional calculus because of its several applications in many fields, such as physics, chemistry, engineering, and so on. See for example ^{[9,10,11,19,23,24,25]}.

Theory and applications of nonlinear fractional partial differential equations (NFPDEs) play an important role in the various fields of engineering and science, including fluid flow, diffusion, viscoelasticity, quantum mechanics, electromagnetic, electrochemistry, biological population models and other applications. The exact solutions of NFPDEs are sometimes too complicated to be attained by conventional techniques due to the computational complexities of nonlinear parts involving them. Therefore, to search of solutions for NFPDEs there are variety of numerical and analytical methods found in literature, among them: Adomian decomposition method (ADM) ^[22] variational iteration method (VIM) ^[6], new iterative method (NIM) ^[12], reduced differential transform method (RDTM) ^[2], homotopy analysis method (HAM) ^[3], homotopy perturbation method (HPM) ^[8]. The residual power series method (RPSM), that was first proposed by Omar Abu Arqub ^[1], is implemented to obtaine analytic approximate solutions of fractional partial differential equations and convergence of RPSM for these equations is considered ^[5,7,17,21].

The main aim of this paper is to apply the fractional residual power series method (FRPSM) to find approximate analytical solutions of nonlinear time-fractional wave-like equations with variable coefficients in the form

with the initial conditions

where $D_{t}^{2\alpha } = D_{t}^{\alpha }D_{t}^{\alpha }$ is the Caputo time-fractional derivative operator of order $2\alpha,$ $\frac{1}{2} < \alpha \leq 1,$ $u = \left\{ u(X, t), X = (x_{1}, x_{2}, ..., x_{N})\in \mathbb{R}^{N}, t\geq 0, N\in \mathbb{N}^{\ast }\right\},$ $F_{1ij}, G_{1i}$ $i, j\in \left\{1, 2, ..., N\right\}$ are nonlinear functions of $X, t$ and $u,$ $F_{2ij}, G_{2i}$ $i, j\in \left\{ 1, 2, ..., N\right\}$ are nonlinear functions of derivatives of $u$ with respect to $x_{i}$ and $x_{j}$ $i, j\in \left\{1, 2, ..., N\right\},$ respectively. Also $H, S$ are nonlinear functions and $k, m, p$ are integers. When $\alpha = 1$, the equation (1.1) reduces to the classical wave-like equations with variable coefficients.

Recently, we have used many numerical techniques to solve this kind of equations, where the Caputo time-fractional derivative operator is $D_{t}^{\alpha }, 1 < \alpha \leq 2$. Note that, the solution of Eqs. (1.1)-(1.2) obtained by the FRPSM is quite different from the solutions found in ^{[12,13,14,15]}.

The rest of the paper is structured as follows: In Section 2, we present basic definitions and properties of fractional calculus theory and fractional power series. In Section 3, we introduce our results of fractional residual power series method (FRPSM) for the nonlinear time-fractional wave-like equations (1.1) with the initial conditions (1.2). In Section 4, we propose three numerical examples in order to show the validity and effectiveness of this approach. In Section 5, we discuss our obtained results represented by figures and table. Finally, conclusions are drawn in the last section.

2.   Basic definitions of fractional calculus theory

In this section, we give the necessary notations and basic definitions and properties of fractional calculus theory, which are used further in this paper. For more details, see ^[16,18,20].

Definition 2.1. A real function $u(X, t), X\in \mathbb{R}^{N}, N\in \mathbb{N}^{\ast }, t\in \mathbb{R}^{+}$, is considered to be in the space $C_{\mu }(\mathbb{R}^{N}\times \mathbb{R}^{+}),$ $\mu \in$ $\mathbb{R},$ if there exists a real number $p > \mu,$ so that $u(X, t) = t^{p}v(X, t)$, where $v$ $\in C\left(\mathbb{R}^{N}\times \mathbb{R}^{+}\right)$, and it is said to be in the space $C_{\mu }^{n}$ if $u^{\left(n\right) }\in C_{\mu }(\mathbb{R}^{N}\times \mathbb{R}^{+}), n\in \mathbb{N}.$

Definition 2.2. The Riemann-Liouville fractional integral operator of order $\alpha > 0$ of $u\in C_{\mu }(\mathbb{R}^{N}\times \mathbb{R}^{+}), \mu \geq -1$, is defined as follows

Definition 2.3. The Caputo time-fractional derivative operator of order $\alpha > 0$ of $\ u\in C_{-1}^{n}(\mathbb{R}^{N}\times \mathbb{R}^{+}), n\in \mathbb{N},$ is defined as follows

The following are the basic properties of the Caputo time-fractional derivative operator which we will need here.

Let $n-1 < \alpha \leq n$ and $\beta \geq -1.$ Then

$(1)$

$(2)$

For the Riemann-Liouville fractional integral and Caputo time-fractional derivative, we have the following relation

Now, we introduce some definitions and theorems related to the fractional power series (FPS) which are used in this paper. For more details, see ^[4].

Definition 2.4. A power series of the form

where $m-1 < \alpha \leq m$ and $t\geq t_{0}\;$is called the multiple fractional power series (MFPS) about $t_{0}$, where $t$ is a variable and $c_{n}(X)$ are constants called the coefficients of the series.

Theorem 2.1. Suppose that $u(X, t)$ has a MFPS representation at $t = t_{0}$ of the form

and $R$ is the radius of convergence of the MFPS.

If $u\in C\left(\mathbb{R}^{N}\mathbb{\times }\left[t_{0}, t_{0}+R\right) \right)$ and $D_{t}^{n\alpha }u\in C\left(\mathbb{R}^{N}\mathbb{\times }\left(t_{0}, t_{0}+R\right) \right)$ for $n = 0, 1, 2, ...,$ then the coefficients $C_{n}(X)$ will take the form of

where $D_{t}^{n\alpha } = D_{t}^{\alpha }.D_{t}^{\alpha }.....D_{t}^{\alpha }$ ($n$-times).

3.   FRPSM for time-fractional wave-like equations

Theorem 3.1. Consider the nonlinear time-fractional wave-like equations (1.1) with the initial conditions (1.2). Then, the solution of Eqs. (1.1)-(1.2) is given in the form of infinite series which converges rapidly to the exact solution as follows

where $f_{n}(X)$ are the coefficients of the series have been constructed by FRPSM and $R$ is the radius of convergence.

Proof. We consider the following nonlinear time-fractional wave-like equations (1.1) with the initial conditions (1.2).

First we define

Eq. (1.1) is written in the form

The FRPSM assumes the solution for Eq. (3.1) as a multiple fractional power series about the initial point $t = 0$, as follows

where $R$ is the radius of convergence of the MFPS.

In the next step, the $k^{th}$ truncated series of $u(X, t)$ that is $u_{k}(X, t)$ can be written as

Since the initial conditions in Eq. (1.2). Then, the approximate solution to (3.1) can be written in the form of

where $f_{0}(X)+f_{1}(X)\frac{t^{\alpha }}{\Gamma (\alpha +1)}$ is considered to be the $1^{st}$ FRPS approximate solution of $u(X, t).$

Then $u_{k}(X, t)$ could be reformulated as

Now, we define the residual function as

and the $k^{th}$ truncated residual function as

It is clear that Res$(X, t) = 0$ and $\underset{k\longrightarrow \infty }{\lim}$Res$_{k}(X, t) =$Res$(X, t)$ for each $X\in \mathbb{R}^{N}$ and $t\geq 0.$ In fact this lead to $D_{t}^{(n-2)\alpha }$Res$(X, t) = 0$ for $n = 2, 3, 4, ..., k$ because the fractional derivative of a constant is zero in the Caputo sense. Also, the fractional derivative $D_{t}^{(n-2)\alpha }$ of Res$(X, t)$ and Res$_{k}(X, t)$ are matching at $t = 0$ for each $n = 2, 3, 4, ..., k,$ that is,

To clarify the FRPS technique, we substitute the $k^{th}$ truncated series of $u(X, t)$ into Eq. (3.6), find the fractional derivative formula $D_{t}^{(n-2)\alpha }$ of Res$_{k}(X, t)$ and then, we solve the obtained algebraic (3.7), to get the required coefficients $f_{n}(X), n = 2, 3, 4, ...$in Eq. (3.4). Thus the $u_{k}(X, t)$ approximate solutions can be obtained respectively.

4.   Numerical examples

In this section, we describe the method explained in the Section 3. Three numerical examples of nonlinear time-fractional wave-like equations with variable coefficients are considered to validate the capability, reliability and efficiency of FRPSM.

Example 4.1. Consider the 2-dimensional nonlinear time-fractional wave-like equation with variable coefficients

with the initial conditions

where $D_{t}^{2\alpha }$ is the Caputo fractional derivative operator of order $2\alpha,$ $u$ is a function of $x, y, t\in \mathbb{R}\times \mathbb{R\times R}^{+}.$

For $\alpha = 1,$ the exact solution of Eqs. (4.1)-(4.2) is given by ^[14]

According to FRPSM described in Section 3, by applying on the Eqs. (4.1)-(4.2), we have

First, the $1^{st}$ FRPS approximate solution of $u(x, y, t)$ is

Secondly, construct the $k^{th}$ truncated series and $k^{th}$ residual function of Eqs. (4.1)-(4.2) as follow

By (3.7), we have

Taking $k = 2$ in (4.6), we obtain

Then, the $2^{nd}$ truncated approximate solution will be

In a similar way, taking $k = 3, 4, 5$ in (4.6), we have

Then the $5^{th}$ order truncated approximate solution of Eqs. (4.1)-(4.2) can be obtained as follows

Following the same step, then the solution of Eqs. (4.1)-(4.2) can be expressed by

When $\alpha = 1$, the exact solution is

Remark 4.1. Comparing our obtained result (4.7) with the results in ^{[12,13,14,15]}, it can be seen that the result is new.

Example 4.2. Consider the following nonlinear time-fractional wave-like equation with variable coefficients

with the initial conditions

where $D_{t}^{2\alpha }$is the Caputo fractional derivative operator of order $2\alpha,$ and $u$ is a function of $x, t\in \left] 0, 1\right[\times \mathbb{R}^{+}.$

For $\alpha = 1,$ the exact solution of Eqs. (4.8)-(4.9) is given by ^[14]

According to FRPSM described in Section 3, by applying on the Eqs. (4.8)-(4.9), we have

First, the $1^{st}$ FRPS approximate solution of $u(x, t)$ is

Secondly, construct the $k^{th}$ truncated series and $k^{th}$ residual function of Eqs. (4.8)-(4.9) as follow

By (3.7), we have

Taking $k = 2$ in (4.13), we obtain

Then the $2^{nd}$ truncated approximate solution will be

In a similar way, taking $k = 3, 4, 5$ in (4.13), we have

Then the $5^{th}$ order truncated approximate solution of Eqs. (4.8)-(4.9) can be obtained as follows:

Following the same step, then the solution of Eqs. (4.8)-(4.9) can be expressed by

When $\alpha = 1$, the exact solution is

Remark 4.2. Comparing our obtained result (4.14) with the results in ^{[12,13,14,15]}, it can be seen that the result is new.

Example 4.3 Consider the following one dimensional nonlinear time-fractional wave-like equation with variable coefficients

with the initial conditions

where $D_{t}^{2\alpha }$is the Caputo fractional derivative operator oforder $2\alpha,$ and $u$ is a function of $x, t\in \left] 0, 1\right[\times \mathbb{R}^{+}.$

For $\alpha = 1,$ the exact solution of Eqs. (4.15)-(4.16) is given by ^[14]

According to FRPSM described in Section 3, by applying on the Eqs. (4.15)-(4.16), we have

First, the $1^{st}$ FRPS approximate solution of $u(x, t)$ is

Secondly, construct the $k^{th}$ truncated series and $k^{th}$ residual function of Eqs. (4.15)-(4.16) as follow

By (3.7), we have

Taking $k = 2$ in (4.18), we obtain

Then the $2^{nd}$ truncated approximate solution will be

In a similar way, taking $k = 3, 4, 5$ in (4.20), we have

Then the $5^{th}$ order truncated approximate solution of Eqs. (4.15)-(4.16) can be obtained as follows:

Following the same step, then the solution of Eqs. (4.15)-(4.16) can be expressed by

When $\alpha = 1$, the exact solution is

Remark 4.3. Comparing our obtained result (4.21) with the results in ^{[12,13,14,15]}, it can be seen that the result is new.

5.   Numerical results and discussion

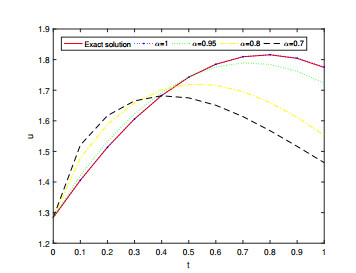
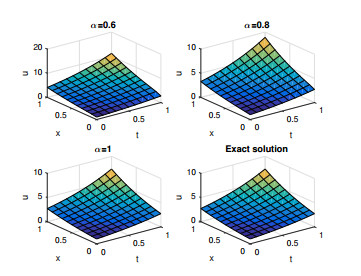
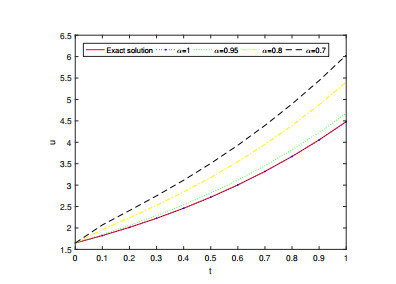
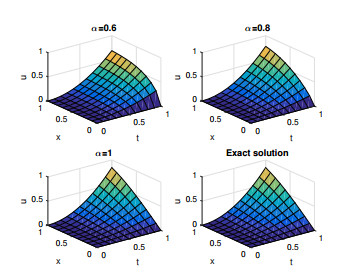
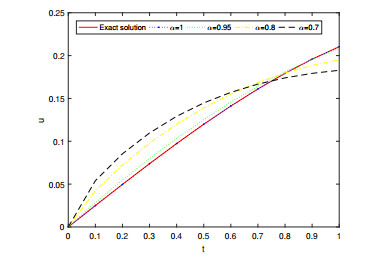
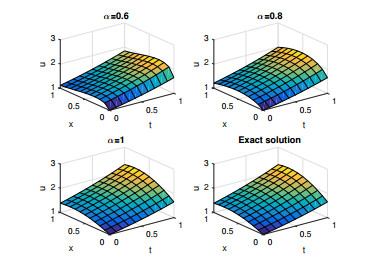
In this section, we discuss and evaluate the numerical results of the approximate solutions for Examples 4.1, 4.2 and 4.3 respectively. Figures 1, 3 and 5 represents the surface graph of the $5^{th}$ FRPSM approximate solution at $\alpha = 0.6, 0.8, 1$ and the exact solution. Figures 2, 4 and 6 represents the behavior of the $5^{th}$ FRPSM approximate solution at $\alpha = 0.7, 0.8, 0.95, 1$ and the exact solution. These figures afirm that when the order of the fractional derivative $\alpha$ approaches $1$, the approximate solutions obtained by FRPSM approach the exact solutions.

Tables 1–3 represents the numerical values of the $5^{th}$ FRPSM approximate solution for different values of $\alpha$ and the exact solution. These tables clarifies the convergence of the approximate solutions to the exact solutions.

6.   Conclusion

In this paper, fractional residual power series method (FRPSM) is successfully applied to find approximate analytical solutions of time-fractional wave-like equations with variables coefficients. This method was tested on three numerical examples. Numerical results obtained confirm the easily, accurately and efficiency of the proposed method. The advantage of the FRPSM is that it reduces significantly the numerical computations to find approximate analytical solutions for this type of equations compared to current methods such as the perturbation technique, differential transform method (DTM) and Adomian decomposition method (ADM), thus, we can conclude that, the FRPSM is simple, effective, and practically method for solving many other nonlinear fractional partial differential equations.

Acknowledgments

The authors are thankful to a Professor Hamouche Zakia and to the anonymous referees for their careful checking of the details and for their valuable suggestions and comments which cause substantial improvements in the paper.