A conservative semi-Lagrangian finite difference WENO scheme based on exponential integrator for one-dimensional scalar nonlinear hyperbolic equations

1.   Introduction

In this paper, we are interested in semi-Lagrangian (SL) finite difference (FD) schemes for solving nonlinear hyperbolic conservation laws (HCL)

The SL scheme updates the solution by following the characteristics, either forwardly [10,25], or backwardly [19,14], where for (1) the characteristic equation is defined as

The classical backward SL scheme traces the characteristics back to a previous time level and then updates the solution with interpolation, or polynomial reconstruction. Based on its solution space, there are SL FD schemes [26,29], SL finite volume (FV) schemes [9,12], SL spectral element methods [32,13], SL discontinuous Galerkin (DG) finite element methods [23,3], SL particle methods [8], etc.

For SL schemes, mass conservation is an important property for certain applications, such as in kinetic simulations [9,2], weather forecasting [27,15], fluid dynamics [29,12], etc. For finite volume schemes and finite element methods, it is more natural to enforce the discrete mass conservation, by working with the integral form for finite volume schemes [12], or the weak form for finite element methods [2]. For finite difference schemes, it is much more challenging [18]. A conservative SL finite difference scheme based on the flux difference form was proposed in [21]. A maximum principle preserving limiter was applied to ensure the $L_\infty$ stability in [29]. However, the method in [21] only considers the linear or quasilinear advection equation with $f(u) = a(x,t)\,u$ in (1), where $a(x,t)$ is a known function. The extension to high dimensional problems is from Strang splitting. This method has later been generalized to nonlinear hyperbolic problems with the idea from an Eulerian-Lagrangian scheme [16]. On the other hand, a multi-dimensional SLFD scheme without dimensional splitting has been developed based on a predictor-corrector approach [20], and applied to the kinetic Vlasov-Poisson equation. It was later been generalized to the incompressible flow and Guiding-center model problems [30]. Here the predictor-corrector repeatedly utilizes the material derivatives and replaces time derivatives by spatial derivatives from the equation, in a similar idea of a Lax-Wendroff approach. A high order approximation of the characteristic equation is built upon low order predictions of its solution. A conservative correction of the scheme was proposed in [31], which is still based on the flux difference form, and the temporal integrals of the numerical fluxes are approximated by numerical quadrature rules. The scheme has also been used to solve the BGK model of the Boltzmann equation [1]. However, since it traces numerical quadrature points along the temporal integration, the fully discrete conservative scheme in [31,1] will subject to time step restrictions, which has been analyzed by Fourier analysis in [31].

For SLFD schemes solving nonlinear hyperbolic problems, the main difficulty lies on the characteristic speed depending on the unknown solution, such as in (2), especially for high dimensional problems. Except the predictor-corrector approach in [20], there are also some other methods proposed to achieve high order in time. One is the class of multi-step schemes based on backward differential formulas (BDF), such as the Adams-Moulton and Adams-Bashforth schemes [14]. Another is based on commutator-free Runge-Kutta exponential integrators (RKEI) [5,6]. However, both methods in literature do not have mass conservation. In this paper, we will adopt the RKEI method and combine it with the SLFD scheme in [21] to develop conservative SLFD-RKEI schemes for solving the nonlinear hyperbolic problems. The RKEI method has also recently been coupled with SLDG scheme for solving the Vlasov equations [2].

The RKEI method was first proposed in [7], which is designed for nonlinear ordinary differential equations (ODEs). The idea is to mimic the exponential solution for linear ODEs, and write the nonlinear function as a coefficient multiplying the unknown solution. Then the coefficient is frozen at previous given time levels, so that the resulting ODE have explicit exponential solutions. Later, the RKEI method was realized to be equivalent to the semi-Lagrangian scheme for partial differential equations (PDEs) [5,6]. In this paper, we propose to combine it with the conservative SLFD scheme [21] under the flux difference form. However, different from [31], the temporal integral is transferred to a spatial integral at the previous time level with know solutions, owing to the divergence theorem. WENO interpolations and numerical flux reconstructions [21] are used to ensure essentially non-oscillatory properties. Other methods, such as Hermite WENO schemes (HWENO) [4] may also be applied. However, we would emphasize that in order to achieve large time step condition, we have to combine the WENO interpolation and flux reconstruction, so that the common integration in the left and right fluxes can be canceled exactly [21,18]. This cancellation typically due to the fact, for the one-dimensional problem the spatial integrals in the reconstructions of the left and right fluxes are along the same line (only one dimension). This is not the case for two and higher dimensions. The extension to high dimensional problems is not straightforward. Although dimensional splittings can still be used, they suffer from low order splitting errors and we do not pursue them here.

The rest of the paper is organized as follows. In Section 2, the model equation will be described. The SLFD scheme in [21] and the RKEI method [7] will first be recalled in Section 3, after that conservative SLFD schemes for solving (1) will be presented. In Section 4, numerical experiments will be performed to demonstrate the effectiveness of our proposed methods. Conclusion remarks will be made in Section 5.

2.   Model equation

We start with the hyperbolic equations in the advective form,

where $u = u(x,t)$ and $V(u)(x,t)$ is the advection speed which may depend on the unknown $u$. The solution of (3) propagates along characteristics, which can be defined as

When $V$ does not depend on the unknown $u$, namely, in the linear or quasilinear form, the characteristics of (4) are given and can be computed a prior, so that the solution of (3) can be determined from the characteristics by tracing it back to its initial or boundary values. However, when $V$ does depend on the unknown $u$, (3) becomes a nonlinear hyperbolic equation, e.g., in (1) $V(u)(x,t) = f'(u)$. Even initially the solution $u$ is smooth, the characteristics are changing with the solution $u$. At some later time, the characteristics would intersect and discontinuities are formed, such as shock waves. This is well-known for nonlinear hyperbolic equations [17].

However, numerical schemes designed according to the advective form (3) cannot provide a correct shock speed for shock waves. It is important instead using the following conservative form

(5) shares the same characteristic equation as (3) for the same problem. But only in the linear or quasilinear case, $a$ would be the same as $V$. For nonlinear hyperbolic equations, usually it is not. For example, for the nonlinear Burgers' equation,

$V(u)(x,t) = u$ in (3), while $a(u)(x,t) = \frac{u}{2}$ in (5). However $u$ is the right characteristic speed for both of them.

In the following, for our numerical scheme design, we consider (4) as the characteristic equation for (3). For the conservative equation (5), instead of (4), we use a pseudo characteristic equation

Taking the Burgers' equation as an example, we consider

for (3), while

for (5). Similarly for other nonlinear hyperbolic equations.

3.   Numerical scheme

In this section, we will describe how to design conservative SLFD WENO schemes, based on the RKEI method. We first recall the conservative SLFD scheme defined for the quasilinear hyperbolic equation in [21], then we will present the framework of RKEI method proposed in [5]. After that, we will show how to get conservative schemes by coupling these two methods.

3.1.   Conservative SLFD scheme

The conservative SLFD scheme starts from the conservative equation (5). Assuming we already have the solution at time level $t_n$, integrating (5) from $t_n$ to $t_{n+1}$, we get

Denoting

and defining

we obtain

where $\Delta x$ could be referred as the spatial mesh size.

At a given point $x = x_i$, (10) becomes

A conservative finite difference scheme can be provided as follows

where $\widehat{h}_{i+\frac{1}{2}}$ is a numerical flux approximating $h(x_i+ \frac{ \Delta x}{2})$ and $u_i^n$ approximates $u(x_i,t_n)$ accordingly. $\widehat{h}_{i+\frac{1}{2}}$ can be obtained from $\{H_i\}$ via a high order finite difference WENO reconstruction, which will be described afterward. From (11), we have

It is important on how to get high order approximations of (16), as we only know the solution at time level $t_n$. In this paper, a semi-Lagrangian scheme based on solving the characteristic equations (7) is used.

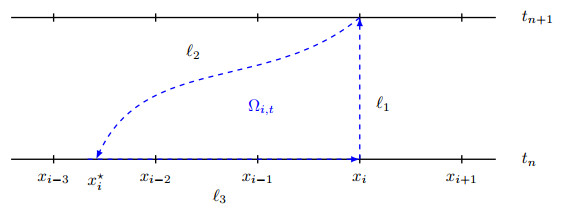
Let's introduce a spatio-temporal region $\Omega_{i,t}$, which is associated to the point $x_i$ and time levels from $t_n$ to $t_{n+1}$. The region is displayed in Fig. 3.1. The curves $\ell_1$ and $\ell_3$ are along the time and space directions respectively, while $\ell_2$ is the curve defined from the characteristic equation (4). From the definition, we know that the outward normal direction along $\ell_2$ is $(-1/a,1)$.

Now if we integrate the conservative equation (5) over the region $\Omega_{i,t}$, that is

Denoting $\nabla_{t,x} = ( \partial t,\nabla_x)$, and from the divergence theorem, we get

where $\mathbf{n}$ is the outward unit normal vector along each curve, and this equation yields

So if we can solve the characteristic equation (7) to find the root $x_i^{\ast}$, we can do the integration in (18) to get the value $H_i$. After that, we reconstruct $\{\widehat{h}_{i+\frac12}\}$ from $\{H_i\}$, the solution $u_i^{n+1}$ is then updated from (15). We denote this conservative updating process as "SLFDc", that is

In [21], only $a(x,t)$ is considered. As $a(x,t)$ is given, classical Runge-Kutta methods can be used to solve (7). When $a(u)(x,t)$ depends on $u$, since we do not have the values $u$ at intermediate stages, Runge-Kutta methods cannot be directly applied in the SL settings. In [31], a high order predictor-corrector approach is proposed. However, that approach is problem dependent and algebraically a little complicated to extend to higher order (e.g., 4th order and up). Here we will adopt the RKEI method developed in [5], which can be more conveniently extended to high order, and we will present it in the next subsection.

On the other hand, another type of SLFD scheme can base on the nonconservative advective form (3). This scheme is to solve the characteristic equation (4) to get $x_i^{\ast}$, then interpolate the value at $x_i^{\ast}$ to update the solution $u^{n+1}_i$ at the next time level, e.g., the approach used in [5]. However, due to interpolating errors, this type SLFD scheme does not have mass conservation. Here we refer this update as "SLFDn", that is

The nonconservative approach cannot get a right shock speed for nonlinear hyperbolic equations. Moreover, it is not appropriate for long time simulations [19]. In our numerical schemes proposed in the following, we could combine "SLFDc" and "SLFDn" to achieve a high order conservative SLFD scheme for the nonlinear hyperbolic equations.

3.2.   RKEI time method

In this subsection, we first briefly review the RKEI method, which was proposed to solve nonlinear ODEs [7]. For more details, we refer to [7,5,2].

We consider a nonlinear initial value ODE problem of size $N$,

where $C(Y)$ is a matrix-value function of size $N\times N$, which may depend on the solution of $Y(t)$. The idea of RKEI method is to freeze the coefficient matrix $C(Y)$ at a given time step, or linear composition of explicitly known values, to obtain a linearized problem, and then apply the exponential integrator method to update the solution from $Y^n$ to $Y^{n+1}$. $Y^n$ is the numerical solution at time level $t_n$. For a first order scheme, it is

where $C^n = C(Y^n)$ and $\Delta t = t_{n+1}-t_n$ is the time step.

To achieve high order accuracy, a class of commutator-free RKEI methods with multi-stages can be used. For an $s$-stage RKEI method, the algorithm flow chart is summarized as follows

In the subindex of $\alpha^k_{rJ^(r)}$, $J^{(r)}$ represents the number of exponentials one has to take per RK stage. The RKEI method can be represented by the Butcher tableau in Table 1.

Example 3.1. A 3rd order RKEI method in [5] can be represented by the following Butcher tableau,

with which, the RKEI scheme for the nonlinear ODE system (21) reads

here $J^{(r)} = 1$ for $r = 1,\ldots,3$ and $J = 2$.

Example 3.2. A 4th order RKEI method in [5] can be represented by the following Butcher tableau,

correspondingly, the RKEI scheme for the nonlinear ODE system (21) reads

here $J^{(r)} = 1$ for $r = 1,\ldots,3$, $J^{(4)} = 2$ and $J = 2$.

3.3.   Conservative SLFD-RKEI scheme

The RKEI method for linear ODEs is later recognized to be equivalent to an SL scheme for updating the solution for linear transport problems. The method is then coupled with spectral Galerkin method and applied to convection-diffusion problems [7], incompressible Navier-Stokes equations [6]. Very recently, it has been coupled with SLDG methods, and applied to the Vlasov-Poisson system and guiding-center model problems [2].

Here we will couple the RKEI method with the SLFD scheme, to get a high order SLFD-RKEI scheme for solving the nonlinear hyperbolic equations. The difficulty here is that for SL schemes under the finite difference framework, it is not easy to achieve the following properties simultaneously, high order, conservative, large time steps and ability to solve nonlinear hyperbolic equations. Our method proposed here for the one-dimensional hyperbolic equations, will have these properties.

Two types of conservative schemes can be proposed. One is that we only do a conservative correction at the last stage as compared to a nonconservative one. The other is we do it at every stage. Taking the 3rd order RKEI scheme in Table 2 as an example, the first SLFD-RKEI scheme reads as follows

We denote this scheme as "SLFDc1". The other is

and we denote it as "SLFDc2". The nonconservative scheme with SLFDn at every stage is still denoted as "SLFDn".

We note that for above schemes at each stage, we freeze $V(u)(x,t)$ or $a(u)(x,t)$ with linear composition of explicitly known values of $u$ at its corresponding time stages, but leaving $x$ as a changing variable. However we only know the values of $u$ at grid points $\{x_i\}$. For $x$ different from the grid points, an interpolation is needed. With the frozen characteristic speed, the characteristic equation (4) or (7), which now is an explicit ODE, can be solved by a high order Runge-Kutta method in a backward way. Let us take the solution to the characteristic equation as $X(t)$, and we introduce $w(X(t))$ as the velocity function. Detailed procedures for a first order scheme and a 3rd order scheme corresponding to (23) are given as follows:

● for a first order RKEI scheme, it has only one stage, the characteristic equation is

It can be solved with an Euler forward scheme, that is, we let $w(x_i) = w(X(t_{n+1}))\approx w(X(t))$, then

After that we call "SLFDc" to update $u^{n+1}$ from $u^n$;

● for a 3rd order RKEI scheme, it has three stages. For each stage, we have:

- Stage 1: The characteristic equation is

We solve it with a 3rd order Runge-Kutta scheme to get

- Stage 2: The characteristic equation is

We solve it with a 3rd order Runge-Kutta scheme to get

- Stage 3: This stage has two steps. The first step has the characteristic equation

We solve it with a 3rd order Runge-Kutta scheme to get

Then we call "SLFDc" to obtain $u^{(3)}$ based on $u^n$. The second step has the characteristic equation

Similarly, we solve it with a 3rd order Runge-Kutta scheme to get

and we call "SLFDc" to update $u^{n+1}$. Here it is starting from $u^{(3)}$ instead of $u^n$.

In Stage 1 and Stage 2, $\mathcal{I}u(x_i^{(\ell)},t_n)$ for $\ell = 1,2$ is an linear interpolation operator. Corresponding to the 5th order WENO reconstruction in the Appendix A.2, a 6th order interpolation with equal points on both sides of $x^{(\ell)}_i$ is used.

A similar procedure can be applied to other types of RKEI schemes, e.g., the 4th order in Table 3. "SLFDc2" will have every stage as Stage 3 above. Here we all omit them to save space.

4.   Numerical test

In this section, numerical examples for one dimensional linear and nonlinear hyperbolic equations are presented to verify the effectiveness of our algorithms. Three schemes are considered. For the 3rd order RKEI scheme (2), "SLFDc1" corresponds to (23), "SLFDc2" corresponds to (24), and "SLFDn" will have "SLFDn" instead of "SLFDc" in the last stage of (23). The schemes with 4th order RKEI (3) can be defined correspondingly.

The formal 5th order finite difference WENO reconstruction in the Appendix A.2 is used, which is a combination of the interpolation and flux reconstruction, and in this way we will not subject to time step restrictions. We note here this 5th order WENO scheme achieves 5th order when $a(u)(x,t)$ is a constant, but gives 3rd order otherwise, as no optimal linear weights exist. For more details, we refer to the appendix or [19]. We denote the mesh size as $N$, the final time $T$ and the time step is taken as

Here "CFL" refers to the CFL number as used in an Eulerian scheme.

4.1.   Linear case

First we consider the following linear equation with $a(u)(x,t) = 1$

We take the initial condition $u(x,0) = \sin(\pi x)$ and periodic boundary condition. The corresponding exact solution is $u(x,t) = \sin(\pi x-\pi t)$. The final time is set to be $T = 2.5$ and $\text{CFL} = 4.5$ is used.

For this example, the characteristic equation (7) can be solved exactly, no temporal errors exist. This example is used to test the spatial orders. In Table 1, we show the errors in $L_1$ and $L_{\infty}$ norms and the corresponding orders. We can observe that the 5th orders are obtained as expected.

4.2.   Quasilinear case

In this example, we consider the quasilinear hyperbolic equation with a variable coefficient

If we take the initial condition $u(x,0) = 1$ and periodic boundary condition, the exact solution can be given by [21]

For this example, the RKEI method for solving the characteristic equation (7) becomes the classic RK method. We consider both the 3rd order RKEI scheme with Butcher tableau (2) and the 4th order RKEI scheme with Butcher tableau (3).

For this quasilinear case, a large CFL number is still allowed. We take $\text{CFL} = 4.5$ and compute the solution up to time $T = 1.5$. In Table 2, we show the errors in $L_1$ and $L_{\infty}$ norms as mesh refinements, with their corresponding convergence orders. As we can see, with the mesh much refined, 3rd order accuracies are obtained for both 3rd order RKEI and 4th order RKEI schemes, which demonstrate the leading order is 3rd order in space.

For this problem, we also try to test the temporal orders. We take a very refined mesh size $N = 900$. In order to clearly see the temporal orders, we take very large CFL numbers from $26$ to $30$ so that the temporal errors dominate. The errors in $L_1$ and $L_\infty$ norms and the corresponding orders are presented in Table 3. The desired temporal orders are obtained.

4.3.   Nonlinear case

In the third example, we consider the nonlinear hyperbolic equation. We simply choose the Burger's equation

We take the initial condition $u(x,0) = 0.5+\sin(\pi x)$ and periodic boundary condition. For this example, since it is a nonlinear hyperbolic problem, we only take relatively large CFL numbers up to $3$ in the following, although the scheme is designed to be stable for arbitrary large CFL numbers.

We first compute the solution up to $T = \frac{0.5}{\pi}$ when the solution is still smooth [17]. For this nonlinear problem, the RKEI scheme will play its role. First we show the errors and orders for the three schemes "SLFDn", "SLFDc1" and "SLFDc2", with $L_1$ and $L_\infty$ norms in Table 4 and Table 5 for the 3rd order RKEI scheme (2), and with $L_1$ and $L_\infty$ norms in Table 6 and Table 7 for the 4th order RKEI scheme (3), respectively. For the nonlinear problem, we take $\text{CFL} = 1.5$. At least 3rd order convergence for three schemes are all obtained. However, if we compare the absolute errors, we can find that generally SLFDn has the smallest errors, SLFDc2 has the largest, while SLFDc1 is in between. This is expected, as nonconservative updating involves less interpolation and reconstruction errors than the conservative one. So SLFDc1 is better than SLFDc2 on this aspect.

Then we would like to verify that the three schemes coupled with RKEI, can achieve high order in time for this nonlinear problem. In Table 8, we show the errors and orders for the nonconservative SLFDn scheme with 3rd order RKEI (2) and 4th order RKEI (3), relatively large CFL numbers from $2.6$ to $3$ are used. We take $N = 800$ and we measure the errors on the grid points $|N-400|>100$, as we can find that around the position where $u = 0$, it has large errors. This is due to the fact that at the position where $u = 0$, the RKEI scheme directly gives $x^*_i = x_i$, which means the position $u = 0$ will not move in the nonconservative scheme. If the initial values happened to not contain this point, it still affects the solution close to it. We show another case evolving to shock solutions afterward. We plot the errors for $N = 320$ in Fig. 1, for the 3rd order RKEI scheme and 4th order RKEI scheme respectively. The plots clearly shows large errors around $u = 0$. Similarly for the following conservative schemes. With the measurement away from $u = 0$, we can see 3rd order and 4th order can be obtained.

We now compare the errors and orders for the two conservatives schemes, with 3rd order RKEI (2) and 4th order RKEI (3), in Table 9 and Table 10, respectively. We take CFL numbers from $1.6$ to $2$ for the 3rd order and $2.6$ to $3$ for the 4th order. We take $N = 800$ and the errors are measured in the same way as above. We can find that the conservative scheme SLFDc2 with conservative updating at each stage can achieve 3rd order and almost 4th order in time. Note here we only have 3rd order in space, the order will degenerate as CFL getting smaller. The SLFDc1 scheme seems to lose order as compared to SLFDc2. However, we should notice that SLFDc1 has smaller absolute errors as compared to SLFDc2. The lost order might be due to the pollute errors around $u = 0$. But it is still more accurate in time as compared to SLFDc2. From the tables 8-10 and Fig. 1, we can also find that the 4th order RKEI has much better accuracy than the 3rd order RKEI.

Finally we compute the solution to $T = \frac{2}{\pi}$, where the shock wave is already formed. We take $\text{CFL} = 1.5$ and $N = 80$. We compare the two conservative schemes with the nonconservative scheme in Fig. 2, where the 3rd order RKEI scheme with (2) and 4th order scheme with (3) are used respectively. We simply take a 2nd order linear interpolation for the nonconservative scheme. We can see that the two conservative schemes can capture the correct shock speed for both cases. However, the nonconservative scheme cannot, which is essentially the limitation of nonconservative schemes for hyperbolic conservation laws [17].

We further consider another initial condition $\sqrt{2}/2+\sin(\pi x)$, and we take $N = 88$. In this case, there is one grid where $u = 0$ initially. We take $\text{CFL} = 1.5$ and compute the solution to $T = 2/\pi$ with these three schemes. In Fig. 3, we show the results at $T = 0.7/\pi$, $1.3/\pi$ and $2/\pi$. At $T = 0.7/\pi$, the solution is still smooth, all three schemes work well. Then at $T = 1.3/\pi$, the shock forms, both conservative schemes capture the shock very well, however we can find that the nonconservative scheme keeps a point with value to be $0$. As the time further evolves to $T = 2/\pi$, the point with value $0$ is still there for the nonconservative scheme, and it causes large oscillations of the solution, also the shock front is not valid. They are not the case for the two conservative schemes. The reason is what we mentioned above, when $u = 0$, the nonconservative scheme cannot evolve this point. These two tests with shock waves clearly show the advantage and robustness of our conservative approach over the nonconservative one.

Remark 1. For nonlinear hyperbolic problems, large time steps might be beneficial when the dominant time scales are much larger than the characteristic-based time scales [11]. However, when discontinuous solutions exist, such as shock waves are formed, large time steps might still be allowed in some circumstances, e.g., if you track the characteristics very accurately to get an entropy satisfying solution and use total variation bounded (TVB) reconstructions [22]. Here we simply take a relatively large $\text{CFL} = 1.5$ without pursuing this aspect, and numerical tests show it works in our current settings.

5.   Conclusions

In this paper, we propose two conservative SLFD schemes for nonlinear scalar hyperbolic conservation laws, which is a combination of the conservative SLFD scheme developed for the quasilinear equation and RKEI scheme for nonlinear ODEs. The resulting schemes are conservative, allow large CFL numbers and can deal with the nonlinear equation. In our numerical tests, we have verified that the conservative schemes can achieve the same error levels as the nonconservative one. 3rd and 4th order in time can be obtained. However, for shock wave solution, the conservative schemes are more robust in shock capturing and avoid the actionless point $u = 0$. Besides, the conservative scheme with conservation correction at the last stage shows to be better than the other one with conservation updating at every stage. However, in this work, only one-dimensional problems are considered. The extension to high dimensions is not straightforward, due to the difficulty appeared in the spatial reconstructions. This will be subject to our future work.

Another interesting direction would be applying the conservative SLFD schemes for hyperbolic systems, e.g., the shallow water equations. However, current SL schemes for hyperbolic systems are, e.g., either under the Lagrangian framework which is similar to Lagrangian schemes [28], or updating the Riemann invariants along characteristics [33]. However, the two approaches both are nonconservative and they resort to Eulerian approach for mass conservation. So applying our current conservative SLFD schemes to hyperbolic system is highly nontrivial, and we leave it to our future investigation.

Appendix A

In this appendix, for completeness, we recall the finite difference WENO reconstruction in [19]. After we solve the characteristic equation (7) to get $x^{\ast}_i$, we need to reconstruct a polynomial of $u$ to do the integration in (18), we denote this procedure as $R_1$. Then from $\{H_i\}$, we will reconstruct $\{h_{i+\frac{1}{2}}^{\pm}\}$ based on the direction of the characteristics, which is denoted as $R_2$. The final flux $\{\hat{h}_{i+\frac{1}{2}}\}$ in (15) is obtained by combining these two reconstructions, which we denote as

We note that it is important to combine these two reconstructions, especially to achieve large time step without subject to stability restrictions.

For simplicity, we denote the characteristic speed in (7) simply as $a$.

A.1.   First order reconstruction

We split it into two cases, $|a|\Delta t\leq\Delta x$ and $|a|\Delta t>\Delta x$:

Case 1. $|a|\Delta t\leq\Delta x$: if $a\geq0$, $x_i^*\leq x_i$,

if $a<0$, $x_i^*> x_i$,

Case 2. $|a|\Delta t>\Delta x$, let $i^*$ be the index satisfying $x_i^*\in(x_{i^*-1},x_{i^*}]$:

when $a\geq0$,

when $a<0$,

A.2.   Fifth order reconstruction

We only consider $a>0$, the case $a<0$ can be obtained symmetrically.

First, we consider $a\Delta t\leq\Delta x$. One chooses three three-point stencils

The reconstruction $R = R_1\circ R_2$ is as follows:

1. reconstruction $h^{(j)}(x_{i+\frac{1}{2}})$ for $j = 1,2,3$:

where $\xi_j = (x_j-x_j^\ast)/\Delta x,\, j = i-2,...,i+2.$

2. compute the linear weights if $a$ is a constant:

in this case, all $\{\xi_j\}$ $(j = -2,...,2)$ are the same, which we write as $\xi.$

However when $a(u)(x,t)$ is not a constant, no optimal linear weights to achieve 5th order exist. We take

which are used to ensure the non-oscillatory performance [24].

3. compute the smoothness indicator:

4. compute the nonlinear weights.

5. get the numerical flux.

When $a\Delta t>\Delta x$, let $i^\ast$ be the index such that $x_i^{\ast}\in[x_{i^\ast-1},x_{i^\ast}]$, we can write the flux $\widehat{h}_{i+\frac12}$ as

where $\widehat{h}_{i^\ast+\frac{1}{2}}$ will be reconstructed as the case $a\Delta t <\Delta x$ with $\{u_{i^\ast-2},...,u_{i^\ast+2}\}$.