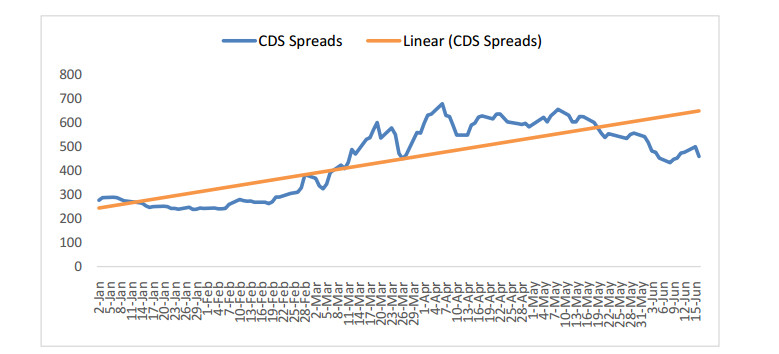
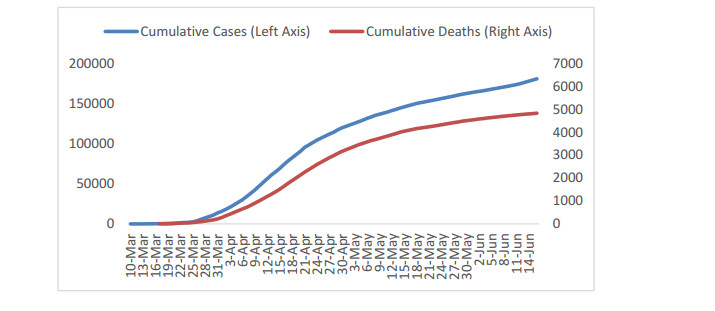
This study examines how sovereign CDS spreads of Turkey behave in Covid-19 pandemic times by considering that CDS spreads reflect the riskiness, vulnerability, financial stability, and macroeconomic stability of countries and CDS spreads of most of the emerging countries have increased with the emergence of Covid-19 pandemic. Therefore, the study focuses on the year 2020 which includes before Covid-19 and Covid-19 pandemic times periods. In this context, daily data between 12.06.2019 and 06.16.2020, 6 independent variables, and 6 Covid-19 situations are analyzed by employing Multivariate Adaptive Regression Splines (MARS) method. The findings reveal that (i) influential factors on Turkey's CDS spreads are BIST100 index, VIX index, MSCI Turkey index, and USD/TL foreign exchange rates for the period which is before Covid-19 pandemic times; (ii) MSCI emerging market index, number of new deaths from Covid-19, USD/TL foreign exchange rates, weighted average cost of funds, number of new cases from Covid-19, and VIX index have effect on Turkey's CDS spreads in Covid-19 pandemic times, respectively; (iii) on the other hand, number of cumulative cases, number of cumulative deaths, and measures do not have effect on Turkey's CDS spreads in any period. Taking precautions to decrease negative effects on Turkey's CDS spreads by considering the importance of deaths number from Covid-19 pandemic is very important. Hence, Turkey could stimulate foreign portfolio investment inflows with decreasing CDS spreads.
1.
Introduction
Hepatitis B is a disease that manifests itself as an inflammation of the liver caused by HBV. This virus belongs to the hepadnaviridae family [1]. It is a worldwide disease [2] affecting approximately 2 billion people and is considered to be about 50 to 100 times more contagious than HIV [3]. The disease is a serious public health problem in Africa [2] in general and, more specifically, in Cameroon, which is among the 17 most infected African countries with a prevalence that has increased from 10% in 2012 to 11.9% in 2017 [4], with some regions having a prevalence higher than 20%. Although effective treatments exist [5], HBV causes more than 800,000 deaths annually [5] and is classified into 10 genotypes ranging from A to J [5]. The transmission pathways of HBV include exposition to infectious blood, vaginal secretions during sexual intercourse, and other body fluids such as semen, as well as from infected mothers to infants (see [5] and references therein). The transmission process of HBV can also occur indirectly via contaminated surfaces and objects, since it can remain stable and infectious on environmental surfaces for at least seven days [6]. To stop the increase in the spread of this disease, the World Health Organization (WHO) has put in place a strategy targeting HBV [7]. It is expected that the deployment of this strategy will contribute in a substantial way to the global reduction of HBV infections, which is an important part of the 2030 sustainable development agenda driven by the United Nations [7,8].
The current modeling efforts in infectious disease dynamics is predominantly focused on monoscale modeling [9] as opposed to multiscale modeling [10,11]. For details of the advantages of multiscale models over single-scale models, see the published works [9,12]. However, a theory that provides the foundation for development of multiscale models from a pathogen-centered perspective has been successfully formulated [10,11]. But, despite this conceptual breakthrough in the development of multiscale models of infectious disease dynamics, the current modeling approach is still predominantly single-scale modeling because of limitations in the mathematical technology for development of multiscale models. As a result, several single-scale models for HBV have been developed at the between-cell scale by researchers. In this case, we can cite as examples the works in [13,14,15,16,17]. Such single-scale models of infectious disease dynamics at cell level propose mathematical models which describe the interaction between susceptible cells, infected cells, and free virus. The weakness of these monoscale models is that they disregard the within-cell scale viral replication process and the subsequent shedding of the virus into the between-cell scale.
To date, the techniques of modern molecular biology have also produced much knowledge about the replication and transmission processes of HBV and some fine details about its life cycle at cell level of organization [18,19]. To complement this detailed knowledge, the techniques of multiscale modeling need to be adopted in order to facilitate a comprehensive analysis and interpretation of dynamical processes of HBV, which include the viral replication and transmission processes, at cell level of organization. Such multiscale models integrate the within-cell scale where the viral replication process occurs, the between-cell scale where the viral transmission process occurs, and the interplay between these two scales of viral dynamics. These multiscale models of HBV at cell level of organization of a disease system [20,21] can help in understanding the effectiveness of therapies, from efficacy data when the therapies are administered at different stages of the life cycle of HBV in order to predict when treatment should be initiated, treatment scheme, dosage, duration of treatment, and periodicity of treatment. In order to develop multiscale models of infectious disease dynamics, it is necessary to consider infectious disease systems as a complex system consisting of three subsystem [12,22,23]: the host, the pathogen, and the environmental subsystems. The replication-transmission relativity theory [10,11], a theory formulated to guide the creation of multiple scales models, stipulates that infectious systems should be segmented into seven principal organizational levels. These include [10,12,22]: the cell, tissue, organ, microecosystem, whole-organism, macrocommunity, and macroecosystem levels. In line with the dictates of the replication-transmission relativity theory, each hierarchical level of organization consists of two scales: a microscale and macroscale, which influence each other in a reciprocal manner through the interaction of four key disease processes, which are [12,23]: pathogen infection/super-infection, pathogen replication, pathogen shedding/shedding, and pathogen transmission. At the cell level of organization, like all other levels of organization of an infectious disease system, five different categories of multiscale models of infectious disease dynamics are identified as follows [22]:
[a.] Individual-based multiscale models (IMSMs): These models, while developed at the cell level of organization, do not explicitly merge the within-cell and the between-cell scales. Only the within-cell scale is explicitly incorporated into the multiscale model. In this category of multiscale models, the between-cell scale is only observed as emergent behavior of the within-cell scale entities. This category uses simultaneous framework [22,23].
[b.] Nested multiscale models (NMSMs): The multiscale models developed in this category at the cell level of organization explicitly integrate the within-cell scale and the between-cell scale. In this case, the between-host scale influences the within-cell scale by a once off inflow of initial infectious agent inoculum dose from the between-cell scale to the within-cell scale through the process of infection, while the within-cell scale influences the between-cell scale by the outflow of the infectious agent from the within-cell scale to between-cell scale through the process of infectious agent excretion or shedding. This category uses serial integration framework [22]. Further, the within-cell scale sub-model and the between-cell scale sub-model must be described by the same mathematical formalism. See also [9,24,25,26,27].
[c.] Embedded multiscale models (EMSMs): The multiscale models developed in this category at the cell level of organization also explicitly integrate the within-cell scale and the between-cell scale. In this category, the between-cell scale influences the within-cell scale through the continuous inflow of infectious agent from the between-cell scale to the within-cell scale through the process of super-infection, that is, repeated infection of the within-cell scale before it recovers from the initial infectious episode. However, the within-cell scale influences the between-cell scale through the outflow of the infectious agent from the within-cell scale to between-cell scale through the process of infectious agent excretion or shedding. This category uses the embedded integration framework [22,23]. The within-cell scale sub-model and the between-cell scale sub-model must also be described by the same mathematical representation [28,29].
[d.] Hybrid multiscale models (HMSMs): The multiscale models developed in this category at the cell level of organization explicitly integrate the within-cell scale and the between-cell scale either as in NMSMs or as in EMSMs. However, the main distinguishing feature between these two categories of multiple scale models (i.e., NMSMs and EMSMs) and HMSMs is that in HMSMs the within-cell scale sub-model and between-cell scale sub-model are described by different mathematical representations. Examples of such paired descriptions are deterministic/stochastic, discrete time/continuous time, mechanistic/phenomenological, ODE/PDE, ODE/ABM, ODE/CA, etc. [30,31]. In addition, this category uses a multi-domain integration framework [22,23].
[e.] Coupled multiscale models (CMSMs): The multiscale models developed in this category at the cell level of organization integrate the within-cell scale and between-cell scale in the context of multiple infectious agent species and/or multiple cell species. Consequently, this category of multiscale models employs models from the four other categories of multiscale modeling, that is, IMSMs, NMSMs, EMSMs, and HMSMs as sub-models [31,32]. Further, this category uses parallel integration framework [22,23].
In this study, we focus on the NMSMs category, whose multiscale models can be subdivided into three main classes as follows [22,27]:
[a.] Class 1: Transformation-based nested multiscale models (TRAN-NMSMs): In this class, multiscale models are formulated by dividing the total population of infected cells into several subclasses. These subclasses represent the different stages of the pathogen's life cycle within an infected cell.
[b.] Class 2: Unidirectional coupling-based nested multiscale models (UNID-NMSMs): For this class of multiscale models, sub-models are coupled as in this article, where the between-cell scale is linked to the within-cell scale through a once off inflow of initial viral infective inoculum dose from the between-cell scale to the within-cell scale through the process of infection, while the within-cell scale is linked to the between-cell scale through the outflow of the virus from the within-cell scale to between-cell scale through the process of viral shedding or excretion.
[c.] Class 3: Simplification-based nested multiscale models (SIMP-NMSMs): In this class of multiscale models, the within-cell scale sub-model is streamlined, for instance, by condensing it into a single composite parameter that influences the between-cell scale sub-model, typically through methods like singular perturbation analysis [27].
In this article, we are more interested in developing a NMSM for HBV at the lowest level of biological organization of living systems, which is the cell level, in line with the dictates of the replication-transmission relativity theory [10,11]. The published paper [26] is a pioneering work in the field of multiscale modeling of viral infections, specifically in the context of poliovirus at the cell level of organization. This multiscale model integrates the intracellular-scale replication of poliovirus and the intercellular-scale population transmission dynamics of the virus. This multiscale model was further simplified into a SIMP-NMSMs by reducing the within-cell scale sub-model into a composite parameter that feeds into the between-cell sub-model. In the same paper [26], it is also demonstrated how the dynamics of the virus at two scales interact to generate compromises in the life cycle strategy of the poliovirus, without taking into account the mortality of the host. Information derived from poliovirus studies indicates that viruses may struggle to reconcile the conflicting interests that exist among various selection scales at cell level of organization.
This ground-breaking work on multiscale modeling of viral infections [26] was followed by the work [33]. The authors proposed a multiscale model that integrates the within-cell scale and the between-cell scale by using integro-partial differential equations where the within-cell sub-model and the between-cell sub-model are linked through time-since-infection [22]. The examination of this multiple-scales model reveals that, unlike typical monoscale models, the balance of cell populations offers a more instinctive and adaptable approach for integrating events at both intracellular and intercellular scales during viral infections. This enhanced ability to depict biological measurement trends yields a more methodical and quantifiable insight into the spread of viral infections and the most effective methods for managing their dissemination. The authors in [32] introduced a simple cytoimmuno-epidemiological model of HCV, which is homogeneously described by a system of ODEs where the within-cell scale is unidirectionnally coupled to the between-cell scale sub-model; this model is classified as a UNID-NMSM.
The work in [30] introduced one of the first cell-level multiscale models for HIV-1 disease dynamics. For this multiscale model, the within-cell scale is described by an ODE sub-model while the between-cell scale is described by a delay differential equation (DDE) sub-model. The within-cell scale sub-model is coupled to the between-cell scale sub-model based on class 2 of NMSMs approach. Therefore, the multiscale model is categorized as a UNID-HMSM. The multiscale model was used to simulate in vitro experiments that simultaneously include A3G-Vif interactions at the within-cell scale and T cell-HIV interactions at between-cell scale. As far as we are aware, there is an absence of multiscale modeling studies of Hepatitis B at cell level. The work in this article is intended to address this gap in knowledge on multiscale modeling of viral infections by developing a multiscale model of HBV at cell level of organization. In particular, the objective is to develop a NMSM that can used to test the impact of HBV therapies in the control of this disease system. The rest of the paper is subdivided in five sections. Section 2 deals with the derivation of the nested multiscale model. Here, we initially present the between-cell sub-model, followed by the within-cell sub-model. Furthermore, we link the two sub-models by using the nested multiscale models category approach. Finally, the full multiscale model is simplified. In Section 3 we study the positivity of the solutions, and the stability of the equilibrium of the simplified NMSM, and also perform sensitivity analysis. In Section 4, we present numerical results that establish the influence of within-cell parameters on between-cell scale variables through shedding and the influence of between-cell scale on within-cell scale through initial infection. Then, we end the paper with concluding remarks in Sections 5.
2.
Derivation of the nested multiscale model
2.1. The between-cell sub-model of HBV
The between-cell sub-model of HBV is described by the interaction of susceptible cells T, infected cells Y, and the virus V (see [13]). We make the following assumptions based on [13]:
[a.] Transmission is only through contact of viral load V and susceptible cells T.
[b.] We suppose that, infection follows a mass action principle.
[c.] The dynamics of T, Y, and V are assumed to unfold at a slower time scale t compared to the intracellular scale sub-model so that T=T(t),Y=Y(t) and V=V(t).
[d.] The mean count of virions in every infected cell is represented by ^Nc, serving as an indicator for the infectious capacity of an infected cell.
Based on these assumptions, the sub-model of HBV transmission dynamics at the between-cell scale becomes:
The first equation of system (2.1) models the dynamics of healthy cells. Here, Λw models the rate at which susceptible cells are produced. The population of susceptible cells reduces through infection at rate θc and decay at rate δw. The second equation of system (2.1) models the dynamics of infected cells. This population grows via infection and diminishes due to natural decay at a rate δw, and additional decay at rate δℓ due to infection so that the average lifespan of HBV infected cell is 1/(δw+δℓ). The third equation of system (2.1) models viral load. This population increases through shedding of HBV virus by infected cells into the extracellular environment and through burst at rate η1α4^Nc. It also decreases due to natural decay at rate δV. In this work, we show that ^Nc is a composite parameter which can be derived from a multiscale model system. It is a parameter consisting of multiple parameters that determine viral dynamics within an infected cell, and this makes the single-scale model (2.1) unrealistic. Given the difficulty in estimating ^Nc using monoscale models, we propose a multiple-scales model in this study that can be deployed to estimate its value.
2.2. The within-cell sub-model of HBV
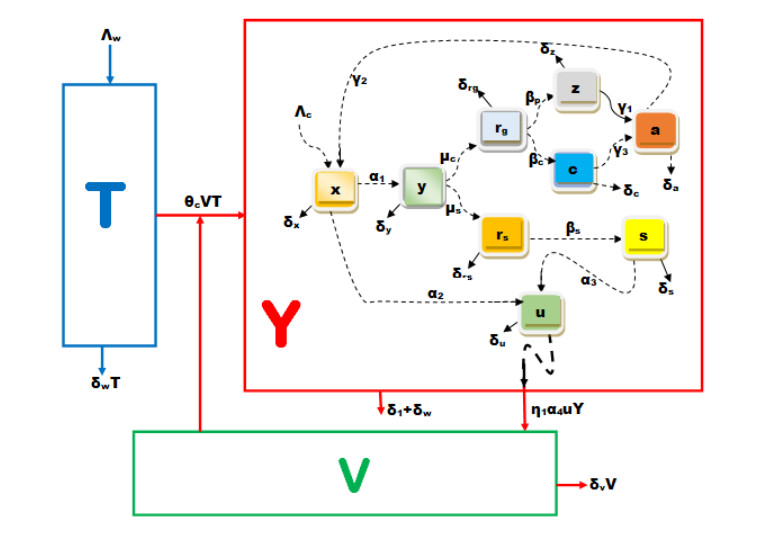
For the derivation of this nested multiscale model, the within-cell is adopted from the work of [20], whose work was based on deriving the life cycle of HBV at cell level. We derive our model based on this work. We make modifications that are based on multiscale considerations. Nevertheless, it is important to note that the multiscale consideration introduced is the excretion/shedding rate α4, which is important for multiscale modeling since the within-cell scale sub-model is linked to the between-cell scale sub-model through pathogen excretion/shedding [23]. The resulting within-cell scale sub-model is based on life cycle of HBV as follows: The viral entry is facilitated by cell receptors. Once in the liver cell, the virus degrades and releases the DNA of the viral genome (compartment x). This DNA is then transported at rate (α1) to rcDNA where it is repaired and converted into cccDNA (compartment y). The cccDNA is transcripted into pgRNA (compartment rg) at rate μc, mRNA and precRNA (compartment rs) at rate μs.The mRNA is translated at rate βs into HBsAg (compartment s) while the pgRNA is translated into polymerase (compartment z) and core proteins (compartment c). These are encapsidated at rates γ1 and γ3 into compartment a and then move to core particles at rate γ2, which include synthesis of the negative and positive strand. The immature nucleocapsids are either associated with surface antigen (compartment u) at rate α2 and α3 and excreted at rate α4 into the bloodstream as virion or recycled in the nucleus to promote overproduction of cccDNA. The meaning of all these variables are listed in Table 1 and we make the following assumptions:
[a.] There is a supply from extracellular virus at rate Λc, which models the super-infection of the infected cell.
[b.] Infection of cells occurs solely through interaction with the extracellular viral load V.
[c.] The within-cell scale disease processes occur at fast time scale τ in comparison to the variables of the between-cell scale sub-model. Hence, we have: x=x(τ), y=y(τ), rg=rg(τ), c=c(τ), a=a(τ), rs=rs(τ), s=s(τ), z=z(τ), u=u(τ).
[d.] There is no replication of HBV at between-cell scale.
[e.] The within-cell scale variable u(τ) is a proxy for individual cell infectiousness.
Based on the life cycle and the previous assumptions, the within-cell scale sub-model is thus written as follows:
2.3. Integrating the between-cell scale and the within-cell scale sub-models of HBV dynamics into a single nested multiscale model
After presenting the two sub-models of HBV at between-cell scale and within-cell scale dynamics that describe separately the two key processes of HBV, transmission process and replication process [10,11], which occur at two different scales in the two previous subsections, we now integrate the two sub-models of the two scales into a single multiscale model as presented in the conceptual diagram in Figure 1. To do that, we replace the composite parameter that phenomenologically models the within-cell scale virus replication process by the variable u(τ). Then, we have the following full nested multiscale model.
The multiscale model for HBV disease dynamics, as defined by system (2.3), is classified as class 2 of nested multiple-scales model. This classification is based on the categorization of multiple-scales models for infectious disease systems as outlined in [22,23].
2.4. Simplifying the multiscale model at cell level
Observing the full multiple-scales model system (2.3), it is clear that there are two separate time scales. The first is the between-cell time scale, which pertains to the transmission process of HBV among cells that occurs at slow time scale t. The second is the within-cell time scale, which is linked to the replication process of HBV at the within-cell scale at fast time scale τ. This multiscale model needs to be simplified through singular perturbation analysis in order to reduce some computational challenges associated with numerical methods for solving it. A key challenge for solving the full nested multiscale model (2.3) of HBV dynamics across the two different scales using numerical methods is that there is a timescale mismatch over the within-cell scale and the between-cell scale.
This suggests that, to solve the nested multiple-scales model (2.3) for HBV dynamics, numerical methods are necessary that use discretization techniques, where each scale utilizes specific methods in terms of length and/or time. However, a significant challenge in applying these methods across multiple scales is that different scales would necessitate different grid densities and time steps. This variation can complicate the transfer of information between the different scales. Up to this point, several methods have been developed to reduce dimensions, including statistical methods like principal component analysis, response and statistical surrogate modeling, and approaches grounded in dynamical systems, including the theory of central manifolds and analysis of rapid and gradual scale changes [22]. However, the complexity of the multiple-scales model system (2.3) can be lessened by expressing the fast and slow time scales in relation to each other using the equation t=ϵτ, where 0 <ϵ≪1 and ϵ. In this equation, ϵ is a constant that underscores the rapid time-scale dynamics of the intra-cellular model in comparison to the slower time-scale dynamics of the inter-cellular scale. We also assume a steady additional death rate of infected cells at rate δℓ. As a result, the complete multiple-scales model system (2.3) is transformed to become:
In what follows, we estimate the value of the composite parameter ^Nc by setting ϵ=0 in the final nine equations of multiscale model system (2.4) so that the within-cell scale becomes independent of time, and the nine last equations of the multiscale model system (2.4) can be re-written as follows:
Setting ϵ=0, Eq (2.4) becomes:
From system (2.5), we get:
with
Furthermore, the singular perturbation analysis helped us to reduce the within-cell scale sub-model system into algebraic expressions (2.5), which can be solved to give expressions (2.7). The aforementioned expressions can be incorporated into the parameters of the intercellular-scale sub-model, resulting in:
Here, ˜u is an approximation of u that is the total number of extracellular virions excreted. We now let Nc=˜u so that
This can be understood as the mean quantity of intracellular viral load at the endemic equilibrium, which is ready for excretion to the extracellular environment by each infected cell. Consequently, the simplified multiple-scales model is as follows:
Based on the categorization of multiscale models [22,23], the multiscale model (2.9) is a nested multiscale model of class 3 (SIMP-NMSM). In the next section, we analyze the simplified multiscale model system (2.9).
3.
Mathematical analysis of the multiscale model
3.1. Existence of a positively invariant set
Theorem 1. Given that the initial conditions of the model system (2.9) are positive, then all solutions remain positive for all t>0.
Proof. From the first equation, we get a differential inequality given by equation:
Now, letting s=sup{t>0,T>0,Y>0,V>0}∈[0,t] and integrating Eq (3.2), we have:
Thus the solution of Eq (3.1) is given by:
This implies that:
We use the same approach to show that:
For the third equation described below:
We then use separation of variables to obtain the following solution:
We thus have:
We thus conclude that any positive initial value condition of model (2.8) will then have a positive solution for all t≥0.
□
Theorem 2. The region
is positively invariant for the multiscale model (2.9) with non-negative initial conditions in R3+.
Proof. Since all the variables of the multiscale model given by Eq (2.9) describe cell populations and viral load, they are positive and all the parameters are non-negative. It can be demonstrated that if the initial values are non-negative, then the solutions of the multiple-scales model will also be non-negative. Letting X=T+Y, and adding the two first equations of system (2.8), we then have:
It follows that,
From which we get,
Where X(0) and V(0) represent the values of total cell population and the community viral load at cell level at the initial values of these variables. Taking the limit as time gets large, we then have:
Hence, all feasible solutions of model (2.9) enter the region Ω, where
In this region, the multiscale model described by (2.9) is epidemiologically and mathematically well posed. This means that every solution of Eq (2.9) with non-negative initial conditions in Ω remains in Ω for all t>0.
□
3.2. Equilibrium state and the basic reproduction number
Theorem 3. The disease-free equilibrium,
is globally asymptotically stable for R0<1.
Proof. We obtain the disease-free equilibrium by setting the left-hand side of Eq (2.9) equal to zero and Y=V=0. Thus, we obtain:
Which gives:
We thus have that the disease-free equilibrium is given by:
where E0 denotes the disease-free equilibrium of model (2.9). This equilibrium is used to compute the threshold number R0, which is the basic reproduction number, defined as the expected number of secondary infections produced by a single infectious individual during their entire infectious period [34]. This number is then conveniently used to study the endemic steady state. To calculate R0, we used the next generation matrix approach by using the article of [35]. In order to determine the basic reproductive number R0 of Eq (2.9), we then decomposed J(E0) into two matrices F and V such that : J(E0)=F−V, where F represent the paths to infection and V the remaining dynamics corresponding to compartments Y and V, where F and V are defined as:
Hence,
Considering that the basic reproductive number is the principal eigenvalue of the FV−1 matrix, we therefore conclude that
This basic reproduction number can be re-written as:
where
and
We therefore conclude that, based on these two expressions, the cytoimmuno-epidemiological parameters of HBV contribute to the infection of liver cells. To show the stability of DFE, we define the following Lyapunov function:
The derivative of L1(t) corresponding to the model solutions is:
Using the fact that Λw=δwT0 the derivative of L1 becomes:
We choose a1 such that:
And using the fact that V=0 at DFE, we thus have the following expression:
Upon simplification and rearrangements of terms in the above Eq (3.25), we will obtain:
˙L1=0 iff T=T0 and Y=0. Since T<T0, it is clear that ˙L1≤0 whenever R0<1. This implies that L1 is a Lyapunov function. Hence, by the principle of invariance of LaSalle, we conclude that the DFE is GAS. □
3.3. The endemic equilibrium's stability analysis
Theorem 4. The unique endemic equilibrium
is asymptotically globally stable for R0>1.
Proof. To show the result, we define the following Lyapunov function of Goh-Volterra type [36]:
Using the inequality 1−z+ln(z)<0 for z>0 with equality if and only if z=1, the derivative of L2(t) corresponding to the model solutions gives:
It follows from direct calculation that,
Substituting Eqs (3.28)–(3.30) into Eq (3.27), we get:
since −z+log(z)≤−1, ∀z>0, we thus have that ˙L2≤0. Thus, by LaSalle's invariance principle, we can say that the endemic equilibrium is GAS. □
3.4. Sensitivity analysis
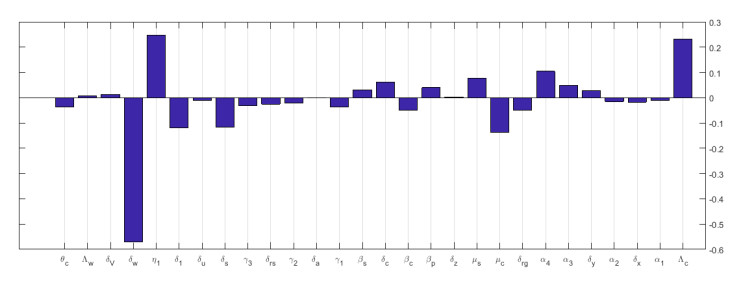
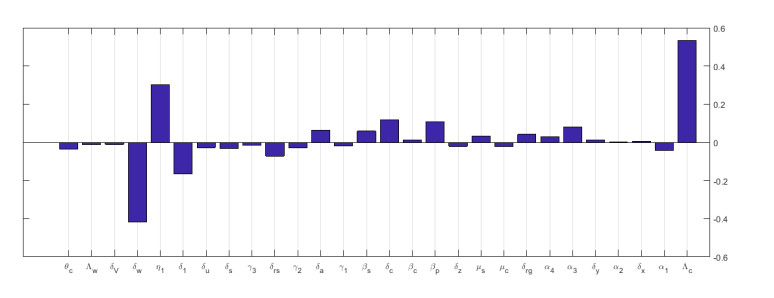
The parameters values used to evaluate the multiscale model for HBV in this study are given in Table 2. Due to uncertainty of these parameter values, here we conduct sensitivity analysis based on two disease dynamics metrics, the basic reproductive number R0 and the endemic value of the between-cell scale viral load ˜V, derived from the simplified nested multiscale model given by model (2.9) with respect to all the 28 parameters in order to inform health planners about prevention and optimal treatment of HBV. Numerous studies have underscored the significance of sensitivity analysis in pinpointing the key parameters that can be targeted for managing, eliminating, or even eradicating a disease. For that, we used the Latin hypercube (LHS) and partial rank correlation coefficient (PRCCs). Per run, we used 1000 simulations to study the impact of each parameter on the basic reproduction number and the endemic value of CVL. From Figures 2 and 3 we note that both R0 and ˜V are highly sensitive to the within-cell scale parameter Λc, which models the super-infection rate. This means that the use of interferon-alpha, which blocks the novo infection, will likely reduce infection. On the other hand, Figures 2 and 3 also show that both R0 and ˜V are highly sensitive to the between-cell scale parameters δw,η1. We also see that some parameters of the multiscale model at cell level have positive (Λc,η1) and negative (δ1,δw or μc) sensitivity index. Parameters with positive PRCCs will increase the value of both R0 and ˜V when they are increased, while those with negative PRCCs will decrease when they are increased.
[a.] At between-cell: R0 is highly sensitive to the variation of between-cell scale parameters δw, and η1 while ˜V is highly sensitive to the variation of between-cell scale parameter δw, η1 and δ1.
[b.] At within-cell: R0 is highly sensitive to the variation of within-cell scale parameters Λc and μc while ˜V is highly sensitive to Λc.
Based on sensitivity analysis of R0, which characterizes the disease dynamics at the onset of infection, this study indicates that at the initial stages of hepatitis B virus infection, it is crucial to consider medical interventions like drugs (including reverse transcriptase inhibitors and nucleos(t)ide analogues). These interventions aim to limit viral replication and prevent new infections, offering the greatest benefits in terms of reducing cell-to-cell transmission. In addition to that, care should be taken during data collection at between-cell scale if we want to improve the accuracy of these parameters.
4.
Numerical simulations
4.1. The impact of intracellular-scale parameters on intercellular-scale variables
In this section, we showcase numerical simulations of the multiple-scales model as defined by Eq (2.9) using parameter values as given in Table 2. We demonstrate the reciprocal influence between the intracellular scale and the intercellular scale through a positive feedback mechanism. Specifically, we highlight the impact of the four intracellular scale parameters (Λc,βp,βs,α4 and μc) on the between-cell scale variables (T,Y, and V).
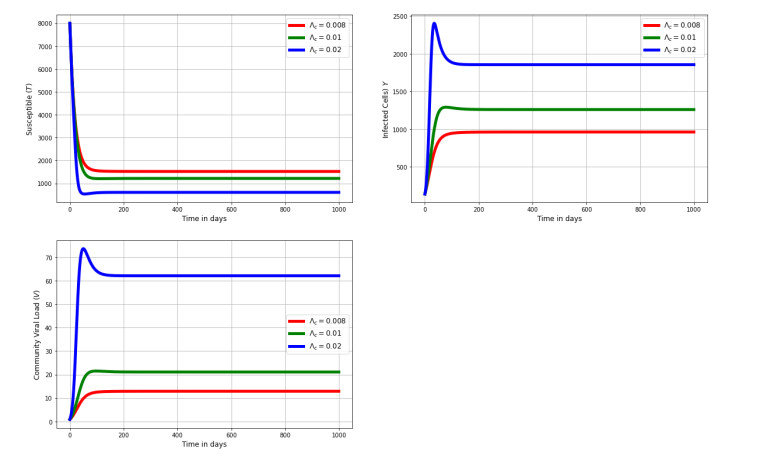
Figure 4 illustrates the variation in healthy cells, infected cells, and between-cells scale viral load for different values of super-infection rate Λc. The numerical findings indicate that these between-cell scale variables are influenced by the between-cell scale parameter Λc. The findings also reveal that as the rate of super-infection increases, the population of infected cells increase and the transmission of virus among cells also increases.
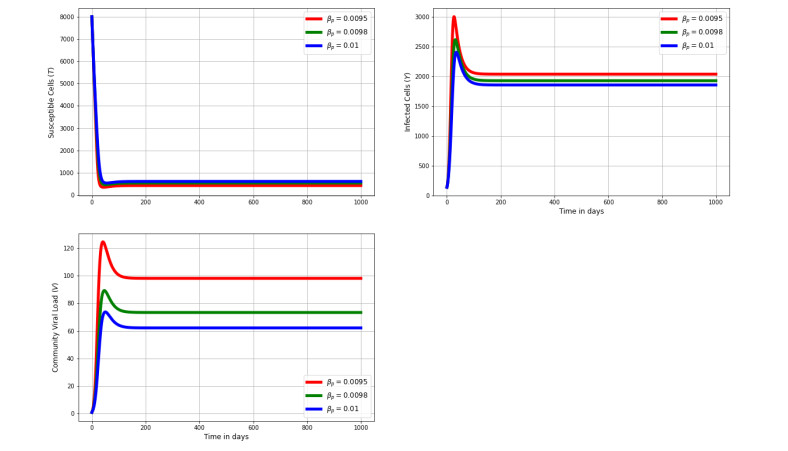
Figure 5 shows the impact of varying target cells, infected cells, and between-cell scale viral load for different values of translation rate of pgRNA to polymerase. The numerical findings indicate that the intercellular scale variables are affected by the intracellular scale parameter βp. The findings also show that as the rate of translation decreases, the population of infected cells increases and the transmission at the between-cell scale viral load also increases.
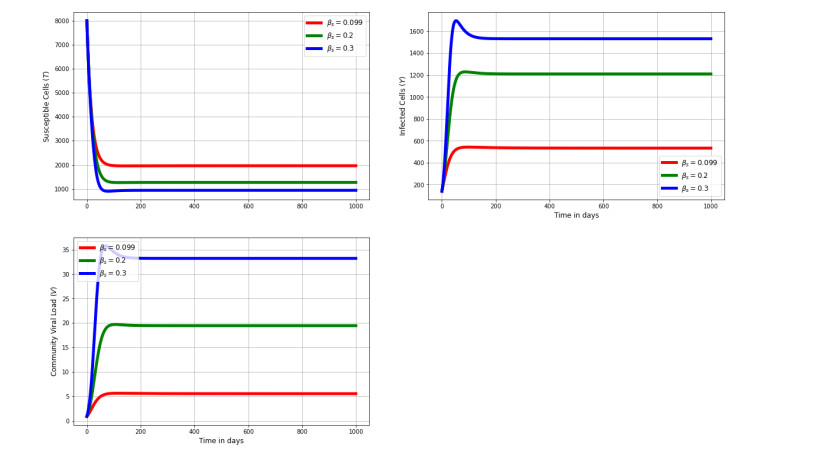
Figure 6 shows the impact of varying target cells, infected cells, and between-cell scale viral load for different values of translation rate of mRNA to surface antigen. The numerical findings confirm that the intercellular scale variables are affected by the intracellular scale parameter βs. The results also show that as the rate of translation increases, the population of infected cells and the between-cell scale viral load also increases.
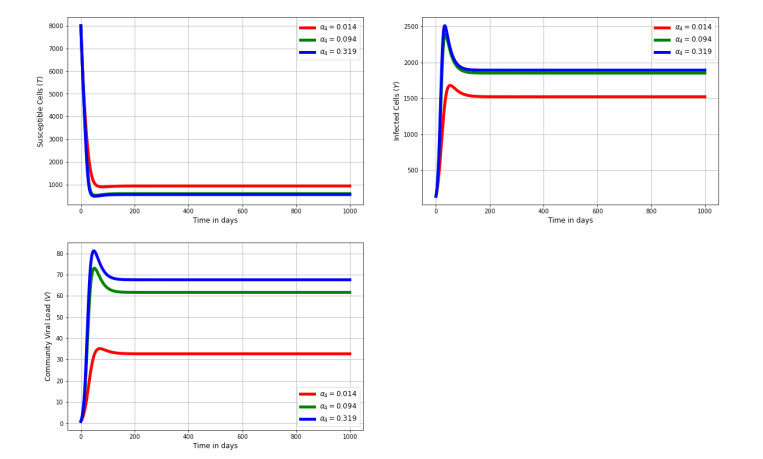
Figure 7 shows the impact of varying target cells, infected cells, and community viral load for different values of shedding rate α4. The numerical findings indicate that the intercellular scale variables are affected by the intracellular scale parameter α4. The findings also reveal that an increase in the shedding rate leads to an increase in the population of infected cells and enhances transmission at the intercellular scale.
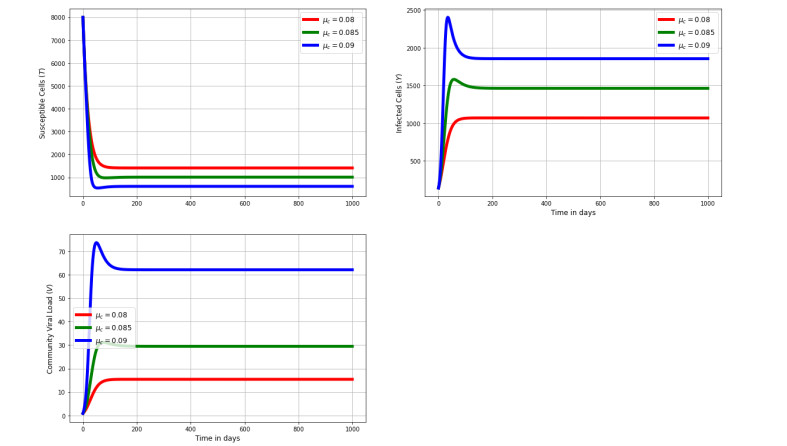
Figure 8 shows the impact of varying target cells, infected cells, and between-cell scale viral load for different values of transcription rate from cccDNA to pgRNA (μc). The numerical findings indicate that the intercellular variables are affected by the intracellular scale parameter μc. The results also show that as the transcription rate increases, the population of infected cells and between-cell scale viral load also increases.
5.
Discussion and conclusions
HBV is a directly and highly transmissible viral infection responsible for approximately 800,000 deaths annually. Even though WHO has put in place a strategy to fight against this viral infection, more effort is needed by developing countries in order to completely eradicate this disease. Mathematical models have been developed and utilized as essential tools to understand the clinical course of infectious diseases. Some of them have been used to control or even to eradicate these diseases. However, the major contribution of this paper is the development of a nested multiscale model as mathematical technology that can be deployed to evaluate the control, elimination, or even eradication of HBV infection from a complex systems perspective. The analytical results and the numerical simulations presented in this study confirm the need for deploying a multiscale modeling approach in understanding the dynamics of HBV infection. Numerical simulations show that, as the infection rate increases, the infected cells population and the viral load at between-cell scale also increase and, in turn, fuel infection at within-cell scale. This establishes a multiscale cycle involving a positive feedback mechanism between viral transmission processes at between-cell scale and viral replication process at within-cell scale. Since multiscale modeling based on the application of the replication-transmission relativity theory [10,11] incorporates both pathogen transmission process and pathogen replication process as the main drivers of disease dynamics, we used the multiscale model developed in this study to estimate a composite parameter Nc that estimates viral replication process at within-cell scale by reducing the dimension of the full nested multiscale model. In general, viral replication process at within-cell scale of a viral disease system involves seven main stages: [a.] attachment, [b.] penetration, [c.] uncoating, [d.] replication, [e.] assembly, [f.] maturation, and [g.] release or excretion/shedding of new virions. We conducted a sensitivity analysis on the two primary disease dynamics metrics, the basic reproduction number R0 and the endemic quantity of the intercellular scale viral load ˜V. These metrics were derived from the simplified nested multiple-scales model. The goal was to identify the most influential parameters affecting HBV infection dynamics at the cellular level of this disease system. This analysis allowed us to pinpoint the key parameters at both the intracellular scale and intercellular scale, that is, intervention targets that are highly sensitive to HBV disease dynamics. We thus conclude that interventions aimed at reducing the rate of cell infection, such as the use of protease inhibitors (PIs), which has been demonstrated to be efficient in blocking the novo infection can produce optimum impact in the control and prevention of HBV. However, like any other modeling study, the work here leaves room for further improvements. This is because the modeling work here is based on the replication-transmission relativity theory [10,11], which only considers pathogen-centered disease processes in infectious disease dynamics. A more elaborate multiscale model of HBV infection dynamics can be developed based on the universal theory for multiscale modeling of infectious disease dynamics [37]. We think that this study lays the groundwork for more comprehensive multiple-scales models that can be used to guide the management, elimination, or even eradication of HBV infection at cell level of organization.
Use of AI tools declaration
The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.
Acknowledgments
H. L. Wamba Makeng would like to thank the EMS-Simons for Africa and the Modelling Health and Environmental Linkages Research Group (MHELRG) of Department of Mathematical and Computational Sciences, University of Venda, South Africa where part of this work was done.
W. Garira would acknowledges financial support from the South Africa National Research Foundation (NRF) for its financial support, Grant No. IPRR (UID 81235).
Conflict of interest
The authors declare there is no conflict of interest.









 DownLoad:
DownLoad: