Interaction between hydrogen sulfide, nitric oxide, and carbon monoxide pathways in the bovine isolated retina

Abbreviations: ${A_{ij}}$: area of wall cell ($i, j$), m²; $e$: energy carried by sample Monte Carlo bundle, W; Eb(T): spectral blackbody emissive power at temperature T, W/(m²·m); $H$: total exercise times; $L$: length of the domain, m; M, N: lattice indices in square mesh corresponding to x, y position, respectively; n: refractive index of medium; ${N_{ij}}$: number of sample bundles emitted by cell ($i, j$); ${N_{ij \to k{\kern 1pt} l}}$: number of sample bundles emitted by cell ($i, j$) and absorbed by cell ($k, l$); $N_{ij}^*$: number of sample bundles emitted by cell ($i, j$) in the BDMC method; $N_{ij \to kl}^*$: number of sample bundles emitted by cell ($i, j$) and absorbed by cell ($k, l$)in the BDMC method; ${N_0}$: the number density of sampling bundles for a reference case; ${N_r}$: the number of sample bundles chosen for a reference volume cell ${V_r}$; $P$: performance parameter for Monte Carlo simulation; $R{D_{\lambda, ij \to kl}}$: radiative exchange factor of cell ($i, j$) to cell ($k, l$) for non-gray medium in the TMC method; ${\overline {RD} _{\lambda, ij \to kl}}$: modified form of $R{D_{\lambda, ij \to kl}}$; $R{D_{ij \to kl}}$: radiative exchange factor of cell ($i, j$) to cell ($k, l$) for gray medium in the TMC method; ${\overline {RD} _{ij \to kl}}$: modified form of $R{D_{ij \to kl}}$; $RD_{ij \to kl}^ * $: radiative exchange factor of cell ($i, j$) to cell ($k, l$) in the BDMC method; $\overline {RD} _{ij \to kl}^ * $: modified form of $RD_{ij \to kl}^ * $; ${s_n}$, ${\hat s_n}$: bundles trajectories and coupled bundles trajectories; $t$: time, s; $T$: absolute temperature, K; ${V_{ij}}$: volume of medium cell ($i, j$), m3; ${W_{ij}}$: bundle weight of cell ($i, j$); ${\delta _{ij \to \, kl}}$: reciprocity error of a couple of radiative exchange factor by the TMC method; $\delta _{ij \to \, kl}^ * $: reciprocity error of a couple of radiative exchange factor by the BDMC method; $\Delta P$: variation of performance parameter; ${\Delta _r}$: relative error of reciprocity; ${\varepsilon _\lambda }$: spectral emissivity; ${{\mathit{\Phi }} _{\lambda, ij}}$: spectral radiative energy emitted from cell ${V_{ij}}$ (or ${A_{ij}}$); ${{\mathit{\Phi }} _{\lambda, ij \to \, kl}}$: spectral radiative energy emitted from cell ${V_{ij}}$ (or ${A_{ij}}$), that is absorbed by cell ${V_{kl}}$ (or ${A_{kl}}$); ${\mathit{\Phi }} _{ij \leftrightarrow kl}^ * $: net radiative energy exchange, W; $\gamma $: standard deviation; ${\kappa _{a\lambda }}$: spectral absorption coefficient of medium; ${\kappa _e}$: extinction coefficient, m^-1; $\sigma $: Stefan-Boltzmann constant, $\left({\sigma = 5.67 \times {{10}^{ - 8}} {\rm{W/{m^2}{K^4}}}} \right)$; $\tau $: optical thickness $(\tau = {\kappa _e}L)$; $\omega $: scattering albedo of medium. Subscripts, $a$: medium absorption; $h$: hth sampling; $i{\kern 1pt} {\kern 1pt}, \, {\kern 1pt} j$: order number of cell; r: reference cell; $w$: wall

1.   Introduction

Radiative heat transfer in participating medium is described by radiative transfer equation (RTE), which is an integro-differential equation. Many methods have been developed to solve the RTE, the common used numerical methods such as the discrete ordinate method (DOM) and the finite volume method (FVM), rely on both spatial discretization and angular discretization, which are difficult to solve the RTE with high accuracy. Monte Carlo (MC) method is a stochastic statistical method based on the physical processes, it has been applied to solve radiative heat transfer in various participating media ^{[1,2,3,4,5,6]}. Moreover, the results predicted by MC method can often be treated as benchmark solutions due to its high accuracy of solution ^[7,8].

However, for the statistical nature of the MC method, the high computational cost is still a considerable disadvantage of MC simulation. Many attempts have been made in order to improve the computational efficiency of the method ^[9]. For example, several sampling approaches were developed to improve the speed of convergence, such as the importance sampling method ^[10], the rejection sampling method ^[11], the differential sampling method ^[12] and the weight-equivalent sampling method ^[13]. In addition, parallel computing technique was introduced into the MC simulation to improve computation efficiency evidently ^[1,9]. Howell ^[9] analyzed the advantages of various programming strategies of the MC method for radiative heat transfer in absorbing and scattering medium. All of these improvements were mainly mathematical efforts and hardware improvement of computer, which are universal to the MC simulations.

It has been noticed that the physical feature of thermal radiation transfer can also provide possibility to improve the MC simulation of radiative heat transfer in participating medium. For example, Walters ^[14] developed a reverse method based on the reciprocity principle for radiative heat transfer in a generalized enclosure containing an absorbing, emitting and scattering medium, the reverse method was proved to be efficient. Cherkaoui et al. ^[15,16] developed a net exchange Monte Carlo method based on a net-exchange formulation, provided an efficient way of systematically fulfilling the reciprocity principle, the computing time was proved much smaller than the conventional Monte Carlo approach. Lataillade ^[17] and his cooperators applied the net exchange Monte Carlo approach for radiative heat transfer in optically thick medium with spectral dependent radiative properties. Eymet et al. ^[18] extended this method to absorbing, emitting, and scattering media. Tessé et al. ^[19] improved the forward Monte Carlo (FMC) method based on the reciprocity principle, the method was used for radiative transfer in real gases, and proved to be a better choice for optically thick or nearly isothermal media compared with the forward Monte Carlo method. In addition, the reverse Monte Carlo (RMC) methods, based on the reversibility of radiative transfer trajectory, has been developed to solve the radiative transfer in absorbing and scattering media ^{[20,21,22,23,24]}. Kovtanyuk et al. ^[25] presented a recursive algorithm based on modification of Monte Carlo method, the modified method was used to solve the coupled radiative and conductive heat transfer in an absorbing and scattering medium, and was proved to be more accurate. Soucasse et al. ^[26] proposed a Monte Carlo formulation for radiative transfer in quasi-isothermal media which consists in directly computing the difference between the actual radiative field and the equilibrium radiative field at the minimum temperature in the medium.

In the present study, a bidirectional Monte Carlo (BDMC) method based on reversibility of bundle trajectory and reciprocity of radiative energy exchange was developed to solve thermal radiation transfer in absorbing and scattering medium. Two types of sampling models for MC simulation were presented, namely the equivalent sampling and the weight sampling. The equivalent sampling was chosen for the uniform mesh while the weight sampling was more suitable to the non-uniform mesh. The bidirectional information of tracing a sampling bundle was utilized by the BDMC method, the solution precision or efficiency can be evidently improved. Radiative heat transfer in a two-dimensional rectangular domain with absorbing and scattering media was solved by the BDMC method and the TMC method, respectively. The radiative exchange factors and the temperature profiles were investigated, in addition, the performance parameter defined by Howell ^[9] was also calculated to evaluate the two MC methods.

2.   Description and formulation

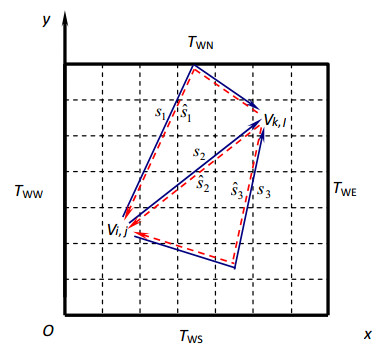
Radiative heat transfer in a two-dimensional (2-D) rectangular domain with absorbing, emitting and/or scattering medium was investigated. Figure 1 shows the 2-D rectangular geometry as well as the coordinate system. The four walls were assumed to be diffuse and gray. Radiative properties, such as the absorption coefficient, the scattering coefficient were assumed to be constant. The rectangular domain was divided into M × N = MN cells, any of which was depicted by V_ij (medium cell) or A_ij (wall cell), wherein the subscripts I∈[1, M] and j∈[1, N]. Monte Carlo method has robust adaptability and can be extended to more complex cases.

2.2.   The TMC method and radiative exchange factor

In the present study, the radiative exchange factor $R{D_{\lambda, \; ij \to kl}}$ was introduced to decouple the solution of radiative transfer from that of the temperature profile. It was defined as a fraction of the spectral radiative energy emitted from cell V_ij (or A_ij), that is absorbed by cell V_kl (or A_kl) ^[27,28].

As Eq 1, where ${{\mathit{\Phi }} _{\lambda, ij}}$ is the spectral radiative energy emitted from cell V_ij (or A_ij), ${{\mathit{\Phi }} _{\lambda, ij \to kl}}$ is the spectral radiative energy emitted from cell V_ij (or A_ij), and absorbed by cell V_kl (or A_kl), taking into account possible wall reflections. It is obvious that the conservation relation $\sum\limits_{k = 1, l = 1}^{M, N} {R{D_{\lambda, ij \to kl}}} = 1$ is tenable according to the definition of radiative exchange factors. Note that the radiative exchange factor depends only on the system geometry and the radiative properties distribution of the medium ^[29]. The reciprocity relation between a couple of radiative exchange factors was given by ^[30].

or

As Eqs 2 and 3, where, ${\kappa _{a\lambda }}$ is the spectral absorption coefficient of the medium, while ${\varepsilon _\lambda }$ is the spectral emissivity of the boundary wall. For convenience, the radiative exchange factors were usually modified as

or

here, Eqs 4 and 5 are used for volume and wall cells, respectively. The reciprocity relation can be written as

As Eq 6, after solving the radiative exchange factors, the net radiative energy exchange ${\mathit{\Phi }} _{ij \leftrightarrow kl}^ * $ from ${V_{ij}}$ to ${V_{kl}}$ can be calculated from

As Eq 7, where, is the Stefan-Boltzmann constant ( = 5.67×10^-8 W/m²K⁴), E_bλ(T) is the spectral blackbody emissive power at temperature T.

In the MC simulation, ${\mathit{\Phi } _{\lambda, ij}}$ is represented by a large number of independent sampling bundles, the propagating process of each sampling bundle can be tracked and counted. For example, the number of total sampling bundles for ${{\mathit{\Phi }} _{\lambda, ij}}$ is ${N_{ij}}$, each bundle with the same energy of ${e_{ij}} = {{\mathit{\Phi }} _{\lambda, ij}}/{N_{ij}}$. If ${N_{ij \to kl}}$ bundles among them are finally absorbed by ${V_{kl}}$, then, ${{\mathit{\Phi }} _{\lambda, ij \to kl}} = {e_{ij}} \cdot {N_{ij \to kl}}$, the radiative exchange factor can be calculated from ^[31].

As Eq 8, the number ${N_{ij \to kl}}$ can be counted from the MC simulation, however, only an approximate value of ${N_{ij \to kl}}$ can be obtained because of the pseudo randomicity ^[32] in the sampling process. In fact, the reciprocity correlation shown in Eq 6 cannot be strictly satisfied, and random errors always exist. In order to obtain more accurate results, one need to increase the sampling bundles ${N_{ij}}$, which results in the increasing computing cost.

In the TMC method, the propagation trajectories of ${N_{ij}}$ sampling bundles for cell ${V_{ij}}$ are tracked and counted to get the value of ${N_{ij \to kl}}$ for any cell ${V_{kl}}$. Similarly, the number ${N_{kl \to \, ij}}$ is obtained after tracing another ${N_{kl}}$ propagation trajectories of the sampling bundles for cell ${V_{kl}}$. Wherein, only the forward propagation information of a trajectory is used, the number of sampling bundles for cell ${V_{ij}}$ is ${N_{ij}}$.

According to the reversibility of light propagation, for a tracing trajectory from ${V_{kl}}$ to ${V_{ij}}$, a bundle from ${V_{ij}}$ can also propagate to ${V_{kl}}$ along the reverse direction of the tracing trajectory. The information of the reverse direction can be used in the MC simulation, the bidirectional information can be obtained from the forward tracing, which results in the development of the present BDMC method.

2.2.   The BDMC method and the equivalent sampling

In order to simplify the description of the BDMC method, the formula in the following sections were given for gray medium with gray walls. The basic idea of BDMC is to calculate the radiative exchange factor by the reversibility of light beams. According to the reversibility of light beams, the transmission path of the bundles received by cells can also be used as the transmission path of the bundles transmitted by cells. In this way, the effective information of sampling bundles if fully utilized without increasing the number of sampling bundles and calculation amount. Theoretically, the statistical sampling bundles in calculation can be doubled. And it can better satisfy the relationship of the reciprocal of radiative exchange factor. Figure 1 shows the schematic diagram of radiative transfer in a rectangular domain with participating medium in the BDMC method, it can be noticed that there are ${N_{ij}}$ tracing trajectories departing from cell ${V_{ij}}$, and $\sum\limits_{k = 1, l = 1}^{M, N} {{N_{kl \to \, ij}}} $ tracing trajectories getting into cell ${V_{ij}}$ at the same time. According to the reversibility of bundle trajectories, there must be $\sum\limits_{k = 1, l = 1}^{M, N} {{N_{kl \to \, ij}}} $ tracing trajectories depart from cell ${V_{ij}}$ in the reverse directions. It is believed that the $\sum\limits_{k = 1, l = 1}^{M, N} {{N_{kl \to \, ij}}} $ trajectories are independent of the emitted ${N_{ij}}$ trajectories because of the randomness of the sampling process. Thus, the number of total sampling bundles for ${V_{ij}}$ can be counted anew as

while the number of bundles emitted by ${V_{ij}}$ and absorbed by ${V_{kl}}$ is counted anew as

then, the radiative exchange factor $RD_{ij \to kl}^ * $ in the BDMC method can be calculated by

where, $RD_{ij \to kl}^ * $ is used to denote the radiative exchange factor in the BDMC method. The information of the bidirectional trajectories has been used, as is shown in Eq 11, it indicates that the effective sampling bundles are increased, while the computing cost remains unchanged. Therefore, more accurate results can be predicted from Eq 11 than that from Eq 8 under the same computing cost.

It should be pointed out that Eqs 9 and 11 are valid only if the sampling bundles for cell V_ij and any other cells are equivalent. According to the reversibility of light beams, the transmission path of the bundles received by cells can also be used as the transmission path of the bundles transmitted by cells. In this way, the effective information of sampling bundles if fully utilized without increasing the number of sampling bundles and calculation amount. In other words, the forward and reverse bundles in the BDMC method should have the same contribution for radiative exchange factors calculation. To use Eq 11, the equivalent sampling was introduced, in which the number of sampling bundles for cell (i, j) was determined by

where ${N_0}$ is the sampling density for a reference case defined as

where, ${N_r}$ is the number of sample bundles of the reference cell ${V_r}$, the subscript r refers to the reference cell.

2.3.   Error analysis and weight sampling

The bidirectional counting of sampling bundles employed in the BDMC method is equivalent to double the sampling number if the random error does not exist. In fact, any of the Monte Carlo methods always accompanied by random error. For the BDMC method, that leads to $N_{ij}^ * \ne 2{N_{ij}}$ and the energy of a bundle is not strictly equal to other cells. For any cell, it can be easily demonstrated by Eq 11, and the radiative exchange factors calculated by the BDMC method satisfied the conservation relation strictly. But the reciprocity relation between a couple of radiative exchange factors cannot be satisfied strictly. According to Eq 11, the following equation can be obtained

According to Eq 8, for gray medium, ${N_{ij \to kl}} = {N_{ij}}R{D_{ij \to kl}}$, ${N_{kl \to ij}} = {N_{kl}}R{D_{kl \to ij}}$. Therefore,

replace N_ij and N_kl according to Eq 12, in addition, considering Eqs 4 and 5, then Eq 15 can be transformed into

where, $\overline {RD} _{ij \to kl}^ * $ and $\overline {RD} _{kl \to ij}^ * $ are the modified forms for $RD_{ij \to kl}^ * $ and $RD_{kl \to ij}^ * $, respectively.

Supposing the reciprocity errors for a couple of radiative exchange factors ${\overline {RD} _{ij \to \, kl}}$ and ${\overline {RD} _{kl \to \, ij}}$ predicted in the TMC method are ${\delta _{ij \to \, kl}}$ and ${\delta _{kl \to \, ij}}$, respectively, one can write

where, it is obvious that ${\delta _{kl \to ij\, }} = - {\delta _{ij \to \, kl}}$.

For radiative exchange factors predicted in the BDMC method, similar equations can be written as follows

where, $\delta _{ij \to \, kl}^ * $ and $\delta _{kl \to \, ij}^ * $ are the reciprocity errors for a couple of radiative exchange factors $\overline {RD} _{ij \to \, kl}^ * $ and $\overline {RD} _{kl \to \, ij}^ * $ in the BDMC method, and $\delta {_{kl \to ij}^ * } = - \delta _{ij \to \, kl}^ * $.Combine Eqs 16–18, then

Considering the conservation relation $\sum\limits_{i = 1, j = 1}^{M, N} {R{D_{\lambda, kl \to ij}}} = 1$, $\sum\limits_{k = 1, l = 1}^{M, N} {R{D_{\lambda, ij \to kl}}} = 1$, ${\delta _{kl \to ij\, }} = - {\delta _{ij \to \, kl}}$, $\delta {_{kl \to ij}^ * } = - \delta _{ij \to \, kl}^ * $ and Eq 4, then, $\sum\limits_{i = 1, j = 1}^{M, N} {{{\overline {RD} }_{kl \to \, ij}} = } 4{({\kappa _a})_{kl}}{V_{kl}}$, and $\sum\limits_{k = 1, l = 1}^{M, N} {{{\overline {RD} }_{ij \to \, kl}}} = 4{({\kappa _a})_{ij}}{V_{ij}}$, moreover, considering Eq 18, the following error relation can be derived from Eq 19

therefore,

Because of the randomicity of the reciprocity error ${\delta _{ij \to \, kl}}$, the value of $\left| {\sum\limits_{k = 1, l = 1}^{M, N} {{\delta _{ij \to \, kl}}} } \right|$ would be very close to 0 if M and N tend to infinity. The formulae $\left| {\sum\limits_{k = 1, l = 1}^{M, N} {{\delta _{ij \to \, kl}}} } \right| = O\left({\left| {{\delta _{ij \to \, kl}}} \right|} \right)$ and $\left| {\sum\limits_{k = 1, l = 1}^{M, N} {{\delta _{ij \to \, kl}}} } \right| = O\left({\left| {{\delta _{ij \to \, kl}}} \right|} \right)$ would be valid for most of the discrete elements as $M \times N$ was large in the present study, where $O\left({\left| {{\delta _{ij \to \, kl}}} \right|} \right)$ is less than $\left| {{\delta _{ij \to \, kl}}} \right|$. Note that the values of $RD_{ij \to kl}^ * $ and $RD_{kl \to ij}^ * $ do not greater than unity, therefore

The reciprocity error for a couple of radiative exchange factors predicted by the BDMC method is always smaller than those predicted by the TMC method.

For some cases, the equivalent sampling may be inconvenient or inaccurate. For example, if the differences of apparent radiation characteristics and/or cell volume are very large among different cells, the equivalent sampling will result in a very small sampling number for a cell, and may be a very large sampling number for another. The former is not expected for the statistical analysis, while the latter increase computational cost.

The weight sampling was introduced into the BDMC method to avoid the above shortages of the equivalent sampling. For weight sampling, the number of sampling bundles for a cell was determined only based on the statistical request, but the weight of a sampling bundle was taken into account in the final statistical calculation. If the number of sampling bundles for cell V_ij was N_ij, then, its bundle weight W_ij was defined as

where N_r is the number of sample bundles for reference cell V_r. Then, the radiative exchange factor $RD_{ij \to kl}^ * $ in the BDMC method should be calculated by

Eq 11 should be substituted by Eq 24 if the weight sampling is employed.

3.   Numerical analysis on the BDMC method

Radiative transfer in a rectangular domain with absorbing, emitting and isotropic scattering gray medium was solved separately by the BDMC method and the TMC method. The radiative exchange factors, the radiative equilibrium temperature profiles, and the performance parameter defined by Farmer and Howell ^[1,9], predicted by the BDMC method were compared with those predicted by the TMC method. In addition, the performance of the equivalent sampling and the weight sampling in the MC simulation were also examined.

The radiative properties of the medium considered were supposed to be uniform and depicted by constant extinction coefficient ${\kappa _e}$, scattering albedo $\omega $, and refractive index n = 1.0. The length and width of the rectangular domain were ${L_x} = {L_y} = L$. Optical thickness was defined as $\tau = {\kappa _e}L$. The walls were assumed to be diffuse and gray, with constant emissivity of $\varepsilon $. The surfaces were imposed to constant temperature of ${T_{WE}}$, ${T_{WW}}$, ${T_{WN}}$, and ${T_{WS}}$, respectively, see Figure 1. The dimensionless coordinates were defined as $X = x/{L_x}$, and $Y = y/{L_y}$. The simulations were conducted using both uniform and non-uniform grids. The discrete parameters of the two types of mesh systems were listed in Table 1, where, x_c = y_c were the width and length of the largest volume cell in the non-uniform mesh system, and x_c = y_c, the parameter K = 1.04, M = N = 21, the mesh sizes in the non-uniform mesh system were expressed as $\Delta {x_{ij}} = \frac{{\Delta {x_c}}}{{{K^{\left| {i - 11} \right|}}}}$, and $\Delta {y_{ij}} = \frac{{\Delta {y_c}}}{{{K^{\left| {j - 11} \right|}}}}$. For medium cells, i.e., $i \in [2, M-1]$, and $j \in [2, N-1]$, the maximum width of the cells was $\Delta {x_{i, j}} = \Delta {x_c}$ for i = 11, and the minimum width of the cells was $\Delta {x_{i, j}} = \frac{{\Delta {x_c}}}{{{K^9}}}$ for i = 2 or 20. Similarly, the maximum length of the cells was $\Delta {y_{i, j}} = \Delta {y_c}$ for j = 11, while the minimum length of the cells was $\Delta {y_{i, j}} = \frac{{\Delta {y_c}}}{{{K^9}}}$ for j = 2 or 20. The maximum/minimum ratio of the mesh size is $\left({\Delta {x_c} \cdot \Delta {y_c}} \right)/\left({\frac{{\Delta {x_c}}}{{{K^9}}} \cdot \frac{{\Delta {y_c}}}{{{K^9}}}} \right)$ = 2.026.

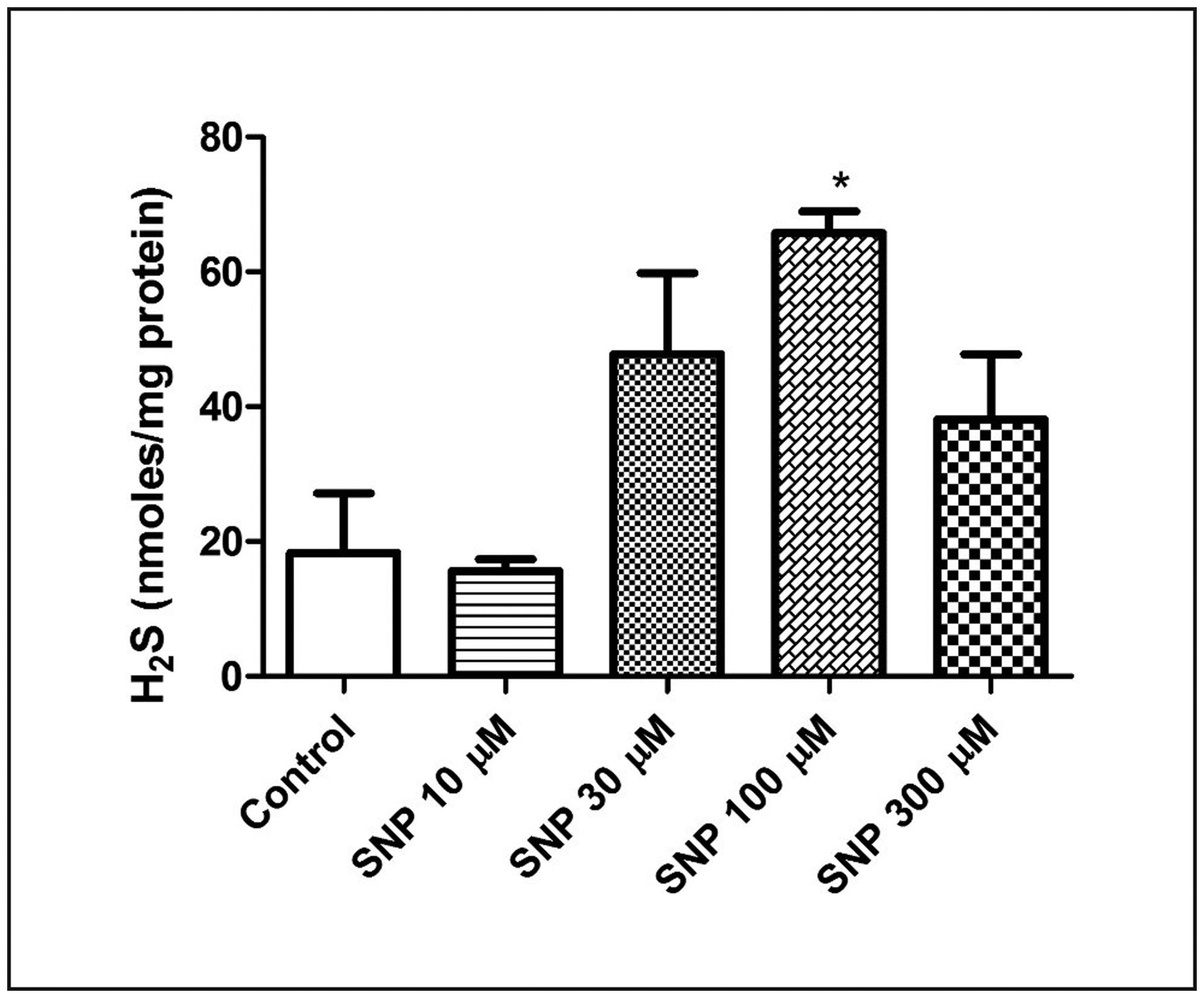
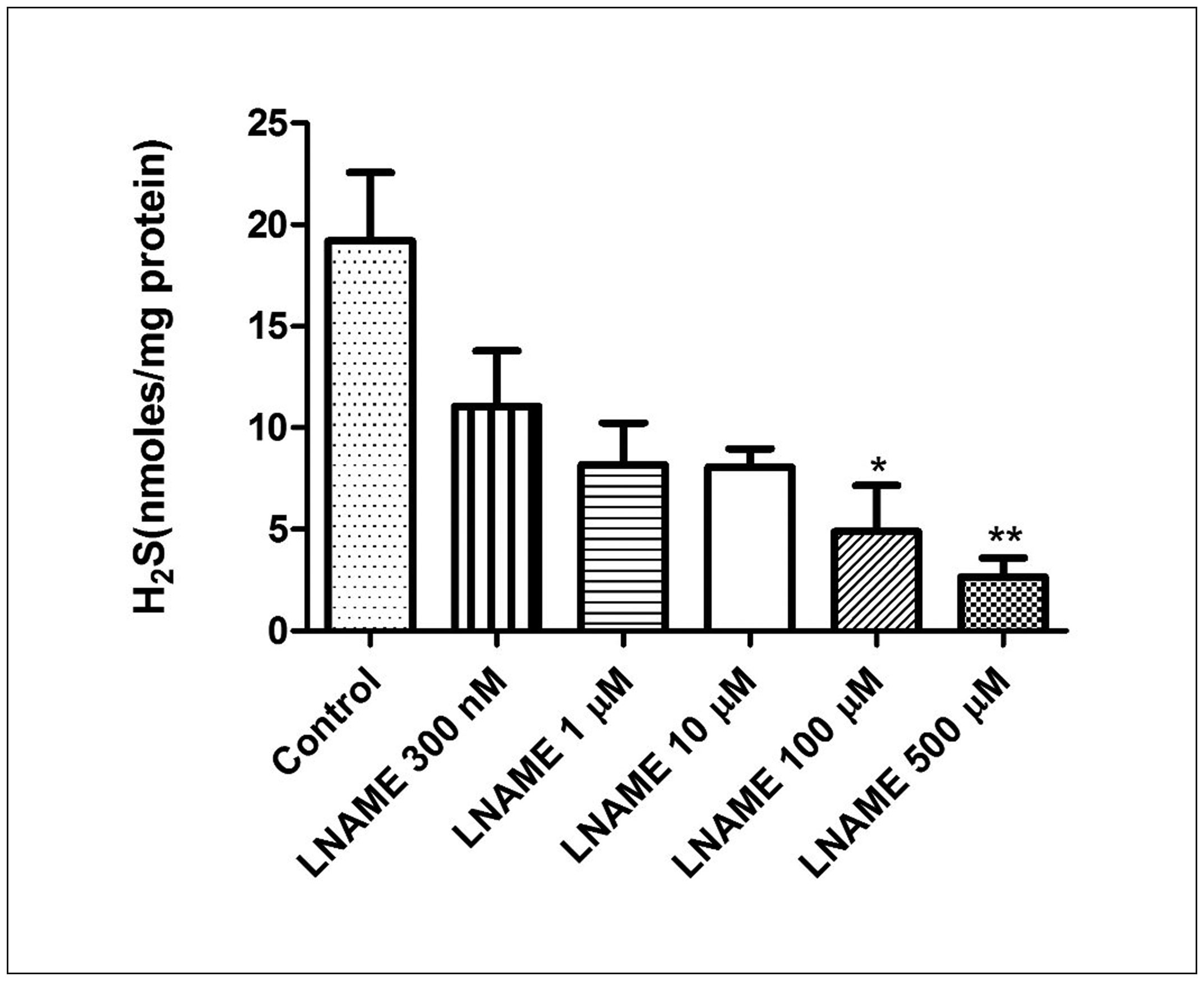
The sampling bundles needed in the MC simulation should be estimated as the results were calculated based on statistical computation. Figures 2 and 3 show the radiative equilibrium temperature profiles at dimensionless locations of Y = 0.3 and Y = 0.5 predicted by the TMC method with different sampling bundles of N_b = 10⁴, 10⁵, and 10⁶, respectively. Figure 2 shows the results for absorbing medium, while the results shown in Figure 3 were for absorbing and isotropic scattering medium with scattering albedo of = 0.5. For both the two cases, the wall temperatures were imposed separately as T_WE = T_WW = 1000 K and T_WN = T_WS = 1500 K, the emissivity of the walls were assumed to be constant and equal to 0.5, the optical thickness = k_eL = 15. For both the absorbing and absorbing-scattering medium, the predicted temperature profiles were found to be close to each other for different sampling bundles of N_b = 10⁴, 10⁵, and 10⁶, moreover, the temperature difference for N_b = 10⁵ and N_b = 10⁶ were less than 0.5%, therefore, the results were considered to reach convergence for sampling bundles N_b = 10⁵ in the present study, and the sampling bundles of N_b = 10⁵ was also chosen as the reference sampling bundles N_r in the BDMC method.

3.1.   Examination of radiative exchange factors

In this section, the radiative exchange factors predicted by the BDMC method were compared with those predicted by the TMC method, the numerical simulations were implemented using both uniform and non-uniform grids, meanwhile, the equivalent sampling and the weight sampling were also employed separately. The predicted radiative exchange factors always satisfy the conservation relation strictly, therefore, only the reciprocity for radiative exchange factors was examined in the present study. The relative error of the reciprocity for a couple of radiative exchange factors was defined as

where, ${\overline {RD} _{ij \to kl}}$ refers not only to the modified form of the radiative exchange factors given by Eq 8 for the TMC method, but also to those given by Eq 11 (BDMC method, equivalent sampling) and by Eq 24 (BDMC method, weight sampling).

Table 2 shows the modified radiative exchange factors predicted by the BDMC method and the TMC method employing the equivalent sampling and the uniform grids as well as the corresponding relative error D_r defined by Eq 25. The emissivity of the walls were taken as = 0.5, the optical thicknesses of the rectangle medium along the length and width direction were $\tau = 1.0$, the reference sampling bundles was taken as ${N_r} = {10^5}$. It indicates that the reciprocity error for a couple of radiative exchange factors predicted by the BDMC method was at least an order of magnitude less than those predicted by the TMC method with the same sampling bundles. The maximum relative error for all the elements considered did not exceed 0.58% in the BDMC method, while it reached 30.1% in the TMC method.

Table 3 shows the radiative exchange factors predicted by the BDMC method using the equivalent sampling and the weight sampling in a non-uniform mesh system. The computing parameters were $\varepsilon = 0.5$, $\tau = 1.0$, $\omega = 0.0$, and ${N_r} = {10^5}$. The reciprocity error for a couple of radiative exchange factors predicted by the BDMC method with the equivalent sampling was unacceptable for the non-uniform mesh, it indicates that the equivalent sampling was not recommended to solve radiative transfer in the BDMC method with non-uniform grids. If there is obvious difference of heat capacity between cells, the equivalent sampling will lead to big difference of sampling number for the same cells. The calculation accuracy will come under influence if the equivalent sampling is applied. However, the BDMC method with the weight sampling can predict quite satisfactory results for all the cells considered.

Table 4 shows the radiative exchange factors predicted by the BDMC method and the TMC method employing the weight sampling and the non-uniform grids. It can be seen that the reciprocity error in the TMC method was larger than those in the BDMC method for all the cells considered. The BDMC method showed greatly superior to the TMC method when the weight sampling and the non-uniform grids was used.

3.2.   Examination of radiative equilibrium temperature profiles

The advantage of the BDMC method was further verified by comparing the predicted temperature profiles. For gray medium, the radiative equilibrium temperature ${T_{ij}}$ of cell (i, j) satisfies the energy equation

or

Utilizing the predictions of radiative exchange factors, the radiative equilibrium temperature profile can be solved iteratively from Eq 26 or Eq 27. In the iteration, the iteration is stopped by setting the residuals. The number of iterations is not certain, which is related to the residuals.

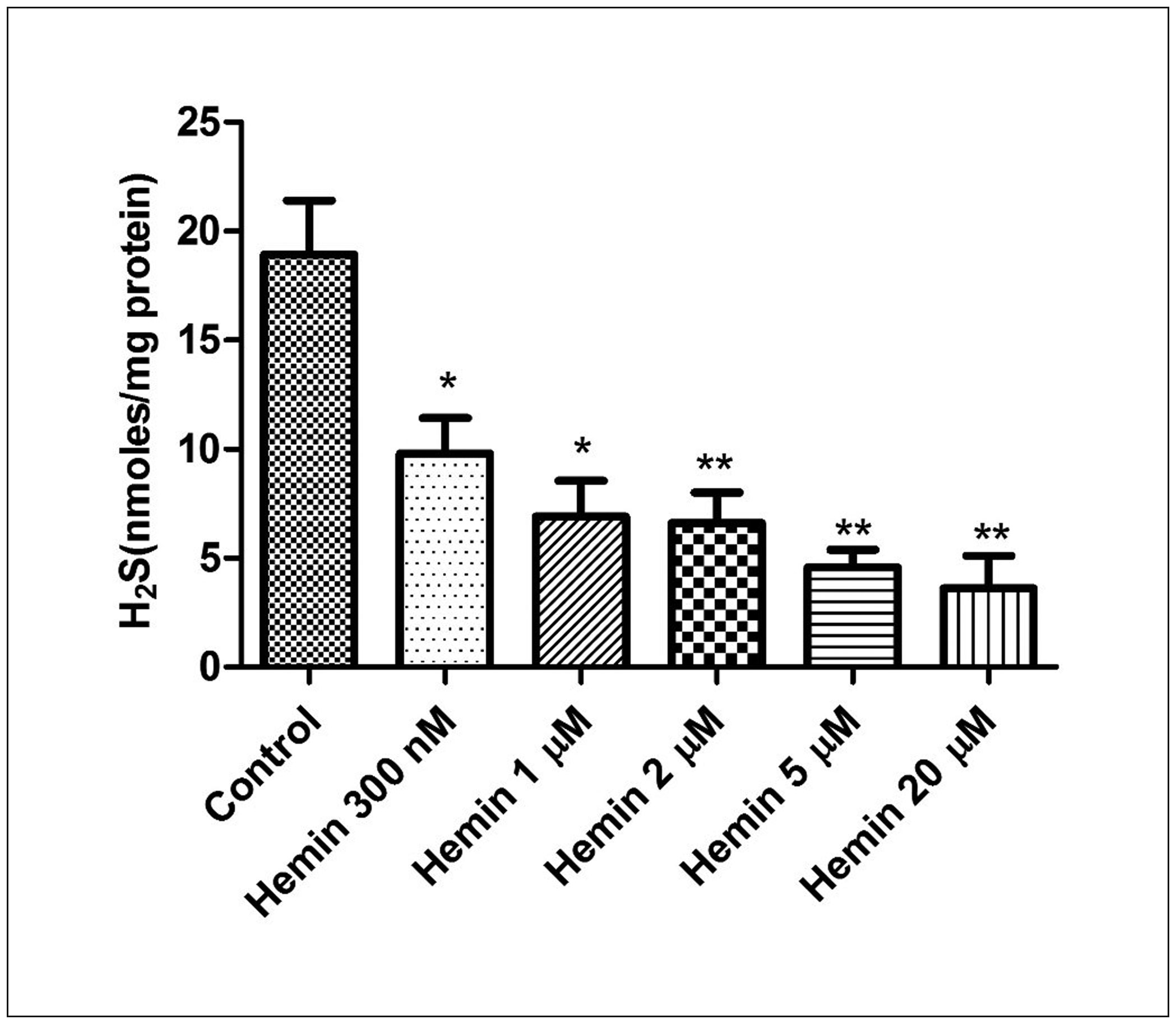
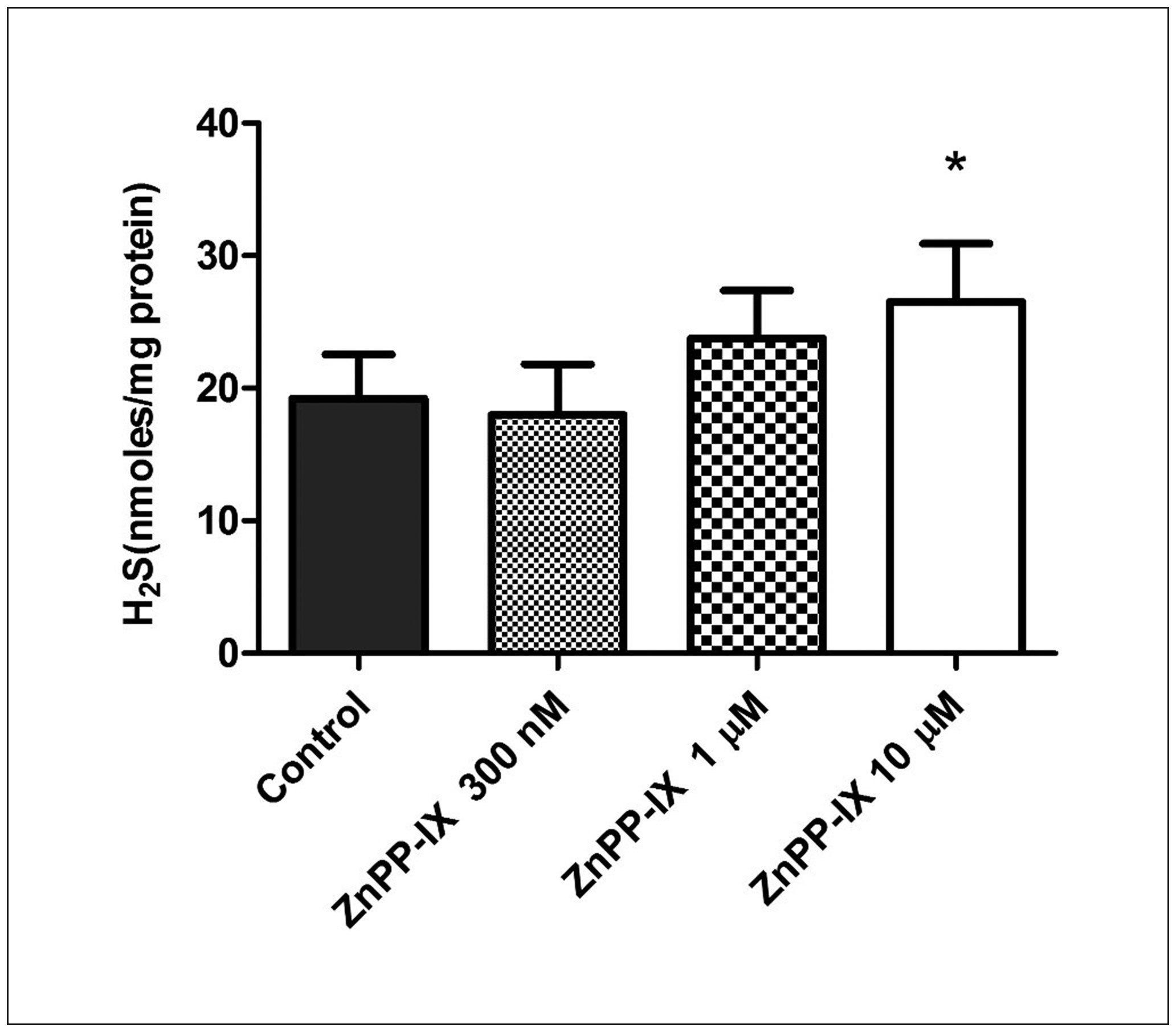
Figure 4 shows the radiative equilibrium temperature profiles for an absorbing, emitting, and non-scattering medium predicted by the TMC method and the BDMC method employing the equivalent sampling and the uniform grids. The wall temperatures were imposed separately as T_WE = T_WW =1000 K and T_WN = T_WS =1500 K, the emissivity of the walls were assumed to be constant and equal to 0.5, the optical thickness = k_eL_x = k_eL_y = 15. First, the BDMC predictions were very close to the TMC predictions, it indicates that the development of the present BDMC for predicting temperature profiles is correct, in addition, the BDMC predictions were shown smoother than those predicted by the TMC method, the BDMC method converged faster than the TMC method. Similar superior of the BDMC method to the TMC method can be seen from Figure 5, where the weight sampling and the non-uniform grids were employed and the medium was absorbing and isotropic scattering with scattering albedo of = 0.5.

Figure 6 shows the comparison of temperature profiles predicted by the BDMC method with non-uniform grids employing different sampling models of the equivalent sampling and the weight sampling. The temperature profiles predicted by using the weight sampling was smooth, while the predictions using equivalent sampling model contains some small rectangles, this may due to the fact that the number of the sampling bundles for different cells employing equivalent sampling were significantly different, which lead to large random error and affected the temperature profiles.

Figure 7 shows the radiative equilibrium temperature profiles predicted by the TMC method and the BDMC method with a relative small number of weight sampling bundles using the non-uniform grids. The temperature profiles predicted by the TMC method became unacceptable as the reference sampling bundles decreased to N_r = 10³, while the BDMC method can still predict better results, the BDMC method converged faster than the TMC method. Therefore, the BDMC method would be a better choice if the sampling bundles for radiation computation is limited or efficient computation is required.

3.3.   Performance parameter analysis

Farmer and Howell introduced the performance parameter P to evaluate various MC methods or strategies ^[1,9], the performance parameter was defined as

where, t is the CPU time spent by the concerned MC simulation and ${\gamma ^2}$ is the variance of the results. A good method or strategy for the MC simulation tends to minimize the performance parameter P. The variance ${\gamma ^2}$ is given by

where, $\gamma _h^2$ is the variance of the hth exercise, $h \in [1, H]$, and H is the total exercise times, $\gamma _h^2$ can be calculated from

where, ${\left({{{\overline {RD} }_{ij \to \, kl}}} \right)_h}$ is the predicted value of ${\overline {RD} _{ij \to \, kl}}$ in the hth exercise, and ${\left({{{\overline {RD} }_{ij \to \, kl}}} \right)_a}$ is the "exact value" of ${\overline {RD} _{ij \to \, kl}}$.

It has been discussed that the acceptable numerical results can be obtained if the sampling bundles N_b in the MC simulation reached 10⁵. In order to compute the performance parameters for the TMC method and the BDMC method, the "exact solution" of the radiative exchange factors should be firstly obtained. The approximate "exact solution" can be obtained by increasing the sampling bundles of the MC simulation due to the high precision of the MC method. To do so, the reference sampling bundles were taken as N_r = 10⁶ and N_r = 10⁸, respectively, the predicted results for the two cases were found to be nearly unchanged, and the maximum relative error for any of the radiative exchange factors correspond to different cells was less than 0.1% as the reference sampling bundles N_r increased from 10⁶ to 10⁸. Therefore, the results employing N_r = 10⁸ were treated as the "exact solution" in the present study.

For each exercise, only the initial random number and sampling order were changed, therefore, the CPU time spent by each exercise should be nearly unchanged. The total exercise times was set as H = 10. The performance parameter of the BDMC method and the TMC method were written as ${{\rm{P}}_{BDM}}$ and ${{\rm{P}}_{TM}}$, respectively, while the performance increment $\Delta {\rm{P}}$ was defined as

Table 5 reports the performance parameter for the TMC method and the BDMC method using the equivalent sampling and the uniform grids. It indicates that the performance parameter for the TMC method was always larger than that for the BDMC method, in addition, the performance increment decrease with the increasing sampling bundles. Table 6 shows the performance parameter for the TMC method and the BDMC method employing the weight sampling and the non-uniform grids. Similar conclusions can be drawn as those employing the equivalent sampling and the uniform grids.

Table 7 shows the performance parameter for the BDMC method with equivalent sampling and the weight sampling using the non-uniform grids. The performance parameter for BDMC with the equivalent sampling was found to be larger than that with the weight sampling, this indicate that the weight sampling was more suitable for non-uniform grids in the BDMC simulations.

4.   Conclusions

The BDMC method along with the equivalent sampling and the weight sampling were developed to solve radiative transfer in absorbing and scattering medium. The BDMC method approximately doubles the information from the bundle tracing to possess a high efficiency by making the best use of the reversibility of the bundle trajectory. The formula for the BDMC method and the corresponding error analysis were derived and presented. Radiative heat transfer in a two-dimensional rectangular domain of absorbing and/or scattering medium were solved by the TMC method and the BDMC method, respectively. The reciprocity of the radiative exchange factors, the radiative equilibrium temperature profiles, and the performance parameter predicted by the two MC methods were examined and compared. The results showed that (1) the BDMC method can greatly improve the reciprocity satisfaction of radiative exchange factors, which is helpful for temperature profile solution, (2) the BDMC method was more accurate or efficient than the TMC method, (3) in the BDMC simulations, the weight sampling was found to be more flexible than the equivalent sampling.

Acknowledgments

The authors acknowledge the financial support by National Science Foundation of China (No. 51776052) and Aeronautical Science Foundation of China (No.201927077002).

Conflict of interest

The authors declare no conflict of interest.

Author Contributions

Xiaofeng Zhang: Software, Formal analysis Data Curation, Writing - Original Draft, Visualization. Qing Ai: Conceptualization, Methodology, Validation, Resources, Writing - Review & Editing, Supervision, Funding acquisition. Kuilong Song: Validation, Formal analysis, Writing - Review & Editing, Heping Tan: Writing - Review & Editing, Supervision, Project administration.