Abbreviations: QS, quorum sensing; AHL, acyl homoserine lactone; MDR, multidrug resistant; EPS, extracellular polymeric substance; PNAG, poly-β-(1,6)-N-acetyl glucosamine; OH-dDHL, N-(3-hydroxy-dodecanoyl)-L-homoserine lactone; HSL, homoserine lactone
1. Introduction
Acinetobacter is a Gram-negative, strictly aerobic, non-motile, non-fermentative bacteria found in soil and water. It belongs to the family Moraxellaceae (consisting 8 genera including Acinetobacter) under the order Pseudomonadales. Recently, Acinetobacter has evolved as a multidrug resistant (MDR) opportunistic nosocomial pathogen and its outbreaks have been reported throughout the world [1]. The common infections caused by this organism are pneumonia, bacteremia, urinary tract and surgical wound infections [2]. The omnipresence and tendency to persist on human skin and dry inanimate objects for extended period of time and the ability to evolve resistance factors by its versatile genetic machinery makes Acinetobacter one of the common, most successful pathogen in the modern healthcare system [3]. In addition, its genetic potential to transfer diverse antibiotic resistance determinants presents Acinetobacter spp. infections a challenge for physicians and clinical microbiologists [4]. The incidence of Acinetobacter infection varies with season and there is a high isolation rate in summer compared to winter [5]. Few strains such as A. radioresistens, A. baumannii andA. lwoffii are highly resistant to desiccation [6]. To date, more than 31 named and unnamed species have been described, of which the clinically important ones are A. baumannii, A. pittii (formerly Acinetobacter gen. sp. 3), and A. noscomialis (formerly Acinetobacter gen. sp. 13TU [7].
Acinetobacterspecies are responsible for both community and health care—associated infections (HAIs), and the infection rate in the population is alarmingly high (28.6%), second only to Staphylococcus aureus (30.9%) [8]. There is an equal distribution of Acinetobacter infections in pediatric and adult cases [9]. It has been reported that this bacterium can colonize the wounds and cause severe infections in emergency situations like war and traumatic disasters such as earthquakes (Centers for Disease Control and Prevention, 2004). The presence of Acinetobacter is demonstrated in body lice, fleas and ticks, proposing the role of these vectors in the transmission of community acquired diseases especially in populations living in poor-hygiene conditions [10]. The strain acquires antibiotic resistance mainly through the production of β-lactamases and aminoglycoside-modifying enzymes [3]. In addition, diminished expression of outer membrane proteins, up-regulation of efflux pumps and mutations in topoisomerases play an important role in antibiotic resistance [3]. The accumulation of multiple mechanisms of resistance leads to the development of MDR strains. The complex interactions of MDR, the ability to spread rapidly and transfer resistance elements, regulation by quorum sensing (QS), persistence through biofilm formation and resistance to desiccation contribute to increasing difficulties in treating infections caused by these organisms. In this review, we discuss the current state of knowledge of QS and the recent dev
elopments in controlling this group of pathogenic bacteria with special emphasis on quorum quenching.
2. Virulence Factors, Biofilm Formation and Pathogenicity
The three major factors which lend to the persistence of A. baumanni in the hospital environment include multidrug resistance, resistance to desiccation and disinfections. A. baumanni has the ability to colonize abiotic substrata, including those in the hospital environment [11] and to grow as biofilm [9]. It also adheres to biotic surfaces such as human epithelial cells and erythrocytes, which may be a target during respiratory infections, or Candida albicans filaments [12,13]. The formation of pilus like structures appear to be important for adherence and this is the first step in the colonization process of A. baumanni. It has been reported that the common source of Acinetobacter bacteremia is intravascular catheters and the respiratory tract [2]. The outgrowth of A. baumanni on the mucosal surface of intravascular catheters and endotracheal tubes results in biofilm formation, which increases the risk of infection of the blood stream and airways [11].
Biofilm is a complex multicellular three dimensional structure within which the cells are embedded in a self-produced matrix of extracellular polymeric substance (EPS). The EPS comprises of carbohydrates, nucleic acids, proteins, and other macromolecules [14]. Biofilm phenotype of the pathogen promotes survival and persistence of the bacteria by resisting antimicrobials. The ability to form biofilm is an effective strategy under stressed conditions like host invasion or following antibiotic treatment [15]. It has been noticed that Acinetobacter produce a specific form of biofilm known as pellicle, which is apparent at the liquid/air interface. The pellicle formation is relevant in the persistence of A. baumanni in environments other than within the host niches. The mechanisms by which the biofilms are less susceptible to antimicrobial agents are still not clear. It is proposed that there might be less penetration of antimicrobial agents to cells of biofilm or the cells growing slowly due to organism’s slow metabolism. The glycocalyx, which is mainly composed of exopolysaccharides, provides certain degree of protection against environmental threats, including chemically reactive disinfectants such as chlorine, iodine, peroxygens, and for highly charged antibiotics, such as glycopeptides, by acting as a barrier to the cells that are deep within the biofilm [16]. β-lactamases are enzymes that hydrolyze β-lactams and in some cases, these enzymes are derepressed in the biofilm mode of growth. Thus, the enzyme concentrated in the extracellular polymer matrix hydrolyze the drug as it penetrates [17]. The introduction of mutations in the antibiotic target molecules in bacteria also contribute to the increased drug resistance of biofilms [17]. In addition, it has been revealed that gene transfer happens quite frequently in biofilms compared to that in the planktonic growth [18]. The formation of biofilm is a multistep process, involving adhesion of bacterial cells on to the surface followed by intercellular aggregation by exopolysaccharide, specific proteins and accessory macromolecules [19]. Biofilm formation is cell density dependent at which cells co-ordinate through quorum sensing molecules, resulting in biofilm formation [14]. The exact mechanisms by which biofilm associated organisms elicit disease is not known. However, the proposed mechanisms include the detachment of cells from indwelling medical device biofilms leading to blood stream or urinary tract infections, resistance to the host immune system and the production of endotoxins [20].
Apart from multidrug resistance, biofilm formation is positively correlated with the expression of several virulence factors, including the outer membrane protein OmpA, the extracellular polysaccharide poly-β-(1,6)-N-acetyl glucosamine (PNAG), type I pili, a homologue of the staphylococcal biofilm-associated protein (Bap) and the outer membrane protein CarO [11,21,22,23,24,25]. The outer membrane protein, OmpA plays an important role in the interaction of the pathogen with human and Candida cells, in addition to its role in biofilm formation on plastics [24]. In addition, the OmpA protein seems to act a part in adherence and invasion of host epithelial cells, contributing to the dissemination of A. baumanni infection [27]. In the environment, OmpA facilitates the persistence and survival of A. baumannii by involving in biofilm formation and surface motility [24,28]. The surface-associated virulence factors play a crucial role in biofilm formation as well as protection from host-defense mechanisms [23]. PNAG forms the major component of the biofilms in Acinetobacter spp. and is critical for the formation of fully developed biofilms [23]. The deletion mutant of PNAG displayed the loss of biofilm phenotype, which was restored by complementation. PNAG seems to be having profound roles in colonization, virulence and immune evasion in infections [29]. In addition to its role in cell-to-cell adherence [30], PNAG is reported to be a critical virulence factor [31], which confers resistance to antibiotics and protects the cells against the innate host immune mediators [32]. The type I pili is likely to have a role in adherence to abiotic surfaces that precedes initiation of biofilm formation in A. baumannii [11]. The pili assembly is encoded by the csu operon comprised of a gene cluster that contains six ORFs: csuAB-A-B-C-D-E [11]. The expression of this operon is under the control of a two-component system, bfmRS, comprising a sensor kinase encoded by bfmS and a response regulator bfmR [33]. It has been reported that the increased transcription of the bfmS and bfmR genes enhance the expression of the pili assembly system which is required for twitching motility in A. baumannii [34]. The accompaniment pili expression and twitching motility assists A. baumannii to attach easily to abiotic surface and form biofilms. Bap is a membrane protein that has a role to play in cell-cell communication and biofilm maturation [22]. The CarO protein constitutes a pore channel for the influx of carbapenems, the alteration of which disturbs the assimilation of β-lactam [35]. It has been revealed that the disruption of carO gene by the IS elements lead to loss of activity of CarO protein resulting in carbapenem resistance in A. baumannii [36]. In addition to the cell surface proteins, those involved in histidine metabolism (like urocanase) are also implicated in biofilm formation [26]. The general stress response and resistance to heat shock and desiccation is controlled by the protein, RecA [37].
3. Quorum Sensing
Quorum sensing is a widespread regulatory mechanism by which bacterial cells communicate each other, producing signaling molecules called autoinducers. These are small, diffusible, hormone-like molecules produced by bacteria to monitor population density and to activate adaptations [38]. QS relies mainly on cell density and upon reaching a critical concentration of signaling molecules, the cell-to-cell communication is established. The autoinducers specifically bind to transcriptional regulators leading to altered expression of various proteins in the entire population [39]. There is a specific correlation between QS and the production of virulence factors, motility, nodulation, plasmid transfer, antibiotic production, bioemulsan production, bioluminescence and biofilm formation [40]. The QS system facilitates the population to live and proliferate in a better environment with effective intercellular communication.
3.1. Quorum sensing molecules
Gram-negative bacteria including Acinetobacter predominantly produce acyl homoserine lactones (AHLs) as signal molecules for intraspecies communication that are best characterized till date. In addition to AHLs, other signaling molecules such as 2-heptyl-3-hydroxy-4-quinolone and diketopiperazines are also synthesized by Gram-negative bacteria [41]. AHLs differ in their length of carbon chain; short chain AHLs (4-8 carbon atoms) can easily diffuse through the cell membrane while the long chain AHLs (10-14 carbon atoms) need active transport system to pass through the membrane [42]. At a specific density of AHLs in the surrounding environment, the signaling molecules bind to specific receptor proteins, activating the QS machinery [43]. The first autoinducer molecule was detected in the bioluminescent marine bacterium Vibrio fischeri [44]. Acinetobacter produce upto five different QS signal molecules, which are detected in greater abundance in the stationary phase [45]. It has been reported that Acinetobacter QS signals are not homogenously distributed among species [46], thus the distinction of virulent and non-virulent strains based on QS signals is not possible. However, one particular sensor, the Rf1-type sensor was detected in most of the strains belonging to A. calcoaceticus - A.baumannii complex [46]. The study reveals that 63% of the Acinetobacter strains tested produced more than one AHL. In a recent study, majority of the A. baumanni clinical isolates tested produced more than six different signals [47] and only one type was detected abundantly among them. The culture conditions also affect the AHL production enormously as four AHLs were identified in A. calcoaceticus BD413 when grown on minimal media and three when grown on minimal media with 0.1% tryptone [45]. Although the Acinetobacter strains produce more than one AHL, only one autoinducer synthase is discovered so far [48]. This suggests that the autoinducer synthase in Acinetobacter has low specificity and may be synthesizing other AHLs with different side chain length as well.
3.2. Mechanism of quorum sensing
The first autoinducer and its cognate regulatory circuit was discovered in Vibrio fischeri and the system comprises of two proteins belonging to the LuxI and LuxR protein families [49]. The autoinducer synthesized by the LuxI directly interacts with the LuxR protein and this complex binds to a specific cis-acting sequence of a promoter called lux-box leading to the regulation of expression of QS target genes [50]. Since the expression of luxI is also activated by the AHL-bound LuxR, once the QS circuit is activated, the autoinducer production is induced and the surrounding environment is saturated with signal molecule. This autoinduction positive feedback loop is a hallmark of quorum sensing systems as it enforces synchrony as the population switches from low cell density to high cell density [49]. The LuxI/LuxR regulatory system of V. fischeri is considered the paradigm for gene regulation by QS in Gram-negative bacteria. Homologs of luxI and luxR have been identified in many bacterial genomes and they control the expression of genes in a population density-dependent manner [51,52].
QS machinery in A. baumannii is mediated by a two component system, AbaI/AbaR which is homologous to the typical LuxI/LuxR system found in Gram-negative bacteria. The system comprises of a sensor protein, AbaI that functions as autoinducer synthase, and AbaR that functions as receptor protein for AHL inducing a cascade of reactions. A putative lux-box (CTGTAAATTCTTACAG) for the binding of AbaR was detected in A. baumannii centered 67 bp upstream of the start codon of abaI [48]. The abI gene of A. baumannii strain M2 has been characterized and it was reported that the strain produce N-(3-hydroxydodecanoyl)-L-homoserine lactone (3-hydroxy-C12-HSL) [48]. The production of AHL at the transcriptional level was activated by A. baumannii culture supernatant or by synthetic 3-hydroxy-C12-HSL. The abaI mutant failed to produce any detectable AHL and the biofilm production was impaired (40% reduction). The biofilm formation in the abI mutant was restored to that of wild-type by the exogenous addition of purified AHL, indicating the role of QS in biofilm development [48]. Another study also pointed out the production of biofilm in biofilm-negative clinical isolates with the suppementation of AHL exogenously [47]. The complete genome sequencing of A. baummannii 17978 revealed that AbaI and acetyl transferases may be the sole participants for the production of AHLs with varying chemical structure [48].
A comparative analysis of the autoinducer synthases in Gram negative bacteria showed that abaI is 45% identical to the autoinducer synthases of environemental isolates such as Halothiobacillus neapolitanus, Acidithiobacillus ferrooxidans ATCC 23270, Thiobacillus ferrooxidans, Pseudomonas sp. (pmr), Ralstonia solanacearum and Burkholderia ambifaria MC40-6 [53]. However, the RhlI and LasI proteins of pathogenic Pseudomonas aeruginosa strains showed only 26.3% and 27.5% identity respectively with AbaI. The environmental isolate, Pseudomonas sp. RW10S displayed 47.3% similarity with AbaI. A greater percent identity of AbaI to autoinducer synthases of environmental isolates than those of pathogenic isolates suggests that abaI of Acinetobacter might have evolved from the environmental isolates. Genes involved in QS are distributed discontinuously among bacteria, implying that they are subjected to loss or horizontal transfer [54]. The extraordinary ability to acquire foreign DNA and the natural competence of Acinetobacter enable the organism to acquire genetic information from other organisms [55]. It has been reported that A. baumannii acquired a significant amount of genetic information implicated in drug resistance and pathogenesis [56].
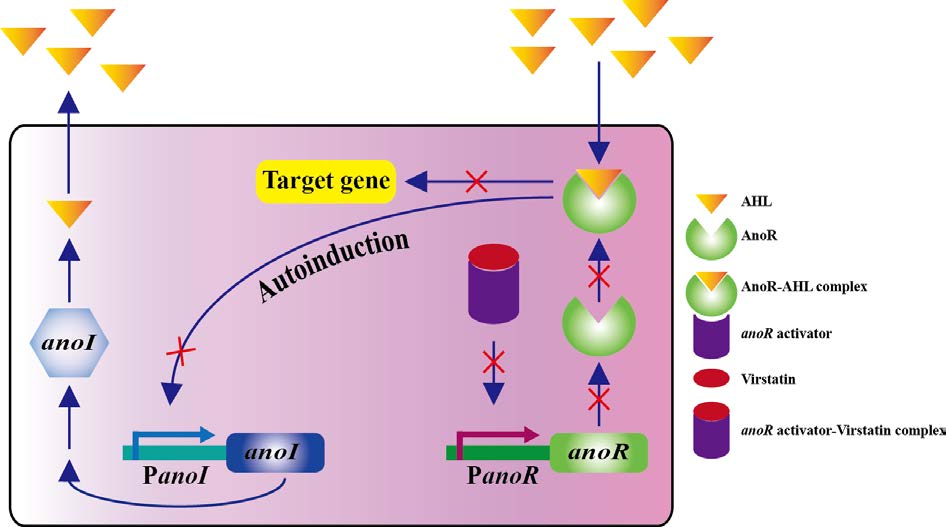
Recently, a homologue of the AbaI/AbaR regulatory system, denoted as AnoIR was characterized in A. noscomialis [57]. The putative LuxI (AnoI) and LuxR (AnoR) sequences were 94% identical in amino acid sequence to that of A. baumannii AbaI and AbaR. The anoR, gene encoding the putative luxR-type transcriptional regulator was transcribed divergently from the putative luxI. The strain produced N-(3-hydroxy-dodecanoyl)-L-homoserine lactone (OH-dDHL) as a signaling molecule. The anoI mutant was not able to synthesize OH-dDHL, indicating that AnoI is needed for the production of AHL. In addition, the expression of anoI was derepressed in the anoR mutant, suggesting the role of AnoR as activator of anoI in A. noscomialis. The biofilm formation and surface motility were impaired in the anoR mutant compared to that of wild-type. Functional complementation of anoR in the anoR mutant lead to the restoration of biofilm formation and motility to that of wild-type, emphasizing the role of anoR in the expression of anoI.
3.3. Quorum sensing and antibiotic resistance
The ability of A. baumannii to acquire drug resistance mechanisms helps them to prevail in hospital environment and also facilitates the emergence of multidrug resistant strains. There are a number of alarming reports describing the pandrug resistance of A. baumannii [58,59]. QS plays an important role in multidrug resistance in the following ways; upregulating both biofilm associated EPS matrix and efflux pump genes [60,61]. It has been suggested that EPS acts as a barrier against antibiotics, preventing their access into the bacterial community. It has been noticed that majority of the clinical isolates tested producing strong biofilm were multidrug resistant [15]. This clearly shows that there is a significant association between biofilms and multidrug resistance. Biofilm colonies are known for their resistance to suprainhibitory concentrations of antibiotics. However, studies on Pseudomonas have reported the enhanced production of biofilm upon exposure to subminimal inhibitory concentrations of macrolide antibiotics [62]. The QS molecules help in replication and transfer of plasmids that mainly carry antibiotic resistance genes [47]. The biofilm forming capacity and multidrug resistance contributes to the endurance and dispersion of A. baumannii in hospital settings.
The correlation between efflux pump and multidrug resistance is well studied in E. coli. It has been noted that the overexpression of E. coli luxR homologue SdiA [63] lead to the overexpression of AcrAB efflux pump, positively influencing multidrug resistance [64]. The sdiA null mutants are hypersensitive to drugs and have low level of AcrB protein. In P. aeruginosa, MexAB-OprM efflux pump is controlled in response to the cell density [65]. At a high population density, the QS system is activated producing the autoinducer C4-HSL. The autoinducer enhances the transcription of MexAB-OprM efflux pump independently either inducing the expresion of mexAB-oprM operon or inactivating the MexR repressor [65]. The MexAB mutants displayed intracellular accumulation of C12-HSL indicating how QS signals form part of efflux pump network. In A. baumanni, the major efflux system is the resistance-nodulation-cell division (RND)-type which shares 47% similarity with the MexAB pumps. A number of studies have reported the role of the three RND systems, AdeABC, AdeIJK, and AdeFGH in the transport of virulence factors and antibiotics in A. baumannii [66,67,68]. In addition, the strain produce C12-HSL as QS molecule suggesting a link between efflux pumps and QS that contributes multiple drug resistance [69]. Recently, He et al. [70] reported biofilm formation with the overexpression of AdeFGH pump. Another study in P. aeruginosa depicted the involvement of RpoS in multidrug resistance and the strain lacking RpoS showed decreased resistance to ofloxacin [71]. The expression of RpoS is under the control of the global regulator Hfq. The genome analysis of Acinetobacter shows evidence for the presence of both RpoS and Hfq though their interconnecting role is not yet investigated. In addition, it has been reported that 2’-Amino-acetophenone (2-AA) produced from P. aeruginosa induced the accumulation of antibiotic tolerant persister cells of A. baumannii [72].
4. Quorum Quenching and Future Perspectives
QS is a global regulatory mechanism impacting the expression of wide array of pathways that in turn enhance survival and persistence of Acinetobacter in hostile environmental conditions, such as desiccation, nutrient starvation and antimicrobial tratments. Accordingly, disruption of the QS-based inter-cellular communication (known as quorum quenching) would be the appropriate target for designing new therapeutic schemes [73]. Inhibition of the QS signals which further regulates biofilm production or expression of virulence genes has been effectively targeted for the development of novel therapeutics [74]. Use of AHL analogues and AbaR antagonists to inhibit quorum sensing pathway by attenuating biofilm formation and motility has been proven to be a valid strategy [75]. This kind of approach is very attractive since these compounds restrict quorum sensing without affecting bacterial growth, hence lower the risk of resistance development. In 2013, Saroj et. al., reported the utility of sub-inhibitory concentrations of streptomycin to inhibit quorum sensing in A. baumannii [76]. It is proposed that streptomycin could act as an antagonist of AbaR preventing the positive feedback activation of abaI by the active AHL-AbaR complex. Recently, in two independent studies, Chabane et al. (2014) and Oh et al. (2015) reported the efficacy of virstatin, a small organic molecule as an inhibitor of biofilm formation and motility in A. baumannii and A. noscomialis respectively [57,77]. It was noticed that virstatin inhibits the expression of anoR, which inturn controls the expression of anoI (Figure 1). Virstatin might be blocking one of the transcriptional regulators of anoR and further studies are needed on the regulatory mechanism of anoR in order to understand the effect of virstatin. Screening of derivatives related to virstatin would be a promising step to develop more effective inhibitors of QS. There are reports on the utilization of a number of natural compounds as quorum sensing inhibitors that interfere with AHL receptors, including Patulin/ Clavacin, vanillin and allin [78,79,80]. Cyclic di-GMP (c-di-GMP) is a second messenger signal essential for biofilm formation. It was reported that the antagonists of diguanylate cyclase enzyme that synthesize c-di-GMP inhibit QS and biofilm formation in A. baumannii [81].
Quorum quenching can also be achieved by the utilization of enzymes called AHL lactonases which degrade the quorum signal [82]. Recently, genetically engineered AHL lactonase was efffectively used for the disruption of biofilm formation (with reduction in biomass and thickness) in A. baumannii [83]. A decrease in biofilm could be translated to more effective antibiotic therapies due to increased susceptibility of bacterial cells towards antibiotic treatment. This work represents the first successful account of biofilm disruption using genetically engineered quorum quenching enzymes. Another approach for disrupting the QS system could be by exploiting the pathway for the synthesis of AHLs. For instance, the enoyl-acyl carrier protein reductase (FabI), which is important for AHL acyl chain formation, can be succesfully inhibited by triclosan at lower concentrations [84]. Also, the inhibitors targeting the iron acquisition system could be a promising tool against A. baumannii as iron metabolism and biofilm formation are closely related [85].
Studies related to quorum quenching in Acinetobacter are limited and the lack of quorum sensing inhibitors for this clinically significant pathogen is a mounting concern, especially with the continued evolution of MDR strains. Since the emergence of MDR strains limits or leave on treatment options for infected patients, development of novel strategies based on quorum quenching are necessary to combat the rising incidence of MDR bacterial infections. Fortunately, at this point of time, we may not have to look beyond existing strategies, as many Gram-negative bacteria share similar quorum sensing mechanisms. The substantial literature coverage of quorum quenching enzymes is promising as these enzymes can be screened for the potential ones for controlling biofilm in Acinetobacter sp.. Moreover, bacteria share many common AHLs; hence the enzymatic degradation of these molecules might be useful in broad spectrum control of pathogenicity in various bacteria [86]. It has been pointed out that quorum quenching enzymes do exhibit substrate specificity [87]. However, there are exceptions among AHL acylases: AiiC acylase from Anabaena sp. is promiscous with the capacity to degrade AHLs ranging from 4 to 14 carbons in the acyl chain [88]. There are also broad spectrum lactonase; QsdA lactonase fromRhodococcus erythropolis can degrade AHLs with acyl chain length ranging from 6 to 14 carbons [89]. The genetically engineered GKL lactonase from Geobacillus kaustophilus with enhanced catalytic acitivity degrades AHLs ranging from 6-12 carbon in acyl chain length [90]. The recombinant lactonase displayed improved hydrolytic activity upto 72-fold against longer AHLs and a newly acquired C4-HSL activity. The directed evolution methods applied for the identification of the improved lactonase could be employed for engineering novel substrate specificities in the existing quorum quenching enzyme scaffolds.
Eventhough QS inhibitors are effective in preventing virulence factor expression, reducing motility and biofilm formation and altering membrane permeability, bacteria do prevail after treatment. Hence, to improve their therapeutic potential, QS inhibitors need to be applied along with antibiotics for both anti-virulence and anti-bacterial effects. Some inhibitors are reported to increase susceptibility to antibiotics in P. aeruginosa, though the combined treatment was rarely tested [91]. The studies directed to the search for medicinal plants illustrated anti-quorum sensing activity in the extracts of Melaleuca alternifolia, Piper betle, Quercus infectoria, Rhizophora mucronata, or Terminalia sp. against A. baumannii [92]. Since these plant extracts exhibit quorum quenching property at subinhibitory concentrations, they could be explored for their anti quorum potential [93].
5. Conclusion
Significant advances have been made in understanding the mechanism of bacterial communicaiton in the past few years. This review discusses the current understanding of quorum sensing mechanism in Acinetobacter sp., the development of biofilm formation and various factors regulating biofilm formation. The quorum sensing mechanism is elucidated in detail with special emphasis on various physiological functions controlled by QS such as biofilm formation, motility, production of virulence factors, development of antibiotic resistance and competence that helps in gene transfer. Finally, various quorum quenching strategies are addressed, including inhibition of QS molecules synthesis, accumulation and detection. Disruption of QS is widely accepted as an anti-virulence approach as it is non-bactericidal and therefore, doesn’t increase the antibiotic resistance of strains. It is highly recommended to optimize the current quorum quenching strategies as there is a growing concern about bacterial resistance against anti-virulence methods [94]. Further studies are needed in order to completely understand the regulatory circuit of QS in depth and the molecular mechanisms of mutations that confer added advantage of increased antibiotic resistance. Understanding QS and its role in virulence will help to find out new biomolecules targeting QS. Moreover, further studies in the development of anti-virulence strategies should be proceeded with care to avoid undesired phenotypes with enhanced virulence and antibiotic resistance.
Acknowledgements
This research was supported by a grant of the Korea Health Technology R&D Project through the Korea Health Industry Development Institute (KHIDI), funded by the Ministry of Health & Welfare, Republic of Korea (grant number : HI14C0257) and Basic Science Research Program through the National Research Foundation of Korea(NRF) funded by the Ministry of Education(NRF-2014R1A6A1029617)
Conflict of interest
Authors declare no conflict of interests in this paper.









 DownLoad:
DownLoad: