In this paper, a new mathematical model (a system of delay differential equation) is proposed to describe dynamical behaviors of malaria in an infected host with red blood cells (RBCs), infected red blood cells (iRBCs) and immune factors. The basic reproduction number ℜ0 of the malaria infection is derived. If ℜ0≤1, the uninfected equilibrium E0 is globally asymptotically stable. If ℜ0>1, there exists two kinds of infection equilibria. The conditions of these equilibria with respect to the existence, stability and uniform persistence are given. Furthermore, fluctuations occur when the model undergoes Hopf bifurcation, and periodic solution appears near the positive equilibrium. The direction and stability of Hopf bifurcation are also obtained by applying the center manifold method and the normal form theory. Numerical simulations are provided to demonstrate the theoretical results.
1.
Introduction
Malaria is one of the most dangerous global health problems. It causes millions of infections every year, and more than 1.1 million people died from the disease, especially infants, young children and pregnant women (WHO [1]). The mainly affected group is children under the age of five, accounting for 82% of all malaria deaths. It is endemic in the tropical and subtropical regions of the world, and people in Africa are at the risk of such disease accounting for 27% of the world's malaria infections (WHO [1]). It is reported that about every 30 seconds, a child's life will be threatened by such disease. Although some children are survived, they still suffer miserable physical problems, such as hearing impairment and brain damage. Meanwhile, pregnant women are also susceptible to malaria infection, which can cause maternal mortality, low birth weight in infants as well as maternal anaemia. According to the statistics, it caused an estimated 243 million malaria cases led to an estimated 863,000 deaths in 2008 (WHO [1]).
Malaria infection is mainly induced by the following four malaria parasites: P. falciparum, P. malariae, P. ovale and P. vivax. Among them, P. falciparum is responsible for almost all of the deaths attributed to malaria [2]. And anopheles is a vector of malaria. Once the infected anopheles bites the host, the malaria parasites first penetrate liver cells of the host and then move into the blood, where they multiply and undergo replication cycles in the red blood cells. After 10-14 days or more, the malaria parasites develop and mature in the biting mosquitos until they can infect others. When malaria parasites evolve in the host, they can stimulate the activity of immune cells which produce an immune response.
In the past few years, lots of efforts have been carried out to control and prevent such disease [3]. However, people living in high epidemic areas are still hardly to obtain effective malaria prevention, diagnosis and treatment. As the emergence of malaria drug resistant strains and insecticide resistant mosquitoes, how to prevent and control malaria infection is still a problem. The main detriment of plasmodium in the host occurs in the blood-stage, where the parasites will develop and reproduce. In order to clarify the mechanism, many mathematical models have been employed to describe the dynamics of malaria infection.
The first model was proposed by Hetzel and Anderson [4] which studied the performance of a mathematical model for the blood phase of malaria infection with a single strain. Analyzing the cells population dynamics in the absence of a host immune response, the authors demonstrated a relationship between host and parasite parameters, which defined a criterion for the successful invasion and persistence of the parasite. Hetzel and Anderson [4] indicated some important parameters, such as the production rates of merozoite and erythrocyte, the mortality rates of merozoite and erythrocyte as well as the invasion rate of merozoite.
In 2011, Li et al. [5] studied the dynamics for malaria parasites infection in the host blood-stage. Considered that the clearance of host immune cells was restricted by concentration, the following model was established:
where H,I,M and E are population of red blood cells, infected red blood cells, malaria parasites and immunity effectors, respectively. d1,δ,μ and d2 represent the decay rate of H(t), I(t), M(t) and E(t) respectively. λ, α and r are production rate of H(t), infection of H(t) by M(t), product rate of M(t) respectively. p1,p2,k1,k2,β and γ represent the removal rate of I(t) and M(t) by E(t), proliferation rate of E(t) by I(t) and M(T), 1β means half saturation constant for I(t) and 1γ is half saturation constant for M(t) respectively. In [5], the authors showed that there existed a threshold value ℜ0 and the malaria-free equilibrium was globally asymptotically stable if ℜ0<1, if ℜ0>1, there existed two kinds of infection equilibria: malaria infection equilibrium (without specific immune response) and positive equilibrium (with specific immune response). Conditions on the existence and stability of both infection equilibria are given. Moreover, it indicated that the model could undergo Hopf bifurcation at the positive equilibrium and exhibit periodic oscillations.
A malaria model between human and mosquitoes was established by Xiao and Zou [6] which presented an important conclusion that two malaria parasites may co-exist in the same region but not in the same host.
In 2016, Chang [7] made a great progress in the study of the innate immune mechanism of plasmodium falciparum escaping the immune clearance in the host. Innate immune response is the first line for host to defense pathogen invasion. After being stimulated by the red blood cells, the host neutrophils release chromatin and lysosomal granules in the cytoplasm to form a reticular structure (NETs) in a way of active death (Netosis). NETs can capture and kill infected red blood cells. At the same time, plasmodium degrades NETs by secreting DNA enzymes (TatD-like DNase) to escape host immune elimination. Chang [7] indicated that TatD-like DNase was an important factor in the survival of malaria parasites as well as a potential candidate for malaria vaccine.
In terms of a great deal of literatures in malaria infection [8,9,10,11,12], we focus on some more important factors and hope to establish new models that can be used to study malaria infection in a host from different perspectives. Liu [13] considered three dynamical variables of populations: RBCs T(t), iRBCs I(t) and the immunity effectors (NETs) M(t). Here the model reads as
The variables and parameters are given in the table below.
The main results of model (1.1) have been shown in [13]. And here, we just simply introduce the results as below.
(ⅰ) If ℜ0<1, then the infection-free equilibrium is globally asymptotically stable.
(ⅱ) If 1<ℜ0<1+d3μd1β, then the infection equilibrium (without specific immune response) is globally asymptotically stable.
(ⅲ) If ℜ0>1+d3μd1β, then the infection equilibrium (with specific immune response) is globally asymptotically stable.
However, in real life, malaria infection does not tend to a fixed state over time, it turns out that some diseases will recur over a period of time or even change periodically. That means, it is not a good way to study the dynamics of malaria in host by using an ordinary differential equation model. Hence, in order to describe the time lag of the generation of immune factors, we consider adding a delay term to model (1.1). The delay differential equation model is as follows.
Compared with model (1.1), this model adds a time delay τ in the production item of immune factors βI(t)M(t). In the following analysis, we calculated the characteristic root of the characteristic transcendental equation and found that the stability of positive equilibrium is changed from stable to unstable, and thus the Hopf bifurcation occurs.
This paper is organized as follows. In section 2, we propose a delay differential equation model for the within-host dynamics of malaria infection based on the basic reproduction number, existence of equilibria, stability of infection-free equilibrium E0 and infection equilibria E1,E∗ as well as persistence of positive equilibrium E∗. Section 3 is devoted to exhibit periodic oscillations due to the Hopf bifurcation at the positive equilibrium E∗. Specifically, by choosing immune response delay as bifurcation parameter, we can demonstrate that a limit cycle occurs via Hopf bifurcation when the time delay τ passes through the critical value. The direction and stability of Hopf bifurcation are derived by applying the center manifold method and the normal form theory. In section 4, some numerical simulations are presented to interpret our main results biologically. A short discussion on research results is also given in this section.
2.
Global dynamical properties of the model
Consider the delay differential equation model
The initial conditions of (2.1) are given as
where (φ1,φ2,φ3)∈C([−τ,0],R3+), the Banach space of continuous functions map the interval [−τ,0] into R3+. By fundamental theory of functional differential equation (Kuang [14]), there exists a unique solution (T(t),I(t),M(t)) of (2.1) with initial conditions (2.2).
Upon the positivity and boundedness of solutions for model (2.1), we claim the following result.
Theorem 2.1. Let (T(t),I(t),M(t)) be the solution of model (2.1) with initial conditions (2.2), then T(t),I(t),M(t) are positive and ultimately bounded for all t≥0.
Proof. The positivity of the model (2.1) follows directly from Theorem 3.4 [15]. As for the boundedness of solutions to the model (2.1) with initial conditions (2.2), we denote
By the positivity of solutions, we have
where m=min{d1,d2,d3}. Hence, it comes
This implies that T(t),I(t),M(t) are ultimately bounded.
Next, we define threshold values ℜ0 and ℜ1. For model (2.1), the basic reproduction number of iRBCs, which describes the average number of newly infected cells generated by one infected cell during its lifespan, is defined by
and the immune response threshold value is defined as below
We will see that ℜ0 and ℜ1 play key roles in determining the existence and stability of equilibria of the model (2.1). Actually, let
The following results can be verified by direct calculations.
(ⅰ) If ℜ0≤1, then (2.1) always has a unique infection-free equilibrium E0=(T0,0,0), where T0=λd1.
(ⅱ) If 1<ℜ0≤ℜ1, then (2.1) has two equilibria, E0 and infection equilibrium (without specific immune response) E1=(T1,I1,0), where T1=d2μ and I1=λμ−d1d2d2μ=d1(ℜ0−1)μ.
(ⅲ) If ℜ0>ℜ1, then (2.1) has three equilibria, E0,E1 and infection equilibrium (with specific immune response) E∗=(T∗,I∗,M∗) respectively, where T∗=λβd1β+d3μ,I∗=d3β and M∗=λμβ−d1d2β−d2d3μd1αβ+d3αμ=d1d2β(ℜ0−ℜ1)d1αβ+d3αμ.
Now, we investigate the stability of the equilibria of model (2.1). Consider the linearization of the model (2.1) at E=(T(t),I(t),M(t)),
where x(t)=(T(t),I(t),M(t))T,
The characteristic equation of (2.5) is formulated as (Hale [16])
Theorem 2.2. If ℜ0<1, then the infection-free equilibrium E0 of model (2.1) is locally asymptotically stable. Moreover, E0 is unstable if ℜ0>1.
Proof. By substituting E0 in (2.5), (2.6), (2.7) and (2.8), we obtain the following characteristic equation
Clearly, Λ1=−d1, Λ2=−d3 and
which dominates the stability of E0. If ℜ0<1, then Λ3<0. Therefore, when ℜ0<1, all eigenvalues of model (2.1) have negative real parts and hence, equilibrium E0 is locally asymptotically stable. In addition, when ℜ0>1, we have Λ3>0, which means E0 is unstable.
Theorem 2.3. If ℜ0≤1, then the infection-free equilibrium E0 of model (2.1) is globally asymptotically stable.
Proof. Define Lyapunov functional V0 as follows
Differentiating V0 with time t along the model (2.1), then
Obviously, if ℜ0≤1, then dV0dt≤0 for any T(t),I(t) and M(t). In addition, dV0dt=0 if and only if T(t)=T0,I(t)=0 and M(t)=0. Let Γ be the largest invariant set of {(T(t),I(t),M(t)∈R3+∣dV0dt=0}, we easily get Γ={E0}. According to LaSalles invariance principle (Kuang [14]), it follows that equilibrium E0 is globally asymptotically stable when ℜ0≤1. This completes the proof.
Theorem 2.4. If 1<ℜ0<ℜ1, then the infection equilibrium (without specific immune response) E1 of model (2.1) is locally asymptotically stable.
Proof. By substituting E1 into (2.5), (2.6), (2.7) and (2.8), we have the following characteristic equation
It is easy to check that Λ2+d1ℜ0Λ+d1d2(ℜ0−1)=0 has two eigenvalues Λ1 and Λ2 with negative real parts if 1<ℜ0<ℜ1. We assume that Λ=a+ib satisfies
Substituting Λ=a+ib into (2.10) and separating the real and imaginary parts, we obtain
Assume that a≥0, when 1<ℜ0<ℜ1, then a<d3[e−aτcos(bτ)−1] from the right hand side of the first equation of (2.11). This contradicts the assumption. So we get a<0, i.e. ReΛ3<0. Thus, all eigenvalues of equation (2.9) have negative real parts and equilibrium E1 is locally asymptotically stable.
Theorem 2.5. If 1<ℜ0≤ℜ1, then the infection equilibrium (without specific immune response) E1 of model (2.1) is globally asymptotically stable.
Proof. Define Lyapunov functional V1 as follows
Differentiating V1 with time t along model (2.1), then
Obviously, if 1<ℜ0≤ℜ1, then dV1dt≤0 for any T(t),I(t) and M(t). In addition, dV1dt=0 if and only if T(t)=T1,I(t)=I1 and M(t)=0. By LaSalles invariance principle (Kuang [14]), equilibrium E1 is globally asymptotically stable when 1<ℜ0≤ℜ1. The proof is completed.
Next, we study the stability of the infected equilibrium (with specific immune response), which is denoted by positive equilibrium E∗. Recall that the positive equilibrium E∗ exists if and only if ℜ0>ℜ1. At equilibrium E∗, the characteristic equation for the corresponding linearized model of (2.1) is
where
When τ=0, equation (2.12) becomes
where
Clearly, (A+A1)(B+B1)>C+C1. By Hurwitz criteria, all eigenvalues of equation (2.13) have negative real parts, which leads to the local stability of equilibrium E∗ when τ=0. In fact, in this case, E∗ is also globally stable.
Theorem 2.6. If ℜ0>ℜ1 and τ=0, then the infection equilibrium (with specific immune response) E∗ of model (2.1) is globally asymptotically stable.
Proof. Define Lyapunov functional V∗ that
Differentiating V∗ with respect to t along model (2.1), we get
If ℜ0>ℜ1, then dV∗dt≤0 for any T(t),I(t) and M(t). In addition, dV∗dt=0 if and only if T(t)=T∗,I(t)=I∗ and M(t)=M∗. By using LaSalles invariance principle (Kuang [14]), equilibrium E∗ is globally asymptotically stable when ℜ0>ℜ1. This completes the proof.
Now we consider the stability of the equilibrium E∗ if ℜ0>ℜ1 and τ>0. By theorem 4.4 of Hal Smith [15], for small enough delay, the characteristic roots of (2.12) are either very near the eigenvalues of (2.13) or having more negative real parts than any of the eigenvalues of (2.13). Hence, when the delay is small the equilibrium E∗ is locally asymptotically stable.
When ℜ0>ℜ1, for any τ>0, zero is not a root of (2.12). Note that any complex roots to the equations (2.12) appear in pairs, and all roots of (2.12) have negative real parts if τ=0. Therefore, any root of (2.12) has negative real part for sufficiently small τ. Assume that there exists τ=τ∗, such that (2.12) has a pair of pure imaginary roots, denoted by Λ=±ωi,(ω>0). Substituting Λ=ωi into (2.12), we have,
Separate the real and imaginary parts,
It follows that
Let z=ω2, it follows that
where
By calculating p1,q1 and r1, we obtain
Equation (2.15) has no positive roots if it satisfies p1>0,r1>0,p1q1−r1>0 (Hurwitz criterion). Hence, τ∗ doesn't exist. It follows that all solutions of equation (2.15) have negative real part and E∗ is locally asymptotically stable for any τ>0. Therefore, we have the following theorem.
Theorem 2.7. If ℜ0>ℜ1 and p1>0,r1>0,p1q1−r1>0, then the infection equilibrium E∗ is locally asymptotically stable for any τ>0.
Theorem 2.8. If ℜ0>ℜ1 and r1<0, there exists τ∗>0, such that equation (2.15) has a pair of conjugate purely imaginary roots ±ω∗i when τ<τ∗. Moreover, the infection equilibrium E∗ is locally asymptotically stable if τ<τ∗.
Proof. We know that if r1<0, then equation (2.15) has at least one positive root and not more than three positive roots. Assume that equation (2.15) has three positive roots, denoted by zk,k=1,2,3, it follows that
where k=1,2,3,n∈Z+. Suppose that
When τ=τ∗, equation (2.15) has a pair of conjugate purely imaginary roots. Note that all roots of equation (2.15) have negative real part if τ=0, and all roots of equation (2.15) have negative real part if τ<τ∗, which follows from the continuous dependence of the solution on τ.
In what follows, we study the persistence of equilibrium E∗, following the analysis of Wang et al. [17].
Lemma 2.1. Let X be a locally compact metric space and it is the union of two disjoint subsets X1 and X2, with X2 be compact in X, X1 be open and forward invariant under the continuous semiflow Φ on X. Assume that
has an acyclic isolated covering M=∪mk=1Mk. If each part Mk of M is a weak repeller for X1, then X2 is a uniform strong repeller for X1.
Theorem 2.9. If ℜ0>ℜ1, then M is uniformly persistent, that is, there exists a positive constant σ, such that the positive solutions of model (2.1) satisfy lim inft→∞M(t)>σ.
Proof. By Theorem 2.1, model (2.1) is point dissipative. Let
To prove Theorem 2.9, we need to show that X2 is uniformly strong repeller for X1. It suffice to verify the conditions of Lemma 2.1. Obviously, X is locally compact, X2 is compact and X1 is forward invariant. In addition, there are two equilibria E0=(λd1,0,0) and E1=(d2μ,λμ−d1d2d2μ,0) in X2. Consider
By Theorem 2.5, E11=(T1,I1)=(d2μ,λμ−d1d2d2μ) is globally asymptotically stable for solutions (T(t),I(t)) to (2.16) with positive initial value if 1<ℜ0≤ℜ1. In addition, let Y={(T,0)|T≥0}, then Y is positively invariant for (2.16) and the solutions to (2.16) in Y approach E00=(T0,0)=(λd1,0) as t→∞, it becomes zero or unbounded as t→−∞. Therefore, it follows that
Thus, we know that M is acyclic in X2. From theorem 2.4, 2.5 and the Jacobian matrix at E00, it is easy to check that E00 and E11 are hyperbolic if ℜ0>ℜ1, which implies that E00 and E11 are isolated in X2. From what has been discussed above, Ω2 has an acyclic isolated covering M=E00∪E11.
Next, we need to show that each part Mk(k=1,2) of M is a weak repeller for X1. It suffice to show that Ws(E11)⋂X1=∅ and Ws(E00)⋂X1=∅, where Ws(E11) denotes the stable manifold of E11, and Ws(E00) denotes the stable manifold of E00. Suppose Ws(E11)⋂X1≠∅, then there is a solution of model (2.1) such that limt→∞(T(t),I(t),M(t))→E11. Therefore, from the third equation of model (2.1) that for any ε>0, there exists t0>0, then we obtain
Note that
then for t≥t0 and M′(t)≥g(ε)M. Since ℜ0>ℜ1, we can choose ε sufficiently small such that g(ε)>0. Thus, (2.17) shows that M(t)→∞ as t→∞. This contradicts the ultimate boundedness of Theorem 2.1. Hence, Ws(E11)⋂X1=∅. Similarly, we can prove Ws(E00)⋂X1=∅.
3.
Hopf bifurcation
In the following, we shall determine when the equilibrium E∗ becomes unstable and Hopf bifurcation occurs. We will seek conditions which guarantee characteristic equation (2.15) to have a root with negative real part as well as a pair of conjugate purely imaginary roots.
Theorem 3.1. Suppose ℜ0>ℜ1 and r1<0, then there exists τ∗>0. If τ>τ∗, there is a Hopf bifurcation of model (2.1) from equilibrium E∗ as τ passes through the critical value τ∗.
Proof. Consider the derivative of eigenvalue on real axis across section of positive equilibrium point E∗ on τ=τ∗ ([18]). Assume that Λ(τ)=ξ(τ)+iω(τ) is the eigenvalue of equation (2.15) at τ near τ∗ and calculate the derivative of equation (2.15) on τ, we obtain ([19])
This gives
For ξ(τ∗)=0 and ω(τ∗)=ω∗, then
where Z=[b21ω2∗+(C1−A1ω2∗)2]ω2∗>0. Since z3∗+p1z2∗+q1z∗+r1=0 and r1<0, then 3z2∗+2p1z∗+q1>0 if either p1≥0 or q1≤0. So we have
if either p1≥0 or q1≤0.
Remark 3.1. By theorem 3.1, we can extend that if there exists p1,q1 and r1, which makes z3∗+p1z2∗+q1z∗+r1=0 and z∗Z(3z2∗+2p1z∗+q1)>0 hold. Then periodic solutions are bifurcated near the positive equilibrium E∗.
We have already shown the existence of Hopf bifurcation. Next, we will give a formula by using the center manifold theorem and the normal form theory to determine the direction of Hopf bifurcation and stability of periodic solutions.
Let v(t)=T(τt)−T∗,x(t)=I(τt)−I∗ and y(t)=M(τt)−M∗. Then (2.1) can be rewritten as
where
A=(−d1−μI∗−μT∗0μI∗0−αI∗00−d3),
B=(0000000βM∗βI∗),
F(vt,xt,yt,τ)=(−τμv(t)x(t)τμv(t)x(t)−ταx(t)y(t)τβx(t−1)y(t−1)−τd3M∗).
Let ˆτ be the critical value of τ where model (2.1) undergoes a Hopf bifurcation at E∗. Assume τ=ˆτ+h, then h=0 is the Hopf bifurcation value of (2.1).
Choose the phase space C=C([−1,0],R3). Define L(h):C→R3 by
From the Riesz representation theorem, there exists a matrix whose components are bounded variation functions η(θ,h):[−1,0]→R3,θ∈[−1,0], such that
We select η(θ,h)=(ˆτ+h)Aδ(θ)−(ˆτ+h)Bδ(θ+1), where
For ϕ∈C1([−1,0],R3), we give
such that
Then (3.1) can be rewritten as
For φ∈C1([0,1],(C3)∗), define
And for ϕ∈C([−1,0],C3) with φ∈C([0,1],(C3)∗), define
then A∗ and A(0) are adjoint operators, such that ⟨φ,Aϕ⟩=⟨A∗φ,ϕ⟩. Let q(θ) and q∗(s) be the eigenvectors of A and A∗ corresponding to iwˆτ and −iwˆτ respectively. Via direct calculation, we obtain following result.
Lemma 3.1. q(θ)=(1,α1,β1)Teiˆwˆτθ is the eigenvector of operator A on iˆwˆτ, q∗(s)=¯D(1,α2,β2)Teiˆwˆτs is the eigenvector of operator A∗ on −iˆwˆτ, and ⟨q∗,q⟩=1,⟨q∗,ˉq⟩=0, where α1=−iˆw+d1+μI∗μT∗, β1=−iˆwα1−μI∗αI∗, α2=−iˆw+d1+μI∗μI∗, β2=−iˆwα2+μT∗eiˆwˆτβM∗.
Proof. Let q(θ)=(1,α1,β1)Teiˆwˆτθ be an eigenvector of operator A on iˆwˆτ, it follows from Aq(0)=iˆwˆτq(0), then
The calculation shows that α1=−iˆw+d1+μI∗μT∗, β1=−iˆwα1−μI∗αI∗. Similarly, we can obtain α2=−iˆw+d1+μI∗μI∗, β2=−iˆwα2+μT∗eiˆwˆτβM∗.
To ensure ⟨q∗,q⟩=1, we only need
The details have been given in Hassard et al. [20] corroborated ⟨q∗,ˉq⟩=0. Here we are not going to repeat it. The proof is completed.
Following the algorithm in Hassard et al. [20], we first compute the coordinates to describe the center manifold C0 at h=0. Let μt=(vt,xt,yt)T be the solution of (3.1) when τ=ˆτ, i.e. when h=0. Define
On the center manifold C0, it shows
where
z and ˉz represent the local coordinates for the center manifold C0 in the direction of q∗ and ˉq∗. Note that W is real if ut is real, and here, we only consider real solutions. For the solution ut∈C0 of (3.1), since h=0,
We rewrite the above equation as
where
From (3.2) and (3.3), we have
where
Expanding the above series and comparing the coefficients, it yields
Note that
and
Direct substitution and comparing the coefficients with (3.4) shows that
We still need to compute W20(θ) and W11(θ). For θ∈[−1,0], it comes
Comparing the coefficients with (3.5), we found that
and
It follows from (3.6) that
Then solving the above equation, we get
Similarly,
where E1 and E2 are both two-dimensional vectors and can be determined by setting θ=0 in H. In fact, since
we have
and
It follows from (3.6) and the definition of A that
and
Substituting (3.7), (3.8) into the above two equations respectively yields
where I is the 3×3 identity matrix. Consequently, g21 can be expressed in terms of the parameters and delay ˆτ. Then the following values can be computed,
Utilizing the results of Hassard et al. [20], we make a conclusion as follows.
Theorem 3.2.
(ⅰ) If μ2>0(<0), then the Hopf bifurcation is supercritical (subcritical).
(ⅱ) If β2<0(>0), then the bifurcating periodic solutions are stable (unstable).
4.
Simulations, biological explanations and discussions
In order to interpret the conclusions from a quantitative perspective, the dynamics of malaria infection in the host by numerical simulations will be analyzed in the following. In this section, we use matlab to find the numerical solutions of the model (2.1) and analyze the effect of basic reproduction number ℜ0 and the immune response reproduction number ℜ1 on malaria infection.
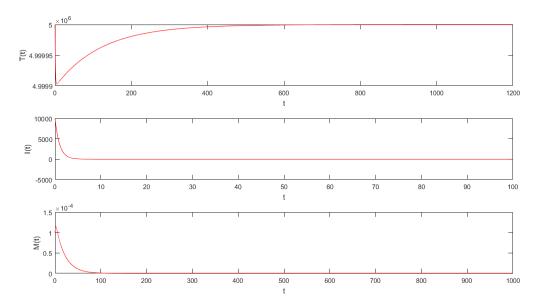
With parameters values given in Table 1 and Table 2, we get ℜ0=0.0025<1. Hence, Theorem 2.3 indicates that the infection-free equilibrium E0 is globally asymptotically stable. Meanwhile, this result shows that iRBCs can be eliminated by immune response in host infected with malaria, such that malaria infection can not be established within a host if ℜ0≤1 (see Figure 1).
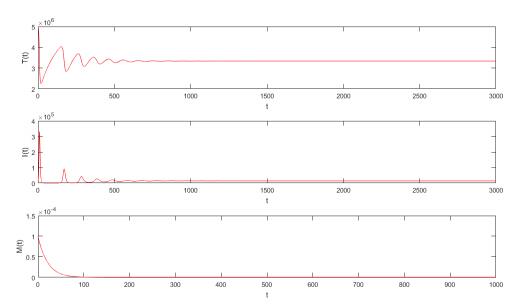
Taking u=3×10−7,β=1.5×10−8 and the other parameters values as in Table 1 and Table 2, we get ℜ0=1.5 and ℜ1≈121. The infection equilibrium (without specific immune response) E1 is globally asymptotically stable. It means that the generation of immune factors in the host are degraded immediately, which ultimately leads to the failure of the immune factors in the host, that is, immune factors do not remove the iRBCs in the host completely, such that malaria infection can be established in the host if ℜ0>1 (see Figure 2).
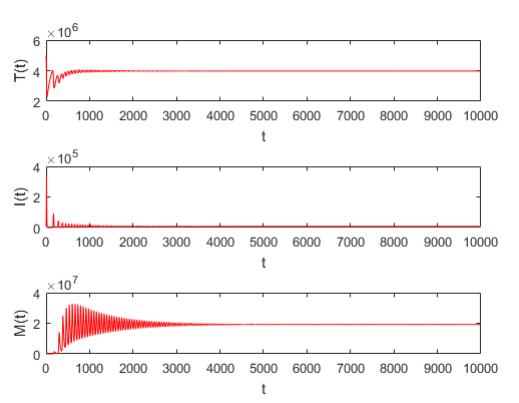
Taking τ=0,u=3×10−7,β=7×10−6 and the other parameters values as in Table 1 and Table 2, we get ℜ0=1.5 and ℜ1≈1.26. The infection equilibrium (with specific immune response) E∗ is globally asymptotically stable. It shows that immune factors play roles in the host, but the number of immune factors and iRBCs will eventually tend to a dynamic balance. Immune factors can not completely eliminate the iRBCs in the host, such that malaria infection can be established in the host if τ=0 and ℜ0≥ℜ1 (see Figure 3).
When all parameters values are as in Figure 3 with τ=0.1, we can find the solution curve is the same as Figure 3. It means that there is no great change in the stability of the equilibrium E∗ when the time delay τ is small. Immune factors can not completely eliminate the iRBCs in the host, so malaria infection can be established in the host if τ=0.1 and ℜ0>ℜ1 (see Figure 4).
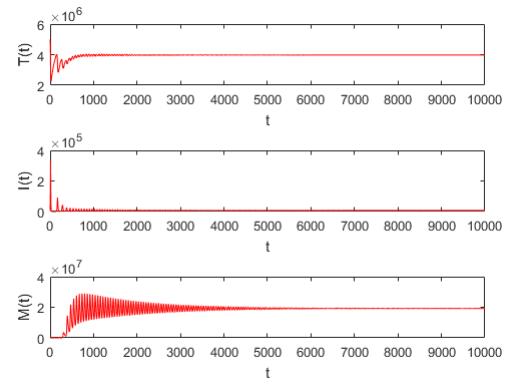
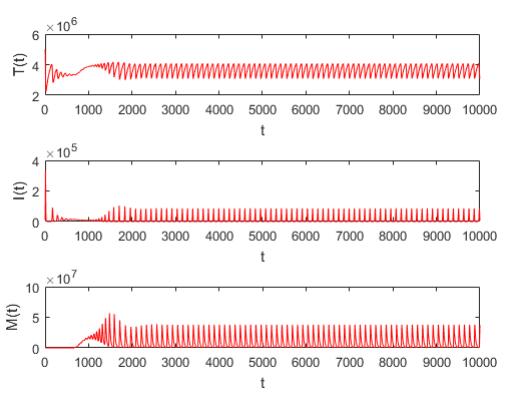
When τ increases and passes through τ∗≈0.238. For example, taking τ=2, we get ℜ0=1.5,ℜ1≈1.26 and E∗ becomes unstable. Theorem 3.1 implies that model (2.1) undergoes Hopf bifurcation and a periodic solution appears. It means that in the previous period of relative stability, the number of iRBCs is very small. Meanwhile, the number of immune factors is small as well, the iRBCs in the host has not been cleared completely. We consider that the incubation period for malaria leads to the number of iRBCs rising again after a period of time. Maybe that is why malaria might rekindle in the host (see Figure 5).
In this paper, we have discussed a malaria infection model with time delay.
For the model (2.1), immune response delay τ plays a important role in the stability of the equilibrium E∗. We derive the basic reproduction number ℜ0 for the malaria infection and establish that the dynamics are completely determined by the basic reproduction number ℜ0. The results show that when ℜ0≤1, the infection-free equilibrium E0 is globally asymptotically stable for any delay τ. It signifies that the malaria is cleared and immune response is not active. When 1<ℜ0≤ℜ1, the infection equilibrium E1 without immune response exists and it is globally asymptotically stable for any delay τ, which means that the immune response would not be activated and malaria infection can be established in the host. When ℜ0>ℜ1, some results are given as below:
(ⅰ) If τ=0, the infection equilibrium with immune response E∗ is globally asymptotically stable.
(ⅱ) If τ<τ∗, the infection equilibrium with immune response E∗ is locally asymptotically stable.
(ⅲ) If model (2.1) satisfies theorem 3.1 or remark 3.1, the dynamical behaviors of equilibrium E∗ will occur and locally asymptotically stable becomes unstable and Hopf bifurcation appears. By choosing immune response delay as bifurcation parameter, we have demonstrated that a limit cycle occurs via Hopf bifurcation, when the delay passes through the critical value τ∗. This explains the fact that the immune response delay plays negative role in controlling disease progression. The direction and stability of Hopf bifurcation is derived by applying the center manifold method and the normal form theory.
Moreover, we study the uniform persistence of infection equilibrium E∗.
Numerical simulations are also provided to demonstrate these theoretical results. Finally, we hope that our work will be helpful to the study of malaria infection.
Acknowledgements
The authors wish to thank two anonymous reviewers for their very helpful comments. QD, JL and ZG were supported by National Science Foundation of China (No. 11771104), Program for Chang Jiang Scholars and Innovative Research Team in University (IRT-16R16).
Conflict of interest
All authors declare no conflicts of interest in this paper.









 DownLoad:
DownLoad: