The known nonlinear mathematical model of the Glassy-winged Sharpshooter is considered. It is assumed that this model is influenced by stochastic perturbations of the white noise type and these perturbations are directly proportional to the deviation of the system state from the positive equilibrium point. A necessary and sufficient condition for asymptotic mean square stability of the equilibrium point of the linear part of the considered stochastic differential equation is obtained. This condition is at the same time a sufficient one for stability in probability of the equilibrium point of the initial nonlinear equation. Numerical calculations and figures illustrate the obtained results.
1.
Introduction
Nowadays, the real-world optimization problems we face in scientific research, engineering and even daily life are becoming more and more complicated. Demand for fast, accurate and robust optimizer has been on the rise among researchers in the various fields for several decades. Dating back to 1940s, diverse traditional operations research approaches such as linear programming (LP), nonlinear programming (NLP), integer programming or dynamic programming (DP) were first applied to solve complex optimization problems. In the following decades, some iterative methods such as Newton's method, Conjugate gradient method, and Gradient descent method were proposed as well. The methods mentioned above can be categorized into the exact methods. Unfortunately, these exact methods have limitations for solving real-world problems. For instance, gradient-based methods can only find local optimum, whereas most of the real world problems have multiple local optimums. For another instance, when dealing with large-scale NP-hard problems, exact methods cannot obtain the global optimum in polynomial time. These limitations are the stumbling blocks for their successful applications to real-world problems.
Fortunately, people can always get inspirations from nature. For some nature-inspired approximation methods, although they cannot guarantee to obtain the global optimum, they can obtain the near global optimum of the large-scale problems in reasonable time. Therefore, they are more suitable for practical applications than those exact methods. Meta-heuristics are the most important classes in the approximation methods, they are considered as high-level techniques or strategies that intend to combine lower-level techniques and tactics for exploration and exploitation of the huge solution space [1]. Most of the meta-heuristics combine the randomness and rules to imitate the natural or social phenomena, and the research on the meta-heuristic algorithms is one of the hottest topics in the current academic community. The inspiration sources of popular meta-heuristics include animal behavior (e.g., particle swarm optimization (PSO) [2], ant colony optimization (ACO) [3], artificial bee colony (ABC) [4], and cuckoo search (CS) [5]), biological evolutionary process (e.g., the genetic algorithm (GA) [6] and the differential evolution (DE) [7]), physical process (e.g., simulated annealing (SA) [8]), and chemical process (e.g., chemical reaction optimization (CRO) [9]). Over the last decades, many outstanding meta-heuristic algorithms have been successfully applied to various real-world problems and obtained better solutions than traditional methods.
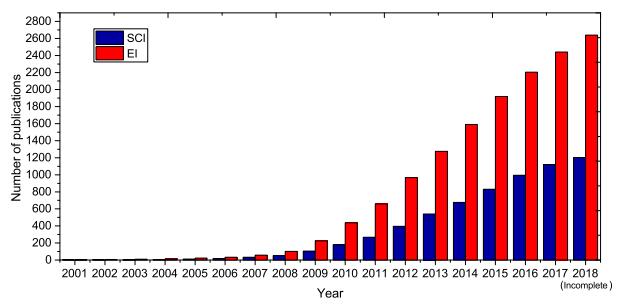
Harmony search (HS) algorithm is one of the most popular meta-heuristic algorithms [10]. It was inspired by the music improvisation process in which the musicians continuously adjust the pitch of their instruments to get a better harmony. The music improvisation process is similar to the search process of global optimization problems that each decision variable continuously adjust its value during the search process to converge to the global optimum. HS is a successful meta-heuristics optimization algorithm, which is simple in concept, easy in implementation with few parameters. Since its inception in 2001, HS has drawn the attention of many researchers all over the world. Figure 1 depicts the accumulated number of SCI and EI publications on HS from 2001 to 2018. It indicates that the researches on HS are now at the stage of rapid growth. The international communication activity on HS has been also proved a big success, the fourth international conference on HS was successfully held in India, Feb 2018. During the latest decade, HS has been successfully applied in various fields, such as Renewable energy systems [11,12,13,14], system reliability problems [15], robot path planning [16,17], hyper-parameter optimization of deep neural networks [18,19], and others [20,21,22].
The manufacturing industry is the foundation for a nation's economy and it has powerful influences on people's daily lives. As one of the emerging new technologies, intelligent manufacturing has game-changing impacts on the whole manufacturing industry. The purpose of intelligent manufacturing is to optimize production and product transactions by making full use of advanced information and manufacturing technologies and finally upgrades the whole life cycle of a typical product [23]. Within an intelligent manufacturing system, lots of decisions need to be made, from product design to supply chain and from the level of manufacturing operation to the level of manufacturing system management etc. In recent years, meta-heuristic algorithms are becoming popular methods to achieve those optimal decisions [24,25,26,27,28,29]. Of course, HS is among them.
Although there are already some literature review articles on the HS algorithm [30,31,32,33,34,35], the survey on HS applications to intelligent manufacturing was not covered. Actually, after searching on databases such as IEEE, Elsevier, Springer, and Taylor & Francis, we found about 40 articles in recent years related to the HS applications within the scope of intelligent manufacturing, including production scheduling, design optimization, industrial wireless sensors network, assembly sequence planning, automated guided vehicle (AGV) etc. It is of great interests to survey these innovative applications. In addition, the latest four years (2015-2018) have witnessed the rapid development of HS variants. It is also important to summarize the new progress in HS variants development. Hence, the major aim of this review paper is to present an intensive but not comprehensive review of the latest developments of HS variants and their applications within the scope of intelligent manufacturing, and then, to identify some potential research trends.
The remainder of this paper is organized as follows: Section 2 introduces the basic idea of the HS algorithm with its some prominent variants. Section 3 summarizes some of the latest HS variants for function optimization. Section 4 gives an overview of the innovative HS applications in the field of intelligent manufacturing. Finally, section 5 gives the concluding remarks and some potential future research directions.
2.
Harmony search algorithm with its prominent variants
2.1. Harmony search algorithm
In the HS algorithm, each solution is represented by a "harmony" with an $ n $-dimension real vector. There are four main steps in HS, namely initialization, improvisation, harmony memory update, and termination check. In the first step, an initial population of harmony vectors is randomly generated and stored in a harmony memory (HM). In the second step, a new candidate harmony is improvised based on all the solutions in HM by using memory consideration, pitch adjustment, and random re-initialization. In the third step, the worst harmony vector in HM is replaced by the new candidate harmony if the new candidate harmony has better fitness. In the fourth step, HS will stop if the predefined stopping criterion is reached, otherwise go back to step 2. The pseudo code of HS illustrated is in Figure 2. There are several differences between HS and other meta-heuristic algorithms such as GA and DE: (1) each newly generated harmony in HS can learn from all individuals from the harmony memory, however, in algorithms such as GA and DE, the child individual is generated by the crossover operation from two parent individuals; (2) even a small number of harmony memory size in HS (similar with population size in GA and DE) can work efficiently, while GA and DE always need a large population size to maintain the population diversity; (3) HS always abandons the worst individual in harmony memory for update, whereas GA and DE follows the principles of Darwinian natural selection for population update, in which only the individual with better fitness can be survived.
2.2. Improved harmony search algorithm (IHS)
The IHS algorithm was firstly proposed by M. Mahdavi, et al.[37], in which the memory consideration, pitch adjustment and random selection are same with the original HS algorithm, but the parameter values of $ PAR $ and $ BW $ are dynamically updated as follows:
where $ PAR(t) $ is the pitch adjustment rate in generation $ t $, $ PAR_{min} $ and $ PAR_{max} $ are the minimum and maximum adjustment rate, respectively.
2.3. Global-best harmony search algorithm (GHS)
Inspired by the concept of swarm intelligence as proposed in Particle Swarm Optimization (PSO) [2], Omran and Mahadavi [38] proposed another variant of HS algorithm, named the global-best harmony search (GHS) algorithm. In GHS, the new harmony $ \mathit{\boldsymbol{X}}_{new} $ is generated by directly learning from the current best pitch within the HM to simplify the pitch adjustment procedure. GHS has exactly the same steps as the IHS with the exception that step of improvising the new harmony is modified as shown in Figure 3.
2.4. Self-adaptive global-best harmony search algorithm (SGHS)
Based on the GHS, Pan et al. [39] proposed a self-adaptive global-best harmony search (SGHS) algorithm. SGHS employs a new improvisation scheme and an adaptive parameter tuning method. It does not require a precise set of specific values for the critical parameters $ HMCR $, $ PAR $ and $ BW $ in accordance with problem's characteristics and complexity. Instead, the $ HMCR $ and $ PAR $ are dynamically adjusted within a suitable range by recording their historical values corresponding to generated harmonies entering the HM. The value of the $ BW $ parameter is decreased with increasing generations by a dynamic method. The computational procedure of SGHS is shown in Figure 4.
2.5. Novel global-best harmony search algorithm (NGHS)
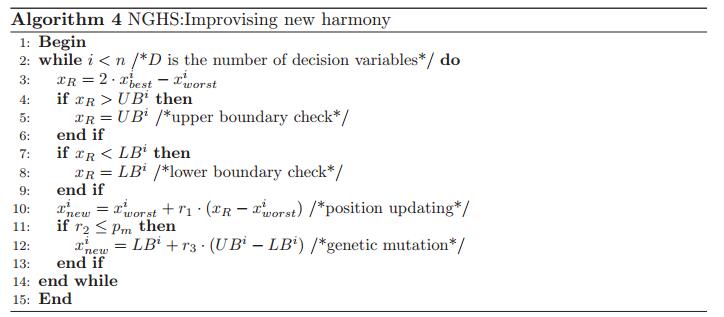
Zou et al. [40] proposed a different variant of HS named novel global harmony search (NGHS) algorithm. The structure of NGHS is much different from the original HS, where the parameters like $ HMCR $ and $ PAR $ are deleted, and a genetic mutation operation with a very low probability ($ Pm $) is introduced. Furthermore, a new updating strategy is proposed in NGHS. Figure 5 depicts the improvisation procedure of the NGHS.
3.
Latest HS variants for continuous optimization problems
When searching for the recent HS-related publications in SCI database, we found that most of HS papers incorporate some modifications to the original HS algorithm without targeting any specific application scenario but the numerical benchmarks for continuous optimization. Considering that the proportion of this kind of article is huge, we will summarize this part first. Beyond the HS variants listed in the last section, there are also many other interesting variants of HS, which can be found in previous review literature, e.g. Alia and Mandava [32] and the references therein. Fortunately, HS has more and more attention from researchers all over the world and so many interesting new HS variants were developed in recent years, as summarized in Table.1. Hence, this section aims at shedding some light on the latest HS variants. Nevertheless, the readers are still recommended to resort to any of the previous reviews to get a broader insight into the HS developing history.
3.1. Variants based on different parameter setting strategies
Parameter settings have a big impact on the performance of the HS algorithm. For instance, a smaller value of $ HMCR $ can lead the algorithm focusing on exploration in the whole search space while a larger value of $ HMCR $ can lead the algorithm focusing on local exploitation. The proper selection of HS parameter values is considered as one of the challenging tasks not only for the HS algorithm but also for other meta-heuristics. The major reason is that parameter setting strategy is problem dependent, one parameter setting strategy is suitable for one problem but may perform badly for another. However, this challenge drives the research into new directions of HS: dynamic and adaptive parameter setting strategies of HS algorithm. Actually, a lot of remarkable progress have been achieved in this area, e.g. IHS proposed by Mahdavi, Fesanghary and Damangir [37], SGHS proposed by Pan et al. [39]. In this subsection, some new progress in this area will be summarized.
Chen, Pan and Li [41] proposed a new variant of HS with dynamic control parameters named NDHS. The proposed NDHS includes a new pitch adjustment scheme that parameters $ PAR $ and $ BW $ are dynamically adapted. The first parameter $ PAR $ is changed dynamically with the generation number as follows:
The second parameter $ BW $ is composed of two stages. During the first stage, the $ BW $ value is changed based on the selected pitch $ x^i_{new} $ to explore within the entire search space. During the second stage, the $ BW $ value is computed by the distance between $ x^i_{new} $ and a randomly selected pitch $ x^i_{a} $ in HM. $ BW $ is represented by a piece wise function:
Enayatifar et al. [42] proposed a new HS variant based on the learning automata named LAHS. In LAHS, the learning ability is used to select parameters based on spontaneous reactions. At first, all the parameter values are uniform randomly generated. Then, a reinforcement signal is sent back after each fitness evaluation, if the fitness value is improved, the signal will be a reward one, otherwise, it will be a punishing one. The automaton learning mechanism employs this feedback to update the existing parameters probability distributions. By repeating this action, the probability distribution of better parameters will be increased, and the most favorable parameter values are eventually determined. Kattan and Abdullah [43] proposed a dynamic self-adaptive HS algorithm, which utilizes two different methods to dynamically adapt the values of the $ PAR $ and $ BW $ during the optimization process. The proposed approach introduces a best-to-worst ($ BtW $) ratio ($ 0 < BtW < 1 $) of the current HM. The $ BtW $ ratio is calculated as follows:
The $ BtW $ ratio shows the quality of the current solutions in HM. A high $ BtW $ value indicates that the quality of the current HM solutions is approaching that of the current best. In the new approach, $ PAR $ value decreases or increases in response to the computed $ BtW $ ratio as follows:
If the $ BtW $ value decreases, indicating bigger quality difference on solutions in current HM, then the $ PAR $ value increases to enhance the local exploitation. If the $ BtW $ value increases, indicating smaller quality difference on solutions in current HM, so the $ PAR $ value decreases to enlarge the search space and solutions diversity. For the other parameter $ BW $, the new approach using a dynamic bandwidth value ($ DBW $) that considers each dimension of harmony vector separately:
Wang and Yan [45] proposed a global best HS algorithm with control parameters co-evolution based on PSO (PSO-CE-GHS). In their proposed method, parameters like $ HMCR $ and $ PAR $ are considered as symbiotic individuals of the original individuals. During the evolutionary process, these two symbiotic individuals are co-evolved by PSO. As a result, with the evolution of the HM in PSO-CE-GHS, these two parameters are dynamically and self-adaptively adjusted and the real-time optimum control parameters are obtained. Khalili et al. [47] proposed a global dynamic HS algorithm named GDHS. In GDHS, both HMCR and PAR are dynamically adjusted during the searching process as follows:
$ HMCR $ and $ PAR $ increase during the first half iterations and decrease during the second half iterations.
Another HS variant was proposed by Kumar, Chhabra and Kumar [48]. In their research, the impact of dynamic parameters on the algorithm performance is investigated. Dynamic parameters with linear and exponential forms are tested in four groups of tests. Results show that linear change in $ HMCR $ and exponential change in $ PAR $ outperforms other techniques in a noisy and scalable environment.
Wang et al. [52] proposed a new HS variant based on dual strategies and adaptive parameters (DSAHS). In DSAHS, the initial value of the parameter $ HMCR $ is set to 0.95 and the parameter $ PAR $ is set to 0.5. During the search, $ HMCR $ and $ PAR $ are automated tuned based on the feedback of the fitness of new harmony, if the current HM is updated, the values are kept unchanged, otherwise $ HMCR $ randomly picks a value in a range of $ (0.9, 1.0) $ and $ PAR $ randomly selects a value in a range of $ (0.1, 1.0) $.
Guo et al. [53] proposed an adaptive HS with best-based strategy (ABHS). ABHS adopts a similar parameter control strategy with DSAHS. In ABHS, the initial value of the parameter $ HMCR $ is randomly generated in a range of $ (0.9, 1.0) $ and the parameter $ PAR $ is randomly generated in a range of $ (0.3, 1.0) $. During each iteration, $ HMCR $ and $ PAR $ are re-initialized with a low probability of $ 0.1 $.
3.2. Variants with different selection strategies
Selection is a vital component for Evolutionary Algorithms. It decides the survivability of the individuals during the search and drives the search toward the global optimum [81], which is consistent with the principles of Darwinian natural selection. Several selection strategies have been proposed to improve the performances of EAs, such as the tournament, linear rank, exponential rank and proportional etc. [55]. All these selection strategies utilized the principle of "survival of the fittest" to obtain better search performances.
In HS algorithm, the principle of "survival of the fittest" can be found in the procedure of harmony memory updating, where the HS has to decide whether to substitute the worst harmony with the improvised new one. However, memory consideration in the step of improvising new harmony is not based on the goodness of the harmonies, and thus the selection process is completely random. Drawing on the successful experience of other EAs, some novel selection methods in memory consideration may have the potential of obtaining better performances.
Al-Betar et al. [54] proposed several novel selection schemes to replace the random selection scheme in memory consideration, namely global-best selection scheme, tournament selection scheme, linear rank selection scheme, exponential rank selection scheme and proportional selection scheme. The novel selection strategy used the natural selection principle of "survival of the fittest" to improvise new harmony by learning from the excellent solutions stored in HM. Computational results showed that the novel selection schemes directly influenced the performance of HS. One of the consequences is that the parameters like $ PAR $ and $ HMS $ became less sensitive. However, limitations can be found in the proportional selection scheme that it is not applicable when the negative objective function value is possible. To overcome the drawbacks, Al-Betar, et al. [55] proposed a scaled proportional selection scheme. They also carefully analyzed the influences of the parameters in different selection methods. They found an appropriate setting of these parameters could enhance the HS performance.
Based on the above research, Castelli [56] proposed a geometric selective harmony search (GSHS). The unique characteristic of GSHS is in three perspectives: first, a selection procedure inspired by Genetic Algorithms (GAs) and Genetic Programming (GP) is used; second, new harmony improvisation process that linearly combines the information of two harmonies; and third, GSHS uses a newly defined mutation operator. The new algorithm is named "geometric" because the authors want to highlight its properties of the memory consideration process and the newly defined mutation operation. The major difference between GSHS and other selection-based HS is that the tournament selection procedure is used to choose two different solutions and the pieces of information present in both two parent solutions were taken into consideration to generate the candidate harmony.
3.3. Variants based on modification of HS structure
Some other novel HS variants are based on the modification of its basic structure. Kaveh and Ahangaran [58] proposed a social HS for continuous optimization. The main difference between social HS and the basic HS appears at the step of pitch adjustment, where social HS uses the normal distribution for adjusting the new harmony found by the memory consideration rule. El-Abd [62] proposed an improved global-best HS (IGHS) based on the GHS. The author thought that HS should emphasize exploration at the initial search stage and emphasize exploitation at the end stage. Hence, two different distributions were introduced into HS, namely Gauss distribution and normal distribution. The two modified improvisation strategies are shown as follows:
where $ Gauss(0, 1) $ is a Gaussian random number with a mean of 0 and a standard deviation of 1.
where $ \phi $ is a random number uniformly distributed in the range [0, 1].
Hasan et al. [63] carefully analyzed the influence of different mutation operations on HS performance, and finally found polynomial mutation improved the performance of HS significantly.
Valian, Tavakoli and Mohanna [64] proposed an intelligent global HS (IGHS) based on NGHS. IGHS modified the improvisation step of the NGHS by employing the concept of swarm intelligence. In IGHS, parameters $ HMCR $ and $ PAR $ were used to the improvisation procedure.
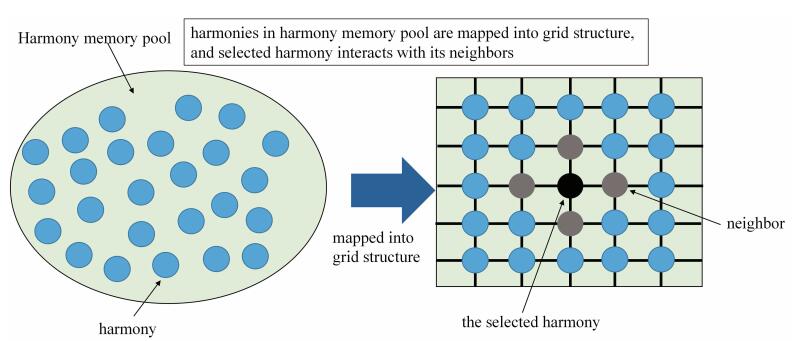
Inspired by the idea of the cellular automata (CA) [82], Al-Betar, et al. [60] proposed the cellular HS. The essential idea of the CA model is to simulate macro-behavior by the micro-dynamics, which is produced by the interaction of a population of individuals who are connected in particular neighborhood structures [83]. In cellular HS, HM was arranged as a two-dimensional toroidal grid, and the improvisation process was adjusted to interact with the neighborhoods of specific individuals. One of the advantages of the structured population is that it can maintain a high level of diversity during the search process. Figure 6 shows the schematic drawing of cellular HS.
Yi et al. [67] presented a modified HS (MHS) for continuous optimization problems. In MHS, the HM is divided into two groups based on the fitness: the better group and the worse group. The new harmonies are generated by intersecting mutation operations between harmonies from the better group and the worse group. MHS also introduces a cellular local search to enhance the exploitation power.
Yadav, Kumar, Panda and Chang [50] proposed an intelligent tuned HS (ITHS). ITHS borrowed the concepts from the decision-making in a group. In ITHS, the HM was first divided into two sub-populations based on their fitness values, and then the proper pitch adjustment strategy based on its HM was automatically selected. The authors also carefully studied the influence of the parameters on HS performance.
Some other multi-population based structures also have been introduced into HS. Turky and Abdullah [65] proposed a multi-population HS with an external archive (MHSA-ExtArchive) to solve dynamic optimization problems. In MHSA-ExtArchive, the HM is divided into several sub-populations and each sub-population took charge exploring or exploiting the search space. Moreover, an external archive is used to save the current best individual for later use. In their later work, another multi-population structured HS called dual-population multi operators HS (DPMO-HSA) was proposed [84]. In DPMO-HSA, the population is first divided into two population, one is responsible for exploration and the other is responsible for exploitation. DPMO-HSA also introduces multi-pitch adjustment operators to in order to handle different landscapes. Ashrafi and Dariane [61] proposed a novel HS variant named melody search (MS) which has a very different structure with the classical HS. The MS algorithm was inspired by the musical performance processes that group members from a musical group interact with each other to find the best series of pitches within a melodic line. The major difference between MS and HS is that MS employs several memories, called Player Memory (PM). The main body of MS consists of two computation phases, the initial phase and the second phase. In the initial phase, each music player can improvise melody without the influence of others; whereas, in the second phase, music players interact with each other, which acts like group performance. The structure of MS is very similar to multi-population HS. Another multi-population based HS variant is the island-based HS (iHS), which was proposed by Al-Betar et al. [66]. It learns the concepts of island model that has been adopted in evolutionary algorithms (EAs). In iHS, The HM is divided into several sub-populations (islands) and each island evolves independently for a number of iterations. Periodically, information can be shared between different islands by using the migration process, which is responsible for exchanging certain individuals across islands controlled by the migration rate and the migration frequency. The above three HS variants share the similar algorithm structure and both have improved performance. The main reason for their success is that both of them maintain the population diversity by means of tracking different trajectory through the search space. The multi-population based algorithm structure is also very suitable for parallel implementation, which helps reduce the computational costs.
The opposition-based learning strategy also has been embedded into the HS structure [57,69]. Ouyang et al. [69] proposed a new HS variant based on local opposition-learning where during the improvisation process, an opposite new harmony is generated along with the new harmony.
3.4. Variants based on hybridization with other meta-heuristics
Hybridization of different meta-heuristics is an efficient way to enhance the performances. It can integrate their advantages and cover their shortcomings. In this section, some latest hybrid HS variants are introduced.
Tuo, Yong and Zhou [71]proposed a hybrid HS with Teaching and Learning based optimization (TLBO) method named HSTL. HS was also hybridized with Bat algorithm [85], Biogeography-based optimization [72], Cuckoo Search algorithm [73], ant colony optimization algorithm [76], simulated annealing algorithm [78], mine blast algorithm [79], and differential evolution [80]. Yuan et al. [74] proposed a hybrid parallel chaos optimization with HS (PCOA+HS). The authors considered that the moving step of PCOA is always big, so HS was employed as a local search optimizer to improve the solution accuracy. Zhang et al. [77] proposed a memetic algorithm based on cooperative particle swarm optimization and modified harmony search algorithm for non-separable multi-modal optimization problems.
4.
Review of HS applications to intelligent manufacturing
4.1. Survey of distribution for HS applications within the intelligent manufacturing scope
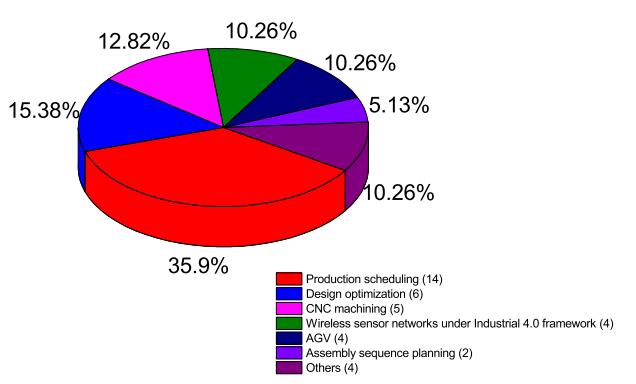
In this section, the distribution of HS applications to intelligent manufacturing area is analyzed. To achieve this goal, we collected 39 related papers that have been published during recent years (especially during the latest 3 years from 2015 to 2018) in databases of IEEE, Elsevier, Springer and Taylor & Francis. We found that the applications of HS approach cover the topics such as production scheduling, design optimization, CNC machining, wireless sensor networks under Industrial 4.0 framework, automated guided vehicles, assembly sequence planning, and others. To show an overview of the spread of HS applications within the intelligent manufacturing area, Figure 7 depicts the distribution of HS applications. As shown in Figure 7, application in production scheduling comprises the greatest proportion (35.9%), followed by Design optimization (15.38%). As the supplementary illustration of Figure 7, Table 2 gives a detailed classification of articles in the different application area.
4.2. Production scheduling
Production scheduling can be defined as "allocation of available production resources to carry out manufacturing tasks in an efficient manner" [125]. The purpose of production scheduling is to maximize the efficiency of the operation and reduce costs. Actually, production scheduling can be divided into several specific problems, such as single machine scheduling problem, permutation flow shop scheduling problem (PFSP), job shop scheduling problem (JSP), and flexible job shop scheduling problem (FJSP). Unfortunately, production scheduling is an intractable NP-hard optimization problem, even in its simplest forms [126]. It has been widely investigated in the research community over decades [127,128,129,130]. Recently, one of the research trends is employing meta-heuristic methods to solve these problems [129,131,132,28,29]. As an effective meta-heuristic method, the HS algorithm also has been applied in solving production-scheduling problems. In this section, some research works about HS applications to production scheduling are summarized.
Single machine scheduling is the process of assigning a group of tasks to a single machine. The performance measures of the tasks in the single machine-scheduling problem include tardiness, earliness, lateness and flow time. In the real-life Just-In-Time (JIT) production and delivery situations, each job is expected to be completed as close to its due date as possible, neither too early nor too late. In recent research, the well-known restrictive single-machine earliness/tardiness scheduling problem in JIT production is investigated by Liu and Zhou [90]. In this work, the total penalty of earliness and tardiness is taken as the objective function to be minimized. To tackle this problem, a hybrid method combines permutation-based HS with a variable neighborhood search is proposed. While in another research work, Zammori et al. [92] considered a more realistic situation in the single machine scheduling problem where the single machine is characterized by a time increasing failure rate, and both reactive and planned maintenance tasks are taking into account. To solve this problem, the authors proposed a two stages approach: at the first stage, the optimal number of maintenance tasks is computed aiming to maximize machine's availability; then, the near-optimal jobs maintenance sequence is obtained by a newly developed HS.
The permutation flow shop scheduling problem (PFSP) is another typical scheduling problem, in which the processing order of the jobs on the resources is the same for each subsequent step of processing. PFSP widely exists in modern industries and has been extensively discussed in academical research and practical applications [133,134]. Zhao et al. [97] proposed a hybrid HS with efficient job sequence scheme and variable neighborhood search (VNS) named HHS for the permutation flow shop scheduling problems. HHS first uses the smallest order value rule based on the random-key to convert the continues harmony vectors to discrete job permutations. Other techniques such as the opposition-based learning technique and a novel variable neighborhood search with efficient insert and swap structures are also adopted.
The flexible job shop scheduling problem (FJSP) is an extension of the classic JSP, in which operations are allowed to be processed by any machine from a given set, rather than one specified machine. Compared with the classical JSP, FJSP contains job assignment sub-problem, which makes the search space larger, hence it is more complicated than the classic JSP. A recent work conducted by Yuan et al. [91] presents the application of the HS algorithm for solving FJSP by minimizing the makespan. In their proposed method, a two-vector code method is used to represent machine assignment and operation sequence, and then a harmony vector is mapped into a feasible active schedule through active decoding. A problem dependent local search method is also utilized to enhance the local exploitation. Maroosi et al. [95] proposed a parallel and distributed HS framework (MIHS) based on membrane systems for FJSP. In MIHS, the individual solutions within each membrane on different cores evolve independently according to the HS operations. In addition, individuals between different membranes can exchange their information with each other. Although parallel HS frameworks have already been proposed such as island model-based HS and multi-population HS, the membrane-based parallelism is more flexible and general. While in another research, Gao et al. [86] proposed a Pareto-based grouping HS algorithm for solving multi-objective FJSP with makespan and earliness-tardiness criteria. The authors thought the small-sized HM works better than a large one for the HS algorithm, so they divided the HM into several sub-HMs in a dynamic way. They also proposed two different local search methods to enhance the search-ability and reduce the search space. In their later work, the objectives of FJSP are formulated as a weighted combination of the maximum makespan and the mean of earliness and tardiness [88]. To solve this problem, a discrete HS (DHS) with novel methods for generating initial machine assignment tasks and improvising new harmonies was proposed. To enhance the exploitation ability, several local search methods are embedded into DHS. The fuzzy or uncertainty of processing time has vital engineering implication in re-manufacturing engineering and it's also one of seven characteristics of re-manufacturing. It is of great interests to study the fuzzy or uncertain operation processing time in FJSP. Gao et al. [87] studied the FJSP with fuzzy processing time the in re-manufacturing process and proposed an effective discrete HS to minimize the maximum fuzzy completion time.
HS algorithm has also been applied to other types of production scheduling problems, e.g. Li et al. [93] proposed a hybrid HS algorithm for solving multi-objective flowline manufacturing cell scheduling problem (FMCSP) with total tardiness and mean total flow time minimization. They adapted a one-point crossover operator for population diversification and the iterative local search method for further improving the solution. Guo et al. [96] proposed a harmony search-based memetic algorithm for integrated production and transportation scheduling (IPTS) in make-to-order (MTO) manufacturing. The IPTS is a joint problem that simultaneously considers how to assign jobs to machines and how to deliver the finished products to customers. In IPTS, production and transportation operations are highly integrated to improve the supply chain performance and therefore achieve higher supply chain sustainability [135]. In their work, a HS-based memetic algorithm with certain heuristic procedures is proposed to convert the IPTS problem into an order assignment problem. Gao et al. [89] studied the scheduling and rescheduling problems with increasing processing time and new job insertion in the re-manufacturing process. Re-manufacturing is the process of disassembly and recovery of products, which requires repair, reprocessing or replacement of worn-out or obsolete components and modules [136]. Re-manufacturing is a cost-effective solution to address the environmental, legislative and competitive pressures in the modern manufacturing industry. In their work, the problem is formulated as a bi-objective optimization problem which needs to simultaneously minimize the maximum completion time and the mean of earliness and tardiness. A discrete HS algorithm equipped with an experience-based strategy, rescheduling strategies, and a local search method is thus designed to solve the problem.
Energy is one of the most important resources for manufacturing enterprises and the energy consumption in the industrial sector is huge. In China, manufacturing enterprises consume almost 50% of national electricity energy [137]. Huge industrial energy consumption is one of the most significant factors that lead to environmental deterioration. Therefore, manufacturing companies have made efforts to improve energy efficiency during the manufacturing process. There are several ways to reduce the energy consumption, such as machine level, product level, and manufacturing system level, among which, reducing the energy consumption through the manufacturing system level with energy-efficient production planning and scheduling is one of the most cost-effective ways since it can be accomplished with much less financial investment. Following this research line, Garcia et al. [94] proposed a discrete HS algorithm with random-key encoding scheme for energy-efficient production scheduling with limited availability of shared resources.
4.3. Design optimization
Product design is an important part of the manufacturing process. Digital and intelligent product design is the pathway to achieve intelligent manufacturing. Product design optimization, the purpose of which is to obtain the best possible design of the product under given conditions or constraints. However, product design optimization is challenging. The reasons are fourfold: (1) the number of design variables can be very large; (2) the problems are often subjected to many nonlinear constraints; (3) the objectives and constraints are sometimes computationally-expensive to evaluate; (4) multiple objectives may need to be considered simultaneously. We found several previous works covered this field, such as constrained design optimization[21,36], surrogate-assisted design optimization [103,104,102] and topology optimization [100,138,101].
Mun et al. [21] proposed a modified HS with constraint fitness priority-based ranking method for constrained design problems. Yi et al. [36] proposed a parallel chaotic local search enhanced HS with Deb's constraint-handling technique for constrained design problems.
Nowadays, with the rapid development of computer technology, advanced simulation techniques such as computational fluid dynamics (CFD) and finite element analysis (FEA) have been applied to product design optimization. Although simulations can significantly reduce the experimental cost, they are often computationally expensive. Therefore, surrogate-based design optimization methods (SBDO) have been proposed. The basic idea of SBDO is to build a computationally cheap approximation (surrogate) of the computationally-expensive simulation model and use the surrogate to help search for the optimal design. Keshtegar et al. [103] developed an off-line SBDO method based on adaptive dynamic HS algorithm and second-order polynomial regression for optimal design of aircraft panels. In their work, a surrogate model is built before the optimization procedure and it will not be updated during optimization. In their later work, an improved on-line SBDO method based on a Gaussian global best HS and second-order polynomial regression is developed. In this updated work, the surrogate model is updated after each run of HS. The aforementioned SBDO methods are based on a single high-fidelity model, whereas besides the high-fidelity (HF) models there are also some low-fidelity (LF) models. Thus, it's possible to build a surrogate model based on both the HF and LF models, this is call variable-fidelity (VF) surrogate. VF surrogate enjoys the advantages of higher prediction accuracy and lower computational cost. The selection of sample points of VF approximation (nested design), has a direct impact on the performance of VF surrogate. Thus a proper nested design for variable-fidelity approximation is essential. However, the nested design problem is an NP-hard combination optimization problem. Yi et al. [102] developed a sampling approach based on successive local enumeration (SLE) and discrete novel global best HS (NGHS) algorithm (SLE-NGHS). In SLE-NGHS, the LF samples are generated by SLE and then the HF samples are selected from LF sample by using NGHS.
As one of the three main categories in design optimization, topology optimization is the most efficient way of reducing weight. Recent years, applications of HS to solve the topology optimization problems have been found in the literature, such as Lee et al. [101] applied HS to static stiffness topology optimization problems, Lee et al. [100] applied HS for dynamic topology optimization problems.
4.4. Assembly sequence planning
Assembly is an important process within product manufacturing, where different components are assembled one by one and finally become the complete product. Within the products assembly process, the assembly sequence plays a key role, inappropriate assembly sequence may cause low productivity and sometimes even violate the assembly constraints. Therefore, developing intelligent assembly sequence planning (ASP) techniques to improve productivity and product quality is very important. Unfortunately, ASP is an NP-hard combination optimization problem where the search space will increase exponentially with the number of parts increase. For example, even for a small scale of products assembly process with only 15 parts, the number of possible solution can reach $ 15! = 1.3077 \times 10^{12} $. To solve the ASP problem efficiently, and automatically, some soft-computing methods such as meta-heuristic algorithms have been introduced to solve this problem [139]. Although meta-heuristic algorithms cannot guarantee to find the global optimum, they are still widely used in practice because they are able to access near-optimal solution effectively for large-scale problems. There are two fundamental procedures to solve the ASP problem, the first one is to build an appropriate mathematical optimization model for ASP, the second one is to develop an optimization scheme to solve the problem. Li et al.[106] proposed an improved HS for solving ASP problem. In their work, an existing optimization model is adopted and a structure based encoding method is designed to represent the assembly sequence. The opposition-based learning (OBL) strategy and a local search are also used to enhance the performance of HS. In their later work, another encoding method based on the largest position value rule is designed [107]. The new encoding method is very similar with the random key technique, where the assembly sequence is determined by the ascending order of the values in the first row within a harmony.
4.5. Automated guided vehicle (AGV) applications
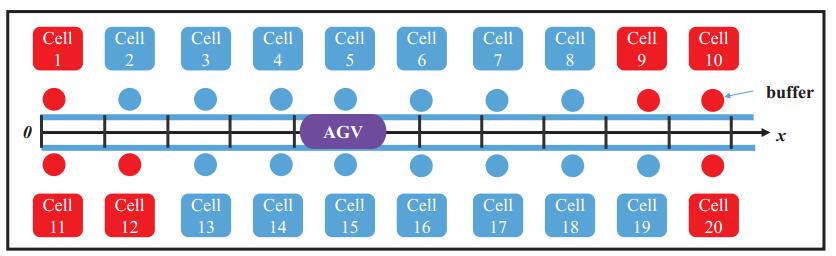
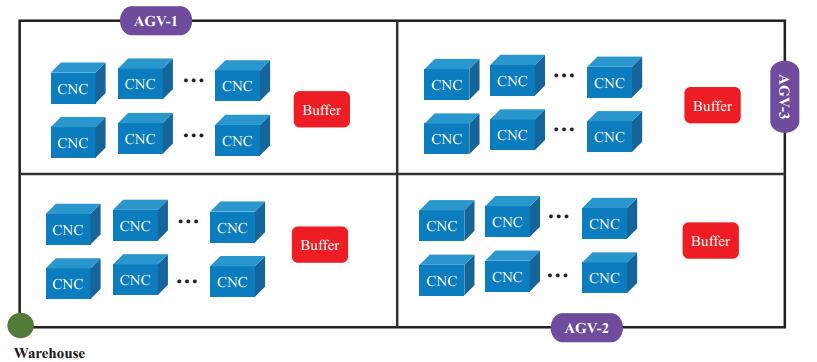
The automated guided vehicle (AGV) has been widely used in nowadays manufacturing factories to transport cutting tools and materials between warehouse and workstations. AGV is one of the most efficient solutions for material handling because of their routing flexibility, space utilization, and safety. Most of the currently used AGVs are line followers, where they usually follow the painted line on the floor that guides them to their destinations. It seems to be an easy task to scheduling AGVs tasks on the fixed lines, however, it's far from the truth. The amount of possible scheduling solutions increases exponentially with the number of computer numerical control (CNC) machines, thus the AGV scheduling problem (AGVSP) is NP-hard. The problem will become even more complicated when multiple AGVs work cooperatively because the task assignment is needed in addition to task scheduling. Li et al. [108] studied the single AGV scheduling problem in a CNC production line. As shown in Figure 8, the AGV moves back and forth on the fixed line to transport material to CNC cells. An appropriate task sequence is needed so that the total travel distance of AGV is minimized and the impact on CNC productivity is also minimized at the same time. In their work, the optimization objective is formulated as the weighted sum of the the total travel distance of AGV and standard deviation of the waiting time of CNC material buffers. An improved HS with discrete encoding, dynamic parameter control strategy and local search is proposed to solve the problem then. Li et al. [109] considered a more complicated situation where multiple AGVs work cooperatively within the production workshop of an industry 4.0 manufacturing factory, which is called the tasks assigning and sequencing problem of multiple AGVs (AGVASP). Figure 9 shows the schematic diagram the workshop layout. In the workshop, the cells will send the demand signal for production materials or cutting tools immediately when the buffer inventories are under a certain level. When the central control system receives the request, AGVs will be scheduled to deliver the production materials or cutting tools. AGVs must deliver the required materials or cutting tools in time so that the pause of CNC machining can be avoided. In their work, the optimization objective of AGVASP is formulated as the weighted sum of (a) the total walking distance of all AGVs, (b) the standard deviation of the workload of all AGVs, and (c) the standard deviation of the difference between the calculated delivery time and the required latest delivery time. The objective is also subjected to several constraints such as each task can only be performed by one AGV, the total workload of a single AGV cannot exceed its maximum capacity. To solve the AGVASP problem, an improved HS with discrete encoding harmony is proposed. In their proposed approach, the task sequence is represented by a harmony, and then the harmony is further divided into several segments which represent the task assignments.
An another recent interesting HS applications to AGV is conducted by Mahaleh and Mirroshandel [110], where the HS is used for path detection for vision-based AGV. For a vision-based line follower AGV, AGV must extract the path information from captured images and follow the track. In specific, the path detection and tracking system must find a certain number of points inside every captured image that are distributed evenly inside the path area. After that, a regression model can be used to determine the shape of the matching path. This problem is actually a complicated combination optimization problem which has an extremely huge number of possible combinations. For instance, a single $ 320 \times 240 $ image has $ 76,800 $ individual pixels. If only 10 pixels were chosen to be the solution, the number of possible combinations will reach $ 2.2262\times 10^{22} $. In their experiment, the HS is employed for path detection on a differential two-wheeled robot. The experimental results show HS successfully complete the real-time image processing task and outperforms Genetic algorithm in every aspect.
4.6. CNC Machining
CNC machining is a manufacturing process in which the movement of tools and machinery is dictated pre-programmed computer software. The process can be used to control a range of complex machinery and three-dimensional cutting tasks can be accomplished in a single set of prompts. We found several recent research works on HS from the databases are related to CNC machining, which includes machining parameter optimization[113,114], tool indexing problem [116] and tool path planning for 5-axis flank milling[115]. In this section, these research works are summarized.
Abhishek et al. [113] studied the optimal drilling parameters tuning problem for drilling of polyester composite plates. In their work, the analysis of variance (ANOVA) approach is first performed to assess the effects of drilling parameters on multiple responses such as thrust, torque and delamination factor of the drilled composite product. After that, the obtained multiple responses are converted into a single response with the help of a fuzzy inference system (FIS). In the final step, the HS is employed to search for the optimal drilling parameter combinations. Another similar research work is conducted by Kumari et al. [114], in which they study the effects of different turning parameters like spindle speed, feed rate and depth of cut on turning performance during dry turning of AISI D2 Steel using PVD coated carbide tool.
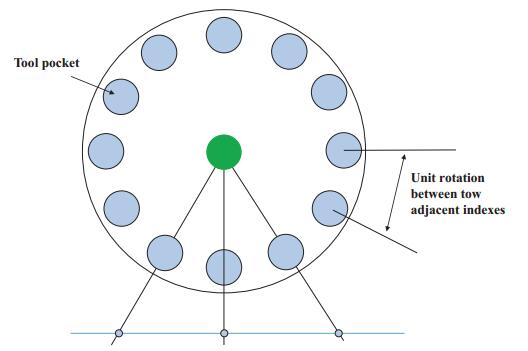
In CNC machining operation, the total processing time of a job is the sum of the cutting times by the various tools available and the time required for changing the tools. The cutting time for a specific job is constant, however, the time required for changing tools is flexible and it can be optimized. Significant improvements in the total processing time can be achieved by reducing the tool changing time. In a manufacturing system, machining operations require many tools in a specific order to complete a job. Different types of tools are available in the turret of the CNC machine. Figure 10 depicts the schematic diagram of tools that are kept in tool pockets. During the tool changing operation, the required tool is brought into place by rotating the turret. The total time consumption for rotations of the turret is called non-machining time. Therefore, the aim of the tool indexing problem (TIP) is to find an optimal tool index so that the total non-machining time is minimized [140]. The TIP problem is also known as an NP-hard problem [141]. Recently, Atta [116] proposed a customized HS algorithm with a harmony refinement strategy to solve the TIP problem. The computational results on 27 test instances show the performance of the proposed approach is excellent. It has improved the best-known solutions for 16 instances out of 27 instances. The proposed approach also requires less computational times compared to previous methods.
Nowadays, 5-axis CNC machining is widely used in the manufacturing industry. As a key to high machining quality and productivity in 5-axis flank milling of ruled surfaces, optimization-driven tool path planning can effectively reduce the geometrical errors on the finished surface. However, to solve the tool path planning problem is a challenging task with a large number of decision variables. Recently, Yi et al. [115] proposed a novel approach to generating an optimized tool path for 5-axis flank finishing cut based on a geometric decomposition strategy and multi-population HS algorithm. In their research, the machined surface is first geometrically divided into several segments and then a multi-population HS with local search method is used to optimize the tool paths in the corresponding sub-surfaces independently. In the proposed multi-population HS, updated tool paths are shared between neighbor sub-populations. The multi-population HS structure also makes it suitable for parallel implementations. The experimental results show the proposed approach can access high accurate machining accuracy. An improved version of the approach also has been implemented on the supercomputing platform which can obtain similar machining accuracy but with the computational time reduced to one minute or even less.
4.7. Wireless sensor networks under Industrial 4.0 framework
Cyber-physical systems (CPS) and the Internet of things (IoT) are the foundations for Industrial 4.0 framework. Within the Industrial 4.0 smart factories, cyber-physical systems monitor physical processes, create a virtual copy of the physical world and make decentralized decisions. With the help of the IoT, cyber-physical systems communicate and cooperate with each other and with humans in real-time both internally and across organizational services offered and used by participants of the value chain [142]. With the advantages such as low cost, scalability, flexibility, and alarm monitoring, industrial wireless sensors network (IWSN) has become one of the pathways to achieve Industry 4.0 smart factory settings. However, some technical challenges still existed during the practical applications of IWSN, for example, harsh environment, reliability and latency, and energy limits. Hence, lots of approaches have been proposed for improving the performance of IWSN from different aspects. We found several recent HS related works fall into this scope, which includes energy-efficient deployment and scheduling [117], energy-efficient routing [118], node placement [119,120]. In this section, these works will be summarized.
Lin et al. [117] studied the joint deployment and scheduling problem for a large-scale group-based IWSN. As wireless sensors are equipped with batteries with limited power, it thus needs to plan sleep schedules of sensors for saving energy, however, the schedules are influenced significantly by the deployment of IWSN. In their work, a two-stage optimization procedure based on hybrid HS and genetic algorithm is proposed to solve the problem. Zeng et al. [118] studied the energy-efficient routing problem for WSN, where the objective is to find a route from the source node to the sink node that has the minimum energy consumption. In their work, an improved HS with variable harmony length encoding is proposed to this problem. Wang et al. [119] studied the multi-objective node placement problem to guarantee the reliability and real time of IWSN. In their work, the node placement problem is formulated as an NP-hard tri-objective binary optimization problem with constraints. To solve the problem, a multi-objective binary differential HS is proposed. Another similar work was conducted by Alia et al. [120]. In their work, the node deployment problem is formulated as a single objective optimization problem, where the objective is to find the optimal deployment positions for sensor nodes, such that coverage is maximized.
4.8. Other topics in intelligent manufacturing
We also found some other HS applications in intelligent manufacturing. Lin et al. [121] studied the problem of rare faults forecasting for critical components in a LED manufacturing industry. In their work, operating conditions of particle filters are first monitored and collected by industrial sensors. After that, a pre-process procedure on those data is performed by data filtering and clustering. Then, a hybrid approach based on grey forecasting and HS is used to fit the curve of the aging condition of a particle filter. Lin et al. [123] studied the integrated order planning (IOP) problem in steel-making continuous casting-hot rolling production of multiple plants, which is a large-scale many-objective optimization problem with four conflicting objectives. In their work, a many-objective global-best harmony search (KGHS) algorithm with a knee point-driven Pareto optimization is proposed to solve this problem. The manufacturing facility layout problem is important in the manufacturing industry, appropriate facility layout in the factories will save lots of material transportation cost and bring higher productivity. Kang et al. [122] studied the layout design problem of an unequal area facility. In their work, the facility layout is represented as an allocation of blocks with restrictions in terms of an unequal area and rectangular shape. In addition, an effective facility layout representation is proposed by a slicing tree representation. The HS algorithm is then used to generate quality solutions. In another work [124], a comparative study is conducted between the HS and genetic algorithm for solving the max-cut problem.
5.
Conclusions and potential future research directions
As one of the popular meta-heuristic algorithms, HS has attracted the attention of many researchers from all over the world. Over the last decade, large numbers of research works have been conducted on HS modifications and their applications. In this paper, a general overview of the latest developments in the HS variants with their applications to intelligent manufacturing has been presented.
Although the rapid growth of HS researches proves that the research on HS has reached a remarkable state, there are still many challenges and potential applications areas continually emerging for the HS. Here, we analyze some potential future research directions both for HS variants and their applications within intelligent manufacturing.
Regarding the research of HS variants, we summarize the following potential research directions:
(1) Theoretical analysis of HS. Comparing with other outstanding population-based algorithms such as GA, PSO, and DE, the theoretical analysis work of HS variants is relatively poor. Actually, only sporadic researches are found in the HS literature, e.g. Das et al. [143] studied the relationship between the exploration power and parameters in HS. Based on this foundation, Gao et al. [144] analyzed the probabilistic convergence properties of HS and completed the population convergence proof. As the foundation of HS, the theoretical properties of HS should be further analyzed in future.
(2) Ensemble selection methods in memory consideration for HS. Inspired by the natural principle of the "survival of the fittest", Al-Betar et al. [54,55] carefully analyzed different selection methods in memory consideration for HS. One interesting thing is that one selection method is only effective for problems with specific characteristics. In the field of machine learning, ensemble methods [145] based on a variety of classification methodologies are employed to improve the overall classification performance. It would be interesting to address the question: "Can HS algorithm also utilizes an ensemble concept that makes use of a pool of different selection methods to obtain better performance?".
(3) Large-scale global optimization problems. Many real-world optimization problems tackle with a large number of decision variables (generally speaking, the number of decision variables is more than 100), known as large-scale global optimization problems (LSGO) [146]. Normally, the standard meta-heuristic algorithms will suffer from the main deficiency for solving LSGO problems. There are two main reasons: the first, the increasing of the problem size increases the landscape complexity; the second, the search space exponentially increases with the problem dimension. The approaches for solving LSGO problems can be categorized into two directions, namely, decomposition methods based on "divide-and-conquer" approach, and non-decomposition based methods. HS variants combined with cooperative co-evolution strategy for LSGO may be one of the potential future research directions.
(4) Parameter-free HS and intelligent parameter control methods for HS. As we know, the performance of HS is sensitive to its parameters. Although many different parameter setting strategies have been proposed in previous studies, most of these strategies still need manual intervention. More intelligent parameter setting techniques such as parameter-free HS and parameter control methods [147] should be developed in the future so that those engineers who have little knowledge of HS will be enabled to easily apply HS to solve problems in their own fields.
Regarding intelligent manufacturing, HS can be applied to solve more complicated problems at a new age. Nowadays manufacturing is embracing the 4th industrial evolution, with the help of CPS, IoT, and cloud computing, the whole manufacturing process will be totally different. We can expect more and more HS applications in intelligent manufacturing, from product design to supply chain and from the level of manufacturing operation to the level of manufacturing system management. In detail, we think HS will continue to contribute in the following areas:
(1) Applications to IWSN. IWSN is one of the fundamental technologies in Industry 4.0. Although HS has been applied to this area, such as energy-efficient routing, sensor node deployment, and joint deployment and scheduling, the challenge remains. Thus, we can expect in the future that HS will be applied to make the IWSN becomes more reliable and energy-efficient.
(2) In the near future, AGVs which can only follow the painted lines will be upgraded to more intelligent automated mobile robots (AMRs). These AMRs are equipped with advanced sensors that can automatically recognize components, learn the environment, make decisions by self, and work cooperatively. In the future, HS can be applied to improve the performance of AMR systems through ways such as self-localization, route planning, task assignment.
(3) Sustainable manufacturing is also one of topic for future manufacturing. Development of energy-efficient machining operation, production planning and scheduling is one of the pathways toward the goal. Therefore, HS can be applied to areas such as energy-efficient motion planning for industrial robots, energy-efficient tool path planning for CNC machining, and energy-efficient production scheduling.
(4) Intelligent decision-making incorporates with AI big-data analytic methods. With the large increase of advanced sensors in the manufacturing system, massive data will be generated. The effective use of these data with the help of advanced technologies such as AI and big-data analytic methods will improve manufacturing efficiency. Therefore, one of the future research directions is to use HS incorporate with AI big-data analytic methods to build intelligent algorithms for decision-making in manufacturing systems.
Acknowledgments
This research is supported by the National Natural Science Foundation of China (NSFC) under Grant No. 51805495, and the Open Project from the State Key Laboratory of Digital Manufacturing Equipment and Technology, Grant No. DMETKF2018010.
Conflict of interest
The authors have declared that no conflict of interest exists.









 DownLoad:
DownLoad: