Persistence metrics for a river population in a two-dimensional benthic-drift model

Yu Jin; Qihua Huang; Julia Blackburn; Mark A. Lewis; Yu Jin; Qihua Huang; Julia Blackburn; Mark A. Lewis

doi:10.3934/math.2019.6.1768

AIMS Mathematics

2019, Volume 4, Issue 6: 1768-1795. doi: 10.3934/math.2019.6.1768

Previous Article Next Article

Research article Special Issues

Persistence metrics for a river population in a two-dimensional benthic-drift model

1.
Department of Mathematics, University of Nebraska-Lincoln, Lincoln, NE, 68588, USA
2.
School of Mathematical and Statistical Sciences, Southwest University, Chongqing 400715, China
3.
School of Mathematical and Statistical Sciences, Hubei University of Science and Technology, Xianning 437100, China
4.
Department of Civil and Environmental Engineering, University of Alberta Edmonton, AB, T6G 1H9, Canada
5.
Center for Mathematical Biology, Department of Mathematical and Statistical Sciences, University of Alberta, Edmonton, AB, T6G 2G1, Canada
6.
Department of Biological Sciences, University of Alberta, Edmonton, AB, T6G 2E9, Canada

Received: 24 April 2019 Accepted: 19 November 2019 Published: 31 December 2019
MSC : 35K10, 47A75, 92B05

The study of population persistence in river ecosystems is key for understanding population dynamics, invasions, and instream flow needs. In this paper, we extend theories of persistence measures for population models in one-dimensional rivers to a benthic-drift model in two-dimensional depth-averaged rivers. We define the fundamental niche and the source and sink metric, and establish the net reproductive rate R₀ to determine global persistence of a population in a spatially heterogeneous two-dimensional river. We then couple the benthic-drift model into the two-dimensional computational river model, River2D, to study the growth and persistence of a population and its source and sink regions in a river. The theory developed in this study extends existing R₀ analysis to spatially heterogeneous two-dimensional models. The River2D program provides a method to analyze the impact of river morphology on population persistence in a realistic river. The theory and program derived here can be applied to species in real rivers.
- benthic-drift population model,
- next generation operator,
- persistence,
- net reproductive rate,
- River2D
Citation: Yu Jin, Qihua Huang, Julia Blackburn, Mark A. Lewis. Persistence metrics for a river population in a two-dimensional benthic-drift model[J]. AIMS Mathematics, 2019, 4(6): 1768-1795. doi: 10.3934/math.2019.6.1768

Related Papers:

Abstract

The study of population persistence in river ecosystems is key for understanding population dynamics, invasions, and instream flow needs. In this paper, we extend theories of persistence measures for population models in one-dimensional rivers to a benthic-drift model in two-dimensional depth-averaged rivers. We define the fundamental niche and the source and sink metric, and establish the net reproductive rate R₀ to determine global persistence of a population in a spatially heterogeneous two-dimensional river. We then couple the benthic-drift model into the two-dimensional computational river model, River2D, to study the growth and persistence of a population and its source and sink regions in a river. The theory developed in this study extends existing R₀ analysis to spatially heterogeneous two-dimensional models. The River2D program provides a method to analyze the impact of river morphology on population persistence in a realistic river. The theory and program derived here can be applied to species in real rivers.

References

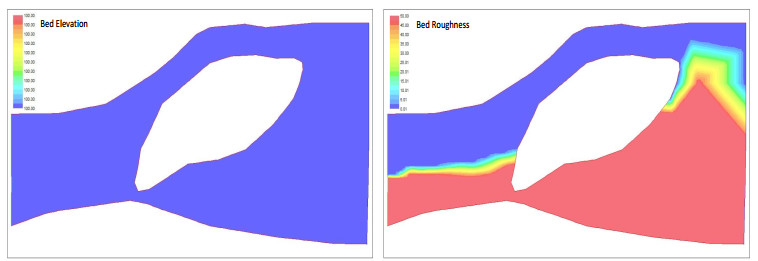
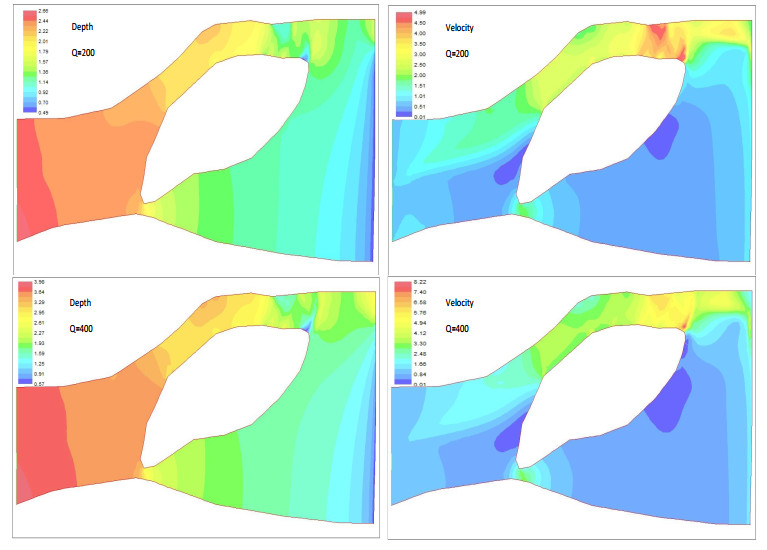
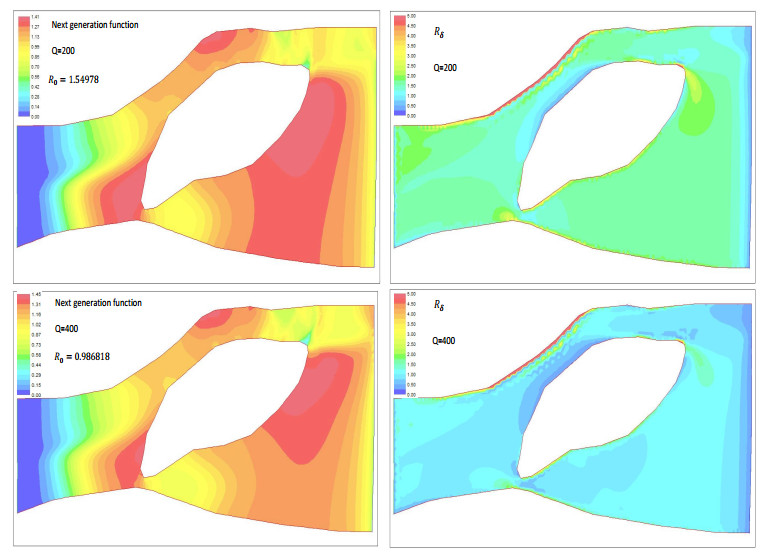
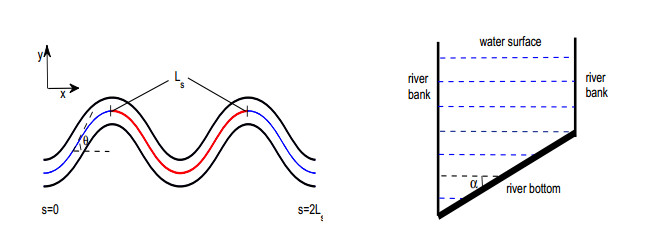
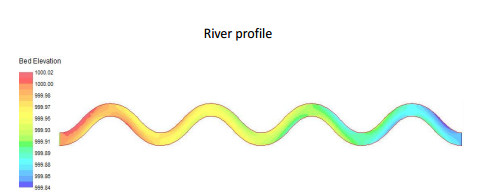
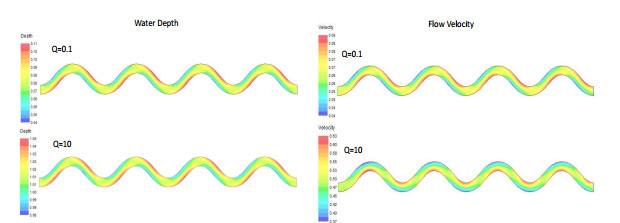
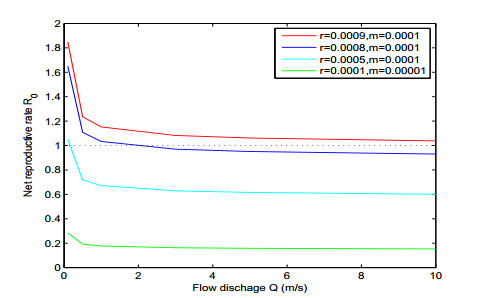
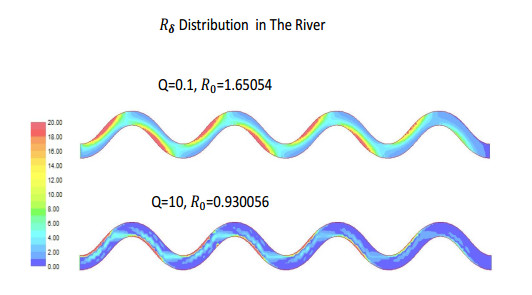
[1]	J. D. Allan, Stream Ecology: Structure and Function of Running Waters, Chapman & Hall, London, 1995.
[2]	K. E. Anderson, L. R. Harrisonb, R. M. Nisbet, et al. Modeling the influence of flow on invertebrate drift across spatial scales using a 2D hydraulic model and a 1D population model, Ecol. Model., 265 (2013), 207-220. doi: 10.1016/j.ecolmodel.2013.06.011
[3]	K. E. Anderson, A. J. Paul, E. McCauley, et al. Instream flow needs in streams and rivers: The importance of understanding ecological dynamics, Front. Ecol. Environ., 4 (2006), 309-318. doi: 10.1890/1540-9295(2006)4[309:IFNISA]2.0.CO;2
[4]	J. D. Armstrong, P. S. Kemp, G. J. A. Kennedy, et al. Habitat requirements of Atlantic salmon and brown trout in rivers and streams, Fish. Res., 62 (2003), 143-170. doi: 10.1016/S0165-7836(02)00160-1
[5]	K. E. Bencala, R. A. Walters, Simulation of solute transport in a mountain poop-and-riffle stream: A transient storage model, Water Resour. Res., 19 (1983), 718-724. doi: 10.1029/WR019i003p00718
[6]	D. J. Booker, Hydraulic modelling of fish habitat in urban rivers during high flows, Hydrol. Process., 17 (2003), 577-599. doi: 10.1002/hyp.1138
[7]	A. N. Brooks, T. J. R. Hughes, Steamline upwind/Petrov-Galerkin formulations for convection dominated flows with particular emphasis on the imcompressible Navier-Stokes equations, Comput. Method. Appl. Mech. Eng., 32 (1982), 199-259. doi: 10.1016/0045-7825(82)90071-8
[8]	N. J. Clifford, O. P. Harmar, G. Harvey, et al. Physical habitat, eco-hydraulics and river design: A review and re-evaluation of some popular concepts and methods, Aquat. Conserv., 16 (2006), 389-408. doi: 10.1002/aqc.736
[9]	J. M. Cushing, Y. Zhou, The net reproductive value and stability in matrix population models, Nat. Resour. Model., 8 (1994), 297-333. doi: 10.1111/j.1939-7445.1994.tb00188.x
[10]	D. L. DeAngelis, M. Loreaub, D. Neergaardc, et al. Modelling nutrient-periphyton dynamics in streams: The importance of transient storage zones, Ecol. Model., 80 (1995), 149-160. doi: 10.1016/0304-3800(94)00066-Q
[11]	MIKE 21 Flow Model FM: Particle Tracking Module, User Guide, Horsholm, Denmark, 2011, pp. 56.
[12]	MIKE 21 Flow Model FM: Particle Tracking Module, Step-by-step training guide, Horsholm, Denmark, 2011, pp. 48.
[13]	J. M. Elliott, Time spent in the drift by downstream-dispersing invertebrates in a Lake District stream, Freshwater Biol., 47 (2002), 97-106. doi: 10.1046/j.1365-2427.2002.00784.x
[14]	L. Gallien, T. Münkemüller, C. H. Albert, et al. Predicting potential distributions of invasive species: Where to go from here?, Divers. Distrib., 16 (2010), 331-342. doi: 10.1111/j.1472-4642.2010.00652.x
[15]	A. Ghanem, P. M. Steffler, F. E. Hicks, et al. 1995, Dry area treatment for two-dimensional finite element shallow flow modeling, Proceeding of the 12th Canadian Hydrotechnical Conference, Ottawa, Ontario, June, 1995, pp.10.
[16]	A. Ghanem, P. M. Steffler, F. E. Hicks, et al. Two dimensional finite element model for aquatic habitats, Water Resources Engineering Report 95-S1, Department of Civil Engineering, University of Alberta, 1995, pp. 189.
[17]	R. Guenther, J. Lee, Partial Differential Equations of Mathematical Physics and Integral Equations, Dover, New York, 1996.
[18]	J. W. Hayes, N. F. Hughes, L. H. Kelly, Process-based modelling of invertebrate drift transport, net energy intake and reach carrying capacity for drift-feeding salmonids, Ecol. Model., 207 (2007), 171-188. doi: 10.1016/j.ecolmodel.2007.04.032
[19]	F. M. Hilker, M. A. Lewis, Predator-prey systems in streams and rivers, Theor. Ecol., 3 (2010), 175-193. doi: 10.1007/s12080-009-0062-4
[20]	Q. Huang, Y. Jin, M. A. Lewis, R₀ Analysis of a Benthic-Drift Model for a Stream Population, SIAM J. Appl. Dyn. Syst., 15 (2016), 287-321. doi: 10.1137/15M1014486
[21]	I. Ibanez, E. Gornish, L. Buckley, et al. Moving forward in global-change ecology: Capitalizing on natural variability, Ecol. Evol., 3 (2013), 170-181. doi: 10.1002/ece3.433
[22]	Y. Jin, F. M. Hilker, P. M. Steffler, et al. Seasonal invasion dynamics in a spatially heterogeneous river with fluctuating flows, Bull. Math. Biol., 76 (2014), 1522-1565. doi: 10.1007/s11538-014-9957-3
[23]	Y. Jin, M. A. Lewis, Seasonal influences on population spread and persistence in streams: Critical domain size, SIAM J. Appl. Math., 71 (2011), 1241-1262. doi: 10.1137/100788033
[24]	Y. Jin, M. A. Lewis, Seasonal influences on population spread and persistence in streams: Spreading speeds, J. Math. Biol., 65 (2012), 403-439. doi: 10.1007/s00285-011-0465-x
[25]	M. Krkosěk, M. A. Lewis, An R₀ theory for source-sink dynamics with application to Dreissena competition, Theor. Ecol., 3 (2010), 25-43. doi: 10.1007/s12080-009-0051-7
[26]	J. Lancaster, B. J. Downes, Linking the hydraulic world of individual organisms to ecological processes: Putting ecology into ecohydraulics, River Res. Appl., 26 (2010), 385-403. doi: 10.1002/rra.1274
[27]	L. B. Leopold, W. B. Langbein, River Meanders, Sci. Am., 214 (1966), 60-73.
[28]	F. Lutscher, M. A. Lewis, E. McCauley, Effects of heterogeneity on spread and persistence in rivers, Bull. Math. Biol., 68 (2006), 2129-2160. doi: 10.1007/s11538-006-9100-1
[29]	F. Lutscher, R. M. Nisbet, E. Pachepsky, Population persistence in the face of advection, Theor. Ecol., 3 (2010), 271-284. doi: 10.1007/s12080-009-0068-y
[30]	D. A. Lytle, D. M. Merritt, Hydrologic regimes and riparian forests: A structured population model for cottonwood, Ecology, 85 (2004), 2493-2503. doi: 10.1890/04-0282
[31]	H. M. McKenzie, Y. Jin, J. Jacobsen, et al. R₀ Analysis of a Spationtemporal Model for a Stream Population, SIAM J. Appl. Dyn. Syst., 11 (2012), 567-596. doi: 10.1137/100802189
[32]	R. T. Milhous, T. J. Waddle, Physical Habitat Simulation (PHABSIM) Software for Windows (v.1.5.1), Fort Collins, CO: USGS Fort Collins Science Center, 2012.
[33]	A. M. Mouton, M. Schneider, J. Depestele, et al. Fish habitat modelling as a tool for river management, Ecol. Eng., 29 (2007), 305-315. doi: 10.1016/j.ecoleng.2006.11.002
[34]	K. Müller, Investigations on the organic drift in North Swedish streams, Report of the Institute of Freshwater Research, Drottningholm, 34 (1954), 133-148.
[35]	K. Müller, The colonization cycle of freshwater insects, Oecologica, 53 (1982), 202-207.
[36]	T. Nagaya, Y. Shiraishi, K. Onitsuka, et al. Evaluation of suitable hydraulic conditions for spawning of ayu with horizontal 2D numerical simulation and PHABSIM, Ecol. Model., 215 (2008), 133-143. doi: 10.1016/j.ecolmodel.2008.02.043
[37]	S. A. Nazirov, A. A. Abduazizov, Approximate calculation of the multiple integrals' value by repeated application of Gauss and Simpson's quadrature formulas, Appl. Math. Sci., 7 (2013), 4223-4235.
[38]	E. Pachepsky, F. Lutscher, R. M. Nisbet, et al. Persistence, spread and the drift paradox, Theor. Popul. Biol., 67 (2005), 61-73. doi: 10.1016/j.tpb.2004.09.001
[39]	V. B. Pasour, S. P. Ellner, Computational and analytic perspectives on the drift paradox, SIAM J. Appl. Dyn. Syst., 9 (2010), 333-356. doi: 10.1137/09075500X
[40]	N. L. Poff, J. K. H. Zimmerman, Ecological responses to altered flow regimes: A literature review to inform the science and management of environmental flows, Freshwater. Biol., 55 (2010), 194-205. doi: 10.1111/j.1365-2427.2009.02272.x
[41]	D. Speirs, W. Gurney, Population persistence in rivers and estuaries, Ecology, 82 (2001), 1219-1237. doi: 10.1890/0012-9658(2001)082[1219:PPIRAE]2.0.CO;2
[42]	I. Stakgold, Green's Functions and Boundary Value Problems, 2 Eds., Wiley, New York, 1998.
[43]	P. Steffler, J. Blackburn, Two-dimensional depth averaged model of river hydrodynamics and Fish habitat, River2D User's Manual, University of Albert, Canada, 2002.
[44]	T. J. Stohlgren, P. Ma, S. Kumar, et al. Ensemble habitat mapping of invasive plant species, Risk Anal., 30 (2010), 224-235. doi: 10.1111/j.1539-6924.2009.01343.x
[45]	A. H. Stroud, Approximate Calculation of Multiple Integrals, Prentice-Hall Inc., 1971.
[46]	C. B. Talbert, M.K. Talbert, User Manual for SAHM package for Vis Trails, US Geological Survey, 2012.
[47]	H. Thieme, Spectral bound and reproductive number for infinite-dimensional population structure and time heterogeneity, SIAM J. Appl. Math., 70 (2010), 188-211.
[48]	F. Wang, B. Lin, Modelling habitat suitability for fish in the fluvial and lacustrine regions of a new Eco-City, SIAM J. Appl. Math., 267 (2013), 115-126.
[49]	W. Wang, X. Q. Zhao, Basic reproduction numbers for reaction-diffusion epidemic models, SIAM J. Appl. Dyn. Syst., 11 (2012), 1652-1673. doi: 10.1137/120872942
[50]	L. L. Wehmeyer, C. R. Wagner, Relation between Flows and Dissolved Oxygen in the Roanoke River between Roanoke Rapids Dam and Jamesville, North Carolina, 2005-2009, Scientific Scientific Investigations Report, Department of the Interior, U.S. Geological Survey, 2011. Available from: https://pubs.usgs.gov/sir/2011/5040/pdf/sir2011-5040.pdf.

Reader Comments

your name:*

Email:*
© 2019 the Author(s), licensee AIMS Press. This is an open access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0)