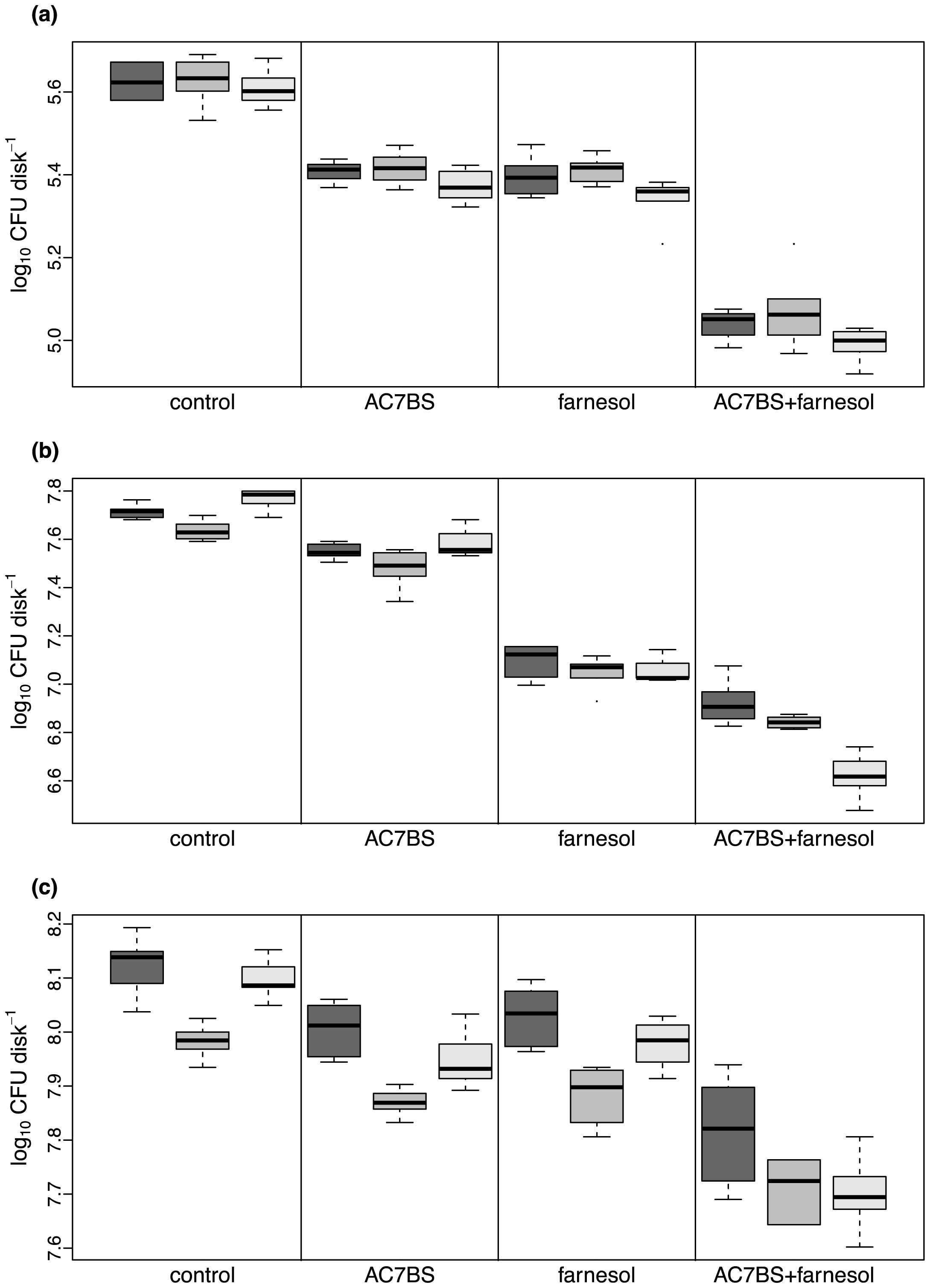
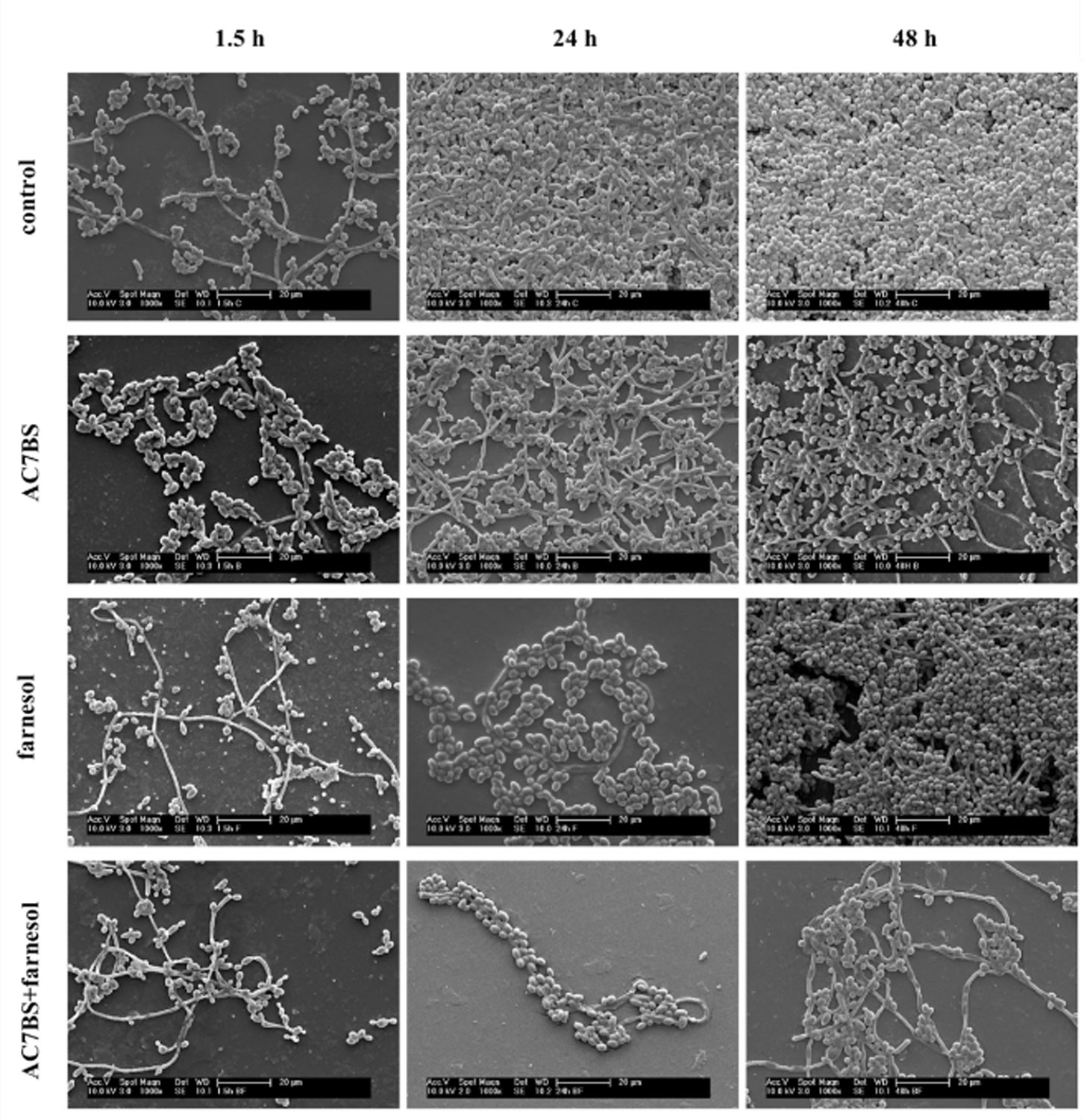
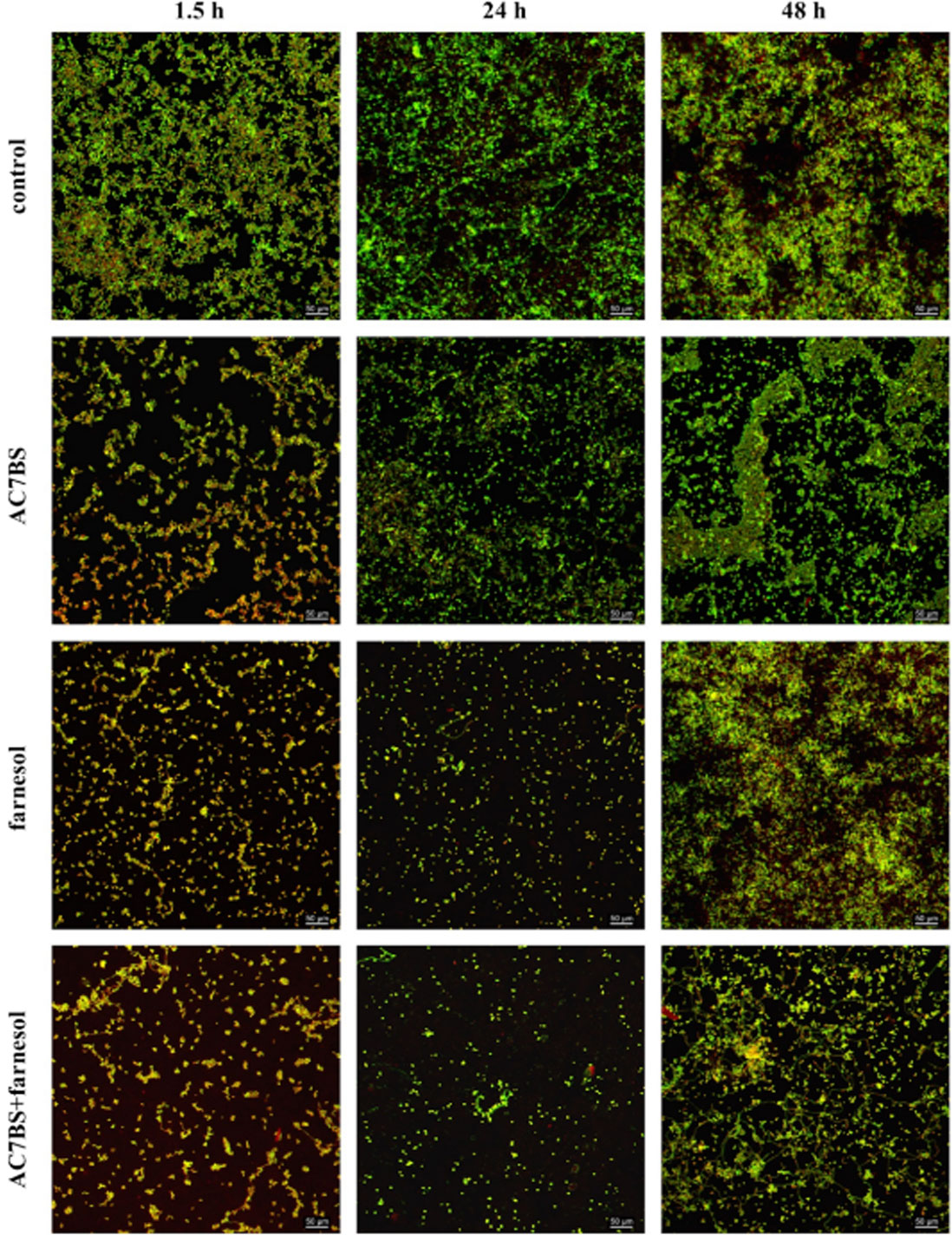
Biosurfactants affect interaction of microorganisms with material surfaces by altering interfacial properties, and have recently attract the attention of the scientific community for their use as anti-adhesive and anti-biofilm agents. The work studied the synergistic effect of a lipopeptide from Bacillus subtilis AC7 (AC7BS) combined with the quorum sensing molecule farnesol to counteract Candida albicans biofilms on silicone elastomer in simulated physiological conditions. The anti-adhesive and anti-biofilm properties of AC7BS, farnesol and their combination was evaluated after 1.5, 24 and 48 h by the viable count method on three C. albicans strains. Moreover, fungal biofilm was characterised by both scanning electron microscopy (SEM) and confocal laser scanning microscopy (CLSM). By combining the two molecules, a synergistic effect was observed with a significant reduction of C. albicans adhesion up to 74% at 1.5 h and of biofilm growth up to 93% at 24 h and 60% at 48 h. SEM and CLSM confirmed the synergistic anti-adhesive and anti-biofilm activity. Similar trends for the percentage of biofilm covered surface and biofilm mean thickness were observed. No cytotoxicity on eukaryotic cells was detected after exposures to AC7BS concentrations up to 0.5 mg ml−1. Results demonstrated that the combination of the two molecules significantly inhibit both C. albicans initial adhesion and biofilm growth on silicone. Biosurfactant AC7 in combination with farnesol is a hopeful coating to prevent C. albicans medical device-associated infection.
1.
Introduction
In real life, elastic collision systems with friction and clearance are widely used in mechanical systems, vehicle engineering and other fields; and, the vibro-impact system is a kind of common nonlinear dynamical system. For the parameter optimization design and service life extension of nonsmooth mechanical systems with clearance and restrictions, the study of collision and vibration is extremely important. Numerous academics have investigated vibro-impact systems to better understand their dynamic structure, which can be useful for engineering applications.
In mechanical engineering, friction is widely used in dynamic design, controlling high-precision positioning systems, transferring power or torque and decelerating high-speed rotating components. Sometimes, friction is unnecessary because friction produces noise, affects work accuracy and stability, reduces mechanical efficiency and influences the productivity of machinery and equipment. People hope to avoid the adverse factors caused by friction, to the greatest extent, so as to enhance the mechanical system's dynamic performance. In 1930, Hartog [1] analyzed nonsmooth dynamical systems impacted by viscous damping and Coulomb friction. Feeny and Moon [2] obtained that a forced oscillator's dynamics with velocity- and displacement-related Coulomb friction force could be simplified into one-dimensional mapping dynamics in some parameter ranges in 1993. Popp et al.[3] used a frictional oscillator model to study bifurcation behavior and chaotic paths under different system parameters. In the 1990s, the dynamics of multiple frictional oscillators were described by Galvanetto [4,5]. An invariance principle that can be applied to a Coulomb friction oscillator was investigated by Alvarez et al.[6]. In 2006, Sinou et al.[7] discussed the nonlinear dynamics in a complex aircraft braking model. In 2007, Martinez and Alvarez [8] proposed a controller for a two-degree-of-freedom (2-DOF) mechanical system that has unactuated discontinuous joint friction. Through theoretical studies and experimental verification, an attempt was made to use vibration-related friction to improve the efficiency of the relevant equipment in [9]. The analytical criterion for the dry friction oscillator with SDOF (single-degree-of-freedom) stick-slip periodic solution was obtained in [10]. Fang and Jian [11] investigated the relationships among the other factors, external Coulomb dry friction and system's steady-state motion through a model of a vibration-driven system. In the same year, Liu and Wen [12] proposed a kind of controller and proved the closed-loop system's asymptotic stability by establishing an SDOF mass-spring-friction dynamical model. Based on Coulomb friction, Saadabad et al.[13] deduced and simplified the dynamic motion equation for the microrobot and obtained the causes for the stick-slip motion of the microrobot.
The collision phenomenon exists widely in various mechanical devices, and the nonlinear motion caused by a collision is the main reason for mechanical components' fatigue and structural damage. Vibro-impact systems' dynamic behavior is significantly impacted by a collision. Therefore, it is of great importance to study the impact system's dynamic behavior by combining qualitative and quantitative methods. In 1990, Balachandran and Nayfeh [14] addressed the flexible L-shaped beam-mass structure's dynamic plane response at a low excitation level. A few years later, the thin-walled structure's dynamics under impact stimulation were taken into account by Balachandran et al.[15,16]. Two elastic balls colliding dynamically in a viscous fluid were analyzed by Zhang et al.[17]. In 2007, by applying the mechanics principle, Liu et al.[18] used the mass-spring model of dynamic cloth to describe a collision response process. In [19], a dynamic collision detection algorithm was proposed for the behaviors of the virtual battlefield. The impact dynamics characteristics of large concrete blocks were studied experimentally by Ma et al.[20]. The authors of [21] addressed the impact force performance of a vibro-impact system under various stimulation frequencies. Bichri et al.[22] analytically and numerically investigated the most reasonable method for regulating the vibro-impact dynamics of a single-sided Hertzian contact forced oscillator in 2011. The author of [23] developed and applied an enhanced single-unit vibro-impact system in their investigation. In 2018, the chaotic properties of a nonlinear energy sink system with vibration and impact were analyzed by Li et al. [24].
The degree of freedom and periodicity affect how the vibro-impact system behaves dynamically. In 1970, Harris [25] analyzed the existence of the ideal spring-mass system infinite period motion with two and multiple degrees of freedom. Campen et al.[26] discussed the periodically excited mechanical system's long-term behavior. Vorst et al. [27] examined a sophisticated multiple-degree-of-freedom (multi-DOF) beam system with an intermediate elastic stop in 1996. In [28,29], Natsiavas and Verros examined a class of nonlinear SDOF oscillator periodic motions' stability and their dynamics. In 2002, Janin and Lamarque [30] examined an SDOF shock oscillator's stability. Arsenault and Gosselin [31] analyzed the planar 2-DOF tensegrity mechanism's dynamical model and proposed a preliminary control scheme. In 2007, sliding motion's switching conditions of forced linear oscillators with periodicity and dry friction were proposed by Luo and Gegg [32]. In addition, Luo et al.[33] employed the Poincaré map to examine the vibro-impact system's nonlinear dynamics while taking into account an n-DOF system that was subjected to periodic stimulation. In 2008, the 2-DOF dry friction oscillator's characteristics were studied by Pascal [34]. In 2012, Luo and Huang [35] discussed a nonlinear oscillator's discontinuous dynamics. Igumnov et al.[36] analyzed the dynamics of a friction system located in a rough belt. In a time-delayed, periodically driven, twin-well Duffing oscillator, Xing and Luo [37] discussed bifurcation trees with period-3 motions to chaos.
With regard to discontinuous dynamical systems, Filippov [38,39] discussed the right-hand sides discontinuous differential equation solutions' existence and uniqueness. It is not sufficient to study the complex dynamic behavior of nonsmooth dynamical systems only by applying Filippov's theory. To explore the flow's local singularity closer to the separation boundary in more detail through the use of connectable and accessible sub-domains, a local theory of nonsmooth dynamical systems is explored by Luo [40]. Luo and Gegg [41] investigated the periodic motion of a vibrator moving in a periodic vibration band with dry friction and gave the grazing and stick bifurcations in the same year. Under the condition of flow barriers existing in discontinuous dynamic systems, the condition of flow passing through a separation boundary was studied by Luo [42]. In addition, by using the set-valued vector field theory, Luo [43] has provided the sliding motion's switching conditions on the separation boundary. In [44], the G-function was designed to study discontinuous dynamical systems' singularity. In 2009, Luo [45] clearly described the dynamic regions' discontinuous dynamical system theory. The analytical parameters of sliding flow and nonsliding flow at the velocity boundary were reported in [46]. Luo [47] systematically elaborated the flow switching theory in 2010. The flow barrier theory was established by Luo [48] for discontinuous dynamical systems. Currently, a growing number of academics are starting to explore several dynamical systems by using the flow switching theory. In 2015, Fu and Zhang [49] investigated inclined impact oscillator's behavior with periodic excitation. In 2017, based on the local theory of flow at the corner in discontinuous dynamical systems, the analytical criteria for switching impact-alike chatter at corners were discovered by Huang and Luo [50]. Fan et al.[51] looked into a switching control law-based friction-induced oscillator. [52,53,54] explored the $ 2 $-DOF friction oscillators' motion switching conditions on the separation boundary. In addition, more and more scholars are studying the bifurcation characteristics of dynamical systems; for instance, Li et al.[55] investigated various sliding bifurcations by using the discontinuous predator-prey model in 2021.
However, more needs to be said about the local singularity created at the separation boundary of some dynamical systems. In this research, an in-depth study of the dynamic behavior of a class of 2-DOF frictional vibration systems with asymmetric elastic constraints is conducted. Compared with the physical models studied previously, the model studied in this paper considers the following factors: (ⅰ) negative feedback that makes the system more stable; (ⅱ) simultaneous occurrence of left and right elastic collisions; (ⅲ) flow barriers existing at velocity boundaries, which results in more complex conditions for the disappearance of sliding motion.
The study of the model discussed in this paper differs from the research on the vibro-impact models in earlier studies, and the motion switching on the separation boundary for this kind of system has not yet been thoroughly researched. We will give the switching criteria for an oscillator at the separation boundaries. Moreover, we provide numerical simulations for some typical motions and the sliding bifurcation scene in order to vividly show the diversity and complexity of the oscillator's motion. The motion states of objects become more strongly connected and the corresponding boundaries and domains become more time-dependent as the degrees of freedom and number of discontinuous factors increase; thus, we investigate the 2-DOF system by using the approach of first individually studying each object in the system before combining them to analyze the behavior of the entire system.
At present, there are relatively few studies on the application of the flow switchability theory to the 2-DOF system in which the elastic impact on the left and right sides may occur simultaneously; this paper enriches this theory. This kind of elastic collision system is close to what occurs in practical engineering applications. The study serves as an original and deep investigation into the discontinuous dynamics of a class of 2-DOF frictional vibration systems with asymmetric elastic constraints through the application of strict mathematical consideration, which can deepen the understanding of machine collision-related systems and is beneficial to improve the stability and the service life of machines.
The article has the following structure. The physical model of a 2-DOF frictional vibration system with asymmetric elastic restrictions is introduced, and the system's various motion states are listed in Section 3. In Section 4, the domain and boundary of the oscillators are divided by using the absolute and relative phase spaces associated with the discontinuity or nonsmoothness of the system, and the vector equation in each domain is obtained. In Section 5, the flow switchability theory and flow barrier theory are used to present the analytical criteria for the motion switching at the separation boundary. Additionally, numerical simulations are presented to demonstrate the analytical criteria in Section 6. Section 7 depicts the scene of sliding bifurcation as the excitation frequency and amplitude change. The entire article is summarized at the end in Section 8.
2.
Explanation of symbols
For a clearer understanding of the content of this article, Table 1 summarizes the definitions of the symbols used in this paper.
3.
Dynamical model
3.1. Physical model
A 2-DOF frictional vibration system with asymmetric elastic constraints is depicted in Figure 1, and it mainly consists of two masses $ m_1 $ and $ m_2 $. A variable spring with stiffness coefficients $ K_1 $ and $ K_2 $, as well as a variable damper with stiffness coefficients $ C_1 $ and $ C_2 $, are used to attach the mass $ m_1 $ to the right vertical wall, and the distance between the linear spring with stiffness coefficient $ K_6 $ and the mass $ m_1 $'s equilibrium position is $ d_1 $. A variable spring with stiffness coefficients of $ K_4 $ and $ K_5 $, as well as a variable damper with stiffness coefficients of $ C_4 $ and $ C_5 $, are used to attach the mass $ m_2 $ to the left vertical wall.
In addition, there is an elastic constraint connected to the right end of the mass $ m_2 $, where this constraint is made up of a linear damper $ C_3 $ and a linear spring $ K_3 $, and this constraint's distance from the mass $ m_1 $ is $ d $ when both the object $ m_1 $ and the object $ m_2 $ are in the equilibrium position. In the physical model, springs $ K_2 $ and $ K_5 $ and dampers $ C_2 $ and $ C_5 $ are nonlinear spring-dampers cubic term. When converting potential energy, the nonlinear spring-damper exhibits little deformation, which is conducive to regulating the motion of mechanical parts, mitigating collision or vibration and storing energy.
The nonlinear spring-damper model is widely utilized as a shock absorber in construction, machinery, aerospace and other areas because it can precisely reflect the energy loss during collision processes. $ x_{1} $ and $ x_{2} $ respectively represent the object $ m_1 $'s and the object $ m_2 $'s horizontal displacements; and, the mass $ m_i $ $ (i\in\{1, 2\}) $ is motivated by the periodic force $ F_{i} = Q_{i}\sin(\Omega t+\varphi_{i})+B_{i} $, with the negative feedback
where $ Q_{i} $ and $ P_{i} $ are the excitation amplitude and positive constant force, respectively, $ \Omega $ is the frequency, $ \varphi_{i} $ is the initial phase and the mass $ m_i $'s velocity is $ \dot{x}_{i} $ = $ dx_{i} $/$ dt $.
Figure 2 illustrates the friction model; the kinetic friction coefficient is $ \mu_{k} $ and $ \mu_{s} $ is the static friction coefficient, where the friction force between the mass $ m_i $ $ (i\in\{1, 2\}) $ and the ground is defined as
where $ F_N^{(i)} $ ($ F_N^{(i)} = m_{i}g $, $ g $ is the acceleration of gravity) is the normal force acting on the object $ m_i $ $ (i\in\{1, 2\}) $. In addition, the static friction force ranges from $ [-\mu_{s}F_N^{(i)}, \mu_{s}F_N^{(i)}] $.
3.2. Analysis of oscillator's motion
The following notations are given for convenience:
where $ i = 1, 2 $.
Based on whether the object $ m_1 $ touches the constraint ($ K_3 $, $ C_3 $) on the left or the constraint ($ K_6 $) on the right, we can easily obtain the non-friction forces $ F_{s}^{(1)} $ and $ F_{s}^{(2)} $ affecting the objects $ m_1 $ and $ m_2 $, respectively; and, the expressions of $ F_{s}^{(1)} $ and $ F_{s}^{(2)} $ are as follows:
According to the above discussion, the 2-DOF frictional vibration system with asymmetric elastic constraints has 16 states of motion, which are listed below.
(ⅰ) When the object $ m_1 $ and the object $ m_2 $ are not interacting (i.e., $ {x}_{1}-{x}_{2} > -d) $ and the object $ m_1 $ is not touching the right elastic constraint $ K_6 $ (i.e., $ {x}_{1} < d_1) $, the system has four states of motion: i.e., $ \dot {x}_{1}\ne 0, \, \dot {x}_{2}\ne 0 $ (the object $ m_1 $'s free-flight motion or nonsliding motion and the object $ m_2 $'s free-flight motion or nonsliding motion); $ \dot {x}_{1} = 0, \, \dot {x}_{2}\neq 0 $ (the object $ m_1 $'s sliding motion and the object $ m_2 $'s free-flight motion or nonsliding motion); $ \dot {x}_{1}\neq 0, \, \dot {x}_{2} = 0 $ (the object $ m_1 $'s free-flight motion or nonsliding motion and the object $ m_2 $'s sliding motion); $ {\rm or} $ $ \dot {x}_{1} = 0, \, \dot {x}_{2} = 0 $ (the object $ m_1 $'s sliding motion and the object $ m_2 $'s sliding motion).
(ⅱ) When the object $ m_1 $ and the object $ m_2 $ are not interacting (i.e., $ {x}_{1}-{x}_{2} > -d) $ and the right elastic constraint $ K_6 $ is touched by the object $ m_1 $ (i.e., $ {x}_{1}\geq d_1) $, the system has four states of motion: i.e., $ \dot {x}_{1}\ne 0, \, \dot {x}_{2}\ne 0 $ (the object $ m_1 $'s right stick-nonsliding motion and the object $ m_2 $'s free-flight motion or nonsliding motion); $ \dot {x}_{1} = 0, \, \dot {x}_{2}\neq 0 $ (the object $ m_1 $'s right stick-sliding motion and the object $ m_2 $'s free-flight motion or nonsliding motion); $ \dot {x}_{1}\neq 0, \, \dot {x}_{2} = 0 $ (the object $ m_1 $'s right stick-nonsliding motion and the object $ m_2 $'s sliding motion); $ {\rm or} $ $ \dot {x}_{1} = 0, \, \dot {x}_{2} = 0 $ (the object $ m_1 $'s right stick-sliding motion and the object $ m_2 $'s sliding motion).
(ⅲ) When the object $ m_1 $ is interacting with the object $ m_2 $ (i.e., $ {x}_{1}-{x}_{2}\leqslant -d) $ and the object $ m_1 $ is not touching the right elastic constraint $ K_6 $ (i.e., $ {x}_{1} < d_1) $, the system has four states of motion: i.e., $ \dot {x}_{1}\ne 0, \, \dot {x}_{2}\ne 0 $ (the object $ m_1 $'s left stick-nonsliding motion and the object $ m_2 $'s stick-nonsliding motion); $ \dot {x}_{1} = 0, \, \dot {x}_{2}\neq 0 $ (the object $ m_1 $'s left stick-sliding motion and the object $ m_2 $'s stick-nonsliding motion); $ \dot {x}_{1}\neq 0, \, \dot {x}_{2} = 0 $ (the object $ m_1 $'s left stick-nonsliding motion and the object $ m_2 $'s stick-sliding motion); $ {\rm or} $ $ \dot {x}_{1} = 0, \, \dot {x}_{2} = 0 $ (the object $ m_1 $'s left stick-sliding motion and the object $ m_2 $'s stick-sliding motion).
(ⅳ) When the object $ m_1 $ is interacting with the object $ m_2 $ (i.e., $ {x}_{1}-{x}_{2}\leqslant -d) $ and the right elastic constraint $ K_6 $ is touched by the object $ m_1 $ (i.e., $ {x}_{1}\geq d_1) $, the system has four states of motion: i.e., $ \dot {x}_{1}\ne 0, \, \dot {x}_{2}\ne 0 $ (the object $ m_1 $'s double stick-nonsliding motion and the object $ m_2 $'s stick-nonsliding motion); $ \dot {x}_{1} = 0, \, \dot {x}_{2}\neq 0 $ (the object $ m_1 $'s double stick-sliding motion and the object $ m_2 $'s stick-nonsliding motion); $ \dot {x}_{1}\neq 0, \, \dot {x}_{2} = 0 $ (the object $ m_1 $'s double stick-nonsliding motion and the object $ m_2 $'s stick-sliding motion); $ {\rm or} $ $ \dot {x}_{1} = 0, \, \dot {x}_{2} = 0 $ (the object $ m_1 $'s double stick-sliding motion and the object $ m_2 $'s stick-sliding motion).
4.
Phase space partition and vector equations
The oscillator's motion in the 2-DOF dynamic system is complex and discontinuous because of dry friction, the unequal coefficients of static/dynamic friction and elastic impacts. With the purpose of conducting a more thorough analysis of the separation boundary's motion switching issue in this discontinuous dynamical system, the domains and boundaries shall be initially defined in absolute and relative coordinates, respectively, so that two objects maintain continuous motion in each domain; then, by introducing vector fields of the two objects in the phase space, the two object's motion equations can be expressed as vectors.
4.1. Phase space partition
According to whether the mass $ m_{1} $ makes the left stick motion (i.e., whether the mass $ m_{2} $ makes the stick motion), the oscillator's motion in phase space has the following domain and boundary division.
$ Case \, I$: Without left stick motion for the mass $ m_{1} $.
The mass $ m_{1} $'s four domains are represented as
and the associated boundaries are described as
Figure 3a represents the mass $ m_{1} $'s above domains and boundaries. The domains $ \Omega_1^{(1)} $ and $ \Omega_2^{(1)} $ indicate the free-flight domains, which are symbolized by yellow and light blue, respectively; the right stick domains $ \Omega_3^{(1)} $ and $ \Omega_4^{(1)} $ are represented by purple and orange, respectively; the black dashed line and black dotted line are used to depict the velocity boundaries $ \partial\Omega_{12}^{(1)} $ and $ \partial\Omega_{34}^{(1)} $, respectively; red dashed lines signify the right stick displacement boundaries $ \partial\Omega_{13}^{(1)} $ and $ \partial\Omega_{24}^{(1)} $; and, the permanent boundary $ \partial\Omega_{i\infty}^{(1)}\, \, (i \in \{1, 2\}) $ is represented by the pink dashed curve.
The two domains of the mass $ m_{2} $ are expressed as
and the associated boundaries are specified as
In this case, Figure 3b represents the mass $ m_{2} $'s above domains and boundaries. The domains $ \Omega_1^{(2)} $ and $ \Omega_2^{(2)} $ indicate the free-flight domains, which are shown by yellow and light blue, respectively; the black dashed line designates the velocity boundary, which is $ \partial\Omega_{12}^{(2)} $; and, the permanent boundary is represented by the pink dashed line, which is $ \partial\Omega_{i\infty}^{(2)}\, \, (i \in \{1, 2\}) $.
$ Case \, II\, $: With left stick motion for the mass $ m_{1} $.
The mass $ m_{1} $'s eight domains are expressed as
and the associated boundaries are characterized as
Figure 4a represents the mass $ m_{1} $'s above domains and boundaries. The free-flight domains are represented by the domains $ \Omega_1^{(1)} $ and $ \Omega_2^{(1)} $, which are symbolized by yellow and light blue, respectively; purple and orange respectively represent the right stick domains $ \Omega_3^{(1)} $ and $ \Omega_4^{(1)} $; the left stick domains $ \Omega_5^{(1)} $ and $ \Omega_6^{(1)} $ are represented by pink and green, respectively; dark blue and gray respectively represent the double stick domains $ \Omega_7^{(1)} $ and $ \Omega_8^{(1)} $; the velocity boundaries $ \partial\Omega_{56}^{(1)} $, $ \partial\Omega_{34}^{(1)} $ and $ \partial\Omega_{78}^{(1)} $ are depicted by a black dotted-dashed line, black dotted line and orange dashed line, respectively; pink dashed lines denote the left stick displacement boundaries $ \partial\Omega_{15}^{(1)} $, $ \partial\Omega_{37}^{(1)} $, $ \partial\Omega_{48}^{(1)} $ and $ \partial\Omega_{26}^{(1)} $; and, red dashed lines denote the right stick displacement boundaries $ \partial\Omega_{13}^{(1)} $, $ \partial\Omega_{57}^{(1)} $, $ \partial\Omega_{68}^{(1)} $ and $ \partial\Omega_{24}^{(1)} $.
The mass $ m_{2} $'s four domains are represented as
and the corresponding boundaries are characterized as
Figure 4b displays the mass $ m_{2} $'s above domains and boundaries. The domains $ \Omega_1^{(2)} $ and $ \Omega_2^{(2)} $ indicate the free-flight domains, which are symbolized by yellow and light blue, respectively; the domains $ \Omega_5^{(2)} $ and $ \Omega_6^{(2)} $ indicate the stick domains, which are symbolized by pink and green, respectively; the velocity boundary is demonstrated by the $ \partial\Omega_{12}^{(2)} $, which is shown by the black dashed line; the black dotted-dashed line, which can be seen as the boundary $ \partial\Omega_{56}^{(2)} $, denotes the velocity boundary; the pink dashed lines at the boundaries $ \partial\Omega_{15}^{(2)} $ and $ \partial\Omega_{26}^{(2)} $ denote the stick boundaries.
4.2. Vector equations
Based on the boundaries and domains specified by using absolute coordinates, it is easy to transform the mass $ m_i $'s $ (i \in \{1, 2\}) $ motion equation into the vector form given by
for the mass $ m_{1} $'s non-left stick motion (i.e., it is also the mass $ m_{2} $'s non-stick motion), and
for the mass $ m_{1} $'s left stick motion (i.e., it is also the mass $ m_{2} $'s stick motion), where
Here, $ \delta _1 = 0 $ represents the following motions of the oscillator at the velocity boundaries: the sliding motion at the boundary $ \partial\Omega_{12}^{(1)} $, the right stick-sliding motion at the boundary $ \partial\Omega_{34}^{(1)} $, the left stick-sliding motion at the boundary $ \partial\Omega_{56}^{(1)} $ and the double stick-sliding motion at the boundary $ \partial\Omega_{78}^{(1)} $ for the mass $ m_{1} $; $ \delta _2 = 0 $ indicates the following motions of the oscillator at the velocity boundaries: the sliding motion at the boundary $ \partial\Omega_{12}^{(2)} $, and the stick-sliding motion at the boundary $ \partial\Omega_{56}^{(2)} $ for the mass $ m_{2} $. In this instance, the force on the mass $ m_i $ $ (i \in \{1, 2\}) $ per unit of mass is
Free movement of object $ m_{i} $ $ (i \in \{1, 2\}) $ in domains $ \Omega_{1}^{(i)} $ and $ \Omega_{2}^{(i)} $ is indicated by $ \delta_i = 1, 2 $ $ (i \in \{1, 2\}) $, respectively; in domain $ \Omega_{3}^{(1)} $ and $ \Omega_{4}^{(1)} $, the object $ m_{1} $ executes the right stick motion, as indicated by $ \delta _1 = 3, 4 $. The forces exerted on the masses $ m_{i} $ $ (i = 1, 2) $ per unit of mass are
$ \delta_i = 5, 6 $ $ (i \in \{1, 2\}) $ expresses that, in domains $ \Omega_{5}^{(i)} $ and $ \Omega_{6}^{(i)} $, the object $ m_{1} $ performs the left stick motion and the object $ m_{2} $ performs the stick motion, respectively; in domains $ \Omega_{7}^{(1)} $ and $ \Omega_{8}^{(1)} $, the object $ m_{1} $ performs the double stick motion, as indicated by $ \delta _1 = 7, 8 $. The forces exerted on the masses $ m_{i} $ $ (i = 1, 2) $ per unit of mass are
Since the displacement boundary is tied to time in absolute coordinates, relative coordinates must be introduced to fully examine the two masses' switching rules at the displacement boundary. The following is a list of the relative variables:
Because the object $ m_{1} $'s left stick motion appears and vanishes along with the object $ m_{2} $'s stick motion, it is possible to determine the situation of the object $ m_{2} $'s stick motion by studying the object $ m_{1} $'s left stick motion, where the domains for the mass $ m_{1} $ are defined as follows in relative coordinates:
and the associated velocity boundaries and displacement boundaries are characterized as
The division of the mass $ m_{1} $'s domains and boundaries in relative coordinates are illustrated in Figure 5. The displacement boundaries $ \partial\Omega_{15}^{(1)} $, $ \partial\Omega_{37}^{(1)} $, $ \partial\Omega_{48}^{(1)} $and $ \partial\Omega_{26}^{(1)} $ become straight lines, which is conducive to analyzing the stick motion's switching conditions. The object $ m_{1} $'s motion equation can be represented in vector form by using the relative coordinates for regions and boundaries, i.e.,
for the mass $ m_{1} $'s non-left stick motion (i.e., it is also the mass $ m_{2} $'s non-stick motion), and
for the mass $ m_{1} $'s left stick motion (i.e., it is also the mass $ m_{2} $'s stick motion), where
Similar to the absolute coordinates, $ \delta_i $ $ (i\in \{1, 2\}) $ has the same meaning. It is simple to obtain the motion equations of (4.18)–(4.20) in the relative coordinates, in accordance with the equations of motion in absolute coordinates.
Because the discontinuous dynamical system presented in this paper has unequal static and dynamic friction forces, the velocity boundaries represented by $ \partial\Omega_{\alpha \beta }^{(i)} $ $ (i = 1, (\alpha, \beta)\in\{(1, 2), (3, 4), (5, 6), (7, 8)\} $, and $ i = 2, (\alpha, \beta)\in\{(1, 2), (5, 6)\}) $ have flow barriers. The flow barrier vector fields for $ {\mathbf{x}}_{m}^{(i)} = (x_{m}^{(i)}, \dot{x}_{m}^{(i)})\in\partial\Omega_{\alpha \beta }^{(i)} $ $ (i = 1, (\alpha, \beta)\in\{(1, 2), (3, 4), (5, 6), (7, 8)\} $, and $ i = 2, (\alpha, \beta)\in\{(1, 2), (5, 6)\}) $ at time $ t_{m} $ are given as
where
for the mass $ m_{1} $'s non-left stick motion (i.e., it is also the mass $ m_{2} $'s non-stick motion), and
where
for the mass $ m_{1} $'s left stick motion (i.e., it is also the mass $ m_{2} $'s stick motion), and
The $ \delta $-side $ (\delta \in \{1, 2, 3, 4, 5, 6, 7, 8\}) $ boundary flow barriers for $ {\mathbf{x}}_{m}^{(i)} = (x_{m}^{(i)}, \dot{x}_{m}^{(i)})\in\partial\Omega_{\alpha \beta }^{(i)}, $ $ i = 1, (\alpha, \beta)\in\{(1, 2), (3, 4), (5, 6), (7, 8)\} $; and $ i = 2, (\alpha, \beta)\in\{(1, 2), (5, 6)\}) $ at time $ t_{m} $ are given below.
If $ \tau ^{(\delta)} = \tau_{1} ^{(\delta)} $, the expression for the flow barrier can be obtained by replacing $ \tau ^{(\delta)} $ in Eq (4.22) or Eq (4.24) with $ \tau_{1} ^{(\delta)} $; and if $ \tau ^{(\delta)} = \tau_{2} ^{(\delta)} $, the expression for the flow barrier can be obtained by applying
for the mass $ m_{1} $'s non-left stick motion (i.e., it is also the mass $ m_{2} $'s non-stick motion), and
for the mass $ m_{1} $'s left stick motion (i.e., it is also the mass $ m_{2} $'s stick motion).
5.
Analytical conditions
This section will discuss the flow switchability conditions on discontinuous/nonsmooth boundaries for this $ 2 $-DOF frictional vibration system. At the separation boundaries, the normal vectors and the $ {\rm G} $-functions are first given; then, the switching criteria of flow are provided.
In absolute coordinates, the normal vectors of the displacement boundaries $ \partial\Omega_{ln}^{(1)}\, \, ((l, n)\in\{(1, 3), (2, 4), (5, 7), (6, 8)\}) $ and the velocity boundaries $ \partial\Omega_{\alpha \beta }^{(i)}\, \, ((\alpha, \beta)\in\{(1, 2), (3, 4), (5, 6), (7, 8)\}\, \, {\rm if}\, i = 1;\, {\rm and}\, \, (\alpha, \beta)\in\{(1, 2), (5, 6)\}\, {\rm if}\, i = 2) $ are respectively provided as
where $ \bigtriangledown = (\frac{\partial}{\partial x}, \frac{\partial}{\partial \dot{x}})^{\rm T}. $
In relative coordinates, the normal vectors of the displacement boundaries $ \partial\Omega_{ln}^{(1)}\, \, ((l, n)\in\{(1, 5), (2, 6), (3, 7), \\(4, 8)\}) $ are denoted by
where $ \bigtriangledown = (\frac{\partial}{\partial x}, \frac{\partial}{\partial \dot{x}})^{\rm T}. $
We assume, for simplicity, that the mass $ m_i $'s $ (i \in \{1, 2\}) $ motion flow arrives at the separation boundary point $ {\mathbf{x}}_m^{(i)} $ at time $ t_m $, and $ t_{m\pm} = t_{m}\pm0. $
Definition 5.1. At the velocity boundary $ \partial\Omega_{\alpha \beta }^{(i)}\, \, $$ (\alpha \neq \beta \in \{1, 2\}\, {\rm or}\, \{3, 4\}\, {\rm or}\, \{5, 6\}\, {\rm or}\, \{7, 8\}\, {\rm if}\, i = 1; \alpha \neq \beta \in\{1, 2\}\, {\rm or}\, \{5, 6\} \, \, {\rm if}\, i = 2) $, the following is a list of the $ 0 $th-order and first-order $ {\rm G} $-functions at time $ t_m $ in absolute coordinates:
where $ \alpha \neq \beta \in\{1, 2\}\, {\rm or}\, \{3, 4\}\, {\rm if}\, i = 1; \alpha \neq \beta \in\{1, 2\}\, {\rm if}\, i = 2, \delta \in\{\alpha, \beta \} $; and,
where $ \alpha \neq \beta \in\{5, 6\}\, {\rm or}\, \{7, 8\}\, {\rm if}\, i = 1; \alpha \neq \beta \in\{5, 6\}\, {\rm if}\, i = 2, \delta \in\{\alpha, \beta \}. $ Here, $ {\mathbf{x}}_{i}^{(\delta)}(t_{m\pm}) = {\mathbf{x}}_{i}^{(0)}(t_{m}) = {\mathbf{x}}_{\it m}^{(i)}\in \partial\Omega_{\alpha\beta }^{(i)} $ $ (\alpha \neq \beta \in\{1, 2\}\, {\rm or}\, \{3, 4\}\, {\rm or}\, \{5, 6\}\, {\rm or}\, \{7, 8\} \, {\rm if} \, i = 1; $ $ \alpha\neq\beta \in\{1, 2\}\, {\rm or}\, \{5, 6\}\, \, {\rm if}\, i = 2). $
Definition 5.2. In absolute coordinates, at the displacement boundary $ \partial\Omega_{l n }^{(1)}\, \, $$ (l\neq n\in\{1, 3\}\, {\rm or}\, \{2, 4\}\, {\rm or}\, \{5, 7\}\, {\rm or}\, \{6, 8\}) $, the following is a list of the $ 0 $th-order and first-order $ {\rm G} $-functions at time $ t_m $:
where $ l\neq n \in\{1, 3\}\, {\rm or}\, \{2, 4\}, \delta \in\{l, n\} $; and,
where $ l\neq n \in\{5, 7\}\, {\rm or}\, \{6, 8\}, \delta \in\{l, n\}. $
Here, $ {\mathbf{x}}_{1}^{(\delta)}(t_{m\pm}) = {\mathbf{x}}_{1}^{(0)}(t_{m}) = {\mathbf{x}}_{\it m}^{(1)}\in \partial\Omega_{ln }^{(1)} $ $ (l\neq n\in\{1, 3\}\, {\rm or}\, \{2, 4\}\, {\rm or}\, \{5, 7\}\, {\rm or}\, \{6, 8\}) $.
Definition 5.3. At the velocity boundary with the flow barrier $ \partial\Omega_{\alpha \beta }^{(i)}\, \, $$ (\alpha \neq \beta \in\{1, 2\}\, {\rm or}\, \{3, 4\}\, {\rm or}\, \{5, 6\}\, {\rm or}\, \{7, 8\}\, {\rm if}\, i = 1; \alpha \neq \beta \in\{1, 2\}\, {\rm or}\, \{5, 6\}\, \, {\rm if}\, i = 2) $, the following is a list of the $ 0 $th-order and first-order $ {\rm G} $-functions at time $ t_m $ in absolute coordinates:
for $ \alpha \neq \beta \in\{1, 2\}\, {\rm or}\, \{3, 4\}\, {\rm if}\, i = 1; \alpha \neq \beta \in\{1, 2\}\, {\rm if}\, i = 2, \delta \in\{\alpha, \beta \} $; and,
for $ \alpha \neq \beta \in\{5, 6\}\, {\rm or}\, \{7, 8\}\, {\rm if}\, i = 1; \alpha \neq \beta \in\{5, 6\}\, {\rm if}\, i = 2, \delta \in\{\alpha, \beta \}. $
Here, $ {\mathbf{x}}_{i}^{(\delta)}(t_{m\pm}) = {\mathbf{x}}_{i}^{(0)}(t_{m}) = {\mathbf{x}}_{\it m}^{(i)}\in \partial\Omega_{\alpha\beta }^{(i)} $ $ (\alpha \neq \beta \in\{1, 2\}\, {\rm or}\, \{3, 4\}\, {\rm or}\, \{5, 6\}\, {\rm or}\, \{7, 8\}\, {\rm if} \, i = 1; \alpha \neq \beta \in\{1, 2\}\, {\rm or}\, \{5, 6\}\, \, {\rm if}\, i = 2) $.
Definition 5.4. In relative coordinates, at the displacement boundary $ \partial\Omega_{l n }^{(1)}\, \, $$ (l\neq n\in\{1, 5\}\, {\rm or}\, \{2, 6\}\, {\rm or}\, \{3, 7\}\, {\rm or}\, \{4, 8\}) $, the following is a list of the $ 0 $th-order and first-order $ {\rm G} $-functions at time $ t_m $:
for $ \delta \in\{1, 2, 3, 4\} $; and,
for $ \delta \in\{5, 6, 7, 8\} $.
Here, $ {\mathbf{z}}_{1}^{(\delta) }(t_{m\pm}) = {\mathbf{z}}_{ 1}^{(0)}(t_{m}) = {\mathbf{z}}_{\it m}^{(1)}\in \partial\Omega_{ln }^{(1)} $ $ (l\neq n\in\{1, 5\}\, {\rm or} \, \{2, 6\}\, {\rm or}\, \{3, 7\}\, {\rm or}\, \{4, 8\}) $.
5.1. At velocity boundaries in absolute coordinates
After the above discussion, one is able to determine the analytical criteria of the sliding motion, grazing flow and passable motion at the velocity boundary $ \partial\Omega_{\alpha \beta }^{(i)}\, \, $$ (\alpha \neq \beta \in\{1, 2\}\, {\rm or}\, \{3, 4\}\, {\rm or}\, \{5, 6\}\, {\rm or}\, \{7, 8\}\, {\rm if}\, i = 1; \alpha \neq \beta \in\{1, 2\}\, {\rm or}\, \{5, 6\}\, \, {\rm if}\, i = 2) $ for this $ 2 $-DOF frictional vibration system.
Theorem 5.1. The passable motion's flow from $ \Omega_{\alpha }^{(i)} $ to $ \Omega_{\beta }^{(i)} $ at $ \mathbf{x}_m^{(i)}\in\partial\Omega_{\alpha \beta }^{(i)} $ $ (\alpha \neq \beta \in\{1, 2\}\, {\rm or}\, \{3, 4\}\, {\rm or}\, \{5, 6\}\, {\rm or}\, \{7, 8\}\, {\rm if}\, i = 1; \alpha \neq \beta \in\{1, 2\}\, {\rm or}\, \{5, 6\}\, \, {\rm if}\, i = 2) $ at time $ t_m $ occurs if and only if
Proof. At the time $ t_{m} $, the flow of motion that has reached the boundary. The mass $ m_i $ $ (i \in \{1, 2\}) $ is in motion on the ground with a nonzero speed before or after $ t_{m} $, and, at time $ t_{m} $, the mass $ m_i $'s $ (i \in \{1, 2\}) $ velocity is zero. At time $ t_{m} $, based on Luo's theory of flow switchability [42], the passable motion to occur at $ \mathbf{x}_m^{(i)}\in\partial\Omega_{12 }^{(i)} $ $ (i\in\{1, 2\}) $ satisfies the following criteria:
With Eq (5.2) and Eq (5.4), one obtains
From Eqs (5.14) and (5.15), the passable-flow-appearing conditions in Eq (5.12) for $ \alpha = 1 $ and $ \beta = 2 $ are obtained. Similar methods can be used to generate the other criteria in Eqs (5.12) and (5.13).□
Theorem 5.2. (i) The sliding motion at $ \mathbf{x}_m^{(i)}\in\partial\Omega_{12}^{(i)} $ $ (i\in\{1, 2\}) $ at time $ t_m $ exists if and only if
(ii) The mass $ m_{1} $'s right stick-sliding motion at $ \mathbf{x}_m^{(1)}\in\partial\Omega_{34 }^{(1)} $ at time $ t_m $ exists if and only if
(iii) The mass $ m_{1} $'s left stick-sliding motion or the mass $ m_{2} $'s stick-sliding motion at $ \mathbf{x}_m^{(i)}\in\partial\Omega_{56 }^{(i)} $ $ (i\in\{1, 2\}) $ at time $ t_m $ exists if and only if
(iv) The mass $ m_{1} $'s double stick-sliding motion at $ \mathbf{x}_m^{(1)}\in\partial\Omega_{78 }^{(1)} $ at time $ t_m $ exists if and only if
Proof. With relation to the ground, the object $ m_i\, \, (i\in\{1, 2\}) $ is immobile; according to Luo's flow switchability theory [42], at the velocity boundary, a sink flow will be present. The mass $ m_{1} $'s left stick-sliding motion existing at $ \mathbf{x}_m^{(1)}\in\partial\Omega_{56 }^{(1)} $ or the mass $ m_{2} $'s stick-sliding motion existing at $ \mathbf{x}_m^{(2)}\in\partial\Omega_{56 }^{(2)} $ at time $ t_m $ satisfies the following conditions:
With Eqs (5.2) and (5.5), one obtains
From Eqs (5.20) and (5.21), the case of (ⅲ) holds. The other cases of (ⅰ), (ⅱ) or (ⅳ) can be demonstrated similarly.□
In the following theorems, the semi-passable flow's boundary motion spanning domain $ \Omega_\alpha $ and domain $ \Omega_\beta $ is denoted by $ \overrightarrow{\partial\Omega}_{\alpha \beta } $, and the first-class non-passable flow's boundary is depicted by $ \widetilde{\partial\Omega}_{\alpha \beta } $.
Theorem 5.3. (i) The sliding motion at $ \mathbf{x}_m^{(i)}\in\overrightarrow{\partial\Omega}_{12 }^{(i)} $ $ \rm or $ $ \overrightarrow{\partial\Omega}_{21 }^{(i)} $ $ (i\in\{1, 2\}) $ at time $ t_m $ appears if and only if
(ii) The mass $ m_{1} $'s right stick-sliding motion at $ \mathbf{x}_m^{(1)}\in\overrightarrow{\partial\Omega}_{34 }^{(1)} $ $ \rm or $ $ \overrightarrow{\partial\Omega}_{43 }^{(1)} $ at time $ t_m $ appears if and only if
(iii) The mass $ m_{1} $'s left stick-sliding motion or the mass $ m_{2} $'s stick-sliding motion at $ \mathbf{x}_m^{(i)}\in\overrightarrow{\partial\Omega}_{56 }^{(i)} $ $ \rm or $ $ \overrightarrow{\partial\Omega}_{65 }^{(i)} $ $ (i\in\{1, 2\}) $ at time $ t_m $ appears if and only if
(iv) The mass $ m_{1} $'s double stick-sliding motion at $ \mathbf{x}_m^{(1)}\in\overrightarrow{\partial\Omega}_{78 }^{(1)} $ $ \rm or $ $ \overrightarrow{\partial\Omega}_{87}^{(1)} $ at time $ t_m $ appears if and only if
Proof. At time $ t_m $, based on Luo's theory of flow switchability [42], the sliding motion to appear at $ \mathbf{x}_m^{(i)}\in\overrightarrow{\partial\Omega}_{21}^{(i)} $ $ (i\in\{1, 2\}) $ satisfies the following conditions:
Equations (5.2) and (5.4) provide
From Eqs (5.15), (5.26) and (5.27), the sliding motion-appearing conditions in Eq (5.22) for $ \alpha = 1 $ and $ \beta = 2 $ are established. Similar results can be derived for the other circumstances in Eqs (5.23)–(5.25).□
Theorem 5.4. (i) The sliding motion at $ \mathbf{x}_m^{(i)}\in\widetilde{\partial\Omega}_{12 }^{(i)} $ $ (i\in\{1, 2\}) $ at time $ t_m $ vanishes if and only if
from$ \ \widetilde{\partial\Omega}_{12 }^{(i)}\rightarrow \Omega_{\delta }^{(i)} $, where $ \bar\delta \neq\delta \in\{1, 2 \}. $
(ii) The mass $ m_{1} $'s right stick-sliding motion at $ \mathbf{x}_m^{(1)} \in \widetilde{\partial\Omega}_{34 }^{(1)} $ at time $ t_m $ vanishes if and only if
from$ \, \ \widetilde{\partial\Omega}_{34 }^{(1)}\rightarrow \Omega_{4 }^{(1)}; $
from$ \, \ \widetilde{\partial\Omega}_{34 }^{(1)}\rightarrow \Omega_{3 }^{(1)}. $
(iii) The mass $ m_{1} $'s left stick-sliding motion or the mass $ m_{2} $'s stick-sliding motion at $ \mathbf{x}_m^{(i)}\in\widetilde{\partial\Omega}_{56 }^{(i)} $ $ (i\in\{1, 2\}) $ at time $ t_m $ vanishes if and only if
from$ \, \ \widetilde{\partial\Omega}_{56 }^{(i)}\rightarrow \Omega_{\delta }^{(i)}, $ where $ \bar\delta \neq\delta \in\{5, 6 \}. $
(iv) The mass $ m_{1} $'s double stick-sliding motion at $ \mathbf{x}_m^{(1)}\in\widetilde{\partial\Omega}_{78 }^{(1)} $ at time $ t_m $ vanishes if and only if
from$ \, \ \widetilde{\partial\Omega}_{78 }^{(1)}\rightarrow \Omega_{8 }^{(1)}; $
from$ \, \ \widetilde{\partial\Omega}_{78 }^{(1)}\rightarrow \Omega_{7 }^{(1)}. $
Proof. At the time $ t_{m} $, the mass $ m_i $'s $ (i\in\{1, 2\}) $ non-friction force is equivalent to the maximal static friction force, and, after time $ t_{m} $, the maximal static friction force is less than the non-friction force; also, the mass $ m_1 $'s left stick-sliding motion or the mass $ m_2 $'s stick-sliding motion vanishes at time $ t_{m} $. Based on Luo's flow switchability theory [42], the mass $ m_{1} $'s left stick-sliding motion vanishing at $ \mathbf{x}_m^{(1)}\in\widetilde{\partial\Omega}_{56 }^{(1)} $ or the mass $ m_{2} $'s stick-sliding motion vanishing at $ \mathbf{x}_m^{(2)}\in\widetilde{\partial\Omega}_{56 }^{(2)} $ with the flow barrier at time $ t_m $ satisfies the following conditions:
from $ \widetilde{\partial\Omega}_{56 }^{(i)}\rightarrow \Omega_{6 }^{(i)}; $
from$ \ \widetilde{\partial\Omega}_{56 }^{(i)}\rightarrow \Omega_{5 }^{(i)}, $ where $ i \in\{1, 2 \} $, as shown in Figure 6. Equations (4.23), (5.2) and (5.9) yield
where $ \delta \in\{5, 6 \}. $
From Eqs (5.21) and (5.34)–(5.36), the case of (ⅲ) holds. The other cases of (ⅰ), (ⅱ) or (ⅳ) can also be demonstrated in a similar manner.□
Theorem 5.5. The grazing flow at $ \mathbf{x}_m^{(i)}\in\partial\Omega_{\alpha \beta }^{(i)} $ $ (\alpha \neq \beta \in\{1, 2\}\, {\rm or}\, \{3, 4\}\, \, {\rm or}\, \{5, 6\}\, \, {\rm or}\, \{7, 8\}\, {\rm if}\, i = 1; \alpha \neq \beta \in\{1, 2\}\, {\rm or}\, \{5, 6\}\, \, {\rm if}\, i = 2) $ at time $ t_m $ occurs if and only if
Proof. The grazing motion happens if the object $ m_i $'s $ (i\in\{1, 2\}) $ motion direction with reference to the ground has the same before and after time $ t_m $, and if the object $ m_i $'s $ (i\in\{1, 2\}) $ velocity is zero at time $ t_m $. Based on Luo's theory of flow switchability [42], at time $ t_m $, the grazing flow to occur at $ \mathbf{x}_m^{(i)}\in\partial\Omega_{12 }^{(i)} $ $ (i\in\{1, 2\}) $ satisfies the following criteria:
From Eqs (5.15), (5.27) and (5.39), Eq (5.37) for $ \alpha = 1 $ and $ \beta = 2 $ is proved. The other sufficient and necessary criteria in Eqs (5.37) and (5.38) can be acquired in a comparable manner.□
5.2. At displacement boundaries in absolute coordinates
This section discusses the conditions that lead to the happening and vanishing of the mass $ m_1 $'s right-only stick motion and double stick motion.
Theorem 5.6. (i) The right-only stick motion at $ \mathbf{x}_m^{(1)}\in\partial\Omega_{13 }^{(1)} $ at time $ t_m $ occurs if and only if
(ii) The right-only stick motion at $ \mathbf{x}_m^{(1)}\in\partial\Omega_{24 }^{(1)} $ at time $ t_m $ vanishes if and only if
Proof. If the mass $ m_1 $ is not touching the left damper $ C_3 $ and spring $ K_3 $ (i.e., the mass $ m_1 $ is moving freely) but the mass $ m_1 $ is touching the right spring $ K_6 $, the right stick motion occurs; when the mass $ m_1 $ is separated from the spring $ K_6 $, the right stick motion vanishes. Based on Luo's theory of flow switchability [42], the right-only stick motion that occurs at $ \mathbf{x}_m^{(1)}\in\partial\Omega_{13 }^{(1)} $ at time $ t_m $ satisfies the following criteria:
and, the right-only stick motion that vanishes at $ \mathbf{x}_m^{(1)}\in\partial\Omega_{24 }^{(1)} $ at time $ t_m $ satisfies the following conditions:
Equations (5.1) and (5.6) provide
From Eqs (5.42)–(5.44), the cases of (ⅰ) and (ⅱ) hold.□
Theorem 5.7. (i) When the mass $ m_1 $ is in left stick motion, double stick motion at $ \mathbf{x}_m^{(1)}\in\partial\Omega_{57 }^{(1)} $ at time $ t_m $ occurs if and only if
(ii) The mass $ m_1 $'s double stick motion at $ \mathbf{x}_m^{(1)}\in\partial\Omega_{68 }^{(1)} $ changes to the left stick motion at time $ t_m $ if and only if
Proof. If the mass $ m_1 $ is touching the left damper $ C_3 $ and spring $ K_3 $ (i.e., the mass $ m_1 $ is in the left stick motion), the double stick motion occurs when the mass $ m_1 $ touches the right spring $ K_6 $ and they move together. When the mass $ m_1 $ is separated from the spring $ K_6 $, the mass $ m_1 $ loses double stick motion. Based on Luo's flow switchability theory [42], the double stick motion occurring at $ \mathbf{x}_m^{(1)}\in\partial\Omega_{57 }^{(1)} $ at time $ t_m $ satisfies the following criteria:
and, the criteria for the double stick motion to vanish at $ \mathbf{x}_m^{(1)}\in\partial\Omega_{68 }^{(1)} $ at time $ t_m $ are given by
One obtains the following by using Eqs (5.1) and (5.7):
From Eqs (5.47)–(5.49), the conditions in Eqs (5.45) and (5.46) can be met, as indicated in Figure 7.□
5.3. At displacement boundaries in relative coordinates
This subsection includes the criteria that lead to the mass $ m_1 $'s left stick motion and double stick motion occurring and disappearing in the free state or the right stick state.
Theorem 5.8. (i) The left-only stick motion at $ \mathbf{z}_m^{(1)}\in\partial\Omega_{26 }^{(1)} $ at time $ t_m $ occurs if and only if
(ii) The left-only stick motion at $ \mathbf{z}_m^{(1)}\in\partial\Omega_{15 }^{(1)} $ at time $ t_m $ vanishes if and only if
Proof. If the mass $ m_1 $ is not touching the spring $ K_6 $ on the right (i.e., the mass $ m_1 $ is in free-flight motion), the left stick motion occurs when the mass $ m_1 $ touches the left damper $ C_3 $ and spring $ K_3 $. When the mass $ m_1 $ is separated from the left damper $ C_3 $ and spring $ K_3 $, the mass $ m_1 $ loses the left stick motion. Based on Luo's theory of flow switchability [42], the left-only stick motion that occurs at $ \mathbf{z}_m^{(1)}\in\partial\Omega_{26}^{(1)} $ at time $ t_m $ satisfies the following conditions:
and, the left-only stick motion that vanishes at $ \mathbf{z}_m^{(1)}\in\partial\Omega_{15}^{(1)} $ at time $ t_m $ satisfies the following conditions:
Equations (5.3), (5.10) and (5.11) yield
For the mass $ m_1 $, from Eqs (5.52)–(5.54), the conditions in Eqs (5.50) and (5.51) for the occurrence and vanishment of the left-only stick motion can be acquired.□
Theorem 5.9. (i) When the mass $ m_1 $ is in right stick motion, the double stick motion at $ \mathbf{z}_m^{(1)}\in\partial\Omega_{48 }^{(1)} $ at time $ t_m $ occurs if and only if
(ii) The mass $ m_1 $'s double stick motion at $ \mathbf{z}_m^{(1)}\in\partial\Omega_{37 }^{(1)} $ changes to the right stick motion at time $ t_m $ if and only if
Proof. If the mass $ m_1 $ is touching the right spring $ K_6 $ (i.e., the mass $ m_1 $ is in the right stick motion), and the mass $ m_1 $ touches the left damper $ C_3 $ and spring $ K_3 $, the double stick motion happens. When the mass $ m_1 $ is separated from the left damper $ C_3 $ and spring $ K_3 $, the mass $ m_1 $ loses the double stick motion. Based on Luo's flow switchability theory [42], the double stick motion that occurs at $ \mathbf{z}_m^{(1)}\in\partial\Omega_{48}^{(1)} $ at time $ t_m $ satisfies the following criteria:
and the double stick motion that vanishes at $ \mathbf{z}_m^{(1)}\in\partial\Omega_{37}^{(1)} $ at time $ t_m $ satisfies the following criteria:
as demonstrated in Figure 8. Equations (5.3), (5.10) and (5.11) yield
From Eqs (5.57)–(5.59), the cases of (ⅰ) and (ⅱ) hold. □
Remark 5.1. Similar to the geometric diagrams for the analytic conditions for Theorems 5.4, 5.7 and 5.9, the geometric diagrams for the analytic conditions for other theorems can also be drawn.
6.
Numerical simulations
Numerical simulations of the sliding, grazing, left stick and periodic motions are illustrated in Figures 9–13, respectively, to help better understand the discontinuous dynamical system's switching conditions in this paper. Figures 9a–13a describe the displacement versus time curves; the velocity versus time curves are represented by Figures 9b–13b; the phase space trajectories are demonstrated in Figures 9c–13c; Figures 9d–13d display the G-function versus time histories. In Figures 9–13, green-filled circles serve as representations of the movement starting points of the masses $ m_1 $ and $ m_2 $. Additionally, yellow-, white- and red-filled circles are used to illustrate the switching spots. The black and blue dashed lines show the velocity boundaries; the red dashed lines can be seen as the displacement boundaries; the blue and black solid curves respectively illustrate how the objects $ m_1 $ and $ m_2 $ moved. In Figures 9d–13d, the solid and dashed curves respectively depict the objects $ m_1 $'s and $ m_2 $'s real and imaginary responses to forces, and the differently colored curves depict the forces influencing the objects $ m_1 $ and $ m_2 $ in various domains.
Instance $ \bf{1} $ (Sliding motion): Based on a set of system parameters $ m_1 = 1 $ kg, $ m_2 = 1 $ kg, $ C_1 = 0.05 $ N$ \cdot $s/m, $ C_2 = 0.05 $ N$ \cdot $s$ ^3 $/m$ ^3 $, $ C_3 = 1 $ N$ \cdot $s/m, $ C_4 = 0.05 $ N$ \cdot $s/m, $ C_5 = 0.05 $ N$ \cdot $s$ ^3 $/m$ ^3 $, $ K_1 = 0.6 $ N/m, $ K_2 = 1 $ N/m$ ^3 $, $ K_3 = 2 $ N/m, $ K_4 = 1.5 $ N/m, $ K_5 = 1 $ N/m$ ^3 $, $ K_6 = 1 $ N/m, $ \mu_k = 0.1 $, $ \mu_s = 0.2 $, $ d = 5 $ m, $ d_1 = 4.5 $ m, $ Q_{1} = 30 $ N, $ Q_{2} = 71 $ N, $ \varphi_{1} = \varphi_{2} = 0 $ rad, $ P_{1} = P_{2} = \pi/8 $ N, $ \Omega = 1.6 $ rad/s and $ g = 9.8 $ m/s$ ^2 $ and initial states of $ t_0 = 1 $ s, $ {\dot{x}}_{1} = 0 $ m/s, $ x_{1} = 3 $ m, $ {\dot{x}}_{2} = 0 $ m/s and $ x_{2} = 4 $ m, Figure 9 depicts the objects $ m_1 $'s and $ m_2 $'s sliding motion. The shaded part denotes that the object $ m_1 $ or the object $ m_2 $ is performing a sliding motion. It is observed in Figure 9b that, at the initial time $ t_0 = 1 $ s, the masses $ m_1 $ and $ m_2 $ move at a constant speed of zero, and Figure 9d shows the forces $ F_{2}^{(1)} > 0 $ and $ F_{2}^{(2)} < 0 $, which means that Theorem 5.2's Eq (5.16) is satisfied. Because the velocity boundary $ \partial\Omega_{12}^{(2)} $ has flow barriers, within the time interval (1 s, 1.1749 s), the displacement of the mass $ m_2 $ does not change. At time $ t_1 = 1.1749 $ s, according to the force $ F_{2}^{(0\succ 0_{1})} $ in Figure 9d, we obtain the first-order G-function $ D{F_{2}^{(0\succ 0_{1 })}} < 0 $, and there are the forces $ F_{2}^{(1)} < 0 $, $ F_{2}^{(0\succ 0_{2 })} < 0 $ and $ F_{2}^{(0\succ 0_{1 })} = 0 $, which satisfy the conditions of Eq (5.28) in Theorem 5.4 for sliding motion disappearing for the mass $ m_2 $; thus, the object $ m_2 $ will move out of the velocity boundary and enter the domain $ \Omega_{1}^{(2)} $. According to Figure 9b, the mass $ m_2 $ is free to travel throughout the domain $ \Omega_{1}^{(2)} $ during the time window (1.1749 s, 1.9 s). In addition, similar to the mass $ m_2 $'s analysis method, the object $ m_1 $ makes the sliding motion in the time interval (1 s, 1.2821 s). At time $ t_2 = 1.2821 $ s, the object $ m_1 $ will move out of the boundary $ \partial\Omega_{12}^{(1)} $; during the time interval (1.2821 s, 1.9 s) shown in Figure 9b, the mass $ m_1 $ is free to travel throughout the domain $ \Omega_{2}^{(1)} $.
Instance $ \bf{2} $ (Grazing motion): To demonstrate that the mass $ m_2 $ is performing the grazing motion at the boundary $ \partial\Omega_{12}^{(2)} $, the parameters of the system were chosen as $ m_1 = 1 $ kg, $ m_2 = 1 $ kg, $ C_1 = 0.05 $ N$ \cdot $s/m, $ C_2 = 0.05 $ N$ \cdot $s$ ^3 $/m$ ^3 $, $ C_3 = 1 $ N$ \cdot $s/m, $ C_4 = 0.05 $ N$ \cdot $s/m, $ C_5 = 0.05 $ N$ \cdot $s$ ^3 $/m$ ^3 $, $ K_1 = 1 $ N/m, $ K_2 = 1 $ N/m$ ^3 $, $ K_3 = 2 $ N/m, $ K_4 = 1 $ N/m, $ K_5 = 1 $ N/m$ ^3 $, $ K_6 = 1 $ N/m, $ \mu_k = 0.15 $, $ \mu_s = 0.2 $, $ d = 4 $ m, $ d_1 = 3 $ m, $ Q_{1} = 10 $ N, $ Q_{2} = 10 $ N, $ \varphi_{1} = \varphi_{2} = 0 $ rad, $ P_{1} = P_{2} = \pi/30 $ N, $ \Omega = 2.6 $ rad/s and $ g = 9.8 $ m/s$ ^2 $, and the initial conditions were selected as $ t_0 = 3 $ s, $ {\dot{x}}_{1} = 3 $ m/s, $ x_{1} = 2 $ m, $ {\dot{x}}_{2} = -10 $ m/s and $ x_{2} = 1 $ m. During the time window (3 s, 3.813 s), the mass $ m_2 $ is free to travel throughout the domain $ \Omega_{1}^{(2)} $, and, at the instant $ t_1 = 3.813 $ s, it reaches the boundary $ \partial\Omega_{12}^{(2)} $, as observed in Figure 10b. Figure 10d demonstrates that there is $ F_{2}^{(1)} = 0 $, and, according to the slope of the curve of the force $ F_{2}^{(1)} $, at time $ t_1 $, we obtain the first-order G-function $ D{F_{2}^{(1)}} < 0 $, which satisfies Eq (5.37) in Theorem 5.5. In other words, the mass $ m_2 $ is performing grazing motion at time $ t_1 $. After $ t_1 = 3.813 $ s, the mass $ m_2 $ returns to the domain $ \Omega_{1}^{(2)} $ and continues to perform free motion until time $ t_2 = 4.5 $ s in Figure 10b. During the time window (3 s, 3.325 s), the mass $ m_1 $ is free to travel in the domain $ \Omega_{1}^{(1)} $. According to Eq (5.12) in Theorem 5.1 and the forces $ F_{1}^{(1)} < 0 $ and $ F_{1}^{(2)} < 0 $ plotted in Figure 10d, the mass $ m_1 $ will move out of the boundary $ \partial\Omega_{12}^{(1)} $ and into the domain $ \Omega_{2}^{(1)} $ at $ t = 3.325 $ s. Until $ t_4 = 4.5 $ s, the object $ m_1 $ continues to travel about the domain $ \Omega_{2}^{(1)} $.
Instance $ \bf{3} $ (Left stick motion): Select a set of system parameters $ m_1 = 2 $ kg, $ m_2 = 2 $ kg, $ C_1 = 0.05 $ N$ \cdot $s/m, $ C_2 = 0.05 $ N$ \cdot $s$ ^3 $/m$ ^3 $, $ C_3 = 1 $ N$ \cdot $s/m, $ C_4 = 1 $ N$ \cdot $s/m, $ C_5 = 0.05 $ N$ \cdot $s$ ^3 $/m$ ^3 $, $ K_1 = 1 $ N/m, $ K_2 = 1 $ N/m$ ^3 $, $ K_3 = 2 $ N/m, $ K_4 = 3 $ N/m, $ K_5 = 2 $ N/m$ ^3 $, $ K_6 = 1 $ N/m, $ \mu_k = 0.2 $, $ \mu_s = 0.25 $, $ d = 1.5 $ m, $ d_1 = 5.5 $ m, $ Q_{1} = 16 $ N, $ Q_{2} = 25 $ N, $ \varphi_{1} = \varphi_{2} = 0 $ rad, $ P_{1} = P_{2} = \pi/6 $ N, $ \Omega = 2.6 $ rad/s and $ g = 9.8 $ m/s$ ^2 $ and initial conditions of $ t_0 = 1.5 $ s, $ {\dot{x}}_{1} = 2 $ m/s, $ x_{1} = 3.5 $ m, $ {\dot{x}}_{2} = -1 $ m/s and $ x_{2} = 3 $ m to illustrate the mass $ m_1 $'s left stick motion in Figure 11. According to Figure 11a, in the time interval (1.5 s, 3.0215 s), the difference in displacement $ x_{1}-x_{2} > -d $ indicates that the objects $ m_1 $ and $ m_2 $ are in free motion. Figure 11b illustrates that the mass $ m_1 $ enters into the domain $ \Omega_{2}^{(1)} $ at $ t = 1.5622 $ s; then, the mass $ m_1 $ enters into the domain $ \Omega_{1}^{(1)} $ at $ t = 2.8501 $ s. At $ t = 2.5471 $ s, the mass $ m_2 $ can enter into the domain $ \Omega_{2}^{(2)} $ via the boundary $ \partial\Omega_{12}^{(2)} $. Figure 11a, c demonstrates, with a relative velocity of $ \dot{x}_{1} -\dot{x}_{2} < 0 $, that the mass $ m_1 $ arrives at the displacement boundary at $ t_1 = 3.0215 $ s. Therefore, the conditions of Eq (5.50) of Theorem 5.8 are met, so the mass $ m_1 $ enters the left stick domain. In the time interval (3.0251 s, 3.7786 s), the left stick-nonsliding motion is performed by the mass $ m_1 $, whereas the stick-nonsliding motion is performed by the mass $ m_2 $. At the switching time $ t_2 = 3.7786 $ s, the objects $ m_1 $ and $ m_2 $ enter the free domains in accordance with Eq (5.51) in Theorem 5.8 and $ \dot{x}_{1} -\dot{x}_{2} > 0 $, as shown in Figure 11c. In addition, the object $ m_2 $ completes a passable motion in the stick motion's process at $ t = 3.7019 $ s; it is shown in Figure 11b.
Instance $ \bf{4} $ (Passable periodic motion): Using a set of parameters $ m_1 = 1 $ kg, $ m_2 = 1 $ kg, $ C_1 = 0.05 $ N$ \cdot $s/m, $ C_2 = 0.05 $ N$ \cdot $s$ ^3 $/m$ ^3 $, $ C_3 = 1 $ N$ \cdot $s/m, $ C_4 = 2 $ N$ \cdot $s/m, $ C_5 = 0.05 $ N$ \cdot $s$ ^3 $/m$ ^3 $, $ K_1 = 1 $ N/m, $ K_2 = 1 $ N/m$ ^3 $, $ K_3 = 2 $ N/m, $ K_4 = 1 $ N/m, $ K_5 = 1 $ N/m$ ^3 $, $ K_6 = 1 $ N/m, $ \mu_k = 0.2 $, $ \mu_s = 0.26 $, $ d = 4.5 $ m, $ d_1 = 4 $ m, $ Q_{1} = 12.3268 $ N, $ Q_{2} = 17 $ N, $ \varphi_{1} = \pi $ rad, $ \varphi_{2} = 0 $ rad, $ P_{1} = P_{2} = \pi/3 $ N, $ \Omega = 2.6 $ rad/s and $ g = 9.8 $ m/s$ ^2 $ and initial conditions of $ t_0 = 1.3322 $ s, $ {\dot{x}}_{1} = 0 $ m/s, $ x_{1} = -2.3661 $ m, $ {\dot{x}}_{2} = 0 $ m/s and $ x_{2} = 1.7095 $ m, Figure 12 illustrates the objects $ m_1 $'s and $ m_2 $'s passable periodic motion. At $ t_0 = 1.3322 $ s, the object $ m_1 $ is at the boundary $ \partial\Omega_{12}^{(1)} $ and the object $ m_2 $ is at the boundary $ \partial\Omega_{12}^{(2)} $, as shown in Figure 12b, c, respectively. As exhibited in Figure 12d, there are the forces $ F_{2}^{(1)} < 0 $ and $ F_{2}^{(2)} < 0 $ at time $ t_0 $; according to Theorem 5.1's Eq (5.12), the mass $ m_2 $ enters the domain $ \Omega_{1}^{(2)} $. During the time window (1.3322 s, 2.5402 s), the mass $ m_2 $ is free to travel throughout the domain $ \Omega_{1}^{(2)} $. At $ t_1 = 2.5402 $ s, the mass $ m_2 $ arrives at the velocity boundary $ \partial\Omega_{12}^{(2)} $, and in Figure 12b, d, as a result of the forces $ F_{2}^{(1)} > 0 $ and $ F_{2}^{(2)} > 0 $, the mass $ m_2 $ launches into the domain $ \Omega_{2}^{(2)} $. During the time window (2.5402 s, 3.7485 s), the mass $ m_2 $ is free to travel in the domain $ \Omega_{2}^{(2)} $. Figure 12a, b illustrate that, at time $ t_2 = 3.7485 $ s, the mass $ m_2 $ returns to the starting location. Similar to the motion of the mass $ m_2 $, at $ t_0 = 1.3322 $ s, the mass $ m_1 $ will enter $ \Omega_{1}^{(1)} $ owing to the forces $ F_{1}^{(1)} > 0 $ and $ F_{1}^{(2)} > 0 $ in Figure 12d and Theorem 5.1's Eq (5.12); thus, the mass $ m_1 $ is free to wander around the domain $ \Omega_{1}^{(1)} $; then, the mass $ m_1 $ goes across the boundary $ \partial\Omega_{12}^{(1)} $ to the domain $ \Omega_{2}^{(1)} $ and returns to the original position. After that, the masses $ m_1 $ and $ m_2 $ begin the second period.
Instance $ \bf{5} $ (Right-stick periodic motion): As illustrated in Figure 13, we selected the parameters $ m_1 = 1.021 $ kg, $ m_2 = 1 $ kg, $ C_1 = 0.05 $ N$ \cdot $s/m, $ C_2 = 0.05 $ N$ \cdot $s$ ^3 $/m$ ^3 $, $ C_3 = 1 $ N$ \cdot $s/m, $ C_4 = 2 $ N$ \cdot $s/m, $ C_5 = 0.05 $ N$ \cdot $s$ ^3 $/m$ ^3 $, $ K_1 = 1 $ N/m, $ K_2 = 1 $ N/m$ ^3 $, $ K_3 = 2 $ N/m, $ K_4 = 1 $ N/m, $ K_5 = 1 $ N/m$ ^3 $, $ K_6 = 1 $ N/m, $ \mu_k = 0.2 $, $ \mu_s = 0.25 $, $ d = 4.5 $ m, $ d_1 = 1.8 $ m, $ Q_{1} = 12.39 $ N, $ Q_{2} = 17 $ N, $ \varphi_{1} = \pi $ rad, $ \varphi_{2} = 0 $ rad, $ P_{1} = P_{2} = \pi/3 $ N, $ \Omega = 2.6 $ rad/s and $ g = 9.8 $ m/s$ ^2 $ and initial conditions of $ t_0 = 1.3322 $ s, $ {\dot{x}}_{1} = 0 $ m/s, $ x_{1} = -2.3724 $ m, $ {\dot{x}}_{2} = 0 $ m/s and $ x_{2} = 1.7096 $ m to account for the mass $ m_1 $'s right-stick periodic motion. As exhibited in Figure 13b, at the initial moment $ t_0 = 1.3322 $ s, the objects $ m_1 $ and $ m_2 $ are both at the boundaries $ \partial\Omega_{12}^{(1)} $ and $ \partial\Omega_{12}^{(2)} $, respectively. The object $ m_1 $ will launch into the domain $ \Omega_{1}^{(1)} $ at the initial moment according to Eq (5.12) in Theorem 5.1 and the forces $ F_{1}^{(1)} > 0 $ and $ F_{1}^{(2)} > 0 $ in Figure 13d. As shown in Figure 13a, during the time window (1.3322 s, 2.2966 s), the mass $ m_1 $ is free to travel throughout the domain $ \Omega_{1}^{(1)} $ until the mass $ m_1 $ reaches the displacement boundary $ \partial\Omega_{13}^{(1)} $. Considering this with Figure 13b, the mass $ m_1 $ is moving at a velocity that is greater than zero, so the criteria in Eq (5.40) of Theorem 5.6 for the occurrence of the right-stick motion are met. Therefore, within the time interval (2.2966 s, 2.5399 s), in the domain $ \Omega_{3}^{(1)} $, the mass $ m_1 $ exhibits right-stick nonsliding motion. At the time $ t_2 = 2.5399 $ s, there are forces $ F_{1}^{(3)} < 0 $ and $ F_{1}^{(4)} < 0 $ in Figure 13d that satisfy the conditions of Theorem 5.1's Eq (5.12); thus, the object $ m_1 $ crosses the boundary $ \partial\Omega_{34}^{(1)} $ and into the domain $ \Omega_{4}^{(1)} $. During a certain time (2.5399 s, 2.7973 s), the object $ m_1 $ is free to travel throughout $ \Omega_{4}^{(1)} $ in Figure 13b. At $ t_3 = 2.7973 $ s, the mass $ m_1 $ leaves displacement boundary $ \partial\Omega_{24}^{(1)} $ since its velocity is less than zero according to Figure 13b and Eq (5.41) of Theorem 5.6. Therefore, the mass $ m_1 $ is free to travel throughout the domain $ \Omega_{2}^{(1)} $ during the time window (2.7973 s, 3.7490 s). At the time $ t_4 = 3.7490 $ s, the second period is initiated when the mass $ m_1 $ returns to the starting location. While the object $ m_1 $ conducts the right-stick periodic motion, the object $ m_2 $ performs passable periodic motion.
7.
Scene of sliding bifurcation
In nonlinear dynamical systems, the sliding bifurcation may lead to a change in the topology of the steady-state solution of the system, which has a significant impact on the system's dynamical behavior. Studying sliding bifurcation will help one to better analyze the stability of the system's periodic motion, and this section will give the object $ m_2 $'s sliding bifurcation at the velocity boundary $ \partial\Omega_{12}^{(2)} $ for the excitation amplitude and frequency.
We chose the parameters $ m_1 = 1 $ kg, $ m_2 = 1 $ kg, $ C_1 = 0.05 $ N$ \cdot $s/m, $ C_2 = 0.05 $ N$ \cdot $s$ ^3 $/m$ ^3 $, $ C_3 = 1 $ N$ \cdot $s/m, $ C_4 = 0.05 $ N$ \cdot $s/m, $ C_5 = 0.05 $ N$ \cdot $s$ ^3 $/m$ ^3 $, $ K_1 = 0.6 $ N/m, $ K_2 = 1 $ N/m$ ^3 $, $ K_3 = 2 $ N/m, $ K_4 = 1.5 $ N/m, $ K_5 = 1 $ N/m$ ^3 $, $ K_6 = 1 $ N/m, $ \mu_k = 0.1 $, $ \mu_s = 0.2 $, $ d = 5 $ m, $ d_1 = 4.5 $ m, $ Q_{1} = 30 $ N, $ \varphi_{1} = \varphi_{2} = 0 $ rad, $ P_{1} = P_{2} = \pi/8 $ N and $ g = 9.8 $ m/s$ ^2 $. Using Theorem 5.2, when $ Q_{2} = 71 $ N and $ \Omega $ is in the range of $ [1.3, 1.85] $, the object $ m_2 $'s sliding bifurcation for the excitation frequency is as depicted in Figure 14a. In addition, Figure 14b depicts the sliding bifurcation of the object $ m_2 $ for the excitation amplitude within the region of $ Q_2 \in [68.5, 72] $ and $ \Omega = 1.6 $ rad/s.
8.
Conclusions
In this paper, we have investigated the discontinuous dynamical behaviors of a class of 2-DOF systems, where such a system has asymmetric elastic constraints. Due to collision and friction, the dynamic system is nonsmooth at the displacement boundary and discontinuous at the velocity boundary. Under the condition of the nonsmoothness and discontinuities, to specify a continuous dynamical system in each domain, the phase plane of the oscillator was divided into various boundaries and domains. The 2-DOF frictional vibration system's switchability and local singularity of flows to the dynamic boundaries have been explored in depth; additionally, by using the flow switching theory for discontinuous dynamical systems, we have analyzed the switching criteria for typical motions at the separation boundary in this work. Additionally, numerical simulations of many typical motions were performed to show how the motion of the object varies at the nonsmooth or discontinuous boundary, and the object sliding bifurcation scene is depicted in this paper. These results help us to better understand such 2-DOF system's complex dynamic behaviors.
The 2-DOF system possesses the following features:
(ⅰ) The cushioning functions of the linear and nonlinear dampers and the linear and nonlinear springs are considered.
(ⅱ) The negative feedback acting on the object depends on the velocity of the object, which has more applications in reality.
(ⅲ) The system has different static and kinetic friction forces, which causes flow barriers to exist.
(ⅳ) Since two objects can interact with each other through a spring and damper, the system's motion states are more intricate.
Through rigorous mathematical analysis, we have aimed to provide a thorough and original exploration of the discontinuous dynamics for a class of $ 2 $-DOF frictional vibration systems with asymmetric elastic constraints; it might deepen our comprehension of the 2-DOF system. Vibro-impact systems can be seen in the industry, imcluding in impact vibration rollers, impact vibration dampers, vibration conveyors, etc. Therefore, studying the dynamic properties of a vibration system where friction and elastic collision coexist is extremely important to reveal the consequences of elastic collision. The results of this paper can provide some theoretical references for the mechanical systems with asymmetric elastic constraints, dynamic parameter optimization and noise reduction.
Use of AI tools declaration
The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.
Acknowledgments
This research was supported by the National Natural Science Foundation of China (No. 11971275) and the Natural Science Foundation of Shandong Province, China (No. ZR2019MA048).
Conflict of interests
The authors declare that they have no competing interests.









 DownLoad:
DownLoad: