The Functions of Sleep

1.   Introduction

This paper concerns a one-dimensional model of solid-fluid interaction:

Here $ f(u) = u^2/2 $, and $ \delta(x) $ denotes the Dirac delta measure concentrated at $ x = 0 $. The function $ u = u(x,t) $ models the velocity of the fluid, $ h_k(t) $ models the location of the $ k $th solid particle at time $ t $, $ \lambda_k >0 $ is a drag coefficient associated with the $ k $th particle, and $ m_k >0 $ is the mass of the $ k $th particle. Study of the single-particle version of (1.1) was initiated in [11], and has been the subject of a number of additional papers.

The fluid velocity is governed by the inviscid Burgers equation $ u_t + f(u)_x = 0 $, and the particle-fluid coupling is due to friction, more specifically the drag terms $ \lambda_k \left(u - h_k' \right) $ which appear in both the PDE and the ODEs in (1.1). Since there is no viscosity, the velocity $ u(x,t) $ admits entropy weak solutions, meaning that shock waves occur. This leads to complex interactions between the resulting shock wave and the particles. When multiple particles are present there are interesting features of the solutions that include particles drafting and passing by one another; see Figure 4 or Figure 5.

There are some difficulties associated with (1.1), in addition to the well-known ones associated with a nonlinear conservation law. The source terms on the right side of the first equation are nonconservative products of distributions; their meaning is not immediately clear. The differential equations appearing in the second line are coupled to the conservation law. Due to discontinuities in $ u $ the meaning of the right side of the DE's is also not readily apparent. There are related difficulties in designing practical numerical algorithms.

Notwithstanding these difficulties there has been much progress on the single-particle version of (1.1). A notion of solution has been developed, well-posedness has been proven, and numerical algorithms have been designed whose approximations are known to converge to the unique solution. In this paper we focus on the multiple-particle problem, which has not been studied as thoroughly. We propose a notion of entropy solution suitable for multiple particles, present a Lax-Friedrichs difference scheme for the multiple-particle problem, and prove that the resulting approximations converge to an entropy solution. This is accomplished under the assumption that the particle paths do not intersect except possibly at a set of times whose Lebesgue measure is zero.

Reference [4] developed a unifying framework for the jump conditions that hold across a spatial flux discontinuity for a conservation law with discontinuous flux, using the theory of $ L^1 $-dissipative ($ L^1 \rm{D} $) admissibility germs. The relevant $ L^1 \rm{D} $ admissible germ for the problem discussed here is $ \mathcal{G}(\lambda,c) $, which was identified in [7].

Definition 1.1 (the germ $ \mathcal{G}(\lambda,c) $, [7]] The germ $ \mathcal{G}(\lambda,c) $ is the subset of $ \mathbb{R}^2 $ defined by

Reference [6] gives a definition of entropy solution for the single-particle version of (1.1). The following is a direct generalization of that definition to the multiple-particle problem.

Definition 1.2 (entropy solution).

(ⅰ) Given $ h_k \in W^{1,\infty}([0,T], \mathbb{R}) $, $ k = 1,\ldots,K $, let $ \Gamma = \bigcup_{k = 1}^K \{(h_k(t),t)):t \in [0,T) \} $. A function $ u $ is a solution of the first equation of (1.1) with initial data $ u_0 $ if $ u \in L^{\infty}( \Pi_T) \cap C([0,T]); L^1_{\mathrm{loc}}( \mathbb{R})) $, if $ u $ is a Kružkov entropy solution in $ \Pi_T \setminus \Gamma $ of the Burgers equation with initial data $ u_0 $, and if for a.e. $ t\in (0,T) $ the one-sided traces of $ u $ at each particle position satisfy

(ⅱ) A function $ h_k $ is a solution of the second equation of (1.1) with initial data $ (h_{k,0},v_{k,0}) $ if $ h_k \in W^{2,\infty}([0,T]) $, if $ h_k(0) = h_{k,0} $, $ h_k'(0) = v_{k,0} $, and if given given $ u $ a Kružkov entropy solution of the Burgers equation in $ \Pi_T \setminus \Gamma $ we have for a.e. $ t \in (0,T) $

(ⅲ) With the notation $ \vec{h} = (h_1,\ldots,h_K) $, a pair $ (u, \vec{h}) $ satisfying (ⅰ) and (ⅱ) above is an entropy solution of the system (1.1).

Remark 1. Definition 1.2 requires strong one-sided traces $ u(h_k(t)^{\pm},t) $ along each path $ x = h_k(t) $. Assuming that the particle trajectories do not intersect except possibly on a subset of $ (0,T) $ having Lebesgue measure zero, the results of [13] guarantee existence of the required traces. This is due to the regularity of the paths $ x = h_k(t) $ and the fact that $ u $ is a Kružkov entropy solution of the Burgers equation in $ \Pi_T \setminus \Gamma $.

Assumption 1.1. The initial data satisfies $ u_0 \in \rm{BV}( \mathbb{R}) $.

Above we have used the notation $ \rm{BV}( \mathbb{R}) $ to denote the set of functions of bounded variation on $ \mathbb{R} $, i.e., those functions $ \rho: \mathbb{R} \mapsto \mathbb{R} $ for which

where the $ \sup $ extends over all $ M\ge 1 $ and all partitions $ \{\xi_0< \xi_1< \ldots < \xi_M \} $ of $ \mathbb{R} $.

Theorem 1.3 (Main theorem). The Lax-Friedrichs scheme described in Section 2 produces approximations that converge as the mesh size approaches zero, along a subsequence, to a pair $ (u, \vec{h}) $ where $ u \in L^{\infty}( \Pi_T) \cap C([0,T]; L^1_{\mathrm{loc}}( \mathbb{R})) $ and $ h_k \in W^{2,\infty}([0,T]) $, $ k = 1,\ldots,K $. If the particle trajectories $ h_k(t) $ do not intersect except possibly on a subset of $ (0,T) $ having Lebesgue measure zero, then $ (u, \vec{h}) $ is an entropy solution in the sense of Definition 1.2.

As mentioned above, there has been significant progress on the single-particle version of (1.1) [1,5,6,7,11]. The study of (1.1) started with reference [11]. Among other things the authors completely solved the Riemann problem for $ K = 1 $, and described the asymptotic behavior of solutions.

In reference [5], the authors introduce two finite volume methods for computing approximate solutions. One is a Glimm-like scheme, and the other is a well-balanced scheme that uses nonrectangular space-time cells near the interface. These methods employ random sampling for placing the particle at a mesh interface at each time step. The nonconservative source term is handled by using a certain well-balanced scheme that was analyzed in [7]. They avoid the use of a moving mesh, and also avoid the use of a Riemann solver for the full model. The case of multiple particles is addressed, and is handled via a splitting method.

Reference [14] presents a finite volume scheme that is based on the well-balanced scheme of [5,7], but uses an adaptive stencil as an alternative to using a moving grid. The multiple-particle case is handled by splitting.

Reference [7] proves well-posedness for the problem

This is a simplification of (1.1), but its analysis provides an important step in analyzing the full problem. As mentioned above the germ $ \mathcal{G}(\lambda,c) $, which is required for the correct defintion of entropy solution, was identified in [7].

Reference [6] proves well-posedness of the model (1.1) for $ K = 1 $, assuming that the initial data is of bounded variation. Approximate solutions are generated via a wave-front tracking algorithm. Definition 1.2 is a direct generalization of the definition for $ K = 1 $ appearing in [6].

Reference [1] presents a class of finite volume schemes for (1.1) when $ K = 1 $. The schemes are similar to those in [5], but a moving grid is used, which keeps the particle located at a fixed cell boundary. The approximations are shown to converge to the unique entropy solution.

References [2] and [3] concern a generalized version of (1.1) (again, for $ K = 1 $), where the fluid is governed by the inviscid compressible Euler equations.

Reference [10] specifically deals with a multiple-particle problem. The authors prove well-posedness for a version of (1.1) where the particle paths $ h_k(t) $ are given, i.e., the second equation of (1.1) does not appear.

Let $ H(\cdot) $ denote the Heaviside function, i.e., the characteristic function of $ [0,\infty) $. The system (1.1) has the following equivalent formulation [5,11]:

Although the splitting approach for multiple particles used in [5] and [14] gives good numerical results, extending the convergence analysis from the single-particle to the multiple-particle problem seems difficult. Various bounds required for convergence are not preserved by the splitting steps. The numerical schemes in those papers are based on the model (1.1). In this paper we instead discretize (1.6), using Lax-Friedrichs differencing for each of the PDEs. The advantage of this approach is that the case of multiple particles is accommodated without splitting. This makes it possible to obtain a number of estimates which taken together give a convergence proof for the multiple-particle model. On the other hand, while the schemes of [1], [5], and [14] give very sharply resolved shocks at the particle locations, our Lax-Friedrichs method results in a substantial amount of smearing. With this in mind, we additionally propose a higher resolution version of the scheme, based on MUSCL processing.

The rest of the paper is organized as follows. In Section 2 we describe the Lax-Friedrichs scheme mentioned above. In Section 3 we prove convergence, modulo a subsequence, of the approximations for $ u $, as well as the approximations for $ h_k $. In Section 4 we prove convergence of the approximations for $ w_k $. In Section 5 we verify that the subsequential limit $ u $ is a Kružkov entropy solution in $ \Pi_T \setminus \Gamma $ and satisfies the jump condition (1.3). In Section 6 we prove that the limit $ h_k $ satisfies the differential equation (1.4). Section 6 concludes with the proof of Theorem 1.3. Section 7 describes the MUSCL processing mentioned above. Section 8 presents the results of some numerical experiments.

2.   The Lax-Friedrichs scheme applied to (1.6)

We use a uniform spatial mesh size $ \Delta x $, and temporal step size $ \Delta t $. Define

where the integer $ N $ is such that $ N \Delta t \in [T, T + \Delta t) $. Define $ I_j = [x_j - \Delta x/2, x_j + \Delta x /2) $, $ I^n = [t^n, t^{n+1}) $. Let $ \chi_j(x) $ denote the characteristic function of $ I_j $, and $ \chi^n(t) $ the characteristic function of $ I^n $ We denote by $ U_j^n $ the finite difference approximation of $ u(x_j,t^n) $, $ U_j^n \approx u(x_j,t^n) $. Similarly $ W_{k,j}^n \approx w_k(x_j,t^n) $. Let $ \{Q_j^n\} $ be a grid-defined function such as $ \{U_j^n\} $ or $ \{W_{k,j}^n\} $. We will use the following notational abbreviations:

Let $ v_0(x) $ denote the initial data $ u_0(x) $ or $ H(x-h_{k,0}) $. The data $ v_0(x) $ is discretized via $ V_j^0 = {1 \over {\Delta x}}\int_{I_j} v_0(x)\, dx $, implying that

With the notation $ v^0_{\min} = \inf_{y \in \mathbb{R}}v_0(y) $, $ v^0_{\max} = \sup_{y \in \mathbb{R}}v_0(y) $, we have $ -\infty < v^0_{\min} $, $ v^0_{\max} < \infty $. Due to our method of discretizing $ v_0 $, $ v^0_{\min} \le V^0_{\min} $, $ V^0_{\max} \le v^0_{\max} $, $ \left\|{V^0}\right\|_{\infty} \le \left\|{v_0}\right\|_{\infty} $, and $ \sum_{j \in \mathbb{Z}} \left|{\Delta_+ V_j^0}\right| \le \operatorname*{TV}(v_0) $.

We extend $ \{U_j^n \} $ and $ \{W_{k,j}^n \} $ from grid-defined functions to functions defined on all of $ \Pi_T $ via

Similarly,

where $ c_k^n \approx h_k'(t^n) $ and $ h_k^n \approx h_k(t^n) $, with the initialization $ (h_k^0,c_k^0) = (h_{k,0},v_{k,0}) $

Let $ \mu = \Delta t / \Delta x $. The algorithm that we propose discretizes the first two equations of (1.6) via the Lax-Friedrichs scheme, the third equation using Euler's method:

Here

where $ q $ is a parameter. For our purposes $ q \in (0,1/2] $. The numerical fluxes in (2.7) result by applying the Lax-Friedrichs flux [12] to $ f(u) = u^2/2 $ and $ g_k^n(w) = c_k^n w $.

Remark 2. The scheme (2.6) preserves solutions where the fluid velocity and particle velocities are equal to the same constant: $ U^n_j = v $ for all $ j \in \mathbb{Z} $, $ c^n_k = v $ for $ k = 1,\ldots,K $.

Remark 3. Some explanation of the third equation of (2.6) is in order. Based on the third equation of (1.6), the third equation of (2.6) should be (approximately) equivalent to

where $ \tilde{u}(h_k(t^n),t^n) \approx u(h_k(t^n),t^n) $. To see that the third equation of (2.6) is actually of this form, note that since $ W_{k,j}^n \approx H(x_j-h_k(t^n)) $, the grid function $ \{(1/2)(W^n_{k,j+1}-W^n_{k,j-1})/ \Delta x \} $ approximates $ \delta(x-h_k(t^n)) $, a delta function concentrated at $ x = h_k(t^n) $. In particular, we expect $ (1/2) \sum_{j \in \mathbb{Z}} \left(W^n_{k,j+1}-W^n_{k,j-1} \right) \approx 1 $ (in fact this holds with ``$ \approx $'' replaced by ``$ = $''; this follows from (3.5) of Lemma 3.1), and so we can write the third equation of (2.6) in the form

Thus, by defining

we have the desired approximation $ \tilde{u}(h_k(t^n),t^n) \approx u(h_k(t^n),t^n) $. Clearly there are other, possibly simpler, methods of discretizating the third equation of (1.6). The reason for choosing this particular approximation is to ensure the discrete conservation of momentum property discussed below.

From the first two equations of (1.1) it follows that, at least formally, the total momentum of the system is conserved:

The scheme (2.6) enforces a discrete version of (2.8).

Proposition 1. Assume that there is a $ 0<J\in \mathbb{Z} $ such that $ U_j^n = 0 $ for $ \left|{j}\right| > J $, and that $ \left\|{U^n}\right\|_{\infty} < \infty $. Define the discrete momentum:

The discrete momentum is conserved: $ \mathcal{M}^{n+1} = \mathcal{M}^n $ for $ 0 \le n \le N $.

Proof. Multiplying by $ \Delta x $ and summing the first equation of (2.6) over $ j \in \mathbb{Z} $ gives

Multiplying the third equation of (2.6) by $ m_k $ and then summing over $ k $ gives

The proof is completed by adding (2.10) and (2.11).

Define

Lemma 2.1. $ Z_j^n $ satisfies the following (equivalent) evolution equations:

Remark 4. From (1.6) and the definition $ z = u + \sum_{k = 1}^K \lambda_k w_k $, one can derive (formally) the PDE

Evidently (2.13) is a discretization of (2.15).

Remark 5. It is clear by inspection of either (2.13) or (2.14) that the scheme (2.6) preserves solutions of the form $ Z^n_j = \rm{constant} $.

Proof. Using (2.12) and (2.6) we find that

Next we use

Substituting (2.17) into (2.16) and canceling $ (\mu/2) \sum_{k = 1}^K \lambda_k c_k^n(W_{k,j+1}^n - W_{k,j-1}^n ) $, the result is

The identity (2.14) is immediate from (2.18).

For the proof of (2.13), we start from the second equality of (2.18) and substitute $ \hat{U}_j^n = \hat{Z}_j^n - \sum_{k = 1}^K \lambda_k \hat{W}^n_{k,j} $, which results in

The identity (2.13) now follows directly from (2.19).

3.   Convergence of $ u^{ \Delta} $ and $ h_k^{ \Delta} $

Let $ \Delta = (\Delta x, \Delta t) $. For our convergence analysis we will assume that $ \Delta \rightarrow 0 $ with $ \mu $ fixed, and satisfying the following CFL condition:

Additionally we assume that

which will be satisfied automatically for $ \Delta $ sufficiently small.

Define $ z_0(x) = u_0(x) + \sum_{k = 1}^K \lambda_k H(x-h_k(0)) $. Due to the method of discretizing $ u_0 $ and $ H(x-h_k(0)) $, it follows from from (2.12) that $ Z_j^0 = {1 \over {\Delta x}}\int_{I_j} z_0(x)\, dx $. Using the notation $ z^0_{\min} = \inf_{y \in \mathbb{R}}z_0(y) $, $ z^0_{\max} = \sup_{y \in \mathbb{R}}z_0(y) $, we have $ -\infty< z^0_{\min} $, $ z^0_{\max} < \infty $, and $ z^0_{\min} \le Z^0_{\min} $, $ Z^0_{\max} \le z^0_{\max} $, and $ \left\|{Z^0}\right\|_{\infty} \le \left\|{z_0}\right\|_{\infty} $.

Lemma 3.1. The following properties hold:

Proof. The proof is by induction on $ n $. Clearly all of (3.3), (3.4), (3.5), and (3.6) hold at $ n = 0 $. Assume that those assertions hold at time step $ n $. From (3.1) and the induction hypothesis it follows that

To prove that (3.3) holds at time step $ n+1 $ we rewrite (2.14) using incremental coefficients:

where

Using $ \hat{U}_j^n = \hat{Z}_j^n - \sum_{k = 1}^K \lambda_k \hat{W}^n_{k,j} $, and $ \hat{W}^n_{k,j} \in [0,1] $ we see that $ C_{ j+1/2}^n \ge 0 $, $ D_{ j-1/2}^n \ge 0 $ due to (3.7). At the same time $ C_{ j+1/2}^n + D_{ j-1/2}^n = q \le 1/2 $. Next we rewrite (3.8):

From (3.10) it is clear that $ Z_j^{n+1} $ is a convex combination of $ Z_{j+1}^{n} $, $ Z_j^{n} $, $ Z_{j-1}^{n} $, implying that $ Z^n_{\min} \le Z_{j}^{n+1} \le Z^n_{\max} $. Invoking the induction hypothesis then completes the proof of (3.3) for $ n+1 $.

Next we prove that (3.5) holds for $ n+1 $. We rewrite the second equation of (2.6):

where

By (3.7) we have $ \alpha_k^n \ge 0 $, $ \beta_k^n \ge 0 $, and (3.1) implies $ \alpha_k^n + \beta_k^n = q \le 1/2 $. Thus $ W_{k,j}^{n+1} $ is a convex combination of $ W_{k,j-1}^n, W_{k,j}^n, W_{k,j+1}^n $, implying that $ W_{k,j}^{n+1} \in [0,1] $ after invoking the induction hypothesis. By differencing (3.11) we get

Invoking the induction hypothesis again yields $ \Delta_+ W_{k,j}^{n+1} \ge 0 $. Finally, summing (3.13) over $ j $ and then applying the induction hypothesis yields $ \sum_{j \in \mathbb{Z}} \Delta_+W_{k,j}^{n+1} = 1 $.

To prove (3.4) holds at $ n+1 $, we employ the result of the previous two paragraphs. Recalling (2.12), the proven bound on $ Z_j^{n+1} $ is equivalent to

It is readily verified that $ u^0_{\min} \le z^0_{\min} $ and $ z^0_{\max} \le u^0_{\max} + \sum_{k = 1}^K \lambda_k $. Replacing $ z^0_{\min} $ and $ z^0_{\max} $ in (3.14), the result is

Recalling that $ \lambda_k>0 $ and $ W_{k,j}^{n+1} \in [0,1] $, it is clear that (3.4) holds.

To verify that (3.6) holds for $ n+1 $, we start with the third formula of (2.6), from which it is evident that

The induction hypothesis yields $ \sum_{j \in \mathbb{Z}} \left(W^n_{k,j+1}-W^n_{k,j-1} \right) = 2 $, and so after taking absolute values, and applying (3.2), equation (3.16) becomes

from which the desired inequality follows readily.

Lemma 3.2. $ U_j^n $ and $ Z_j^n $ satisfy spatial variation bounds:

and

Proof. We claim that the scheme is a so-called Total Variation Decreasing (TVD) scheme with respect to the variable $ Z_j^n $, i.e.,

To prove the claim we use (3.8). We have shown that $ C_{ j+1/2}^n, D_{ j+1/2}^n \ge 0 $. It suffices by a standard result [12,p. 116] to show that $ C_{ j+1/2}^n+ D_{ j+1/2}^n \le 1 $. Using (3.9) we find that

Here we have used (3.1) to get the last inequality. The desired bound then results by recalling that $ q\le 1/2 $. Then by induction it follows from (3.18) that

It is readily verified using (2.12) that

Then (3.18) follows from (3.22) and the $ n = 0 $ version of (3.23), along with the fact that $ \sum_{j \in \mathbb{Z}}\left|{\Delta_+ U_j^0}\right| \le \operatorname*{TV}(u_0) $. Finally, (3.19) results from (3.18) and (3.23).

Lemma 3.3. The following time continuity estimate holds:

where the constant $ B $ is independent of $ \Delta $.

Proof. Rearranging the first equation of (2.6), and using (2.17) to rewrite $ \Delta_- \bar{f}_{ j+1/2}^n $ yields

After taking absolute values, applying the triangle inequality, then using the bounds on $ c_k^n $ and $ \hat{U}_j^n $ provided by Lemma 3.1, we sum over $ j \in \mathbb{Z} $. The result is

where $ B_1 $ and $ B_2 $ are $ \Delta $-independent constants. The proof is completed by invoking Lemma 3.2, along with the observation that $ \sum_{j \in \mathbb{Z}} \left|{W_{k,j+1}^n - W_{k,j-1}^n}\right| = 2 $, which follows from (3.5).

Lemma 3.4. The particle velocity approximations satisfy the following bound:

Proof.

We start with the third formula of (2.6). Subtracting $ c_k^n $ from both sides, taking absolute values, and then using the triangle inequality, the result is

The proof of (3.27) is completed using (3.4) and (3.6).

Lemma 3.5. The approximations $ u^{ \Delta} $ converge boundedly a.e. and in $ L^1_{ \mathrm{loc}}( \Pi_T) $ as $ \Delta \rightarrow 0 $, along a subsequence, to some $ u \in L^{\infty}( \Pi_T) \cap C([0,T]; L^1_{\mathrm{loc}}( \mathbb{R})) $. For each $ k \in \{1,\ldots, K\} $ the sequence $ h_k^{ \Delta} $ converges (along the same subsequence) in $ W^{1,\infty}([0,T]) $ to some $ h_k \in W^{2,\infty}([0,T]) $, and $ c_k^{ \Delta} $ converges (also along the same subsequence) to $ h_k' $ in $ L^1_{\mathrm{loc}}((0,T)) $.

Proof. The proof is a standard argument (e.g., the proof of Proposition 2.4 of [1]) using Lemmas 3.1, 3.2, and 3.3 for the $ u $ portion, and Lemmas 3.1 and 3.4 for the $ h_k $ portion.

Remark 6. In Sections 5 and 6 we will assume that the particle trajectories do not intersect except possibly on a subset of $ (0,T) $ having Lebesgue measure zero. The convergence result above holds without any assumptions about particle path intersections.

In what follows $ (u,\vec{h}) $ refers to a fixed subsequential limit of the type whose existence is guaranteed by Lemma 3.5. When taking the limit as $ \Delta \rightarrow 0 $ it is understood to be along this fixed subsequence.

4.   Convergence of $ w_k^{ \Delta} $ and $ z^{ \Delta} $

Lemma 4.1. $ W_{k,j}^n $ satisfies a spatial variation bound and a time continuity estimate for each $ k \in \{1, \ldots, K\} $:

Proof. The first part of (4.1) is evident from (3.5). For the second part of (4.1), we write (3.11) in the form

Taking absolute values, and recalling from the proof of Lemma 3.1 that $ \alpha_k^n, \beta_k^n \in [0,1] $ yields

Then summing over $ j \in \mathbb{Z} $ and using $ \sum_{j \in \mathbb{Z}} \left|{\Delta_+W_{k,j}^n}\right| = 1 $, $ \alpha_k^n + \beta_k^n \le 1/2 $, gives the second part of (4.1)

Lemma 4.2. As $ \Delta \rightarrow 0 $, $ w_k^{ \Delta}(x,t) \rightarrow H(x-h_k(t)) $ boundedly a.e. and in $ L^1_{ \mathrm{loc}}( \Pi_T) $ for each $ k \in \{1, \ldots, K\} $.

Proof. Lemma 4.1 along with $ W_{k,j}^n \in [0,1] $ (Lemma 3.1) guarantees that $ w_k^{ \Delta} $ converges along a subsequence in $ L^1_{ \mathrm{loc}}( \mathbb{R}_+ \times \mathbb{R}) $ and boundedly a.e. to some $ w_k \in L^{\infty}( \Pi_T) \cap C([0,T]; L^1_{\mathrm{loc}}( \mathbb{R})) $.

A standard Lax-Wendroff calculation [9] proves that $ w_k $ is a weak solution of

One such weak solution is $ w_k(x,t) = H(x-h_k(t)) $. We will show that this is the only weak solution and the proof will be complete. Assume that $ w_k $ and $ \tilde{w}_k $ are both weak solutions of (4.4). This implies that for every $ \phi \in C_0^{\infty}( \mathbb{R} \times [0,T]) $,

Fix $ \psi \in C_0^{\infty}( \mathbb{R} \times [0,T]) $. Let

It is readily verified that $ \phi_t + h_k'(t) \phi_x = \psi $, $ \phi(\cdot,T) = 0 $. Substituting into (4.5), we have

Since (4.7) holds for any $ \psi \in C_0^{\infty}( \mathbb{R} \times [0,T]) $, we conclude that $ w = \tilde{w} $ a.e.

The following lemma is a direct consequence of (2.12), Lemma 3.5, and Lemma 4.2.

Lemma 4.3. Define $ z(x,t) = u(x,t) + \sum_{k = 1}^K \lambda_k H(x-h_k(t)) $. As $ \Delta \rightarrow 0 $, $ z^{ \Delta}(x,t) \rightarrow z(x,t) $ boundedly a.e. and in $ L^1_{ \mathrm{loc}}( \Pi_T) $.

5.   Jump and entropy conditions for $ u $

In this section we verify that the subsequential limit $ u $ is a Kružkov entropy solution in $ \Pi_T \setminus \Gamma $ and satisfies the jump condition (1.3).

Here and in Section 6 we will employ the test function $ 0 \le \psi_{\delta}(x) \in \mathcal{C}_0^{\infty}( \mathbb{R}) $, $ \delta>0 $, such that $ \psi_{\delta}(0) = 1 $, $ \rm{supp}(\psi_{\delta}) = [-\delta,\delta] $, and

where $ \eta_{\delta} $ denotes the standard $ C^{\infty}( \mathbb{R}) $ mollifier:

Assumption 5.1. Assume that the particle trajectories do not intersect except possibly on a subset $ F \subset (0,T) $ having Lebesgue measure zero.

Remark 7. The set $ F $ has the form $ F = \cup_{i \ne j} F_{i,j} $, where

Since each of the particle paths $ t\mapsto h_k(t) $ is continuous, each $ F_{i,j} $ is closed, and thus $ F $ is also a closed subset of $ (0,T) $. There are no particle path intersections in the open set $ E: = (0,T) \setminus F $. $ E $ is a countable disjoint union of open intervals, $ E = \cup_{\mathsf{m} = 1}^{\mathsf{M}} (a_\mathsf{m},b_\mathsf{m}) $, where $ 1\le \mathsf{M} \le \infty $ and each $ (a_\mathsf{m},b_\mathsf{m}) \subseteq (0,T) $. By Assumption 2, $ E $ is of full measure, $ \rm{meas}((0,T) \setminus E) = 0 $.

Lemma 5.1. Define $ \mathcal{U} = [ u^0_{\min}-\sum_{k = 1}^K \lambda_k, u^0_{\max} + \sum_{k = 1}^K \lambda_k] $. Referring to (2.6), let $ G(U_{j+1}^n,U_j^n,U_{j-1}^n) = U_j^n - \mu \Delta_- \bar{f}^n_{ j+1/2} $. Then $ G $ is nondecreasing with respect to each of $ U_{j+1}^n,U_j^n,U_{j-1}^n $ if $ U_{j+1}^n,U_j^n,U_{j-1}^n \in \mathcal{U} $. Referring to (2.13)$ , Z_j^{n+1} $ is nondecreasing with respect to each of $ Z_{j+1}^n,Z_j^n,Z_{j-1}^n $ if $ Z_{j+1}^n,Z_j^n,Z_{j-1}^n \in [ z^0_{\min}, z^0_{\max}] $.

Proof. The partial derivatives of $ G $ are

Clearly $ {\partial G}/{\partial U_j^n}\ge 0 $ since $ q \le 1/2 $. For $ {\partial U_j^{n+1}}/{\partial U_{j\pm1}^n} $,

In view of (5.4) and (3.1) it is clear that $ \partial G / \partial U_{j\pm1}^n \ge 0 $.

For $ Z_j^{n+1} $ we use (2.13) to compute

It is readily verified that each of these partial derivatives is nonnegative using (3.1) and the fact that $ \hat{W}_{k,j}^n \in [0,1] $.

The following lemma is a straightforward consequence of (3.5) and Lemma 4.2.

Lemma 5.2. Define

$ S_j^n $ has the following properties:

and as $ \Delta \rightarrow 0 $, $ S^{ \Delta}(x,t) \rightarrow \sum_{k = 1}^K \lambda_kH(x-h_k(t)) $ boundedly a.e. and in $ L^1_{ \mathrm{loc}}( \Pi_T) $.

Lemma 5.3. The following discrete entropy inequalities hold for all $ \kappa \in [ z^0_{\min}, z^0_{\max}] $:

Proof. Writing (2.13) in the form $ Z_j^{n+1} = P(Z_{j+1}^n,Z_j^n,Z_{j-1}^n) $, it is readily apparent that $ P(\kappa,\kappa,\kappa) = \kappa $. Using this observation the proof is a standard calculation [8,9], using the fact that $ P $ is a nondecreasing function of all three arguments (Lemma 5.1).

Lemma 5.4. The limit solution $ u $ satisfies the jump condition (1.3) for a.e. $ t \in (0,T) $ and each $ k \in {1, \ldots, K} $.

Proof. We start with the first inequality in (5.8), and use the identity

This results in

Since $ \Delta_{\pm} S_j^n\ge 0 $, we have

and so we can replace (5.10) by

Following the proof of the Lax-Wendroff theorem [9], let $ \phi $ be a nonnegative test function with $ \phi(x,0) = 0 $, and $ \phi_j^n : = \phi(x_j,t^n) $. We multiply (5.12) by $ \phi_j^n \Delta x $, and then sum over $ j \in \mathbb{Z} $, $ n \ge 0 $. After summation by parts the result is

Letting $ \Delta \downarrow 0 $ and recalling $ z^{ \Delta} \rightarrow z $, $ S^{ \Delta} \rightarrow \sum_{k = 1}^K \lambda_k H(x-h_k(t)) $ yields

After simplifying the last integral the result is

A similar calculation starting from the second inequality of (5.8) yields

Recalling Assumption 5.1 and Remark 7, fix an interval $ \mathcal{I}_{\mathsf{m}}: = (a_{\mathsf{m}}, b_{\mathsf{m}}) \subseteq (0,T) $ where there are no path intersections, and fix a particle path, indexed by $ k $. For this calculation we will use the abbreviations $ z^{\pm}(t) = z(h_k(t)^{\pm},t) $ and $ c_k(t) = h_k'(t) $. The ordering of the particles does not change in $ \mathcal{I}_{\mathsf{m}} $, so we can assume that the particles are labeled so that

Let $ \phi(x,t) = \psi_{\delta}(x-h_k(t))\rho(t) $, where $ 0 \le \rho \in C_0^{\infty}(\mathcal{I}_{\mathsf{m}}) $. Letting $ \delta \downarrow 0 $ in (5.15) yields

where $ \gamma_k = \sum_{l<k} \lambda_l $, and we have abbreviated $ z^{\pm} = z^{\pm}(t) $, $ c_k = c_k(t) $. Another such test function calculation, this time with (5.16) results in

Continuing with the abbreviation $ z^{\pm} = z^{\pm}(t) $, $ c_k = c_k(t) $, for a.e. $ t \in \mathcal{I}_\mathsf{m} $ we have

Fix a time $ t\in \mathcal{I}_\mathsf{m} $ where (5.20), (5.21) hold. If $ z^- = z^+ $ then (5.20) and (5.21) are satisfied. So assume for now that $ z^- \neq z^+ $. Substituting $ z^- \le \kappa \le z^+ $ into (5.20) and then (5.21) gives

where $ \tilde{c}_k = c_k + \gamma_k $. Repeating this calculation with $ z^+ \le \kappa \le z^- $, we find that

Plugging $ \kappa = z^- $ into the first inequality of (5.22) and then into the first inequality of (5.23), and recalling $ f(z) = z^2/2 $, yields

The second inequality of (5.22) (for $ z^-< z^+ $) or the second inequality of (5.23) (for $ z^- > z^+) $ implies that in either case

Substituting $ \kappa = z^+ $ into the second inequalities of (5.22) and (5.23) yields

Finally, with $ \epsilon>0 $, we substitute $ \kappa = z^+ - \epsilon $ into the first inequality of (5.22), and $ \kappa = z^+ + \epsilon $ into the first inequality of (5.23). Sending $ \epsilon \downarrow 0 $ results in

Thus either $ z^+ = z^- $ or all of (5.24), (5.25), (5.26), (5.27) hold. Let $ u^{\pm} = u(h_k(t)^{\pm},t) $. Substituting $ z^- = u^- + \gamma_k $, $ z^+ = u^+ + \gamma_k + \lambda_k $ into these relationships we have shown that either

or

Recalling Definition 1.1, and that $ c_k = h_k'(t) $, it is evident from (5.28), (5.29) that

and this holds for a.e. $ t \in \mathcal{I}_\mathsf{m} $. The proof is completed by repeating this argument for each $ k \in \{1,\ldots,K\} $ and each $ \mathsf{m} \in \{1, \ldots, \mathsf{M}\} $.

Lemma 5.5. The following discrete entropy inequality holds for each $ \kappa \in \mathbb{R} $:

where $ \bar{F}\left(U_{j+1}^{n},U_j^{n} \right) = \bar{f}(U_{j+1}^n \vee \kappa,U_{j}^n \vee \kappa) - \bar{f}(U_{j+1}^n \wedge \kappa,U_{j}^n \wedge \kappa) $.

Proof. First assume that $ \kappa \in \mathcal{U} = [ u^0_{\min}-\sum_{k = 1}^K \lambda_k, u^0_{\max} + \sum_{k = 1}^K \lambda_k] $. We write the first equation of (2.6) in the form

where

Invoking the monotonicity of $ G $ (Lemma 5.1), a standard calculation [8,9] yields

for $ \kappa \in \mathcal{U} $. Substituting $ V_j^{n+1} = U_j^{n+1} - Q_j^n $, and using the triangle inequality yields (5.31), assuming $ \kappa \in \mathcal{U} $.

Now take the case where $ \kappa \notin \mathcal{U} $, say $ \kappa < u^0_{\min} - \sum_{k = 1}^K \lambda_k $. In that case (5.31) reduces to

which, recalling the first equation of (2.6), is clearly satisfied. The case where $ \kappa > u^0_{\max} + \sum_{k = 1}^K \lambda_k $ is handled similarly.

Lemma 5.6. The limit $ u $ is a Kružkov entropy solution in $ \Pi_T \setminus \Gamma $ of the Burgers equation with initial data $ u_0 $.

Proof. Define $ F(a,b) = f(a\vee b)-f(a\wedge b) = \operatorname*{sgn}(a-b)(a^2/2 - b^2/2) $. We must show that $ u $ satisfies

for every $ \kappa \in \mathbb{R} $ and every nonnegative test function $ \phi \in C_0^{\infty}\left( \mathbb{R} \times [0,T) \setminus \Gamma \right) $.

The proof is based on the discrete entropy inequality (5.31). Due to the bounds on $ U_j^n $ and $ c_k^n $ (Lemma 3.1), we have for some $ B>0 $ which independent of $ \Delta $,

Substituting into (5.31) the result is

Multiplying by $ \phi_j^n = \phi(x_j,t^n) $ and then summing by parts we find that

Letting $ \Delta \rightarrow 0 $, and using $ u^{ \Delta} \rightarrow u $, $ w_k^{ \Delta} \rightarrow H(x-h_k(t)) $, results in

The proof is finished by observing that $ \int_{ \mathbb{R}} H(x-h_k(t)) \phi_x \,dx = 0 $, since $ \phi(h_k(t),t) = 0 $.

6.   Differential equation for $ h_k $ and proof of the main theorem

In this section we prove that the limit $ h_k $ satisfies the differential equation (1.4). This section also contains the proof of Theorem 1.3. Assumption 5.1 (restriction on particle intersections) remains in effect in this section.

Lemma 6.1. The limit $ h_k(t) $ satisfies the differential equation (1.4) for each $ k \in {1,\ldots,K} $ and a.e. $ t \in (0,T) $. Also, $ (h_k(0),h_k'(0)) = (h_{k,0},v_{k,0}) $.

Proof. Fix a particle with index $ k $, $ 1\le k \le K $. Let $ a_k^n = (c_k^{n+1}-c_k^n)/\Delta t $. The third equation of (2.6) yields

Define $ \psi_j^n = \psi_{\delta}(x_j - h_k(t^n)) $, where $ \psi_{\delta} $ is defined by (5.1). Let $ \xi(t) \in \mathcal{C}^{\infty}_0((0,T)) $ and define $ \xi^n = \xi(t^n) $. We re-write (6.1) in the form

Next we multiply by $ \xi^n \Delta t $ and sum over $ n: $

We solve for $ \left(c_k^n - \hat{U}_j^n \right) \left(W^n_{k,j+1}-W^n_{k,j-1} \right) $ in the first equation of (2.6),

and substitute into the first sum on the right side of (6.3). The result is

Summing the left side of (6.5) by parts, we find that

Letting $ \Delta \downarrow 0 $ in (6.6), and using $ c_k^{ \Delta} \rightarrow h_k' $, the result is

and for $ \mathcal{S}_1 $, summation by parts followed by sending $ \Delta \rightarrow 0 $ yields

We next estimate $ \mathcal{S}_2 $. Fix $ l \ne k $. It suffices to estimate $ \mathcal{S}_{2,l} $, where

Since $ c_l^n $ and $ \hat{U}_j^n $ are bounded (Lemma 3.1), and $ \left(W^n_{l,j+1}-W^n_{l,j-1} \right) \ge 0 $, $ \psi_j^n \ge 0 $,

where $ B $ is some positive number independent of $ \delta $ and $ \Delta $. Summation by parts yields

The first sum on the right is telescoping and is equal to zero. Thus, referring back to (6.10) we have

Letting $ \Delta \rightarrow 0 $ yields

Recalling that $ w_l(x,t) = H(x-h_l(t)) $, we find that

Substituting into (6.13) yields the desired estimate of $ \mathcal{S}_{2,l} $:

We claim that $ \mathcal{S}_3 \rightarrow 0 $. Since $ c_k^n $ and $ \hat{U}_j^n $ are bounded (Lemma 3.1), and $ \psi_j^n \le 1 $, $ W^n_{k,j+1}-W^n_{k,j-1} \ge 0 $,

where $ B $ is some positive number independent of the mesh size $ \Delta $. Using the formula (6.11) with $ 1-\psi_j^n $ replacing $ \psi_j^n $,

In the second term on the right side we have used $ \Delta_+(1-\psi_{j}^n) = -\Delta_+\psi_{j}^n $. The first sum on the right is telescoping and is equal to $ 2 $. Thus, referring back to (6.16) we have

Letting $ \Delta \rightarrow 0 $ yields

Substituting $ w_k(x,t) = H(x-h_k(t)) $, and using $ \psi_{\delta}(0) = 1 $, the result is

Plugging (6.20) into (6.19) completes the proof of the claim.

Combining $ \mathcal{S}_3 \rightarrow 0 $ with (6.7), (6.8), and (6.15) we have

where

Next we consider the limit when $ \delta \rightarrow 0 $ in (6.21), (6.22). Due to Assumption 5.1 (restriction on particle intersections), if $ l \neq k $ then $ \left|{h_l(t)-h_k(t)}\right|>0 $ for a.e. $ t \in (0,T) $ and thus

with the result that $ R_k \rightarrow 0. $ Let

A straightforward calculation using (5.1), (5.2) gives

and

The result is that (6.21) becomes

After integrating the left side by parts the result is

implying that (1.4) holds for a.e. $ t \in [0,T] $.

The observation that for all $ \Delta >0 $, $ h^{ \Delta}_k(0) = h_{k,0} $ and $ c^{ \Delta}_k(0) = v_{k,0} $ proves the assertion that $ (h_k(0),h_k'(0)) = (h_{k,0},v_{k,0}) $.

Proof of the main theorem.

Proof. Lemma 3.5 provides the convergence portion of Theorem 1.3. That the limit $ (u,\vec{h}) $ is an entropy solution results from Lemmas 5.4, 5.6, and 6.1.

Remark 8. For the single-particle case, Theorem 8 of [6] states that Definition 1.2 is sufficient for uniqueness. Thus if $ K = 1 $, the Lax-Friedrichs approximations $ (u^{ \Delta}, h_1^{ \Delta}) $ converge to the unique entropy solution, and convergence is along the entire computed sequence, not just a subsequence.

7.   Improved resolution via MUSCL processing

It is possible to somewhat reduce the excessively diffusive nature of Lax-Friedrichs differencing without adding too much complexity by using the MUSCL approach. Our incorporation of MUSCL processing is standard [12]. Let $ \mathcal{M}(\cdot,\cdot) $ denote the minmod function:

We replace the numerical fluxes $ \bar{f}^n_{ j+1/2} $, $ \bar{g}^n_{k, j+1/2} $ in (2.7) by

where

We do not presently have any convergence results or even stability estimates for the resulting scheme with MUSCL processing incorporated. A moderate amount of numerical experience indicates that the algorithm produces approximations that converge to the same solution as the basic algorithm of Section 2.

8.   Numerical examples

Following are a few numerical examples. We refer to the scheme of Section 2 as the basic scheme, and the modified scheme of Section 7 as the MUSCL scheme. We used $ q = 1/2 $ in all examples.

Example 8.1. This is a single-particle Riemann problem, with

The exact solution is available for comparison, using the results of [11]. See Figure 1. The approximations appear to improve when the mesh size is halved, as expected. It is also apparent that the MUSCL scheme is more accurate than the basic one.

The sharp transition at $ x\approx 0.8 $ is a shock that is collocated with the particle. With our Lax-Friedrichs scheme there is some smearing of the shock. We must rely on a very small mesh size, even with the MUSCL version, to obtain a very sharp transition. The schemes of [1], [5], and [14] resolve this type of shock (i.e., the shock is collocated with the particle) with no smearing.

Example 8.2. This is another single-particle Riemann problem with

As in the previous example the exact solution is available via [11]. This example displays a spurious kink, see Figure 2, that appears in some cases where a particle's velocity $ h_k'(t) $ lies between $ u(h_k^-(t),t) $ and $ u(h_k^+(t),t) $. The kink is probably due to the large numerical viscosity of the Lax-Friedrichs scheme. The size of the kink diminishes, as expected, when the mesh shrinks. Also the MUSCL approximation has a smaller kink than the basic approximation.

Example 8.3. This is a two-particle example with $ z(x,t) = \rm{constant} = \hat{z} $. It is possible to explicitly solve this type of problem. With $ z(x,t) = \hat{z} $, we have $ u(x,t) = \hat{z} - \lambda_1 H(x-h_1(t)) - \lambda_2 H(x-h_2(t)) $. Thus the problem reduces to determining the particle paths $ h_1(t) $ and $ h_2(t) $. This can be accomplished using the differential equations (1.4), which become

Here

where

Assume that the particle trajectories do not intersect except for a finite set of times $ \tau_\nu $ with $ 0<\tau_1< \ldots< \tau_M < T $. Define $ \tau_0 = 0 $, $ \tau_{M+1} = T $, and let $ r_k = \lambda_k/m_k $. The solution of (8.3), (8.4), (8.5) can be expressed piecewise. For $ t \in (\tau_\nu,\tau_{\nu+1}) $ the solution is

The parameters used in this example are

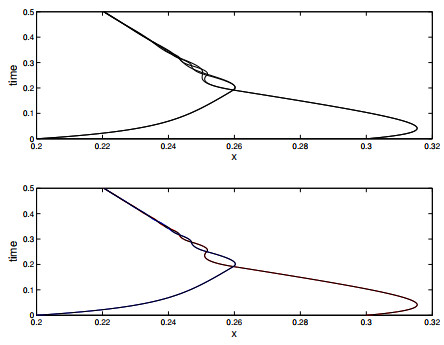
See Figures 3 and 4. From Figure 3 it appears that the MUSCL scheme is more accurate than the basic scheme, as expected. We also see that the discrete $ L^1 $ error in $ u $ decreases as we decrease the mesh size. Figure 4 shows the approximate and exact particle trajectories. At the level of discretization shown, the particle trajectories produced by the basic scheme do not quite agree with the exact trajectories. This discrepancy diminishes when the mesh size is decreased (not shown), but convergence is slow. For the MUSCL scheme the resolution is better; the exact and computed trajectories are not visually distinguishable at this level of grid refinement.

Example 8.4. This is another two-particle example. This time the particles are initially heading toward each other, and the fluid is initially at rest. Unlike the previous example the true solution is not known. In Figure 5 we show the particle trajectories at three levels of grid refinement. It appears that the particle trajectories are converging as the mesh size is refined. The MUSCL scheme is better able to resolve the fine details of the trajectory, especially after the first crossing of trajectories.

The initial fluid velocity is zero, $ u_0(x) = 0 $. The other parameters of the problem are

Acknowledgments

The author thanks an anonymous referee for providing the now improved version of Assumption 5.1, and sharing ideas about how to weaken Assumption 5.1 for future efforts to address much more general particle interaction scenarios.