1. Introduction
While the atmosphere, a complex natural gaseous system, has been an essential key to support life on earth, air pollution is recognized as a threat to human health as well as to the earth's ecosystems. Among all those particles in air, particles less than 2.5 micrometers in diameter are called"fine" particles, i.e. PM$_{2.5}$. Tiny size results in its ability to travel deeply into the respiratory tract, reaching the lungs and causing worsen medical conditions such as asthma and heart disease. Sources of fine particles include all types of combustion, including motor vehicles, power plants, residential wood burnSing, forest fires, agricultural burning, and some industrial processes [1].
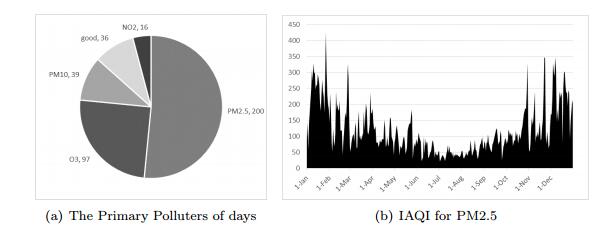
Ever since urban air quality is listed as one of the world's worst toxic pollution problems in the 2008 Blacksmith Institute World's Worst Polluted Places report, increasing number of air quality monitoring stations were established to inform people the real-time concentration of air pollutants, such as PM2.5, O$_3$, PM$_{10}$, NO$_2$, etc, in developing countries like China, Brazil, and India. Among all air pollutants(Wuhan), PM2.5 has been most severe one as illustrated in Figure. 1(a). On the other hand in February 2012, China set limits for the first time on PM2.5 in the released ambient air quality standard, GB 3095-2012 1. PM2.5 is now among the most anxious concern in the field of air management.
1 GB3095-2012 Ambient Air Quality Standards, released by Ministry of Environmental Protection of the People's Republic of China in 02.2012
Unfortunately, current air quality monitoring stations are still insufficient because such a station is in great cost of money, land, and human resources while building and maintaining. Even Beijing, the captain of China, only has 22 stations covering a $50\times50km$ land and each station is in duty of more than $113km^2$ in average. Moreover, urban air quality varies by locations non-linearly and is straightly influenced by multiple complex factors, such as meteorology, traffic, and urban structures. According to the statistics on the air quality index (AQI) recorded from January 1,2013 to January 1,2014 in Beijing [10], the average deviation between the maximum and minimum concentration of PM2.5 from the 22 stations at the same time-stamp stayed larger than 100, which almost denotes a two-level gap, i.e., the gap between moderate and unhealthy, during over $50\%$ of time. Figure 1(b) further presents the distribution of the daily average PM2.5 concentration in Wuhan cross one year, which well demonstrates the skew of air quality within a year in urban spaces.
Although many statistic-based models have been proposed by environment scientists to approximate the quantitative link from factors like traffic and wind to air quality, empirical assumptions and parameters on which they based may not be applicable to all urban environments. Some methodologies, e.g., methodology based on crowd and participatory sensing using sensor-equipped mobile phones, could only work for a very few kinds of gas like CO$_2$ but not applicable to aerosols and other pollutants, including PM2.5. Besides, it usually needs a relatively long sensing period (e.g., 1$\sim$2 hours) before generating an accurate concentration. However, there usually exists regular patter in human activities, i.e. most human activities will repeats daily. This motivates us to mine the concentration change of PM2.5 using time series methodologies.
In this paper, we analyse and decompose the real-time PM2.5 concentration data within one year according to time series decomposition theory and infer the future fine-grained air quality information throughout a city using historical and real-time air quality data reported by existing monitor stations. We also product stochastic modelling in fitting and forecasting. We take two methodologies into comparison and discuss their strong and weak points respectively in PM2.5 prediction.
Contributions. The contribution of this paper is as follows:
1. We propose a practical system of time series based PM2.5 predication on the foundation of limited real-time data without expensive devices. Predicating fine particles like PM2.5 can give an effective support on air quality management. Our experimental result demonstrates the effectiveness of our method.
2. We compare and analyse the characters of two essentially-distinct methods applying to PM2.5. The varies on PM2.5 are intrinsically caused by complex human activities and deterministic and stochastic methods can separately excavate different aspects of hidden pattern of human activities.
Organizations. The rest of paper is organized as follows: Section 2 introduces the background material. Section 3 and 4 present in detail the progress of deterministic and stochastic predication, respectively. Section 5 discusses the characters of two methods. The related work and conclusion is in Section 6 and 7.
2. Preliminary
This section presentd the basic conpects related to this research.
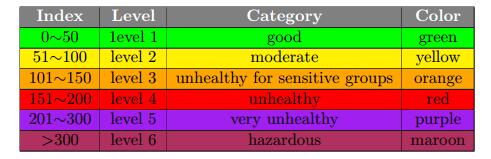
Definition 2.1. Air Quality Index (AQI). AQI is a number used by government agencies to communicate to the public how polluted the air is currently. As the AQI increases, an increasingly large percentage of the population is likely to experience increasingly severe adverse health effects. To compute the AQI requires an air pollutant concentration from a monitor or model. The function used to convert from air pollutant concentration to AQI varies by pollutants, and is different in different countries. Air quality index values are divided into ranges, and each range is assigned a descriptor and a color code. In this paper, we use the standard issued by Ministry of Environmental Protection, People's Republic of China2, as shown in Table 1. The descriptor of each AQI level is regarded as the class to be inferred and the color is employed in the following visualization figures.
Table 1. Air Quality Index.
2 HJ 633-2012 Technical Regulation on Ambient Air Quality Index (on trial), released by Ministry of Environmental Protection of the People's Republic of China in 02.2012
Specifically, the calculation for AQI follows Equation (1) below:
|
$
\text{AQI} = \max \left\{ {{\rm{IAQ}}{{\rm{I}}_1},{\rm{IAQ}}{{\rm{I}}_2}, \cdots ,{\rm{IAQ}}{{\rm{I}}_n}} \right\}
$
|
(1)
|
where IAQI stands for the sub-indicators of air quality and $n$ indicates the number of polluters.
Recall the AQI of Wuhan in 2013, PM2.5 contributed to the primary pollutant over most of the days (illustrate in Figure 1(a)). In this paper, we concentrate the prediction on IAQI for PM2.5 only as it is the culprit of air pollution. However, our time-series based method is straightforward to be extended to AQI prediction.
3. Deterministic modelling and predicting
3.1. Identification
In order to de-constructs the time series into notional components, we identify and construct a number if component series where each represent a certain characteristic or type of behaviour as follows:
-the Trend Component T that reflects the long term progression of the series
-the Cyclical Component C that describes repeated but non-periodic fluctuations
-the Seasonal Component S reflecting seasonality
-the Irregular Component I (or "noise") that describes random, irregular influences. It represents the residuals of the time series after the other components have been removed.
Since cyclicality identification needs complex process and is less-productive, we here consecrate on identifying compositions in the order of trend, seasonality, and irregularity.
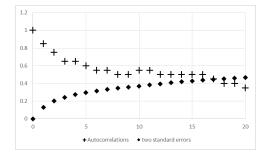
Trend identification. Figure 2 exhibits the autocorrelation of time series. We find that the auto-correlation coefficient attenuation of PM$_{2.5}$ is not evident (the value lower than the two time standard deviation only after 17 steps), different from stationary time series whose auto-correlation coefficient will quickly decay to zero with delay periods increasing. Thus we consider it a non-stationary time series.
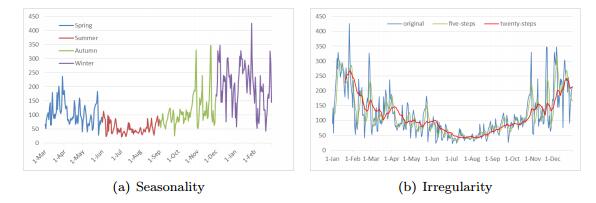
Seasonality identification. We denote spring, summer, fall and winter respectively in blue, green, red and green in Figure 3(a). It is easily observed that significant difference exists in PM$_{2.5}$ time series among four seasons, i.e.seasonal component of time series. Specifically, summer enjoys good quality with less PM$_{2.5}$ concentration, whilst most days in winter encounter poor situation and witness drastic fluctuations. Fall sees the transition from summer to winter. The IAQI in spring is moderate, severe than summer and better than fall.
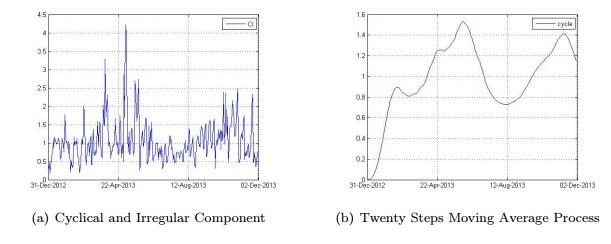
Irregularity identification. Figure 3(b) demonstrates the data after 5(green) and 20(red) intervals moving average process. It is clearly discerned the random fluctuations decreases more as the intervals increasing. Therefore, it is considered that irregularity exists in the time series.
3.2. Decomposition.
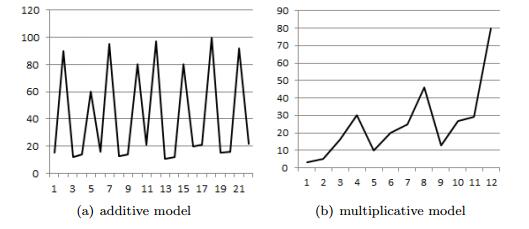
Currently, there are a variety of time-series decomposition models, each of which suits one specific shape. Figure 3.1 shows the tendency feature of two models, namely additive model and multiplicative model [9]. We pick up multiplicative model to decompose the time series of PM2.5 as it is easily observed that PM2.5 time series is roughly actinomorphic. This leads us assume that the PM2.5 can be decomposed into multiplicative model, i.e., $PM_{2.5} = T \times S \times C \times I$.
Trend analysis. Since both trend and seasonality are observed in the data, we first minimize irregularity influence via 20 intervals moving average process and then use Seasonal multivariate regression model fitting.
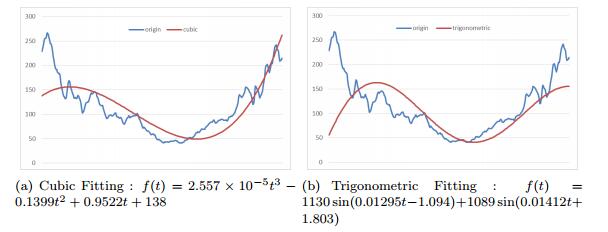
Figure 5 illustrates the fitting curve from cubic curve (Figure 5(a)) and trigonometric (Figure 5(b)) curve fitting separately. According to fitting goodness in Table. 2, cuber curve fitting is considered with best fitting result. However, unpractical upward trend is observed in the final form of the cubic curve. Comparatively, although the fitting result from triangle curve is not as good as cuber curve's, it is still determined that triangle curve fitting as the final trend substitute. So the trend fitting equation can be written as:
|
$
ST(t)=1130sin(0.01295t−1.094)+1089sin(0.01412t+1.803)
$
|
(2)
|
Table 2. Goodness of Fitting.
| Curve Fitting | SSE | R-Square | Adjusted R-square | RMSE |
| Cubic Fitting | $4.214\times 10^4$ | 0.9544 | 0.954 | 11.3 |
| Trigonometric Fitting | $2.901\times 10^5$ | 0.6862 | 0.6814 | 29.74 |
Seasonality analysis. During the process of moving average, not only irregular component but also part of seasonal component can be removed. On the one hand, we aim to remove irregular component to eliminate its interference on other components. On the other hand, we need to maintain seasonal component. To guarantee the effectiveness of prediction, we should add a factor, representing the removed seasonal component. Specifically, we define the generalized seasonal index ${b_i}$ to supply the incomplete seasonal component. We first remove the trend component from the series by subtracting the trend fitting equation value of $t$-th day from the real data of $t$-th day. In this way, the remained PM$_{2.5}$ concentration is of no trend component and can be seen as a mixture of irregular, seasonal and cyclical components. We then derive the Generalized seasonal index ${b_i}$ by utilizing the remained PM$_{2.5}$ concentration.
Definition 3.1. (Generalized seasonal index). The average remained PM$_{2.5}$ concentration of all $t$-th day in all months during $i$-th season (denoted by $b_i = b_i(t)$). $i = 1, 2, 3, 4$ denotes Spring, Summer, Fall, and Winter separately. Table 3 presents specific daily generalized seasonal indexes.
Table 3. Generalized Seasonal Index.
| Date | Sp. | Sum. | Fall | Win. |
| 1st |
-44.33 |
9.14 |
-3.75 |
9.66 |
| 2nd |
8.44 |
10.61 |
-4.37 |
25.82 |
| 3rd |
-37.76 |
5.76 |
-10.01 |
49.94 |
| 4th |
-39.62 |
-19.09 |
-11.33 |
37.69 |
| 5th |
-45.78 |
-48.95 |
2.67 |
79.07 |
| 6th |
6.07 |
-54.47 |
-4.02 |
0.41 |
| 7th |
9.61 |
-46.65 |
3.93 |
5.38 |
| 8th |
-2.16 |
-23.5 |
-7.46 |
-62.35 |
| 9th |
-1.25 |
-37.69 |
-0.54 |
-22.83 |
| 10th |
85.68 |
-16.87 |
15.69 |
-56.35 |
| 11th |
70.64 |
-18.72 |
19.23 |
-65.58 |
| 12th |
50.94 |
-7.57 |
29.42 |
-56.18 |
| 13th |
22.6 |
-14.76 |
14.93 |
-92.15 |
| 14th |
31.94 |
-40.61 |
14.41 |
-79.5 |
| 15th |
36.3 |
-18.13 |
11.21 |
-76.88 |
| 16th |
21.35 |
-18.32 |
-1.35 |
-79.65 |
| 17th |
20.75 |
-17.18 |
15.41 |
-68.78 |
| 18th |
36.49 |
-9.71 |
2.14 |
-57.29 |
| 19th |
-28.07 |
8.43 |
13.85 |
-30.17 |
| 20th |
-6.62 |
7.24 |
4.54 |
9.57 |
| 21st |
31.84 |
5.7 |
0.54 |
3.27 |
| 22nd |
55.66 |
31.84 |
-23.15 |
-91.08 |
| 23rd |
28.83 |
26.97 |
-0.19 |
-110.79 |
| 24th |
14.35 |
-11.58 |
6.74 |
-100.22 |
| 25th |
21.88 |
-23.79 |
10.32 |
-106.02 |
| 26th |
94.76 |
-16 |
2.21 |
-106.87 |
| 27th |
167.66 |
-25.22 |
13.4 |
-89.42 |
| 28th |
60.24 |
-30.44 |
9.25 |
-46.69 |
| 29th |
8.84 |
-11 |
9.73 |
-24.06 |
| 30th |
-0.55 |
-22.23 |
22.52 |
-63.51 |
| 31st |
19.49 |
-14.87 |
38.36 |
-42 |
Note that we utilize mean to decrease the interference from irregular and cyclical component. Thus ${b_i}$ can be treated as a supplement of the removed seasonal component. We then add ${b_i}$ to the trend fitting equation (Equation (2)). The improved model can be presented as:
|
$
ST(t)=1130sin(0.01295t−1.094)+1089sin(0.01412t+1.803)+α4∑i=1Qibi
$
|
(3)
|
where $\alpha \in \left( {0, 1} \right)$ is the weight of seasonal influence and
|
$
{Q_i} = {1,if t∈i-th season0,otherwise.
$
|
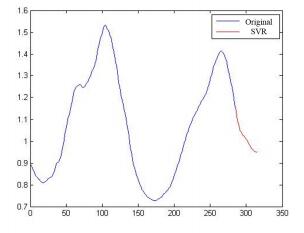
Cyclicality analysis. The naive method to detect cyclical component is observing to see whether any cyclicality exsits in the remaining series after removing trend and seasonal components. However, most of real-world time series does not show strict repeated model in every cyclical time points. As in our case, few cyclical can be detected after removing trend and seasonality ($\alpha = 0.5$, see Figure. 6(a)) and 20 intervals moving average (see Figure. 6(b)).
As a matter of fact, real-word time series can be seen as cyclicality under certain degree of confidence and to detect that kind of cyclicality in PM2.5, we use autoregressive support vector regression (SVR_AR) with RBF kernel function, i.e., $e^{\gamma{\|\| {u - v} \|\|}^2}$. It has been proved in many real-word applications that autoregressive support vector regression can well support series with certain cyclicality.
We apply cross validation method to select and verify the value of the parameter. Specifically, we divide the dataset equally into 10 parts and repeat the following operation for ten times. At $i$-th($i = 1, 2, ..., 10$) time, we use the $i$-th part of data as testing set and the rest 9 parts of data as the training set. We test the accuracy and observe when the penalty term equals $8$ and $\gamma = 2$, the result is of the highest accuracy.
3.3. Time series prediction
Thus, the final predication model can be indicated as
|
$
PM_{2.5} = ST(t)\cdot C(t)
$
|
(4)
|
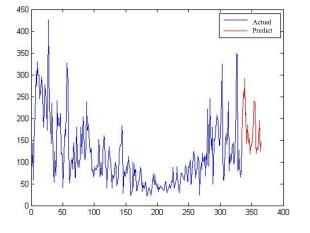
where ST(t) is calculated according to Equation 3 and C(t) can be fitted from SVR_AR) with RBF(the penalty term equals $8$ and $\gamma = 2$). Figure 8 demonstrates the deterministic predication in December.
4. Stochastic modelling and predicting
4.1. Method
The basic approach for stochastic modelling is as follow:
Definition 4.1. (Box-Jenkins model identification). The Box–Jenkins method applies autoregressive moving average ARMA or ARIMA models to find the best fit of a time-series model to past values of a time series.
The original model uses an iterative three-stage modeling approach:
(1). Model identification and model selection: guaranteeing stationariness of the variables, identifying seasonality in the dependent series (seasonally differencing it if necessary), and using plots of the autocorrelation and partial autocorrelation functions of the dependent time series to determine autoregressive(if any) or moving average component.
(2). Parameter estimation: computationally arriving at coefficients that best fit the selected ARIMA model. The maximum likelihood estimation or non-linear least-squares estimation are most common methods.
(3). Model checking: testing the estimated model conformity with the specifications of a stationary univariate process. In particular, the residuals should be independent of each other and constant in mean and variance over time. If inadequate, return to step one and attempt to build a better model.
ARIMA(autoregressive integrated moving average) model can be used in time series prediction based on a limited number of observations. The basic intuition behind ARIMA is that non-stationary sequence firstly built stationary via differencing of appropriate order and then realize fitting in ARMA model. Since sequence after differencing is equal to the weighted summation of sequence before differencing, sequence after differencing can be written in ${\nabla ^d}{x_t} = \mathop \sum \limits_{i = 0}^d {( - 1)^i}C_d^i{x_{t - i}}$, in which $C_d^i = \frac{{d!}}{{i!\left( {d - i} \right)!}}$. And such sequence can be fitted in ARMA(autoregressive moving average) model. The whole process is called autoregressive integrated moving average, in short, ARIMA.
Definition 4.2. (ARIMA$(p, d, q)$ model). Any model that fits stricture below can be called ARIMA$(p, d, q)$ model.
|
$
\left\{ {Φ(B)∇dxt=Θ(B)εtE(εt)=0,Var(εt)=σ2ε,E(εsεt)=0,s≠tExsεt=0,∀s<t
} \right.
$
|
(5)
|
in which ${\nabla ^d} = {\left( {1 - {\rm{B}}} \right)^d}$. ${\rm{\Phi }}\left( B \right) = 1 - {\phi _1}B - \ldots - {\phi _p}{B^p}$ is autoregressive coefficient polynomial and ${\rm{\Theta }}\left( B \right) = 1 - {\theta _1}B - \ldots - {\theta _q}{B^q}$ is moving average coefficient polynomial of $ARMA(p, q)$ model.
$ARIMA(p, d, q)$ can also be written in a short one as :
|
$
{\nabla ^d}{x_t} = \frac{{{\rm{\Theta }}(B)}}{{{\rm{\Phi }}\left( B \right)}}{\varepsilon _t}
$
|
(6)
|
while ${\varepsilon _t}$ is white noise sequence with zero mean. It is clear that ARIMA is a combination of differencing and ARMA model.
4.2. Experiment and result
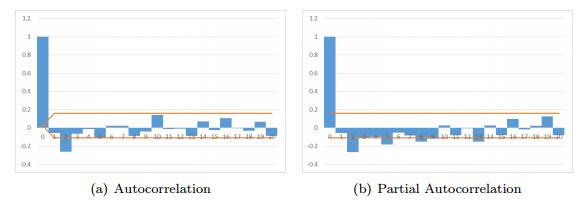
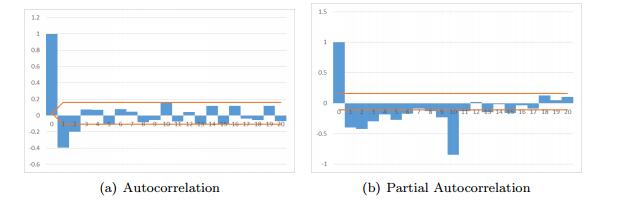
Order identification. Since the observed data is identified in-stationary, we utilize differencing approach to achieve stationary. We chose first-order and second-order differencing separately and compared their accuracy. Figure 9 and Figure 10 shows the autocorrelation coefficient and partial correlation coefficient in 20 steps of first-order and second-order differencing. The 2 times of standard deviation of corresponding coefficients is represented by red line in each figures.
It can be observed in both results from first-order (Figure 9) and second-order (Figure 10) that the autocorrelation coefficients when the steps over 2 are all within 2 times of standard deviation (Figure 9(a) and 10(a)). Tailing can be identified since the autocorrelation coefficient is gradually close to zero, thus q = 2. As for partial correlation coefficient, it is less than 2 times of standard deviation when the steps are over 19 and it is gradually close to 0, tailing can be identified, thus p = 19 (Figure 9(b) and 10(b)). Therefore according to Table 4, the model can be identified as ARIMA $(19, 1, 2)$ and ARIMA$(19, 2, 2)$.
Table 4. Theoretical Model of $ARMA(p, q)$.
| Model | ACF | PACF |
| White Noise | $\rho_k=0$ | $\rho_k^*=0$ |
| $AR(p)$ | attenuated to zero (geometric or volatility) | censored after the $p$-order: $\rho_k^*=0, k>p$ |
| $MA(q)$ | censored after the $q$-order: $\rho_k=0, k>q$ | attenuated to zero (geometric or volatility) |
| $ARMA(p, q)$ | attenuated to zero (geometric or volatility) after $q$-order | attenuated to zero (geometric or volatility) after $p$-order |
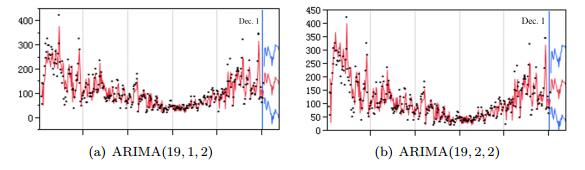
Model fitting and prediction. The prediction results under $95\%$ confidence level and its upper and lower limits are as follows (Figure 11).
Residual test. For ARIMA$(19, 1, 2)$, residual autocorrelation and partial correlation coefficient of 21 order are still greater than 2 times of standard deviation. The effect of random error on fitting and prediction is not completely eliminated. For ARIMA$(19, 2, 2)$, residual autocorrelation and partial correlation coefficients of all orders are less than 2 times of standard deviation and is gradually close to zero. The effect of random error on fitting and prediction is completely eliminated. Thus it can be determined that ARIMA (19, 2, 2) is more reasonable than ARIMA (19, 1, 2) in comparison of AIC (Akaike information method), SBC (Schwartz Bias), and the error of prediction.
5. Discussion
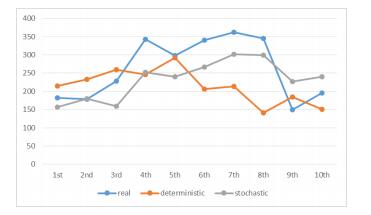
The two previous models are evaluated according to the real-time urban PM2.5 concentrations data obtained in Wuhan from December 1 to 10,2013. As can be seen from the Figure 12, stochastic time series analysis method results in better fitting.
Deterministic time series analysis method is relatively simple and lead to a more in-depth understanding of time series various characteristics. It allows more flexibility, which on the other hand means that it needs more empirically determination of parameters. Namely, it works with a certain degree of subjectivity, in which assumptions are required in advance and the tiny inaccurate in assumption could cause large deviations.
Stochastic time series analysis method leads a higher accuracy and stronger generalization ability. Comparatively, the process of stochastic time series analysis method is more fixed. However, the vague process also leads to difficulty in understanding and analysing the results.
6. Related work
We brief related work in four directions.
Classical bottom-up emission models. There are two major "bottom-up" methods in calculating air quality via the observed emission from ground surfaces. The most common one is referencing to the nearby air quality monitor stations, usually applied by public websites reporting AQIs. However, it is with low accuracy since air quality varies non-linearly as illustrated before. The other are classical dispersion models. Gaussian Plume models, Operational Street Canyon models, and Computational Fluid Dynamics are most widely used in this methodology. These models are in most cases a function of meteorology, street geometry, receptor locations, traffic volumes, and emission factors (e.g., g/km per single vehicle), based on a number of empirical assumptions and parameters that might not be applicable to all urban environments[6].
Satellite remote sensing. Satellite remote sensing of surface air quality is regarded as top-down methods in this field, such as[4] and [5]. However, despite its high cost, the result can only the air quality of atmosphere rather than the ground one.
Crowd sensing. Significant efforts[3], [2] have been devoted to crowd sensing and it may be a potential solution solving air pollution in the future. The devices for PM2.5 and NO$_2$ so far are not easily portable and requires a long period sensing time.
Urban computing. Big data has attracted a series of researches on urban computing to promote urban life quality, including managing air pollution. Data from varies aspects such as human mobility data and POIs[7], taxi trajectories[11], GPS-equipped vehicles[8] can be used to product useful pattern in urban life. This kind of method is based on sufficient urban data, sometimes private, which are difficult to acquire. Becides, it is in need of a long time in pre-processing of cleaning and reducing.
Different from classical models, methods with highly-required devices and tremendous data processing, our method offers a simple but efficient aspect in inferring air quality. Effectiveness is guaranteed on the basis of real-time data without expensive device and long time pre-processing.
7. Conclution
In this paper, from the perspective of time series, we infer the fine-granularity air quality in a city based on the historical reported PM2.5 concentrations from air quality monitor stations. Using deterministic and stochastic theories, we make two predications. In deterministic point of view, we identify and decompose the historical reported PM2.5 concentrations into trend, seasonality, cyclical and irregular factors, based on which we calculate the PM2.5 concentrations equation. In stochastic point of view, we compare the first-order and second-order differencing methods and compute the quantitative models. Finally, we analyse the strong and weak points of deterministic and stochastic methodologies and reach the conclusion that stochastic is more accurate for PM2.5 concentrations predication.









 DownLoad:
DownLoad: