Stability estimates for scalar conservation laws with moving flux constraints

1.   Introduction

Motivated by the modeling of moving bottlenecks in traffic flow, which can be caused by a large, slow moving vehicle, we consider the Cauchy problem for a scalar conservation law with moving flux constraint

where $t\mapsto y(t)$ is a given trajectory, starting from $y(0)=y_0$, and

with $\rho_\alpha({\dot y})$ such that $f'(\rho_\alpha ({\dot y})/\alpha)= \dot y$. Systems of the form (1) arise in the modeling of moving bottlenecks in vehicular traffic [12,16]: $\rho=\rho(t,x) \in [0, R]$ is the scalar conserved quantity and represents the traffic density, whose maximum attainable value is $R$. The flux function $f:[0,R]\to\mathbb{R}^+$ is assumed to be strictly concave, Lipschitz continuous and such that $f(0)=f(R)=0$. The time-dependent variable $y$ denotes the constraint position. In the present paper we consider a weakly coupled PDE-ODE system, in the sense that we assume that the constraint trajectory is given, and it does not depend on the solution of (1a).

Let us detail the meaning of inequality (1c). A moving flux constraint located at $x=y(t)$ acts as an obstacle, thus hindering the flow as expressed by the unilateral constraint (1c). There, $\alpha\in \ ]0,1[$ is the dimensionless reduction rate of the road capacity (the maximal allowed density) at the bottleneck position. The inequality (1c) is derived by studying the problem in the constraint reference frame, i.e., setting ${\tilde \rho}(t,x):=\rho(t,x+y(t))$ and rewriting the conservation law (1a) as

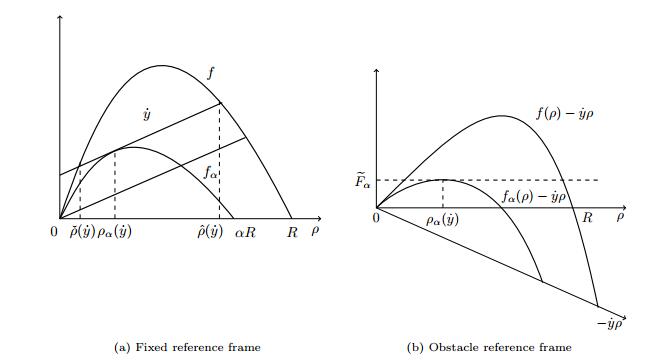
In fact, let $f_\alpha : [0,\alpha R]\to\mathbb{R}^+$ be the rescaled flux function describing the reduced flow at $x=y(t)$, defined by $f_\alpha(\rho) = \alpha f({\rho}/{\alpha}),$ and let ${\rho}_\alpha({\dot y})\in \ ]0,\alpha R[$ such that

with $F_{\alpha}(\rho)=f_{\alpha}(\rho)-\dot{y}\rho$, see Figure 1. Notice that, for (4) to have a solution in $]0,\alpha R[$, we will need to assume that $\dot y (t) < f'(0)$ for $t\geq 0$. Then setting $\widetilde F_{\alpha}({\dot y}):=F_{\alpha}(\rho_{\alpha}({\dot y}))$ we recover (2). Imposing that in the obstacle reference frame the flux $F$ is less than the maximum value of the flux of the reduced flow, one gets (1c). Notice that the inequality (1c) is always satisfied if

since its left-hand side is $0$. Moreover, it is well defined even if $\rho$ has a jump at $y(t)$, because of the Rankine-Hugoniot conditions.

Problem (3), (1b), (1c), can therefore be recast in the framework of conservation laws with fix local constraint, first introduced in [10], then developed in [2,4] for scalar equations and extended in [3,14,13] to systems. Following [12,Definition 4.1] and [6,Definition 1 and 2], solutions of (1) are defined as follows.

Definition 1.1. Let $y\in \mathbf{W^{1,\infty}}(\mathbb{R}^+;\mathbb{R})$ with $0\leq {\dot y} < f'(0)$ and $\rho_0\in \mathbf{L}^1\cap\mathbf{L}^\infty (\mathbb{R};[0,R])$ be given. A function $\rho \in \mathcal{C}^0\left( \mathbb{R}^+; \mathbf{L}^1 (\mathbb{R};[0,R])\right)$ is a solution to (1) if

1. $\rho$ satisfies Kružkov entropy conditions [15] on $\left(\mathbb{R}^+\times\mathbb{R}\right) \setminus \left\{ (t,y(t)) \colon t\in\mathbb{R}^+ \right\}$, i.e. for every $k\in {[0,R]}$ and for all $\varphi\in\mathcal{C}^1_c(\mathbb{R}^2; \mathbb{R}^+)$ and $\varphi(t,y(t))=0$, $t>0$,

2. for a. e. $t>0$ the left and right traces of $\rho$ at $x=y(t)$ satisfy

Notice that the left and right traces in (5b) do exist, see [4,Section 2].

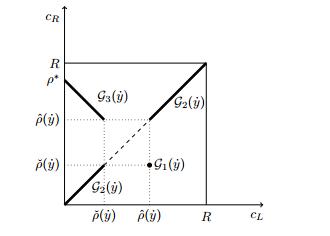
The set $\mathcal{G}_\alpha(\dot{y})$ in (5b) is defined as follows, see [4,5,6].

Definition 1.2. The admissibility germ $\mathcal{G}_\alpha (\dot{y}) \subset [0,R]^2$ for (1a), (1c) is the union $\mathcal{G}_\alpha (\dot{y}):= \mathcal{G}_1 (\dot{y})\cup \mathcal{G}_2 (\dot{y})\cup \mathcal{G}_3 (\dot{y})$, where

We refer the reader to Figure 2 for a graphical representation of $\mathcal{G}_\alpha (\dot{y})$

The equivalence between Definition 1.1 and [12,Definition 4.1] can be proved as in [4,Proposition 2.6].

Systems of the type (1) arise in the modeling of moving bottlenecks in traffic flows, see [12,16] and Section 3 below, where they are coupled with an ODE depending on the downstream traffic velocity and describing the trajectory of a slow moving vehicle (a bus or a truck) acting as a bottleneck.

This paper is a first step towards establishing well-posedness for the strongly coupled models [12,16]. Section 2 presents the main result, stating the $\mathbf{L}^1$ Lipschitz continuous dependence of solutions of (1) from the initial data and the constraint trajectory. Section 3 describes in details the related traffic flow model with moving bottleneck. Technical proof details are deferred to Appendix A.

2.   Lipschitz continuous dependence of BV solutions with respect to ${\dot y}$

Let us fix the constraint trajectory $y\in \mathbf{W^{1,\infty}}(\mathbb{R}^+;\mathbb{R})$ with $0\leq {\dot y} < f'(0)$ and the initial datum $\rho_0\in{\rm {BV}}(\mathbb{R};[0,R])$, and let $\rho\in {\mathcal{C}^0\left( \mathbb{R}^+; \mathbf{L}^1 (\mathbb{R};[0,R])\right)}$ be a solution of (1) in the sense of Definition 1.1. Applying the coordinate transformation $\tilde\rho(t,x):=\rho(t,x+y(t))$, ${\tilde \rho}$ is a weak entropy solution of the problem

in the sense of [4,Proposition 2.6(A)] where we have set $F(\tilde\rho):= f(\tilde\rho) - \dot{y}\, \tilde\rho$. Existence and uniqueness for (6) are proved in [4,10]. In particular, we have that for every $k\in {[0,R]}$ and for all $\varphi\in\mathcal{C}^1_c(\mathbb{R}^2; \mathbb{R}^+)$ such that $\varphi(t,0)=0$, $t>0$,

where we have set

and

see [4,Proposition 2.6]. Moreover, we note that, since $\alpha < 1$ and $f$ is strictly concave, we have

Remark 1. Solution to (6) are not in ${\rm {BV}}$ in general (see [1,10]), but thanks to the strict inequality in (7) and since $y\in \mathbf{W^{1,\infty}}(\mathbb{R}^+;\mathbb{R})$ implies ${\dot y}\in{\rm {BV}}_{loc}(\mathbb{R}^+)$, we can conclude that $\tilde\rho(t,\cdot)\in {\rm {BV}}(\mathbb{R};[0,R])$ for any $t>0$, as in [12].

We compare solutions of (6) corresponding to different constraint trajectories $y$ and $z$.

Theorem 2.1. Assume $y,z\in {\mathbf{W^{1,\infty}}(\mathbb{R}^+;\mathbb{R})}$, with $0\leq \dot{y}, \dot{z} < f'(0)$, $\tilde\rho_0,\tilde\sigma_0\in\mathbf{L}^\infty(\mathbb{R},[0,R])$ and $\tilde\rho_0 -\tilde\sigma_0\in\mathbf{L}^1(\mathbb{R})$. Let $\tilde\rho,\tilde\sigma \in {\mathcal{C}^0\left( \mathbb{R}^+; \mathbf{L}^1 (\mathbb{R};[0,R])\right)}$ be solutions of (6) corresponding respectively to $y,\tilde\rho_0$ and $z,\tilde\sigma_0$. Moreover, let $C_t=\sup_{s\in[0,t]} TV(\tilde\rho(s,\cdot))$ be finite. Then we have

Proof. The two solutions $\tilde\rho$, $\tilde\sigma$ satisfy

in $\mathcal{D}'(\mathbb{R}^+\times\mathbb{R}^*)$ (where we have noted $\mathbb{R}^*=\mathbb{R}\setminus\{0\}$). Following the proofs of [6,Lemma 15] and [7,Theorem 3.1] we observe that

therefore

Applying the classical Kružkov doubling of variables technique [15], with a test function $\psi\in\mathcal{C}^1_c(\mathbb{R}^2; \mathbb{R}^+)$ such that $\psi(t,0)=0$, we deduce the following Kato inequality

We now choose the test function $\psi (t,x)= \theta_\varepsilon (x) \xi(t,x)$, where $\xi \in\mathcal{C}^1_c(\mathbb{R}^2; \mathbb{R}^+)$ is an approximation of the characteristic function of the trapezoid

(where $L\geq \sup_{\rho\in[0,R], s\in[0,t]}\left|f'(\rho)-\dot{z}(s)\right|$ and $M\in\mathbb{R}$, $M>0$) and $\theta_\varepsilon$ a smooth approximation of $x\to \min\{ \left|x\right|/\varepsilon, 1\}$. Following the proof of [10,Proposition 4.4] and letting $\varepsilon\searrow 0$ we get

By Lemma A.1, the last integrand can be bounded by

Letting $M\to \infty$, we recover (8).

We are now able to state the well-posedness of problem (1).

Corollary 1. Assume $y,z\in \mathbf{W^{1,\infty}}(\mathbb{R}^+;\mathbb{R})$, with $0\leq \dot{y}, \dot{z} < f'(0)$, $\rho_0,\sigma_0\in\mathbf{L}^\infty(\mathbb{R},[0,R])$ and $\rho_0 -\sigma_0\in\mathbf{L}^1(\mathbb{R})$. Let $\rho,\sigma \in {\mathcal{C}^0\left( \mathbb{R}^+; \mathbf{L}^1 (\mathbb{R};[0,R])\right)}$ be solutions of (1) corresponding respectively to $y,\rho_0$ and $z,\sigma_0$. Moreover, let $C_t=\sup_{s\in[0,t]} TV(\rho(s,\cdot))$ be finite. Then we have

Proof. Setting

for any $t>0$ we get

Therefore, by (8), we get

where we have used the estimate $\left|y(t) - z(t)\right| \leq \left|y(0) - z(0)\right| + \int_0^t \left|{\dot y}(s) - {\dot z}(s)\right|ds$.

3.   Application to traffic modeling

Setting

where $v(\rho)=V(1-\rho/R)$ is the mean traffic speed, $V$ being the maximal velocity allowed on the road, problem (1) can be used to describe the situation of a moving bottleneck along a road, see [12]. In this case, we get $f_\alpha(\rho) = V \rho \left(1-\frac{\rho}{\alpha R}\right)$ and $\rho_\alpha ({\dot y})=\frac{\alpha R}{2} \left(1-\frac{\dot y}{V}\right),$ so that

Let us suppose that a slow and large vehicle, like for example a bus or a truck moves on the road. The slow vehicle, that in the following we will refer as "the bus", reduces the road capacity and moves with a trajectory given by the following ODE:

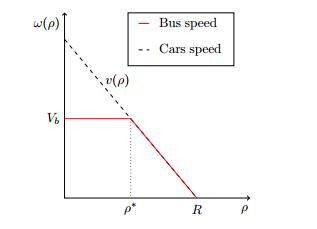
where the velocity of the bus is given by the following traffic density dependent function (see Figure 3)

This means that if the traffic is not too congested, the bus moves at its own maximal speed $V_b<V$. When the surrounding traffic density becomes too high, the bus adapts its velocity accordingly. In particular, it is not possible for the bus to overtake the cars.

Solutions of the coupled system (1), (14) for general initial data are defined as follows.

Definition 3.1. A couple $(\rho,y)\in {\mathcal{C}^0\left( \mathbb{R}^+; \mathbf{L}^1 (\mathbb{R};[0,R])\right)} \times \mathbf{W^{1,1}}(\mathbb{R}^+;\mathbb{R})$ is a solution to (1) if

1. $\rho$ satisfies Kružkov entropy conditions [15] on $\left(\mathbb{R}^+\times\mathbb{R}\right) \setminus \left\{ (t,y(t)) \colon t\in\mathbb{R}^+ \right\}$, i.e. for every $k\in{[0,R]}$ and for all $\varphi\in\mathcal{C}^1_c(\mathbb{R}^2; \mathbb{R}^+)$ and $\varphi(t,y(t))=0$, $t>0$,

2. for a. e. $t>0$ the one-sided traces of $\rho$ at $x=y(t)$ satisfy

3. $y$ is a Carathéodory solution of (14), i.e. for a.e. $t\in\mathbb{R}^+$

The proof of existence of solutions for the general Cauchy problem (1) strongly coupled with the bus trajectory (14) with ${\rm {BV}}$ initial data can be found in [12]. For completeness, we recall the definition of the solution of a Riemann problem, as given in [12]. Let us consider a Riemann type initial datum

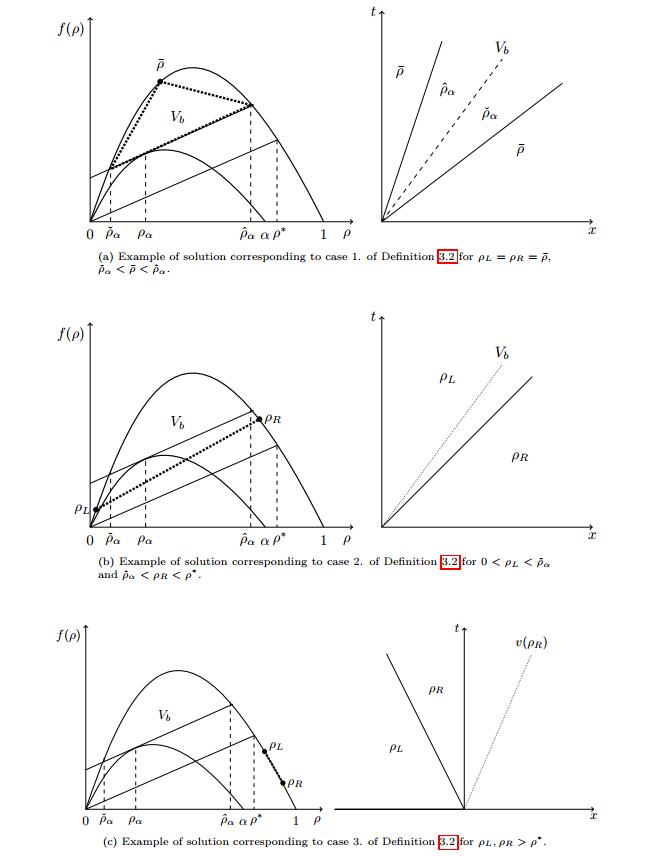
Denote by $\mathcal{R}$ the standard (i.e., without the constraint (1c)) Riemann solver for (1a)-(1b)-(17), i.e., the (right continuous) map $(t,x)\mapsto \mathcal{R}(\rho_L,\rho_R)({x}/{t})$ given by the standard weak entropy solution, see for instance [8,Chapter 5]. Moreover, assume that ${\dot y}$ is constant and let $\check{\rho}=\check\rho({\dot y})$ and $\hat{\rho}=\hat\rho({\dot y})$, with $\check{\rho} \leq \hat{\rho}$, be the intersection points of the flux function $f(\rho)$ with the line $f_\alpha(\rho_\alpha)+{\dot y}(\rho-\rho_\alpha)$ (see Figure 1(a)):

Definition 3.2. The constrained Riemann solver $\mathcal{R}^\alpha : [0,R]^2 \to \mathbf{L}^loc1(\mathbb{R};[0,R])$ corresponding to (1), (14), (17) is defined as follows.

1. If $f(\mathcal{R}(\rho_L,\rho_R)(V_{b}))> F_\alpha+V_{b}\mathcal{R}(\rho_L,\rho_R)(V_{b})$, then

2. If $V_{b}\mathcal{R}(\rho_L,\rho_R)(V_{b})\leq f(\mathcal{R}(\rho_L,\rho_R)(V_{b}))\leq F_\alpha+V_{b}\mathcal{R}(\rho_L,\rho_R)(V_{b})$, then

3. If $f(\mathcal{R}(\rho_L,\rho_R)(V_{b})) < V_{b}\mathcal{R}(\rho_L,\rho_R)(V_{b})$, i.e., $v(\mathcal{R}(\rho_L,\rho_R)(V_b))< V_b$ then

Note that, when the constraint is enforced (point 1. in the above definition), a non-classical shock arises between $\hat{\rho}(V_b)$ and $\check{\rho}(V_b)$, which satisfies the Rankine-Hugoniot condition but violates the Lax entropy condition, see Figure 4 for an example.

Remark 2. Unfortunately, no result about the Lipschitz continuous dependence of the solution $y=y(t)$ of (14) from the solution $\rho=\rho(t,x)$ of (1) is known at present. Related results [9,11] concerning uniqueness and continuous dependence for ODEs of the form (14) hold under hypothesis on the speed function $\omega$ that are not satisfied by (15).

Appendix A. Proof of (12).

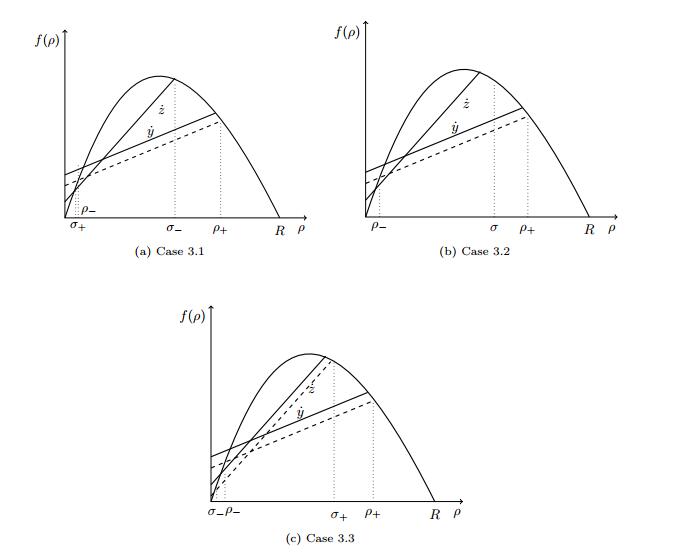
Lemma A.1 For any $(\rho_-,\rho_+)\in\mathcal{G}_\alpha (\dot{y})$ and $(\sigma_-,\sigma_+)\in\mathcal{G}_\alpha (\dot{z})$, it holds

Proof. First of all, let us remark that

where

Without loss of generality, we can assume ${\dot y} < {\dot z}$. Therefore we get

We distinguish the following cases:

1. $(\rho_-,\rho_+)\in\mathcal{G}_1({\dot y})$: we observe that

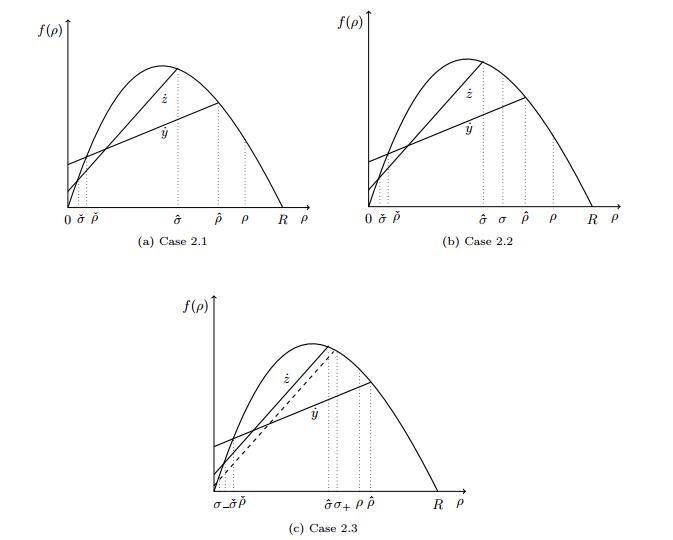
Depending on the values of $\sigma_-$, $\sigma_+$, different situations can occur as shown in Figure 5:

1.1 $(\sigma_-,\sigma_+)\in\mathcal{G}_1({\dot z})$: in this case $\sigma_-=\hat\sigma, ~\sigma_+=\check\sigma$, as shown in Figure 5a and $f(\sigma_-) - {\dot z}\sigma_- = f(\sigma_+) - {\dot z}\sigma_+ = F_\alpha({\dot z}),$ therefore

1.2 $(\sigma_-,\sigma_+)\in\mathcal{G}_2({\dot z})$: we set

The following cases can occur:

● $0\leq\sigma\leq\check\sigma$:

● $\hat\sigma\leq\sigma\leq\hat\rho$, see Figure 5b:

● $\hat\rho\leq\sigma\leq R$:

1.3 $(\sigma_-,\sigma_+)\in\mathcal{G}_3({\dot z})$: we set

We observe that ${\rm {sgn}}(\rho_+ - \sigma_+) < 0$ and ${\rm {sgn}}(\rho_- - \sigma_-) > 0$, see Figure 5c. Therefore

2. $(\rho_-,\rho_+)\in\mathcal{G}_2({\dot y})$: we set

as illustrated in Figure 6.

2.1 $(\sigma_-,\sigma_+)\in\mathcal{G}_1({\dot z})$:

● $0\leq\rho\leq\check\sigma$:

● $\check\sigma\leq\rho\leq\check\rho$, this case is displayed in Figure 6a:

● $\hat\rho\leq\rho\leq R$:

2.2 $(\sigma_-,\sigma_+)\in\mathcal{G}_2({\dot z})$, illustrated in Figure 6b:

We observe that ${\rm {sgn}}(\rho_+-\sigma_+)= {\rm {sgn}}(\rho_--\sigma_-) = {\rm {sgn}}(\rho-\sigma)$, therefore

2.3 $(\sigma_-,\sigma_+)\in\mathcal{G}_3({\dot z})$ shown in Figure 6c: If ${\rm {sgn}}(\rho-\sigma_+) = {\rm {sgn}}(\rho-\sigma_-)$, we get

Otherwise, we have that $\sigma_-\leq\rho\leq\check\rho$ or $\hat\rho\leq\rho\leq\sigma_+$. In this case

by the concavity of $f$. Therefore, (19)≤0 by (20).

3. $(\rho_-,\rho_+)\in\mathcal{G}_3({\dot y})$: we set

See Figure 7, for a graphical representation.

3.1 $(\sigma_-,\sigma_+)\in\mathcal{G}_1({\dot z})$, see Figure 7a.

3.2 $(\sigma_-,\sigma_+)\in\mathcal{G}_2({\dot z})$: If ${\rm {sgn}}(\rho_+-\sigma) = {\rm {sgn}}(\rho_--\sigma)$, we get

Otherwise as shown in Figure 7b, we have that $\rho_-\leq\sigma\leq\check\sigma$ or $\hat\sigma\leq\sigma\leq\rho_+$. In this case

Moreover, we observe that $\lambda(\rho_-,\sigma_-) > {\dot y}$. Indeed

Therefore, by (20)

3.3 $(\sigma_-,\sigma_+)\in\mathcal{G}_3({\dot z})$:

We observe that one of the following relations must hold

For an example see Figure 7c. Therefore

again by concavity of $f$. Hence (19)≤0 by (20).

Acknowledgments

The authors are grateful to Boris Andreianov for suggesting links with the results in [6]. The authors also thank the two anonymous referees for the careful revision and the insightful comments, which were of great help in improving the paper.