General constrained conservation laws. Application to pedestrian flow modeling

1.   Introduction

Since a basic within-host viral infection model introduced by Nowak et al. ^[1], the dynamics of viral infection such as hepatitis B virus (HBV), hepatitis C virus (HCV) and human immunodeficiency virus (HIV) infection models have been widely studied by incorporating various biological factors. Consider age as a continuous variable, writing the production rate of viral particles and the death rate of productively infected cells as two continuous functions of age, Nelson et al. ^[2] studied a HIV infection model with infection-age, the model is described as follows:

with the boundary and initial condition

where $ T(t) $ and $ V(t) $ denote the densities of uninfected target cell and free viruses at time $ t $, respectively; $ i(t, a) $ denote the density of infected cells at time $ t $ with infection-age $ a $. The parameters of model (1.1) are biologically explained in Table 1.

Nelson et al. analyzed the local stability of the model by evaluating eigenvalues and its related characteristic equation. In ^[3], Rong et al. extended the model with combination antiretroviral therapy, and analyzed the local stability of the model. Huang et al. ^[4] have been further investigated the global stability of the model (1.1) with (1.2) by using Lyapunov direct method and LaSalle invariance principle. For some recent works on viral models with age structure, we refer readers to the papers^{[5,6,7,8,9,10,11,12,13]}.

Recently, experimental work ^[14] shows that direct cell-to-cell transmission also contributes to the viral persistence. In a more recent work ^[15], the authors reveals that environmental restrictions limit infection by cell-free virions but promote cell-associated HIV-1 transmission. In fact, cell-to-cell transmission could be also found in other viral infection for human and animals. For example, hepatitis C virus ^[16]; bovine viral diarrhea virus ^[17]; vaccinia virus ^[18]. Due to this fact, Lai and Zou ^[19] formulated a HIV-1 viral model with direct cell-to-cell transmission and studied the global threshold dynamics. Yang et al. ^[20] studied a cell-to-cell virus model with three distributed delays, they also obtained the global stability of each equilibrium for the model. Wang et al. ^[21] investigated an age-structured HIV model with virus-to-cell infection and cell-to-cell transmission, the model takes the following form:

with the boundary and initial condition

By constructing suitable Lyapunov functional, Wang et al. were able to complete a global analysis for the model (1.3). In ^[22], Zhang and Liu studied the Hopf bifurcation of an age-structured HIV model with cell-to-cell transmission and logistic growth.

In viral infection, the host immune system play a critical part on the progress of the infection. The role of the immune system is to fight off pathogenic organisms within the host, for example, cytotoxic T lymphocyte cells (CTLs) attack infected cells, and antibody cells attack viruses (humoral immunity response). In ^[23], Murase et al. studied an viral infection model with humoral immunity response:

where $ T(t) $, $ I(t) $, $ V(t) $ and $ Z(t) $ denote the densities of uninfected cells, infected cells, free viruses and humoral immunity response released by B cells, respectively; the viruses are removed at rate $ k Z $ by the humoral immunity response; the humoral immunity response are activated in proportion to $ h V(t) $ and removed at rate $ \mu_3 $. The global dynamics of model (1.5) were obtain in ^[23]. Consider the delay between viral entry into a cell and the maturation delay of the newly produced viruses, Wang et al. ^[24] studied a virus model with two delays and humoral immunity response. They established the global dynamics based on two threshold parameters, and they found that the three equilibria are globally asymptotically stable under some conditions. For another delay, which is the time that antigenic stimulation needs for generating immunity response, Wang et al. ^[25] considered another virus model with delay and humoral immunity response, they found that this delay could lead to a Hopf bifurcation at the infected equilibrium with immunity. In ^[26], Kajiwara et al. proposed a age-structured viral infection model contains humoral immunity response and the effect of absorption of pathogens into uninfected cells, they also proved the global stability of each equilibria. Duan and Yuan ^[30] considered an infection-age viral model with saturation humoral immune response, the local and global stability of this model are obtained. Additionally, for the virus model with CTL immune response, we refer readers to the papers ^{[27,28,29,31,32,33,34]} and the reference therein.

Based on the above facts, we propose an age-structured viral infection model with cell-to-cell transmission and general humoral immune response in this paper. Precisely, we study the following model:

with the boundary and initial condition

where $ L_+^1 $ is the set of integrable functions from $ (0, +\infty) $ into $ [0, +\infty) $. $ T(t) $, $ V(t) $ and $ Z(t) $ denote the densities of uninfected target cell, free viruses and antibody responses released from B cells at time $ t $, respectively; $ i(t, a) $ denotes the density of infected cells at time $ t $ with infection-age $ a $; $ k(a) $ denote the infection rate of productively infected cells with age a; $ q V(t)f(Z(t)) $ is the neutralization rate of viruses and $ c V(t)f(Z(t)) $ is the activation rate of antibody responses. The antibody responses vanish at rate $ \mu_3 $. Other parameters of model (1.6) have the same biological meaning in the Table 1.

We made the following assumption on parameters and nonlinear function $ f: \mathbb{R}\rightarrow\mathbb{R} $.

(A1) $ k(a), \ \delta(a), \ \theta(a), \ p(a), \ c(a)\in L_+^{\infty}(0, \infty) $, with respective essential supremums $ \bar{k}, \ \bar{\delta}, \bar{\theta}, \ \bar{p}, \ \bar{c} $ and respective essential infimums $ \tilde{k}, \ \tilde{\delta}, \ \tilde{\theta}, \ \tilde{p}, \ \tilde{c}. $

(A2) $ f(Z)\geqslant 0 $ for $ Z\geqslant 0 $, $ f(Z) = 0 $ if and only if $ Z = 0 $; $ f $ is Lipschitz continuous on $ \mathbb{R}_+ $.

(A3) $ f(Z) $ is differentiable such that $ f'(Z) > 0 $ and $ f(Z) $ is concave down on $ \mathbb{R}_+ $.

Here are some examples on function $ f(Z) $ satisfies (A2) and (A3):

(ⅰ) $ f(Z(t)) = Z(t) $ which is the bilinear function (see ^[23]);

(ⅱ) Saturation immune response function $ f(Z(t)) = \frac{Z(t)}{h+Z(t)} $ (see ^[30]).

The paper is organized as follows. In Section 2, we introduce the existence and uniqueness of the solutions to system (1.6), the steady state and reproduction numbers are also determined in this section; In Section 3, we show that system (1.6) is asymptotically smooth; Section 4 is devoted to proving the local stability of each steady state; uniform persistence and global stability of each steady state is considered in Section 5; We perform a numerical simulation of a special case in Section 6; Section 7 provide some brief discussions.

2.   Preliminaries

In this section, we show the existence and uniqueness of the solutions to system (1.6) by a standard method ^[36] (see also ^[37,38]), which is to rewrite system (1.6) as an abstract Cauchy problem.

2.1.   Integrated solution

For convenience, we first denote the following notations.

It is easy to see that

Set the following spaces:

with the following norm

Furthermore, define

Let $ A: \text{Dom}(A)\subset \mathcal{X} \rightarrow \mathcal{X} $ be the following linear operator:

with $ \text{Dom}(A) = \mathbb{R} \times \{0\} \times W^{1, 1}(0, +\infty) \times \mathbb{R} \times \mathbb{R}. $ In the following, we apply the method in ^[36] since $ \overline{ \text{Dom(A)}} = \mathcal{X}_0 $ is not dense in $ \mathcal{X} $. Consider the nonlinear map $ F: \text{Dom}(A)\rightarrow \mathcal{X} $ defined by

One can see that $ F $ is Lipschitz continuous on bounded sets. Let

where $ \text{T} $ represents transposition. Then we can rewrite system (1.6) as the following abstract Cauchy problem:

In order to use the method in ^[36], we need to show that $ A $ is a Hille-Yosida operator. Denote $ \rho(A) $ be the resolvent set of $ A $. The definition of Hille-Yosida operator is:

Definition 2.1. (See [36,Definition 2.4.1]) A linear operator $ A: \text{Dom}(A)\subset \mathcal{X} \rightarrow \mathcal{X} $ on a Banach space $ (\mathcal{X}, \|\cdot\|) $ (densely defined or not) is called a Hille-Yosida operator if there exist real constants $ M\geqslant1 $, and $ \omega\in\mathbb{R} $, such that $ (\omega, +\infty)\subseteq\rho(A) $, and

Now, we prove the following lemma.

Lemma 2.1. The operator $ A $ defined in (2.1) is a Hille-Yosida operator.

Proof. Let

by some simple calculations, we have

and

Denote $ \zeta = \left(\left( $$\begin{array}{c} \hat{\varphi}_0 \\ \hat{\varphi}(a) \\ \end{array}$$ \right), \hat{\phi}_1, \hat{\phi}_2, \hat{\phi}_3\right)^ \text{T} $, then

where $ \mu = \min\{\mu_1, \mu_2, \mu_3, \tilde{\delta}\} $. By the Definition 2.1, the operator $ A $ is a Hille-Yosida operator. This ends the proof.

Let $ X_0 = \left(T_0, \left( $$\begin{array}{c} 0 \\ i_0 \\ \end{array}$$ \right), V_0, Z_0\right)^ \text{T}\in \mathcal{X}_{0+}, $ by using [36,Theorem 5.2.7] (see also in ^[37,39]), we have the following theorem.

Theorem 2.1. There exists a uniquely determined semi-flow $ \{U(t)\}_{t\geqslant 0} $ on $ \mathcal{X}_{0+} $ such that for each $ X_0 $, there exists a unique continuous map $ U\in C([0, +\infty), \mathcal{X}_{0+}) $ which is an integrated solution of Cauchy problem (2.2), that is

Let

where $ \mu_0 = \min\{\mu_1, \tilde{\delta}\} $ and $ \hat{\mu} = \min\left\{\mu_2, \mu_3\right\} $. We show that $ \Omega $ is a positively invariant set under semi-flow $ \{U(t)\}_{t\geqslant 0}. $

Theorem 2.2. $ \Omega $ is a positively invariant set under semi-flow $ \{U(t)\}_{t\geqslant 0}. $ Moreover the semi-flow $ \{U(t)\}_{t\geqslant 0} $ is point dissipative and $ \Omega $ attracts all positive solutions of (2.2) in $ \mathcal{X}_{0+} $.

Proof. Integrating the second equation of (1.6) along the characteristic line $ t-a = $constant, yields

Then

Note that $ \Gamma(0) = 1 $ and $ \Gamma'(a) = -\delta(a)\Gamma(a) $, thus

One has that

We have

From the third and forth equations of (1.6), it is easy to check

Hence

where $ \Pi = \frac{\Lambda}{\mu_0}\left(1 + \frac{\bar{p}}{\hat{\mu}} + \frac{c\bar{P}}{q\hat{\mu}}\right) $. Therefore, for any solution of (2.2) satisfying $ X_0\in \Omega $ and $ U(t)X_0\in \Omega $ for all $ t\geqslant0 $, $ \Omega $ is a positively invariant set under semi-flow $ \{U(t)\}_{t\geqslant 0}. $ Moreover the semi-flow $ \{U(t)\}_{t\geqslant 0} $ is point dissipative and $ \Omega $ attracts all positive solutions of (2.2) in $ \mathcal{X}_{0+} $.

2.2.   Steady state

In this subsection, we concern with the existence of steady states for system (1.6). Obviously, the system (1.6) always has a virus-free steady state $ E_0 = (T_0, 0, 0, 0) = (\frac{\Lambda}{\mu_1}, 0, 0, 0) $. $ E^0 $ is the unique equilibrium if $ \Re_0 \leqslant 1 $, where $ \Re_0 = \frac{\beta T_0 \mathcal{P}}{\mu_2} + T_0 \mathcal{K} $ is the basic reproduction number of system (1.6). If $ \Re_0 > 1 $, there exists an immune-inactivated infection steady state $ E_1 = (T_1^*, i_1^*(a), V_1^*, 0), $ which is the same situation in ^[21], that is,

There also exists another immune-activated infection steady state $ E_2 = (T_2^*, i_2^*(a), V_2^*, Z_2^*), $ which is satisfies

where

By some calculations, we have

From the third equation of (2.7), yields

Substituting (2.8) and (2.9) into the first equation of (2.7) one has that

and

In the following, we show that $ Z_2^* > 0 $. In fact, combining the last two equations of (2.7) give us

Denote

and

Then

It is easy to check $ \frac{ \text{d} \Phi(Z^*)}{ \text{d} Z^*} < 0 $ and $ \lim_{Z^* \rightarrow +\infty}\Phi(Z^*) \rightarrow -\infty $. Hence, there is only one positive root for (2.12) if $ \Re_1 > 1 $. By the expressions of $ \Re_0 $ and $ \Re_1 $, we have $ \Re_1 > 0 \Rightarrow \Re_0 > 1, $ then there is the following theorem on the existence of steady states.

Theorem 2.3. For system (1.6), there are two threshold parameters $ \Re_0 $ and $ \Re_1 $ such that

(ⅰ) if $ \Re_0 \leq 1, $ there exists only one positive steady state $ E_0 $;

(ⅱ) if $ \Re_1 < 1 < \Re_0, $ there exists two positive steady states $ E_0 $ and $ E_1^* $;

(ⅲ) if $ \Re_1 > 1, $ there exists three positive steady states $ E_0, $ $ E_1^* $ and $ E_2^* $.

The following lemma on immune-inactivated infection steady state and immune-activated infection steady state will be used in the proof of global stability.

Lemma 2.2. The immune-inactivated infection steady state $ (T_1^*, i_1^*(a), V_1^*, 0) $ satisfies

and immune-activated infection steady state $ (T_2^*, i_2^*(a), V_2^*, Z_2^*) $ satisfies

Proof. For the immune-inactivated infection steady state $ (T_1^*, i_1^*(a), V_1^*, 0) $, it follows from the third equation of (2.6), we have

Recall that $ i(t, 0) = \beta T(t) V(t) + \int_0^\infty k(a)T(t)i(t, a) \text{d}a $ in (1.7), hence

Thus, (2.13) holds true. The proof of Eq (2.14) is similar to (2.13), so we omitted it. This ends the proof.

3.   Asymptotically smooth

In this section, we show that the semi-flow $ \{U(t)\}_{t\geqslant0} $ is asymptotically smooth. Since the state space $ \mathcal{X}_{0+} $ is the infinite dimensional Banach space, we need the semi-flow $ \{U(t)\}_{t\geqslant0} $ is asymptotically smooth to proof the global stability of each steady states. Rewrite $ U: = \Phi+\Psi $, where

with

We are now in the position to prove the following theorem.

Theorem 3.1. For any $ X_0\in \Omega $, $ \{U(t)X_0: t\geqslant0\} $ has compact closure in $ \mathcal{X} $ if the following two conditions hold:

(ⅰ) There exists a function $ \Delta: \mathbb{R}_+\times\mathbb{R}_+\rightarrow\mathbb{R}_+ $ such that for any $ r > 0 $, $ \lim_{t\rightarrow\infty}\Delta(t, r) = 0 $, and if $ X_0\in\Omega $ with $ \|X_0\|_{\mathcal{X}}\leqslant r $, then $ \|\Phi(t)X_0\|_{\mathcal{X}}\leqslant \Delta (t, r) $ for $ t\geqslant0 $;

(ⅱ) For $ t\geqslant0 $, $ \Psi(t)X_0 $ maps any bounded sets of $ \Omega $ into sets with compact closure in $ \mathcal{X} $.

Proof. Step Ⅰ, to show that (ⅰ) holds.

Let $ \Delta(t, r): = e^{-\tilde{\delta}t}r $, it is obvious that $ \lim_{t\rightarrow\infty}\Delta(t, r) = 0 $. Then for $ X_0\in\Omega $ satisfying $ \|X_0\|_{\mathcal{X}}\leqslant r $, we have

This completes the proof of condition (ⅰ).

Step Ⅱ, to show that (ⅱ) holds.

We just have to show that $ \varpi_2(t, a) $ remains in a precompact subset of $ L_+^1(0, \infty). $ In order to prove it, we should show the following conditions hold [40,Theorem B.2]:

(a) The supremum of $ \int_0^\infty \varpi_2(t, a) \text{d}a $ with respect to $ X_0\in \Omega $ is finite;

(b) $ \lim_{u\rightarrow\infty} \int_u^\infty \varpi_2(t, a) \text{d}a = 0 $ uniformly with respect to $ X_0\in \Omega $;

(c) $ \lim_{u\rightarrow0^+} \int_0^\infty (\varpi_2(t, a+u)-\varpi_2(t, a) \text{d}a = 0 $ uniformly with respect to $ X_0\in \Omega $;

(d) $ \lim_{u\rightarrow0^+} \int_u^\infty \varpi_2(t, a) \text{d}a = 0 $ uniformly with respect to $ X_0\in \Omega $.

Conditions (a), (b) and (d) hold since $ \varpi_2(t, a)\leqslant \left(\frac{\beta \bar{p}}{\hat{\mu}}+\bar{k}\right)\frac{\Lambda^2}{\mu_0^2} $. Next, we verify condition (c). For sufficiently small $ u\in(0, t), $ set $ K(t) = \int_0^\infty k(a)i(t, a) \text{d}a $, we have

Since $ \Gamma(a) $ is non-increasing function with respect to $ a $ and $ 0\leqslant\Gamma(a)\leqslant1 $, we have

Then

where

Thanks to the argument in [41,Proposition 6], $ T(\cdot)V(\cdot) $ and $ T(\cdot)K(\cdot) $ are Lipschitz on $ \mathbb{R}_+ $. Let $ M_1 $ and $ M_2 $ be the Lipschitz coefficients of $ T(\cdot)V(\cdot) $ and $ T(\cdot)K(\cdot) $ respectively. Then

Hence

which converges to 0 as $ u\rightarrow0^+ $, the condition (c) holds. Let $ \mathcal{Y}\subset\mathcal{X} $ be a bounded closed set and $ B $ be a bound for $ \mathcal{Y} $, where $ B\geqslant A $. It is easy to check $ M_1 $ and $ M_2 $ are only depend on $ A $, that is $ M_1 $ and $ M_2 $ are independent on $ \mathcal{X} $. Consequently, $ \varpi_2(t, a) $ remains in a precompact subset $ \mathcal{Y} $ of $ L_1^+(0, +\infty) $ and thus

which has compact closure in $ \mathcal{X} $. The proof is completed.

4.   Local stability of steady states

In this section, we show the local stability of system (1.6) at each steady states.

4.1.   Local stability of virus-free steady state

Theorem 4.1. If $ \Re_0 < 1 $, then the virus-free steady state $ E_0 $ of system (1.6) is locally asymptotically stable.

Proof. Denote $ \bar{T}_1(t) = T(t) - T_0 $, $ \bar{i}_1(t, a) = i(t, a) $, $ \bar{V}_1(t) = V(t) $ and $ \bar{Z}_1(t) = Z(t) $, the linearized equation of (1.6) at $ E_0 $ as follows:

Let the solution of (4.1) has the following exponential form:

then

Solve the second equation of (4.2) yields

We can write the characteristic equation as following

where

Since $ \lambda = - \mu_1 < 0 $, then we only need to consider the root of $ \Delta(\lambda) = 0 $. By way of contradiction, we assume that it has an eigenvalue $ \lambda_0 $ with $ Re(\lambda_0)\geqslant 0. $ We have

Hence,

which is impossible because $ \Re_0 = \frac{\beta T_0 \mathcal{P}}{\mu_2} + T_0 \mathcal{K} < 1. $ This completes the proof.

4.2.   Local stability of immune-inactivated steady state

Theorem 4.2. If $ \Re_1 < 1 < \Re_0 $, then the immune-inactivated steady state $ E^*_1 $ of system (1.6) is locally asymptotically stable.

Proof. Denote $ \bar{T}_2(t) = T(t) - T_1^* $, $ \bar{i}_2(t, a) = i(t, a)-i^*_1(a) $, $ \bar{V}_1(t) = V(t)-V_1^* $ and $ \bar{Z}_2(t) = Z(t) $, the linearized equation of (1.6) at $ E_1^* $ as follows:

Let $ \bar{T}_2(t) = \bar{T}_2 e^{\lambda t} $, $ \bar{V}_2(t) = \bar{V}_2 e^{\lambda t} $, $ \bar{Z}_2(t) = \bar{Z}_2 e^{\lambda t} $ and $ \bar{i}_2(t, a) = \bar{i}_2(a) e^{\lambda t} $, thus we have the following characteristic equation:

Note that $ \Re_1 < 1 $ and using (2.6), we can obtain that $ \mu_3-cf'(0)V_1^* > 0 $, then the characteristic equation is equivalent to

By way of contradiction, we assume that it has an eigenvalue $ \lambda_0 $ with $ Re(\lambda_0)\geqslant 0. $ Obviously, $ \lambda = -\mu_1 $ and $ \lambda = -\mu_2 $ are not the roots of (4.4) and note that

Then we have

which is impossible since $ V_1^* > 0 $ and $ i_1^*(a) > 0 $. Accordingly, the immune-inactivated steady state $ E^*_1 $ of system (1.6) is local asymptotically stable if $ \Re_1 < 1 < \Re_0 $.

4.3.   Local stability of immune-activated steady state

Theorem 4.3. If $ \Re_1 > 1 $, then the immune-activated steady state $ E^*_2 $ of system (1.6) is locally asymptotically stable.

Proof. Applying similar method in the proof of the Theorem (4.2), we have the characteristic equation as following:

By way of contradiction, we assume that it has an eigenvalue $ \lambda_0 $ with $ Re(\lambda_0)\geqslant 0. $ From the concavity of function $ f $ in (A2), we have $ \mu_3 - cV_2^*f'(Z_2^*) \geqslant 0 $ since $ \mu_3Z_2^* - cV_2^*f(Z_2^*) = 0 $. Note that $ \lambda = -\mu_1 $, $ \lambda = -(\mu_2+qf(Z_2^*)) $ and $ \lambda = cV_2^*f'(Z_2^*)-\mu_3 $ are not the roots of (4.5), then we can rewrite (4.5) as

where

Then

which is contradictory. Here we use the fact:

This completes the proof.

5.   Global stability of steady states

In this section, we discuss the global stability of system (1.6) by using Lyapunov direct method and LaSalle invariance principle. We first give the result on uniform persistence.

Theorem 5.1. Assume that $ \Re_0 > 1 $. Then there exists a constant $ \zeta > 0 $ such that

for each $ X_0\in\mathcal{X} $.

The proof of Theorem 5.1 is similar with that in [21,Section 4] or ^[30], so we omit the details. In the following, we proof the global stability of each steady states.

5.1.   Global stability of virus-free steady state

Theorem 5.2. The virus-free steady state $ E_0 $ of system (1.6) is globally asymptotically stable if $ \Re_0 < 1 $.

Proof. Let

By direct calculations, we have $ \alpha_1(0) = \Re_0 $ and $ \alpha_1'(a) = \delta(a)\alpha(a) - \left(\frac{\beta T^0}{\mu_2}p(a) + T^0 k(a)\right) $. Define the following Lyapunov functional:

where

Calculating the derivatives of $ H_1(t) $ and $ H_2(t) $ along system (1.6), we have

and

thus

if $ \Re_0 < 1 $. Note that $ \frac{ \text{d}H(t)}{ \text{d}t}|_{(1.6)} = 0 $ implies that $ T(t) = T_0 $, $ i(t, 0) = 0 $ and $ Z(t) = 0 $, then the largest invariant subset of $ \left\{\frac{ \text{d}H(t)}{ \text{d}t}|_{(1.6)} = 0\right\} $ is $ \{E_0\} $. Therefore, the virus-free steady state $ E_0 $ of system (1.6) is global asymptotically stable if $ \Re_0 < 1 $ by Lyapunov-LaSalle theorem. This ends the proof.

5.2.   Global stability of immune-inactivated steady state

Theorem 5.3. The immune-inactivated steady state $ E_1^* = (T_1^*, i_1^*(a), V_1^*, 0) $ of system (1.6) is globally asymptotically stable if $ \Re_1 < 1 < \Re_0 $.

Proof. Let

Define the following Lyapunov functional:

where

The derivative of $ W_1(t) $ is calculated as follows:

Note that

which leads to

By some calculations, we have

and using the fact that

Hence

Then we have the derivative of $ W_2(t) $ as follows:

For $ W_3(t) $, we have

Hence,

Recalling that $ V_1^* = \int_0^\infty \frac{p(a)}{\mu_2}i_1^*(a) \text{d}a $ and $ i_1^*(0) = \beta T_1^* V_1^* + \int_0^\infty k(a)T_1^*i_1^*(a) \text{d}a $. Substituting (2.13) into (5.11), after some calculations and rearranging the equation yield

Note that

Thus $ \frac{ \text{d}W(t)}{ \text{d}t}|_{(1.6)} \leqslant 0 $ when $ \Re_1 < 1 < \Re_0 $, $ \frac{ \text{d}W(t)}{ \text{d}t} = 0 $ if and only if $ (T(t), i(t, a), V(t), Z(t)) = (T_1^*, i_1^*(a), V_1^*, 0). $ Applying Lyapunov-LaSalle theorem, the immune-inactivated steady state $ E_1^* = (T_1^*, i_1^*(a), V_1^*, 0) $ of system (1.6) is globally asymptotically stable if $ \Re_1 < 1 < \Re_0 $.

5.3.   Global stability of immune-activated steady state

Theorem 5.4. The immune-activated steady state $ E_2^* = (T_2^*, i_2^*(a), V_2^*, Z_2^*) $ of system (1.6) is globally asymptotically stable if $ \Re_1 > 1 $.

Proof. Let

Define the Lyapunov functional as follows

where

Using the results in the proof of Theorem (5.3), after some calculations, we have the derivative of $ L(t) $ as follows:

It follows from follows (A2) and (A3) that $ \left(\frac{Z(t)}{Z_2^*}-\frac{f(Z(t))}{f(Z_2^*)}\right)\left(\frac{f(Z_2^*)}{f(Z(t))}-1\right)\leqslant0 $, thus $ \frac{ \text{d}L(t)}{ \text{d}t}|_{(1.6)} \leqslant 0 $ and $ \frac{ \text{d}L(t)}{ \text{d}t} = 0 $ if and only if $ (T(t), i(t, a), V(t), Z(t)) = (T_2^*, i_2^*(a), V_2^*, Z_2^*). $ Therefore, the immune-activated steady state $ E_2 $ of system (1.6) is global asymptotically stable if $ \Re_1 > 1 $ by Lyapunov-LaSalle theorem.

6.   Special case and numerical simulation

6.1.   Example

In this subsection, as special case for the age-infection model (1.6) and (1.7) with general nonlinear immune response $ f(Z) $, we introduce the following age-infection model with saturation immune response function, which have been used for modeling HIV infection in ^[30,42].

with the boundary and initial condition

The model without cell-to-cell transmission of system (6.1) with (6.2) has been studied in ^[30]. It is easy to see that $ f(Z) = \frac{Z(t)}{h+Z(t)} $ satisfy (A2) and (A3). System (6.1) with (6.2) is a special case of the original system (1.6) and (1.7).

The virus-free equilibrium of system (6.1) with (6.2) is similar to the previous one, $ E_{01} = (T_0, 0, 0, 0) $, where $ T_0 = \frac{\Lambda}{\mu_1} $. By some calculation, we obtain the basic reproduction number and immune-activated reproduction number of system (6.1) with (6.2) as $ \Re_{01} = \frac{\beta T_0 \mathcal{P}}{\mu_2} + T_0 \mathcal{K} $ and $ \Re_{11} = \frac{\Lambda c \mathcal{P}}{h\mu_2\mu_3}\left(1-\frac{1}{\Re_0}\right) $, respectively. We have the following corollary:

Corollary 6.1. For system (6.1) with (6.2), there are two threshold parameters $ \Re_{01} $ and $ \Re_{11} $ with $ \Re_{01} > \Re_{11} $ such that

(ⅰ) If $ \Re_{01} < 1 $, there exists a virus-free steady state $ E_{01} $, and $ E_{01} $ is globally asymptotically stable;

(ⅱ) If $ \Re_{11} < 1 < \Re_{01} $, there exists a immune-inactivated steady state $ E_{11} $ which is globally asymptotically stable;

(ⅲ) If $ \Re_{11} > 1 $, there exists a immune-activated steady state $ E_{21} $ which is globally asymptotically stable.

6.2.   Numerical simulation

In this subsection, we perform some numerical simulations to the validity of the theoretical result of this paper. Specifically, we focus on the age-infection model with saturation immune response function (see model (6.1)).

The parameter values will be used in numerical simulation are listed in Table 2. Furthermore, we set the maximum age for the viral production as $ a^† = 10 $ and we set

and

Thus, the averages of $ \delta(a) $, $ p(a) $ and $ k(a) $ are $ 0.03 $, $ 2.9 $ and $ 0.0003 $, which are the same in ^[43,20].

Numerical simulation shows the following three cases:

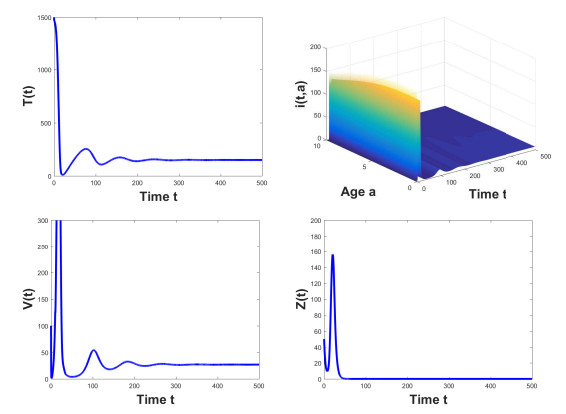
Case 1: Choose parameter values as in Case 1 of Table 2, then we can calculate the basic reproduction number as $ \Re_0\approx0.8093 < 1 $. Corollary 1 asserts that the virus-free steady state of system (6.1) with (6.2) is globally asymptotically stable. From Figure 1, one can observe that the levels of all compartmental individuals tend to stable values, where $ T(t) $, $ V(t) $, $ i(t, a) $ and $ Z(t) $ converge to a virus-free steady states (100, 0, 0, 0).

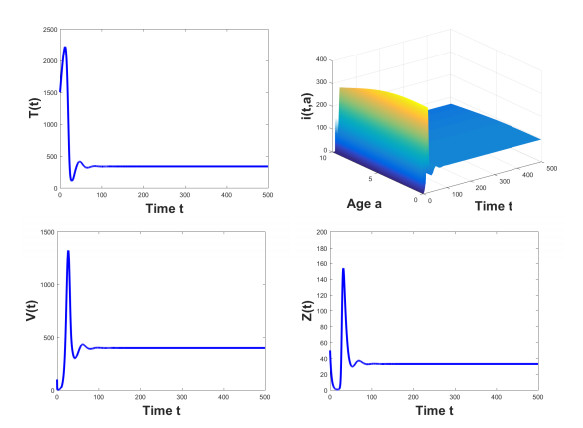
Case 2: Choose parameter values as in Case 2 of Table 2. By some computing, we can obtain that $ \Re_0 \approx 5.3952 > 1 > \Re_1\approx 0.9040 $. From Corollary 1, we derive that immune-inactivated infection steady state is globally asymptotically stable. Numerical simulation illustrates this fact (see Figure 2).

Case 3: Choose parameter values as in Case 3 of Table 2. Similarly, we can obtain that $ \Re_0 \approx 29.9893 > 1 $ and $ \Re_1\approx 1.3408 > 1 $. Numerical simulation shows that the levels of all compartmental individuals tend to stable values (see Figure 3), that is, immune-inactivated infection steady state is globally asymptotically stable.

7.   Conclusion and discussion

In this paper, we proposed and investigated an age-structured within-host viral infection model with cell-to-cell transmission and general humoral immunity response. We have shown that the global stability of equilibria of model (1.6) are determined by the corresponding basic reproduction numbers $ \Re_0 $ and the basic immune reproductive number $ \Re_1 $. That is, when $ \Re_0 < 1 $, the virus-free steady state is globally asymptotically stable, which means that the viruses are cleared and immune response is not active; when $ \Re_1 < 1 < \Re_0 $, the immune-inactivated infection steady state exists and is globally asymptotically stable, which means that viral infection becomes chronic and humoral immune response would not be activated; and when $ \Re_1 > 1 $, the immune-activated infection steady state exists and is globally asymptotically stable, in this case the infection causes a persistent humoral immune response and is chronic.

Now, we show the relevance of model formulations between our age-structured model (1.6) and the standard ODE models. We consider $ \delta(a)\equiv\delta $, $ k(a)\equiv k $ and $ p(a)\equiv p $ in model (1.6). Letting

Recall that

then we have

here we assume that $ \lim_{a\rightarrow\infty}i(t, a) = 0 $, which means that there is no biological individual can live forever. Thus, system (1.6) is equivalent to the following ODE model as

which is the model studied by ^[23] when $ f(Z) = Z $ and $ k = 0 $. In fact, we have not found the above model in any existing literatures, but we think it has the same dynamic behavior with (1.6).

It is necessary to mention it here, in the proof of Lemma 4.1, there may exists zero eigenvalue if $ R_0 = 1 $, and it may lead to more complex dynamic behavior. For example, Qesmi et al. ^[46] propose a mathematical model describing the dynamics of hepatitis B or C virus infection with age-structure, and they found that when $ \Re_0 = 1 $, the system may undergo a backward bifurcation. In a recent work ^[22], Zhang and Liu studied an age-structured HIV model with cell-to-cell transmission and logistic growth in uninfected cells. They have shown that there exists Hopf bifurcation of the model by using the Hopf bifurcation theory for semilinear equations with non-dense domain. Introducing logistic growth in uninfected cells to model (1.6), it will be interesting to investigate the existence of a Hopf bifurcation. We leave the above two studies for future consideration.

Acknowledgments

The authors are very grateful to the editors and two reviewers for their valuable comments and suggestions that have helped us improving the presentation of this paper. The authors were supported by Natural Science Foundation of China (11871179; 11771374).

Conflict of interest

All authors declare no conflicts of interest in this paper.