Coupled systems with Ambrosetti-Prodi-type differential equations

1.   Introduction

This paper focuses on the search for sufficient conditions to require nonlinearities in order to be able to discuss, depending on the parameters, the existence of solutions for coupled systems of nonlinear second-order differential equations, of the type

for $x\in \left[ 0, 1\right]$, with $f, h:\left[ 0, 1\right] \times \mathbb{R} ^{4}\rightarrow \mathbb{R}$, $m, n:\left[ 0, 1\right] \rightarrow \mathbb{R} ^{+}$ continuous functions and $\mu, \lambda$ are real parameter, along with boundary conditions

where $a_{i}, b_{i}, c_{i}, d_{i}, A_{i}, B_{i}\in \mathbb{R},$ $i = 1, 2,$ such that $a_{i}^{2}+b_{i} > 0$, $c_{i}^{2}+d_{i} > 0,$ for $i$ fixed, and $b_{i}, d_{i}\geq 0.$

Coupled systems of second-order differential equations were studied by many authors, not only from a mathematical point of view, as in, for example, ^[1,2,3,4], but also to model some real phenomena, as, for instance, Lokta-Volterra models, reaction diffusion processes, prey-predator systems, Sturm-Liouville problems, mathematical biology, chemical systems, as in ^[5,6,7,8,9]. Moreover, in the last few years, fractional calculus has had an increasing application to several real processes, as in ^[10,11,12].

Ambrosetti-Prodi-type problems, introduced in ^[13,14], have been applied to several types of boundary conditions, as it can be seen in, for example: ^[15,16], to separated two-point and three-point boundary value problems; ^[17,18], for Neuman's conditions; ^{[19,20,21,22,23,24]} to periodic solutions; ^[25], for parametric problems with $(p, q)$ -Laplace operator; ^[26], with asymptotic assumptions; ^[27], for fractional Laplacian; ^[28], with asymptotic sign-changed nonlinearities, among others.

Motivated by these works, we consider for the first time, as far as we know, a coupled second-order system composed of two Ambrosetti-Prodi-type differential equations together with two-point boundary conditions. The arguments are based on the lower and upper solutions method ^{[29,30,31,32,33]}, which requires a new definition of lower and upper functions to overcome the couple variation on the nonlinearities (see Definition 2.1). A Nagumo condition (see, for example, ^[34,35,36]) plays an important role to control the first derivatives variation, and the theory of the topological degree (see, for instance, ^[37,38]) is the main tool to prove the existence of solution for the parameters' values such that there are lower and upper solutions for (E), (B). Therefore, the main result is an existence and localization theorem, as it provides not only the existence of a solution, but also a range where the solution varies.

The paper is organized as follows: Section 2 contains the functional framework, a definition of upper-lower solutions, the Nagumo conditions and "a priori" estimates of the first derivative of the unknown functions. In Section 3 we present an existence and location result and an example to show the applicability of the main theorem. Section 4 applies our main result to a stationary version of the model presented in ^[39,40] for complex interactions in social media, the mechanisms and dynamics of information diffusion in online social networks.

2.   Definitions and auxiliary results

In this section, some definitions and lemmas will be introduced for the subsequent analysis, we consider the following functional framework.

Let $X = C^{1}[0, 1]$ be the usual Banach space equipped with the norm $\Vert \cdot \Vert _{C^{1}}$, defined by

where

and $X^{2} = C^{1}[0, 1]\times C^{1}[0, 1]$ with the norm

To apply the lower and upper solutions method, depending on the values of the parameters $\mu$ and $\lambda$, we introduce a new type of lower and upper definition:

Definition 2.1. Let $a_{i}, b_{i}, c_{i}, d_{i}, A_{i}, B_{i}\in \mathbb{R},$ such that $a_{i}^{2}+b_{i} > 0$, $c_{i}^{2}+d_{i} > 0$ and $b_{i}, d_{i}\geq 0$, for $i = 1, 2$.

A pair of functions $(\gamma_1, \gamma_2) \in (C^2(]0, 1[)\cap C^1([0, 1]))^2$ is a lower solution of problem (E)-(B) if, for all $x\in \left[ 0, 1 \right]$,

and

A pair of functions is an upper solution of problem (E)-(B) if the reversed inequalities are verified.

The so-called Nagumo condition establishes an "a priori" estimation for the first derivatives of the solutions of (E), provided that they satisfy adequate bounds, and is adapted here for coupled systems.

Definition 2.2. Let $\gamma _{i}(x), {\text{ }}\Gamma _{i}(x), {\text{ }}i = 1, 2$, be continuous functions such that

and consider the sets

The continuous functions $f, h:[0, 1]\times \mathbb{R}^{4}\rightarrow \mathbb{R }$ satisfy a Nagumo-type condition relative to the intervals $[\gamma _{1}(x), \Gamma _{1}(x)]$ and $[\gamma _{2}(x), \Gamma _{2}(x)]$, for all $x\in \left[ 0, 1\right],$ if there are $k_{1}$, $k_{2}$, such that

and continuous positive functions $\varphi, \psi :[0, +\infty)\rightarrow (0, +\infty)$, verifying

such that

The priori estimates for the first derivatives are given by the next lemma.

Lemma 2.1. Suppose that the continuous functions $f, h:[0, 1]\times \mathbb{ R}^{4}\rightarrow \mathbb{R}$ satisfy a Nagumo type condition relative to the intervals $[\gamma _{1}(x), \Gamma _{1}(x)]$ and $[\gamma _{2}(x), \Gamma _{2}(x)],$ for all $x\in \left[ 0, 1\right]$.

Then for every solution $(u, v)\in (C^2[0, 1])^2$ of (E) verifying

there are $N_1, N_2 > 0$ (depending only on the parameters $\mu$ and $\lambda$ and the functions $m,$ $n,$ $\; \gamma_1, \; \Gamma_1, \; \gamma_2, \; \Gamma_2, \; \varphi$ and $\psi$), such that

Proof. Let $(u(x), v(x))$ be a solution of (E) verifying (2.5). By the Mean Value Theorem, there are $x_{0}, x_{1}\in \lbrack 0, 1]$ such that

If

then it is enough to define $N_{1}: = k_{1}$ and the proof is complete.

Moreover, the case $|u^{\prime }(x)| > k_{1}, {\text{ }}\forall x\in \lbrack 0, 1]$, is not possible. In fact, if $u^{\prime }(x) > k_{1}, {\text{ }}\forall x\in \lbrack 0, 1]$, we obtain, by (N2), (2.5) and (2.3), the contradiction

If $u^{\prime }(x) < -k_{1}, {\text{ }}\forall x\in \lbrack 0, 1]$, the contradiction is similar.

Consider $N_{i} > k_{i}$, for each $i = 1, 2$, such that

and assume that there are $x_{2}, x_{3}\in \lbrack 0, 1]$ with $x_{2} < x_{3}$, such that

By continuity of $u^{\prime }(x)$, there exists $x_{4}\in \lbrack x_{2}, x_{3}]$ such that $u^{\prime }(x_{4}) = k_{1}$.

By a convenient change of variable and using (E) and (N2),

and by (N)

Therefore $u^{\prime }(x_{3}) < N_{1},$ and as $x_{3}$ is taken arbitrarily, then $u^{\prime }(x) < N_{1}$, for the values of $x$ whenever $u^{\prime }(x) > k_{1}$.

The case for $x_{2} > x_{3}$ follows similar arguments.

The other possible case where

can be proved by the previous techniques. Therefore $\Vert u^{\prime }\Vert \leq N_{1}$.

By a similar method, it can be shown that $\Vert v^{\prime }\Vert \leq N_{2}$.

Remark 2.1. From the previous demonstration, it follows that $N_{1}$ and $N_{2}$ can be considered independently of $\mu$ and $\lambda$, since $\mu$ and $\lambda$ belong to a bounded set.

3.   Main result

The first theorem is an existence and localization result:

Theorem 3.1. Let $f, h:[0, 1]\times \mathbb{R}^{4}\rightarrow \mathbb{R}$ be continuous functions. If there are lower and upper solutions of (E)-(B), $(\gamma _{1}, \gamma _{2})$ and $(\Gamma _{1}, \Gamma _{2})$, respectively, according Definition 2.1, such that

and $f$ and $h$ verify Nagumo conditions as in Definition 2.2, relative to the intervals $[\gamma _{1}(x), \Gamma _{1}(x)]$ and $[\gamma _{2}(x), \Gamma _{2}(x)]$, for all $x\in \left[ 0, 1\right],$ with

for $x\in \left[ 0, 1\right],$ $\forall z_{1}\in \mathbb{R},$

and

for $x\in \left[ 0, 1\right],$ $\forall y_{1}\in \mathbb{R},$

Then there is at least a pair $(u(x), v(x))\in (C^{2}[0, 1])^{2}$ solution of (E)-(B) and, moreover,

Proof. Define the functions $\alpha, \beta :[0, 1]\times \mathbb{R}\rightarrow \mathbb{R}$ given by

and

For $\theta, \vartheta \in \lbrack 0, 1],$ consider the truncated and perturbed auxiliary problem formed by the equations

for $x\in ]0, 1[$, and the boundary conditions

where $a_{i}, b_{i}, c_{i}, d_{i}, A_{i}, B_{i}\in \mathbb{R},$ $i = 1, 2,$ such that $a_{i}^{2}+b_{i} > 0$, $c_{i}^{2}+d_{i} > 0$ and $b_{i}, d_{i}\geq 0.$Take $r_{i} > 0$, $i = 1, 2$, such that, $\forall x\in \lbrack 0, 1]$,

and

Claim 1. Every solution $(u(x), v(x))$ of the problems (3.6) and (3.7) verifies

independently of $\theta, \vartheta \in \lbrack 0, 1]$ . Assume, by contradiction, that there exist $\theta \in \lbrack 0, 1],$ $\left(u(x), v(x)\right)$ solution of (3.6) and (3.7) and $x\in \lbrack 0, 1]$ such that $|u(x)|\geq r_{1}$.If $u(x)\geq r_{1}$, define

For $x_{0}\in ]0, 1[$ and $\theta \in ]0, 1],$ $u^{\prime }(x_{0}) = 0$ and $u^{\prime \prime }(x_{0})\leq 0.$ By (3.8), we have the following contradiction

If $\theta = 0,$ the contradiction arises from

If $x_{0} = 0,$ then

and $u^{\prime }(0^{+}) = u^{\prime }(0)\leq 0.$ By (3.7) and (3.9), we have

If $x_{0} = 1$ a contradiction is obtained analogously.

Then $u(x) < r_{1}$ for $x\in \lbrack 0, 1]$ and regardless of $\ \theta$. The other possible case where

can be proved by similar techniques.

Therefore $|u(x)| < r_{1}$ for all $x\in \lbrack 0, 1],$ regardless of $\theta$.

By a similar method, it can be proved that $|v(x)| < r_{2}$ for all $x\in \lbrack 0, 1]$ regardless of $\vartheta$.

Claim 2. For every solution $(u(x), v(x))$ of the problems (3.6) and (3.7),

independently of $\theta, \vartheta \in \lbrack 0, 1],$ with $N_{1}$ and $N_{2}$ given by Lemma 2.1.

Define the continuous functions $F_{\theta }, H_{\vartheta }{\text{ }}: [0, 1]\times \mathbb{R}^{4}\rightarrow \mathbb{R}$, by

and

with $y_{0}\in \lbrack -r_{1}, r_{1}]$ and $z_{0}\in \lbrack -r_{2}, r_{2}]$.

As the functions $f, h:[0, 1]\times \mathbb{R}^{4}\rightarrow \mathbb{R}$ satisfy a Nagumo-type condition relative to the intervals $[\gamma _{1}(x), \Gamma _{1}(x)]$ and $[\gamma _{2}(x), \Gamma _{2}(x)]$, then

and

Therefore for continuous positive functions $\varphi _{\ast }, \psi _{\ast }:[0, +\infty)\rightarrow (0, +\infty)$, given by

then, clearly, $F_{\theta }$ and $H_{\vartheta }$ satisfy Nagumo conditions in the sets

and, by (N1), we have

and

Therefore, by Lemma 2.1,

independently of $\theta, \vartheta \in \lbrack 0, 1]$.

Claim 3. The problems (3.6) and (3.7), for $\theta = 1$ and $\vartheta = 1$, has at least one solution $(u, v)$.

Define the operators

given by

and

given by

being

and

Since $\mathcal{L}$ is invertible, we define the completely continuous operator

given by

For $M: = \max \{r_{1}, r_{2}, N_{1}, N_{2}\}$ consider the set

By Claims 1 and 2, for all $\theta, \vartheta \in \lbrack 0, 1]$, the degree $d(\mathcal{I}-\mathcal{T}_{(\theta, \vartheta)}, \Omega _{1}, 0)$ is well defined, and, by homotopy invariance,

As the equation $(u, v) = \mathcal{T}_{(0, 0)}(u, v)$ admits only the null solution, then, by degree theory,

and, in particular, the equation $(u, v) = \mathcal{T}_{(1, 1)}(u, v)$ has at least one solution.

That is, the problem is composed of the equations

and the boundary conditions

has at least one solution $(u_{1}(x), v_{1}(x))$ in $\Omega _{1}$.

Claim 4. The functions $u_{1}(x)$ and $v_{1}(x)$ are a solution of the initial problem (E), (B).

In fact, if the pair $(u_{1}(x), v_{1}(x))\in (C^{2}[0, 1])^{2}$ is a solution of (3.10) and (3.11), it will be also a solution of the initial problems (E) and (B), provided that

Suppose, by contradiction, that there exists $x\in \lbrack 0, 1]$ such that $u_{1}(x) > \Gamma _{1}(x)$, and define

If $x_{1}\in ]0, 1[$ then

and we have, by Definition 2.1, the following contradiction

For $x_{1} = 0,$

and

By the boundary conditions (3.11) and Definition 2.1, this contradiction is obtained

So, $x_{1}\neq 0$ and by a similar method it is shown that $x_{1}\neq 1$. Therefore

Defining

it can be proved that $u_{1}(x)\geq \gamma _{1}(x)$, for all $x\in \lbrack 0, 1]$, by an analogous process.

Using the same technique, it can be shown that

So, $(u_{1}(x), v_{1}(x))$ is a solution of (E)-(B), for the values of $\mu, \lambda \in \mathbb{R}$, such that there are lower and upper solutions according to Definition 2.1.

Example 3.1. Consider the system

for $x\in \left[ 0, 1\right]$, and $\mu, \lambda$ are real parameter, along with boundary conditions

The functions $\gamma _{1}, \gamma _{2}, \Gamma _{1}, \Gamma _{2}:[0, 1]\rightarrow \mathbb{R}$, given by

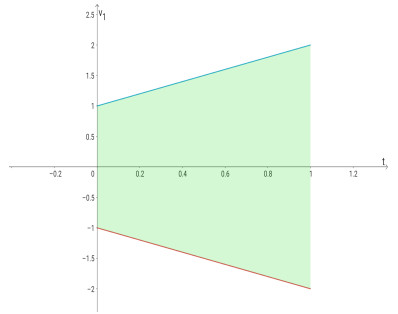
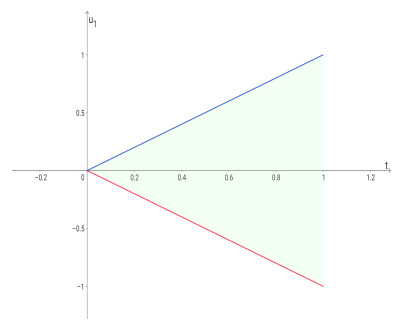
are, respectively, lower and upper solutions of (3.12) and (3.13) for $\mu$ and $\lambda$ such that

The functions

and

are continuous and satisfy the Nagumo conditions (N1) and (N2). By Theorem 3.1, the problems (3.12) and (3.13) has at least one solution $(u_{1}(x), v_{1}(x)),$ which verifies

Figures 1 and 2 show the admissible region for solution $(u_{1}(x), v_{1}(x)).$

4.   Application to the diffusion of information in social media

In ^[39,40], the authors study the process of disseminating information in social media to obtain, mathematical predictability in news dissemination to increase the efficiency of the distribution of positive information and, at the same time, reduce information unwanted. In short, it is considered a model to describe the flow of information, based on two similar news sources, that spread with logistic growth independently together with an additional effect one over the other.

It is addressed that, for a given piece of information initiated by two specific users called sources, the density of influenced users in the network depends on the distance $x$ to any source. Based on this model we consider the following stationary system

together with the boundary conditions

where $b_{i}, d_{i}, r_{i}, K_{i}\in \mathbb{R}^{+}$ and $\alpha _{i}\geq 0,$ $i = 1, 2$, having the following meaning:

● $u$ and $v$ are the density of information from the different sources

● $d_{1}, d_{2}$ represent the popularity of the two pieces of information;

● $r_{1}, r_{2}$ are the speed with which information spreads within groups of users with the same distance;

● $K_{1}, K_{2}$ represents the carrying capacity, which is the maximum possible density of influenced users;

● $\alpha _{1}$ measures the positive effect of news $v$ on $u$ and $\alpha _{2}$ measures the positive effect of news $u$ on $v$;

● $m, n:\left[ 0, 1\right] \rightarrow \mathbb{R}^{+}$ are continuous functions, $\mu, \lambda$ real parameters, both relating with distance of each source.

● $b_{1},$ $b_{2}$ are related with the initial spread of each source.

Define

consider $K_{1} = 1$ and $K_{2} = 1,$ in the sense that the maximum load capacity is $100%,$ and, as a numeric example, assume that

Then the functions

are, respectively, lower and upper solutions of problems (4.1) and (4.2) for

and

Moreover, the problems (4.1) and (4.2) are particular cases of (E), (B), with

and

These functions verify the Nagumo conditions (N1) and (N2), relative to the intervals $y_{0}\in \lbrack \gamma _{1}(x), \Gamma _{1}(x)]$ and $z_{0}\in \lbrack \gamma _{2}(x), \Gamma _{2}(x)]$, as

and, trivially,

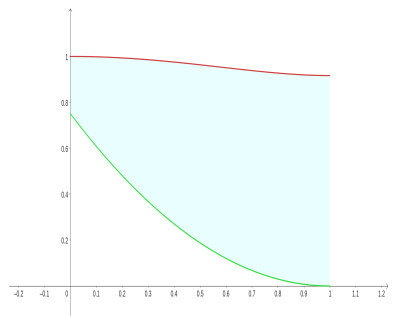
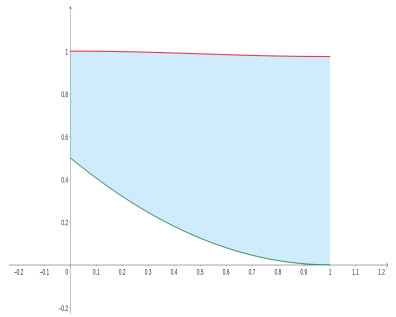
So by Theorem 3.1 the problems (4.1) and (4.2) have at least one solution $(u(x), v(x)),$ for the values of $\mu$ and $\lambda$ verifying (4.3) and (4.4), such that

and

for all $x\in \lbrack 0, 1]$.

The Figures 3 and 4 show the regions where this solution lies.

5.   Discussion

As far as we know, it is the first paper where Ambrosetti-Prodi differential equations are considered in couple systems with different parameters, therefore with present a preliminary study where the solvability of such problems is obtained for parameters' values for which there are lower and upper solutions. There are a lot of open issues such as how the Ambosetti-Prodi alternative could be done for coupled systems, and what are the sufficient conditions on the nonlinearities to discuss the existence, non-existence, and multiplicity of coupled systems solutions

We highlight two aspects in this work:

● A new definition type of lower and upper solutions for coupled systems (see Definition 2.1), which overcomes the nonlinear dependence on the two unknown functions and is will be crucial for future work;

● In the presence of such lower and upper solutions the parameters always belong to bounded sets, as it is illustrated in Example 3.1 and in the application.

6.   Conclusions

The main result allows us to evaluate some parameter values for which there are lower and upper solutions, and, therefore, it shows that, for these values, there is also, at least, a solution and this solution is localized in a strip bounded by lower and upper solutions.

The lower and upper solutions method seems to be a powerful tool to deal with these Amprosetti-Prodi type problems, as it allows not only some estimations on both parameters for which there are solutions of the coupled systems, but also because it provides strips for the localization of such solutions.

In fact, this localization tool, in our opinion, has been undervalued, as it maybe very useful to know some qualitative properties of the unknown functions.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This research was partially supported by national funds through the Fundação para a Ciência e Tecnologia, FCT, under the project UIDB/04674/2020.

Conflict of interest

F. Minhós is the Guest Editor of special issue "Boundary Value Problems and Applications" for AIMS Mathematics. F. Minhós was not involved in the editorial review and the decision to publish this article.