Periodic boundary value problem involving sequential fractional derivatives in Banach space

Xinwei Su; Shuqin Zhang; Lixin Zhang; Xinwei Su; Shuqin Zhang; Lixin Zhang

doi:10.3934/math.2020481

AIMS Mathematics

2020, Volume 5, Issue 6: 7510-7530. doi: 10.3934/math.2020481

Previous Article Next Article

Research article

Periodic boundary value problem involving sequential fractional derivatives in Banach space

1.
Department of Mathematics, China University of Mining and Technology-Beijing, 100083, Ding No.11 Xueyuan Road, Haidian District, Beijing, China
2.
Department of Basic Courses, Beijing Union University, 100101, No.97 Beisihuan East Road, Chaoyang District, Beijing, China

Received: 10 July 2020 Accepted: 17 September 2020 Published: 23 September 2020
MSC : 26A33, 34B15

In this paper, by the method of upper and lower solutions coupled with the monotone iterative technique, we investigate the existence and uniqueness results of solutions for a periodic boundary value problem of nonlinear fractional differential equation involving conformable sequential fractional derivatives in Banach space. An example is given to illustrate our main result.

Keywords:

Citation: Xinwei Su, Shuqin Zhang, Lixin Zhang. Periodic boundary value problem involving sequential fractional derivatives in Banach space[J]. AIMS Mathematics, 2020, 5(6): 7510-7530. doi: 10.3934/math.2020481

Related Papers:

[1]	Laura Grumann, Mara Madaleno, Elisabete Vieira . The green finance dilemma: No impact without risk – a multiple case study on renewable energy investments. Green Finance, 2024, 6(3): 457-483. doi: 10.3934/GF.2024018
[2]	Mukul Bhatnagar, Sanjay Taneja, Ercan Özen . A wave of green start-ups in India—The study of green finance as a support system for sustainable entrepreneurship. Green Finance, 2022, 4(2): 253-273. doi: 10.3934/GF.2022012
[3]	Biljana Ilić, Dragica Stojanovic, Gordana Djukic . Green economy: mobilization of international capital for financing projects of renewable energy sources. Green Finance, 2019, 1(2): 94-109. doi: 10.3934/GF.2019.2.94
[4]	Amanda-Leigh O'Connell, Johan Schot . Operationalizing transformative capacity: State policy and the financing of sustainable energy transitions in developing countries. Green Finance, 2024, 6(4): 666-697. doi: 10.3934/GF.2024026
[5]	Shahinur Rahman, Iqbal Hossain Moral, Mehedi Hassan, Gazi Shakhawat Hossain, Rumana Perveen . A systematic review of green finance in the banking industry: perspectives from a developing country. Green Finance, 2022, 4(3): 347-363. doi: 10.3934/GF.2022017
[6]	João Moura, Isabel Soares . Financing low-carbon hydrogen: The role of public policies and strategies in the EU, UK and USA. Green Finance, 2023, 5(2): 265-297. doi: 10.3934/GF.2023011
[7]	Goshu Desalegn . Insuring a greener future: How green insurance drives investment in sustainable projects in developing countries?. Green Finance, 2023, 5(2): 195-210. doi: 10.3934/GF.2023008
[8]	Raja Elyn Maryam Raja Ezuma, Nitanan Koshy Matthew . The perspectives of stakeholders on the effectiveness of green financing schemes in Malaysia. Green Finance, 2022, 4(4): 450-473. doi: 10.3934/GF.2022022
[9]	Fu-Hsaun Chen . Green finance and gender equality: Keys to achieving sustainable development. Green Finance, 2024, 6(4): 585-611. doi: 10.3934/GF.2024022
[10]	Yafei Wang, Jing Liu, Xiaoran Yang, Ming Shi, Rong Ran . The mechanism of green finance's impact on enterprises' sustainable green innovation. Green Finance, 2023, 5(3): 452-478. doi: 10.3934/GF.2023018

Abstract

1. Introduction

Nature-inspired algorithms are well-known algorithms for finding near-optimal solutions to optimization problems. These algorithms have successfully solved optimization problems in different domains ^[1,2]. The natural behaviors or events among living creatures inspire these nature-inspired algorithms Examples of such events include the mountain gazelle's social behavior, and the behavior of birds, monkeys, and other animals in the wildlife ^[3]. These algorithms have shown promise in solving real-world engineering problems and problems in many fields. Among the plethora of algorithms that have been designed by researchers over the years, new algorithms are still of interest among optimization enthusiasts to solve the common problem of these algorithms, which are mainly entrapped in local optima solutions and slow convergences. The Coot Optimization Algorithm (COA) has shown promise in solving these difficulties in classical nature-inspired algorithms. COA is inspired by the social lifestyle exhibited by coots. It is an effective and straightforward metaheuristic algorithm to find near-optimal solutions ^[4]. Despite the great prosperity of COA, it suffers from a slow convergence in solving very complex problems ^[5]. This weakness caused COA to require an extremely high number of iterations to produce substantially good results, especially on large-scale complex optimization problems ^[5,6].

The poor balance of the exploration and exploitation stages significantly contributes to the slow convergence ^[6,7]. While exploitation guarantees the refinement of solutions in attractive parts of the search space, exploration is essential for the global search and to prevent a premature convergence to the local optima ^[8]. An imbalance between these two stages can seriously impair the algorithm's effectiveness, thus resulting in wasted searches and higher processing expenses that ultimately yield less-than-ideal outcomes ^[9].

In the literature, scholars have employed a range of corrective measures to enhance the performance of certain algorithms that have comparable shortcomings ^[10,11]. A typical example is the truncation parameter selection technique, which was adopted to improve the general performance of the Mountain Gazelle Optimizer (MGO) on standard benchmark test functions ^[12]. To enhance the overall performance of the Gorilla Troop Optimizer (GTO), A. Bright et al. ^[13] integrated a step adaptive simulation concept into the GTO.

In the case of the COA, Aslan et al. ^[14] proposed a modification by integrating a randomized mutation technique into the original COA to enhance its global search ability. However, excessive randomization within algorithms causes significant instabilities. Additionally, R. R. Mostafa et al. ^[7] modified COA by introducing an opposition-based learning and an orthogonal-based learning approach to improve the algorithm's performance. Moreover, authors in ^[15] proposed control randomization and a transition factor-based strategy to enhance the COA. This modification was geared towards solving the battery parameters estimation problem. Hence, its performance in a variety of optimization fields was not established.

Similarly, this work seeks to modify the COA to improve its general performance through an adaptive sigmoid increasing inertia weight in the "Leader Movement" phase ^[16]. This is a crucial stage of the COA because it determines how the coots are led by their leader coot on the surface of the water. This influences the dynamics of the search as a whole ^[6]. The integrated adaptive weight is intended to dynamically balance the exploration and exploitation mechanisms throughout the search process.

To achieve this aim, the exploration is dominant at the early stages of the optimization search process and then gradually improves the exploitation mechanism in the later stages. Therefore, the adaptive sigmoid rising inertia weight is designed to begin with a smaller value and gradually increase ^[16].

The rest of the paper is organized as follows: the original COA and the proposed modification are presented in Section 2; the performance of the simulation's outcome is discussed in Section 3; and lastly, Section 4 concludes the paper by providing a thorough synopsis of the research and suggestions for potential future studies as recommendations.

2. Adaptive sigmoid increasing inertia weight-based modification of COA

This section presents the methodological approach followed in this research, which consists of the original COA, the proposed modification, and the test implementation.

2.1. The original coot optimization algorithm

The COA mimics the behavior of American coots as they navigate through seas or lakes. American coots have four distinct movement strategies: random movement, chain formation, moving toward group leader positions, or leading the group ^[6]. The initial generation is created randomly using Eqs (1) and (2):

$CootPos\left(i\right) = rand\left(1, d\right)\times \left(ub-lb\right)+lb ,$

(1)

$lob = \left[{lob}_{1}, {lob}_{1}, \dots , {lob}_{d}\right], uob = \left[{uob}_{1}, {uob}_{2}, \dots , {uob}_{d}\right] ,$

(2)

where CootPos denotes the position of the ith coot, d represents the dimension number, uob and lob signify the upper and lower boundaries, respectively, and rand denotes a random vector within the range [0, 1].

Random movement:

If coots exhibit random movement, then they will consequently migrate towards a position denoted as Q, which can be determined through Eq (3):

$Q = rand\left(1, d\right)\times \left(ub-lb\right)+lb .$

(3)

To prevent getting trapped in local optimal areas, if coots encounter a failure within a local region, then they will employ a position as determined through Eq (4):

$CootPos\left(i\right) = CootPos\left(i\right)+A\times R2\times \left(Q-CootPos\left(i\right)\right) ,$

(4)

where R2 ∈ [0, 1] and A can be calculated using Eq (5):

$A = 1-L\times \left(\frac{1}{Iter}\right) ,$

(5)

where L and Iter represent the current iteration and the maximum number of iterations, respectively.

Chain movement:

To mathematically represent the movement of the chain phase, we address the following equation, denoted as Eq (6):

$CootPos\left(i\right) = 0.5\times \left(CootPos\left(i-1\right)+CootPos\left(i\right)\right).$

(6)

Moving towards group leader:

When adjusting its position according to the leader's position, the coot's movement is governed by the following equation, denoted as Eq (7):

$K = 1+\left(iMODNL\right) .$

(7)

Here, $i$ represents the total number of coots, NL represents the number of leaders, and K denotes a specific leader. The update process utilizes the following equation, referred to as Eq (8):

$CootPos\left(i\right) = LeaderPos\left(K\right)+2\times R1\times \mathrm{cos}\left(2R\pi \right)\times \left(LeaderPos\left(K\right)-CootPos\left(i\right)\right).$

(8)

Leading the group by the leader (Leader movement):

Finally, to update their positions, the leaders employ the following Eq (9): to update their positions.

$LeaderPos\left(i\right) = \left\{\begin{array}{c}B\times R3\times \mathrm{cos}\left(2R\pi \right)\times \left(gBest-LeaderPos\left(i\right)\right)+gBest,\ \ if\ R4 < 0.5, \\ B\times R3\times \mathrm{cos}\left(2R\pi \right)\times \left(gBest-LeaderPos\left(i\right)\right)-gBest,\ \ if\ R4\ge 0.5, \end{array}\right.$

(9)

where gBest is the best position, R ∈ [−1, 1], both R3 and R4 ∈ [0, 1], B can be calculated using Eq (10):

$B = 2-L\times \left(\frac{1}{Iter}\right) ,$

(10)

where L represents the current iteration, and Iter represents the maximum number of iterations.

2.2. Proposed modification

The original COA has a great potential of being adopted for applications in various optimization fields ^[7]. However, the COA has a slow convergence, which makes it require a lot of iterations to produce a good optimization result ^[6]. This drawback is caused by a poor exploration and exploitation balance to ensure an efficient search.

To remedy this weakness, an adoptive sigmoid increasing inertia weight ^[16] is incorporated in the Leader Movement phase. This phase of the original COA is expressed in Eq (9), which indicates how the leader coots lead the coots' group to move on the water surface. The proposed weight is incorporated as shown in Eq (11):

$LeaderPos\left(i\right) = \left\{\begin{array}{l}B\times R3\times \mathrm{cos}\left(2R\pi \right)\times \left(gBest-LeaderPos\left(i\right)\right)+gBest, \ \ \ \ \ \ \ if\ R4 < 0.5, \\ B\times R3\times \mathrm{cos}\left(2R\pi \right)\times \left(gBest-LeaderPos\left(i\right)\right)-\omega \times gBest, \ if\ R4\ge 0.5, \end{array}\right.$

(11)

where the value of the weight, $\omega$ , is calculated using the sigmoid increasing inertia weight expressed in Eq (12):

$\omega \left(i\right) = {\omega }_{min}+\frac{{\omega }_{max}-{\omega }_{min}}{1+{e}^{a-b\times \frac{i}{MaxIter}}} ,$

(12)

where a and b are parameters for adjustment, which are carefully chosen through numerical simulations. The weights ${\omega }_{min}$ and ${\omega }_{max}$ represent the minimum and maximum weight values, respectively, and i and MaxIter represent the current iteration and the maximum number of iterations, respectively.

Finally, $\omega \left(i\right)$ represents the adaptive weight value at the ith iteration. The proposed weight is integrated in Eq (11) when R4 ≥ 0.5 to gain the full benefit of the inertia weight technique while avoiding its drawback of a possible premature convergence. In algorithms with the inertia weight techniques, they might converge too quickly to suboptimal solutions, especially when the weight parameter is not tuned properly. However, they are good at providing an effective and fast convergence to global solutions when properly implemented. To tap the good qualities of the coot technique, the developers of the algorithm incorporated the weighting factor when R4 ≥ 0.5. In this contribution, the eight has been designed to ensure the versatility of the algorithm during each iteration while avoiding its weaknesses. Depending on the value of R4, Eq (11) is executed with the proposed weight, where the good qualities can be utilized, or without the weight, where the algorithm can freely search within the space without solely focusing on the temporarily best individual members of the population.

The implementation (pseudocode) of the modified COA (mCOA) is presented as shown in Algorithm 1:

Algorithm 1. The pseudo-code of mCOA.
Initialize the first coot population randomly using Eqs (1) and (2).
Initialize the parameters of P=0.5, NL (Number of leaders), Ncoot (Number of coots), ${\mathrm{\omega }}_{\mathrm{m}\mathrm{i}\mathrm{n}}$ , ${\mathrm{\omega }}_{\mathrm{m}\mathrm{a}\mathrm{x}}$ , a, b, and MaxIter (max iteration).
Random selection of coot leaders.
Calculate the fitness of coots and leaders.
Find the best coot or leader as the global optimum (gBest).
While (Iter $\le$ MaxIter)
Calculate A, B, and $\omega$ using Eqs (5), (10), and (12) respectively.
If rand $<$ P
R1, R2, and R3 are random vectors along the dimensions of the problem.
Else
R1, R2, and R3 are random numbers.
End
For i=1 to the number of coots
Calculate K by Eq (7).
If rand $>$ 0.5
Update the positions of the coots by Eq (8)
Else
If rand $<$ 0.5 i $\ne$ 1
Update the positions of the coots by Eq (6)
else
Update the positions of the coots by Eq (4)
End-if
End-for
Calculate the fitness of the coot
If the fitness $<$ the fitness of leader(k)
Temp = leader(k); leader(k)=coot; coot=Temp
End
End-????
For the number of leaders
If rand $<$ 0.5
Update the position of the leader by Eq (11.1)
Else
Update the position of the leader by Eq (11.2)
End-if
If the fitness of the leader $<$ gBest
Temp =gBest; gBest=leader; leader=Temp; (update Global optimum)
End-if
End
Iter=Iter+1;
End-while

The pseudo-code serves as a guide for the implementation of the proposed mCOA.

3. Simulation test setup on benchmark functions

The proposed mCOA was tested on thirteen commonly used standard benchmark test functions to establish its performance ^[17]. The test functions consist of the same functions used in the literature of the original COA, the details of which can be found in the reference ^[6]. The algorithm was coded in the MATLAB software (R2018a), using an HP Pavilion laptop computer with AMD A-8-6410 APU, an AMD Radeon R5 Graphics processor of a 2.00GHz clock speed, a RAM size of 4.00GB, and a 64-bit operating system. Table 1 provides detailed information on the benchmark function.

Table 1. Detail information of benchmark functions.

No.	Function	Search range	Global optimum	Dimension
1	F1	[-100,100]	0	30
2	F2	[-10, 10]	0	30
3	F3	[-100,100]	0	30
4	F4	[-100,100]	0	30
5	F5	[-30, 30]	0	30
6	F6	[-100,100]	0	30
7	F7	[-1.28, 1.28]	0	30
8	F8	[-500,500]	-12,569	30
9	F9	[-5.12, 5.12]	0	30
10	F10	[-32, 32]	0	30
11	F11	[-600,600]	0	30
12	F12	[-50, 50]	0	30
13	F13	[-50, 50]	0	30

| Show Table

DownLoad: CSV

The simulation parameter settings used in the simulation experiment are presented in Table 2. These contain all the parameter settings used in the simulation of the original COA in the literature to facilitate a fair comparison.

Table 2. Simulation parameters settings.

Parameter	Value
Population size	30
a	0.5
B	1.2
${\omega }_{min}$	0.001
${\omega }_{max}$	0.8
Maximum iteration	1000
Number of runs	30

| Show Table

DownLoad: CSV

On each test function, the simulation was executed thirty (30) times, and some relevant statistical indicators were calculated, including the best value (Min), the worst value (Max), the mean value (Avg), and the standard deviation (Std). This depicts the possible best performance, the worst performance, the average performance, and the possible deviation when applied to a real-world optimization problem. Since no algorithm has been deemed globally optimal, relatively better-performing algorithms were searched for based on these statistical indicators ^[18].

To establish the efficacy of the proposed mCOA, the simulation results were compared to the original COA and some other state-of-the-art metaheuristic algorithms in ^[6], namely the genetic algorithm (GA) and the particle swarm optimization (PSO) algorithm. The comparison of simulation results on the thirteen (13) test functions are presented in Table 3, where the boldened numbers represent the best performances.

Table 3. Results comparison on benchmark functions.

Function		GA	PSO	COA	mCOA
F1	Min	1.5245E+00	9.3905E-08	2.8240E-47	3.9156E-165
	Max	7.4966E+00	5.0237E-05	4.3670E-23	1.114 E-104
	Avg	3.6872E+00	2.8706E-06	1.4570E-24	3.7133 E-106
	Std	1.3063E+00	9.0693E-06	7.9728E-24	2.0339 E-105
F2	Min	2.2110E-01	1.1259E-04	4.0984E-24	3.6289 E-86
	Max	6.5960E-01	1.0800E-02	9.0834E-13	3.3722 E-51
	Avg	4.7510E-01	1.8000E-03	5.6782E-14	1.1241 E-52
	Std	1.0590E-01	2.4000E-03	1.8801E-22	6.1568 E-52
F3	Min	2.8924E+03	3.1124E+01	9.1935E-48	1.829E-161
	Max	1.1739E+04	4.5637E+02	8.5873E-22	5.1103E-76
	Avg	5.1669E+03	1.5501E+02	2.8626E-23	1.7034E-77
	Std	2.1462E+03	1.0194E+02	1.5678E-22	9.3301E-77
F4	Min	4.9927E+00	1.0955E+00	9.1191E-25	5.5155E-82
	Max	2.1162E+01	6.1639E+00	3.0541E-12	3.8707E -34
	Avg	9.1426E+00	2.5264E+00	1.4861E-13	1.2902E-35
	Std	3.0510E+00	1.0886E+00	6.0000E-13	7.0669E-35
F5	Min	1.7212E+02	1.6161E+01	2.8344E+01	2.7475E+01
	Max	9.0158E+02	1.0518E+02	6.6751E+01	2.8597E+01
	Avg	4.1400E+02	3.7766E+01	3.1804E+01	2.8173E+01
	Std	1.7821E+02	2.4842E+01	7.8738E+00	2.5579E-01
F6	Min	1.5385E+00	3.8856E-08	4.7900E-02	2.8573E-03
	Max	7.5916E+00	9.8496E-06	5.4550E-01	2.1669E-02
	Avg	3.6049E+00	1.5514E-06	1.9360E-01	7.6979E-03
	Std	1.5701E+00	2.4394E-06	1.2700E-01	3.7623E-03
F7	Min	5.5600E-02	1.0200E-02	3.0816E-04	9.8849E-05
	Max	2.0180E-01	5.6100E-02	2.2100E-02	3.7090E-03
	Avg	1.2240E-01	2.5300E-02	4.4000E-03	1.1750E-03
	Std	3.9000E-02	1.0300E-02	4.8000E-03	1.0394E-03
F8	Min	-1.1491E+04	-7.8895E+03	-9.2190E+03	-8.9888E+03
	Max	-1.0316E+04	-4.8503E+03	-6.3040E+03	-6.3108E+03
	Avg	-1.0872E+04	-6.5312E-03	-7.5838E+03	-7.4229E+03
	Std	3.0684E+02	8.0228E+02	7.3974+02	6.1435E+02
F9	Min	2.8791E+00	9.5516E+01	0.0000E+00	0.0000E+00
	Max	1.4370E+01	9.5516E+01	5.0591E-12	0.0000E+00
	Avg	7.7912E+00	4.8255E+01	1.8948E-13	0.0000E+00
	Std	2.8269E+00	1.6229E+01	9.2219E-13	0.0000E+00
F10	Min	3.2410E-01	4.6059E-05	8.8818E-16	8.8818E-16
	Max	1.6306E+00	2.8136E+00	1.9263E-08	4.4409E-15
	Avg	7.3590E-01	1.2718E+00	6.4475E-10	1.2434E-15
	Std	3.1770E-01	8.2150E-01	3.5164E-09	1.0840E-15
F11	Min	9.1080E-01	3.8588E-08	0.0000E+00	0.0000E+00
	Max	1.0681E+00	7.0900E-02	6.1950E-14	0.0000E+00
	Avg	1.0221E+00	1.4800E-02	2.1057E-15	0.0000E+00
	Std	3.0900E-02	1.6700E-02	1.1305E-14	0.0000E+00
F12	Min	2.9000E-03	3.0857E-01	1.2000E-03	5.3217E-05
	Max	2.4180E-01	9.3380E-01	1.3627E+00	5.4852E-04
	Avg	3.1500E-02	1.7650E-01	9.7700E-02	1.4757E-04
	Std	4.5400E-02	2.4850E-01	2.8540E-01	1.1308E-04
F13	Min	7.6300E-02	3.4979E-07	7.0200E-02	4.2545E-03
	Max	6.1460E-01	6.2250E-01	2.9777E+00	2.8156E+00
	Avg	3.0580E-01	3.4600E-02	5.4750E-01	2.3575E-01
	Std	1.3670E-01	1.1420E-01	5.7420E-01	5.2133E-01

| Show Table

DownLoad: CSV

4. Results

The results presented in Table 2 show the performance of the proposed mCOA compared to GA, PSO, and COA. It produced improvements for the GA, PSO, and COA on functions F1–F12. In these test functions, the mCOA produced the least values of the min, max, avg, and std, which indicates a better performance for minimization optimization problems, and represents ten (10) out of the thirteen (13) benchmark test functions tested. This represents an average performance of 76.92% on the test functions. For the cases of F6 and F13, the PSO outperformed the other algorithms, while the GA outperformed the other algorithms on F13.

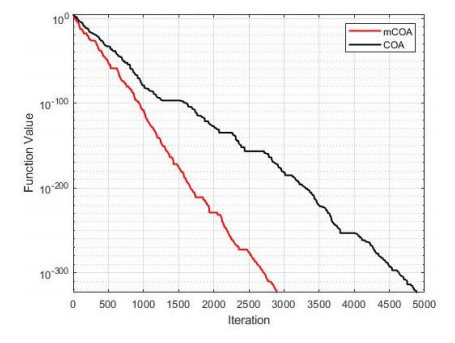
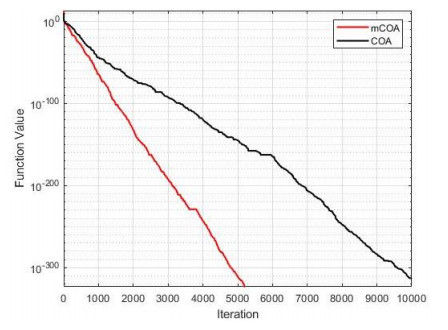
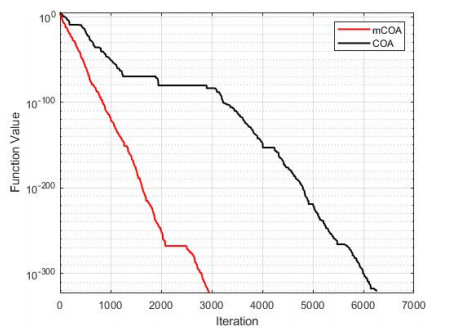
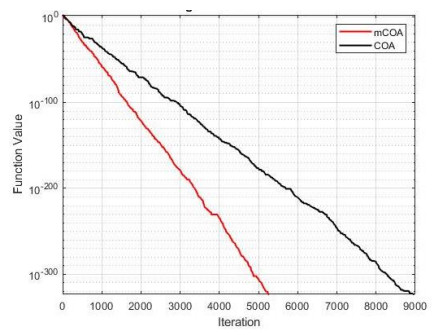
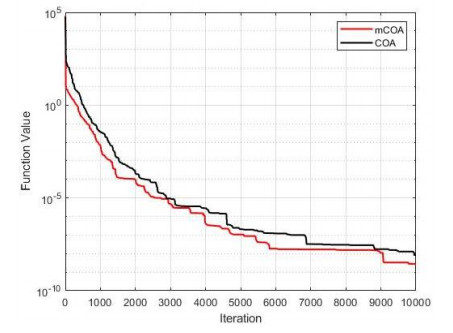
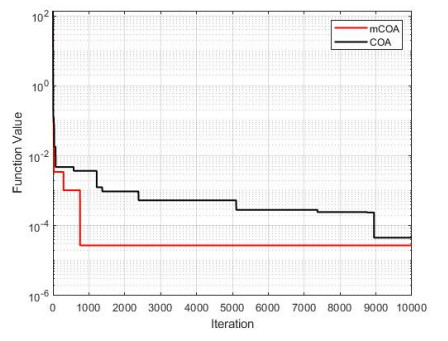
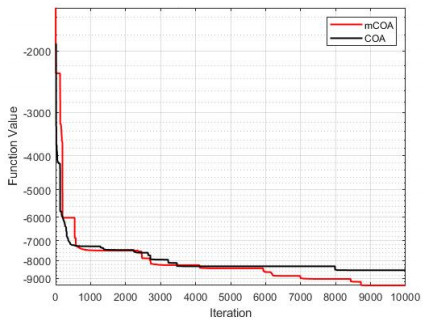
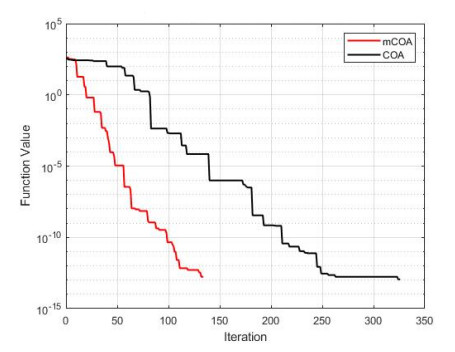
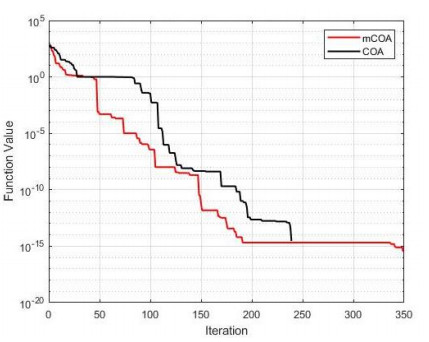
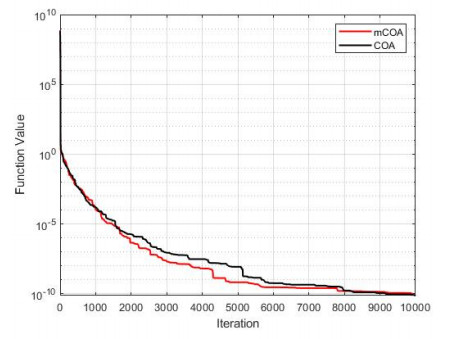
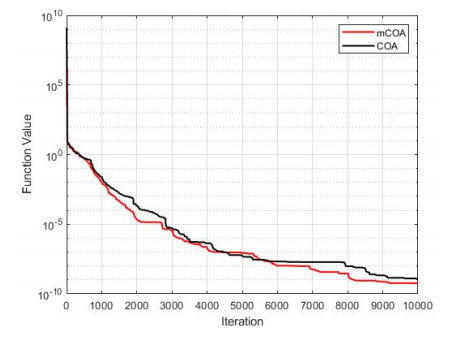
The convergence of the two algorithms is presented in Figures 1–13, which indicate the convergence process from the first iteration to the last iteration. This provides a clearer comparison of the performances of the two algorithms to effectively justify the superior performance of the mCOA over the COA.

Figure 1. Convergence characteristics of function F1.

DownLoad: Full-Size Img PowerPoint

Figure 2. Convergence characteristics of function F2.

DownLoad: Full-Size Img PowerPoint

Figure 3. Convergence characteristics of function F3.

DownLoad: Full-Size Img PowerPoint

Figure 4. Convergence characteristics of function F4.

DownLoad: Full-Size Img PowerPoint

Figure 5. Convergence characteristics of function F5.

DownLoad: Full-Size Img PowerPoint

Figure 6. Convergence characteristics of function F6.

DownLoad: Full-Size Img PowerPoint

Figure 7. Convergence characteristics of function F7.

DownLoad: Full-Size Img PowerPoint

Figure 8. Convergence characteristics of function F8.

DownLoad: Full-Size Img PowerPoint

Figure 9. Convergence characteristics of function F9.

DownLoad: Full-Size Img PowerPoint

Figure 10. Convergence characteristics of function F10.

DownLoad: Full-Size Img PowerPoint

Figure 11. Convergence characteristics of function F11.

DownLoad: Full-Size Img PowerPoint

Figure 12. Convergence characteristics of function F12.

DownLoad: Full-Size Img PowerPoint

Figure 13. Convergence characteristics of function F13.

DownLoad: Full-Size Img PowerPoint

In F1–F4, F7, F9, and F10, the mCOA has better convergence characteristics than the COA with a great margin. It starts performing better effectively from the initial iteration to the final iteration, thus producing a better final optimization value on these benchmark functions. In the cases of F6, F8, and F11–F13, the mCOA produced a slightly better convergence, on average, than the COA. The two algorithms, mCOA and COA, produced fast convergences in F5.

5. Conclusions

A modification of the COA was developed to improve its global performance by incorporating an adaptive sigmoid inertia weight-based technique in the exploration phase. The mCOA was tested on the same 13 standard benchmark test functions used for the original COA. The simulation outcome using the MATLAB software was compared to that of the COA, PSO algorithm, and the GA. The mCOA outperformed the other algorithms on most of the test functions, with a score of 10 out of the 13 functions, while maintaining a competitive performance on the other 3 test functions. Therefore, an enhanced version of the COA was developed for a better global performance. Based on the exceptional simulation performance of the mCOA, it is recommended for applications in real-life optimization problems, especially in the field of engineering without any reservation.

All tests were obtained by Matlab software publicly available in https://github.com/etwumasi/code_appendix.

Conflict of interest

All authors declare no conflict of interest regarding the publication of this paper.

References

[1]	K. S. Miller, B. Ross, An Introduction to the Fractional Calculus and Fractional Differential Equations, Wiley and Sons, New York, 1993.
[2]	Z. L. Wei, Q. D. Li, J. L. Che, Initial value problems for fractional differential equations involving Riemann-Liouville sequential fractional derivative, J. Math. Anal. Appl., 367 (2010), 260-272.
[3]	B. Ahmad, R. Luca, Existence of solutions for a sequential fractional integro-differential system with coupled integral boundary conditions, Chaos Soliton. Fract., 104 (2017), 378-388.
[4]	B. Ahmad, J. J. Nieto, Sequential fractional differential equations with three-point boundary conditions, Comput. Math. Appl., 64 (2012), 3046-3052.
[5]	B. Ahmad, J. J. Nieto, Boundary value problems for a class of sequential integrodifferential equations of fractional order, J. Funct. Space. Appl., 2013 (2013), 1-8.
[6]	B. Ahmad, S. K. Ntouyas, Existence results for a coupled system of Caputo type sequential fractional differential equations with nonlocal integral boundary conditions, Appl. Math. Comput., 266 (2015), 615-622.
[7]	Y. Chen, X. H. Tang, Solvability of sequential fractional order multi-point boundary value problems at resonance, Appl. Math. Comput., 218 (2012), 7638-7648.
[8]	Q. D. Li, H. Su, Z. L. Wei, Existence and uniqueness result for a class of sequential fractional differential equations, J. Appl. Math. Comput., 38 (2012), 641-652.
[9]	C. Promsakon, N. Phuangthong, S. K. Ntouyas, et al. Nonlinear sequential Riemann-Liouville and Caputo fractional differential equations with generalized fractional integral conditions, Adv. Differ. Equ., 2018 (2018), 1-17.
[10]	H. Ye, R. Huang, Initial value problem for nonlinear fractional differential equations with sequential fractional derivative, Adv. Differ. Equ., 2015 (2015), 1-13.
[11]	H. Ye, R. Huang, On the nonlinear fractional differential equations with Caputo sequential fractional derivative, Adv. Math. Phys., 2015 (2015), 1-9.
[12]	O. Abu Arqub, Application of residual power series method for the solution of time-fractional Schrödinger equations in one-dimensional space, Fundam. Inf., 166 (2019), 87-110.
[13]	O. Abu Arqub, Numerical algorithm for the solutions of fractional order systems of Dirichlet function types with comparative analysis, Fundam. Inf., 166 (2019), 111-137.
[14]	O. Abu Arqub, N. Shawagfeh, Application of reproducing kernel algorithm for solving Dirichlet time-fractional diffusion-Gordon types equations in porous media, J. Porous Med., 22 (2019), 411-434.
[15]	A. M. A. El-Sayed, H. H. G. Hashem, E. A. A. Ziada, Picard and Adomian decomposition methods for a quadratic integral equation of fractional order, Comput. Appl. Math., 33 (2014), 95-109.
[16]	A. Lotfi, S. A. Yousefi, A numerical technique for solving a class of fractional variational problems, J. Comput. Appl. Math., 237 (2013), 633-643.
[17]	P. Chen, Y. Li, Monotone iterative technique for a class of semilinear evolution equations with nonlocal conditions, Results Math., 63 (2013), 731-744.
[18]	H. D. Gou, Y. X. Li, Upper and lower solution method for Hilfer fractional evolution equations with nonlocal conditions, Bound. Value Probl., 2019 (2019), 1-25.
[19]	C. Hu, B. Liu, S. Xie, Monotone iterative solutions for nonlinear boundary value problems of fractional differential equations with deviating arguments, Appl. Math. Comput., 222 (2013), 72-81.
[20]	F. A. Mcrae, Monotone iterative technique and existence results for fractional differential equations, Nonlinear Anal., 71 (2009), 6093-6096.
[21]	J. Mu, Y. Li, Monotone interactive technique for impulsive fractional evolution equations, J. Inequal. Appl., 2011 (2011), 1-12.
[22]	G. Wang, Monotone iterative technique for boundary value problems of a nonlinear fractional differential equation with deviating arguments, J. Comput. Appl. Math., 236 (2012), 2425-2430.
[23]	L. Zhang, B. Ahmad, G. Wang, Explicit iterations and extremal solutions for fractional differential equation with nonlinear integral boundary conditions, Appl. Math. Comput., 268 (2015), 338-392.
[24]	C. Z. Bai, Impulsive periodic boundary value problems for fractional differential equation involving Riemann-Liouville sequential fractional derivative, J. Math. Anal. Appl., 384 (2011), 211-231.
[25]	R. Khalil, M. Al-Horani, A. Yousef, et al. A new definition of fractional derivative, J. Comput. Appl. Math., 264 (2014), 65-70.
[26]	T. Abdeljawad, On conformable fractional calculus, J. Comput. Appl. Math., 279 (2015), 57-66.
[27]	D. Zhao, M. Luo, General conformable fractional derivative and its physical interpretation, Calcolo, 54 (2017), 903-917.
[28]	D. R. Anderson, D. J. Ulness, Properties of the Katugampola fractional derivative with potential application in quantum mechanics, J. Math. Phys., 56 (2015), 1-15.
[29]	D. Zhao, X. Pan, M. Luo, A new framework for multivariate general conformable fractional calculus and potential applications, Phys. A, 15 (2018), 271-280.
[30]	S. Yang, L. Wang, S. Q. Zhang, Conformable derivative: application to non-Darcian flow in lowpermeability porous media, Appl. Math. Lett., 79 (2018), 105-110.
[31]	H. W. Zhou, S. Yang, S. Q. Zhang, Conformable derivative approach to anomalous diffusion, Phys. A, 491 (2018), 1001-1013.
[32]	M. Al-Refai, T. Abdeljawad, Fundamental results of conformable Sturm-Liouville eigenvalue problems, Complexity, 2017 (2017), 1-7.
[33]	S. Asawasamrit, S. K. Ntouyas, P. Thiramanus, et al. Periodic boundary value problems for impulsive conformable fractional integro-differential equations, Bound. Value Probl., 2016 (2016), 1-18.
[34]	H. Batarfi, J. Losada, J. J. Nieto, et al. Three-point boundary value problems for conformable fractional differential equations, J. Funct. Space., 2015 (2015), 1-6.
[35]	B. Bayour, D. F. M. Torres, Existence of solution to a local fractional nonlinear differential equation, J. Comput. Appl. Math., 312 (2017), 127-133.
[36]	M. Bouaouid, M. Hannabou, K. Hilal, Nonlocal conformable fractional differential equations with a measure of noncompactness in Banach spaces, J. Math., 2020 (2020), 1-6.
[37]	L. M. Feng, S. R. Sun, Oscillation theorems for three classes of conformable fractional differential equations, Adv. Differ. Equ., 2019 (2019), 1-30.
[38]	A. Jaiswal, D. Bahuguna, Semilinear conformable fractional differential equations in Banach spaces, Differ. Equ. Dyn. Syst., 27 (2019), 313-325.
[39]	M. M. Li, J. R. Wang, D. O'Regan, Existence and Ulam's stability for conformable fractional differential equations with constant coefficients, Bull. Malays. Math. Sci. Soc., 42 (2019), 1791-1812.
[40]	S. M. Meng, Y. J. Cui, Multiplicity results to a conformable fractional differential equations involving integral boundary condition, Complexity, 2019 (2019), 1-8.
[41]	E. Ünal, A. Gökdoğan, Solution of conformable fractional ordinary differential equations via differential transform method, Optik, 128 (2017), 264-273.
[42]	J. F. Wang, C. Z. Bai, Antiperiodic boundary value problems for impulsive fractional functional differential equations via conformable derivative, J. Funct. Space., 2018 (2018), 1-11.
[43]	W. Y. Zhong, L. F. Wang, Positive solutions of conformable fractional differential equations with integral boundary conditions, Bound. Value Probl., 2018 (2018), 1-12.
[44]	W. Y. Zhong, L. F. Wang, Basic theory of initial value problems of conformable fractional differential equations, Adv. Differ. Equ., 2018 (2018), 1-14.
[45]	K. Deimling, Nonlinear Functional Analysis, Springer-Verlag, New York, 1985.
[46]	T. Cardinali, R. Precup, P. Rubbioni, A unified existence theory for evolution equations and systems under nonlocal conditions, J. Math. Anal. Appl., 432(2015), 1039-1057.
[47]	H. P. Heinz, On the behaviour of measure of noncompactness with respect to differentiation and integration of vector-valued functions, Nonlinear Anal., 7 (1983), 1351-1371.
[48]	D. O'Regan, R. Precup, Existence criteria for integral equations in Banach spaces, J. Inequal. Appl., 6 (2001), 77-97.

This article has been cited by:

1.	Cristina Ortega-Rodríguez, Julio Vena-Oya, Jesús Barreal, Barbara Józefowicz, How to finance sustainable tourism: Factors influencing the attitude and willingness to pay green taxes among university students, 2024, 6, 2643-1092, 649, 10.3934/GF.2024025
2.	Isaac Ankrah, Michael Appiah-Kubi, Eric Ofosu Antwi, Ivy Drafor Amenyah, Mohammed Musah, Frank Gyimah Sackey, Richard Asravor, Isaiah Sikayena, A spotlight on fossil fuel lobby and energy transition possibilities in emerging oil-producing economies, 2025, 11, 24058440, e41287, 10.1016/j.heliyon.2024.e41287
3.	Mustafa Raza Rabbani, Madiha Kiran, Zakir Hossen Shaikh, Financing the future: insights into sustainable energy investments through scientific mapping and meta-analysis, 2025, 6, 2662-9984, 10.1007/s43621-024-00788-0
4.	Yu-Wei Lin, Yu-Ting Liu, Li-Cheng Huang, Shing-Chou Lin, Shean-Jen Chen, YongMan Choi, Biomass energy for a sustainable Taiwan: Technologies, policies, and future prospects, 2025, 199, 09619534, 107969, 10.1016/j.biombioe.2025.107969

Reader Comments

Your name:*

Email:*
© 2020 the Author(s), licensee AIMS Press. This is an open access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0)

通讯作者: 陈斌, bchen63@163.com

1.
沈阳化工大学材料科学与工程学院沈阳 110142

AIMS Mathematics

1.8 3.4

Metrics

Article views(3946) PDF downloads(184) Cited by(9)

Preview PDF

Download XML

Export Citation

Article outline

Show full outline

AIMS Mathematics

Periodic boundary value problem involving sequential fractional derivatives in Banach space

Related Papers:

Abstract

1. Introduction

2. Adaptive sigmoid increasing inertia weight-based modification of COA

2.1. The original coot optimization algorithm

2.2. Proposed modification

3. Simulation test setup on benchmark functions

4. Results

5. Conclusions

Conflict of interest

References

This article has been cited by:

Reader Comments

通讯作者: 陈斌, bchen63@163.com

Metrics

Other Articles By Authors

Catalog

AIMS Mathematics

Periodic boundary value problem involving sequential fractional derivatives in Banach space

Related Papers:

Abstract

1. Introduction

2. Adaptive sigmoid increasing inertia weight-based modification of COA

2.1. The original coot optimization algorithm

2.2. Proposed modification

3. Simulation test setup on benchmark functions

4. Results

5. Conclusions

Conflict of interest

References

This article has been cited by:

Reader Comments

通讯作者: 陈斌, bchen63@163.com

Metrics

Other Articles By Authors

Related pages

Tools

Export File

Citation

Format

Content

Catalog