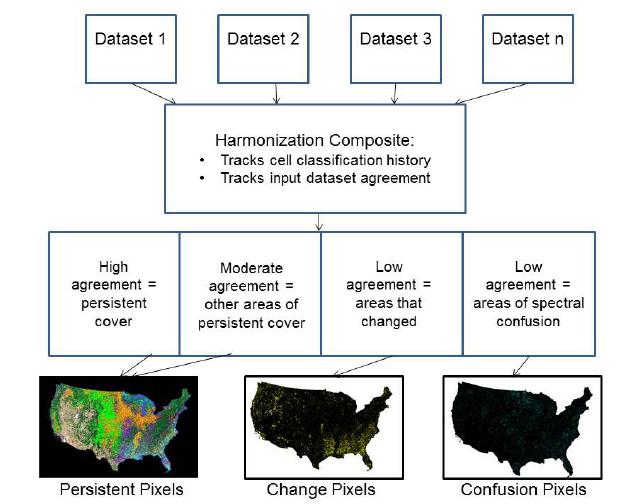
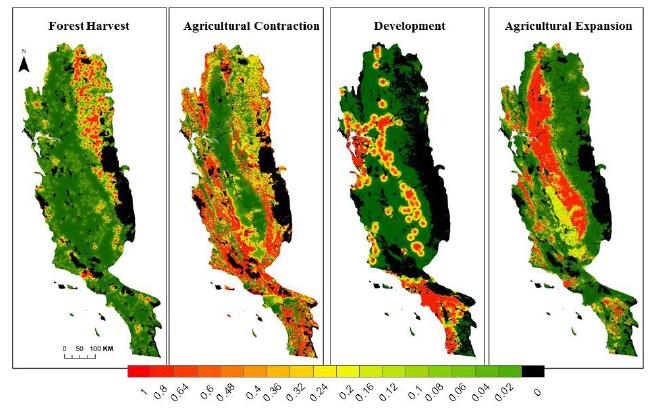
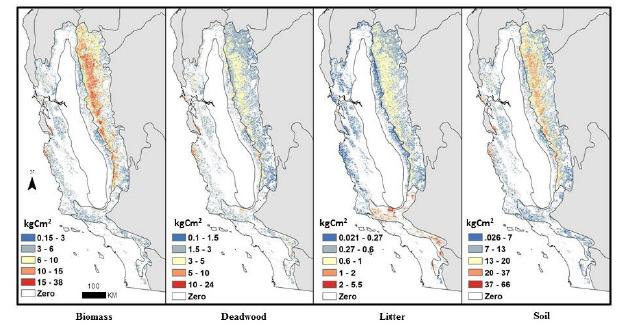
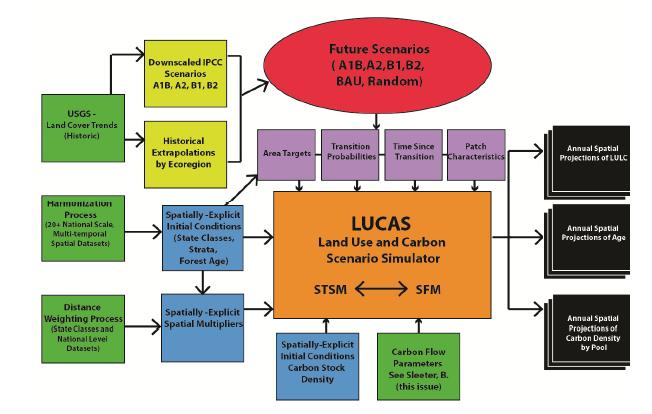
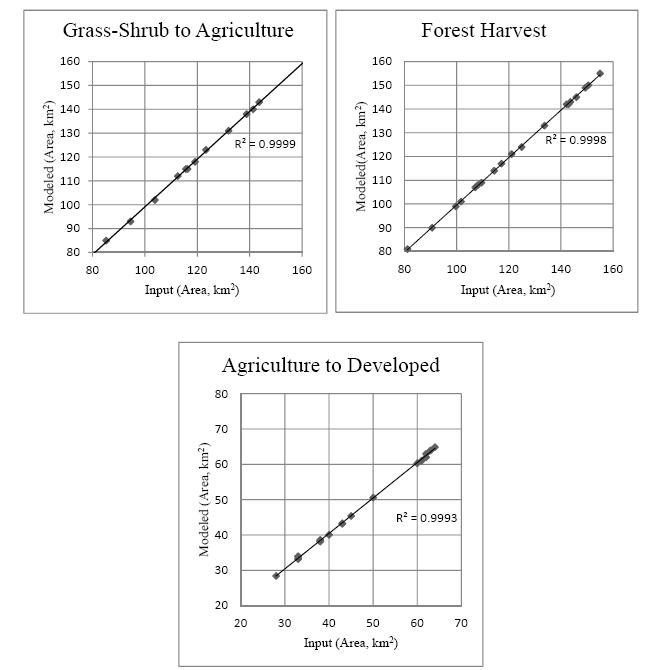
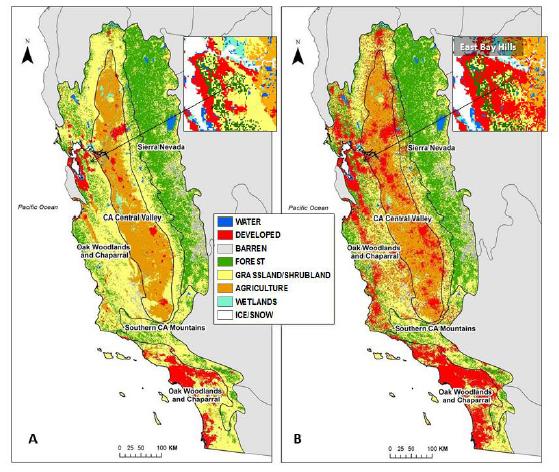
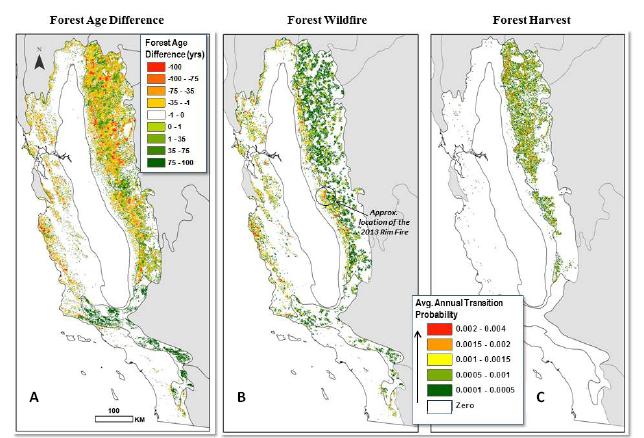
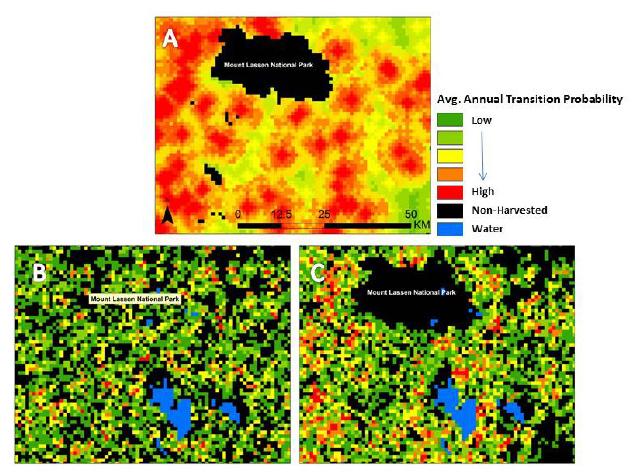
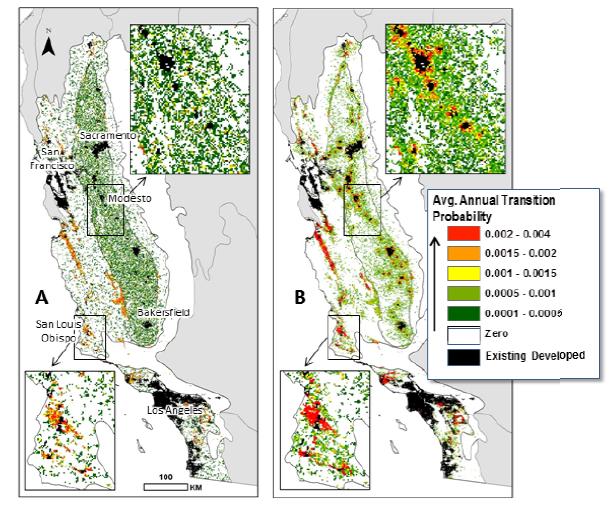
Spatially-explicit state-and-transition simulation models of land use and land cover (LULC) increase our ability to assess regional landscape characteristics and associated carbon dynamics across multiple scenarios. By characterizing appropriate spatial attributes such as forest age and land-use distribution, a state-and-transition model can more effectively simulate the pattern and spread of LULC changes. This manuscript describes the methods and input parameters of the Land Use and Carbon Scenario Simulator (LUCAS), a customized state-and-transition simulation model utilized to assess the relative impacts of LULC on carbon stocks for the conterminous U.S. The methods and input parameters are spatially explicit and describe initial conditions (strata, state classes and forest age), spatial multipliers, and carbon stock density. Initial conditions were derived from harmonization of multi-temporal data characterizing changes in land use as well as land cover. Harmonization combines numerous national-level datasets through a cell-based data fusion process to generate maps of primary LULC categories. Forest age was parameterized using data from the North American Carbon Program and spatially-explicit maps showing the locations of past disturbances (i.e. wildfire and harvest). Spatial multipliers were developed to spatially constrain the location of future LULC transitions. Based on distance-decay theory, maps were generated to guide the placement of changes related to forest harvest, agricultural intensification/extensification, and urbanization. We analyze the spatially-explicit input parameters with a sensitivity analysis, by showing how LUCAS responds to variations in the model input. This manuscript uses Mediterranean California as a regional subset to highlight local to regional aspects of land change, which demonstrates the utility of LUCAS at many scales and applications.
1.
Introduction
Among all the organs in the human body, eyes offer the most sensational feeling which provides us with the scope to praise the beauty and to communicate with others through visual expression. Clear vision plays a vital role in our life. However, due to different eye diseases, sometimes it becomes crucial to maintain a healthy vision. That is why it is important to test different eye components regularly. Amongst diverse components, the retina is the most important ingredient which can exhibit the symptoms of most of the optical disorders. Different morphological properties of retinal blood vessels including branching pattern, length, tortuosity, angular features, and diameter are the basic observation area to detect any eye disease. Study [1] shows that hypertension can be classified by narrow arterioles with bright reflexes. Cardiovascular disease and diabetic retinopathy can be diagnosed by bifurcation angles and tortuosity information.
Accurate blood vessel segmentation is important as well as a challenging task for determining early vision problems. However, different branching patterns, bad contrast, low image resolution make the blood vessel segmentation problem cumbersome. Besides, ill-defined optic disk as well as the random number of the hemorrhage, cotton wool spots, and microaneurysms create noises that lead to false-positive detection. Moreover, it is more troublesome to identify the thin vessels from the background image. Bifurcation, central light reflex, arbitrary branch crossings, contrast variation in the vessel maps are usually the general causes for the failure of the complete isolation of retinal blood vessels from color fundus image.
Matched Filtering [2] methodology based on the characteristics of the blood vessel was the first significant achievement in the field of retinal blood vessel segmentation. Next, the idea of multi-scale approach [3] was developed using a scale-space analysis of the maximum principal curvature. Later on, utilizing morphological reconstruction and vessel centerline detection, the strategy of morphological processing based solution was proposed [4]. Moreover, Machine learning-based techniques were also applied to isolate the vessel tree where a handcrafted feature vector is formed before passed it to a suitable classifier. Nowadays, deep learning-based techniques [5] are dominating this vessel segmentation application akin to most of the segmentation and classification tasks in computer vision.
Wavelet-based methods have already proved their effectiveness in many applications including image denoising, compression, texture analysis, and edge detection. Gabor wavelet, Curvelets [6], Contourlets [7], Shearlets [8] are commonly employed to detect curved like structures which are already applied by many researchers in the application of retinal vessel segmentation. Bendlets [9] is the recent addition to the family of wavelet-based multiscale directional transform technique which can capture curvatures with fewer coefficient values than others.
This paper presents an efficient and robust retinal blood vessel segmentation technique utilizing the new multiscale directional transform methodology named Bendlets. Firstly, some preprocessing steps have been followed to reduce some false outcomes as well as make it suitable for the feature extraction stage. Secondly, in order to enhance the contrast of the input image morphological top-hat and bottom-hat transform are employed which helps to detect the thin vessels more effectively. Thirdly, Bendlet transform is applied on different scales to construct a robust feature vector. Fourthly, a small group of ensemble classifiers is analyzed to find out the most satisfactory classifier. Finally, to improve the accuracy a little bit more, a post-processing step is carried out to fulfill the probable gaps inside the vessel as well as remove the isolated false candidates.
2.
Literature review
The intensity profile along the cross-section of a retinal blood vessel has the Gaussian-shaped curve. Chaudhuri et al. [2] applied a 2-D Gaussian kernel for separating blood vessels from the background. Based on this concept of matched filtering, Hoover et al. [10] designed a piecewise threshold probing algorithm considering some region-based properties. Zhang et al. [11] proposed a combination of zero-mean Gaussian and first-order derivative of the Gaussian filter which resolves some of the limitations of previous methods. Another variation proposed by Odstrcilik et al. [12] where illumination correction and contrast equalization were performed before matched filtering. Chakraborti et al. [13] improved the concept of matched filtering by incorporating orientation histogram and a vesselness filter.
Martinez-Perez et al. [3] started the idea of applying the multi-scale approach in detecting vessel from the background image by using gradient magnitude and maximum principal curvature. Vlachos and Dermatas [14] developed a multi-scale line tracking program from different vessel properties. Nguyen et al. [15] proposed a multi-scale line detection method where the response from eight different scale values is linearly combined to get the final vessel map. In another work, Yanli Hou [16] presented a vessel tree extraction process by utilizing a multi-scale top-hat transform and multi-scale line detection algorithm. Yue et al. [17] made a little optimization in the work of [15] where the improved multi-scale line detector chooses the maximum line response from the available multi-scale windows.
Mendonca and Campilho [4] established the concept of segmenting blood vessels by means of several morphological filters such as multi-scale top-hat transform, region growing process, and multi-scale morphological vessel reconstruction. Miri and Mahloojifar [18] applied connected component analysis and multi-structure elements morphology by reconstruction after using curvelet transform for retinal vessel enhancement. Fraz et al. [19] developed another unique blood vessel segmentation technique where the multidirectional morphological top-hat transform is utilized to enhance the image and morphological bit plane slicing is employed to segment the vessel map. By using morphological component analysis Imani et al. [20] designed another method with combining Morlet wavelet transform and adaptive thresholding. Gao et al. [21] presented an efficient procedure for the vessel segmentation which includes automatic random walks based on centerline extraction.
Pattern classification based methods are more popular than previous approaches. Ricci and Perfetti [22] made a framework using a support vector machine (SVM) where the features are generated from line detectors based on the average grey-level value of the retinal image. Martin et al. [23] assembled a 7-D feature vector for each pixel representation comprised of moment invariants and grey-level features which are trained by neural network classifier. On the other hand, Fan et al. [24] executed a random forest classifier where the feature vector of each candidate pixel is formed from integral channel features.
Although local image feature-based machine learning approaches are satisfactory enough, the feature vector composed of wavelet-based methods is more robust in terms of accuracy. Soares et al. [25] developed the feature vector from a 2-D Morlet wavelet transform and trained it by a Gaussian mixture model classifier. Xu et al. [26] included wavelet and curvelet transform technique to obtain a 12-D feature vector that is trained by SVM. In another work, Fraz et al. [27] made a 9-D feature vector where four features are taken from the Gabor filter response at four different scales.
Ghadiri et al. [28] utilized Non-subsampled Contourlet Transform (NSCT) to extract the vessel tree from the retinal fundus image. Bankhead et al. [29] proposed a wavelet transform to detect the vessel map along with centerline refinement using spline fitting. Azzopardi et al. [30] developed a novel algorithm for vessel segmentation using COSFIRE (Combination of Shifted Filter Response) and DoG (Difference-of-Gaussians) filters. Moreover, Levet et al. [31] proposed applying Shearlet transform with the hysteresis threshold strategy to segment the blood vessel from the input image. Based on elite guided multi-objective artificial bee colony (EMOABC) technique Khomri et al. [32] designed another unsupervised method for retinal vessel segmentation for fundus images.
After the wave of deep learning, most of the applications related to computer vision and NLP are governed by various deep learning methods. R2U-Net [33] using U-Net and Recurrent Residual Convolutional Neural Network (RRCNN) is able to achieve around $ 97\% $ accuracy on the STARE dataset. A Graph Neural Network (GNN) [34] has been introduced to extract the vessel structure utilizing the local appearance and global structure of vessels. However, their performance is not superior as the average accuracy is $ 92.71\% $ and $ 93.78\% $ on DRIVE and STARE databases respectively. IterNet [36] is another deep learning model where multiple iterations of U-Net have been performed and the accuracy is slightly better than R2U-Net [33]. However, deep learning generally uses millions of parameters to learn the model with lots of training data as well as requires a heavy computational load whereas our proposed methodology uses only a limited number of filters which could run in any lightweight system. On the other hand, if the test sample comes from a different domain usually the deep learning-based trained model performs poorly in this case.
3.
Proposed method
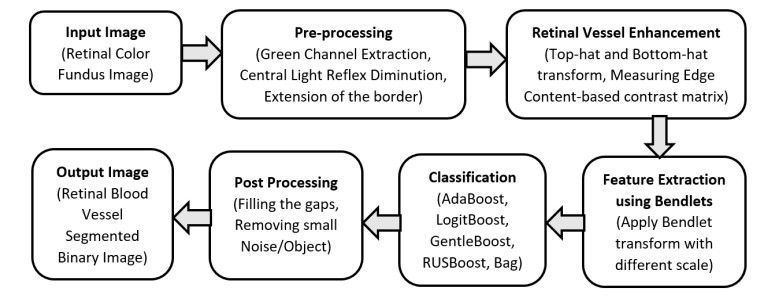
The proposed complete work flow for retinal blood vessel segmentation is illustrated in Figure 1 where the proposed method uses the following basic steps: (1) Pre-processing, (2) Retinal Vessel Enhancement, (3) Feature Extraction using Bendlets, (4) Classification, and (5) Post Processing.
3.1. Pre-processing
Retinal fundus images generally prone to noise, lighting variations, and poor contrast [23]. In order to obtain a better classification result the following actions are executed: (1) Green channel extraction, (2) Central light reflex diminution, and (3) Extension of the border.
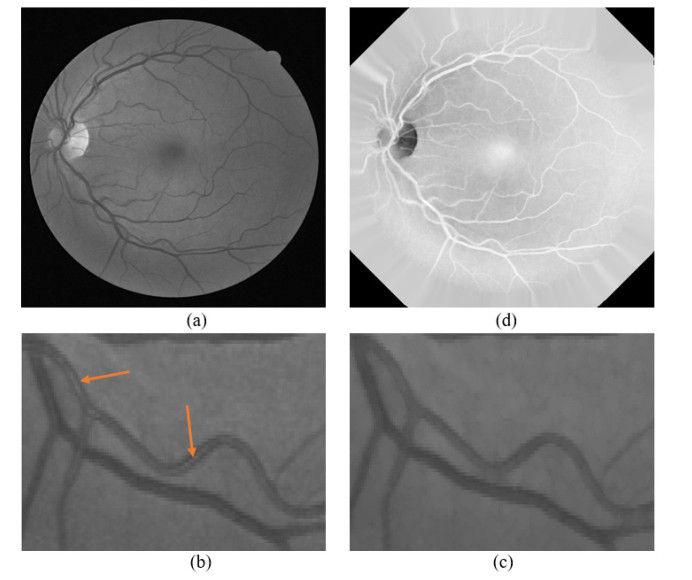
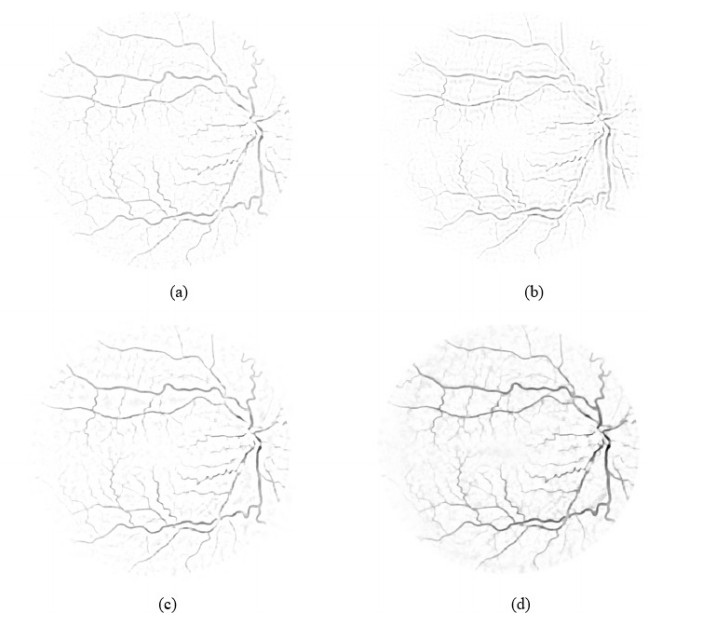
$ (1) $ Green Channel Extraction: The green channel provides the best view for blood vessels compared to other two channels [35]. For this reason, the conversion of RGB color image to Gray-scale image is performed by considering the green plane only, as shown in Figure 2(a).
$ (2) $ Central Light Reflex Diminution: Due to lighting variation, some blood vessels may contain a light streak through the central area of the blood vessel which is known as central light reflex. As a result, the middle portion of the vessel and the background become similar thus creates some false results. To eliminate this central light reflex morphological opening is employed with a two-pixel radius disk-shaped structuring element. The parameter of disk size is kept to the possible lowest value otherwise it could merge the nearest vessels. An example is shown in Figure 2(b), (c) where the effect of central light reflex and its elimination with the help of opening filtering operation is illustrated respectively.
$ (3) $ Extension of Border: The circular-shaped border of the inverted green channel image is expanded to take aside unenvied border effects by the algorithm used in [25]. Otherwise, the output image produces some false-positive results along the border area. Here, an iterative strategy has been followed where the mean value of the pixel’s neighbors inside the aperture is operated to replace the pixels outside the aperture. As a result, an artificially increasing area can be seen along the border, as shown in Figure 2(d).
3.2. Retinal vessel enhancement
The method designed by Kushol et al. [37,38] using morphological operators has been employed to enhance the contrast of the retinal image. At first, the original input image is added with the resultant image of the top-hat transform. Simultaneously, the outcome of the morphological bottom-hat is deducted from the initial image. Equation (3.1) expresses the morphological operations performed to enhance the contrast of the image.
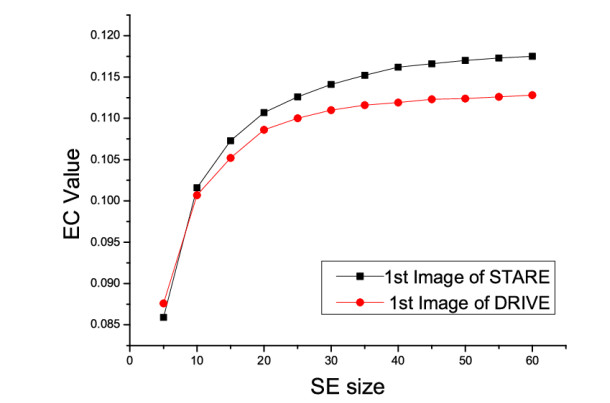
The major contribution of this work is the automatic selection of the structuring element (SE) by means of edge content (EC) based contrast matrix which is computed by the gradient magnitude value. The characteristics of EC with respect to SE is shown in Figure 3 where the graph indicates incrementing the value of SE also results in an increased value of EC at the beginning. However, after a certain period of iterations, the incrementing behavior stops and provides the best contrast-enhanced image.
3.3. Bendlets
Traditional wavelet-based methods can detect point singularities as well as they are useful for multiresolution and proper localization properties. However, they have weaknesses in the case of optimal edge representation. Since the elements are not highly anisotropic it could not yield optimal geometric structure or curved singularities. In order to obtain the curve singularities and hyperplane singularities in higher dimensions, Candes and Donoho first designed curvelet transform [6]. Curvelet elements can be constructed by a parabolic dilation or scale parameter $ a (0 < a < 1) $, a location or translation parameter $ t $, and an orientation $ \theta $ to a shaped function $ \psi $ as shown in Eqs (3.2) and (3.3):
Here, $ D_{a} $ is a parabolic scaling matrix and $ R_{\theta} $ is a rotation by $ \theta $ radians.
Another multiscale directional transform Shearlets also follows the basic principles of wavelets except the isotropic dilation is replaced by anisotropic dilation and shearing. One of the unique characteristics of shearlets is the use of shearing to control directional decision, in contrast to rotation practiced by curvelets. Shearlet elements can be represented by $ \psi_{a, s, t} $ where $ a, s, t $ are the dilation, shearing, and translation variable respectively and can be expressed by Eqs (3.4)–(3.6):
Here, $ A_{a} $ is a scaling (or dilation) matrix and $ S_{s} $ represents shear matrix.
Bendlets can be referred to an extended or second-order shearlet system considering bending as an extra parameter. The basic difference of bendlets compared to classical shearlets appears in $ \alpha $-scaling. If $ a > 0 $ and $ 0\leq \alpha < \infty $ the $ \alpha $-scaling operation is denoted by Eq (3.7):
Here, the variable $ \alpha $ expresses the scaling anisotropy. For instance, the value of $ \alpha = 1 $ indicates isotropic scaling whereas the value of $ \alpha = 1/2 $ means parabolic scaling, and $ \alpha = 0 $ leads to pure directional scaling. Bendlets can accurately determine direction, location, and curvature of a discontinuity curve with an anisotropic scaling of $ 1/3 < \alpha < 1/2 $.
For $ l \quad \varepsilon \quad \mathbb{N} $ and $ r = (r_1, ...., r_l) ^T \varepsilon \quad \mathbb{R}^l $ the $ l – th $ order shearing operator $ S_r^{(l)} \colon \mathbb{R}^2 \rightarrow \mathbb{R}^2 $ is represented by Eq (3.8):
Here, for $ l = 1 $ generates an typical shearing matrix and for $ l = 2 $ the operator contains the characteristics of both shearing and bending.
If $ \psi \quad \varepsilon \quad L^2 (\mathbb{R}^2), l \quad \varepsilon \quad \mathbb{N}, \alpha > 0. $ then a unitary expression of the higher-order shearlet groups $ \mathbb{S}(l, \alpha) $ have the natural representation shown in Eq (3.9):
The parameters $ a, s, $ and $ t $ indicate scale, shear (orientation), and location variable respectively. So, the $ l – th $ order $ \alpha $ –shearlet system is denoted as Eq (3.10):
When $ l = 2 $, the above equation is considered as second-order shearlet transform or bendlet transform. So the bendlet system can be expressed as Eq (3.11) where $ b $ takes the role of bending as an extra parameter.
Bendlets are different from other directional multiscale transforms because of this extra bending parameter which helps to detect curve singularities more efficiently. The shape of bendlet atoms or elements varies according to different parameter values which are depicted in Figure 4 to Figgure 7. In Figure 4(a), Figure 6(b), (c), and Figure 7(a) coefficient values are close to zero because a small amount of edge energy is included in bendlet area. In Figure 4(c), Figure 5(c), and Figure 7(b) bendlet coefficients are moderately high because of the large area of edge energy are enclosed in bendlet. The coefficient response from Figure 6(a) is very high due to entire bendlet frame is enclosed with the edge energy.
In the case of blood vessel segmentation from the retinal fundus image, the aim is to extract vessel-like structure. As we can see from a retinal image, the most occupied region of the image is taken by vessels and they usually do not follow any specific direction. All the time the vessels are changing their direction abruptly and form curved like edge throughout the whole image. Traditional directional wavelets can detect these types of curvature with their elements coefficient response value. As the shape of these elements is a square-like structure, it requires a huge amount of coefficient response to fully capture all the vessels as well as increases the noise inside the image. On the other hand, curvelet and shearlet transform create parabolic rectangular-shaped element according to the parabolic scaling principle $ length^2 \sim width $. As a result, few coefficients are required to fully detect the vessels of an image. Further reduction is possible in the number of coefficients with Bendlets where shearlet elements are bent in different directions by adding one extra parameter bending b. One comparison among traditional wavelets, curvelets, and Bendlets with the number of elements required to capture a little amount of vessel-like region is shown in Figure 8 where we can see wavelet needs around 15 coefficient values, curvelet needs 5 coefficient values and bendlet requires only 3 coefficient values to fully detect the curved region.
3.4. Feature extraction using Bendlets
After applying the bendlet transform, soft thresholding is performed on the coefficient values to retain the large response of the image. Because of the curve like the structure of the bendlet elements, a high response is produced whenever the process finds any vessel-related shape. For different scale values, different reconstructed output images can be obtained by utilizing bendlet transform. However, the scale value of 3, 4, and 5 generate significantly accurate output while reducing unnecessary noise from the background image. Finally, a feature vector of size four is constructed with three different aforementioned scale values of bendlet and another one is taken by subtracting the background from the enhanced image using an averaging filter of size $ 10 \times 10 $. These four features can be expressed in Eqs (3.12)–(3.15):
Here, $ I_{sub} (x, y) $ is the pixel value obtained by subtracting the original enhanced image with average filtered image and $ I_{bendlet} (x, y) $ is the reconstructed image with modified bendlet coefficient values for a given scale information. The individual output for each of these features is shown in Figure 9.
3.5. Classification
In the feature development stage, each pixel from an input image is characterized by a vector in a 4-D feature space as Eq (3.16):
The purpose of classification stage is to assign one candidate pixel to either $ C_v (vessel) $ or $ C_nv(non-vessel) $ class. An efficient and frequently used method in machine learning is ensemble classifiers that combine multiple individual learning models to yield an agammaegate model. The major advantage of an ensemble classifier is having the ability to avoid the mistakes of a single classification model. In a given data set, one individual learning model may result in an over-fitting problem in a specific portion of the data whereas another model can overcome this limitation thus increasing the prediction performance. Moreover, there are mainly two types of ensemble models which are Bagging (subsampling the training data) and Boosting (re-learning with different weights on misclassified instances).
● Bagging (Bootstrap Agammaegation):
To reduce the problem of overfitting as well as variance the Bagging or Bootstrap agammaegation of sample data can be used primarily. However, the Bagging concept is mostly applied in decision tree methods. Each weak learner in Bootstrap agammaegation contains equal weight and it trains individual models from the training set by randomly selecting a subset. For instance, to achieve high accuracy in terms of classification performance the random forest method combines random decision trees with bagging.
● Boosting:
Boosting is a weighted average approach that can be utilized for mitigating bias as well as variance. Boosting algorithms are formed by multiple weak learners which are combined to become a final powerful learner. The weight of each weak learner is recalculated in order to overcome the problem of increased weight from the misclassification result. From the knowledge of previous mislabeled classifiers, the Boosting algorithms generally assemble the learners sequentially. Basically, the overall classification performance can be enhanced by weighing earlier mislabeled examples with higher weight.
Among established Ensemble-agammaegation methods, we have experimented five prominent classifiers. They are AdaBoostM1, LogitBoost, GentleBoost, RUSBoost, and Bag. The Decision Tree type weak learner is used in the ensemble process where the number of ensemble learning cycles is 200.
3.6. Post processing
The resultant image acquired from the classification stage exhibits two common pitfalls. Firstly, the vessel map may contain a few discontinuous line segments due to some obstacles. Secondly, some isolated points could arise because of some pathological objects. The following two steps will solve these predicaments as much as possible and enhance the accuracy a little bit.
3.6.1. Filling the gap inside vessel map
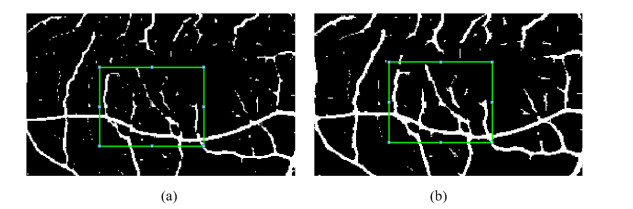
After performing the classification process, some broken vessel segments can be observed which reduces the accuracy of the outcome. To link the broken segments along the vessel pixels, a multiscale line detection algorithm is applied. A window size of $ 15 * 15 $ is considered for each pixel position where 12 lines of length $ L $ are oriented at 12 distinct orientations (with an interval of $ 15^0 $). Three different values 7, 11, and 15 are taken for the value of $ L $ which are linearly combined as proposed in Nguyen et al. [15] to yield the connected vessel tree. Figure 10 depicts the performance of before taking advantage of the line detection scheme and after employing the algorithm.
3.6.2. Irrelevant noise removal
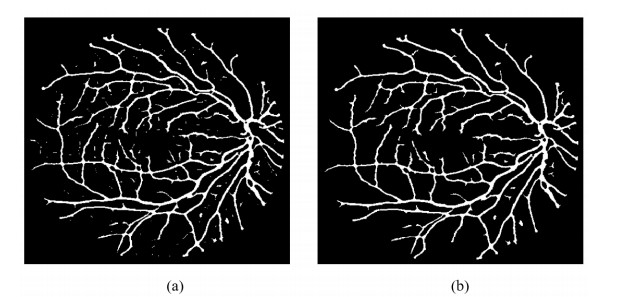
Here, the area of each connected region is measured with the help of morphological area open operation. The accumulation of pixels connected will be removed from the final output if the value of that region is beneath 40 pixels. One sample output after executing the area open operation is given in Figure 11.
4.
Experimental analysis
The proposed method doesn’t require any heavy computational power. The implementation of the proposed idea has been performed in MATLAB R2015a by @2.20 GHz processor consist of 8.00 GB RAM and without any GPU involvement. Two openly accessible benchmark databases are utilized which are DRIVE [39] and STARE [10] database to assess the algorithmic performance of the proposed approach. Moreover, to demonstrate the robustness of our approach a comparative analysis has been incorporated in the latter part of this section.
4.1. Data set
The DRIVE (Digital Retinal Images for Vessel Extraction) dataset has been formulated from a diabetic retinopathy diagnosis program of 400 subjects. With the help of medical experts, 40 ground truth images are created where the first half of the pictures are selected as test subjects and the remaining half of the photographs are chosen for training purposes. On the other hand, the development of the database STARE (STructured Analysis of the Retina) is performed at the University of California. It consists of 20 retinal color photos where two sets of ground truth are designed by two different pathological experts. Here, the first $ 50\% $ of the images are acknowledged as the training set and the later $ 50\% $ of the pictures are recognized as test data in our experiment. The overall summary of the aforementioned two datasets is represented in Table 1.
4.2. Performance Measures
Four types of scenarios can be observed in a two class categorization problem. They are:
(1) True Positive (TP): correct identification
(2) True Negative (TN): correct rejection
(3) False Positive (FP): incorrect identification
(4) False Negative (FN): incorrect rejection
The fundamental statistical measures Sensitivity (recall), Specificity (true negative rate), Precision (positive predictive value), and Accuracy are evaluated to assess the binary classification performance based on these scenarios. In healthcare diagnosis, sensitivity (true positive rate or recall), is the correct identification of samples with the disease whereas specificity (true negative rate) is the correct identification of samples without the disease. Precision (Positive Predictive Value) is the amount of identified items that are relevant and high precision means that an algorithm returned substantially more relevant results than irrelevant. The Accuracy is the fraction of the total number of truly identified pixels and the number of pixels present in the FOV. Sensitivity (Sn), Specificity (Sp), Precision (Pr), and Accuracy (Acc) are measured by Eqs (4.1)–(4.4) respectively.
Table 2 shows the relationship of vessel classification with the above mentioned four events.
4.3. Performance method evaluation
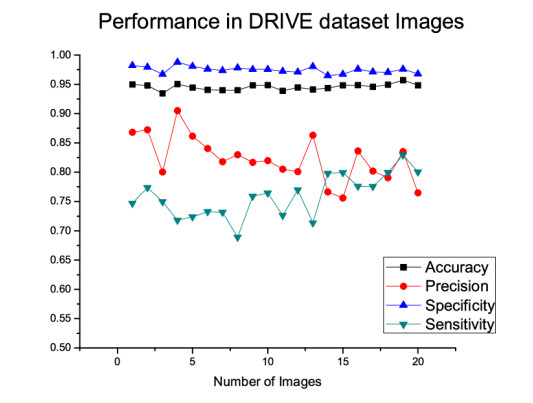
Firstly, the proposed method is assessed by the images of DRIVE database. In the first part of the evaluation, the algorithm is trained by the 20 train set images with 5 established aforementioned ensemble classifiers. Next, a similar feature vector is also designed for the test set images and applied for the classification result with trained data. All ensemble classifiers produce almost similar results in terms of sensitivity, specificity, precision, and accuracy. However, AdaBoost slightly outperforms among other classifiers, and for that reason, the individual performance measures of each of the images of DRIVE dataset represented in Figure 12 is based on the outcome of the AdaBoost classifier. The average sensitivity, specificity, precision, and accuracy achieved in this database are 0.7588, 0.9748, 0.8226, and 0.9456 respectively.
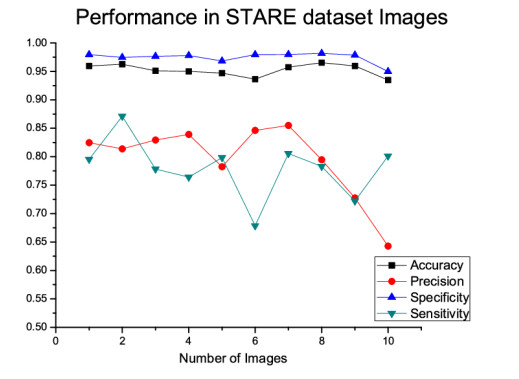
Secondly, the same approach is also performed in the case of STARE dataset where the average sensitivity, specificity, precision, and accuracy achieved are 0.7798, 0.9746, 0.7956, and 0.9528 respectively. The detailed result of the individual image is represented in Figure 13.
4.4. Comparison of segmentation results with different ensemble classifiers
A bunch of ensemble classifier is experimented to find the most accurate result of the blood vessel segmentation. They are AdaBoost, LogitBoost, GentleBoost, RUSBoost, and Bag. Table 3 depicts the complete result of these classifiers based on Average Sn, Sp, Pr, and Acc on DRIVE and STARE database. RUSBoost achieves the highest score on both datasets for Sensitivity whereas AdaBoost and LogitBoost receive the best rate for Specificity and Precision on STARE and DRIVE respectively. Overall, considering the performance of Accuracy AdaBoost clearly outweighs other classifiers in our application and thus employed in our final evaluation assessment.
4.5. Comparison to other methods
Our proposed model is also compared with some auspicious existing works. The comparison of our methodology to other recent methods is shown in Tables 4 and 5 for DRIVE and STARE databases respectively. For a better comparison view, the list is grouped according to the categorization of the literature review section with the ascending order of the publication year. Average Sensitivity (Sn), Specificity (Sp), and Accuracy (Acc) are the performance metrics examined for the comparative analysis.
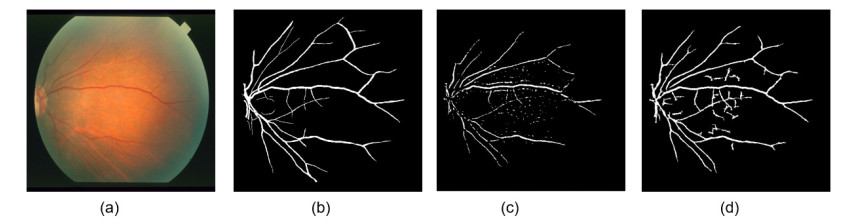
However, our proposed method is compared with some promising research work in terms of cross-training evaluation which also represents the robustness of our algorithm. In the case of cross-training experiment, the test data is completely taken from a different dataset or domain. Table 6 illustrates the comparative average accuracy analysis where the DRIVE test set images are evaluated after training with STARE dataset images and vice versa. Furthermore, ten abnormal images of STARE database are experimented separately and achieved an acceptable score in performance measures. A relative comparison with some recent works is also noted in Table 7 as well as one output result of a pathology image after performing the execution on Matlab is depicted in Figure 14. Figure 14(c), (d) are the output of shearlet and bendlet transform respectively where we can comprehend the latter image can detect more thin vessels from the background image.
5.
Conclusion and future work
Automatic and proper retinal blood vessel segmentation leads to the solution for various optic diseases. As day by day, the number of patients and the necessity of the vessel segmentation is increasing, an automated system can be an alternative to the manual system. Due to different sizes and shapes, it is very challenging to develop an automated system. Introducing Bendlets successfully for the first time in the domain of medical imaging opens the potentiality to use a comparable strategy in a lot of increasingly complex clinical applications. Moreover, analyzing and comparing the group of ensemble classifiers help to decide the best option for training and testing any new dataset images. In the future, we want to extend our research to develop an automated segmentation system for other problems such as 3D MR brain images. Different object detection in the optical images like hemorrhage, exudates, optic disc, cotton wool spots as well as Artery-venous classification, measurement of tortuosity, vessel width, branching angle could be some important topics of interest which could ameliorate the autonomous diagnosis of retinal images. Later on, 3D shape analysis of individual objects and predicting the growth rate of disease could be some advanced focus of the future study. It can also be explored for the disease of Alzheimer's and Amyotrophic Lateral Sclerosis (ALS). But to investigate, researchers need to collect robust clinical datasets at first.
Acknowledgments
The authors extend their appreciation to the Deanship of Scientific Research at King Saud University for funding this work through research group no (RG-1441-394).
Conflict of interest
All authors declare no conflicts of interest in this paper.









 DownLoad:
DownLoad: