We study the motion of discrete interfaces driven by ferromagnetic interactions in a two-dimensional low-contrast periodic environment, by coupling the minimizing movements approach by Almgren, Taylor and Wang and a discrete-to-continuum analysis. As in a recent paper by Braides and Scilla dealing with high-contrast periodic media, we give an example showing that in general the effective motion does not depend only on the $\Gamma$-limit, but also on geometrical features that are not detected in the static description. We show that there exists a critical value $\widetilde{\delta}$ of the contrast parameter $\delta$ above which the discrete motion is constrained and coincides with the high-contrast case. If $\delta<\widetilde{\delta}$ we have a new pinning threshold and a new effective velocity both depending on $\delta$. We also consider the case of non-uniform inclusions distributed into periodic uniform layers.
1.
Introduction
The study of optimal allocation is the kernel part of financial economics since Markowitz's pioneering work [1]. In the existing literature, there are mainly two choices to formulate the optimization rule. The first one is to study the expected utility maximization problem. Most early literature on investment problems focuses on maximizing the expectation of a smooth utility of terminal wealth. The main shortcoming of the optimization problem under a concave utility is that the decision-makers do not distinguish the preferences for gains and losses. Loss aversion, first proposed by [2] within the framework of prospect theory (PT), is defined over gains and losses in wealth relative to a pre-defined reference point, rather than in terms of changes in the absolute level of total wealth itself. Every investor has a reference point that defines relative 'losses' and 'gains'. Tversky and Kahneman [3] demonstrate the loss aversion and risk-seeking behavior by an asymmetric S-shaped utility function, convex in the domain of losses and concave in the domain of gains. Recently, an increasing number of studies have focused on the optimization problem under an S-shaped utility; see [4,5,6,7,8,9]. The concavification technique proposed by [10] allows to alternatively solve a concavified version of the S-shaped utility maximization problem. This technique has been successfully adopted to solve different non-concave utility maximization problems with and without constraints, see [7,11,12].
The second one is to follow the idea of Markowitz [1] to maximize the expected return for a given level of risk. Under this optimization objective, it is very important to develop a performance measure for a risky portfolio. The literature on portfolio performance evaluation is vast. The Sharpe ratio, which is defined as the average return beyond the risk-free rate divided by the standard deviation of its returns, first quantifies the trade-off between risk and reward by variance and mean, respectively. However, it only considers the portfolio return's first- and second-order moments but neglects higher-order ones. Then, alternative performance measures are reward-to-risk ratios representing a fraction where a measure of reward is divided by a measure of risk. Examples of such reward-to-risk ratios include the Sortino ratio (see [13,14]), the Kappa ratios (see [15]) and the Omega ratio (see [16]). It is well-documented that the Omega ratio, which is defined as the ratio between two expectations, is deemed a better performance measurement than the Sharpe ratio and the Sortino ratio since this measure effectively distinguishes between gains and losses relative to an externally specified benchmark. Furthermore, its calculation captures both the upside and downside deviations from a benchmark and has symmetric and asymmetric risk measures characteristics; see [5,17,18]. However, as pointed out in [17], the maximization problem of the Omega ratio is ill-posed. Therefore, they add additional constraints to make the maximization problem well-posed. Lin et al. [18] modify the Omega ratio to include a utility function for over-performance and a penalty function for under-performance in the definition of the performance ratio. They investigate the portfolio selection problem of maximizing the extended Omega ratio. Based on the fractional programming method, they analyze the non-linear fractional optimization problem by solving a family of related non-fractional optimization problems, where the objective functions are the numerator of the original problem minus the denominator multiplied by a penalty parameter. Since they work in a Black-Scholes market, the completeness of the financial market allows them to solve the optimal problems by using the martingale method, which consists of first finding the optimal terminal wealth by solving corresponding simplified static optimization problems and then finding the replicating feasible trading strategies with the martingale representation theorem; see [19,20,21,22].
Under the above-mentioned two optimization rules, one of the crucial norms is the choice of the benchmark, which measures over-performance and under-performance. In [18], the benchmark is a constant. Intuitively, every fund manager is deemed successful if he can beat the market. Therefore, the fund manager might choose any market return, for example, an index, or the level of a portfolio, or any economic indicator, as a benchmark. Lin et al. [18] set the benchmark to be a constant, which can be interpreted as the money market benchmark. Another important benchmark is a value-weighted portfolio with a fixed proportion invested in the risky asset, which implies the return rate of the benchmark is a weighted average of the risk-free rate and the return of stock. Under this specific benchmark, Basak et al. [23] investigate how the benchmark impacts the investment behaviors within the framework of expected utility theory. Motivated by [18,23], we shall consider a performance measure optimization problem with a stochastic benchmark, which is set to be a value-weighted portfolio with a fixed proportion invested in the risky asset. In general, for a stochastic benchmark, it is difficult to derive the closed-form solution for the performance measure maximization problem. However, when the penalty and reward functions are both power functions, the explicit expression for the optimal investment strategy can be obtained by combining the linearization method, the martingale method, the change of measure, and the concavification method.
The main contribution of this paper is that we consider a specific benchmark whose return rate is a weighted average of the risk-free rate and the return of stock. This choice of the stochastic benchmark allows for the derivation of a closed-form expression for the optimal solution to the optimization problem based on performance measures. By making use of a static Lagrangian method in a complete market setting, the optimal solution can be fully determined along with the existence and uniqueness of the Lagrangian multipliers. This paper offers new insights into optimal investment using a performance measure with a stochastic benchmark.
The rest of the paper is organized as follows. In Section 2 we formulate an optimal allocation problem by maximizing a performance measure with a stochastic reference point. In Section 3 we apply the linearization method, the martingale method, the change of measure, and the concavification technique to solve the non-linear optimization problem and derive the optimal investment strategy. In Section 4 we numerically investigate the impacts of some model parameters on the optimal investment strategy. Section 5 concludes.
2.
The model
Consider a finite investment time horizon $ [0, T] $ with $ T > 0. $ Let $ (\Omega, \mathcal{F}, \mathbb{F}, P) $ be a filtered complete probability space with the filtration $ \mathbb{F}: = \{\mathcal{F}_t|0\leq t\leq T\} $ being the natural filtration generated by a standard Brownian motion $ {\{W(t)}\}_{0\leq t \leq T} $ and satisfying the usual conditions. Investors can trade in the financial market at any time, regardless of transaction costs and taxes. Consider a financial market that consists of two tradable securities: a risk -free security $ B(t) $ and a risky asset $ S(t). $ The money market account evolves as:
where $ r > 0 $ is a risk-free interest rate.
The price process of the risky asset is modeled by
where $ \mu > r $ is the stock growth rate and $ \sigma > 0 $ is the volatility of $ S(t). $
Suppose that the initial value of the fund account is $ {x_0} \geqslant 0. $ The fund manager invests in a risk-free asset and a risky asset. Let $ \pi(t) $ be the proportion of wealth invested in the risky asset and $ 1-\pi(t) $ be the proportion of wealth invested in the risk-free cash bond. Then, the wealth process $ X^{\pi}(t) $ satisfies
where $ \varsigma = \frac{\mu-r}{\sigma} $ is the market price of risk.
We next define the set of admissible trading strategies.
Definition 2.1. A portfolio strategy $ \{\pi = \pi(t):t\in [0, T]\} $ is said to be admissible if $ \pi(t) $ is an $ \mathcal{F} $-progressively measurable process, with $ \int_0^T\pi^2(t)dt < +\infty, $ a.s., for all $ t\in [0, T], $ and there exists a unique strong solution $ X^{\pi}(t) $ to (2.3). We denote the set of admissible portfolio strategies by $ \mathcal{A}(x_0) $.
In the literature, there are many performance measures to evaluate the portfolio. The Markowitz mean-variance criterion has been widely applied in portfolio selection. However, the variance cannot distinguish the gains and losses. Furthermore, the returns are often supposed to be normally distributed within the mean-variance framework, which often conflicts with the empirical evidence. In an attempt to account for higher-order characteristics, Keating and Shadwick [16] introduce the Omega ratio. Given a benchmark return level $ \tilde{\theta} $, the Omega for a random return $ R $ is defined as:
where $ (x)_+ = \max\{x, 0\} $ represents the positive part of $ x. $ In contrast to the mean-variance criterion and Sharpe ratio, the Omega ratio distinguishes the gains over a benchmark $ \tilde{\theta} $ and losses below $ \tilde{\theta} $. In addition, the Omega ratio captures all of the higher moments information in the return distribution. The Omega ratio has been widely used in the evaluation of portfolios; see [24,25,26].
If we define the return of the portfolio with value process $ X^{\pi} $ described by (2.3) as follows
then $ \Omega_{\theta}(R) $ defined by (2.4) is equivalent to
where $ \theta = (1+\tilde{\theta})x_0 $ is a benchmark level.
As shown in [17,18], the maximization problem of the Omega ratio is ill-posed. Following the framework in [18] to make the optimization problem bounded, we introduce a weighting function $ U(x) $ over gains and a weighting function $ D(x) $ over losses, respectively. Hence, $ U $ is called the reward function, and $ D $ is called the penalty function. In order to ensure the well-posedness of the problem, similar to [18], we consider $ U $ to be strictly concave. However, $ D $ is not required to be concave or convex.
Consider a stochastic benchmark that evolves dynamically according to the process as follows:
where $ \eta $ is the fixed proportion of wealth invested in the stock at time $ t $.
Consider the performance measure
where the numerator $ \mathbb{E}[U(X^{\pi}(T)-\theta(T))_+] $ measures the benefit from exceeding the benchmark wealth $ \theta(T) $, while the denominator $ \mathbb{E}[D(\theta(T)-X^{\pi}(T))_+] $ penalizes shortfalls. The extended Omega ratio in Eq (2.8) distinguishes the gains and losses by the benchmark $ \theta(T) $. The preferences over gains and losses are represented by different functions $ U $ and $ D $, respectively, which is consistent with the prospect theory proposed by [2].
Note that if $ x_0\geq \theta_0, $ then it may hold that $ X^{\pi}(T)\geq \theta(T) $ only by letting $ \pi(t) = \eta $ for $ t\in[0, T]. $ So here we assume $ x_0 < \theta_0, $ i.e., $ f_0 < 1, $ which means the manager faces a challenging target.
We formulate the manager's portfolio selection problem as follows:
Equation (2.9) distinguishes the gains and losses by the benchmark $ \theta(T) $. Other works including [6,9] are also concerned with gains and losses of a portfolio by S-shaped utility with two different functions. However, as pointed out by [5], the trade-off between gains and losses in the S-shaped utility is subjective, while Eq (2.9) can provide more objective strategies for the manager by presenting the ratio of two expectations, including a utility function and a penalty function.
Remark 2.1. In general, it is difficult to explicitly derive the optimal solution for the expected utility maximization problem with a stochastic benchmark, let alone the optimization problem based on performance measure. Nicolosi [27] solved the expected utility maximization problem when the benchmark is modelled by (2.7) and the utility is a power function. However, it is a highly nontrivial task to solve the optimization problem based on performance measure with a stochastic benchmark.
To explicitly solve the optimization problem (2.9) and to compare our optimal solution with that within the framework of prospect theory, we use the power utilities to capture the preferences over gains and losses, which are also used in [3,7,9,28]:
where $ 0 < \gamma < 1 $ measures the degree of risk aversion and risk seeking with respect to random gains and losses, respectively. The parameter $ A > 1 $ measures the extent to which individuals are loss averse.
Define the relative performance with respect to the benchmark $ \theta $ by
A simple application of Itó's formula gives that
where $ f_0 = \frac{x_0}{\theta_0} < 1 $ and $ \delta(t) = \pi(t)-\eta $ denotes the tracking error.
We call $ \delta = \{\delta(t):t\in [0, T]\} $ admissible if the related $ \pi $ satisfied by $ \pi(t) = \delta(t)+\eta $ is in $ \mathcal{A}(x_0) $. Denote the admissible set of $ \delta $ by $ \tilde{\mathcal{A}}(f_0). $ Then, the optimization problem (2.9) becomes
Define a new measure $ Q $ by
From Girsanov's theorem, we have that the process
is a $ Q $ Brownian motion.
Therefore, (2.8) can be written as
where $ \mathbb{E}^Q[.] $ is an expectation under measure $ Q $, and the dynamics of $ F(t) $ under $ Q $ are given by
Since the market is complete, there exists a unique pricing kernel given by:
where $ \vartheta = \varsigma-(1-\gamma)\sigma\eta. $
The completeness of the market model under consideration allows us to solve the optimization problem via the martingale approach. Then, following [19], we can transform the optimization problem (2.11) into an equivalent one w.r.t. $ Z\hat{ = }F(T): $
where $ \mathcal{M}_{+} $ denotes the set of nonnegative $ \mathcal{F}_T $-measurable random variables.
We denote the feasible set of the optimization problem (2.16) by $ \mathcal{C}(f_0) $:
Problem (2.16) involves solving a terminal static optimization problem over the random variable $ Z\in\mathcal{M}_+ $. Once we obtain the optimal solution $ Z^* $, we can identify the optimal tracking error $ \delta^* $ and the optimal portfolio $ \pi^*. $
Proposition 2.1. Assume that $ Z^* $ is the optimal solution to problem (2.16). Then there exists a tracking error $ \delta^*\in \tilde{\mathcal{A}}(f_0) $ such that $ F^*(T) = Z^* $, a.s..
Proof. As $ Z^* $ is the optimal solution to problem (2.16), it is easy to verify that $ Z^* $ should satisfy $ \mathbb{E}^Q[\xi(T)Z^*] = f_0. $ Otherwise, consider $ \tilde{Z}^* = Z^* + (f_0- \mathbb{E}^Q[\xi(T)Z^*]) $ would still be feasible and yields a larger objective value.
Define the process
Then $ \xi(t)F^*(t) $ is an $ \mathcal{F}- $martingale. From the martingale representation theorem, there exists an $ \mathcal{F} $-progressively measurable process $ \psi = \{\psi(t), 0\leq t\leq T\} $ such that $ \mathbb{E}^Q[\int_0^T\psi^2(t)dt] < \infty $, a.s., and
Combining Eq (2.19) with Eqs (2.14) and (2.15), we can obtain that
The proof is finished. □
Theorem 2.1. Problem (2.11) and problem (2.16) have the same optimal value.
Proof. For any $ F(T)\in \{F(T):F(T)\in\mathcal{M}_+, \mathbb{E}^Q[\xi(T)F(T)] \leq f_0\}, $ from Proposition 2.1 we can conclude that $ F(T)\in \{F(T): \mbox{there exists a}\ \delta\in\tilde{\mathcal{A}}(f_0) \ \mbox{such that}\ F^{\pi}(t)\ \mbox{satisfies}\ (2.14)\}. $ Therefore,
On the other hand, for any $ F(T)\in\{F(T): F^{\pi}(t)\ \mbox{satisfies}\ (2.14)\ \mbox{with}\ \delta\in\tilde{\mathcal{A}}(f_0)\}, $ it is easy to obtain that $ F(T)\in \{F(T):F(T)\in\mathcal{M}_+, \mathbb{E}^Q[\xi(T)F(T)] \leq f_0\}, $ which implies
The proof is completed. □
Theorem 2.4 and Proposition 2.3 show that in order to solve problem (2.11), we only need to investigate problem (2.16) first.
Since the maximization problem (2.16) is non-linear, it is difficult to solve directly. We shall follow [18] to transform the non-linear fractional optimization problem into a non-fractional optimization problem based on the fractional programming method. For any $ \lambda\geq0 $, consider a family of optimization problems:
Remark 2.2. Similar to the proof of Proposition 2.3, it is easy to verify that when problem (2.21) attains the optimal value, the budget constraint is binding, that is
The following result shows that under some suitable conditions of $ v $, the optimal solutions to problems (2.21) and (2.16) are the same.
Theorem 2.2. Assume $ f_{0} < 1 $. For each $ \lambda\geq0 $, let $ Z_{\lambda}^{*} $ be a solution to problem (2.21), and suppose there exists a constant $ \lambda^{*}\geq0 $ such that
Then $ Z^*: = Z_{\lambda^*}^* $ solves problem (2.16), and $ \lambda^* $ is the optimal value.
Proof. The proof is similar to the proof of Proposition 2.3 in [18]. As $ Z_{\lambda^*}^* $ is the solution to the problem (2.21), for any $ Z\in \mathcal{C}(f_0), $ we have
Furthermore, $ \mathbb{E}^Q[\xi(T)Z]\leq f_0 < 1 $ implies that $ Z < 1 $ holds with some positive probability; otherwise, $ f_0\geq \mathbb{E}^Q[\xi(T)Z] \geq \mathbb{E}^Q[\xi(T)] = 1, $ contradicting the assumption that $ f_0 < 1 $. Thus, $ \mathbb{E}^Q[A(1-Z)_+^{\gamma}] > 0 $ and
which concludes the proof. □
Based on Theorem 2.6, it remains to prove the existence of the root of Eq $ v(.; f_0) = 0 $ and solve problem (2.21) after linearization. To prove the existence of $ \lambda^*, $ similar to [18], we need the following results about $ v(.; f_0). $
Proposition 2.2. Suppose $ f_0 < 1 $. Then the function $ v(\lambda; f_0) $ has the following properties:
(a) $ 0 < v(0;f_{0}) < \infty. $
(b) $ v $ is non-increasing in $ \lambda. $
(c) $ v(\lambda; f_0) $ is convex in $ \lambda $ for each fixed $ 0 < f_0 < 1 $.
(d) $ v(\cdot; f_0) $ is Lipschitz continuous.
Proof. The proof is similar to that of Proposition 2.4 in [18]. So we omit it here. □
The following result is useful for the proof of the existence and uniqueness of the root to Eq (2.22).
Lemma 2.1. Define $ M = \sup\limits_{Z\in\mathcal{M}_+, \mathbb{E}^Q[\xi_TZ] = f_0 }\mathbb{E}^Q[(Z_{{\lambda}^{*}}^*-1)_+^{\gamma}] $ and $ m = \inf\limits_{Z\in \mathcal{M}_+, \mathbb{E}^Q[\xi_TZ] = f_0}\mathbb{E}^Q[(1-Z_{{\lambda}^{*}}^*)_+^{\gamma}] $. Then we have $ M < \infty $ and $ m > 0 $.
Proof. For the proof of $ M < \infty $, we refer to [29]. We shall prove $ m > 0. $ It is obvious that $ m\geq 0. $ Suppose $ m = 0 $. Let $ \{Z_n\}\in\mathcal{M}_+ $ with $ \mathbb{E}^Q[\xi_TZ_n] = f_0 $ be a sequence such that $ \lim\limits_{n\to\infty}\mathbb{E}^Q[(1-Z_n)_{+}^{\gamma}] = 0 $. Then $ (1-Z_n)_{+}^{\gamma} $ converges to 0 in probability. Thus, $ (1-Z_n)_{+} $ also converges to 0 in probability. So there is a subsequence $ (1-Z_{n_m})_+ $ which converges to 0 a.s, leading to $ (1-Z_{n_m})_{+} $ also converging to 0 a.s. with respect to a new measure $ \tilde{Q} $ defined by
Note that $ 0\leq (1-Z_{n_m})_{+} \leq 1. $ It follows from the dominated convergence theorem that $ \mathbb{E}^{\tilde{Q}}[(1-Z_{n_m})_+]\rightarrow 0 $, which implies that $ \mathbb{E}^{Q}[\xi(T)(1-Z_{n_m})_+]\rightarrow 0, $ contradicting with the condition $ \mathbb{E}^{\tilde{Q}}[(1-Z_{n_m})_+]\geq \mathbb{E}^{\tilde{Q}}[(1-Z_{n_m})] = 1-f_0 > 0. $ Therefore, $ m = 0. $ □
From Proposition 2.2 and Lemma 2.8, we have the following theorem.
Theorem 2.3. There exists a unique $ \lambda^* > 0 $ such that (2.22) holds.
Proof. Note that the budget constraint is binding at optimality. Thus,
which yields that
Combining (2.23) with Proposition 2.2 yields that there exists a $ \lambda^* \geq 0 $ such that (2.22) holds. Suppose that $ 0 < \lambda_1^* < \lambda_2^* $ are both the roots to (2.22). Then there must exist a $ \lambda_3^* > \lambda_2^* $ such that $ v(\lambda_3^*; f_0) < v(\lambda_2^*; f_0) = 0. $ On the other hand, as
we have
which contradicts with the convexity of $ v $. Hence, the root to (2.22) is unique. □
The analysis in this section motivates us to focus on the linearized problem (2.21).
Remark 2.3. To compare the optimal investment strategies based on performance measure and based on prospect theory, we formulate the S-shaped utility maximization problem (see [30]) as follows:
where $ \theta $ is modelled by (2.7) and
Similar to deriving (2.11), the optimization problem (2.24) can be transformed into
Following a similar argument as in deriving (2.16), problem (2.26) is equivalent to the following problem:
Note that, if $ \lambda = 1 $ in (2.21), then problem (2.27) is the same as problem (2.21). Therefore, we transform the non-linear fractional optimization problem into a family of S-shaped utility maximization problems based on the fractional programming method.
3.
Optimal trading strategy
In this section, we shall use a Lagrangian duality method and a pointwise optimization procedure to solve linearized problem (2.21).
For each $ \lambda\geq0, \beta > 0, $ consider the following optimization problem:
where
We can solve problem (3.1) by resorting to a pointwise optimization procedure. Consider the following related non-randomized version of problem (3.1) as follows: for each $ y > 0 $,
where $ \mathbb{R}_+ $ denotes the set of nonnegative real numbers.
The following result reveals the relationships among the optimal solutions of problems (2.16), (3.1), and (3.3).
Lemma 3.1. For all $ \lambda\geq0, $ we have the following properties:
(a) For all $ \lambda\geq0, y > 0, $ let $ x_{\lambda}^*(y) $ be a Borel measurable function such that $ x_{\lambda}^*(y) $ is an optimal solution to problem (3.3). Then, $ Z_{\lambda, \beta}^*: = x_{\lambda}^*(\beta\xi(T)) $ solves problem (3.1).
(b) Assume that, given $ \lambda\geq0 $, if there exists a constant $ \beta^* $ such that $ Z_{\lambda, \beta^*}^*\in\mathcal{M}_+ $ solves problem (3.1) with $ \mathbb{E}^Q[\xi(T)Z_{\lambda, \beta^*}^*] = f_0 $. Then, $ Z_{\lambda}^*: = Z_{\lambda, \beta^*}^* $ solves problem (2.16).
Proof. We refer to Lemmas 3.1 and 3.2 in [7] for the proof. □
Since $ h_{\lambda} $ is not concave, we shall use a concavification technique as in [9,10] to solve problem (3.3).
The concave envelope of a given function $ f $ with a domain $ G $, denoted by $ f^c $, is defined as follows:
Then, based on Lemma 2.9 of [31], problem (3.3) is equivalent to the following concavified version of (3.3):
Proposition 3.1. The solution to the optimization problem (3.3) is
where
$ \widetilde{z}_\lambda $ is the unique solution to
Proof. Let $ \widetilde{z}_\lambda $ be the tangent point of the straight line starting at $ (0, -A\lambda) $ to the curve $ (x-1)^{\gamma}, x > 1. $ It is easy to verify that there exists a unique solution $ \widetilde{z}_\lambda > 1 $ to Eq (3.8) and $ h_{\lambda}\left(x\right)\leq k_\lambda x-\lambda A $ for $ 0\leq x < \widetilde{z}_\lambda $. From Lemma A.1 of [9], the concave envelope of $ h_{\lambda} $ is given by
Then we can find the point $ x_{\lambda }^{*} \left (y \right) \in\{x|h_{\lambda}(x) = h_{\lambda}^{c}(x)\} $ solving (3.3) and (3.5) for which 0 is in the superdifferential of $ h_{\lambda}^{c}(x)-xy $ given by (3.6). □
By Lemma 3.1, it remains to prove there exists the optimal multiplier $ \beta^* $ with $ \mathbb{E}^Q[\xi(T)Z_{\lambda, \beta^*}^*] = f_0 $ such that $ Z_{\lambda}^*: = Z_{\lambda, \beta^*}^* $ solves problem (2.21).
Theorem 3.1. For each $ \lambda\geq 0, $ there exists a unique constant $ \beta^* > 0 $ such that $ Z_{\lambda}^*: = Z_{\lambda, \beta^*}^* = x_{\lambda}^*(\beta^*\xi(T)) $ with $ \mathbb{E}^Q[\xi(T)Z_{\lambda, \beta^*}^*] = f_0 $, where $ x_{\lambda}^* $ is given by (3.6).
Proof. Define
It is easy to check that $ R_{\lambda}(\beta) < \infty $. Because $ \lim_{\beta\to\infty}x_{\lambda}^*(\beta\xi(T)) = 0 $, $ \lim_{\beta\to0^+}x_{\lambda}^*(\beta\xi(T)) = \infty $ and $ x_{\lambda}^*(\beta\xi(T)) $ is non-negative, we have $ \lim_{\beta\to\infty}R_\lambda(\beta) = 0 $, $ \lim_{\beta\to0^+}R_\lambda(\beta) = \infty $ from the monotonic convergence theorem.
Furthermore, $ R_{\lambda}(\beta) $ is continuous and strictly decreasing in $ \beta. $ Therefore, there exists a unique $ \beta^* > 0 $ such that $ \mathbb{E}^Q[\xi(T)Z_{\lambda, \beta^*}^*] = f_0. $ □
As such, based on Theorems 2.6, 2.9, and 3.3, Lemma 3.1, and Proposition 3.2, we can obtain the optimal solution of the original optimization problem (2.11) by the following procedures:
Step 1: Use the result presented in Proposition 3.2 to obtain the optimal solution $ x_{\lambda}^* $ to the non-random problem (3.3).
Step 2: For the optimal solution $ x_{\lambda}^* $ to the non-random problem (3.3), make use of Lemma 3.1 and Theorem 3.3 to find the unique solution $ \beta^* $ satisfying $ \mathbb{E}^Q[\xi(T)x_{\lambda}^*(\beta^*\xi(T))] = f_0 $ and set $ Z_{\lambda}^* = x_{\lambda}^*(\beta^*\xi(T)). $
Step 3: Using Theorem 2.6 and Theorem 2.9 to get $ \lambda^* $ by solving (2.22) and obtain the corresponding optimal solution $ Z_{\lambda^*}^* $ to problem (2.16).
In what follows, we shall follow the above steps to derive the optimal solution. Set
where $ k_{\lambda} $ is defined by (3.7) and $ \beta_{\lambda }^{*} $ is determined by Eq $ \mathbb{E}^Q[\xi(T)Z_{\lambda, \beta_{\lambda }^{*} }^*] = f_0 $ for each $ \lambda \geq 0 $.
Remark 3.1. The optimal solution to the S-shaped utility maximization problem (2.27) is given by (3.11) just by letting $ \lambda = 1 $. However, for the problem (2.16), it remains to determine the optimal $ \lambda^* $ by solving (2.22).
In order to derive the optimal $ \lambda^*, $ we define
Using (3.11) yields that
and
where $ \Phi $ denotes the standard normal cumulative distribution function,
Based on Theorem 2.9, with the above expressions for $ f_1 $ and $ f_2 $, we can determine a $ \lambda^{*} > 0 $ satisfying
Given $ \lambda^{*} > 0 $, we can derive the optimal solution for the portfolio optimization problem (2.9).
Proposition 3.2. Let $ \lambda^{*} > 0 $ be a constant determined by (3.14). Let $ k_{\lambda^{*}} $ and $ \widetilde z_{\lambda^{*}} $ be defined by (3.7) and (3.8) with $ \lambda $ replaced by $ \lambda^* $. Then the optimal terminal relative performance, the optimal relative performance at time $ t $, and the optimal trading strategy at time $ t $ are given as follows:
(a) The optimal terminal relative performance is
where $ \beta_{\lambda^*}^* $ satisfies $ \mathbb{E}^Q[\xi(T)F^{*}(T)] = f_0 $.
(b) The optimal relative performance at time $ t $, $ 0\leq t < T $, is given by
(c) The optimal portfolio of wealth invested in the risky asset at time $ t $, $ 0\leq t < T $, is given by:
Proof. The optimal terminal relative performance is a direct consequence of Lemma 3.1, Proposition 3.2, and Theorem 3.3. Then, substituting the expression for $ F^*(T) $ into (2.18), we can easily obtain the formula for $ F^*(t) $ by some straightforward calculations.
Based on Proposition 2.3, we let $ F^*(t) = A(\xi(t), t). $ Then applying Ito's formula to $ \xi(t)F^*(t) $ and using (2.19), (2.20) gives the explicit formula for $ \delta^*(t). $ The equality $ \pi^*(t) = \delta^*(t)+\eta $ yields the result. □
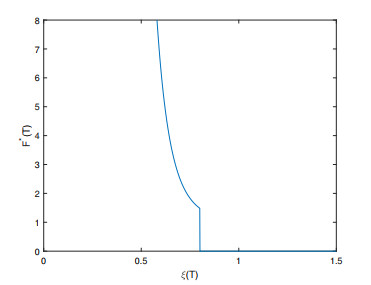
Remark 3.2. From (3.15), we see that $ F^{*}(T) $ takes a two-region form and is a decreasing function of $ \xi(T) $ for different $ \eta $. When the state price density $ \xi(T) $ is relatively low, $ F^{*}(T) $ is similar to the smooth utility; when $ \xi(T) $ increases above a critical value of the price density, $ F^{*}(T) $ drops to 0 since the loss aversion states a risk-seeking preference in the loss domain. This reflects that, as in the S-shaped expected utility optimization problem (see [30]), there is still a moral hazard problem based on performance measures that the manager does not have an incentive to keep the terminal wealth above a minimal positive guarantee. Therefore, to protect the investor's benefits, it is better to incorporate some risk constraints into the optimization problems, which will lead to a much more complex optimization problem. We leave this problem for future research.
4.
Numerical analysis
In this section, we aim to carry out some numerical calculations to investigate the impacts of the model parameters on the optimal investment strategy. We also compare the optimal investment strategy for the non-linear fractional optimization (2.9) with that for the S-shaped utility maximization problem (2.24).
We assume $ A = 2.25 $ and $ \gamma = 0.88 $ as estimated by [3]. For the underlying asset, we pick the CSI 500 index, which is mostly used as the underlying in Chinese OTC markets. According to the empirical data on the financial market, parameter values are chosen as: $ r = 0.03, \mu = 0.07, \sigma = 0.3. $ Assume that the investment horizon is $ T = 5 $ years, the initial wealth and the initial value of the benchmark process are $ x_0 = 100 $ and $ \theta_0 = 150, $ respectively, and the fixed proportion of wealth invested in the risky asset is $ \eta = 0.5. $
Figures 1 and 2 present the optimal terminal relative performance $ F^{*}(T) $ versus $ \xi(T) $ for problems (2.9) and (2.24), respectively. It can be seen from Figures 1 and 2 that for each optimization problem, $ F^{*}(T) $ ends up with zero from a certain value of the price density $ \xi(T) $, which reflects the moral hazard problem that the manager does not have an incentive to ensure that there is any capital in case of the worst economic states. We can see that the optimal terminal relative performance in the good-states region based on performance measure is higher than that based on prospect theory. We can also observe that the states with the optimal terminal relative performance of 0 for problem (2.9) are much more than those for problem (2.24). Note that, comparing problem (2.21) with problem (2.27), for a fixed $ \lambda, $ problem (2.21) is equivalent to an S-shaped utility maximization problem with utility given by $ \overline{U} = x^{\gamma}1_{\{x\geq 0\}}-\lambda A(-x)^{\gamma}1_{\{x < 0\}}, $ where $ \lambda A $ is the loss aversion degree, and it measures the extent to which individuals are loss averse. For problem (2.9), the optimal $ \lambda^* $ determined by (2.22) is about 0.4, which implies that the loss aversion degree based on performance measure is lower than that based on prospect theory. Therefore, the manager, based on performance measure, shall invest more wealth in the risky asset, which leads to a better optimal terminal relative performance in the good-states region and a higher tail risk in the bad-states region.
Figures 3–12 illustrate the effects of some model parameters on the optimal proportion $ \pi^*(0) $. We can conclude from them that when the parameters are fixed, $ \pi^*(0) $ corresponding to problem (2.9) is much higher than that corresponding to problem (2.24), which confirms the result presented in Figures 1 and 2: the manager based on performance measure invests more wealth in the risky asset.
Figures 3 and 4 show the optimal proportion $ \pi^*(0) $ versus $ \eta $ for problem (2.9) and problem (2.24), respectively. We can observe from them that $ \pi^*(0) $ is an increasing function of $ \eta $; this is due to the fact that as the proportion of wealth invested in the risky asset, $ \eta, $ increases, the benchmark becomes more aggressive, and the manager shall decrease the tracking error and invest more in the risky asset to beat the benchmark.
Figures 5 and 6 graph $ \pi^*(0) $ versus $ \mu $ for problem (2.9) and problem (2.24), respectively. We can observe from them that for each optimization problem, $ \pi^*(0) $ is an increasing function of $ \mu $. The reason is that when the stock growth rate $ \mu $ increases, the market price of the risk, $ \varsigma = \frac{\mu-r}{\sigma}, $ increases, which leads to more investment in the risky asset, consistent with economic intuition.
Figures 7 and 8 plot $ \pi^*(0) $ versus $ \sigma $ for problem (2.9) and problem (2.24), respectively. It can be seen from them that for each optimization problem, $ \pi^*(0) $ is a decreasing function of $ \sigma $. When the volatility $ \sigma $ increases, the market price of the risk, $ \varsigma = \frac{\mu-r}{\sigma}, $ decreases. As a result, the manager shall invest less in the risky asset.
Figures 9 and 10 represent $ \pi^*(0) $ versus $ x_0 $ for problem (2.9) and problem (2.24), respectively. We can note from them that for each optimization problem, $ \pi^*(0) $ decreases with $ x_0 $, since an increase in the initial wealth leads the manager to get close to the benchmark, and hence he invests less in the risky asset to reduce the risk.
Figures 11 and 12 graph $ \pi^*(0) $ versus $ \gamma $ for problem (2.9) and problem (2.24), respectively. The parameter $ \gamma $ characterizes both the manager's risk attitude towards gains and the degree of risk aversion attitude towards losses. We can observe that the manager, based on the performance measure, invests more money in the risky asset at the initial time as $ \gamma $ increases, while for the manager based on prospect theory, $ \pi^*(0) $ increases with $ \gamma $ when $ \gamma $ is no more than about 0.5 and decreases with $ \gamma $ when $ \gamma $ is greater than about 0.5. This is due to two effects: the first effect is that when $ \gamma $ decreases, the manager becomes more risk averse in the gain domain, and then he will invest less in the risky asset. The second effect is that the manager also becomes more risk-seeking in the loss domain with $ \gamma $ decreasing, and therefore, he shall invest more in the risky asset to eliminate losses in the loss domain. Figure 11 shows that based on the performance measure, the first effect outweighs the second effect for problem (2.9). Figure 12 presents that based on prospect theory, for a relatively low value of $ \gamma $, the first effect outweighs the second effect, while for a relatively high value of $ \gamma $, the second effect outweighs the first effect.
5.
Conclusions
In this paper, we investigate the optimal portfolio selection problem of a fund manager when he bases decisions on the performance measure comparison to a benchmark. The choice of the benchmark is very crucial in the optimization problem. Extending the constant benchmark in [18], we assume the benchmark to be a value-weighted portfolio with a fixed proportion invested in the risky asset, which implies that the benchmark depends completely on the financial market. In general, it is a highly nontrivial task to solve a non-linear optimization problem with a stochastic benchmark. However, when the penalty and reward functions are both power functions, the stochastic benchmark we consider allows us to derive the optimal investment strategy by combining the linearization method, the martingale method, the change of measure, and the concavification method. Theoretical and numerical results show that the optimal terminal relative performance ends up with zero from a certain value of the price density, which reflects the moral hazard problem. A natural extension of our investigation would be to incorporate some risk constraints, such as, a VaR (value at risk) constraint or an ES (expected shortfall) constraint, into the optimization problem to investigate how the risk constraints impact the optimal investment behaviors of the manager.
Author contributions
Original draft preparation, Chengjin Tang and Jiahao Guo; Supervision, writing-review, editing and project administration, Yinghui Dong. All authors have read and approved the final version of the manuscript for publication.
Use of Generative-AI tools declaration
The authors declare that they have not used Artificial Intelligence (AI) tools in the creation of this article.
Acknowledgments
The research was supported by the Research and Practice Innovation Program for Graduate Students in Jiangsu Province (KYCX24-3408) and the NNSF of China (Grant Nos. 12071335, 12371474).
The author would like to thank the editor and the anonymous reviewers for their valuable comments and suggestions, which have helped to improve the paper.
Conflict of interest
All authors declare no conflicts of interest in this paper.









 DownLoad:
DownLoad:













