Homogenization and dimension reduction of filtration combustion in heterogeneous thin layers

1.   Introduction

In December 2019, a new coronavirus infection, called corona virus disease (COVID-19) by the World Health Organization, was found in Wuhan, Hubei, China ^[1] and soon spread outside of China. Although two rather effective antivirals have been approved by the FDA and monoclonal antibody treatment has been in use for some time and is extremely effective, this viral contamination continues to spread rapidly across globe ^[2,3]. In March 2020 ^{[1,2,4,5,6,7]} the emergency arrived at the pandemic stage as the overall effect was accelerated. The number of cases and deaths with COVID-19 have reached 506 million and 6.2 million worldwide, respectively, as of 21 April 2022. Currently, only vaccines can attenuate the COVID-19 pandemic. Several vaccines, such as Pffizer-BioNtech, Moderna, AstraZeneca, etc., had been developed and approved via Emergency Use Authorization (EUA) worldwide ^[8]. On December 2, 2020, UK became the first country to approve the Pffizer-BioNtech COVID-19 vaccine, and several vaccines were approved under EUA by different countries in early 2021 ^[8].

Mathematical modeling is a useful technique to understand the dynamics of infectious diseases. Mathematical models of evolution of COVID-19 pandemic have been proposed to predict the spread of Covid-19 pandemic such as the peaks, total numbers of infections, and the ending time of COVID-19 epidemic in different countries ^{[9,10,11,12,13]}. Balasubramaniam et al. ^[9] used a stochastic epidemiological model (SEM) along with a machine learning technique to compute the infection rates in populations. Yadav ^[10] employed the well known SIR model, consisting of deterministic ODEs, to predict the peak and ending time of COVID-19 pandemic in India. Hassen et al. ^[11] also employed the SIR model to predict the evolution of COVID-19 cases in the Maghreb Central countries. Bhardwaj ^[12] used the natural exponential function with a time dependent growth rate to estimate the peak dates and the number of total infections in several countries. Jamshidi et al. ^[13] proposed a computational algorithm to predict the number and locations of new epicenters.

Santosh ^[14] pointed out that complex models were needed to study the spread of COVID-19 which depends on many factors such as hospital capacity, testing rate, demographics, population density, poverty, etc. Furthermore, as COVID-19 continues to spread, mathematical models studying pharmaceutical or non-pharmaceutical factors, which can help with reducing effect of the spread and devising the control strategies for fighting COVID-19 pandemic, are as important as the models attempting to predict the future evolution of COVID-19 pandemic ^[15,16,17]. Dawoudi ^[18] proposed a computational algorithm to study coronavirus DNA sequences for discovery of new drugs. Based on the SIR model, Wanjau, Ndam, and Asempapa et al. ^[19,20,21] proposed mathematical models with more sub-populations such as susceptible, exposed, infectious, isolated, and recovered individuals. Asempapa et al. ^[21] further divided some of the above sub-populations into high-risk and low-risk sub-populations. These complex models contain many coupled ODEs with many parameters. However, daily information of these sub-populations, such as the number of isolated individuals, high-risk and low-risk sub-populations, or the number of exposed individuals, is not available in many countries/regions. Estimation of parameters and the plausibility of the model may be hindered by lack of information in many countries/regions.

Rojas-Vallejos ^[22] suggested that mathematical models should not be simpler than necessary, but also not more complex than needed to provide helpful insight. Recently, Alvarez et al. ^[23] have proposed a simple yet novel mathematical model of COVID-19 epidemic to study the effect of social distancing and detection of positive cases in urban areas. The mathematical model considered two populations, population of the cumulative confirmed cases and population of recovery/death. Daily reported data of the number of cumulative cases and the number of recovered or died individuals are available for most countries, making the model plausible for their study. The computational results are interesting. However, the mathematical model has not been correctly formulated. Motivated by the model in ^[23], the purpose of this paper is to build a mathematical model to study the impacts of pharmaceutical factors (vaccination, detection efficiency, and health care capacity) and non-pharmaceutical factors (lock-down and social distancing) on COVID-19 pandemic.

To provide details, the mathematical model is presented in Section 2. Parameter fitting and numerical simulation are performed in Section 3. Finally, a brief conclusion is made in Section 4.

2.   Mathematical model

2.1.   The first-stage model

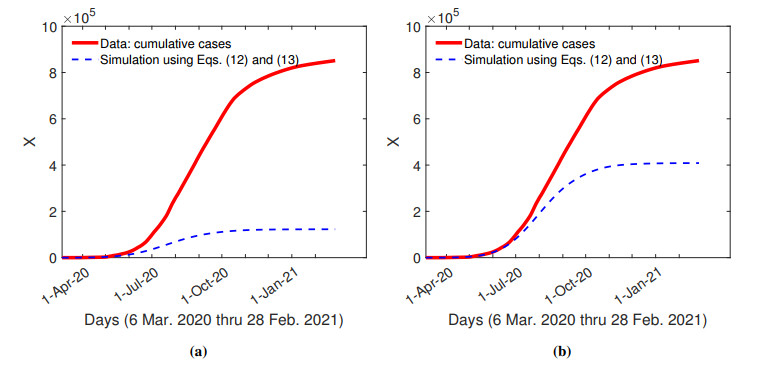
In this paper, a two-stage model is to be constructed. The first-stage model contains two state variables, $ X $ and $ R $, and the impacts of lock-down, social distancing, and testing intensity. The variable $ X $ represents the cumulative COVID-19 cases. The variable $ R $ represents the number of individuals who have been infected but removed from the population and thus do not contribute to the propagation of COVID-19. The construction of first-stage model is motivated by the model proposed by Alvarez et al. ^[23]. However, the mathematical model proposed by Alvarez et al. ^[23] was not correctly formulated nor consistent with the implementation of the solutions in Excel spreadsheets (Supplemental File F1 in ^[23]). The model given in ^[23] is as follows:

where $ P_0 $ is the population of the region, which may be a country, state, or urban area, and $ \mu_0 $ is the intrinsic infection rate. Both $ \sigma $ and $ \alpha $ were modeled by nondecreasing functions of $ t $ ^[23]. The function $ \sigma $ represents the effect of social distancing. The infection rate is reduced by $ \sigma $ due to social distancing effect. In ^[23], Eq (2) describes the rate at which infected patients are retrieved from the general population. It has been assumed in ^[23] that a fraction ($ \alpha $) of infected individuals is effectively removed from the general population with a delay of $ delay\_q $ days from the onset of virus to positive diagnosis. These individuals do not contribute to the propagation of COVID-19. Another fraction ($ 1-\alpha $) of infected individuals is not effectively removed from the general population until their recovery or death after $ delay\_r $ days. It was stated in ^[23] that the second term was formulated by the integral of all infected individuals recovered or died from the onset of the epidemic episode in the region with a delay of $ delay\_r $ days. Apparently, Eq (2) and the above statement do not describe the rate of change of $ R $. Furthermore, Eqs (1) and (2) were converted into equations of differences in ^[23]:

Using the fact that $ X(t) $ is nondecreasing, Eq (4) is equivalent to

if $ delay\_r\geq delay\_q $. The left hand side of Eq (5) represents the increment of the population $ R $ over a time span $ [t, t+\Delta t] $ while the right hand side uses the cumulative infected cases over the whole time span with a delay of a few days $ [0, t-delay\_r] $, multiplied by $ \Delta t $. This shows that Eq (2) was not correctly formulated in ^[23]. Nevertheless, the elements and terms considered in the mathematical model in ^[23] are novel and can be easily applied to construct a modified model to study the evolution of the desease.

Following the construction concept of Eqs (1) and (2) with modification and incorporation of the lock-down effect, the first-stage model proposed in this paper is given by a deterministic system of ODEs with time delays:

where $ \mu_1 $ is the intrinsic infection rate and $ K $ is the number of infected individuals who reside outside of the region and travel to the region. The functions $ \sigma(t) $ and $ \alpha(t) $ represent the same effects as in Eqs (1) and (2). The notations $ delay\_q $ and $ delay\_r $ are replaced by shorter notations $ \tau_1 $ and $ \tau_2 $, respectively.

Equation (6) describes the rate of change in cumulative COVID-19 cases. Assume that it is of similar status of COVID-19 outbreak in neighboring regions. This assumption leads to $ K(t) = \beta_1(X(t)-R(t)) $. Thus $ X(t)-R(t)+K(t) = (1+\beta_1)(X(t)-R(t)) $ where $ \beta_1 $ represents the unlock-down factor. At the stage of implementation of the lock-down orders, $ \beta_1 = 0 $.

Social distancing involves the change of behavior ^[24] and it is difficult for individuals to stick to the social distancing guidelines ^[25]. Implementation of social distancing policy can become effective after people have learned the importance of social distancing ^[26]. This behavioral change can be related to the S-shaped learning curve, measuring an individual who is new to a task ^[27]. The bottom of the S curve indicates slow progressing initially as it requires more time to master new skills. The S curve also describes the strongest resistance to adoption of a change ^[28]. After the learner becomes proficient in the skills, it requires less time to complete the task. The curve eventually levels off, indicating a plateau or new challenges ^[27]. Alvarez et al. ^[23] reported that using a linear ramp between two values over a time period for $ \sigma $ could reproduce the actual progression of COVID-19. The behavioral change of social distancing described above and the formulation of $ \sigma $ given in ^[23] suggest that a sigmoid function, which is regularly used in mathematical modeling, is a good fit for $ \sigma $.

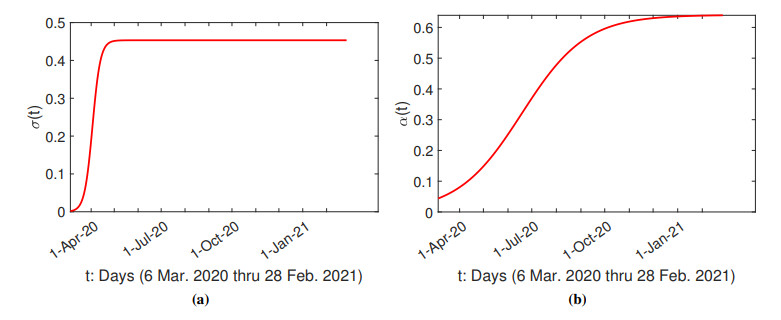
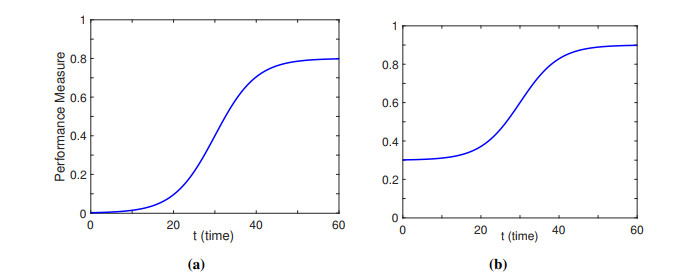
The effect of social distancing $ \sigma(t) $, shown in Figure 1(a), is modeled as follows:

Figure 1.  S-shaped learning curves, plotted using Eq (9), (a) without prior experience ($ M_1 = 0 $, $ t_1 = 30 $, $ k_1 = 0.2 $, and $ L_1 = 0.8 $) and (b) with prior experience ($ M_1 = 0.3 $, $ t_1 = 30 $, $ k_1 = 0.2 $, and $ L_1 = 0.6 $).

DownLoad: Full-Size Img PowerPoint

where $ k_1 $ represents the steepness of the curve, $ t_1 $ is the time point at which the learner reaches the maximum growth rate, and $ L_1 $ represents the maximum performance measure. When a learner develops new skills required for a new task through previous experience, the bottom of the curve might not start with zero performance. In this case, Eq (8) is modified as follows:

where $ M_1 $ is the previous-experience factor. Note that Eq (9) becomes Eq (8) when $ M_1 = 0 $. Thus Eq (9) is used in this paper as it represents a more general case than Eq (8). Figures 1(a), (b) give examples of S-shaped learning curves without and with prior experience, respectively.

Equation (7) describes the rate of change of the removed population $ R $. At the initial stage of COVID-19 outbreak, most countries faced a shortage of testing kits ^[29]. As a result, infected individuals were tested only after the onset of symptoms. The function $ \alpha $ has the same meaning as in Eq (2). Recall that $ \tau_1 $ is the delay from the onset of symptoms to positive diagnosis. The delay takes about 2–5 days ^[23]. We use $ \tau_1 = 4 $ in this paper. It has been reported that the median time to recovery is 13.5 days ^[30]. We assume that these individuals are removed from the general population after their recovery or death with a delay of $ \tau_2 = 14 $ days. From Eq (7), $ 0\leq \alpha(t)\leq 1 $, $ X(t) = 0 $ for $ t < 0 $, and $ dX(t)/dt = 0 $ for $ t < 0 $, we have

Equation (10) shows that $ R(t) $ includes the cumulative infected individuals over the time span $ [0, t-\tau_2] $ and the removed individuals over $ [t-\tau_2, t-\tau_1] $. The expression $ X(t)-R(t) $ represents the infected individuals who are capable of infecting susceptible individuals in the region. Equation (10) also shows that $ X(t)-R(t) $ includes the individuals contracted the disease over $ [t-\tau_1, t] $ and the individuals contracted the disease over $ [t-\tau_2, t-\tau_1] $ who have not been removed from the general population. Since $ X(t) $ is a differentiable, nondecreasing function and bounded above by $ P_0 $, the limit $ lim_{t \rightarrow \infty} X(t) $ exists and $ lim_{t \rightarrow \infty} (dX/dt) = 0 $. Thus, Eq (10) implies $ lim_{t \rightarrow \infty} R(t) = lim_{t \rightarrow \infty} X(t) $; all the infected individuals will be included in the population $ R $ eventually.

The outbreak of COVID-19 is an unprecedented public health crisis affecting all countries worldwide. Testing and treatment strategies are new tasks for health-care workers. Thus, it is reasonable to expect an improvement in effective diagnosis with time. Here, the removal factor $ \alpha(t) $ is also modeled by an S-curve,

The first-stage model becomes

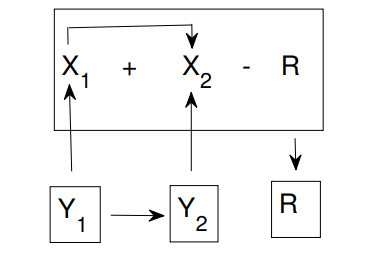
where $ \sigma(t) $ and $ \alpha(t) $ are given as in Eqs (9) and (11), respectively. Figure 2 gives a schematic of Eqs (12) and (13).

Figure 2.  Schematic of Eqs (12) and (13). $ P_0-X $, $ X-R $, and $ R $ represent the susceptible, infectious, and removed populations, respectively.

DownLoad: Full-Size Img PowerPoint

2.2.   The second-stage model

COVID-19 vaccines had been approved by many countries in early 2021 ^[8]. In the second-stage model, four state variables $ X_1 $, $ X_2 $, $ Y_1 $, and $ R $ are considered. The variables $ X_1 $ and $ X_2 $ represent the cumulative COVID-19 cases in unvaccinated and vaccinated sub-populations, respectively. The variable $ Y_1 $ represents the unvaccinated uninfected sub-population. The practical meaning of $ R $ is the same as in Eqs (12) and (13). Many countries have experienced the second wave of COVID-19, and the second wave has caused a dramatic increase in COVID-19 cases which exceed health care capacity ^{[31,32,33,34]}. The second-stage model further considers the factor of health care capacity and is given as follows:

where $ X(t) = X_1(t)+X_2(t) $ represents cumulative infected cases and $ Y_2(t) = P_0-X_1(t)-X_2(t)-Y_1(t) $ represents the vaccinated uninfected sub-population. The function

is a factor related to vaccination rate with the maximum vaccination rate $ \beta_2 $. Note that $ \gamma(t) $ is modeled by an S-curve. Vaccination plays an important role in controlling the spread of the disease. Due to rapid development of COVID-19 vaccines, doubts and worries of vaccination safety lead to hesitancy or refusal initially ^[35]. Many people preferred to wait until others have taken the vaccine ^[36]. However, vaccination willingness changed over time, where vaccination refusal was reported from $ > $70% in March 2020 to $ < $50% in October 2020 ^[36]. Another research study reported an increase in vaccine acceptance during a study period from February to September 2020 ^[37]. The behavioral response to vaccination acceptance can be related to adoption and diffusion of technology which is often described by the S-curve ^[28]. The vaccination rate depends on the size of unvaccinated sub-populations $ X_1 $ and $ Y_1 $. A factor $ X_1/(h_1+X_1) $ is incorporated into the term of vaccination rate. This factor describes the situations that the rate of change of vaccination is determined by vaccination willingness, $ \gamma(t) $, if a considerable population is unvaccinated ($ X_1 > > h_1 $ or $ X_1/(h_1+X_1)\approx 1 $). The rate of change of vaccination decreases and becomes small as majority of the population are vaccinated ($ X_1 < < h_1 $ or $ X_1/(h_1+X_1)\approx 0 $). Furthermore, the factor $ X_1/(h_1+X_1) $ can also prevent the solutions from becoming negative.

Let $ \tau_3 $ be the average number of days that a COVID-19 patient is hospitalized for. The function $ H(t) \in [0, 1] $ represents the utilization factor of health care resources. Due to limited health care resources available for COVID-19 patients, we assume that the portion of COVID-19 patients who can be admitted to hospital depends on $ H(t) $. When $ H(t) < < 1 $ ($ 1-H(t)\approx 1 $), ample health care resources are available for COVID-19 patients; the patients with positive test results can be admitted to hospital. In contrast, $ H(t)\approx 1 $ represents the situation when available health care resources have been fully employed. In this case, few or none COVID-19 patients can be admitted to hospital. Let $ H_{\tau_3}(t) $ represent the number of patients being hospitalized. For simplicity, we shall assume that these patients do not contribute to the propagation of the disease. Since $ (1-H(t))(\alpha(t-\tau_1))(dX(t-\tau_1)/dt) $ represents the rate of change of these individuals,

represents the number of patients being hospitalized at $ t $. We model the utilization factor of health care resources using $ H(t) = \frac{H_{\tau_3}(t)}{h_2+H_{\tau_3}(t)} $ which depends on the number of patients being hospitalized at $ t $. Thus

Since $ \tau_2 $ represents the average time period it requires to recover from the disease, we use $ \tau_3 = \tau_2 $ in this paper.

3.   Parameter fitting and numerical simulation

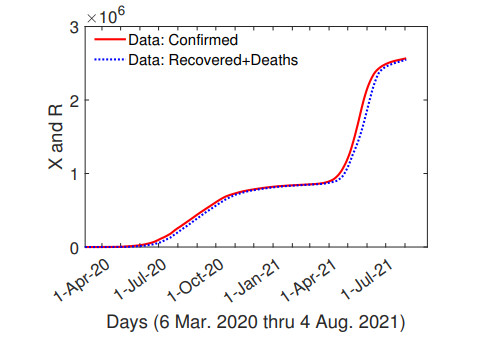
The parameter values in the mathematical model are fitted using the daily reported data of Tamil Nadu of India. The dataset is taken from ^[38], a repository supported by Center for Systems Science and Engineering (CSSE) at Coronavirus Resource Center of John Hopkins University (JHU) through GitHub. The features, in daily reported data, related to Eqs (12) and (13) are "Confirmed", "Deaths", "Recovered" and "Active", where Confirmed equals the sum of Deaths, Recovered, and Active. The data for the feature Confirmed is used to fit the cumulative cases $ X(t) $. Figure 4 shows that the sum of Deaths and Recovered in daily reported data follows the same progression as Confirmed with a delay of roughly 10 days. Note that the mathematical analysis (Eq (10)) agrees with this property. The sum of Deaths and Recovered is used to fit $ R(t) $. In the second-stage model, $ X_2(t)+Y_2(t) $ represents the number of individuals who received at least one dose of vaccine in the data. The vaccination data for Tamil Nadu is not available. To work around this, the daily vaccination data for India is downloaded from ^[39]. Consider populations of $ 7.8 \times 10^7 $ persons and $ 1.4 \times 10^9 $ persons in Tamil Nadu and India, respectively ^[40]. The India Express reported that over 76% of eligible population have received at least one dose of COVID vaccine on 25 November 2021. Daily vaccination data for India shows that 776, 515, 911 individuals (about 55.5% of the population) in India had received at least one dose of COVID vaccine by 25 November 2021. Let $ f = (0.76\cdot 7.8\times 10^7)/(0.555\cdot 1.4\times 10^9) = 0.076 $, and let $ N(t) $ be the number of individuals in India that had been vaccinated. Then, $ fN(t) $ is used to estimate the number of individuals in Tamil Nadu who had been vaccinated. The lock-down dates are taken from lock-down orders posted in https://www.tn.gov.in/go_view/dept/26 by Tamil Nadu government. Two periods of lock-down orders took place in 2020, 8 April 2020 through 15 September 2020 and 28 October 2020 through 30 November 2020.

Figure 3.  Schematic of Eqs (14) and (17). $ X_1 $, $ X_2 $, $ Y_1 $, and $ Y_2 $ represent the numbers of unvaccinated infected, vaccinated infected, unvaccinated susceptible, and vaccinated susceptible individuals, respectively. $ R $ and $ X_1+X_2-R $ represent the removed and infectious populations.

DownLoad: Full-Size Img PowerPoint

Figure 4.  The removed population $ R $ follows the dynamics of the infected population $ X $ with a delay of roughly 10 days.

DownLoad: Full-Size Img PowerPoint

3.1.   Parameter values for the first-stage model

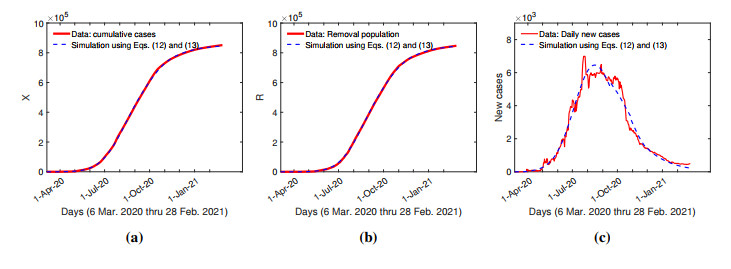
The daily reported data of COVID-19 cases from 6 March 2020 to 28 February 2021 (359 days) along with the lock-down information is used to estimate the parameter values for the first-stage model, Eqs (12) and (13). Let $ T = 359 $ be the number of days from 6 March 2020 to 28 February 2021. Let $ \tilde{X}_i $ and $ \tilde{R}_i $, $ i = 0, 1, \cdots, T $ be Confirmed and the sum of Deaths and Recovered from the daily reported data, respectively. Equations (12) and (13) are integrated over $ [0, T] $ using Euler's method with $ \Delta t = 0.01 $ day. Ten parameters listed in Table 1 are to be fitted using 360 data points. The parameter values are determined by solving the minimization problem $ \min \sqrt{\sum_{i = 0}^T (X(i)-\tilde{X}_i)^2}+\sqrt{\sum_{i = 0}^T (R(i)-\tilde{R}_i)^2} $. The Nelder Mead simplex method ^[41] is employed to solve the least square error of the fitting. The Nelder Mead simplex method is an iterative method. The Matlab build-in functions fminsearch can also fulfill the tasks. In the fitting process, we set 200 for the maximum number of iteration. The fitting process is executed a few times until the evolution of $ X(t) $ and $ R(t) $ agrees with the daily reported data. Figure 5 shows the fitting results with $ \sqrt{\sum_{i = 0}^T (X(i)-\tilde{X}_i)^2}+\sqrt{\sum_{i = 0}^T (R(i)-\tilde{R}_i)^2} = 1.3\times 10^5 $ (persons) and with the parameter values determined and summarized in Table 1. The parameter fitting result shows that the intrinsic infection rate in Tamil Nadu is $ 0.2053 $ day$ ^{-1} $ which is between the growth rates initially and after measures for the regions studied by Alvarez et al. ^[23].

Table 1.  Parameter values in Eqs (12) and (13).

Parameter	Brief Description	Value	Units	Reference
$ P_0 $	$ 7.8\times 10^7 $	Population of Tamil Nadu State, India	individual	[40]
$ \mu_1 $	0.2053	Intrinsic infection rate	Day$ ^{-1} $	fitted with data [38]
$ \beta_1 $	0.0484	Unlock-down factor	Dimensionless	fitted with data [38]
$ M_1 $	0	Pre-experience in $ \sigma $	Dimensionless	fitted with data [38]
$ t_1 $	29	Time parameter in $ \sigma $	Day	fitted with data [38]
$ k_1 $	0.1935	Steepness of $ \sigma $	Day$ ^{-1} $	fitted with data [38]
$ L_1 $	0.4533	Maximum increase in $ \sigma $	Dimensionless	fitted with data [38]
$ M_2 $	0	Pre-experience in $ \alpha $	Dimensionless	fitted with data [38]
$ t_2 $	105	Time parameter in $ \alpha $	Day	fitted with data [38]
$ k_2 $	0.0248	Steepness of $ \alpha $	Day$ ^{-1} $	fitted with data [38]
$ L_2 $	0.6405	Maximum increase in $ \alpha $	Dimensionless	fitted with data
$ \tau_1 $	4	Delay in detection	Day	[23]
$ \tau_2 $	14	Recovery time	Day	[30]

---

 | Show Table

DownLoad: CSV

Figure 5.  Population dynamics for Eqs (12) and (13) with parameter values shown in Table 1. $ X $ and $ R $ represent the infected and removed populations, respectively. The number of new cases are computed using $ X_{i}-X_{i-1} $ and $ X(i)-X(i-1) $, $ i = 1, 2, \cdots T $, for the observations and simulation, respectively.

DownLoad: Full-Size Img PowerPoint

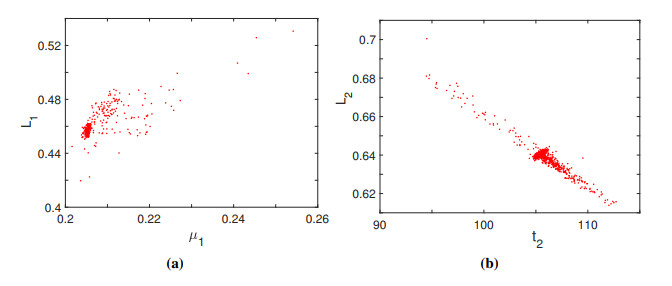
Parameter estimation of dynamical systems is often associated with parameter uncertainty due to data errors and computational errors in parameter fitting processes. The analysis of parameter uncertainty is important as it determines how reliable the model outputs are. Bootstrap method is a popular technique for assessment of parameter uncertainty due to its simplicity. A bootstrapping sampling was proposed for assessment of parameter uncertainty of a mathematical model of population dynamics ^[42]. This method can be directly applied to the analysis of parameter uncertainty in this paper. A random sample with replacement of size $ T+1 $ is drawn over $ \{0, 1, \cdots, T\} $. After discarding the repeated numbers, we have $ 0\leq t_1 < t_2 < \cdots < t_I\leq T $. The parameter values are estimated using the datasets $ \tilde{X}_{t_i} $ and $ \tilde{R}_{t_i} $, $ i = 1, \cdots, I $ with the parameter values listed in Table 1 as the initial guess. The Nelder Mead simplex method is performed for 500 iterations to obtain the bootsrtap estimates of parameter values. The above parameter estimation process with resampling is repeated 1000 times. The bootstrap statistics are shown in Table 2. As about 95% of the data values of a distribution usually fall within 2 standard deviations from the mean. The intervals [Mean-2Std, Mean + 2Std] are given in Table 2. These narrow intervals and small standard deviations show that the bootstrap estimates of parameter values closely distributed around the mean values. The parameter values used for the first-stage model (Table 1) are rather close to these mean values of bootstrap estimates and lie within the intervals of Mean $ \pm $ 2 $ \times $ Std. Further investigation of correlations between parameters has shown that the correlation coefficients of $ \mu_1 $ and $ L_1 $ and of $ t_2 $ and $ L_2 $ are 0.77 and –0.96, respectively. Figure 6 shows the plots of their distributions. These plots also show that these bootstrap estimates are densely distributed around the mean values. All other parameters show no correlation or weak correlation with each other.

Table 2.  Bootstrap statistics, first wave, 1000 bootstrap samples.

Parameter	$ \mu_1 $	$ M_1 $	$ t_1 $	$ k_1 $	$ L_1 $
Mean	0.2064	0	29.3	0.1786	0.4565
Std	0.004	0	0.9	0.0233	0.0081
Mean $ \pm $ 2Std	[0.1984, 0.2144]	[0, 0]	[27.5, 31.1]	[0.1320, 0.2252]	[0.4403, 0.4727]
Parameter	$ \beta_1 $	$ M_2 $	$ t_2 $	$ k_2 $	$ L_2 $
Mean	0.0485	0	105.7	0.0249	0.6395
Std	0.0017	0	2	0.0004	0.0076
Mean $ \pm $ 2Std	[0.0451, 0.0519]	[0, 0]	[101.7, 109.7]	[0.0241, 0.0257]	[0.6243, 0.6547]

---

 | Show Table

DownLoad: CSV

Figure 6.  Two dimensional distributions, using 1000 bootstrap samples, for (a) $ \mu_1 $ and $ L_1 $, and (b) $ t_2 $ and $ L_2 $.

DownLoad: Full-Size Img PowerPoint

3.2.   The effect of lock-down, social distancing, and detection of positive cases

The parameter $ \beta_1 $ is related to the lock-down effect. The infection rate is reduced by $ 1-1/(1+\beta_1) = 4.6\% $ during lock-down, where $ \beta_1 = 0.0484 $. The effect for lock-down is considered insignificant in this paper. The functions $ \sigma(t) $ and $ \alpha(t) $ are plotted in Figure 7 to show the effect of social distancing and efficiency of detection of COVID-19 positive cases, respectively. Figure 7(a) shows that the social distancing factor starts with 0 initially, implying social distancing is considered a new concept in Tamil Nadu during the first wave. The social distancing factor reaches the plateau of 0.4533 around Day 50. Alvarez et al. ^[23] used social distancing factors increasing form 0 on March 10 to 0.75 on March 23, 2000, for New York City (NYC) in their simulation. They also showed that a social distancing factor of about 70% in Mexico City. Compared with the social distancing effect in NYC and Mexico City, our simulation result shows that the social distancing effect in Tamil Nadu increases relatively slowly and levels off at a relatively low level. Chakraborty et al. ^[43] have pointed out that the first wave of COVID-19 infection in India took off in March 2020, and the lack of the use of face covering and compliance with social distancing measures are among significant factors that cause the fast spread of COVID-19 in India.

Figure 7.  The functions (a) $ \sigma(t) $ and (b) $ \alpha(t) $ in Eqs (12) and (13) with parameter values given in Table 1 for $ M_1 $, $ t_1 $, $ k_1 $, $ L_1 $, $ M_2 $, $ t_2 $, $ k_2 $, and $ L_2 $.

DownLoad: Full-Size Img PowerPoint

Figure 7(b) shows that detection of positive cases does not start with zero performance meaning that although COVID-19 is a novel disease, health care professionals adopt new skills through prior experience. The function $ \alpha(t) $ starts with a low level of 0.05 and slowly increases to a plateau of 0.64 over several months. In the simulation example for NYC, Alvarez et al. ^[23] used $ \alpha $ values from 0 to 0.76 in two weeks, from March 20 to April 7, 2020. They also reported that South Korea implemented widespread testing with $ \alpha \approx 0.98 $ in controlling the spread of the disease whereas Mexico City suffered from a low level of testing with $ \alpha = 0.1 $. Compared with NYC and South Korea, the detection of positive cases in Tamil Nadu is relatively ineffective.

To study the effect on the evolution of COVID-19 cases caused by the change in $ \sigma $, we enhance $ L_1 $ by 10%. Let $ L_1 = 0.498 $ and all parameter values are kept the same as in Table 1. Figure 8(a) shows the evolution of cumulative cases $ X(t) $; the spread of COVID-19 can be effectively controlled by improving social distancing behaviors. Next, we enhance $ L_2 $ by 10%. Let $ L_2 = 0.704 $ which increases the detection rate. Figure 8(b) shows that the number of cumulative cases $ X(t) $ decreases dramatically. Comparing Figures 8(a) and (b), the effectiveness in controlling the spread of COVID-19 by enhancing detection rate is not as significant as that by improving social distancing measures. The simulation suggests that implementing non-pharmaceutical interventions may be an effective method to slow the spread of COVID-19.

Figure 8.  The evolution of the cumulative cases produced using Eqs (12) and (13) with all parameter values kept the same as in Table 1 except for (a) $ L_1 = 0.498 $ and (b) $ L_2 = 0.704 $. $ X $ represents the infected population.

DownLoad: Full-Size Img PowerPoint

3.3.   Parameter values for the second-stage model

It has been reported that the efficacy of all COVID-19 vaccines exceeds 70% ^[44], and the RNA based vaccines are highly efficacious, with an efficacy over 92% ^[44,45]. The vaccine efficacy varies over time ^[45]. The vaccination data used in this study contains individuals who have received one or two doses. Based on the above reported efficacy of COVID-19 vaccines, we assume a collective vaccine efficacy of 80% and let $ \mu_2 = 0.2\mu_1 $ in the parameter fitting process. We also assume that the vaccination willingness is the main factor determining the vaccination rate; a relatively small value $ h_1 = 10^4 $ (persons) is used in this paper, compared with the population $ P_0 $ in Tamil Nadu. For the utilization factor of health care resources, $ h_2 = 5\times 10^5 $ (persons) is assumed, which is about one percent of $ P_0 $. The daily reported data of COVID-19 cases and vaccination from 1 March 2021 to 4 August 2021 (156 days) are used to estimate the parameter values for the second-stage model.

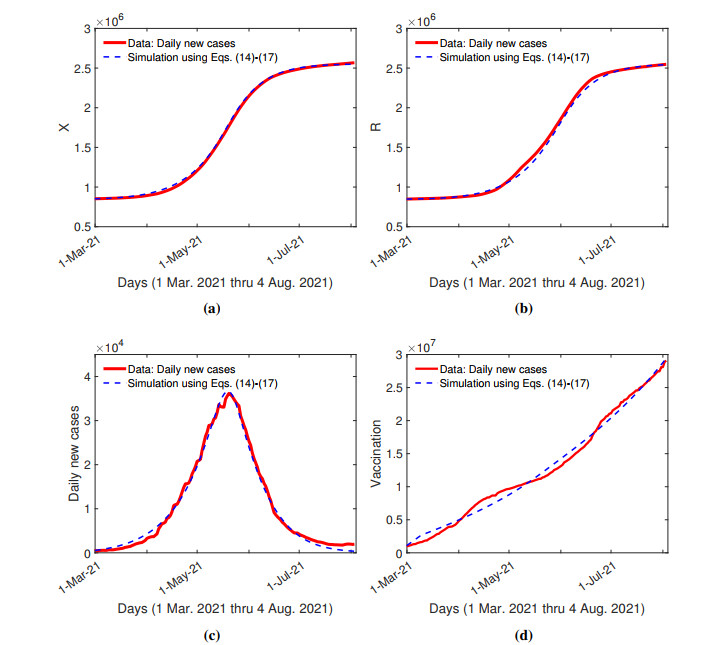
Let $ \tilde{X}_i $, $ i = 0, 1, 2, \cdots, 156 $, be the cumulative COVID-19 cases from daily reported data. We fit $ X_1(t)+X_2(t) $ to $ \tilde{X}_i $. Note that $ X_1(t)+X_2(t) $ represents the cumulative COVID-19 cases in the mathematical model. Let $ \tilde{V}_i $, $ i = 0, 1, 2, \cdots, 156 $, be the number of vaccinated individuals from the vaccination dataset. We fit $ P_0-(X_1(t)+Y_1(t)) $, which represents the number of vaccinated individuals in the mathematical model, to $ \tilde{V}_i $. Let $ \tilde{R}_i $, $ i = 0, 1, 2, \cdots, 156 $, be the sum of Recovery and Deaths from daily reported data. The removed population $ R(t) $ is fitted to $ \tilde{R}_i $. The fitting process is the same as that used for the first-stage model. Equation (20) is approximated by the left-hand sum with $ d\xi = 0.01 $ day. Fourteen parameters listed in Table 3, including $ \mu_1 $, $ \beta_2 $, $ L_i $, $ M_i $, $ k_i $, $ t_i $, $ i = 1, 2, 3 $, are to be fitted. The parameter values are determined by minimizing $ \sqrt{\sum_{i = 0}^T (X_1(i)+X_2(i)-\tilde{X}_i)^2}+\sqrt{\sum_{i = 0}^T (R(i)-\tilde{R}_i)^2}+0.3\times \sqrt{\sum_{i = 0}^T (V(i)-\tilde{V}_i)^2} $, where $ T = 156 $. Figure 9 shows the fitting results with $ \sqrt{\sum_{i = 0}^T (X_1(i)+X_2(i)-\tilde{X}_i)^2}+\sqrt{\sum_{i = 0}^T (R(i)-\tilde{R}_i)^2}+0.3\times \sqrt{\sum_{i = 0}^T (V(i)-\tilde{V}_i)^2} = 3.6\times 10^6 $ (persons) and with the parameter values determined and summarized in Table 3. The infection rate $ \mu_1 = 0.227 $ day$ ^{-1} $ is higher in the second wave than that in the first wave. India scientists have reported mutant variants which are more infectious in the second wave, and India experienced the exponential growth of COVID-19 infection beginning in March 2021 ^[43,46]. Figure 4 shows that in the first and second waves, the number of COVID-19 cases was growing exponentially in March 2020 and March 2021, respectively.

Table 3.  Parameter values in Eqs (14)–(17). HSC represents half saturation constant. HCR represents health care resources.

Parameter	Value	Brief Description	Units	Reference
$ P_0 $	$ 7.8\times 10^7 $	Population of Tamil Nadu State, India	individual	[40]
$ \mu_1 $	0.227	Intrinsic infection rate	Day$ ^{-1} $	fitted with data [38,39]
$ \mu_2 $	0.0454	Infection rate after vaccinated	Day$ ^{-1} $	assumed, based on [44,45]
$ \beta_1 $	0.0484	Unlock-down factor	Dimensionless	fitted with data [38]
$ h_1 $	$ 10^4 $	HSC of vaccination	Individual	assumed
$ M_1 $	0.43	Pre-experience in $ \sigma $	Dimensionless	fitted with data [38,39]
$ t_1 $	83.9	Time parameter in $ \sigma $	Day	fitted with data [38,39]
$ k_1 $	0.2421	Steepness of $ \sigma $	Day$ ^{-1} $	fitted with data [38,39]
$ L_1 $	0.265	Maximum increase in $ \sigma $	Dimensionless	fitted with data [38,39]
$ h_2 $	$ 5\times 10^5 $	HSC of HCR	Individual	assumed
$ M_2 $	0.3491	Pre-experience in $ \alpha $	Dimensionless	fitted with data [38,39]
$ t_2 $	-5.8882	Time parameter in $ \alpha $	Day	fitted with data [38,39]
$ k_2 $	-0.6178	Steepness of $ \alpha $	Day$ ^{-1} $	fitted with data [38,39]
$ L_2 $	0.5406	Maximum increase in $ \alpha $	Dimensionless	fitted with data [38,39]
$ M_3 $	0.0216	Pre-experience in $ \gamma $	Dimensionless	fitted with data [38,39]
$ t_3 $	282.2	Time parameter in $ \gamma $	Day	fitted with data [38,39]
$ k_3 $	0.0163	Steepness of $ \gamma $	Day$ ^{-1} $	fitted with data [38,39]
$ L_3 $	0.7209	Maximum increase in $ \gamma $	Dimensionless	fitted with data [38,39]
$ \beta_2 $	3155833	Maximum vaccination rate	Individual Day$ ^{-1} $	fitted with data [38,39]
$ \tau_1 $	4	Delay in detection	Day	[23]
$ \tau_2 $	14	Recovery time	Day	[30]
$ \tau_3 $	14	Hospitalization time	Day	[30]

---

 | Show Table

DownLoad: CSV

Figure 9.  Population dynamics for (a) the infected population ($ X $ = $ X_1+X_2 $), (b) the removed population ($ R $), (c) new cases ($ X(i)-X(i-1) $, $ i = 1, 2, \cdots, T $), and (d) the vaccinated population ($ P_0-X_1-Y_1 $) with simulation using Eqs (14)–(17) and parameter values given in Table 3.

DownLoad: Full-Size Img PowerPoint

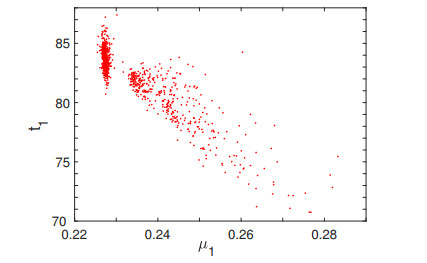
The bootstrap statistics for the parameters of the second-stage model are shown in Table 4. Similarly, small standard deviations for bootstrap estimates are found for the second-stage model. The parameter values used for the second-stage model (Table 3) are rather close to these mean values. The bootstrap statistics show no correlation or weak correlation between all parameters except for $ \mu_1 $ and $ t_1 $ with a correlation coefficient of –0.9 (Figure 10).

Table 4.  Bootstrap statistics, second wave, 1000 bootstrap samples.

Parameter	$ \mu_1 $	$ M_1 $	$ t_1 $	$ k_1 $	$ L_1 $
Mean	0.2339	0.4304	82.2	0.2363	0.2658
Std	0.01	0.0011	2.6	0.0391	0.0082
Mean $ \pm $ 2Std	[0.2139, 0.2539]	[0.4282, 0.4326]	[77, 87.4]	[0.1581, 0.3145]	[0.2494, 0.2822]
Parameter	$ M_2 $	$ t_2 $	$ k_2 $	$ L_2 $
Mean	0.3574	-5.53	-0.6341	0.5625
Std	0.0219	0.52	0.0803	0.0318
Mean $ \pm $ 2Std	[0.3136, 0.4012]	[-6.57, -4.49]	[-0.7947, -0.4735]	[0.4989, 0.6261]
Parameter	$ M_3 $	$ t_3 $	$ k_3 $	$ L_3 $	$ \beta_2 $
Mean	0.0221	282	0.0165	0.7264	$ 3.1757\times 10^6 $
Std	0.0015	7	0.0007	0.0528	$ 1.872\times 10^5 $
Mean $ \pm $ 2Std	[0.0191, 0.0251]	[268,296]	[0.0151, 0.0179]	[0.6208, 0.832]	$ [2.8013, 3.5501]\times 10^6 $

---

 | Show Table

DownLoad: CSV

Figure 10.  Two dimensional distributions for $ \mu_1 $ and $ t_1 $ using 1000 bootstrap samples.

DownLoad: Full-Size Img PowerPoint

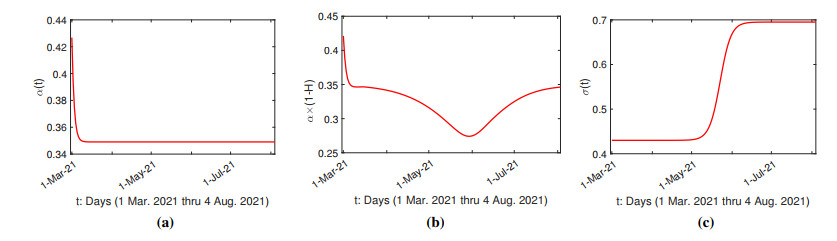
3.4.   The effect of social distancing and detection of positive cases for the second wave

During the second wave, major hospitals faced a shortage of hospital beds, medicines, oxygen and ventilator supplies, leading to high mortality ^[43,46]. The detection rate $ \alpha(t) $, shown in Figure 11(a), is lower compared with that in the first wave (Figure 7(b)). The parameters $ k_2 $ and $ t_2 $ are negative indicating that the detection rate $ \alpha(t) $ is decreasing and $ \alpha(t) $, for $ t\geq 0 $, contains only the lower part of the curve. The detection rate decreases quickly initially, levels off soon, and remains at a low level. Combining this effect with shortage of health care resources, Figure 11(b) shows that the overall rate of hospitalization of the positive cases continue to decrease over time. Shortage of health care resources is one of the factors responsible for fast increased number of cases in Tamil Nadu ^[46]. Jain et al. ^[46] suggested that prevention was better than cure for this disease and the implementation of social distancing and the use of face masks was able to help with controlling the disease. Figure 11(c) shows that during the first two months of the second wave, implementation of social distancing is not effective and remains at the same level as that in the first wave. Then, the social distancing effect increases during May and Jun 2021 and levels off at about 0.7 which is much higher than that during the first wave. Chakraborty et al. ^[43] pointed out that social distancing was not strictly implemented during the first wave in India due to crowded style of living arrangement. Our study shows that people in Tamil Nadu may have learned their lessons and follow social distancing measures after some time in the second wave. Nevertheless, a factor of 0.7 for social distancing measures is not effective compared with other cities studied in ^[23].

Figure 11.  The functions (a) $ \alpha(t) $, (b) $ \alpha \times (1-H) $, and (c) $ \sigma(t) $ in Eqs (14)–(17) with parameter values given in Table 3.

DownLoad: Full-Size Img PowerPoint

4.   Conclusions

In this paper, mathematical models using deterministic ODEs with time delays are proposed for the study of impacts of pharmaceutical and non-pharmaceutical factors on the COVID-19 pandemic for the state of Tamil Nadu, India. The first-stage model, designed for the first wave in the region, considers two populations, the population of infected individuals and the population of removed individuals. The second-stage model, designed for the second wave, considers four populations, unvaccinated infected population, vaccinated infected population, unvaccinated uninfected population, and removed population. Some factors such as social distancing, detection efficiency, and vaccination willingness are modeled by learning curves. Daily reported data supported by CSSE at Coronavirus Resource Center of JHU are used to fit the model ^[38,39] and to determine the parameter values. The model produces a close match to the evolution of COVID-19 in Tamil Nadu (Figures 5 and 9).

The preliminary results obtained from the simulation indicate that the lock down contributed limited effects on controlling the spread of the disease in Tamil Nadu. The social distancing implementation and detection of positive cases are relative ineffective compared with some big cities studied by Alvarez et al. ^[23] in the first wave. These observations are in agreement with the research report that social distancing was not strictly implemented during the first wave in India ^[43]. The implementation of social distancing remains at a low level during the first half period of the second wave but is improved after some time in the second wave (Figure 11(c)). The detection efficiency and hospitalization rate decrease rapidly and remains at low levels over the second wave (Figure 11(a), (b)). Jain et al. ^[46] pointed out that Tamil Nadu faced shortage of health care resources during the second wave of COVID-19. The impacts of other factors will also need to be considered and is currently under future research directions of the authors.

Acknowledgments

A Shankaranarayanan was supported by the Ministry of Science and Technology (MOST) of Taiwan under the grant no. MOST 110-2222-E-035-002; H.-C. Wei was supported by the MOST of Taiwan under the grant no. MOST 110-2115-M-035-004.

Conflict of interest

The authors declare there is no conflict of interest.