A novel numerical method for stochastic conformable fractional differential systems

1.   Introduction

The systematic analysis of reaction-diffusion models started with the seminal work by Kolmogorov, Petrovskii and Piskunov (see ^[1]), to predict the kinetic of gases in a model of combustion and by Fisher (see ^[2]) to understand the mechansims of genes interactions in bioloy. In both cases, the authors proposed a parabolic operator based on the classical order two Laplacian. This operator comes from the application of the Fick law, used to model the global particles motion in a domain. In parallel, the authors established a new conception in the search of solutions which has been of great interest in the last decades. We refer to Travelling Waves solutions. This was a remarkable idea inspired by the fact that any evolution, under the scope of a parabolic operator, shall propagate with a certain velocity (as main driver of the involved dynamics) which may define the shape of the solutions.

Since its very early formulation, the Fisher-KPP model has attracted the interest of applied scientists, as well as theoreticians. In particular, some other principles in connection with diffusion have been considered in ^[3,4,5]. Further, the Fisher- KPP model has been analyzed with more complex forms of operators, see for example the heterogeneous diffusion of a higher-order ^[6], the density and gradient dependant p-Laplacian ^[7] and the non-local diffusion given by a fractional operator ^[8].

Typically, the modelling of diffusion has been focused on the definition of the energy of motion. In the last few decades, the mathematical theories concerning nonlinear operators has developed strongly. This fact has permitted to model diffusion based on the mathematical properties introduced by such operators, along with an identification of the physical observations. In this regard, we can mention the references [9] and [10] where perturbation terms were introduced in the form of nonlinear diffusive operators. Further, in ^[11] and ^[12] the oscillatory behavior of solutions was shown to hold for the perturbed Fisher-Kolmogorov equation. Furthermore, other approaches to diffusion can be observed in the literature; in ^[13] fractional-in-space operators were considered to model anomalous diffusion. The authors started from the standard Brownian motion and they introduced fractional order operator in the sense of the Riesz derivative. In addition, the authors in ^[14] introduced a new Laplace residual power series algorithm to solved a nonlocal diffusion based in the Caputo derivative and it was applied to a biological problem in connection with bacteria growth systems. Some recent techniques based on homotopy and multigrid method have been considered recently to solve difficult diffusion-convection problems (e.g., ^[15,16,17]) as well as techniques based on a wavelet multiscale method ^[18]. In addition, in ^[19], the authors provided new conceptions based on Bayesian analysis to validate the selection of a model for biological applications.

In the presented analysis, we focus our attention on the particular interaction between two biological species, namely invasive-invaded. To this end, we shall consider the definition by the Convention of Biological Diversity (p.1, Ch.1 ^[20]) in what regards with invasive species: "...those alien species which threaten ecosystems, habitats or species".

The invasive-invaded dynamics has been an active area of mathematical research. In ^[21], the authors analyzed the haptotactic cell motion, based on an invasive dynamics to model the formation of melanoma. Further, the study in ^[22] examined the stability of travelling wave solutions based on spectral techniques to predict the cancer formation by haptotaxis processes. In this study, the authors made use of the Evans functions, formulated for a previously linearized diffusion. We should mention that, in the last two references, the diffusion was based on the classical order two Laplacian.

The process of invasion has been typically modelled with the involvement of only two species. Given an invasive species concentration $w$ that arrives at a new territory previously occupied by another species of concentration $v$, the following model concretes some of the further general works by Bramson about Fisher-KPP models (for further discussions, the reader is referred to the techniques exposed in ^[23] by the same author):

where $D_v$ and $D_w$ are the specific diffusion rates of each species, $r_v$ and $r_w$ are the specific rates of increase and the $\alpha$ coefficients are defined the intraspecific and interspecific competition balances.

To introduce a justification of the newly proposed model, we must start from the last model in (1.1) and we considered the following additional principles:

● An invasion may occur in a predominant direction. For instance, in the invasion of a cell, any virus can penetrate through a damage in the cell membrane. Similarly, this can be observed in the invasion of a country which may start by the zones where the supplying goods to the main cities are hosted.

With the intention of modeling the existence of a preferred direction of invasion, we introduce an advection given by the terms $c \cdot \nabla v$ and $c \cdot \nabla w$ in the previously mentioned model studied by Bramson. The advection vector is considered to be the same for both species, as there exists a common front where the species fight.

● Once the invasive species arrives at a the domain to conquer, the invasion process related with diffusion shall be carefully assessed for finding accurate forms of motion. The selection of an adequate diffusion is supported by the mathematical properties of the associated parabolic operator and its possibilities to describe the observations in a real situation. Generally, we can think that the involved diffusion shall be inherently nonlinear and dependant on the population density. Indeed, once the invasive species arrives at the new domain, there exists a propagating dynamics that may not be fully reproduced by the Gaussian order two diffusion (we recall that this operator induces positive solutions everywhere). This observation makes the order of two diffusions imprecise as the positivity property is not fully compatible with the existence of a propagating front in the invasive species, wherein the diffusivity is further heterogeneous. As a consequence, a study has been conducted to select the most appropriate diffusive operator. Namely and for a general and sufficiently regular function $v$, we considered the following operators: Porous Medium Equation ($\nabla \cdot (v^{m-1} \nabla v), m > 1$), Higher-order ($-(- \Delta)^p \, v \, , \, p\geq 2)$, Thin film ($-\nabla \cdot (\vert v \vert^n \nabla \Delta v), \, n > 0$) and p-Laplacian ($\nabla \cdot (\lvert{\nabla v}\rvert^{p-2} \, \nabla v) \, , \, p > 1$).

In addition, we have carried out a review on the existing literature dealing with biological problems formulated with nonlinear diffusion operators. The celebrated model by Keller and Segel (refer to ^[24] for dedicated insights) was considered as a starting point. Herein, the diffusion is given by a density dependant diffusivity. Another related analyses are provided in ^{[25,26,27,28]} where additional dynamics are observed in other scenarios.

Based on the mentioned ideas, the following problem is proposed:

Note that the second equation in (1.2) includes the reproducing term $r_w > 0$ that represents the renewal of forces in the invasive species to make the invasion prosper. It includes, as well, a positive intraspecific term $w$ which includes all forms of generating new invasive agents to conquer the territory. In addition, the interspecific term $\alpha_{wv}$ is the mortality of invasive species because of the action battle with the invaded one. The first equation in (1.2) includes a reproducing term $r_v$ in the invaded species. The intraspecific $\alpha_{vv}$ and interspecific $\alpha_{vw}$ coefficients represent the invaded species death rates because of the action of the invasion. The term $\alpha_{vv}$ can be associated to the deaths due to possible disease and hunger conditions and $\alpha_{vw}$ represents the mortality rate in the battle against the invasive species. All the mentioned coefficients shall be correctly rescaled in a particular application so that the carrying capacity in the medium does not impact the postulated equation.

We should mention that the domain is given in the whole space $\mathbb{R}^d, \, \, d > 1$, no boundary conditions are considered. This is done to study the problem dynamics openly with no additional restrictions at any border. Our attention is then focused on the characterization of the system interaction and the species balance rather than geometrical restrictions. Precisely speaking, there is a restriction in what regards with the behavior at infinity, as we will discuss the problem with the support of a test function that shall be requested to be null, or small in the tail at $\vert x \vert \rightarrow \infty$.

The paper layout is as follows: First, the analysis introduces topics related with the regularity and boundedness of solutions together with their existence and uniqueness. The fact of modeling with a nonlinear diffusion (particularly with a density dependant diffusivity) makes us to introduce the analysis supported by a weak formulation. To this end, we will introduce a test function $\Upsilon \in C^{\infty} (\mathbb{R}^d)$. Afterward, the profiles of solutions are explored within a travelling wave formulation. This permits to understand the involved dynamics given in the species during the invasion.

2.   Regularity and uniqueness of solutions

Definition 1. (Parabolic operator). Consider a function $\aleph \in C^{2+\nu, \, 1+\nu/2} (\mathbb{R}^3 \times (0, T))$ with $\aleph^p \in C^{2+\nu} (\mathbb{R}^d \times (0, T))$ for any $\nu > 0$ and such that $p$ may be either $n$ or $m$ (refer to (1.2)). The following operator $\mathcal{L}$ is given by:

Note that $\varepsilon$ may be $D_v$ or $D_w$ according to the problem (1.2).

The nonlinear diffusion introduced in (1.2) is density dependant with the associated diffusivity terms

where $n > 0$ and $m > 0$. According to ^[29], in case of $n$, $m$ or both are in the interval $(0, 1)$, the problem is driven by a fast diffusion while for any value higher than the unity, the diffusion is referred as slow. This last condition is particularly relevant as, according to ^[29], the slow diffusion induces the existence of a diffusive front for compactly supported functions that propagates in the domain with finite speed. The front may be regarded as a trace, such that in the inner region the invasive species exists while in the outer region the invasive species is null. This is, the invasive one does not arrive at that territory yet. The existence of such a front means that globally the invasive species reach the territory and expand following such a diffusive front.

We should mention that both species are considered to be positive or slightly positive in the propagating front and locally in a time interval $(0, T]$ for a $T$ sufficiently small to preserve the parabolicity of the operator $\mathcal{L}$. Furthermore, the physical interpretation of the problem leads us to assume that both solutions (referring to a volumetric or mass concentrations) are below one and positive at the moment of the interaction. Based on these principles, we can make use of the arguments about uniqueness and regularity of solutions provided in ^{[30,31,32,33]}. In our case, there exists a remarkable difference compared to such references given by the particular invasive-invaded dynamics considered in the independent terms of (1.2).

Based on the discussed local parabolicity of the operator $\mathcal{L}$ for positive or slightly positive solutions, the following holds:

Definition 2. (Maximum and minimum solutions). Assume a set of two pairs of solutions: Maximum solutions, $(\hat{v}, \hat{w})$ $\in C^{2+\nu, \, 1+\nu/2} (\mathbb{R}^d \times (0, T))$, and minimum solutions, $(\tilde{v}, \tilde{w})$ $\in C^{2+\nu, \, 1+\nu/2} (\mathbb{R}^d \times (0, T))$. The set $(\hat{v}, \hat{w})$ of maximum solutions satisfies:

The pair formed by $(\tilde{v}, \tilde{w})$ is a minimum solution, if the following condition holds:

Consider now:

where:

and $\delta_0$ shall comply with:

Given the inner parabolicity of the operator $\mathcal{L}$ for positive solutions and the continuity of the forcing terms, it is possible to state on the following preliminary regularity condition: $(\hat{v}, \hat{w})$ and $(\tilde{v}, \tilde{w})$ $\in L^1 (\mathbb{R}^d \times (0, T))$ (for additional insights refer to ^[34] and Ch. 3 in ^[35]).

Now, consider a sequence of solutions given by $(v^{(i)}, w^{(i)})_{i = 0, 1, 2, ...}$ and defined as per the following set of equations:

The study of existence and uniqueness of each element of the sequence $(v^{(i)}, w^{(i)})_{i = 0, 1, 2, ...}$ to (2.8) follows from standard analysis based on the mixed monotone properties of the independent terms and the inner parabolicity of the operator $\mathcal{L}$ (refer to the Ch. 3 of ^[35] and the Theorems 2.1 and 2.2, Ch. 7 in ^[36]). It should be noted that (2.8) apply to the maximum and minimum solutions in Definition 2 and for any initial condition as stated in (2.6). As a consequence, each element of the sequences satisfies:

In addition, following well known techniques, it is straightforward to show that the sequence is ordered (see Ch. 12 of ^[36]). Then:

Hence, the sequence of maximum solutions $(\hat{v}^{i)}, \hat{w}^{(i)})$ is nonincreasing while the sequence of minimum solutions $(\tilde{v}^{(i)}, \tilde{w}^{(i)})$ is nondecreasing.

Definition 3. (Weak Formulation). Given a test function $\Upsilon \in C^{\infty} (\mathbb{R}^d \times [0, t])$, with $0 < \vartheta < t < T$, the following weak formulation is defined in $[\vartheta, t]$:

Given any spatial ball with radium $R$, the test function is selected such that any spatial derivative is asymptotically null:

for any $\beta = 1, 2, 3...$ and being $x_0 \gg R$.

Consider the locating point $x_0 \gg R$, and the interval $J_x = (x_0, \infty)$. The interval $J_x$ is taken for the definition of the following problem in the test function tail, this is in $J_x \times [0, t]$:

with the following initial conditions:

Consider now the following truncation for any $0 < \delta_1 < 1$:

where $h$ may be $v$ or $w$ and $b$ = $\lbrace n, m \rbrace$. Based on the defined truncation, the following problem ($P^{\Upsilon}_{\delta_1}$) shall be considered:

together with (2.15).

It should be noticed that the functions $v_{\delta_1}$ and $w_{\delta_1}$ are bounded as per the defined truncation. As a consequence, and based on the initial regularity in $\Upsilon$, the inner parabolicity of $\mathcal{L}$ and the monotone behavior of the forcing terms; we can show the existence and uniqueness of $\Upsilon$ by well known techniques (refer to ^[36]) during the evolution in $J_x = (x_0, \infty)$.

The coming intention is to show that any weak solution, as stated in the Definition 3, is bounded given the invasive-invaded interaction expressed in the independent terms. This results is particularly interesting because the quadratic growth rate in the $w-$equation leads to blow-up without competition between species. Even in the case of a high increase in the invasive species (due to the arrival of new troops to fight or new viruses to infect), the invaded species can make the invasion to slow down impeding the potential formation of global or local in time blow-up phenomena. To support this, we show that the solutions are sufficiently smooth under the scope of the weak formulation. That smoothness indicated that the problem can be studied asymptotically in the test function tail without risk of losing regularity.

Theorem 1. Given a pair of weak solutions $(v, w)$, in accordance with (2.11) and (2.12), such a pair is bounded for $(x, t) \in J_x \times [\vartheta, t]$.

Proof. Given an arbitrary positive $\gamma \in \mathbb{R}$, let us define a cut off function as follows:

In addition, it holds that:

Now, take the weak formulations as per (2.11) and (2.12) for $(x, t) \in J_x \times [\vartheta, t]$ together with a test function verifying $\Upsilon(\vartheta) = \Upsilon(t) = 0$. Then, the following problem is given:

To continue, we shall consider that

where $b$ = $\lbrace n, m \rbrace$ and $u$ can take the values of $v$ and $w$, then the following holds:

In order to show the boundedness of $v$ and $w$ in $J_x \times [\vartheta, t]$, we require the boundedness of the integrals in the right hand side of the last equality. To this end, considering the integration for any spatial variable $R \in J_x$, it holds that (see ^[29]):

Then, the following applies:

Assume now the following test function satisfying the conditions: $\Upsilon(\vartheta) = \Upsilon(t) = 0$:

where $\vartheta \leq \tau \leq T$. It should be noted that $\eta$ is selected to ensure the convergence for $R \in J_x$ of the integral as per (2.24). Then, the following holds

It suffices to consider $\eta = \frac{1}{b-1}$ for a finite integral.

Based on the same form of a test function, the following assessment holds for the advection term:

where $M_s = \max_{\tau \in [\vartheta, T]} \lbrace \Upsilon(\cdot, \tau) \rbrace$. In addition, we shall consider that the solutions represent a mass or volumetric concentration and can take the values $0 < v, w < 1$. The last integral converges for any value $\eta > 0$.

Considering now, the assessment done in (2.26), it suffices to take a value for $\eta$ of the form:

In return to the expression (2.22), it applies that:

The right hand terms are formed of finite constants, hence the previous two inequalities allow us to state on the global boundedness of the solutions $(v, w)$ in $J_x \times [\vartheta, t]$.

Now, considering the Definition 2, and supported by the shown boundedness of solutions as stated in the last result, we show the convergence to a limit of the sequences of maximum and minimum solutions.

Theorem 2. Consider the positive initial distributions $(v_0, w_0) > (0, 0)$ for $x \in J_x$. The sequences of solutions given in Definition 2, $(\hat{v}^{(i)}, \hat{w}^{(i)})$ and $(\tilde{v}^{(i)}, \tilde{w}^{(i)})$ $\in C^{2+\nu, \, 1+\nu/2} (J_x \times (0, T))$ converge with a monotone behavior.

Proof. First, we consider the weak formulation in the Definition 3 for each element of the maximum and minimum sequences. For this purpose, assume the test function given in (2.25) and such that $\Upsilon\in C^{\infty} (J_x)$ with $0 < \vartheta < t < T$. The following applies for $(x, t) \in J_x \times [\vartheta, t]$:

such that $\lim_{i \rightarrow \infty} \delta_1 (i) = 0$. Taking the limit and considering the use of the dominated converge theorem, it holds that:

Now, for $\tilde{v}^{(i)}$:

The substraction of the last two equations leads to:

Assume now that we depart from sufficiently close maximum and minimum solutions. It suffices to consider this assumption for one of the two solutions, say $\hat{w}^{(i)} \rightarrow \tilde{w}^{(i)}$, then the equality (2.35) holds provided that $\hat{v}^{(i)} \rightarrow \tilde{v}^{(i)}$.

A similar procedure can be followed for the $w$-equation, so that we end into a similar expression to that in (2.35), but for the solution $w$. Then, we shall consider that the maximum and minimum solutions for $v$ are sufficiently close, this is $\hat{v}^{(i)} \rightarrow \tilde{v}^{(i)}$, then it will hold that $\hat{w}^{(i)} \rightarrow \tilde{w}^{(i)}$.

Further, the limit function preserves the same properties of each element of the converging sequence. As previously pointed, the inner regularity and positivity of the operator $\mathcal{L}$, that is applied to each element of the sequence, allow us to state the following regularity condition for the limit functions:

The coming theorem has the intention of showing the uniqueness of the weak solutions as per the Definition 3.

Theorem 3. Consider the following pair of minimum and positive solutions to (1.2), $(v, w) > (0, 0)$ in $J_x \times [\vartheta, T)$. Such a pair of solutions coincides locally with the pair of maximum and positive solutions, $(\hat{v}, \hat{w}) > (0, 0)$, stating then, the local uniqueness of solutions.

Proof. Consider the following pair of maximum solutions $(\hat{v}, \hat{w})$ in $J_x \times [\vartheta, T)$ taking on from the initial distribution given by:

being $\delta_1 > 0$ small. In addition, the pair $(\hat{v}, \hat{w})$ is defined as:

The pair formed of minimum solutions, and taking on from the initial data $(N(x, 0), w(x, 0)) = (v_0(x), w_0(x))$, is given as:

Assume again a test function satisfying $\Upsilon\in C^{\infty} (J_x)$ and the associated weak formulations for the last set of equations. Making the difference between the maximum and minimum weak solutions, the following applies:

Consider now the definition of the continuous functions given in the following expressions:

Given a fixed value for $x$ and for $\tau = \vartheta < T$, it holds that:

Now, consider the following structure for a smooth test function defined in $0 < \vartheta < t < T$ and satisfying the conditions $\Upsilon(\vartheta) = \Upsilon(t) = 0$:

for finite values of $J_0$ and $\kappa_0$.

It should be noticed that:

where $M_i = \inf_{t \in (\vartheta, T)} \, \lbrace D_t [(t-\vartheta) (t-T)]\rbrace$. For the sake of simplicity in the coming expressions, let us define:

Based on the assessments presented up to now and in return to (2.40) and (2.41), it applies that:

The finite $J_0$ is selected to comply with the following inequality:

Then, it suffices to take:

so that:

and

The expressions (2.40) and (2.41) are rewritten as follows:

The uniqueness of the solutions is proved locally in time. For this purpose, assume that $t \in (\vartheta, \varepsilon_0)$ for $0 < \varepsilon_0 \ll 1$. Furthermore, consider that in the mentioned t-interval, we can introduce, by simple translation, a $\varepsilon_0$-contact between the minimum and maximum solutions for $v$, this is $0 < (\hat{v}-v)(\vartheta) \leq \varepsilon_0$. Now, let us make the first time derivative in (2.55), so that the following applies:

where $M_w = \max_{t \in (\vartheta, T)} \, \lbrace \hat{w} \rbrace$. Note that the difference between the maximal and the minimal solution is certainly positive, but the difference between them may be decreasing over time to ensure the uniqueness of solutions, leading to $\frac{d(\hat{w} - w)}{dt} < 0$. Assume that $A_w = r_w \alpha_{w} 2 M_w + \varepsilon_0 \alpha_{wv}$, then, and making a standard resolution, the following holds:

where the minus sign in the exponential term is introduced to ensure that $\frac{d(\hat{w} - w)}{dt} < 0$. Consider now the expression given in (2.37), $\hat{w}(x, 0) - w(x, 0) = \delta_1$, then:

The local uniqueness is shown for $\delta_1 \rightarrow 0^+$, then it holds that:

The only possible condition in the last expression is given by $\hat{w} = w$, showing then the local uniqueness of the solutions. Now, return to (2.54) and define the constant $A_v = r_v + 2 \alpha_{vv} M_v + \alpha_{vw} M_w$ where $M_v = \max_{t \in (\vartheta, T)} \, \lbrace \hat{v} \rbrace$. It holds that:

Performing the first time derivative and solving the resulting inequality by standard techniques, the following holds:

Making again $\delta_1 \rightarrow 0^+$:

where the only compatible result is to consider $\hat{v} = v$, locally in time.

The analysis provided allows us to conclude on the local in time uniqueness of solutions as initially postulated.

3.   Characterization of the propagating front

The intention now is to provide analytical solutions to describe the propagation of the invasive and invaded species in the domain while they are fighting. As mentioned, the nonlinear diffusion induces the existence of a support in the solutions that propagates with finite speed. The determination of a precise analytical expression to describe the evolution of the front will be of help to further understand the involved dynamics between the species.

It should be noticed that the evolution of the support requires to study the system (1.2) for small values in $v$ and $w$ leading to the following alternative problem:

where $\vert \varepsilon_3 \vert \ll 1$ and compiles the order two terms in the equation for $w$.

The coming theorem aims at providing the spatio-temporal evolution of the support. As it will be shown, there are several propagating modes for each species.

Theorem 4. As a result of the interaction between species and for $\vert v \vert \ll 1, \, \, \vert w \vert \ll 1$, there exist two propagating modes for each species in the $(x, t)$ variables, that have the following structures:

● For the concentration $v$:

● For the concentration $w$:

where

and $v_f$, $w_f$ refer to the levels of species concentration in the propagating front. This is mainly related with the level of individuals of each species effectively fighting.

Proof. First, consider the equation:

The determination of an analytical expression for the support requires to solve the above equation, and this is done with the help of a selfsimilar solution. To this end, assume that the advection coefficient is small, $\vert c \vert \ll 1$. This is a sufficiently accurate approximation in the proximity of the support, where the dynamics is focused on the interaction between species rather than in the transport motility induced by the advection. Nonetheless, the advection term will be kept in the equation during the resolution process as it will have an influence in the diffusive front, but we shall keep in mind the requirement of $\vert c \vert \ll 1$. Then:

Hence, in (3.7)

Balancing the leading terms in the previous equations and considering the exponents in $t$, the following holds:

The following values for $\theta_1$ and $\gamma_1$ are obtained:

Consider again the leading terms in (3.9), then the selfsimilar profile $F$ satisfies the following elliptic equation (where $r_v = 1$ for simplicity):

The family of solutions to the postulated elliptic equation is (see ^[35] for additional insights):

Replacing this last expression in (3.12), and after performing standard assessments, the following values for $A_v$ and $B_v$ are obtained:

Now, we make similar operations for the $w$-equation in (3.1) and considering a small $\varepsilon_3$ in comparison with the other involved terms (diffusion and advection):

where:

The intention is to introduce an analytical expression for the propagating front. For this, we fix two concentration levels for each of the species involved. Let us consider that such fixed values are given by $w = w_f$ (concentration level of the invasive species in the propagating front) and $v = v_f$ (concentration level in the front for the invaded species). Coming again to the selfsimilar expression:

where $F(\xi)$ is as per (3.13) and $\xi = \lvert{x}\rvert t^{-1}$. After making the necessary standard assessments, the following equations describe the evolution of the support:

and

And similarly for the equation in $w$:

It should be noticed that the constants involved in the equations for the front $(n, m, c, A_v, A_w, v_f, w_f)$ shall be obtained supported by experimental observations about the particular dynamics. The constants $A_v$ and $A_w$ are related with the boundedness condition in the initial distributions and can simply take the values of the maximum level of initial invaded and invasive species. Some specific values for the levels $v_f$ and $w_f$ can be obtained from the numerical simulations (see Section 4) if we consider the interacting front where both species are fighting.

4.   Travelling wave solutions

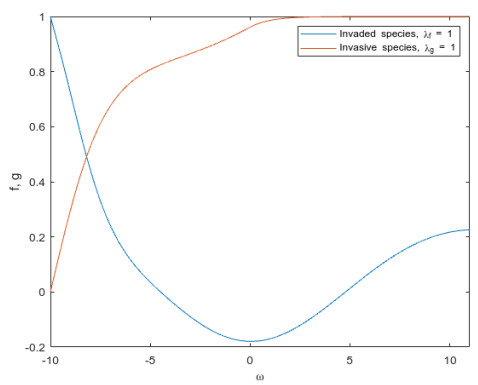
The profiles of travelling waves are expressed as $v(x, t) = f(\omega_1), \, \omega_1 = x \cdot n_d - \lambda_1 t$ and $w(x, t) = g(\omega_2), \, \omega_2 = x \cdot n_d - \lambda_2 t \,$, where $n_d \in \mathbb{R}^d$ is a unitary vector that provides the travelling wave propagation direction and $\lambda_1, \lambda_2$ are defined the propagation speed for each travelling profile that comply with: $f, g: \mathbb{R} \rightarrow (0, \infty)$ and are bounded as it will be shown afterward in the graphical representations. It should be noted that two travelling wave profiles are equivalent under a translation $\omega \rightarrow \omega + \omega_0$ and a symmetry $\omega \rightarrow -\omega$. For the sake of convenience, assume that the vector $n_d = (1, 0, ..., 0)$, then $v(x, t) = f(\omega_1), \, \, \, \, \omega_1 = x - \lambda_1 t \, \in \mathbb{R}$ and $w(x, t) = g(\omega_2), \, \, \, \, \omega_2 = x - \lambda_2 t \, \in \mathbb{R}$.

Consider now $v(x, t) = f(\omega_1)$ and $w(x, t) = g(\omega_2)$, then the problem (1.2) is expressed under the travelling wave profiles formulation:

It is our aim to introduce a numerical analysis to depict the involved dynamics and to represent solutions to the problem (4.1). All the constants given in the model (1.2) are assumed to have particular values:

We should mention that the solutions have been tested for other combinations in the given constants. In this regard, the behavior of the solutions follow similar profiles to that for the values in (4.2). This exercise was done during the ordinary trials in the numerical procedure. We do not reproduce such information here to account for a concise representation. Hence, the parameters, to be modified in the numerical assessments, are the travelling wave speeds in each of the profile, this is $\lambda_1$ and $\lambda_2$.

The numerical simulation is performed with the Matlab function bvp4c. For further details about the intrinsic numerical assessments executed by the function bvp4c, the reader can refer to ^[37].

The domain size of integration has been assumed as $R = 1000$ (although the presented figures will be provided with a zoom in the interacting area) to minimize the impact of the collocation method at the borders. The number of nodes considered was $100,000$ with an absolute error of $10^{-5}$.

The results are compiled in the Figures 1–6 for different combinations in the travelling wave speeds. It shall be noted that the invasive species comes from the right and interact with the invaded species. The interacting front moves from the right to the left (recall that the travelling wave profiles are invariant under a translation) so that the interacting front occupies the whole region until the invaded species cannot support the invasion. In addition, we should mention that the introduction of the nonlinear diffusion may induce oscillations that lead solutions to be outside of the interval $[0, 1]$. In a real application, it is not possible to get values outside of the mentioned interval. Then, for negative values in one of the species, we shall consider that the species concentration vanishes and for values higher than one, the species concentrations reach the maximum allowed in the region.

5.   Conclusions

The initial objectives outlined have been accomplished based on the analytical and numerical assessments provided. The new set of equations in (1.2) were shown to comply with the conditions of regular and unique weak solutions. We obtained exact analytical expressions in the $(x, t)$ variables for the propagating fronts, that modeled the interaction of the species while they were fighting. Eventually, the problem was analyzed within the scope of the travelling waves formulation, and a numerical assessment provided to further understand the interaction between the species. We observed here that a significant difference in the travelling waves speeds, between the involved species, provided an unstable behavior in the solutions.

Acknowledgments

This work has been financed by the CEU San Pablo University, grant number MGI22AOQ.

Conflict of interest

The author declare there is no conflict of interest.