Fundamental theorems of group isomorphism under the framework of complex intuitionistic fuzzy set

1.   Introduction

Recently, researchers have developed numerous mathematical and computational tools to improve scientific research and facilitate decision-making. Group theory is one of the most important parts of algebra and provides a powerful framework for analyzing structures that show up in symmetric form. It has applications in many domains, including theoretical physics and medicine ^[1,2]. Furthermore, it is essential for classifying atoms, regular polyhedral structures, crystal structures, and symmetries of molecules ^[3]. The study of group homomorphism and isomorphism, which connect two groups while keeping their structure, is also part of group theory.

Uncertainty is a vital part of human life, making it impossible to make precise estimates or hypotheses. This analytical error is extremely unfavorable for human intelligence and has led to the development of various mathematical concepts, including fuzzy sets, as useful techniques for addressing this challenge, presented as practical approaches for solving uncertainty-related problems. To overcome this uncertainty of data, Zadeh ^[4] created the notion of fuzzy sets (FS) defined as $\mu \to A : \{(h, \mu(h)); h\in A \}$ where $\mu(h)\in [0, 1]$ is known as the membership value.

Roenfeld ^[5] introduced the fuzzy subgroup notation (FSG); many basic results were established for the homomorphism image and pre-image under a group. The concept of Fuzzy space and fuzzy normal subgroup were investigated ^[6,7]. Mukherjee and Bhattacharya ^[8] established the fuzzy coset and normality of a FSG of a group. Also, conjugate classes were discussed, and FSG was determined to be fuzzy normal if and only if it is (constant) on classes of conjugates of group G. Das ^[9] investigated the idea of level subgroups of a certain group based on the work of Zadeh and Rosenfeld. Dib and Youssef ^[10] developed a new framework with functions, relationships, and fuzzy Cartesian products. Atanassov ^[11] investigated the notation of intuitionistic fuzzy set (IFS) defined as $A = \{(s, \mu(s), \nu(s)); s\in H\}$, where $\mu(s)$ and $\nu(s)$ represent the membership degree (MD) and non-MD of elements of universe set H that belong to $[0, 1]$, and established many basic results. These functions must satisfy: $0 < \mu(s) + \nu(s) \leq1$ and flourished fundamental algebraic tributes. The scientific field found more useful applications of this notion because it deals with two-sided information by increasing non-membership in FS. The subgroups and normal subgroups under the framework of IFS were discussed ^[12,13,14]. Wang et al. ^[15] initiated a new approach based on intuitionistic fuzzy propositional logic (IF), classifications of intuitionistic fuzzy logic proposition (IFLP) formulas, and fundamental features. Moreover, three reasoning methods (the classification methods, the reduction to absurdity method, and the direct proof method) were developed. Alcantud et al. ^[16] developed a method for aggregating IFSs into infinite chains. Also, the scores and accuracy degrees of IF elements were defined. Meng et al. ^[17] used linguistic intuitionistic fuzzy preference relations to solve multi-criteria. Zhou and Xu ^[18] developed the IFS and used it to deal with concerns about decision-making that include risk preference. The concepts of IFS $t$-conorm, IFS t-norm, and IFS relations, Atanassov intuitionistic composition, and operators of t-conorm and t-norm were created by Burillo and Bustince ^[19]. Xiao ^[20] established a novel distance measure for IFSs based on the Jensen-Shannon divergence. It was also shown that nonlinear properties can better tell the difference between IFSs and give more accurate results than other measurement methods. The intuitionistic fuzzy relations, generalization the idea IFS to Pythagorean Fs also used in decision making and the idea of IFS extended by introducing the concepts of Pythagorean fuzzy set ^[21,22]. Jana and Pal ^[24] used the notation of bipolar IF soft sets to study their fundamental characteristics. Also, the intersection and union of two bipolar IF soft sets were presented. Biswas ^[25] developed the idea of intuitionistic FSGs on IFSs, and some important characterizations were explored. Mathematically, in terms of the MD function, extending integers $Z$ to real numbers $R$ is similar to extending crisp sets to FSs. That is, expanding the range of the member function $U$ from 0, 1 to [0, 1] is mathematically similar to expanding $Z$ to $R$. The modifications to the number set did not stop with real numbers. The development of real numbers into the set of complex numbers, $C$, preceded their introduction. Therefore, it is possible to propose that this expansion should serve as the foundation for future FS theory development. In the domain of set theory, the result of such an extension is the complex fuzzy set (CFS), which is defined by a function of MD with complex values. Ramot et al.^[26] explored the novel idea of CFS defined as $\{s, \nu(s) = \mu(s)e^{\iota\theta(s)}:s\in H \}$. The CFS belongs to the range of values that its function in MD may attain. This range is not limited to $[0, 1],$ in contrast to a traditional fuzzy function of MD. Also, it extends to the unit circle in the complex plane. The CFS offers a mathematical framework that describes a set's membership in terms of a complex number. The mathematical definition of the CFS, together with the basic set theory operations that can be performed with it, have been discussed. Alkouri et al. ^[27] established the novel notion of a complex intuitionistic fuzzy set (CIFS) defined as $\{s, \nu(s) = \mu(s)e^{\iota\theta(s)}, \overline{\nu}(s) = \overline{\mu}(s)e^{\iota\overline{\theta}(s)}:s\in H \}$, which is extended by adding a non-MD term to the basic notion of a CFS. Where $\mu(s)\rightarrow [0, 1]$ is the MD of the real part, $\nu(s)\rightarrow [0, 1]$ is the non-MD of the real part, $\theta(s)\rightarrow [0, 2\pi]$ is the MD of the imaginary part, and $\overline{\theta}(s)\rightarrow [0, 2\pi]$ is a non-MD of the imaginary part of a complex number such that $0 < \mu(s) + \nu(s) \leq 1$ and $0 < \theta(s) + \overline{\theta} \leq 2\pi$ for all complex numbers $s\in H$. For both MD and non-MD functions, CIFS can also reach a wider range of values. These ranges are now extended to the unit circle in the complex plane for both functions, instead of just [0, 1] as they are in regular IF functions. Several new uncertainty sets have been established. One of these uncertainty sets is known as the complex Atanassov's intuitionistic fuzzy set (CAIFS), where values for Atanassov's IF functions of MD and non-MD are taken in the complex plane's unit circle. The concept of CIFS by quaternion numbers were investigated and used in decision making ^[28]. Alkouri and Salleh ^[29] established some operations that were extended to the CAIFS. The investigation focused on two major operations and numerous properties. Furthermore, the benefit of applying these two operations to complex numbers was gained by creating a link between the concepts of CFS and CAIFS. Almutairi et al. ^[30] explored the basic components of complex anti-FSGs, pre-image, image, and the vital primary characteristics of complex anti-FSGs. Also, the homomorphic and isomorphic relationships between complex anti-FSGs under group homomorphism were investigated. Latif and Shoaib ^[31] studied Sylow theory under the framework of the $t$-IF subgroup and related properties. They also investigated the fundamental theorems of Sylow theory.

Gulzar et al.^[32,33,34] enhanced the notation of complex intuitionistic fuzzy subgroups (CIFSGs) and level subsets of CIFSs. Moreover, the $t$-intuitionistic fuzzy subgroup, $Q$-complex fuzzy subring, the CIFSGs homomorphic image and pre-image under group homomorphism were explored. Alkouri et al. ^[35] discussed $(\alpha, \beta)$-CFSs, then defined CFSGs, and proved their fundamental algebraic characteristics. Also, $(\alpha, \beta)$-complex fuzzy cosets were presented and used to develop $(\alpha, \beta)$-complex fuzzy normal subgroups. Also, an $(\alpha, \beta)$-complex fuzzy quotient ring was created and the $(\alpha, \beta)$-complex fuzzification of Lagrange's Theorem was proved. Ashraf et al. ^[36] proposed the novel concept of a CI-hesitant-FS to handle uncertain information in real-world complex issues in unit disks and introduced generalized distance measures and weighted generalized distance measures based on the Euclidean, Hamming, and Hausdorff metrics. Dobritsa and Yakh ^[37] developed the concept of clarification, which aided in the early conceptualization of homomorphisms in fuzzy groups. Their study investigated the conditions required to satisfy various characteristics of homomorphisms in conventional groups while also considering properties unique to systems with fuzzy operations. Choudhury et al. ^[38] investigated fuzzy subgroups and discussed the basic structure of fuzzy homomorphisms and isomorphisms between subgroups of groups. Additionally, they introduced the $t$-level image and $t$-level inverse images and established their key findings. Chakrabatty and Khare ^[39] presented a novel concept of fuzzy homomorphism between crisp groups and established a fundamental theorem for FSG isomorphism, leveraging insights from group theory. The study also examined the image and pre-image relationship in FSG, revealing that FSG homomorphisms involve structure-preserving mappings between algebraic structures. The idea of fuzzy subgroups and fuzzy homomorphism with categorical properties was investigated ^[40]. The CIFS is an extended form of the CFS, incorporating the complex degree of non-membership functions, which play an equal role in the decision-making process. The CIFS is also an extension of all these existing theories, such as CFS, IFS, and FS. Furthermore, the concepts of CIFS and CFS are connected in the domain of complex numbers through two distinct procedures.

Motivation for the proposed concept and its contributions:

● Ramot et al. ^[41] created a novel concept of CFS by expanding MD of the functions from the unit interval to the complex plane with the unit disc. The CFS helps in the process of evaluating the system because it considers the amplitude as well as the phase term. Alkouri and Salleh ^[42] extended the concept of CFS to CIFS by introducing complex non-membership degrees of functions and examined their basic properties. The CIFS expands the MD and non-MD values of functions to the unit disc in the complex plane instead of [0, 1] as in the IFS.

● Roenfeld ^[5] presented the notation fuzzy subgroup (FSG) and many basic results were established for the homomorphism image and pre-image under the group. Biswas ^[25] developed the idea of intuitionistic FSGs on IFSs, and some important characterizations were explored.

● Al-Husban and Salleh ^[43] introduced the idea of CF subgroups and CF binary operations, and fundamental results were discussed. Gulzar et al. ^[32] developed the novel notation of CIFSGs, and certain important fundamental results were investigated in detail. Moreover, the homomorphism between two CIFSGs under the influence of CIFS was discussed. Furthermore, the direct product of two CIFSGs was investigated, and some new fundamental characteristics related to the direct product of CIFSG were studied.

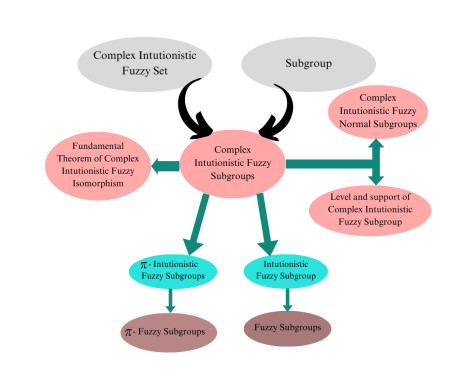
● The idea of CIFS has not yet applied to the advanced algebraic structure of complex intuitionistic fuzzy (CIF) group homomorphisms and isomorphisms. We will talk about the advanced features of CIF homomorphism and isomorphism in this proposed work, which is influenced by group theory. Furthermore, we introduce the normal CIF subgroup of the group and establish examples to explore the concept of the complex intuitionistic fuzzy subgroup. The following Figure 1 depicts the relationship between proposed and existing models. Table 1 shows the comparison between the CIFSs of the proposed and existing models.

Section 2 presents fundamental definitions related to CIFS, along with a relevant result that lays the groundwork for subsequent discussions. Section 3 introduces the concept of support for CIFS, establishes a normal subgroup within the group, and provides relevant illustrations. Section 4 explores the concept of isomorphism in CIFSG and offers a comprehensive examination of three crucial theorems on CIFG homomorphism and isomorphism.

2.   Preliminaries

In this section, we will discuss several fundamental concepts (intuitionistic fuzzy set, union, intersection, image, pre-image, intuitionistic fuzzy subset, and intuitionistic fuzzy normal subgroup) associated with the theory of IFSGs, which will play an important part in our further investigation. Using these definitions, in the main part, we define and investigate the concepts of CIF isomorphism and homomorphism, as well as show the basic CIF isomorphism theorems.

Definition 2.1. ^[44] An IFS $U$ of a universal set $H$ is expressed as $U = \{(s, \mu(s), \nu(s)): s\in H\}$, where $\mu(s)$ and $\nu(s)$ represent the universe $H$ MD and non-MD of element $s$ to $[0, 1]$. These functions must satisfy these requirements: $0 \leq\mu(s) + \nu(s) \leq1$.

Definition 2.2. ^[44] The symbol that represents the product of any two IFS $U$ and $Q$ is $U\circ Q$ and, defined by the value: For any $j\in H$, $U\circ Q = (\mu_{U\circ Q}(j), \nu_{U\circ Q}(j))$

And

Definition 2.3. ^[44] Suppose $U$ and $Q$ are two IFS of sets $S$ and $T$, respectively, and let $w:S\rightarrow T$. Then the image and pre-image of $U$ and $Q$ are defined as:

and $w^{-1}(Q)(g) = Q(w(g))$, $\forall g\in H$.

Definition 2.4. ^[44] An IF subgroup of $L$ is defined as an IF subsetif it satisfies the following conditions:

(1) $\mu(sg)\geq \wedge\{\mu(s), \mu(g)\}$,

(2) $\mu(s^{-1})\geq \mu(s)$,

(3) $\nu(sg)\leq \vee\{\nu(s), \nu(g)\}$,

(4) $\nu(s^{-1})\leq \nu(s)$, $\forall s\in L$.

Definition 2.5. ^[44] If $U$ is IFSG of a group $L$, then

(1) $\mu_{U}(s)\leq \mu_{U}(e)$ and $\nu_{U}(s)\geq \nu_{U}(e)$, $\forall$ $s\in L$, as the identity element of $L$ is denoted by $e$.

(2) $\mu_{U}(sg^{-1}) = \mu_{U}(e)$ and $\nu_{U}(sg^{-1}) = \nu_{U}(e)$ $\Rightarrow$ $\mu_{U}(s) = \mu_{U}(g)$ and $\nu_{U}(s) = \nu_{U}(g)$, $\forall$ $s, g\in L$.

Definition 2.6. ^[44] An IF normal subgroup of $L$ is defined as an IFS of L that satisfies the following factors:

1) $\mu(sg) = \mu(gs)$,

2) $\nu(sg) = \nu(gs)$ $\forall$ $s, g\in L$.

In other terms, an IF normal subgroup of a $L$ is normal $\Leftrightarrow$ $\mu(r^{-1}sr) = \mu(s)$ and $\nu(r^{-1}sr) = \nu(s)$ $\forall$ $s\in U$ and $r\in L$.

We write the IF normal subgroup as IFNSG for convenience.

3.   Fundamental algebraic characteristics of complex intuitionistic fuzzy subgroups

The notions of CIF homomorphisms and isomorphisms for CIFSG are the focus of this section. For these specific FSGs, we explain CIF homomorphism and isomorphism and establish the three basic theorems of CIF isomorphism.

Definition 3.1. If CIFS $U$ of group $L$ satisfies the given conditions, then it is said be a CIFSG of group $L$:

(1) $\mu_{U}(sg)e^{\iota \theta_{U}(sg)}\geq \wedge\{\mu_{U}(s), \mu_{U}(g)\}e^{\iota \wedge\{\theta_{U}(s), \theta_{U}(g)\}}$,

(2) $\mu_{U}(s^{-1})e^{\iota \theta_{U}(s^{-1})}\geq \mu_{U}(s)e^{\iota \theta_{U}(s)}$,

(3) $\nu_{U}(sg)e^{\iota \overline{\theta}_{U}(sg)}\leq \vee\{\nu_{U}(s), \nu_{U}(g)\}e^{\iota \vee\{\overline{\theta}_{U}(s), \overline{\theta}_{U}(g)\}}$,

(4) $\nu_{U}(s^{-1})e^{\iota \overline{\theta}_{U}(s^{-1})}\leq \nu_{U}(s)e^{\iota \overline{\theta}_{U}(s)}$.

Equivalently, a CIFS of $L$ is CIFSG of $L$ if:

$\mu_{U}(sg^{-1})e^{\iota \theta_{U}(sg^{-1})}\geq \wedge\{\mu_{U}(s), \mu_{U}(g)\}e^{\iota \wedge\{\theta_{U}(s), \theta_{U}(g)\}}$ and

$\nu_{U}(sg^{-1^{}})e^{\iota \overline{\theta}_{U}(sg^{-1})}\leq \vee\{\nu_{U}(s), \nu_{U}(g)\}e^{\iota \vee\{\overline{\theta}_{U}(s), \overline{\theta}_{U}(g)\}}$ hold $\forall$ $s, g\in L$.

Example 3.2. Consider $L = S_{3} = \{ i, (12), (13), (23), (123), (132)\}$ be the symmetric group. Consider the CIFS $U$ of $L$ defined by

Where $s\in L$ and $i$ is the identity element of $L$. Clearly, $U$ is CIFSG of group $L$.

Definition 3.3. Let $U$ be a CIFSG of $L$ and $j$ be some fixed element of $L$. The set $jU = \{(g, \mu_{jU}(g), \theta_{jU}(g), \nu_{jU}(g), \overline{\theta}_{jU}(g)):g\in L\}$, where $\mu_{jU}(g) = \mu_{U}(j^{-1}g)$, $\theta_{jU}(g) = \theta_{U}(j^{-1}g)$ and $\nu_{jU}(g) = \nu_{U}(j^{-1}g)$, $\overline{\theta}_{jU}(g) = \overline{\theta}_{U}(j^{-1}g)$ $\forall$ $j\in L$ is called CIF left coset of $L$ is expressed by $U$ and $j$. In the same method, the right CIF coset is defined.

Definition 3.4. Assume that $U$ is a CIFSG of $L$. The set $U$ is called CIF normal subgroup of $L$ if $\mu_{U}(sg) = \mu_{U}(gs)$, $\theta_{U}(sg) = \theta_{U}(gs)$ and $\nu_{U}(sg) = \nu_{U}(gs)$, $\overline{\theta}_{U}(sg) = \overline{\theta}_{U}(gs)$, $\forall$ $s\in L$ or equivalently, $U$ is CIF normal subgroup of a group $L$ normal if and only if $\mu_{U}(s^{-1}gs) = \mu_{U}(g)$, $\theta_{jU}(s^{-1}gs) = \theta_{U}(g)$ and $\nu_{jU}(s^{-1}gs) = \nu_{U}(g)$, $\overline{\theta}_{jU}(s^{-1}gs) = \overline{\theta}_{U}(g)$ $\forall$ $j\in L$.

The above definition implies the following proposition.

Proposition 3.5. Assume that $U$ is a CIFNSG of a group $L$. In view of Definition (3.4), then $\mu_{U}(sg) = \mu_{U}(gs)$, $\theta_{U}(sg) = \theta_{U}(gs)$ and $\nu_{U}(sg) = \nu_{U}(gs)$, $\overline{\theta}_{U}(sg) = \overline{\theta}_{U}(gs)$ $\Leftrightarrow$ $\mu_{U}(r^{-1}sr) = \mu_{U}(s)$, $\theta_{U}(r^{-1}sr) = \theta_{U}(s)$ and $\nu_{U}(r^{-1}sr) = \nu_{U}(s)$, $\overline{\theta}_{U}(r^{-1}sr) = \overline{\theta}_{U}(s)$, holds $\forall$ $s, r\in L$.

Remark 3.6. The intersection of two CIFSGs of a group $L$ is a CIFSG.

Definition 3.7. Assume that $U$ is a CIFS of $H$. The support set $U^{\ast}$ of $U$ is described as: $U^{\ast} = \{j\in H:\mu_{U}(j) > 0, \; \theta_{U}(j) > 0 \; \text{and} \; \nu_{U}(j) < 1, \; \overline{\theta}_{U}(j) < 2\pi\}$.

Remark 3.8. Let $U$ be a CIFSG of $L$. Then $U^{\ast}$ is a subgroup of $L$.

The following outcome shows that CIFNSG's support set is normal.

Theorem 3.9. Assume that $U$ is a CIFSG of $H$. Then $U^{\ast}$ is a NSG of $L$.

Proof. For any element $j\in L$ and $q\in \mu_{U^{\ast}}$, using the Definition (3.7), $\mu_{U^{\ast}}(jqj^{-1}) = \mu_{U^{\ast}}(q) > 0$, we get $jqj^{-1}\in \mu_{U^{\ast}}$. Also, $\theta_{U^{\ast}}(jqj^{-1}) = \theta_{U^{\ast}}(q) > 0$. We obtain $jqj^{-1}\in \theta_{U^{\ast}}$. Similarly, for any element $j\in L$ and $q\in \nu_{U^{\ast}}$. using the definition (3.7), $\nu_{U^{\ast}}(jqj^{-1}) = \nu_{U^{\ast}}(q) < 1$. We have $jqj^{-1}\in \nu_{U^{\ast}}$. Moreover, $\overline{\theta}_{U^{\ast}}(jqj^{-1}) = \overline{\theta}_{U^{\ast}}(q) < 2\pi$. We have $jqj^{-1}\in \overline{\theta}_{U^{\ast}}$. This concludes the proof. □

Theorem 3.10. If $U$ and $Q$ are CIFSG of $L$. Then $(U\cap Q)^{\ast} = U^{\ast}\cap Q^{\ast}$.

Proof. For any element, $i\in (U\cap Q)^{\ast}$. We get $\mu_{U\cap Q}(i) > 0$, $\theta_{U\cap Q}(i) > 0$ and $\nu_{U\cap Q}(i) < 1, \; \; \overline{\theta}_{U\cap Q}(i) < 2\pi$. Implies that $\mu_{U}(i), \mu_{Q}(i) > \wedge\{\mu_{U}(i), \mu_{Q}(i)\} > \mu_{U\cap Q}(i) > 0, \; \; \; \theta_{U}(i), \theta_{Q}(i) > \wedge\{\theta_{U}(i), \theta_{Q}(i)\} > \theta_{U\cap Q}(i) > 0$. And, $\nu_{U}(i), \nu_{Q}(i) < \vee\{\nu_{U}(i), \nu_{Q}(i)\} < \nu_{U\cap Q}(i) < 1, \; \; \overline{\theta}_{U}(i), \overline{\theta}_{Q}(i) < \vee\{\overline{\theta}_{U}(i), \overline{\theta}_{Q}(i)\} < \overline{\theta}_{U\cap Q}(i) < 2\pi$. This implies that $\mu_{U}(i), \mu_{Q}(i) > 0$, $\theta_{U}(i), \theta_{Q}(i) > 0$ and $\nu_{U}(i), \nu_{Q}(i) < 1$, $\overline{\theta}_{U}(i), \overline{\theta}_{Q}(i) < 2\pi$. We have $i\in U^{\ast}\cap Q^{\ast}$.

Consequently, $(U\cap Q)^{\ast}\subseteq U^{\ast}\cap Q^{\ast}$. For any element, $i\in U^{\ast}\cap Q^{\ast}$. Which means that $\mu_{U}(i) > 0$, $\theta_{U}(i) > 0$ and $\mu_{Q}(i) > 0, \; \; \theta_{Q}(i) > 0$. Also $\nu_{U}(i) < 1$, , $\overline{\theta}_{U}(i) < 2\pi$, and $\nu_{Q}(i) < 1$, $\overline{\theta}_{Q}(i) < 2\pi$. Therefore, $\wedge\{\mu_{U}(i), \mu_{Q}(i)\} > 0, \; \wedge\{\theta_{U}(i), \theta_{Q}(i)\} > 0$ and $\vee\{\nu_{U}(i), \nu_{Q}(i)\} < 1, \; \; \vee\{\overline{\theta}_{U}(i), \overline{\theta}_{Q}(i)\} < 1$. We get $\mu_{U\cap Q}(i) > 0, \; \theta_{U\cap Q}(i) > 0$ and $\nu_{U\cap Q}(i) < 1, \; \overline{\theta}_{U\cap Q}(i) < 2\pi$. Thus, $i\in (U\cap Q)^{\ast}$. So, $(U\cap Q)^{\ast}\supseteq U^{\ast}\cap Q^{\ast}$. This concludes the proof. □

The next theorem shows that the support of a CIF normal subgroup is also normal.

Theorem 3.11. Assume that $U$ and $Q$ are the CIFSG of a group $L$, and $U$ is a CINFSG of $Q$. Then $U^{\ast}$ is CIFSG of $Q^{\ast}$.

Proof. For any element $j\in \mu_{U^{\ast}}$ and $g\in \mu_{Q^{\ast}}$. Since $U^{\ast}$ is CIFSG of $Q^{\ast}$, then $\mu_{U^{\ast}}(gjg^{-1}) > \wedge\{\mu_{U^{\ast}}(j), \mu_{Q^{\ast}}(g)\}$ $= \wedge\{\mu_{U^{\ast}}(e), \mu_{Q^{\ast}}(e)\} = \mu_{U^{\ast}}(e) > 0$. We obtain $\mu_{U^{\ast}}(gjg^{-1}) > 0$. For any element $j\in \theta_{U^{\ast}}$ and $q\in \theta_{Q^{\ast}}$, since $U^{\ast}$ is CIFSG of $Q^{\ast}$, we get $\theta_{U^{\ast}}(gjg^{-1}) > \wedge\{\theta_{U^{\ast}}(j), \theta_{Q^{\ast}}(g)\}$ $= \wedge\{\theta_{U^{\ast}}(e), \theta_{Q^{\ast}}(e)\} = \mu_{U^{\ast}}(e) = \theta_{U^{\ast}}(e) > 0$. We have $\theta_{U^{\ast}}(gjg^{-1}) > 0$.

Similarly, for any element $j\in \nu_{U^{\ast}}$ and $g\in \nu_{Q^{\ast}}$, since $U^{\ast}$ is CIFSG of $Q^{\ast}$, we obtain $\nu_{U^{\ast}}(gjg^{-1}) < \vee\{\nu_{U^{\ast}}(j), \nu_{Q^{\ast}}(g)\}$ $= \vee\{\nu_{U^{\ast}}(e), \nu_{Q^{\ast}}(e)\} = \nu_{U^{\ast}}(e) < 1$. We get $\nu_{U^{\ast}}(gjg^{-1}) < 1$. For any element $j\in \overline{\theta}_{U^{\ast}}$ and $g\in \overline{\theta}_{Q^{\ast}}$, since $U^{\ast}$ is CIFSG of $Q^{\ast}$, then $\overline{\theta}_{U^{\ast}}(gjg^{-1}) < \vee\{\overline{\theta}_{U^{\ast}}(j), \overline{\theta}_{Q^{\ast}}(g)\}$ $= \vee\{\overline{\theta}_{U^{\ast}}(e), \overline{\theta}_{Q^{\ast}}(e)\} = \overline{\theta}_{U^{\ast}}(e) < 2\pi$. We have $\overline{\theta}_{U^{\ast}}(gjg^{-1}) < 2\pi$. This concludes the proof. □

The next theorem shows that the epimorphism image of the support set of $U$ is equal to the support of $Q$.

Theorem 3.12. Let $U$ and $Q$ be any two CIFSG of $L$ and $L^{'}$, and $w$ be a epimorphism from $L\rightarrow L^{'}$ as follows $w(U) = Q$. Then $w(U^{\ast}) = Q^{\ast}$.

Proof. As we know $w(U) = Q$. Let $\beta\in w(U^{\ast})\Rightarrow \beta = w(j), \; \; j\in U^{\ast}$. Consider $\mu_{w(U)}(\beta) = \vee\{\mu_{U}(j), j\in w^{-1}(\beta)\} > \mu_{U}(j) > 0$, $\theta_{w(U)}(\beta) = \vee\{\theta_{U}(j), j\in w^{-1}(\beta)\} > \theta_{U}(j) > 0\; and \; \nu_{w(U)}(\beta) = \wedge\{\nu_{U}(j), j\in w^{-1}(\beta)\} < \nu_{U}(j) < 1$, $\overline{\theta}_{w(U)}(\beta) = \wedge\{\overline{\theta}_{U}(j), j\in w^{-1}(\beta)\} < \overline{\theta}_{U}(j) < 2\pi$.

Therefore, $\beta\in Q^{\ast}$ Thus, $w(U^{\ast}) = Q^{\ast}$. In addition, by using the Definition of $(2.3)$ and the fact that $w$ is an epimorphism $w(U^{\ast})\supseteq Q^{\ast}$, this concludes the proof. □

4.   Group homomorphism and isomorphism under the influence of complex intuitionistic fuzzy set

This section explores the concepts of CIF homomorphisms and isomorphisms for CIFSG. We establish the basic theorems of CIF isomorphism and define CIF isomorphism and homomorphism.

Definition 4.1. Assume that $U$ and $Q$ are CIFSG of groups $L$ and $L^{'}$ respectively. A homomorphism $w: U\rightarrow Q$ is known as weak CIF homomorphism of $U$ into $Q$ if $w(U)\subseteq Q$. The case becomes CIF homomorphism from $U$ onto $Q$ if $w(U) = Q$. In this case, $U$ is said to be CIF homomorphic to $Q$ and is represented by $U\approx Q$.

An isomorphism $w: U\rightarrow Q$ is called weak CIF isomorphism from $U\rightarrow Q$ if $w(U)\subseteq Q$. The case becomes CIF isomorphism from $U\rightarrow Q$ if $w(U) = Q$. In this case, $U$ is said to be CIF isomorphic to $Q$ and is expressed by $U\cong Q$.

Now, the homomorphism from CIFSG to its quotient CIFSG is demonstrated by the following result.

Theorem 4.2. Suppose that $O$ is a NSG, $U$ is a $CIFSG$ of a group $L$ and a homomorphism $\eta$ from $L$ to $\frac{L}{O}$. Then $\eta$ is a CIF homomorphism from $U\rightarrow U^{\rho}$, where $U^{\rho}$ is a $CIFSG$ of $\frac{L}{O}$.

Proof. As, we know that, a homomorphism $\eta$ from $L$ to $\frac{L}{O}$ such that $\eta(h)$ = $hO$, $h\in L$. For $hO\in \frac{L}{O}$, we have $\eta(U)(hO) = (\mu_{\eta(U)}(hO), \nu_{\eta(U)}(hO))$. Consider

Which implies $\mu_{\eta(U)} = \mu_{U^{\rho}}$. Also,

We get $\nu_{\eta(U)} = \nu_{U^{\rho}}$. Therefore, $\eta(U) = U^{\rho}$. So, $\eta$ is a CIF homomorphism from $U\rightarrow U^{\rho}$. Thus, we conclude the required result. □

Example 4.3. Assume that the quotient group $\frac{L}{O} = \{O, bO\}$ and $O = \{1, a^{2}, a\}$ is a normal subgroup of $L$, where $L = S_{3} = \{1, b, a, ab, a^{2}, a^{2}b\}$ is the symmetric group of order 6. The IFS $U$ of $L$ is expressed as:

The natural homomorphism $\eta: L\rightarrow \frac{L}{O}$ is defined as: $\eta(h) = hO$, $\forall$ $h\in L$. Define IFSG $U^{\rho}$ of $\frac{L}{O}$ as follows:

Therefore, $\eta(U) = U^{\rho}$. Thus, $\eta$ is a CIF homomorphism of $U\rightarrow U^{\rho}$.

The basic theorem of CIF homomorphism develops a connection between the CIFSG of a quotient group and the CIFSG of a group.

Theorem 4.4. Assume that w is a CIF homomorphism from $U$ onto $Q$ where $U$ and $Q$ are CIFSG of group $L$ and $L^{'}$, respectively. Then the mapping $\phi$ from $\frac{L}{O}\rightarrow L^{'}$ is a CIF homomorphism from $U^{\rho}\rightarrow Q$, where $U_{\rho}$ is a $CIFSG$ of $\frac{L}{O}$.

Proof. Given that w is a CIF homomorphism from $U\rightarrow Q$, where $U$ and $Q$ are $CIFSG$ of $L$ and $L^{'}$ respectively, then $w(U) = Q$. Define a mapping $\phi:\frac{L}{O}\rightarrow L^{'}$ by the rule $\phi(jO) = w(j) = q, \forall j\in L$. The function $\phi$ is a mapping of an image of element $U^{\rho}$ that is defined as:

Hence, we complete the desired result. □

The following example indicates that it is possible to develop a homomorphism between the CIFSG of a group $L^{'}$ and its quotient groups.

Example 4.5. Suppose the permutation group L as $L = \{1, (23), (13), (12), (132), (123)\}$ and $L^{'} = \{1, -1\}$. Explain a homomorphism $w$ from $L$ onto $L^{'}$ as follows:

The CIFS U of L is defined as:

The CIFSG Q of L$^{'}$ is defined as:

In light of the preceding information, one can develop the following relationship: Let,

Therefore, $w(U) = Q$. This implies that $w$ is a CIF homomorphism of $U\rightarrow Q$. The factor group of $L = S_{3}$ is defined as $\frac{L}{O} = \{jO, qO:q =$odd permutation$, j =$even permutation$\}$, where $O$ is a NSG of even permutation of $L$. Define IFS $U^{\rho}$ on $\frac{L}{O}$ as follows:

Define a mapping $\phi : \frac{L}{O}\rightarrow L^{'}$ as follows $\phi(jO) = w(j) = q$ $\forall$ $j\in L$. In light of the preceding information, one can develop the following relationship:

Therefore, $\phi(U^{\rho}) = Q$. Consequently, $\phi$ is a CIF homomorphism of $U^{\rho}$ onto $Q$.

If we choose kernel of the homomorphism, then the above result may be viewed in the form of following remark.

Remark 4.6. Assume that $w$ is a CIF homomorphism from $U\rightarrow Q$, as $U$ and $Q$ are CIFSG of $L$ and $L^{'}$, and $K$ denotes the kernel of $w$. Then the mapping $\phi:\frac{L}{K} \rightarrow L^{'}$ is a CIF homomorphism from $U^{k}\rightarrow Q$, as $U^{k}$ is a CIFSG of $\frac{L}{K}$.

We may create a link between the CIFSG of a group $L^{'}$ and any of its quotient groups, as proved by the following result.

Theorem 4.7. Assume that w is a CIF homomorphism from $U$ onto $Q$, where $U$ and $Q$ are CIFSG of group $L$ and $L^{'}$, respectively, and $O$ is NSG of $L$ with $w(O) = O^{'}$. Then the natural homomorphism $\eta:L^{'} \rightarrow \frac{L^{'}}{O^{'}}$ is a CIF homomorphism from $Q\rightarrow U^{\rho}$ and $\psi = \eta\circ w$ is a CIF homomorphism from $U\rightarrow U^{\rho}$, as $U^{\rho}$ is a $CIFSG$ of $\frac{L^{'}}{O^{'}}$.

Proof. As $\eta$ is a homomorphism from $L \rightarrow \frac{L^{'}}{O^{'}}$. For any $h^{'}O^{'}\in \frac{L^{'}}{O^{'}}$, we get

Since $w$ is a CIF homomorphism from $U$ onto $Q$. $\mu_{(\eta\circ w)(U)}(h^{'}O^{'}) = \mu_{Q}(\eta^{-1}(h^{'}O^{'})) = \mu_{(\eta^{-1})^{-1}(Q)}((h^{'}O^{'})).$ Thus, $\eta$ is a CIF homomorphism from $Q \rightarrow U^{\rho^{'}}$. $\mu_{(\eta)(Q)}((h^{'}O^{'})) = \mu_{U^{\rho^{'}}}((h^{'}O^{'})). \Rightarrow \mu_{(\eta\circ w)(U)}(h^{'}O^{'}) = \mu_{U^{\rho^{'}}}((h^{'}O^{'})). \Rightarrow \mu_{\psi(U)} = \mu_{U^{\rho^{'}}}.$

Since $w$ is a CIF homomorphism from $U$ onto $Q$. $\nu_{(\eta\circ w)(U)}(h^{'}O^{'}) = \nu_{Q}(\eta^{-1}(h^{'}O^{'})) = \nu_{(\eta^{-1})^{-1}(Q)}((h^{'}O^{'})).$ Thus, $\eta$ is a CIF homomorphism from $Q \rightarrow U^{\rho^{'}}$. $= \nu_{(\eta)(Q)}((h^{'}O^{'})) = \nu_{U^{\rho^{'}}}((h^{'}O^{'})). \Rightarrow \nu_{(\eta\circ w)(U)}(h^{'}O^{'}) = \nu_{U^{\rho^{'}}}((h^{'}O^{'})). \Rightarrow \nu_{\psi(U)} = \nu_{U^{\rho^{'}}}.$ Consequently, $\psi = \eta\circ w$ is a CIF homomorphism from $U$ onto $U^{\rho}$. This concludes the proof. □

Under a complex intuitionistic fuzzy epimorphism, the following outcome establishes an essential relationship between the two quotient groups.

Theorem 4.8. Assume that $w$ is a CIF epimorphism from $U$ onto $Q$, where $U$ and $Q$ are CIFSG of group $L$ and $L^{'}$, respectively, and $\eta:L^{'}\rightarrow \frac{L}{O}$ is a natural homomorphism. Then a mapping $\sigma$ from $\frac{L}{O}$ onto $\frac{L^{'}}{O^{'}}$ is a CIF homomorphism, from $U^{\rho}$ onto $U^{\rho^{'}}$ is a CIF homomorphism from $\frac{L}{O}$ $\rightarrow$ $\frac{L^{'}}{O^{'}}$, respectively, and $O = \{j\in L:w(j)\in O^{'}\}.$

Proof. By using Theorem (4.7), we have a mapping $\psi:L\rightarrow \frac{L^{'}}{O^{'}}$, where $\psi$ commutes with $w$ and $\eta$ such that $\psi(h) = (\eta\circ w)(h) = h^{'}O^{'}$ for all $h^{'}\in L^{'}$. Moreover, $\psi(O) = (\eta\circ w)(O) = \eta(w(O)) = \eta(O^{'}) = O^{'}$. Consider, $CIFSG$ $U^{\rho}$ of $\frac{L}{O}$ as: $U^{\rho}(jO) = (\mu_{U^{\rho}}(jO), \nu_{U^{\rho}}(jO))$,

This demonstrates $\psi$ is a CIF homomorphism with $ker \psi = O$. Express a homomorphism $\sigma\rightarrow \frac{L}{O}$ to $\frac{L^{'}}{O^{'}}$ by the rule $\sigma(hO) = h^{'}O^{'}, h\in L, h^{'}\in L^{'}$. Where $\sigma: U^{\rho}\rightarrow U^{\rho}$ is expressed by the rule: $\sigma(U^{\rho})(jO) = (\mu_{\sigma(U^{\rho})}(jO), \nu_{\sigma(U^{\rho})}(jO))$, where

Hence, we obtain the required result. □

Theorem 4.9. Assume that $w$ is a CIF homomorphism from $U$ onto $Q$, where $U$ and $Q$ are CIFSG of groups $L$ and $L^{'}$, consequently with $ker w = K$. Then there exists a CIF isomorphism from $\frac{U}{C}\rightarrow Q$, as $C$ is a CIFNSG of $U$.

Proof. As we know, $w$ is a CIF homomorphism from $U$ to $Q$. Let CIFSG $C$ of $L$ as follows:

Obviously, $C\subseteq U$. Also, $K$ is normal, so $jqj^{-1}\in K$ for any $j\in C$, $q\in L$. Let

If $j\in K$, then $\mu_{C}(j) = 0$, $\nu_{C}(j) = 1$ and $\theta_{C}(j) = 0$, $\overline{\theta}_{C}(j) = 2\pi$. This shows that $C$ is a CIFNSG of $U$. Since $U\approx Q$ $\Rightarrow$ $w(U) = Q$. In view of Theorem (3.12) $w(U^{\ast}) = Q^{\ast}$.

Let $\wr = w_{U^{\ast}}$, then $\wr:U^{\ast}\rightarrow Q^{\ast}$ is a homomorphism with ker $\wr = C^{\ast}$. Then there occurs a isomorphism $\wr$ from $\frac{U^{\ast}}{C^{\ast}}$ to $Q^{\ast}$ $\wr = C^{\ast}$. that can be characterized as $\wr(jC^{\ast})$ = z = $\wr(j) = w(j)$, $\forall$ $j\in U^{\ast}$. For $\wr$, we have $\wr(\frac{U}{C})(z) = (\mu_{\frac{U}{C}}(z), \nu_{\frac{U}{C}}(z))$.

$\overline{\wr}(\frac{U}{C})(z) = (\overline{\mu}_{\frac{U}{C}}(z), \overline{\nu}_{\frac{U}{C}}(z))$. Consider

□

Now, we illustrate the well-known second fundamental theorem of isomorphism under the influence of CIFS.

Theorem 4.10. Assume that $U$ is a CIFNSG and $Q$ is a CIFSG of group $L$ such that $U\subseteq Q$. Then there exists a weak CIF isomorphism between $\frac{Q}{U\cap Q}$, and $\frac{U\circ Q}{U}$.

Proof. By using Theorem (3.11) and the case $U\subseteq Q$, verify the addition of the factor groups $\frac{Q^{\ast}}{U^{\ast}\cap Q^{\ast}}$ and $\frac{U^{\ast}Q^{\ast}}{U^{\ast}}$. Also, by employing second fundamental theorem, then we have: $\frac{Q^{\ast}}{U^{\ast}\cap Q^{\ast}}\cong \frac{U^{\ast}Q^{\ast}}{U^{\ast}}$ The algebraic statement leads us to the observation that there is a group isomorphism $w$ from $\frac{Q^{\ast}}{U^{\ast}\cap Q^{\ast}}$ to $\frac{U^{\ast}\circ Q^{\ast}}{U^{\ast}}$ that is known as $w(j(U\cap Q)^{\ast}) = jU^{\ast}$, $\forall$ $j\in Q^{\ast}$. Consider

Thus, $w(\frac{Q}{U\cap Q}))\subseteq (\frac{(U\circ Q)}{U})$. Consequently, we obtain a weak CIF isomorphism between $\frac{Q}{U\bigcap Q}$ and $\frac{(U\circ Q)}{U}$. □

Now, we show the third fundamental theorem of isomorphism by employing CIFS.

Theorem 4.11. Assume that $U$, $Q$, and $C$ are CIFSG of $L$ such that $U$ and $Q$ are CIFNSG of $C$ with $U\subseteq Q$. Then there exists a CIF isomorphism between $\frac{(\frac{C}{U})}{(\frac{Q}{U})}$ and $(\frac{C}{Q})$.

Proof. By using Theorem (3.11) and the case $U$ and $Q$ are CIFSG of $C$ with $U\subseteq Q$, verify the the addition of the factor groups $\frac{(\frac{C^{\ast}}{U^{\ast}})}{(\frac{Q^{\ast}}{U^{\ast}})}$ and $\frac{C^{\ast}}{Q^{\ast}}$. Also, by employing the third basic isomorphism theorem of group on these specific factor groups results in $\frac{(\frac{C^{\ast}}{U^{\ast}})}{(\frac{Q^{\ast}}{U^{\ast}})}\cong \frac{C^{\ast}}{Q^{\ast}}$. Thus, this statement lead us to the observation that $w$ is the group isomorphism from $\frac{(\frac{C^{\ast}}{U^{\ast}})}{(\frac{Q^{\ast}}{U^{\ast}})}$ to $\frac{C^{\ast}}{Q^{\ast}}$ and describes the following $w(jU^{\ast}.(\frac{Q^{\ast}}{U^{\ast}})) = jQ^{\ast}$, $\forall$ $j\in C^{\ast}$. Consider

And

Hence, we obtain the required result.

□

5.   Conclusions

In this manuscript, we have defined normal CIFSGs, introduced the concept of support for CIFSGs, and proved that the support of a CIF normal subgroup is also normal. Additionally, we have proved that the epimorphic image of support set $A$ equals the support set $B$. We established a relevant generalization of CIF isomorphism between any two CIFSGs. Also, three important isomorphism theorems for CIF subgroups are shown using support sets, along with examples on how they work. The support set property of CIF normal subgroups is of great significance to the development of the algebraic theory of complex fuzzy sets and the potential role of the CIF isomorphism theorem in group theory. In the future, machine learning (ML) and deep learning (DL) will prove to be pivotal in modern technology and innovation due to their ability to process and analyze vast amounts of data, uncover patterns, and make predictions or decisions. We aim to further enhance the speed, efficiency, and versatility of decision-making in complex plans. We will use machine and deep learning techniques, ^[45,46], paving the way for broader adoption and more impactful applications.

Author contributions

Niat Nigar, Muhammad Haris Mateen and Sarka Hoskova-Mayerova: Supervised and conceptualized; Muhammad Jawad: Wrote the original draft; Sarka Hoskova-Mayerova and Bijan Davvaz: Modified and verified the results. All authors have read and approved the final version of the manuscript for publication.

Use of Generative-AI tools declaration

The authors declare that they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

The author thanks the Ministry of Defence of the Czech Republic for the support via grant VAROPS.

Conflict of interest

The authors declare no conflict of interests.