The impact of a Saccharomyces cerevisiae bio-protective strain during cold static clarification on Catarratto wine

1.   Introduction

Population dynamics is one of the main issues of theoretical biomathematics and has aroused the interest of many scholars in the fields of mathematical biology. A lot of methods have been presented and developed to study the evolution of population dynamics. It is clear that establishing mathematical models is the prerequisite for analysis of population dynamics. Until now, researchers have proposed a variety of models, represented by difference equations or differential equations ^[1,2,3].

As is well known, no species can exist in isolation, all populations must be related to the others directly or indirectly, and mutualism, parasitism, competition and predation are the four most widespread direct relationships in the ecosystem ^[4]. Based on these four relationships, researchers have established a variety of models to study the dynamics of the population, such as the Lotka-Volterra models, Leslie-Gower models and predator-prey models ^[5,6,7,8]. In recent years, many researchers began to study more complex and realistic population models and have got some interesting results ^{[9,10,11,12,13,14]}. In ^[15], a predator-prey system with Beddington-DeAngelis functional response was considered, and global asymptotical stability of the positive equilibrium was investigated by using divergency criterion. In ^[16], a ratio-dependent prey-predator model with the Allee effect was proposed, and bifurcation and stability analysis were carried out. Moreover, all possible non-degenerated phase portraits have been displayed. In ^[17], a simple predator-prey interaction where predator population is subjected to harvesting was considered, and different outcomes including switching of stability, oscillation and deterministic extinction were demonstrated.

On the other hand, with the development of fractional calculus, researchers have applied fractional derivatives to various fields ^{[18,19,20,21,22,23,24,25,26,27,28,29]}. Compared with the classical integer-order counterpart, fractional derivative is an outstanding instrument to describe memory and hereditary properties of various materials and processes ^[30]. In ^[31], the fractional-order predator-prey model and the fractional-order rabies model were firstly established. Moreover, existence and uniqueness of solutions, and stability of equilibrium points were studied. A comparison between the proposed fractional-order model and its integer-order counterpart was made. Since then, fractional population models have received extensive attention, and numerous results have been reported in the literature. Some different fractional Lotka-Volterra models are studied in ^[32,33,34]. For more details, see ^{[35,36,37,38]} and the references cited therein. In ^[39], stability of fractional-order nonlinear systems was studied by using Lyapunov direct method with the introduction of generalized Mittag-Leffler stability definition. It provided a new instrument to investigate the dynamics of the fractional population model. After that, the Lyapunov direct method has been widely applied to stability analysis of the fractional population model ^[40,41,42]. For instance, dynamics of a fractional-order predator-prey model incorporating a prey refuge was discussed in ^[40]. Stability of a fractional-order prey-predator system with time-delay and Monod-Haldane functional response was considered in ^[41]. Stability of a fractional-order two-species facultative mutualism model with harvesting was addressed in ^[42]. Some sufficient conditions to ensure the stability of the considered models were obtained in the aforementioned references based on the the Lyapunov direct method. Recent years, variety of interesting fractional-order population models are studied and some significant results were obtained ^[43,44,45].

Due to factors such as reproduction, most of the population systems have memory and hereditary effects. Thus, the fractional-order population system is more realistic than integer-order counterpart. Moreover, the integer-order system can be seemed as a special form of fractional-order system. So the analysis of fractional-order model is more general. Based on the above advantages, a new fractional-order $N$ species model is established in this paper. In order to find general theories, the general functions are used in this model. It can be said that most of the population model can be seemed as a special form of this model. Therefore, it is valuable to analyze the stability of this model. The main contributions of this paper are as follows: First of all, a new generalized fractional order $N$ species network is established to describe the relationship between species in an ecosystem. In addition, the existence, uniqueness and non-negativity of the solution are discussed. Moreover, the algebraic criteria for local stability and global stability are established by using the eigenvalue method and the Lyapunov direct method, respectively. Finally, the theoretical analysis is demonstrate by three examples and numerical simulations.

The rest of this paper is organized as follows. In Section 2, some definitions in fractional calculus and some stability results are introduced. In Section 3, existence, uniqueness, non-negativity of the solutions, and local and global asymptotical stability of the equilibrium point are discussed in depth. In Section 4, some numerical simulation results are presented. Finally, some conclusions are drawn in Section 5.

2.   Preliminaries

In this section, some definitions and lemmas in fractional calculus are recalled, which will be used later.

Definition 1. ^[46] The Caputo fractional derivative of a function $f(t)$ with order $\alpha$ is defined as

where $\alpha > 0$, $t_{ 0}$ is the initial time, $n\in\mathbb{N}$, and $\Gamma$ is the Gamma function.

Lemma 1. ^[47] The equilibrium points $x^*$ of $D^\alpha x(t) = f(x)$ are locally asymptotically stable if all eigenvalues $\lambda_i$ of the Jacobian matrix $J = {\partial f}/{\partial x}$ evaluated at the equilibrium points satisfy $|\arg(\lambda_i)| > \frac{\alpha\pi}{2}$.

Lemma 2. ^[48] Let $x(t)\in\mathbb{R}^+$ be a differentiable function. Then, for any time instant $t\geq t_0$

Lemma 3. ^[49] (Uniform Asymptotic Stability Theorem) Let $x = 0$ be an equilibrium point of $D^\alpha x(t) = f(t, x)$, and let $\Omega\subset R^n$ be a domain containing $x = 0$. Let $V(t, x) : [t, \infty) \times \Omega\rightarrow \mathbb{R}$ be a continuously differentiable function such that

and

for $t\geq0, x\in\Omega$ and $0 < \alpha < 1$, where $W_1(x), W_2(x)$ and $W_3(x)$ are continuous positive definite functions on $\Omega$, then $x = 0$ is uniformly asymptotically stable.

Remark 1. ^[39] If $x = x^\ast$ is the equilibrium point of $D^\alpha x(t) = f(t, x)$ and satisfies the conditions of Lemma 3, then $x = x^\ast$ is uniformly asymptotically stable.

3.   Main result

3.1.   Model description

In ^[50], the following model is considered.

where the functions $a_i(t), b_{ij}(t)$ are assumed to be nonnegative and continuous for $t\in(-\infty, \infty)$. This system is commonly called the Volterra-Lotka system for $N$-competing species. Because of the complex relations between the species, it would be more realistic to change the functions $b_{ij}(t)u_j(t)$ to $f_{ij}(u_j(t))$, so one can build a new population model.

This paper considers the following generalized fractional-order ecosystem model:

where $t_0\geq0$ is the initial time, $x_i(t)$ for $i = 1, 2, 3, \ldots, N$ denotes population density of the species $x_i$ at time $t$, $a_{ij} = \pm 1, 0$. $f_{ij}(x_j(t))$ are continuous, non-negative and differentiable functions.

$f_{ii}(x_i)$ are the specific growth rate of $x_i$ in the absence of other species for $i = 1, 2, 3, \ldots, N$. If $x_i$ represents a producer in ecosystems, one can see that the specific growth rate of $x_i$ is positive, so one makes $a_{ii} > 0( = 1)$. If $x_i$ represents a consumer in ecosystems, one can see that the specific growth rate of $x_i$ is negative, so one makes $a_{ii} < 0( = -1)$. The greater the number of species is, the greater the intra-specific competition will be. So ${df_{ii}(x_i)}/{dx_i} < 0$, if $x_i$ represents a producer and ${df_{ii}(x_i)}/{dx_i}\geq0$, if $x_i$ represents a consumer.

$f_{ij}(x_j)$ are the effect of $x_j$ on $x_i$ in a time unit for $i = 1, 2, 3, \ldots, N$, $i\neq j$. The greater $x_j$ is the greater the impact on $x_i$ will be, so one makes ${df_{ij}(x_j)}/{dx_j} > 0$. It is easy to see that when $x_j = 0$, there is no effect on $x_i$. That is $f_{ij}(x_j) = 0$ for $x_j = 0$.

One can describe the relationship between $x_i$ and $x_j$ by determining the sign of $a_{ij}$ and $a_{ji}$. If $a_{ij} > 0( = 1)$ and $a_{ji} > 0( = 1)$, then the relationship between $x_i$ and $x_j$ is mutualism. If $a_{ij} > 0( = 1)$ and $a_{ji} < 0( = -1)$, then the relationship between $x_i$ and $x_j$ is predation(parasitism) and it can be seen that $x_i$ is the predator(parasite) and $x_j$ is the prey (host). If $a_{ij} < 0( = -1)$ and $a_{ji} < 0( = -1)$, then the relationship between $x_i$ and $x_j$ is competition. If $a_{ij} = 0$ and $a_{ji} = 0$, there is no direct relationship between $x_i$ and $x_j$.

One should consider the significance of system (6), that is the boundedness of $x_i$. So the function $f_{ij}(x_j(t))$ for $i, j = 1, 2, 3, \ldots, n$ should give the restriction of making $x_i$ to be bounded.

Remark 2. If $x_i$ represents a producer, since ${df_{ii}(x_i)}/{dx_i} < 0$ and $f_{ii}(x_i) > 0$, then $f_{ii}(x_i) = b+g(x_i)$ ($g(x_i)$ does not contain a constant term and b is a constant), where $b > 0$ represents growth and ${dg(x_i)}/{dx_i} < 0$. In addition, if the time dependence of coefficients is ignored, Eq (5) can be regarded as a special form of Eq (6) (just set all $x_i$ as a producer, $a_{ii} = 1$, $a_{ij} = -1$, $f_{ij}(x_j) = b_{ij}x_j$ and $\alpha = 1$).

Remark 3. Moreover, let all $x_i$ as a producer, $a_{ii} = 1$, $a_{ij} = -1$, $f_{ii} = k_i-k_ic_{ii}x_i$, $f_{ij} = k_ic_{ij}x_j$ for $i, j = 1, 2, 3$ and $i\neq j$, then Eq (6) is same as the model in ^[32]. Let $x_1$ as a producer and $x_2$ as a consumer, $a_{11}, a_{21} = 1$, $a_{12}, a_{22} = -1$, $f_{11} = r-kx_1$, $f_{12} = x_2$, $f_{21} = \beta x_1$ and $f_{22} = 1$, then Eq (6) is same as system (5) in ^[33]. Let $x_1$ as a producer and $x_2, x_3$ as consumers, $a_{i1} = 1$, $a_{ij} = -1$, $f_{1j} = c_{1j}x_j$, $f_{j1} = c_{j1}x_j$, , $f_{11} = b_1-c_{11}x_1$, $f_{jj} = b_j+c_{jj}x_j$ for $i = 1, 2, 3, j = 2, 3$, $f_{23} = c_{23}x_3$ and $f_{32} = c_{32}x_2$, then Eq (6) is same as system (1) in ^[34]. Just let $a_{23} = a_{32} = 0$, then Eq (6) is same as system (19) in ^[34]. So the models in ^[32,33,34] are special forms of Eq (6).

3.2.   Existence and uniqueness of the solution

Theorem 1. If $x_i(t_0) > 0,$ for $i = 1, \cdots, N$, then is a unique solution $x(t)$ of system (6) in $\mathbb{R}_+^N$ for $t\geq t_0$.

Proof. We study the existence and uniqueness of the solution of system (6) in the region $\Omega\times[0, T]$, where $\Omega = \{(x_1, x_2, \ldots, x_N)\in\mathbb{R}^3:max\{\mid x_1\mid, \mid x_2\mid, \ldots, \mid x_N\mid < M\}\}$ and $T < +\infty$. Denote $X = (x_1(t_1), x_2(t_1), \ldots, x_N(t_1))$ and $\bar{X} = (x_1(t_2), x_2(t_2), \ldots, x_N(t_2))$. Consider a mapping $H(X) = (H_1(X), H_2(X), \ldots, H_N(X))$ where

For any $X, \bar{X}\in\Omega$

where $t\in[t_1, t_2]$ and $L = \max\{M \sum_{j = 1}^N[f_{ji}(x_i(t))-f_{ij}(x_j(t_2))]\}$ for $i = 1, 2, \ldots, n$. Obviously, $H(Z)$ satisfies the Lipschitz condition. Thus, system (6) has a unique solution $x(t)$.

Theorem 2. If $x_i(t_0) > 0,$ for $i = 1, \cdots, N$, then solutions of system (6) are non-negative.

Proof. Let $x_i(t_0) > 0, i = 1, \cdots, N$ in $R_+^N$ be the initial solution of system (6). By contradiction, suppose that there exists a solution $x(t)$ that lies outside of $R_+^N$. The consequence is that $x(t)$ crosses the $x_i$ axis for $i = 1, 2, 3, \ldots, N$.

Assume that $x(t)$ crosses $x_k = 0$, then there exists $t^*$ such that $t^* > t_0$ and $x_k(t^*) = 0$, and there exists $t_1$ sufficiently close to $t^*$ such that $t_1 > t^*$, and $x_k(t) < 0$ for all $t \in(t^*, t_1]$. Based on the $k$-th equation of system (6), one obtains

Since $x(t)$ and $f_{kj}(x_j(t))$ are continuous, one can see that $f_{kj}(x_j(t))$ is bounded on $t\in[t^*, t_1]$.

Assume that $\max |a_{kj}f_{kj}(x_j(t))| = M$. Then

By using the Laplace transform on both sides, one gets

where $E_\alpha$ is the Mittag-Leffler function. Thus, $x(t)\geq 0$ for any $t \geq t_0$, which contradicts the assumption. By using the same method, one gets $x_i(t)$ are non-negative for $i = 1, 2, \ldots, N$.

3.3.   Stability analysis of equilibrium points

In this section, the stability of the equilibrium points will be investigated by using the Lyapunov direct method. The equilibrium points of the model can be obtained from the following equations.

In the following, we will only consider the stability of a certain equilibrium point, for the other equilibrium points can be discussed by the same way.

3.3.1.   Local stability

Assume that $x^*$ is the equilibrium point of system (6), then it has k ($0\leq k\leq N$) components of vector $x^*$ that are not 0. By the operations of row and column, $x^*$ can be written as $x^* = (x_1^*, x_2^*, \ldots, x_k^*, 0, \ldots, 0)$. The Jacobian matrix at $x^*$ is

where $b_{ij} = a_{ij}f^{'}_{ij}(x^*_j)x_i^*$.

Solving the characteristic equation $det(\lambda I-J(x^*)) = 0$ for $\lambda$ to find the eigenvalues of $J(x^*)$, one gets

Let

$M(i, j)$ is the $j-th$ $i-order$ principal minor of $A$ and $a_i = (-1)^i\sum_{j = 1}^{C_k^i}M(i, j)$.

For the sake of discussion, we define $H_j$ as follows

Theorem 3. Suppose that $x^* = (x_1^*, x_2^*, \ldots, x_k^*, 0, \ldots, 0)$ is the equilibrium point of the system (6), then the equilibrium point is locally asymptotically stable, if the following algebraic conditions hold:

1). $\sum_{j = 1}^k a_{ij}f_{ij}(x_j^*)+a_{ii}f_{ii}(x_j^*)\leq0$, for $i = k+1, k+2, \ldots, N$.

2). $a_i$ for $i = 1, 2, \ldots, k$ satisfy $H_j > 0$ for $j = 1, 2, \ldots, k$.

Proof. According to the Hurwitz criterion, if $H_j > 0$ for $j = 1, 2, \ldots, k$, then all eigenvalues of $\lambda^k+a_{1}\lambda^{k-1}+a_{2}\lambda^{k-2}+\cdots+a_{k-1}\lambda+a_k = 0$ have negative real part.

According to $\sum_{j = 1}^k a_{ij}f_{ij}(x_j^*)+a_{ii}f_{ii}(x_j^*)\leq0$, one can see that all eigenvalues of $[(\lambda-\sum_{j = 1}^n a_{k+1'j}f_{k+1'j}(x_j^*)) \cdots(\lambda-\sum_{j = 1}^n a_{nj}f_{nj}(x_j^*))] = 0$ are negative or equal to 0.

Above all, the equilibrium point is locally asymptotically stable.

Remark 4. The conditions of Theorem 3 are sufficient conditions. If $H_j < 0$ and all eigenvalues of $\lambda^k+a_{1}\lambda^{k-1}+a_{2}\lambda^{k-2}+\cdots+a_{k-1}\lambda+a_k = 0$ satisfy the condition in Lemma 1, the equilibrium point is also locally asymptotically stable.

3.3.2.   Global stability

Theorem 4. Suppose that $x^* = (x_1^*, x_2^*, \ldots, x_k^*, 0, \ldots, 0)$ is the equilibrium point of system (6), then $x^*$ is globally asymptotically stable, if the following algebraic conditions hold:

1). $x^*$ satisfy $\sum_{j = 1}^k a_{ij}f_{ij}(x_j^*)+a_{ii}f_{ii}(x_j^*)\leq0$, for $i = k+1, k+2, \ldots, N$.

2). $\exists k_{ij}\geq0$ satisfy $\sum_{j = 1}^n k_{ij} = 1$ for $i, j = 1, 2, \ldots, N$ and $i\neq j$.

3). $\exists c_i > 0$ and $\exists k_{ij}\geq0$ satisfy $2\sqrt{a_{ii}a_{jj}c_ic_jk_{ij}k_{ji}f^{'}_{ii}(x_i^*)f^{'}_{jj}(x_j^*)} > |a_{ij}c_if^{'}_{ij}(x_j^*)+a_{ji}c_jf^{'}_{ji}(x_i^*)|$ for $i, j = 1, 2, \ldots, N$.

Proof. If $\sum_{j = 1}^k a_{ij}f_{ij}(x_j^*)+a_{ii}f_{ii}(x_j^*)\leq 0$, for $i = k+1, k+2, \ldots, N$, that is

Let us consider the following positive definite function about $x^*$

One can subtly choose $c_i > 0$ such that $V$ is a Lyapunov function. By Lemma 2, one obtains

For arbitrary $\varepsilon > 0$, since functions $f_{ij}$ for $i, j = 1, 2, \ldots, n$ are differentiable functions, there exists $\delta > 0$ such that $|x_i -x_i^{\ast}| < \delta$ for $i = 1, 2, \ldots, N$, it implies

Thus

By the arbitrariness of $\varepsilon$, one has

For $i\neq j$, then one has

According to the condition $2\sqrt{a_{ii}a_{jj}c_ic_jk_{ij}k_{ji}f^{'}_{ii}(x_i^*)f^{'}_{jj}(x_j^*)} > |a_{ij}c_if^{'}_{ij}(x_j^*)+a_{ji}c_jf^{'}_{ji}(x_i^*)|$, and $a_{ii}f^{'}_{ii}(x_i) < 0$ for $i = 1, 2, \ldots, n$. So the conditions in Lemma 3 are satisfied, where $W_3(x) = \sum_{i = 1}^n\sum_{j > i}^n\bigg[2|x_i-x_i^*||x_j-x_j^*|\sqrt{a_{ii}a_{jj}c_ic_jk_{ij}k_{ji}f^{'}_{ii}(x_i^*)f^{'}_{jj}(x_j^*)}-(x_i-x_i^*)(x_j-x_j^*)(c_ia_{ij}f_{ij}^{'}(x_j^*)+c_ja_{ji}f_{ji}^{'}(x_i^*))\bigg] > 0$.

Thus, $x^*$ is a globally asymptotically stable equilibrium point for the system (6).

Remark 5. According to theorem 4, one can see that N-order system should have $N(N-1)/2$ conditions at least. So if $N$ is large enough, it is difficult to find the suitable $c_i, k_{ij}$ for $i, j = 1, 2, 3, \ldots, n$ and $i\neq j$.

4.   Numerical simulation

In this section, we will give some examples to demonstrate the theoretical analysis.

Example 1:

Let us consider the functions of the system (6) as follow

Therefore, the system (6) can be denoted by the following Volterra-Lotka competition system:

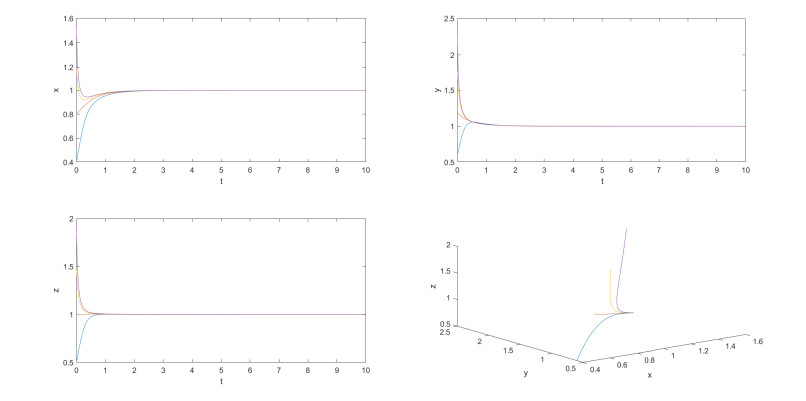
From the parameters of the system, it can be seen that the equilibrium points of the system are $(1, 1, 1)$, $(1, 1, 0)$ and $(1, 0, 0)$. One can see that when $k_{ij} = 0.5$ and $c_i = 1$ for $i, j = 1, 2, 3, i\neq j$, the equilibrium point $x^* = (1, 1, 1)$ can satisfy three conditions in Theorem 4. Other equilibrium points can not satisfy condition 1 in Theorem 4. One selects the initial values as $(0.8, 0.6, 0.4)$, $(1.6, 1.2, 0.8)$, $(2.4, 1.8, 1.2)$ and $(3.2, 2.4, 1.6)$ respectively, and the numerical results are shown in Figure 1. From Figure 1, one can see that the positive equilibrium point (1, 1, 1) of system (23) is globally asymptotically stable.

Example 2:

In this example, one considers the functions $f_{ij}$ of system (6) as nonlinear form:

Therefore, the system (6) can be denoted by the following competition system:

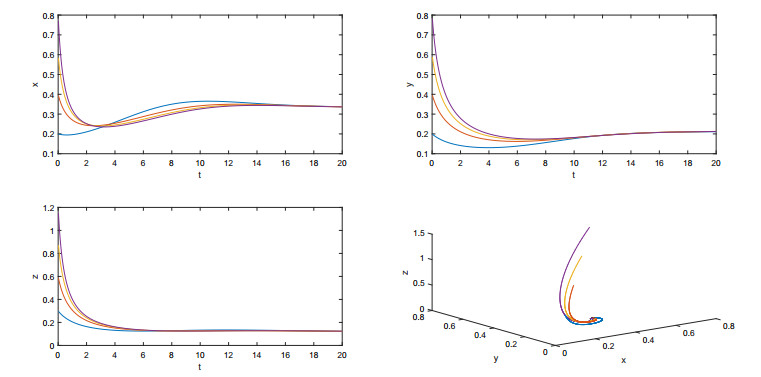
From the parameters of the system, it can be seen that the equilibrium points of the system are $(1, 1, 1)$ and $(0, 0, 0)$. One can see that when $k_{ij} = 0.5$ and $c_i = 2$ for $i, j = 1, 2, 3, i\neq j$, the equilibrium point $x^* = (1, 1, 1)$ can satisfy three conditions in Theorem 4 and the other can not satisfy all conditions in Theorem 4. One selects the initial values as $(0.4, 0.6, 0.5)$, $(0.8, 1.2, 1)$, $(1.2, 1.8, 1.5)$ and $(1.6, 2.4, 2)$ respectively, and the numerical results are shown in Figure 2. From Figure 2, one can see that the positive equilibrium point (1, 1, 1) of system (25) is globally asymptotically stable.

Example 3:

The new example will consider the complex relationships between the species, one selects the functions of the system (6) as follow.

Therefore, the system (6) can be denoted by the following prey-predator system with interspecific competition:

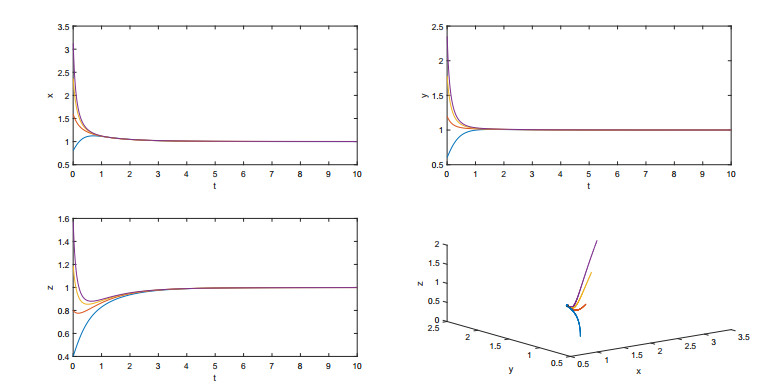
From the parameters of the system, it can be seen that the equilibrium points of the system are $(1/3, 2/9, 1/9)$, $(1/3, 1/3, 0)$ and $(1, 0, 0)$. One can see that when $k_{12} = k_{21} = 0.5$, $k_{32} = k_{23} = 0.8$, $k_{21} = k_{31} = 0.2$ and $c_i = 1$ for $i, j = 1, 2, 3, i\neq j$, the equilibrium point $(1/3, 2/9, 1/9)$ can satisfy three conditions in Theorem 4. One takes initial values $(0.2, 0.2, 0.3)$, $(0.4, 0.4, 0.6)$, $(0.6, 0.6, 0.9)$ and $(0.8, 0.8, 1.2)$ respectively, and the numerical results are shown in Figure 3. From Figure 3, one can see that the positive equilibrium point $(1/3, 2/9, 1/9)$ of system (26) is globally asymptotically stable.

5.   Conclusions

In this paper, one considers a class of generalized fractional population model. Firstly, the existence, uniqueness and non-negative of solutions of the system are proved. Secondly, one provides a sufficient conditions for local stability and globally stability of the equilibrium points. Finally, three examples are given to demonstrate the theoretical analysis. This paper not only extends the integer population models to fractional-order form, but also extends the dimension to n-dimension. The new model can be used to simulate the relationships between various populations in a complex ecosystem. Compared with other population models, our model is more general.

Time delay stays in the biological system widely and may effect the stability of the biological system. Thus, system (6) with time delay is of great research value. It will be our future work.

Acknowledgments

This work was supported by the National Natural Science Foundation of China (Nos. 61573008, 61973199), the Natural Science Foundation of Shandong Province (No. ZR2018MF005), and the SDUST graduate innovation project (No. SDKDYC190353).

Conflict of interest

The author declares no conflicts of interest in this paper.