1.
Introduction
Material emergency dispatching (MED) is the key link of emergency management in disaster areas. Due to the complex and changeable situation of disaster areas, the material demand of affected points will gradually change with the passage of time, which increases the complexity of solving MED problem. As a result, under the influence of dynamic factors, it is difficult for vehicles to complete the material distribution task of all affected point in the shortest time. Therefore, in order to minimize the loss in the disaster area, it is very important to study and formulate a scientific and efficient dispatching scheme.
MED is the practical application of vehicle routing problem (VRP) [1]. At present, the algorithms used to formulate scheduling schemes mainly include accurate algorithm [2,3] and swarm intelligence algorithm [4,5]. Among them, the accurate algorithm mainly includes branch and bound method, column generation method and dynamic programming algorithm, which adopt mathematical methods to solve the problem. This kind of algorithm can obtain the global optimal solution of the problem, but it can only be used to solve small-scale problems [6]. When the scale of the problem becomes larger, the solution time will increase explosively. Compared with the accurate algorithm, swarm intelligence algorithm can obtain the approximate optimal solution of large-scale problems in an acceptable time [7], but the solution performance of the algorithm depends on various manually designed rules, and the performance of the algorithm is difficult to be verified by mathematical theory. Therefore, the relevant mathematical abstraction and modeling methods often have an imbalance between time and performance when solving the problem. In recent years, with the wide application of machine learning technology in computer science and other fields, it provides new ideas for solving VRP and other combinatorial optimization problems [8−11]. For example, deep reinforcement learning (DRL) algorithm is used to solve VRP [12]. Due to the DRL combines the perception ability of deep learning and the decision-making ability of reinforcement learning (RL), it can automatically learn the hidden relationship between data and avoid the limitations caused by manual design features. The DRL algorithm is based on the Encoder-Decoder framework to build the problem-solving model, although recurrent neural network (RNN), long and short term memory (LSTM) network and attention mechanism (AM) [13] are used in the existing framework to build relevant models to solve combinatorial optimization problems, there are still a disadvantage of low performance in solving VRP and other problems. Therefore, Kool et al. [14] used multi head attention mechanism in Encoder-Decoder framework and use REINFORCE algorithm with baseline to train the model, which improved the performance of solving combinatorial optimization problems such as VRP. Even so, when there are dynamic factors in VRP related problems, the fixed model framework will make the extracted node features deviate from the actual features, and the model is difficult to adapt to the changes of uncertain factors.
Due to the dynamic factors in the actual MED problem, the demand of the affected pointers will change dynamically with time under the influence of the disaster. If the above model is used to solve the problem, the node embedding is only calculated once and remains unchanged in the subsequent decoding steps, which making the fixed node embeddings unable to accurately express the current node characteristics when the demand of the effected points changes. Moreover, the existing model only uses the features of the current node to solve the problem, without considering the influence of the previous node information on the current moment. Therefore, this article proposes a dynamic attention mechanism based on improved gated recurrent unit (DAM-IGRU), which updates node embeddings in real time to adapt to the change of node demand, so that the currently known node information can be fully utilized when constructing solutions step by step. In addition, an improved gated recurrent unit (IGRU) is introduced between the encoder and the decoder to express the influence of known node information on the current moment. The reset gate (RG) and update gate (UG) of IGRU is used to weight the node information of the current moment, the previous moment and the initial moment, so as to obtain a higher representation of the node embedding at the current moment.
The rest of this paper is organized as follows. Section 2 describes the existing related work. Section 3 introduces the relevant background knowledge. Section 4 introduces the proposed model. Section 5 shows the experimental results. Section 6 is discussed and analyzed, and the conclusion follows in Section 7.
2.
Related works
To solve VRP, researchers have proposed a variety of algorithms. According to the different solution methods, it can be divided into accurate algorithm, heuristic algorithm and machine learning algorithm.
The accurate algorithm is to establish the corresponding mathematical model for a specific problem and then use mathematical methods to solve it, which is usually used to solve the optimal solution of the problem. To improve the speed of the algorithm to solve the optimal solution of VRP, Fukasawa et al. [15] used the branch pricing algorithm to solve the root node when solving the VRP with limited capacity, and find the lower bound through the column generation method, so as to improve the overall efficiency of the algorithm. Pecin et al. [3] used the branch price and cut method to solve VRP with time window. It uses arc subset instead of node subset to reduce the computational complexity. For improving the quality of the solution, in solving VRP in waste management system, Ceselli et al. [16] proposed a specific accurate algorithm for pricing problem by dynamically generating rows and columns under the framework of branch and bound, so as to improve the quality of solution. Marinelli et al. [2] decomposed the main problem into multiple sub-problems by FCM clustering, and use an accurate algorithm to obtain the two-level solution of each sub-problem, so as to continuously optimize the feasible solution of the problem. Although the exact algorithm can get the optimal solution of the problem, it usually exchanges the quality of the solution at the cost of time and space complexity. Due to the introduction of strict mathematical methods in the solution, the calculation time will increase explosively with the increase of the scale of the problem, resulting in the performance of the exact algorithm is greatly reduced, even unable to find the optimal solution. Therefore, the exact algorithm can only be applied to the small-scale VRP solution.
The heuristic algorithm is proposed relative to the exact algorithm and gives a feasible solution of the combinatorial optimization problem within an acceptable range, but the deviation degree between the feasible solution and the optimal solution can not be estimated. Compared with the traditional exact algorithm, the heuristic algorithm has higher robustness and feasibility in dealing with large-scale VRP. However, this algorithm has some disadvantages such as falling into local extremum and slow convergence speed. To prevent the algorithm from falling into local optimum, Zhang et al. [17] introduced a mutation operator to search the neighborhood of randomly selected solution in ant colony algorithm and used exchange operator, shift operator, and inverse operator to maintain the diversity of population and prevent it from falling into local optimum too early. In addition, when solving the multi-site vehicle routing problem, Yao et al. [18] adopted a scanning strategy to help the ant colony algorithm jump out of the local optimal solution, and introduced crossover operation to expand the search space of the algorithm. To accelerate the convergence speed of the algorithm, Cattaruzza et al. [19] introduced local search algorithm and segmentation algorithm into the genetic algorithm to solve the VRP with time window, and selectively carried out local search on a certain individual to accelerate the convergence speed and thus improve the performance of the genetic algorithm. Wang et al. [20] proposed an adaptive genetic algorithm with local search for solving multi-site VRP. According to the fitness value, the adaptive rate strategy was adopted to update the crossover and mutation probabilities, and combined with local search to accelerate the convergence speed of the algorithm. Although a lot of work has been done to solve the two shortcomings of the algorithm, its solving performance mainly depends on various rules designed by humans, which makes it difficult to achieve the optimal quality of the solution.
With the rapid development and successful application of machine learning technology in the fields of management operations research and computer science, more and more researchers apply it to solve combinatorial optimization problems (such as VRP), and have obtained certain achievement. For example, Hopfield et al. [21] used Hopfield neural network to quickly solve the small-scale traveling salesman problem (TSP), so that the application of neural network in related problems has been widely concerned and discussed by researchers [22]. Researchers have done a lot of work around TSP, VRP and other issues. For example, Vinyas et al. [23] proposed pointer network (PN) and regarded the combinatorial optimization problem as a sequence problem, in which the input is the sequence of nodes and the output is the arrangement of input nodes. In addition, the AM [13] was used to create pointers to input elements, and the softmax probability distribution is used as a "pointer" to represent the variable length sequence, so as to eliminate the limitation that the output length is dependent on the input. In the above work, the recurrence network with non-parametric softmax is trained in a supervised way, and the supervised signals given by the approximate solver are used to train the model, so as to predict the sequence of the visited nodes, but it is difficult to obtain the optimal label of TSP. Therefore, Bello et al. [24] proposed an Encoder-Decoder framework that uses neural network and RL to solve combinational optimization problems, and used the RNN in encoder and decoder respectively. When training the model, the negative path length is used as the reward value, and REINFORCE algorithm is adopted to optimize the parameters of the neural network, which has achieved certain results in solving TSP and other problems. As an extension of TSP, VRP is more difficult to calculate because of its more complex form. In order to solve this problem, Nazari et al. [25] proposed an end-to-end framework using RL algorithm, which is composed of an RNN decoder and an AM. Due to paying attention to the change of node demand during solution, it takes the embedding of static elements as the input of RNN decoder, and inputs the output of RNN and the embedding of dynamic elements into the AM to select the next node. At the same time, Yu et al. [26] constructed a deep neural network model to solve the online VRP. It uses an unsupervised auxiliary network to train the model parameters and form a new neural combination optimization strategy based on RL, so that the trained model can effectively solve the dynamic system. In addition, in order to obtain better models and training methods, Kool et al. [14] proposed an attention-based model that is more effective than PN. The model used the multi head attention mechanism in the Encoder-Decoder framework, and used the REINFORCE algorithm with baseline during model training, which improved the performance of the model to solve combinational optimization problems such as TSP and VRP. In addition, Ma et al. [27] adopted pointer neural network combined with deep learning and RL to solve VRP with task priority and limited resources. According to the actual distribution of nodes, the model continuously learns the mapping relationship between input nodes and output decision-making scheme. Moreover, a global attention mechanism was used in the model to improve the convergence speed and solution performance of the model, which provided a better solution for VRP.
When solving TSP and VRP combinatorial optimization problems, the performance of the above work has better advantages than the traditional heuristic algorithm, which lays a foundation for solving related problems in the future. However, when solving the VRP Problem with dynamic factors, its performance still has some limitations. Therefore, this article will improve the DRL algorithm to adapt to the MED problem with the change of material demand at the actual affected point. Therefore, the following research work will be carried out to improve the effectiveness of the algorithm.
3.
Background
3.1. Encoder-decoder model based on multi-head attention mechanism
The Encoder-Decoder model based on multi head attention mechanism (MHA) [14] uses MHA in encoder and decoder respectively, and obtains node embedding with stronger representation ability after fusion improvement by integrating different results of multiple identical attention. When solving VRP, its encoder is used to generate intermediate node embedding and output access nodes in turn through the decoder. The input feature dimension of VRP problem is dx = 3 (including node coordinates and demand). The initial node embedding (dimension dh = 128) is obtained through linear transformation, and the node embedding is updated through the n-layer attention layer in encoder, and the final embedding hNi and graph embedding ¯hN of each node are obtained by Eqs(3.1)–(3.5).
Where m∈{1,...,M}, M is the number of heads, hi represents the embedding of node i, WmQ∈Rdk×dh, WmK∈Rdk×dh, WmV∈Rdv×dh, WO∈Rdh×dv(dk=dv=dh/M=16) is a learnable parameter, Qmi, Kmi and Vmi are the query vector, key vector and value vector of node the i-th in the m-th head, h'i is the embedding of node i after one attention mechanism, FF is the feedforward sublayer.
In the decoder, the next node to be accessed is selected based on the currently generated partial solution π1:t−1 and each node embedding. The context embedding is calculated according to Eq (3.6), and then the importance of each node for context embedding is calculated respectively, and the node embedding after fusion promotion is obtained through the MHA mechanism. The output probability of the node is obtained by a single head attention mechanism and calculated with Eqs (3.7) and (3.8).
Where WQ∈Rdk×dh, WK∈Rdk×dh, WV∈Rdv×dh, C is used to map the result to [−C,C] (C = 10).
3.2. Gated recurrent unit
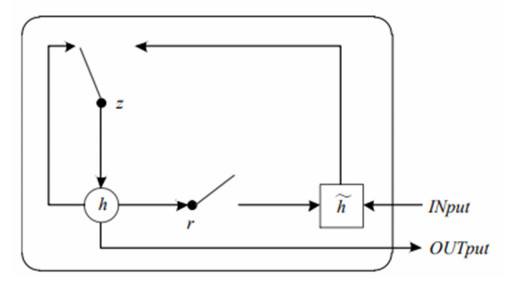
The gated recurrent unit (GRU) [28] aims to solve the gradient disappearance problem in the standard RNN, which can be regarded as the optimization of the structural complexity of the LSTM. The principle of GRU is similar to that of LSTM. Through the gating mechanism, GRU can not only remember the past information, but also selectively forget some unimportant information. In terms of structure, GRU only includes two gating structures: reset gate and update gate. Its structure is shown in Figure 1.
The RG is used to determine how to combine the new input and the previous memory information, and the UG determines how much previous memory information to retain. The RG rt and UG zt can be calculated by Eqs (3.9) and (3.10) respectively:
Where σ is the sigmoid function, xt is the input at time t, ht−1 is the previous hidden state, and Wr, Ur, Wz and Uz are the learned weight matrix respectively.
The candidate hidden status and hidden status can be updated by Eqs (3.11) and (3.12) respectively.
Where φ is the tanh function, W and U are the learnable weight matrix respectively, ⊙ is the Hadamard product, that is, the product of the corresponding elements in the two matrices.
4.
Proposed models
4.1. The structure of proposed model
In the MED problem with dynamic demand, each affected point contains two static features (coordinates) and one dynamic feature (demand). The existing model is mainly used to solve the static problem. The node embedding is only calculated once in the solution, that is, the node features remain unchanged in the subsequent decoding process. Therefore, when the node demand changes, the fixed node embedding will not be able to accurately express the current node characteristics, thus losing some node information and difficult to fit the dynamic characteristics in the problem. In addition, when constructing the solution step by step, the existing model only uses the current node embedding, the previous output node and context embedding. The context embedding is mainly used to reflect the load information of the current vehicle, and does not make full use of the information of the intermediate output node, so that when solving the next output node, the importance between the location of this node and the relative location of other nodes accessed by the current vehicle is ignored.
Therefore, this article proposes the DAM-IGRU. Aiming at the problem of the dynamic change of the demand of the affected points, the model adopts the dynamic Encoder-Decoder framework to recalculate the node embedding in each decoding step, so as to obtain the current accurate node characteristics. At the same time, IGRU is introduced between encoder and decoder, and its RG and UG are used to weighted combine the node information of the previous time, the current time and the initial time to obtain a more representative node embedding, so as to effectively mine the hidden structure information between nodes. The structure of DAM-IGRU model in this article is shown in Figure 2.
In DAM-IGRU model, when the demand of nodes changes, the encoder is used to re-extract the characteristics of nodes to generate new node embedding and graph embedding. In order to reduce the calculation time and improve the efficiency of model solving, only the unselected nodes and distribution centers are calculated when updating the node embedding each time.
When solving the problem, obtain the node embedding hNi and graph embedding ¯hN of all currently unreachable nodes and distribution centers through encoder, and input the node embedding into IGRU. In IGRU, in order to make full use of the known node information and the hidden relationship between nodes, it not only retains the node information at the previous time, but also retains the node information at the initial time, and uses the RG and UG to weight the node embedding at different times, so as to obtain the high-level node embedding with stronger expression ability. The RG is used to determine how to combine the node information of the current time, the memory information of the previous time and the initial time, and the UG determines how much memory information of the previous time and the initial time should be retained. In this article, the improved method shown in Eqs (4.1)–(4.3) was adopted to calculate RG rt and UG zt in IGRU.
Where [0:xt]n−t−1 indicates that the matrix xt is supplemented with zero elements in the first n-t-1 column, [0:ht−1]n−t indicates that the matrix ht−1 is supplemented with zero elements in the first n-t column, t indicates the current decoding step, R[n−t+1:] indicates that the n−t+1 column of matrix R is taken to the last column, and Z[n−t+1:] indicates that the n-t+1 column of matrix Z is taken to the last column. When the Encoder-IGRU-Decoder process is completed once, the access node at the current time will be output. In the next Encoder-IGRU-Decoder process, the node information output at the previous t-2 time will be deleted from the information of the previous time. Therefore, when the node embedding is promoted and fused in IGRU, the number of embedded nodes input each time will differ by 1 from the previous time.
After the corresponding operations of RG and UG, in this article, the current candidate hidden state ˜ht and hidden state ht is calculated by the improved Eqs (4.4) and (4.5). The hidden state ht has two functions: one is to feed back the hidden information to IGRU at the next time, and the other is to embed it into the decoder as the current node. In the decoder, in addition to ht, its input also includes the graph embedding ¯hN obtained by the encoder, which is decoded according to the two kinds of information to obtain the output of the current decoding step.
The basic steps of the DAM-IGRU model are as follows:
Step 1: For the original input node sequence, the initial node embedding of the node at t' = 0 is obtained by linear transformation.
Step 2: The node embedding is input into encoder for coding, and the node embedding and graph embedding after improved fusion are obtained through MHA mechanism.
Step 3: Input the node embedding into IGRU, determine whether to delete or retain the information of t-1 time and initial time by UG, and use the RG to combine the information of t time, t-1 time and initial time, so as to obtain the node embedding with stronger representation ability after improved fusion.
Step 4: Input the node embedding and graph embedding into the decoder to obtain the output probability of all unvisited nodes, and select the node with the highest probability to output.
Step 5: Judge whether the access of all nodes is completed, if the access is completed, it ends, and the complete access sequence is obtained. Otherwise, the demand of unvisited nodes changes, and return to Step 2.
4.2. Model training algorithm
The performance of the DAM-IGRU model is not only related to the model structure, but also related to the model parameters. Therefore, to obtain a high-performance DAM-IGRU model, it is necessary to find the optimal model parameters to maximize the superiority of the model. RL is an important branch of machine learning technology. Through the interaction between the agent and the environment, features can be automatically learned from the data to maximize benefits. REINFORCE is one of the most basic strategy gradient algorithms in RL, which uses stochastic gradient descent to update strategy parameters, that is, given an instance X, the gradient of parameter θ is:
Where L(π∣X) is the path length of the solution to π, and b(X) is the baseline function used to estimate the expected path length of the instance X, which can reduce the gradient variance. During training, the instance X comes from the same distribution, then the gradient of the parameter θ in Eq (4.6) can be approximated by Monte Carlo sampling:
Where B is the batch size, πsi and πgi are the solutions of the instance Xi constructed by sample rollout and greedy rollout, respectively. The specific training algorithm is shown in Algorithm 1.
5.
Experiment results
Our experiments were written in Python 3.8, compiled on PyCharm, and run on an Intel(R) Core(TM) i5-10400f CPU @ 2.10GHz, Windows 10 operating system.
Since the node demand in the MED problem in this paper change dynamically, and the currently public data sets (such as Solomon [29]) lack data to simulate the demand change, the randomly generated data can be used to approximate the demand change of each affected point in the disaster area environment. In addition, in order to comprehensively evaluate the solution performance of the algorithm under different problem sizes, four problem sizes of 10, 20, 50 and 100 are selected [30]. The node positions are evenly and randomly selected in the unit square [0, 1]2, and the node demand is randomly generated between [0, 9] (the demand of the distribution center is 0), and the vehicle loads corresponding to different node numbers are 20, 30, 40 and 50 respectively. According to the solution goal of MED problem, that is, to complete the material distribution task of all disaster affected points in the disaster area in the shortest time, the solution of the problem is measured by the total driving distance of all vehicles when completing this task. The larger the total driving distance is, the higher the cost will be, and for the converse situation, the lower the cost will be.
5.1. Model training
The solution performance of the model is not only related to the model structure, but also depends on the model parameters. Appropriate model parameters can maximize the superiority of the model, so as to obtain better problem solutions when solving problems. Therefore, for improving the solution performance of the model, it is necessary to optimize the model parameters according to the number of nodes. Since REINFORCE is an unsupervised training, this article will perform iterative training on the model under the condition that the baseline is greedy rollout. The hyper-parameters used in the experiment are shown in Table 1, and Figures 3–6 shows the average cost change of the validation set under the baseline greedy rollout when the number of nodes is 10.
As can be seen from Figure 3, during the entire training process, the average cost of the validation set showed a fluctuating downward trend and finally stabilizes. As shown in Figure 4, from the beginning of training to about the 10th time, the average cost of the validation set decreased significantly, and then showed a slow downward trend. It can be seen from Figure 5 that when the number of training times is from 270 to 470, the average cost of the validation set showed a significant downward trend. From Figure 6, it can be seen that the average cost of the validation set still fluctuates at the end of training, but its overall trend has gradually stabilized. This kind of turbulence in training processes is because REINFORCE belongs to unsupervised training, and there is no expected actual data label as a reference. The baseline greedy rollout is added in training to provide a definite benchmark for model training, that is, when the result obtained by using a certain strategy is better than the current benchmark, the probability of the strategy is increased, and vice versa, the probability of the strategy is reduced. Therefore, the average cost of the validation set during the training process of the model shows an oscillating downward trend. And because the algorithm has the ability to learn automatically, it will gradually obtain better model parameters through a lot of training, so that the fluctuation range of the average cost of the verification set will gradually stabilize. That is, it can be considered that better model parameters are obtained through a lot of training on the model.
When using DAM-IGRU model to solve the problem, in order to obtain better model parameters and improve the solution performance of the model, the model is trained under different problem scales, and the corresponding training time and calculation time are shown in Table 2. It can be seen from Table 2 that with the increase of the problem scale, the time required for model training increases significantly, and the corresponding calculation time also increases gradually, but its calculation time is far less than the training time of the model, and the model only needs to be trained once to solve the problem. Therefore, DAM-IGRU model has high solution efficiency.
5.2. IGRU validity verification
In order to verify the effectiveness of IGRU in the model, DAM model without IGRU and DAMIGRU model are used to solve the MED problem respectively. Firstly, when the number of nodes is 10, 20, 50 and 100 respectively, the same super parameters are used to train the DAM model. Then 10 test sets are generated under different node numbers. Each test set contains 2000 samples. Two models are used to calculate the test set respectively. The calculation results are shown in Table 3 and Figure 7.
As can be seen from Figure 7, when DAM and DAM-IGRU models are used to solve problems of different scales, the average cost of problem solving obtained by DAM-IGRU model is significantly better than that of DAM model. According to Table 3, when the number of nodes is 10, 20, 50 and 100, the average cost of the 10 test sets calculated by DAM-IGRU model decreases by 9.78, 7.17, 6.11 and 8.23%, respectively, compared with the DAM model obtained by training under the same hyper-parameter. The difference is whether IGRU is used between the encoder and the decoder. The difference in solution performance between the two may be because IGRU can further improve the fusion of node features, and the obtained node embedding has more representation ability, so as to improve the solution performance of the model, which can show the effectiveness of IGRU in the model to a certain extent. In addition, in terms of calculation time cost, the average time required by DAM-IGRU model is longer than that of DAM model, and the average time difference between the two models increases with the increase of node number. This is because in DAM-IGRU model, the node embedding obtained by encoder needs to be upgraded and integrated through IGRU again, which takes a certain amount of time.
5.3. Model validity verification
In order to verify the effectiveness of the DAM-IGRU model proposed in this article, the elitismbased immigrants ant colony optimization (EIACO) algorithm proposed by Mavrovouniotis et al. [31] is used to solve this problem. The calculation results are shown in Table 4.
As can be seen from Table 4, compared with EIACO algorithm, when calculating MED problems with different nodes, the average cost of the problem solution calculated by DAM-IGRU model is lower. When the problem scale is 10, 20, 50 and 100 respectively, the quality of the problem solution calculated by the DAM-IGRU model is improved by 27.89, 27.94, 28.09 and 28.12% respectively. It can be seen that the DAM-IGRU model has better performance in solving, and the average deviation between the two algorithms increases gradually with the increase of the problem scale. This is because when the problem scale is small, that is, the number of nodes is small, the solution space of the problem is relatively small, and the probability of obtaining a better solution by using EIACO algorithm is relatively large. When the problem scale is large, the solution space of the problem increases explosively, and the trained DAM-IGRU model can effectively deal with the huge solution space, and eliminate the influence of the dynamic change of node demand, so as to obtain a better quality solution.
In addition, it can be seen from Table 4 that the calculation time of DAM-IGRU model and EIACO algorithm increases significantly with the increase of problem scale. However, compared with EIACO algorithm, the average time required for solving DAM-IGRU model is less. Under different node numbers, the solving time is reduced by 4.05, 13.13, 79.01 and 234.67 respectively. It also shows that when dealing with large-scale problems, the well-trained DAM-IGRU model can quickly obtain the corresponding solution by automatically learning the characteristics of input nodes.
6.
Discussion
1) The reason for the difference between the heuristic algorithm and the DAM-IGRU model.
It can be seen from Table 4 that the heuristic algorithm and the DAM-IGRU model have certain differences in solving the same problem, and the reason for this difference may be the different principles on which they solve. The heuristic algorithm iteratively optimizes the solution of the problem according to the rules designed in advance, which makes its solution performance effected by various manually designed rules, and the iterative rules of the algorithm make it easy to fall into local extremum too early. At the same time, with the increase of the scale of the problem, the solution space of the problem increases greatly, which reduces the solution performance of the algorithm under the same parameters (such as the number of iterations of the algorithm), making it difficult to fully explore the solution space of the problem. Compared with the heuristic algorithm, the DAM-IGRU model will automatically learn features from the data, and can mine the deep-level information hidden between the data without manual participation. This method can avoid the limitations of manual design features to a certain extent and improve the solution efficiency of problem. In addition, the experimental analysis also shows that the heuristic algorithms are greatly effected by the parameter setting, and its randomness in the solution spaces search makes the solution different. Therefore, if the optimal parameters of the heuristic algorithm are found for experimental calculation, the quality of the solution may be close to the DAM-IGRU model. In the follow-up work, this problem needs to be deeply studied and analyzed.
2) Time complexity of DAM-IGRU model.
Although the DAM-IGRU model has achieved good results, the encoder is repeatedly used to update the node embedding in the solution process, which increases the time complexity of the algorithm. It can also be seen from Table 3 that the solution time of DAM-IGRU model is increased compared with DAM model. In the experimental calculation, when the decoder outputs an access node, the demand of the remaining unreached nodes will change. In order to obtain the current accurate node embedding, it is necessary to re-encode the node information. Therefore, in the whole solution process, the update times of node embedding are related to the length of the final output sequence. The longer the output sequence is, the more time it takes to solve the problem. In order to reduce the complexity of the problem, this article only considers the increase or decrease of the demand of the existing affected points. But in the actual problem, there may be new affected points. If this situation is taken into account, the complexity of the problem will increase and the time spent in solving may also increase significantly. How to reduce the solving time while improving the solving performance of the model is a problem worthy of our in-depth thinking. In the following work, in view of the high time complexity, we will carry out the optimal solution research on the MED problem with changing demand.
3) Inconsistent data sets caused by changes in node access order and demand
In addition, in the MED problem solved in this article, the demand attribute of the affected point changes dynamically over time, that is, in each decoding step, when one access node is output, the demand of the remaining unreached nodes will change. Therefore, for the same set of initial data (the same coordinates and initial demand), the final demand of each node may not be consistent in the subsequent decoding process due to different output sequences. For example, for a group of nodes (0, 1, 2, 3, 4, 5), assuming that their initial demands are (0, 0.2, 0.1, 0.3, 0.4, 0.3), the model is used to solve the sample. When the first output node is 2, the generated access order is 0–2, and then the demands of the unvisited nodes (1, 3, 4, 5) will change. If the first output node is 3 and the generated access order is 0-3, the demands of the unvisited nodes (1, 2, 4, 5) will change. Therefore, in the comparative experiment, even if the initial data set is the same, with the output of the access sequence, the demand of the remaining unreachable nodes will change continuously, it will lead to the inconsistency of the sample data. In this case, its impact on the experimental results needs to be considered. For example, in Table 3, for the same batch of samples, the calculation result of DAM-IGRU model is better than that of DAM model. In order to minimize the impact of this problem on the results, although we used a large number of samples to train, verify and test the model, it is not known whether this result is still effected by the inconsistency of node demand. And if so, we want to know how much impact it will have. So, in the next step, the demand inconsistent of the unvisited nodes will be further studied based on the change of the output sequence.
7.
Conclusions
In this article, a DAM-IGRU model is proposed to solve the MED problem of changing demand. The model adopts a dynamic Encoder-Decoder structure to adapt to the characteristics of dynamic changes in node demand, and updates the current node characteristics in real time in different decoding steps, so that get accurate node information. In addition, through the introduction of IGRU, the node information of the previous moment, the current moment and the initial moment can be effectively combined, and the hidden structural information between the nodes can be deeply excavated, so as to obtain the node features with more representational ability and improve the solving ability of the model.
Meanwhile, the DAM-IGRU model is applied to the MED problem and compared with the improved heuristic algorithm EIACO. The experimental results show that when solving MED problems of different scales, the DAM-IGRU model can obtain higher quality solutions than EIACO in a shorter time. In addition, through further analysis and discussion of the experimental results, the following conclusions are drawn: 1) DAM-IGRU model and heuristic algorithm have different solving performance due to different basic principles in solving. 2) Compared with the DAM model, since the DAM-IGRU model needs to repeatedly calculate the node embedding, the required solution time will increase to varying degrees. 3) When solving the MED problem, in order to simulate the dynamic change of the demand, it may lead to inconsistency in the data set. For 2) and 3), we will find relevant solutions for these two problems in the future, and further optimize the model to improve its performance.
Acknowledgments
This research was supported by Key Scientific Research Projects of Colleges and Universities in Henan Province (Grant No.22A520003), Innovative Funds Plan of Henan University of Technology (Grant No.2021ZKCJ18).
Conflict of interest
The authors declare there is no conflict of interest.









 DownLoad:
DownLoad:









