Transformer-based cascade networks with spatial and channel reconstruction convolution for deepfake detection

1.   Introduction

Difference equations are the essentials required to understand even the simplest epidemiological model: the SIR-susceptible, infected, recovered-model. This model is a compartmental model, which results in the basic difference equation used to measure the actual reproduction number. It is this basic model that helps us determine whether a pathogen is going to die out or whether we end up having an epidemic. This is also the basis for more complex models, including the SVIR, which requires a vaccinated state, which helps us to estimate the probability of herd immunity.

There has been some recent interest in studying the qualitative analysis of difference equations and system of difference equations. Since the beginning of nineties there has be considerable interest in studying systems of difference equations composed by two or three rational difference equations (see, e.g., [4,5,6,2,8,9,11,10,14,15,17,19,20] and the references therein). However, given the multiplicity of factors involved in any epidemic, it will be important to study systems of difference equations composed by many rational difference equations, which is what we will do in this paper.

In [2], Devault et al. studied the boundedness, global stability and periodic character of solutions of the difference equation

where $m\in\{2, 3,\ldots\}$, p is positive and the initial conditions are positive numbers.

In [20], Zhang et al. investigated the behavior of the following symmetrical system of difference equations

where the parameter $A$ is positive, the initial conditions $x_{i}, y_{i}$ are arbitrary positive numbers for $i = -m,- m + 1,\ldots,0$ and $m\in \mathbb{N}$. While this study is good, we note that the authors did not investigate various device properties, such as the stability nature, the rate of convergence and the asymptotic behavior.

Complement of the work above, in [8], Gümüş studied the global asymptotic stability of positive equilibrium, the rate of convergence of positive solutions and he presented some results about the general behavior of solutions of system (2). Our aim in this paper is to generalize the results concerning equation (1) and system (2) to the system of $p$ nonlinear difference equations

where $A$ is a nonnegative constant and $x_{-m}^{(j)}, x_{-m+1}^{(j)}, \ldots, x_{-1}^{(j)}, x_{0}^{(j)}, j = 1,2,\ldots,p$ are positive real numbers.

The remainder of the paper is organized as follows. In Section (2), we introduce some definitions and notations that will be needed in the sequel. Moreover, we present, in Theorem (2.4), a result concerning the linearized stability that will be useful in the main part of the paper. Section (3) discuses the behavior of positive solutions of system (3) via semi-cycle analysis method. Furthermore, Section (4) is devoted to study the local stability of the equilibrium points and the asymptotic behavior of the solutions when $0\leq A<1, A = 1$ and $A>1$. In Section (5), we turn our attention to estimate the rate of convergence of a solution that converges to the equilibrium point of the system (3) in the region of parameters described by $A>1$. Some numerical examples are carried out to support the analysis results in Section (6). Section (7) summarizes the results of this work, draws conclusions and give some interesting open problems for difference equations theory researchers.

2.   Preliminaries

In this section we recall some definitions and results that will be useful in our investigation, for more details see [3,7,14,13].

Definition 2.1. (see, [14]) A 'string' of sequential terms $\{x^{(j)}_{\mu},\ldots,x^{(j)}_{\nu}\}$, $\mu\geq-1$, $\nu\leq+\infty$ is said to be a positive semi-cycle if $x^{(j)}_{i}\geq \overline{x^{(j)}}$, $i\in\{\mu,\ldots,\nu\}$, $x^{(j)}_{\mu-1}<\overline{x^{(j)}}$ and $x^{(j)}_{\nu+1}<\overline{x^{(j)}}$, $j\in\{1,2,\ldots,p\}$.

A 'string' of sequential terms $\{x^{(j)}_{\mu},\ldots,x^{(j)}_{\nu}\}$, $\mu\geq-1$, $\nu\leq+\infty$ is said to be a negative semi-cycle if $x^{(j)}_{i}< \overline{x^{(j)}}$, $i\in\{\mu,\ldots,\nu\}$, $x^{(j)}_{\mu-1}\geq\overline{x^{(j)}}$ and $x^{(j)}_{\nu+1}\geq\overline{x^{(j)}}$, $j\in\{1,2,\ldots,p\}$.

A 'string' of sequential terms $\left\{(x^{(1)}_{\mu},x^{(2)}_{\mu},\ldots,x^{(p)}_{\mu}),\ldots,(x^{(1)}_{\nu},x^{(2)}_{\nu},\ldots,x^{(p)}_{\nu})\right\}$, $\mu\geq-1$, $\nu\leq+\infty$ is said to be a positive semi-cycle (resp. negative semi-cycle) if if $\{x^{(1)}_{\mu},\ldots,x^{(1)}_{\nu}\}, \ldots,$$\{x^{(p)}_{\mu},\ldots,x^{(p)}_{\nu}\}$ are positive semi-cycles (resp. negative semi-cycles).

A 'string' of sequential terms $\left\{(x^{(1)}_{\mu},x^{(2)}_{\mu},\ldots,x^{(p)}_{\mu}),\ldots,(x^{(1)}_{\nu},x^{(2)}_{\nu},\ldots,x^{(p)}_{\nu})\right\}$, $\mu\geq-1$, $\nu\leq+\infty$ is said to be a positive semi-cycle (resp. negative semi-cycle) with respect to $x^{(q)}_{n}$ and negative semi-cycle (resp. positive semi-cycle) with respect to $x^{(s)}_{n}$ if $\{x^{(q)}_{\mu},\ldots,x^{(q)}_{\nu}\}$ is a positive semi-cycle (resp. negative semi-cycle) and $\{x^{(s)}_{\mu},\ldots,x^{(s)}_{\nu}\}$ is a negative semi-cycle (resp. positive semi-cycle).

Definition 2.2. (see, [14]) A function $x^{(i)}_{n}$ oscillates about $\overline{x^{(i)}}$ if for every $\xi\in \mathbb{N}$ there exist $\mu,\nu \in \mathbb{N}$, $\mu\geq\xi$, $\nu\geq\xi$ such that

We say that a solution $\left\{x^{(1)}_{n},x^{(2)}_{n},\ldots,x^{(p)}_{n}\right\}_{n\geq-m}$ of system (3) oscillates about $(\overline{x^{(1)}},\overline{x^{(2)}},\ldots,\overline{x^{(p)}})$ if $x^{(q)}_{n}$ oscillates about $\overline{x^{(q)}}$, $q\in\{1,2,\ldots,p\}$.

Let $f^{(1)},f^{(2)},\ldots,f^{(p)}$ be $p$ continuously differentiable functions:

where $I_{i},\quad i = 1,2,\ldots,p$ are some intervals of real numbers. Consider the system of difference equations

where $n, k \in \mathbb{N}_{0}$, $\left(x^{(i)}_{-k},x^{(i)}_{-k+1},\ldots,x^{(i)}_{0}\right)\in I_{i}^{k+1},\quad i = 1,2,\ldots,p.$

Define the map

by

where

Let

Then, we can easily see that system (4) is equivalent to the following system written in vector form

Definition 2.3. (see, [13]) Let $(\overline{x^{(1)}},\overline{x^{(2)}},\ldots,\overline{x^{(p)}})$ be an equilibrium point of the map $F$ where $f^{(i)}$, $i = 1,2,\ldots,p$ are continuously differentiable functions at $(\overline{x^{(1)}},\overline{x^{(2)}},\ldots,\overline{x^{(p)}})$. The linearized system of (3) about the equilibrium point $(\overline{x^{(1)}},\overline{x^{(2)}},\ldots,\overline{x^{(p)}})$ is

where $X_{n} = \left(x^{(1)}_{n},x^{(1)}_{n-1},\ldots ,x^{(1)}_{n-k}, x^{(2)}_{n},x^{(2)}_{n-1},\ldots ,x^{(2)}_{n-k},\ldots, x^{(p)}_{n},x^{(p)}_{n-1},\ldots ,x^{(p)}_{n-k}\right)^{T}$ and $B$ is a Jacobian matrix of the system (3) about the equilibrium point $(\overline{x^{(1)}},\overline{x^{(2)}}, \ldots,\overline{x^{(p)}})$.

Theorem 2.4. (see, [13])

1. If all the eigenvalues of the Jacobian matrix $B$ lie in the open unit disk $|\lambda|<1$, then the equilibrium point $\overline{X}$ of system (3) is asymptotically stable.

2. If at least one eigenvalue of the Jacobian matrix $B$ has absolute value greater than one, then the equilibrium point $\overline{X}$ of system (3) is unstable.

3.   Semi-cycle analysis

In this section, we discuss the behavior of positive solutions of system (3) via semi-cycle analysis method. It is easy to see that system (3) has a unique positive equilibrium point $\left(\overline{x^{(1)}},\overline{x^{(2)}},\ldots,\overline{x^{(p)}}\right) = (A+1,A+1,\ldots,A+1)$.

Lemma 3.1. Let $\{(x_{n}^{(1)},x_{n}^{(2)},\ldots,x_{n}^{(p)})\}_{n\geq -m}$ be a solution to system (3). Then, either $\{(x_{n}^{(1)},x_{n}^{(2)},\ldots,x_{n}^{(p)})\}_{n\geq -m}$ consists of a single semi-cycle or $\{(x_{n}^{(1)},x_{n}^{(2)},\ldots, x_{n}^{(p)})\}_{n\geq -m}$ oscillates about the equilibrium $(\overline{x^{(1)}},\overline{x^{(2)}},\ldots,\overline{x^{(p)}}) = (A+1,A+1,\ldots, A+1)$ with semi-cycles having at most $m$ terms.

Proof. Suppose that $\{(x_{n}^{(1)},x_{n}^{(2)},\ldots,x_{n}^{(p)})\}_{n\geq -m}$ has at least two semi-cycles. Then, there exists $n_{0}\geq -m$ such that either

We suppose the first case, that is, $x_{n_{0}}^{(j)}<A+1\leq x_{n_{0}+1}^{(j)}$. The other case is similar and will be omitted. Assume that the positive semi-cycle beginning with the term $(x_{n_{0}+1}^{(1)}, x_{n_{0}+1}^{(2)},\ldots,x_{n_{0}+1}^{(p)})$ have $m$ terms. In this case we have

So, we get from system (3)

The Lemma is proved.

Lemma 3.2. Let $\{(x_{n}^{(1)},x_{n}^{(2)},\ldots,x_{n}^{(p)})\}_{n\geq -m}$ be a solution to system (3) which has $m-1$ sequential semi-cycles of length one. Then, every semi-cycle after this point is of length one.

Proof. Assume that there exists $n_{0}\geq -m$ such that either

or

We will prove the case (6). The case (7) Is identical and will not be included. According to system (3) we obtain

and

The result proceeds by induction. Thus, the proof is completed.

Lemma 3.3. System (3) has no nontrivial periodic solutions of (not necessarily prime) period $m$.

Proof. Suppose that

is a $m$-periodic solution of system (3). It is obvious then that for this solution,

So, the equilibrium solution $\left(\overline{x^{(1)}},\overline{x^{(2)}},\ldots,\overline{x^{(p)}}\right) = (A+1,A+1,\ldots,A+1)$ must be this solution. Thus, the proof is completed.

Lemma 3.4. All non-oscillatory solutions of system (3) converge to the equilibrium $\left(\overline{x^{(1)}},\overline{x^{(2)}},\ldots,\overline{x^{(p)}}\right) = (A+1,A+1,\ldots,A+1)$.

Proof. We assume there exists non-oscillatory solutions of system (3). We will prove this lemma for the case of a single positive semi-cycle, the situation is identical for a single negative semi-cycle, so it will be omitted. Assume that $(x_{n}^{(1)},x_{n}^{(2)},\ldots,x_{n}^{(p)})\geq(\overline{x^{(1)}},\overline{x^{(2)}},\ldots,\overline{x^{(p)}})$ for all $n\geq-m$. From system (3) we have

So, we get

From (8), there exists $\delta_{i}^{(j)}$ for$i = 0, 1,\ldots ,m-1$ such that

Hence,

is a periodic solution of (not necessarily prime period) period $m$. But, from Lemma (3.3), we saw system (3) has no nontrivial periodic solutions of (not necessarily prime period) period $m$. Thus, the solution must be the equilibrium solution. So, the proof is over.

4.   The asymptotic behavior

4.1.   The Case $0<A <1$

Theorem 4.1. Suppose $0<A <1$ and $\{(x_{n}^{(1)},x_{n}^{(2)},\ldots,x_{n}^{(p)})\}_{n\geq -m}$ be a positive solution to system (3). Then the following statements hold.

ⅰ): If $m$ is odd, and $0<x^{(j)}_{2k-1}<1$, $x_{2k}^{(j)}>\frac{1}{1-A}$ for $k = \frac{1-m}{2},\frac{3-m}{2},\ldots,0$, then

ⅱ): If $m$ is odd, and $0<x^{(j)}_{2k}<1$, $x_{2k-1}^{(j)}>\frac{1}{1-A}$ for $k = \frac{1-m}{2},\frac{3-m}{2},\ldots,0$, then

Proof. (ⅰ): From (3), for $i = 1,2,\ldots,p$, we get

By induction, for n $= 0,1,2,\ldots$ and $i = 1,2,\ldots,p$, we obtain

So, from (3) and (9), we have

So

By limiting the inequality (10), we get

On the other hand, from(3), (9) and (11), we get

(ⅱ): The proof is similar to the proof of (ⅰ).

Open Problem. Investigate the asymptotic behavior of the system (3) when $m$ is even.

4.2.   The Case $A=1$

Lemma 4.2. Suppose $A = 1$. Then every positive solution of the system (3) is bounded and persists.

Proof. Let $\{(x_{n}^{(1)},x_{n}^{(2)},\ldots,x_{n}^{(p)})\}_{n\geq -m}$ be a positive solution to system (3). Then, it is clear that for $n\geq1$, $x_{n}^{(j)}>A = 1,\quad j = 1,2,\ldots,p.$ So, we get

where

So, we get

thus, the following is obtained

By induction, we get

Theorem 4.3. Suppose $A = 1$ and $\{(x_{n}^{(1)},x_{n}^{(2)},\ldots,x_{n}^{(p)})\}_{n\geq -m}$ be a positive solution to system (3). Then

Proof. From (12), we can set

We first prove the theorem for $p = 2$. From system (3), we have

which implies

thus, the following equalities are obtained

So, we get that $m_{1} = m_{2}$ and $L_{1} = L_{2}$. Now we suppose that

From system (3), we have

hence, we get

consequently, the following equalities are obtained

So, we get that $m_{p} = m_{p-1}$ and $L_{p} = L_{p-1}$. Thus, the proof completes.

4.3.   The Case $A > 1$

Theorem 4.4. Assume that $A>1$. Then, the unique positive equilibrium $\left(\overline{x^{(1)}},\overline{x^{(2)}},\ldots,\overline{x^{(p)}}\right) = (A+1,A+1,\ldots,A+1)$ of system (3) is locally asymptotically stable.

Proof. The linearized equation of system (3) about the equilibrium point $(\overline{x^{(1)}},\overline{x^{(2)}}, \ldots,\overline{x^{(p)}})$ is

where $X_{n} = (x_{n}^{(1)},x_{n-1}^{(1)},\ldots,x_{n-m}^{(1)}, x_{n}^{(2)},x_{n-1}^{(2)},\ldots,x_{n-m}^{(2)},\ldots,x_{n}^{(p)},x_{n-1}^{(p)},,\ldots,x_{n-m}^{(p)})^{t},$ and $B = (b_{ij})$, $1\leq i,j\leq pm+p$ is an $(pm+p)\times(pm+p)$ matrix such that

where $\mathcal{A}, \mathcal{J }$ and $\mathcal{O}$ are $(m+1)\times(m+1)$ matrix defined as follows

Let $\lambda_{1},\lambda_{2},\ldots,\lambda_{pm+p}$ denote the eigenvalues of matrix $B$ and let

be a diagonal matrix where $d_{1} = d_{m+2} = d_{2m+3} = \cdots = d_{(p-1)m+p} = 1$, $d_{k} = d_{m+1+k} = 1-k\varepsilon$ for $k\in\{1,2,\ldots, \frac{p}{2}(m+1)\}$. Since $A>1$, we can take a positive number $\varepsilon$ such that

It is obvious that $D$ is an invertible matrix. Computing matrix $DBD^{-1}$, we get

where

and

From $d_{1}>d_{2}>\ldots> d_{\frac{p}{2}(m+1)}$ and $d_{\frac{p}{2}(m+1)}+1>d_{\frac{p}{2}(m+1)}+2>\ldots>d_{pm+p}$ we can get that

Moreover, from $A >1$ and (16) we have

It is common knowledge that $B$ has the same eigenvalues as $DBD^{^{-1}}$, we have that

We have that all eigenvalues of $B$ lie inside the unit disk. According to Theorem (2.4) we obtain that the unique positive equilibrium $\left(\overline{x^{(1)}},\overline{x^{(2)}},\ldots,\overline{x^{(p)}}\right) = (A+1,A+1,\ldots,A+1)$ is locally asymptotically stable. Thus, the proof is completed.

To prove the global stability of the positive equilibrium, we need the following lemma.

Lemma 4.5. Suppose $A>1$. Then every positive solution of the system (3) is bounded and persists.

Proof. Let $\{(x_{n}^{(1)},x_{n}^{(2)},\ldots,x_{n}^{(p)})\}_{n\geq -m}$ be a positive solution to system (3). Then, it is clear that for $n\geq1$, $x_{n}^{(j)}>A>1,\quad j = 1,2,\ldots,p.$ So, we get

where

So, we get

thus, the following is obtained

By induction, we get

Theorem 4.6. Assume that $A>1$. Then the positive equilibrium of system (3) is globally asymptotically stable.

Proof. Let $\left\{\left(x_{n}^{(1)},x_{n}^{(2)},\ldots,x_{n}^{(p)}\right)\right\}_{n\geq-m}$ be a solution of system (3). By Theorem (4.4) we need only to prove that the equilibrium point $(A+1,A+1,\ldots,A+1)$ is global attractor, that is

To do this, we prove that for $i = 1,2,\ldots,p$, we have

From Lemma (4.5), we can set

So, from (3) and (13), we have

We first prove the theorem for $p = 2$. From (19), we get

So,

hence

since $A>1$, It follows that

we know that $L_{1}-m_{1}\geq0$ and $L_{2}-m_{2}\geq0$, so we obtain $L_{1} = m_{1}$ and $L_{2} = m_{2}$. Now we assume that the theorem holds for $p-1$, that is $L_{i} = m_{i},\quad i = 1,2,\ldots,p-1$ and prove the theorem for $p$. From (19), we have

So,

Thus, the following inequality is obtained

since $A>1$, $L_{1}-m_{1}\geq0$ and $L_{p}-m_{p}\geq0$, we obtain $L_{p} = m_{p}$, it signify that

Therefore every positive solution $\left\{\left(x_{n}^{(1)},x_{n}^{(2)},\ldots,x_{n}^{(p)}\right)\right\}_{n\geq-1}$ of system (3) tends to $(A+1,A+1,\ldots,A+1)$ as $n\rightarrow +\infty$.

5.   Rate of convergence

In this section, we estimate the rate of convergence of a solution that converges to the equilibrium point $\left(\overline{x^{(1)}},\overline{x^{(2)}},\ldots,\overline{x^{(p)}}\right) = (A+1,A+1,\ldots,A+1)$ of the system (3) in the region of parameters described by $A>1$. We give precise results about the rate of convergence of the solutions that converge to the equilibrium point by using Perron's theorems. The following result gives the rate of convergence of solutions of a system of difference equations

where $X_{n}$ is a $(pm+p)$-dimensional vector, $A\in C^{(pm+p)\times(pm+p)}$ is a constant matrix and $B:\mathbb{Z}^{+}\rightarrow C^{(pm+p)\times(pm+p)}$ is a matrix function satisfying

where $\|.\|$ indicates any matrix norm which is associated with the vector norm $\|.\|$.

Theorem 5.1. (Perron's first Theorem, see [16]) Suppose that condition (21) holds. If $X_{}n$ is a solution of (20), then either $X_{n} = 0$ for all large$n$ or

exists and is equal to the modulus of one of the eigenvalues of matrix $A$.

Theorem 5.2. (Perron's second Theorem, see [16]) Suppose that condition (21) holds. If $X_{}n$ is a solution of (20), then either $X_{n} = 0$ for all large$n$ or

exists and is equal to the modulus of one of the eigenvalues of matrix $A$.

Theorem 5.3. Assume that a solution $\{(x_{n}^{(1)},x_{n}^{(2)},\ldots,x_{n}^{(p)})\}_{n\geq -m}$ of system (3) converges to the equilibrium $(\overline{x^{(1)}},\overline{x^{(2)}},\ldots,\overline{x^{(p)}})$ which is globally asymptotically stable. Then, the error vector

of every solution of system (3) satisfies both of the following asymptotic relations:

where $|\lambda_{i}J_{F}((\overline{x^{(1)}},\overline{x^{(2)}},\ldots,\overline{x^{(p)}}))|$ is equal to the modulus of one the eigenvalues of the Jacobian matrix evaluated at the equilibrium point $(\overline{x^{(1)}},\overline{x^{(2)}},\ldots,\overline{x^{(p)}})$.

Proof. First, we will find a system that satisfies the error terms. The error terms are given as

for $i = 1,2,\ldots,m, j = 1,2,\ldots,p$. Set

Then, system (22) can be written as

where

and the others parameters ${}^{(k)}A_{i}^{(j)}$ are equal zero.

If we consider the limiting case, It is obvious then that

That is

where $\alpha_{n}^{(i)}, \beta_{n}^{(i)}\rightarrow0$ when $n\rightarrow \infty$. Now we have the following system of the form (20)

where $e_{n} = \left(e^{(1)} _{n}, e^{(1)} _{n-1},\ldots,e^{(1)} _{n-m},e^{(2)} _{n}, e^{(2)} _{n-1},\ldots,e^{(2)} _{n-m},\ldots,e^{(p)} _{n}, e^{(p)} _{n-1},\ldots,e^{(p)} _{n-m}\right)^{t}$ and

where

and $\mathcal{A}, \mathcal{J }$ and $\mathcal{O}$ are the $(m+1)\times(m+1)$ matrix defined in (14) and (15).

$\|B_{n}\|\rightarrow 0$ when $n\rightarrow \infty$. Therefore, the limiting system of error terms can be written as

and $\|B_{n}\|\rightarrow 0$ when $n\rightarrow \infty$. This system is exactly the linearized system of (3) evaluated at the equilibrium point $\left(\overline{x^{(1)}},\overline{x^{(2)}},\ldots,\overline{x^{(p)}}\right)$. From Theorems (5.1) and (5.2), the result follows.

6.   Numerical examples

In this section we will consider several interesting numerical examples to verify our theoretical results. These examples shows different types of qualitative behavior of solutions of the system (3). All plots in this section are drawn with Matlab.

Exemple 6.1. Let $m = 1$ and $p = 10$ in system (3), then we obtain the system

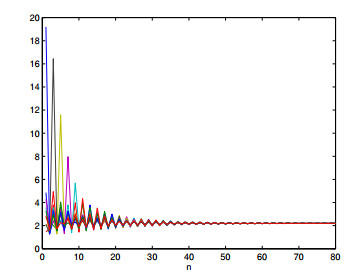
with $A = 1.2>1$ and the initial values $x^{(1)}_{-1} = 3.3, x^{(1)}_{0} = 2, x^{(2)}_{-1} = 1.1, x^{(2)}_{0} = 0.3, x^{(3)}_{-1} = 2.3, x^{(3)}_{0} = 1.5, x^{(4)}_{-1} = 0.5, x^{(4)}_{0} = 2, x^{(5)}_{-1} = 1.9, x^{(5)}_{0} = 0.8, x^{(6)}_{-1} = 4, x^{(6)}_{0} = 1.3, x^{(7)}_{-1} = 1.2, x^{(7)}_{0} = 1.3, x^{(8)}_{-1} = 2.1, x^{(8)}_{0} = 2.3, x^{(9)}_{-1} = 3.6, x^{(9)}_{0} = 0.2, x^{(10)}_{-1} = 2.3, x^{(10)}_{0} = 1.1$. Then the positive equilibrium point $(\overline{x^{(1)}}, \overline{x^{(2)}},\ldots,\overline{x^{(10)}}) =$ $(2.2, 2.2, \ldots, 2.2)$ of system (23)) is globally asymptotically stable (see Figure (1), Theorem (4.4)).

Exemple 6.2. Consider the system (23) with $A = 1$ and the initial values $x^{(1)}_{-1} = 0.3, x^{(1)}_{0} = 1.1, x^{(2)}_{-1} = 1.3, x^{(2)}_{0} = 0.3, x^{(3)}_{-1} = 1.4, x^{(3)}_{0} = 1.5, x^{(4)}_{-1} = 0.5, x^{(4)}_{0} = 2, x^{(5)}_{-1} = 1.9, x^{(5)}_{0} = 0.8, x^{(6)}_{-1} = 4, x^{(6)}_{0} = 1.3, x^{(7)}_{-1} = 1.4, x^{(7)}_{0} = 1.3, x^{(8)}_{-1} = 0.1, x^{(8)}_{0} = 1.1, x^{(9)}_{-1} = 1.6, x^{(9)}_{0} = 1.7, x^{(10)}_{-1} = 1.9, x^{(10)}_{0} = 1.1$. Then the solution oscillates about the positive equilibrium point $(\overline{x^{(1)}}, \overline{x^{(2)}},\ldots,\overline{x^{(10)}}) = (2, 2,\ldots, 2)$ of system (23) with semi-cycles having at most five terms. Also, the equilibrium is not globally asymptotically stable (see Figure (2), Theorem 4.2).

Exemple 6.3. Consider the system (23) with $A = 0.9$ and the initial values $x^{(1)}_{-1} = 1.2, x^{(1)}_{0} = 0.7, x^{(2)}_{-1} = 1.2, x^{(2)}_{0} = 2.3, x^{(3)}_{-1} = 0.4, x^{(3)}_{0} = 1.1, x^{(4)}_{-1} = 0.8, x^{(4)}_{0} = 8, x^{(5)}_{-1} = 1.3, x^{(5)}_{0} = 1.8, x^{(6)}_{-1} = 2.6, x^{(6)}_{0} = 0.9, x^{(7)}_{-1} = 1.4, x^{(7)}_{0} = 1.1, x^{(8)}_{-1} = 0.1, x^{(8)}_{0} = 1.4, x^{(9)}_{-1} = 0.9, x^{(9)}_{0} = 1.3, x^{(10)}_{-1} = 1.2, x^{(10)}_{0} = 2.1$. Then the positive equilibrium point $(\overline{x^{(1)}}, \overline{x^{(2)}},\overline{x^{(3)}},\overline{x^{(4)}}) = (1.9, 1.9,\ldots, 1.9)$ of system (23) is not globally asymptotically stable. Also, this solution is unbounded solution see Figure (3), Theorem 4.2).

Exemple 6.4. Let $m = 5$ and $p = 4$ in system (3), then we obtain the system

with $A = 1.4>1$ and the initial values $x^{(1)}_{-5} = 1.2,x^{(1)}_{-4} = 0.8,x^{(1)}_{-3} = 1.9,x^{(1)}_{-2} = 2.2,x^{(1)}_{-1} = 0.3, x^{(1)}_{0} = 1.7, x^{(2)}_{-5} = 1.3, x^{(2)}_{-4} = 2.4, x^{(2)}_{-3} = 1.2, x^{(2)}_{-2} = 0.5, x^{(2)}_{-1} = 1.6, x^{(2)}_{0} = 2.3, x^{(3)}_{-5} = 0.4,x^{(3)}_{-4} = 1.1,x^{(3)}_{-3} = 1.4,x^{(3)}_{-2} = 2.1, x^{(3)}_{-1} = 0.3, x^{(3)}_{0} = 1.1, x^{(4)}_{-5} = 0.8,x^{(4)}_{-4} = 1.2,x^{(4)}_{-3} = 1.8,x^{(4)}_{-2} = 3.1,x^{(4)}_{-1} = 0.7, x^{(4)}_{0} = 1.8,$. Then the positive equilibrium point $(\overline{x^{(1)}}, \overline{x^{(2)}},\overline{x^{(3)}},\overline{x^{(4)}}) = (2.4, 2.4,2.4, 2.4)$ of system (24)) is globally asymptotically stable (see Figure (4), Theorem (4.4)).

Exemple 6.5. Consider the system (24) with $A = 1$ and the initial values $x^{(1)}_{-5} = 0.4,x^{(1)}_{-4} = 1.3,x^{(1)}_{-3} = 2.9,x^{(1)}_{-2} = 1.2,x^{(1)}_{-1} = 0.8, x^{(1)}_{0} = 1.2,x^{(2)}_{-5} = 0.3, x^{(2)}_{-4} = 1.4, x^{(2)}_{-3} = 1.3 x^{(2)}_{-2} = 0.5, x^{(2)}_{-1} = 1.6, x^{(2)}_{0} = 2.1,x^{(3)}_{-5} = 1.3,x^{(3)}_{-4} = 2.1,x^{(3)}_{-3} = 1.4,x^{(3)}_{-2} = 2.1, x^{(3)}_{-1} = 0.3, x^{(3)}_{0} = 1.5, x^{(4)}_{-5} = 0.6,x^{(4)}_{-4} = 1.2,x^{(4)}_{-3} = 1.3,x^{(4)}_{-2} = 0.8,x^{(4)}_{-1} = 1.7, x^{(4)}_{0} = 0.1,$. Then the solution oscillates about the positive equilibrium point $(\overline{x^{(1)}}, \overline{x^{(2)}},\overline{x^{(3)}},\overline{x^{(4)}}) = (2.4, 2.4, 2.4, 2.4)$ of system (24) with semi-cycles having at most five terms. Also, the equilibrium is not globally asymptotically stable (see Figure (5), Theorem 4.2).

Exemple 6.6. Consider the system (24) with $A = 0.7$ and the initial values $x^{(1)}_{-5} = 1.3,x^{(1)}_{-4} = 0.9,x^{(1)}_{-3} = 2.1,x^{(1)}_{-2} = 0.9,x^{(1)}_{-1} = 0.7, x^{(1)}_{0} = 2.2, x^{(2)}_{-5} = 1.3, x^{(2)}_{-4} = 0.4, x^{(2)}_{-3} = 1.3 x^{(2)}_{-2} = 1.5, x^{(2)}_{-1} = 1.2, x^{(2)}_{0} = 1.1, x^{(3)}_{-5} = 1.7,x^{(3)}_{-4} = 1.6,x^{(3)}_{-3} = 1.5,x^{(3)}_{-2} = 2.3, x^{(3)}_{-1} = 0.9, x^{(3)}_{0} = 1.5, x^{(4)}_{-5} = 0.6,x^{(4)}_{-4} = 1.4,x^{(4)}_{-3} = 2.3,x^{(4)}_{-2} = 3.1,x^{(4)}_{-1} = 2.7, x^{(4)}_{0} = 1.9.$ Then the positive equilibrium point $(\overline{x^{(1)}}, \overline{x^{(2)}},\overline{x^{(3)}},\overline{x^{(4)}}) = (1.7, 1.7, 1.7, 1.7)$ of system (23) is not globally asymptotically stable. Also, this solution is unbounded solution see Figure (6), Theorem 4.2).

7.   Conclusions and some open problems

In the paper, we studied the global behavior of solutions of system (3) composed by $p$ rational difference equations. More exactly, we here study the global asymptotic stability of equilibrium, the rate of convergence of positive solutions. Also, we present some results about the general behavior of solutions of system (3) and some numerical examples are carried out to support the analysis results. Our system generalized the equations and systems studied in [2,8] and [20].

The findings suggest that this approach could also be useful for extended to a system with arbitrary constant different parameters, or to a system with a nonautonomous parameter, or to a system with different parameters and arbitrary powers. So, we will give the following some important open problems for difference equations theory researchers.

Open Problem 1. study the dynamical behaviors of the system of difference equations

where $A_{i}$, $i = 1,2,\ldots,p$ are nonnegative constants and $x_{-m}^{(j)}, x_{-m+1}^{(j)}, \ldots, x_{-1}^{(j)}, x_{0}^{(j)}, j = 1,2,\ldots,p$ are positive real numbers.

Open Problem 2. study the dynamical behaviors of the system of difference equations

where $\alpha_{n}$ is a sequence (this sequence can be chosen as convergent, periodic or bounded), and $x_{-m}^{(j)}, x_{-m+1}^{(j)}, \ldots, x_{-1}^{(j)}, x_{0}^{(j)}, j = 1,2,\ldots,p$ are positive real numbers.

Open Problem 3. study the dynamical behaviors of the system of difference equations

where$n, m, p\in \mathbb{N}_{0}$, $A_{i}$, $i = 1,2,\ldots,p$ are nonnegative constants, the parameters $p_{i}, q_{i}$, $i = 1,2,\ldots,p$ are non-negative and $x_{-m}^{(j)}, x_{-m+1}^{(j)}, \ldots, x_{-1}^{(j)}, x_{0}^{(j)}, j = 1,2,\ldots,p$ are positive real numbers.

Acknowledgment(s)

This work was supported by Directorate General for Scientific Research and Technological Development (DGRSDT), Algeria.