1.
Introduction
The information obtained from various sources is commonly referred to as multi-modal information. At present, research in this field often begins with the aim of combining multi-modal information and maximizing the potential of different modal information in real life to create new cross-modal research areas [1,2,3,4]. The demand for content-based video retrieval has increased with the widespread use of video platforms such as TikTok and YouTube. Cross-modal retrieval [5,6,7] has gained significant attention from scholars in recent years.
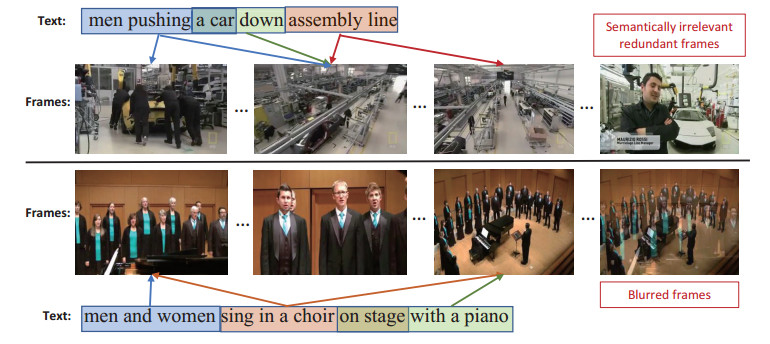
However, text and video modes of conveying information differ significantly. The text conveys information through words or phrases, while video encompasses a broader range of information. The text only partially represents some of the content in a video [8]. When performing sentence and video matching, adopting a more precise approach may be necessary due to redundant frames in videos. For instance, Figure 1 shows two sample videos and their matching text from the MSR-VTT dataset [9]. Observations have shown that some video frames do not match the semantic meaning of the sentences and are deemed redundant components in the text-video matching procedure [10]. This highlights the presence of some bias in the results when matching videos with sentences.
To enhance the precision of text-video retrieval, a proven practical approach involves the elimination of redundant frames and a focused analysis of video subintervals that are semantically linked to the text, as demonstrated by Dong et al. [11]. Consequently, the matching model must possess the capability to extract critical textual content and correctly identify corresponding video segments.However, prevalent methods commonly resort to mean pooling or employ self-attention mechanisms [6,12,13] to derive global feature embeddings for a given sentence and video. These methods exhibit limitations regarding the definition and precise localization of keyframes. This limitation is significant, as it can negatively impact the performance of retrieval tasks, particularly when videos contain content that is not explicitly described in the accompanying text.
This paper presents a novel cross-modal conditional mechanism designed to address two critical issues: feature redundancy within videos and the imbalanced semantic alignment between the two modalities. To tackle these challenges, we propose two key components:
Firstly, we introduce a video feature aggregation module that leverages a text-conditioned attention mechanism. Here, the text features serve as a guiding condition, enhancing the emphasis on keyframes while diminishing the influence of redundant frames. The aggregation process combines numerical values by multiplying attention weights with frame features, resulting in refined video features.
Secondly, we introduce a global-local cross-modal conditional similarity calculation module. This module considers video-sentence features as the global data and frame-word features as the local data. These features are input into the model for similarity calculation, a critical step for text-video matching. This approach enables us to effectively address the overarching topic and the finer details in the matching process.
2.
Related work
2.1. Feature extraction
Text Feature Encoding Previous studies [14,15,16,17] examined the extraction of text features and have achieved exceptional outcomes. The Skip-Gram model [18] begins by considering the central word and predicts its surrounding words, producing text features. This approach not only cuts down the computational effort during the training phase but also elevates the quality of the word-to-vector representation. To enhance the matching between text and images, the Fisher Vector model [19] examines text representation and quantifies it using high-level statistical features for text feature extraction [20]. Furthermore, the GRU model [21] was introduced to address the issue of gradient disappearance in standard RNNs during text encoding. As a result, the GRU model has become a widely utilized text encoder. OpenAI has also made available a graphical pre-training model for CLIP based on contrast learning and has a transformer structure [22]. CLIP model has delivered similarly remarkable results in the coding of text.
Visual Feature Encoding Visual feature extraction is typically carried out using supervised or self-supervised research methods. Recently, there has been growing interest in using a transformer-based image encoder known as the ViT model [23]. While the application of transformers to feature extraction of video content [24,25] is still in its early stages, it has shown potential for enhancing action classification in video text retrieval. Researchers have been exploring new and innovative approaches to enable models with better generalization capabilities [22,49]. Text and video pairs obtained from the internet are collected and formed into large-scale datasets for training. One of the most successful methods is the CLIP model [22], which has achieved state-of-the-art performance in image feature extraction. The pre-trained CLIP model can learn more sophisticated visual concepts and use these features in retrieval tasks. To mitigate the impact of diverse topics in the dataset, a MIL-NCE model [26] based on the CLIP video encoder has been proposed and tested with positive results on the Howto100M [13] dataset. Furthermore, the ClipBERT [49] model, which is based on the MIL-NCE model, employs an end-to-end approach to streamline the pre-processing stage of video-text retrieval. This paper uses a pre-trained CLIP-based ViT model as our video encoder to extract visual features from the video frames. The effectiveness of the feature extraction has been verified through experimental evaluation.
2.2. Text-video retrieval
In cross-modal retrieval, text-video matching plays a key role in bridging vision and language. Text-video matching aims to learn the cross-modal similarity function [27] between text and video, so that related text-video pairs receive higher scores than unrelated ones. Establishing a semantic similarity model that effectively reduces the semantic gap between visual and textual information is crucial for the accuracy of this study [28]. Despite the complex matching patterns and vast semantic differences between images and texts, this remains a challenging research topic. A common approach to overcome this challenge is mapping images and texts into a shared semantic space through a suitable embedding model, i.e., a joint latent space, and then computing cross-modal similarity in this shared space.
Text-video retrieval is typically achieved by integrating a pre-trained language model with a visual model to associate text features with visual features. When dealing with small datasets, incorporating a pre-trained model can improve performance. For instance, the Teachtext model [23] uses multiple text encoders to provide a complementary supervised signal for the retrieval model. MMT [29] and MDMMT [30] were early examples of using transformers for multi-modal video processing, integrating three modal features to accomplish the video retrieval task.
Additionally, some scholars have applied concepts from the data hashing field to tasks involving cross-modal data processing and information retrieval. The ROHLSE model [31] focuses on addressing label noise and exploiting semantic correlations in processing large-scale streaming data. This work presents an innovative approach for hashing streaming data. The DAZSH model [32] introduces a hashing method tailored to the zero-shot problem in cross-modal retrieval. Integrating data features with class attributes effectively captures relationships between known and unknown categories, facilitating the transfer of supervised knowledge. Moreover, a neural network-based approach [33] is designed to learn specific category centers and guide the hashing of multimedia data. Finally, the SKDCH model [34] proposes a semi-supervised knowledge distillation method for cross-modal hashing. It mitigates heterogeneity gaps and enhances discriminability by improving the triplet ranking loss. These studies collectively demonstrate the application of data hashing principles to tackle complex challenges in cross-modal data processing and information retrieval.
Recently, the CLIP model [22] utilized a rich text-image dataset to create a joint text-visual model, which the authors of the CLIP4CLIP model [6] leveraged through transfer learning to achieve state-of-the-art results in video retrieval tasks. In several studies based on the CLIP model [35], the model outperformed most other works [2,12,36], even in a zero-shot manner, showcasing its excellent generalization capabilities in text-video understanding.
Several video feature aggregation methods, including average pooling, self-attention, and multi-modal transformers [4,6], are commonly used in CLIP-based studies and have been shown to match text and images effectively. However, there needs to be more research specifically focused on matching video sub-regions with words [49]. As noted in the previous section, many video frames are semantically irrelevant to the text in matching processes. Thus, using a cross-modal conditional attention mechanism to reduce the impact of redundant frames on retrieval results is the motivation behind this paper's research.
2.3. Cross-modal attention mechanism
In natural language processing, attention mechanisms are widely used to filter redundant information [37]. Similarly, attention mechanisms have been used to enhance the focus on visual and textual local features in cross-modal information-matching tasks. Some researchers have proposed a similarity attention filtration (SAF) module [38] based on attention mechanisms to match images with text. This module applies attention mechanisms to cross-modal feature alignment, aiming to eliminate the interference caused by redundant text-image pairs and enhance image retrieval accuracy. Owing to the remarkable performance of attention mechanisms in the cross-modal domain, certain researchers [39] have developed more intricate bidirectional focused attention networks, building upon this foundation to enhance matching accuracy further. Concurrently, other scholars [40,41] have introduced a recurrent attention mechanism to investigate the correspondence between fine-grained text regions and individual words.
The crucial aspect of implementing the attention model in text-video cross-modal inference lies in embedding the features of both text and video and subsequently identifying frames that align more effectively with text semantics, as demonstrated by Tan et al. [28]. We have incorporated a textual conditional attention module into our cross-modal matching model to achieve this. This module filters out extraneous semantic information within the frames by computing attention weights for each frame, using text semantics as a conditional projection.
3.
Framework
Text-video retrieval can be defined as two tasks: one is retrieving semantically close text by the given video information as the input, named t2v. The other is retrieving semantically similar videos by the sentence given as the input, named v2t. Taking the t2v task as an example, a query text and a set of video sets to be queried are the input data. The model calculates the similarity score between the query text and each video in the video set and finds the video with the best semantic match to return. Similarly, v2t has a similar task. This paper mainly focuses on the t2v task as the leading study. We are dedicated to enhancing the accuracy of text-video retrieval tasks by implementing two pivotal strategies: filtering out irrelevant frames and aggregating key-frames to construct video features, followed by performing a global-local multi-modal feature matching approach.
Figure 2 illustrates the framework of our model for the text-video retrieval task. The text-video retrieval task is quantified into three main components: Data Embedding, Cross-modal Feature Extraction, and Similarity Calculation. In the Data Embedding phase, we feed the input data (including words and frames) into the text encoder ψ and the image encoder ϕ of the CLIP model, obtaining embedded data representations. The Cross-modal Feature Extraction section encompasses two critical steps. Firstly, we employ a self-attention mechanism to extract sentence features from the text. Secondly, we utilize a conditional attention mechanism to filter out redundant and aggregate frames semantically relevant to the text, thereby obtaining more precise video features. In the Similarity Calculation phase, we compute similarity at global and local granularities (i.e., video-sentence and frame-word features) to consider thematic and detail features during the text-video matching process. It is worth noting that the Cross-modal Feature Extraction and Similarity Calculation sections contain two innovative modules introduced in this paper, which are detailed as follows:
Cross-modal Conditional Attention Aggregation Module To process text input t, we pass it through a text encoder ψ to obtain its word embedding Ew. This embedding is then multiplied with the weight matrix query projection WQ, to produce the text query vector Qt. For video input v, it is passed through a video encoder to produce frame embedding Ef. This embedding is then multiplied with the key projection matrix WK and the value projection matrix WV, respectively, to obtain the key embedding of the frames Kv, and the value embedding of the frames Vv. Then we calculate the attention score of the video frames watt, by taking the dot product of Qt and Kv. The attention scores are used to weight the value vectors of the video frames Vv, to produce the self-attention frame feature embedding.
Global-Local Similarity Matching Module proposes a cross-similarity calculation module to perform the text-video matching task. The module integrates cosine similarity and conditional probability models to compute the similarity scores between the different modal data feature embeddings, considering their mutual dependence. The global feature data (text-video) and local feature data (word-frame) are fed into the model separately, producing their similarity scores. The model then aggregates the global and local similarity scores through self-attention to obtain the final matching scores.
4.
Methodology
In this section, we concentrate on the methods for implementing the model presented in the paper. To facilitate a comprehensive understanding of our model, we commence by elucidating the procedure for utilizing the pre-trained CLIP model to encode text and video in Section 4.1. Subsequently, the following two sections introduce pivotal functional components of our model: the Cross-modal Conditional Attention Aggregation Module (Section 4.2) and the Global-Local Similarity Matching Module (Section 4.3). Section 4.2 describes the method for incorporating attention mechanisms into cross-modal feature aggregation to enhance the relevance of video features to text semantics. In Section 4.3, we highlight the limitations of traditional similarity computation method for cross-modal feature matching and propose a novel method for computing the global-local similarity of correlated cross-modal features. Finally, we present the implementations of training objectives with both the two modules in Section 4.4.
4.1. Data embedding
The video can be considered a sequence of images, with each video frame being an individual image. In this study, many pre-trained models have been found to extract features from text and images effectively, enabling cross-modal semantic understanding [6,22]. These models have been pre-trained on large and diverse datasets, allowing us to leverage their excellent performance in feature extraction to simplify the training process of our work.
CLIP models trained on large, richly typed datasets have demonstrated exceptional feature extraction abilities and robust performance in downstream tasks. Numerous studies have shown that CLIP performs well in extracting the rich semantic features of input information [22]. In the task of video feature extraction, individual video frames are embedded in CLIP's joint latent space as images. The video features are obtained by aggregating the embedded features of the individual frames. In this paper, we learn a new joint latent space based on the CLIP model to serve as an encoder for our standard video-text feature extraction.
Given text t and video v as inputs, we first preprocess the video into quantifiable frames vfn and input these frames into the CLIP model as images. CLIP then outputs a text embedding Et and a frame embedding Efnv as encodings. By aggregating the sequence of frame embeddings SF, we can obtain the video embedding EV:
where ψ is CLIP's text encoder, and ϕ is CLIP's image encoder. SetF is the set of frames feature embedding.
Then we can obtain the video's feature embedding by a temporal aggregation function ρ:
Obviously, Et and Efnv are the two outputs of CLIP.
4.2. Cross-modal conditional attention aggregation
Previous research has typically used average pooling or self-attention mechanism when calculating the video embedding by aggregating the frame embeddings [12,29]. However, this approach results in a video embedding that contains many redundant visual features that need to be more relevant to the semantic features of the text. This is because the text has much less semantic information than the video. As a result, these aggregate methods can negatively impact the accuracy of the final similarity computation results.
The aggregation of frame features to obtain the video embedding for use in the similarity calculation model often results in the inclusion of redundant visual features that need to be more relevant to the semantic features of the text. This can negatively impact the accuracy of the final similarity computation results.
This module uses the attention mechanism to extract the video features. We combine the semantic text features to compute the attention weights for the keyframes. This enhances the crucial information in the frames and filters out redundant information, resulting in video features. Firstly, we project the text embedding Et as a query vector Qt∈R1×da. The video embedding obtained from Section 4.1 is then projected as a key vector KF∈R1×da and a value vector VF∈R1×da through dot product operations with matrices WK∈Rd×da and WV∈Rd×da, respectively. The calculations are defined as follows:
where WQ, WK and WV are the parameter matrices obtained from the neural network training.
Finally, by utilizing the cross-modal attention feature aggregation module, we obtain the joint text-video semantic attention scores for each frame, represented as Sfn.
The above equation is the main idea of the aggregation function ρ, and the input video features embedding EV can finally be calculated as follows:
4.3. Global-local similarity matching
In Section 4.1, the CLIP encoder obtains the text feature embedding Et and the set of frame feature embeddings SetF. Section 4.2 then leverages the attention mechanism to aggregate the frame embeddings and get the text-conditional video embedding Ev. Although this approach incorporates semantic text features into the video feature embedding, conventional similarity computation models, such as cosine similarity, can only improve the matching accuracy to a certain extent. It may still need to look at the local semantics expressed in specific keyframes. This section considers the consistency of structure and text word features in semantic expression to address this issue. It combines the similarity computation of both video and sentences to perform text-video matching.
Vector Similarity Function The previous methods of calculating the similarity between features of two different modal data often relied on cosine or Euclidean distance [40]. While these methods can capture relevance to a degree, they cannot detect finer local correspondences between the vectors. Our proposed similarity representation function aims to address this issue by leveraging the local features of the vectors and using cosine similarity calculation as the core component. This enables a more in-depth analysis of the correlation information between the feature representations from different modalities. The similarity function is formulated as follows:
where ‖α1−α2‖2 is the square operation of each element in the result α1−α2, and ‖Wsim|α1−α2|2‖2 is the l2− operation of Wsim|α1−α2|2. The Wsim in the equation is a learnable parameter matrix to obtain the similarity vector.
Text-Video Global Similarity Calculation According to the similarity Eq (4.10), we replace α1 and α2 with the text feature embedding Et and the video feature embedding EV, respectively.
where Wg is the parameter matrix that aims to learn the global similarity through training.
Frame-Text Local Similarity Calculation To exploit the local semantic information in frames, we propose a similarity calculation regarding the similarity between the video's local frames and words.
First, we obtain the cosine similarity Cij of the frame feature vector vi and the word vector tj:
Then, softmax is used to normalize the cosine similarity to obtain the local feature weights βij.
After obtaining the attention weights, we calculate the frames feature representation containing the words' semantic information:
Finally, we compute the frame-text local similarity representation between Vfi and tj using Eq (4.10):
where Wl is also the parameter matrix like Wg.
Local similarity represents the association between capturing a specific word and the frames that make up the video, using finer-grained visual semantic alignment to improve similarity prediction.
4.4. Training objective
We take the widely used ranking loss function [42] as the training objective in our cross-modal retrieval task. Its goal is to evaluate the relative distance between input samples and optimize model training by incorporating the similarity calculation results into the ranking loss. The similarity computation model is defined as sim(), with positive samples (V,T) being the matched video-text pairs and the negative samples being mismatched pairs:
The loss is obtained referring to the ranking loss function:
where:
where va is the anchor sample, representing the reference vector. vp is the sample I or T that matches the reference sample. vn is the sample I′ or T′ that does not match the reference sample. Vector parameters in the Lossl function refer to the frame or text local feature vectors. Vector parameters within the Lossg function refer to the video and text local feature vectors.
5.
Experiments
To validate the effectiveness of our model, in this section, we demonstrate experiments on four widely used text-video retrieval datasets: MSR-VTT [9], LSMDC [44], MSVD [43] and DiDeMo [12]. The model's performance is evaluated by testing its performance in terms of different recall rates, ranking results, and comparing the results with experimental results from existing studies.
5.1. Datasets
MSR-VTT dataset was created by collecting 257 popular video queries from a commercial search engine, with each query including 118 videos. The current version of MSR-VTT offers 10,000 web video clips, totaling 41.2 hours and 200,000 clip-sentence pairs, and each video is annotated with approximately 20 captions. To compare with previous work, 7000 videos were selected for training [13], and 1000 videos were selected for testing [43], following the commonly used segmentation method in current studies. Since no validation set was provided, 1000 videos were randomly selected from MSR-VTT to form the validation set.
LSMDC dataset comprises 118,081 video clips extracted from 202 movies, ranging from two to 30 seconds. The validation set includes 7,408 clips, and the evaluation is performed on a separate test set consisting of 1000 videos from movies that are distinct from those in the training and validation sets.
MSVD dataset comprises 1970 videos ranging from 10 to 25 seconds, and each video is annotated with 40 captions. The videos feature various subjects, including people, animals, actions, and scenes. Each video was annotated by multiple annotators, with approximately 41 annotated sentences per clip and a total of 80,839 sentences. The standard splitting [6] was used, with 1,200 videos for training, 100 videos for validation, and 670 videos for testing.
DiDeMo dataset comprises 10,000 flickr videos, each annotated with 40,000 sentences. In the test set, there are 1000 videos. As per the approach in references, we assess paragraph-to-video retrieval, wherein all sentence descriptions for a video are concatenated to form a single query. Notably, this dataset includes localization annotations (ground truth proposals), and our reported results incorporate these ground truth proposals.
5.2. Implementation details
Data Pre-processing. Different datasets have varying video durations and frame sizes, making standardizing the model input format challenging. This study extracts 12 frames from each video according to a specified time window to resolve this issue. It uses them as representatives of the video content, ensuring a uniform input shape for the model. Additionally, to ensure consistency with previous work [2,6,12] and facilitate testing, the pixel size of each video frame was adjusted to 224×224.
Model Settings. The study employs the CLIP model as its backbone and initializes all encoder parameters based on the pre-trained weights of the CLIP model, as described in [22]. For each video, the ViT-B/32 image encoder of the CLIP model is used to obtain the frame embeddings, while the transformer text encoder of the CLIP model is used to obtain the text embeddings. The CLIP encoder has an output size of 512, which also determines the attention size of the three projection dimensions, which is set to 512. The weight matrices Wq, Wk, and Wv are randomly initialized, and the bias values are set to 0. The output units of the fully connected layer are also set to 512, and a dropout of 0.3 is applied, as described in [45]. The study employs the Adam optimizer [46] for training, with an initial learning rate of 0.00002, and the learning rate is decayed using a cosine schedule, as described in [22].
The recall [12,29] represents the ratio of the valuable fraction in the detection results to that in the dataset. Recall at K was used to measure the model's performance, and recall at 1 (R@1), recall at 5 (R@5), and recall at 10 (R@10) were used as evaluation metrics during testing.
5.3. Results and analysis
In this section, we present the results of the retrieval performance of our model on the MSR-VTT, LSMDC, MSVD and DiDeMo datasets. The aim is to showcase the superiority of our model in comparison to other existing models.
5.3.1. Comparisons on four datasets
Table 1 presents the results of comparative experiments in text-to-video retrieval (R@1/5/10) across four widely utilized public datasets.
Comparing our method's results with existing approaches, we observe that on the MSR-VTT, LSMDC, MSVD, and DiDeMo datasets, our average accuracy rates are 66.4% (+ 0.3%), 43.7% (+ 0.4%), 70.3% (+ 0.2%) and 79.7% (+ 0.4%), respectively. These scores surpass the performance of the models listed in the table across all four datasets, thus validating the effectiveness of the approach presented in this paper.
More accurately, on the LSMDC and DiDeMo datasets, we observed that our model's R@1 results were lower than those of the VINDLU model. Upon analysis, it was discovered that the VINDLU model focuses on effective video-and-language pretraining, utilizing the jointly trained CC3M + WebVid2M dataset containing content domains that are more aligned with MSR-VTT, such as sports, news, and human actions. Consequently, the VINDLU model outperforms our model on the R@1 metric. However, due to our model's enhancements in capturing video themes and details, our overall performance excels over VINDLU on the R@5 and R@10 metrics.
Additionally, it is worth noting that only on the MSR-VTT dataset, the R@10 results of the CLIP4Clip-seqTransf model are slightly higher than our model's results. On all other datasets and metrics, our model outperforms CLIP4Clip-seqTransf. Therefore, it can be considered that our model exhibits better stability in terms of performance compared to CLIP4Clip-seqTransf. Since both CLIP4Clip-seqTransf and our method use CLIP as the backbone, we can attribute the improvement in model performance to the fact that CLIP4Clip-seqTransfer employs a text-agnostic visual feature extraction approach, whereas our model utilizes a frame feature aggregation approach conditioned on text semantics.
Furthermore, on the LSMDC dataset, the retrieval task is more challenging due to the inherently vague textual descriptions of movie scenes. This conclusion can be drawn from the generally lower retrieval scores achieved by previous methods on this dataset. However, our approach outperforms the models listed in the table across all metrics. This demonstrates the significance of our model's ability to aggregate video features conditioned on text semantics. It learns the features of frames most relevant to the text semantics and suppresses the interference of redundant frames in feature aggregation.
5.3.2. Ablation studies
In this section, a series of ablation experiments are conducted to explore the two modules' effects to understand the model's advantages.
Module 1. The embedding module for video feature acquisition, which utilizes a cross-modal attention mechanism to aggregate frame features.
Module 2. The global-local similarity-based computation module.
The comparison experiments were performed on the MSR-VTT dataset.
Cross-modal Feature Aggregation
Table 2 presents the results of the ablation study on the cross-modal feature aggregation module for video feature extraction. The different configurations for the ablation experiments are shown in the table.
In this set of experiments, we compare the performance of our cross-modal aggregation method with that of Mean Aggregation and Self-attention Aggregation. The Mean Aggregation method calculates an unweighted average of the frame feature embeddings, while the Self-attention Aggregation method computes aggregation weights without utilizing textual semantic information and aggregates the frame features using a focused mechanism.
The results of these experiments, as shown in Table 3, reveal an improvement in R@1 values ranging from 1% to 6%. This indicates that our cross-modal attention-based approach to acquiring video features leads to a more accurate capture of the relationships between video frames and text semantics.
Global-Local Similarity Calculation
In the ablation experiments of the similarity calculation module, Table 3 demonstrates the impact of various strategies on similarity analysis and score prediction. The results indicate that using video features obtained from the cross-modal attention feature aggregation method (as outlined in Section 4.3) as input data for the similarity calculation module slightly decreases performance compared to using frame-word local features. This suggests two things: (1) the aggregation process may result in a loss of detailed features, and (2) the slight performance decrease also implies that the aggregated video features can effectively capture the features present in the frames. The global-local similarity calculation approach leads to an improvement of 1–3% in R@1 compared to using either method individually.
Figure 3 displays the attention weights of selected video frames generated by the cross-modal feature aggregation model. As can be observed from the examples, the model's attention mechanism can distinguish the relative importance of each frame's content, assigning lower weights to frames with limited correlation to textual information. In comparison, the self-attention aggregation method can recognize frames with crucial information but fails to differentiate between frames with subtle differences. On the other hand, the mean weighting aggregation method doesn't differentiate between frame.
The line graph in Figure 4 showcases the trend of the weight assigned to the key frames of the first example shown in Figure 3. The results demonstrate that the cross-modal Attention mechanism effectively identifies the frames relevant to the critical information in the video as it assigns higher weights to these frames. On the other hand, the mean aggregation method presents a flat trend, with no significant fluctuations in the weight assignments. In comparison, the self-attention method appears less responsive to the changes in the frame content, leading to a more moderate trend in the graph.
5.3.3. Qualitative results
The results in Figure 5 show the effectiveness of the text-to-video model developed in this study. The first row displays the input query text, while the second shows the ground truth. The remaining rows (3–5) present each query's top 1–3 ranked results. The retrieved video frames are visually similar to the ground truth and semantically align with the given text query, demonstrating the ability of the model to match textual and visual information.
The first column in Figure 5 demonstrates the model's aptitude in retrieving videos accurately related to the query text. The query "doing craft", is reflected in the captions of the retrieved videos, all of which pertain to "craft" and feature a "woman". This indicates that the model can efficiently match text and video topics during retrieval. The second column showcases the model's focus on the critical elements shared between the text and video modalities, as the top-ranked retrieval result, despite not being the ground truth, contains the crucial information from the query, namely a "woman" and a "laptop". Similarly, both the top 2 and top 3 ranked videos in the last column depict a "student" and a "teacher" in a "classroom".
The utilization of cross-modal feature aggregation and global-local similarity calculation in the model elevates the accuracy and sophistication of text-to-video retrieval results. This allows the model to concentrate on the topics and visual aspects of the videos, resulting in a more precise and refined retrieval outcome.
6.
Conclusions
This paper improves the performance of text-video matching by implementing two modules: the cross-modal attention feature aggregation module and the global-local similarity calculation module. The cross-modal attention feature aggregation module leverages the pre-trained CLIP model's multi-modal feature extraction capabilities to extract highly relevant video features, focusing on the frames most pertinent to the text. Meanwhile, the global-local similarity calculation module calculates similarities based on the video-sentence and frame-word granularities, allowing for a more nuanced consideration of both the topic and detail features in the matching process. The experimental results, conducted on the benchmark dataset, clearly demonstrate the efficacy of our proposed modules in capturing both topic and detail features, leading to improvement in text-video matching accuracy. This work contributes to multi-modal representation learning, highlighting the potential of advanced feature aggregation and similarity calculation techniques in enhancing text-video matching. Further research may be necessary to realize our methods in real-world applications fully.
Use of AI tools declaration
The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.
Acknowledgments
The authors would like to acknowledge the support provided by Aerospace HongKa Intelligent Technology (Beijing) CO., LTD.
Conflict of interest
The authors declare there is no conflict of interest.









 DownLoad:
DownLoad:







