Region fine-grained attention network for accurate bone age assessment

1.   Introduction

Worldwide, there are 6.1 million teenagers with developmental abnormalities annually, leading to great trouble for numerous families ^[1]. In this case, growth development monitoring will provide appropriate preventive measures and treatment plans for patients, further effectively preventing the deterioration ^[2]. Bone age assessment, one of the key means of monitoring physical development, can provide strong references for doctors to diagnose the endocrine system and other developmental-related diseases ^[3,4]. Therefore, it is necessary to perform the bone age assessment to monitor adolescent development.

Currently, many methods are proposed for bone age assessment, including manual diagnosis and machine learning-based approaches. In manual diagnosis, the experienced doctors evaluate the bone age based on the reference standards, e.g., Greulich-Pyle (GP) ^[5], Tanner-Whitehouse (TW2) ^[6] and Radius-China (RUS-CHN) ^[7]. However, these methods have large errors and are time-consuming, leading to an overloaded workload for radiologists. For machine learning methods, thanks to the powerful feature extraction capabilities of deep learning techniques, they have already achieved or even surpassed the performance of manual diagnosis methods and are more efficient than radiologists ^{[8,9,10,11,12]}. For example, Wang et al. ^[14] developed a coarse and fine feature joint learning network to perform bone age assessment by capturing long-term dependencies and fusing attention features. However, it is not possible to eliminate the interference caused by the background, resulting in poor performance. Nguyen et al. ^[13] proposed a convolutional neural network (CNN) for bone age assessment using transfer learning from hand radiographs, but it is still far from available in clinical practice. In addition, Liu et al. ^[15] proposed a self-supervised attention network for bone age assessment using specific skeletal regions, e.g., the regions of interest for epiphysis and carpal, while ignoring other areas, such as the metacarpal bone which contains bone age information. Moreover, Ren et al. proposed a regression CNN to automatically assess the pediatric bone age using coarse attention and fine attention maps from hand radiograph ^[16]. However, similar hand radiographs may lead to poor separability, making it difficult for the networks to distinguish them. Furthermore, an attention-guided network is designed to automatically localize the discriminative regions for bone age assessment ^[17], and it performs well on images with significant bone age differences, but shows lower performance on images with successive bone ages.

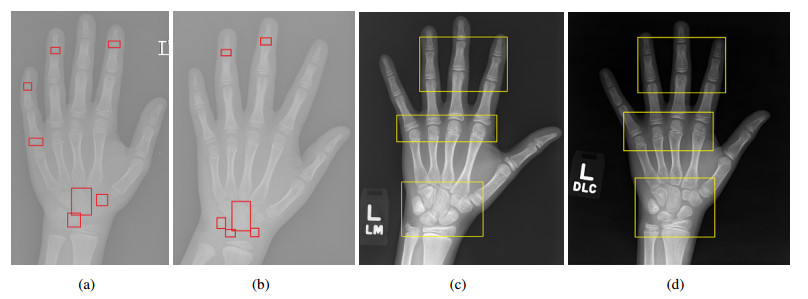
In a word, it is still challenging to perform bone age assessment because of these problems. First, the skeletal regions vary greatly in shape and are prone to background interference ^[18], resulting in some effective feature information being submerged, as shown in Figure 1 (a), (b). Second, hand radiographs with successive bone age are often similar with poor separability ^[19,20] [see Figure 1 (c) (150 months) and (d) (132 months)], leading to larger prediction errors and performance degradation of the networks.

Figure 1.  Examples of hand radiographs. (a) and (b) show the feature bones with significant changes. (c) and (d) describe the hand radiographs with successive bone age, where the characteristic regions are highly similar.

DownLoad: Full-Size Img PowerPoint

To address such problems, a region fine-grained attention network (RFGA-Net) is proposed for bone age assessment, where the region aware attention (RAA) module is developed to distinguish the skeletal regions from the background, and the fine-grained feature attention (FFA) module is devised to identify similar bone radiographs. The main contributions of this paper are described as follows:

$1)$ The RAA module, which can model global spatial dependency, is developed to distinguish the specific skeletal regions from the background.

$2)$ The FFA module, which can recognize critical fine-grained feature regions, is devised to identify similar bone radiographs.

$3)$ The experimental results on the benchmark dataset show the superiority of the proposed RFGA-Net.

The rest of this paper is organized as follows: The proposed RFGA-Net is described in Section 2, while Section 3 gives the experiments and results and the conclusions are shown in Section 4.

2.   RFGA-Net for bone age assessment

In this section, an RFGA-Net is proposed for bone age assessment, as shown in Figure 2, and it contains two key modules: The RAA module and the FFA module, which are described as follows.

Figure 2.  The architecture of the RFGA-Net. First, the RAA module is devised to distinguish the skeletal regions from the background, then the FFA module is developed to discriminate similar bone radiographs. Finally, the regression networks are employed to estimate the bone age by integrating the feature maps and sex information.

DownLoad: Full-Size Img PowerPoint

2.1.   Region aware attention module for skeletal region discrimination

In bone age diagnosis, doctors often determine bone age according to the specific skeletal regions, such as the size and shape of the metacarpal bones ^[21]. However, the large variations and diverse shapes of bones often cause visual fatigue ^[22]. In addition, some small bones are easily over-masked by the background, resulting in misdiagnosis for deep neural networks ^[23]. Correspondingly, the dynamic region convolution can adaptively register target feature regions and achieve target tracking of different sizes ^[24]. Inspired by it, the RAA module was developed to distinguish the specific skeletal regions from the entire bone region by modeling global spatial dependency, where the class dynamic attention convolution was designed to track the different sized hand bones through adaptive feature extraction, as shown in Figure 2, defined as

where CDAC denotes the class dynamic attention convolution, and MPS represents the mask product summation, and the detailed operation is shown in Figure 3, which is described as follows:

Figure 3.  The architecture of the RAA module for global spatial dependency modeling.

DownLoad: Full-Size Img PowerPoint

● Similar to dynamic region-aware convolution for semantic segmentation ^[24], the input feature maps $X$ $\in{\bf R}^{B\times C \times H \times W}$ are first fed into the CDAC to generate the class mask $M$ $\in{\bf R}^{B\times N \times 1\times H \times W}$, where the left branch is developed to generate the convolution kernel $K$ $\in{\bf R}^{(B\times N) \times C \times H \times W}$ and the middle one is designed to obtain the class mask $M$ $\in{\bf R}^{B\times N \times 1\times H \times W}$.

Specifically, in the left branch, the adaptive average pooling, $1\times1$ convolution layer and self-attention are introduced to generate the convolution kernel $K$ $\in{\bf R}^{(B\times N) \times C \times H \times W}$, then the reshaped feature maps $F$ $\in{\bf R}^{1 \times (B\times C) \times H \times W}$ are convoluted with the kernel to obtain the class mask $M$ $\in{\bf R}^{B\times N \times 1\times H \times W}$ after the argmax function, as shown in the middle one of Figure 3.

● The input feature maps $X$ $\in{\bf R}^{B\times C \times H \times W}$ will be processed by the MPS to produce the output feature maps $O$ $\in{\bf R}^{B\times O\times H \times W}$.

Specifically, in the right branch, the input feature maps $X$ $\in{\bf R}^{B\times C \times H \times W}$ are processed by the $1\times1$ convolution and then reshaped to obtain the class feature maps $C$ $\in{\bf R}^{B\times N \times O\times H \times W}$. Finally, the class feature maps $C$ will be multiplied by the mask to obtain the feature maps $O$ $\in{\bf R}^{B\times O\times H \times W}$ after the summation at class dimension.

2.2.   FFA module for similar bone radiograph distinguish

In clinical practice, the size and shape of hand bone areas are utilized to perform bone age assessment ^[25], but a large workload often leads to low efficiency ^[26]. Moreover, similar hand radiographs are always wrongly diagnosed by radiologists ^[27], resulting in significant errors between the predicted bone age and the actual one. Correspondingly, fine-grained feature perception can effectively mine dissimilation information from similar features for image recognition ^[28,29]. Motivated by it, the FFA module is devised to distinguish similar bone radiographs by learning the fine-grained features, as shown in Figure 2, defined as

where FMC and CFA denote the feature map chunking and coordinate fusion attention, respectively, which are shown in detail as follows:

● First, the input feature maps $I$ are divided into identical small feature maps, i.e., FMC (as shown in Figure 2, the feature maps of $16\times 16$ are reshaped into four small ones of $4\times 4$), where the fine-grained features will be transmitted into the self-attention for learning.

● The chunking group feature maps are fed into the linear layer to generate the corresponding group queries (Q), keys (K) and values (V), respectively. Further, the coordinate coefficient position relationship (C) generated from the keys (K) by the linear layer is utilized to model contextual dependencies and avoid spatial information loss caused by chunking.

● Next, the multiplied results of Q and K will be added with the coordinate information C to generate the new group feature maps.

● Finally, the values (V) will multiply with the new group feature map C to obtain the output feature maps.

In ^[28], the destruction and construction are proposed to focus on fine-grained details and learn robust and discriminative features, where the destruction is developed to obliterate some redundant regions to focus on other relevant parts, and the construction is designed to capture and understand the important features. In addition, it can be seen from ^[29] that the RefineMask is proposed to capture more detailed and precise information about the object boundaries and shapes, where the attention mechanism is used to selectively refine the mask predictions for each instance. Differentiated from them, the proposed FFA module is devised to distinguish similar bone radiographs by designing FMC and CFA, where the FMC is performed before attention learning, meaning the FFA can pay more attention to local features to mine the fine-grained features and the coordinate position relationship is utilized to model contextual dependencies and avoid spatial information loss.

3.   Experiments and results analysis

3.1.   Evaluation metric

In the experiments, we use the mean absolute error (MAE) and root mean square error (RMSE) as evaluation metrics to evaluate the performance of bone age assessment ^[16], defined as

and

where $P(n)$ and ${{\widehat P}}(n)$ represent the actual bone age and predicted one, respectively.

3.2.   Dataset

To evaluate the effectiveness of the proposed RFGA-Net, the Radiological Society of North America (RSNA) pediatric bone dataset ^[30] is used as the benchmark, where it consists of the training set with 12,611 images, validation set with 1425 images and test set with 200 images. Furthermore, the RSNA dataset includes images with the ages from zero to 228 months, while the corresponding ground truth is provided for the public with the sex information. In the experiments, the same data partitioning is used for model testing, i.e., the RSNA dataset is divided into the training set, validation set, and testing set with the number of 12,611, 1425 and 200 images, respectively.

3.3.   Implementation details

The proposed RFGA-Net is constructed by Pytorch 1.6.0 ^[31] on a server with two NVIDIA GeForce GTX 3090 GPUs. During the experiments, the stochastic gradient descent (SGD) optimizer ^[32] with an initial learning rate of $4e^{−4}$ is used to optimize the proposed RFGA-Net, where the epoch, batch size and momentum are set as 100, 36, and 0.9, respectively. In addition, the L1Loss (absolute value loss) is regarded as the loss function while the learning rate is optimized by the StepLR (step learning rate) scheduler. Furthermore, all hand radiographs are resized to $576\times576$, then they are normalized by subtracting the mean of [0.485, 0.456, 0.406] and dividing the standard deviation of [0.229, 0.224 0.225], respectively.

3.4.   Comparisons to other SOTA methods

To verify the superiority of the proposed RFGA-Net, nine SOTA (state-of-the-art) methods, i.e., Spampinato et al. ^[33], Deng et al. ^[34], Bui et al. ^[35], Wibisono et al. ^[36], Zhou et al. ^[37], Ren et al. ^[16], Chen et al. ^[17], Li et al. ^[38] and Liu et al. ^[15] are used for bone age assessment, and the results are recorded in Table 1, where the methods of Spampinato et al. ^[33] and Bui et al. ^[35] are tested on the digital hand atlas database^*, while the model proposed by Zhou et al. ^[37] is evaluated on the tailored private hand radiograph dataset, and these approaches, i.e., Deng et al. ^[34], Wibisono et al. ^[36], Ren et al. ^[16], Chen et al. ^[17], Li et al. ^[38] and Liu et al. ^[15], are validated on the RSNA dataset.

^*http://www.ipilab.org/BAAweb/

Table 1.  Results of different methods for bone age assessment on the RSNA dataset.

Methods	MAE (month)	RMSE (month)
Spampinato et al. [33]	9.48	–
Deng et al. [34]	7.34	9.75
Bui et al. [35]	7.08	9.12
Wibisono et al. [36]	6.97	9.34
Zhou et al. [37]	–	6.00
Ren et al. [16]	5.20	–
Chen et al. [17]	4.40	4.78
Li et al. [38]	4.09	–
Liu et al. [15]	3.99	–
RFGA-Net	3.34	4.02

---

 | Show Table

DownLoad: CSV

It can be observed that the RFGA-Net shows the best performance on the RSNA dataset, achieving the MAE of 3.34 months and RMSE of 4.03 months, respectively, demonstrating the superiority of RFGA-Net for bone age assessment. In addition, the proposed RFGA-Net performs better than Ren et al. ^[16] and Liu et al. ^[15], indicating that the proposed region-aware and fine-grained feature attention can assist the self-attention mechanism to focus on the key bone regions, further improving the performance of the network. Moreover, compared to other region-specific guided methods, such as Spampinato et al. ^[33], Deng et al. ^[34], Bui et al. ^[35] and Wibisono et al. ^[36], the proposed RFGA-Net also exhibits better performance because it can adaptively learn information from all bone feature regions.

In addition, the visualized results of the class activation map are given in Figure 4, where the first and third rows represent the raw hand radiography, and the second and last rows correspond to the class activation maps. From it, we can note that the proposed RFGA-Net mainly focuses on the regions of the epiphysis, metacarpal-phalanges, and carpal bones, which is consistent with the diagnosis of radiologists, demonstrating the effectiveness of the proposed RFGA-Net.

Figure 4.  The class activation map of the proposed RFGA-Net for bone age assessment, where the region with red color stands for high attention.

DownLoad: Full-Size Img PowerPoint

3.5.   Ablation studies of the proposed modules in RFGA-Net

In this section, a large number of ablation studies are conducted to verify the effect of the proposed modules in RFGA-Net, including the RAA module and the FFA module, which are described as follows.

3.5.1.   Impact of RAA module

As described in Section 2, the RAA module is devised to distinguish the specific skeletal regions from the entire hand bone. To validate the effect of the RAA module, several experiments are carried out on the RSNA dataset and the results are shown in Table 2, where No.1 is the baseline performance without the RRA and FFA module, and the baseline represents the backbone network of InceptionV3 ^[39]. From it, we can see that the MAE and RMSE can be reduced to 4.19 and 5.61, respectively, after inserting the RRA module into the baseline, showing that the RAA module is beneficial for bone age assessment. In addition, comparing No.3 with No.4 and No.5, we can note that the performance for bone age assessment can be further improved, validating the effectiveness of the proposed RAA module.

Table 2.  Ablation studies of the proposed modules for bone age assessment, where the baseline represents the InceptionV3 ^[39] integrating sex information.

No.	Baseline	RAA	FFA	MAE	RMSE
1	$\checkmark$			5.34	6.85
2	$\checkmark$	$\checkmark$		4.19	5.61
3	$\checkmark$		$\checkmark$	4.49	5.83
4	$\checkmark$	$\checkmark ^2$	$\checkmark ^1$	3.87	4.26
5	$\checkmark$	$\checkmark ^1$	$\checkmark ^2$	3.34	4.02

---

 | Show Table

DownLoad: CSV

Moreover, several class activation maps for testing results are shown in Figure 5, where the first row (A) denotes the raw images, while the second one (B) and the third one (C) represent the baseline and baseline+RAA, respectively. We can observe from it that inserting the RAA module can further assist the network in focusing the bone regions in the hand radiograph, while the baseline network is affected by complex background interference (the entire hand bone region). These excellent results demonstrate that the proposed RAA module can distinguish the skeletal regions from the background, and further improve the performance of bone age assessment.

Figure 5.  Class activation maps of the ablation experiment for the proposed module, where the red color denotes the high attention: A. raw images, B. baseline, C. baseline+RAA, D. baseline+RAA+FFA.

DownLoad: Full-Size Img PowerPoint

3.5.2.   Impact of FFA module

Similarly, as illustrated in Section 2, the FFA module is employed to identify similar bone radiographs. To explore the effect of the FFA module, ablation experiments are carried out on the RSNA dataset and the ablation results are given in Table 2, where the proposed FFA module is embedded into the baseline+RAA to show its superiority for bone age assessment. From Table 2, comparing the second row and the third one, we can note that the MAE and RMSE can be further reduced to 3.34 and 4.02, respectively, indicating that the proposed FFA module is helpful for estimating bone age based on the hand radiography. Similarly, it can be noted from No.2, No.4 and No.5 that adding the FAA module can further improve the performance of the network. For example, comparing No.2 with No.5, the MAE and RMSE can be reduced to 3.34 and 4.02, respectively, showing the superiority of the FAA module. Moreover, it can be seen that adding two modules shows better performance than the single module. For example, we can observe from No.2, No.3 and No.4 that the combination of RAA and FAA can achieve reductions of 0.32 and 0.62 on the MAE, respectively, compared to the single RAA and FAA modules, verifying the effectiveness of the RAA and FAA modules for bone age assessment.

Furthermore, several class activation maps are shown in Figure 5, where the last row denotes the results of baseline+RAA+FFA. It can be found that inserting the FFA module can help the network to locate the fine-grained feature regions, such as carpal and epiphysis regions, which are always ignored by radiologists. In contrast, the baseline+RAA performs feature extraction on the rough region of hand bones. This differentiated attention map proves that the proposed FFA module can distinguish similar bone radiographs by capturing fine-grained features.

3.5.3.   Impact of order of RAA and FFA module

The order of the proposed RAA and FFA modules is also crucial for bone age assessment. To explore the effect of the order, the order of RAA before FFA and the opposite one is tested on the RSNA dataset. The results are listed in No.4 and No.5 of Table 2, where No.4 represents the order of the FFA module before the RAA module, and the opposite one is shown in No.5. From the results, we can find that the performance of No.5 is better than that of No.4. Thus, we can conclude that the order of RAA before FFA performs better than the opposite one, and it is used in the proposed RFGA-Net for bone age assessment.

3.5.4.   Impact of sex information

Here, a series of experiments are performed to explore the impact of the sex information, where the sex information is added to the ablation experiments of the proposed modules. The predicted results for bone age are shown in Table 3. It can be seen from it that compared with the basic module, incorporating sex information can improve the performance of the network. For example, from No.3 and No.4, the MAE and RMSE can be reduced to 4.19 and 5.61 from 4.83 and 6.18, respectively after adding the sex information to Baseline+RAA. These substantial performance improvements demonstrate that adding sex information into the network can further advance the capability of bone age assessment. Therefore, the sex information is used as input for the proposed RFGA-Net for bone age assessment.

Table 3.  Ablation studies of the sex information for bone age assessment.

No.	Mode	MAE	RMSE
1	Baseline	5.76	7.19
2	Baseline+Sex	5.34	6.85
3	Baseline+RAA	4.83	6.18
4	Baseline+RAA+Sex	4.19	5.61
5	Baseline+FAA	4.94	6.54
6	Baseline+FFA+Sex	4.49	5.83
7	Baseline+RAA+FFA	3.88	4.29
8	Baseline+RAA+FFA+Sex	3.34	4.02

---

 | Show Table

DownLoad: CSV

4.   Conclusions

In this paper, an RFGA-Net was proposed for bone age assessment, where the RAA module was designed to distinguish the skeletal regions from the background and the FFA module was developed to identify similar bone radiographs. Extensive experiments conducted on the RSNA dataset showed the superiority of the proposed RFGA-Net, further providing accurate references for radiologists to perform bone age assessment.

Use of AI tools declaration

The authors declare that they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgements

This work was supported in part by the National Natural Science Foundation of China under Grant 71802055.

Conflicts of interest

No potential conflict of interest.