DCT-Net: An effective method to diagnose retinal tears from B-scan ultrasound images

1.   Introduction

With the development and progress of society, along with the increasing pace of life, the incidence of depression and anxiety has become increasingly common in everyday life. Depression, also known as major depressive disorder (MDD), is classified according to the diagnostic criteria for depressive disorders outlined in the Fifth Edition of the Diagnostic and Statistical Manual of Mental Disorders (DSM-5) ^[1]. The severity of depression is categorized into mild, moderate, and severe depressive disorders. Mild depressive disorder is clinically characterized by symptoms such as feelings of sadness, loss of interest, fatigue, and difficulty concentrating; however, these symptoms do not significantly interfere with the individual's daily life. Moderate depressive disorder is associated with more severe symptoms, including profound sadness, feelings of helplessness, low self-esteem, sleep disturbances, and changes in appetite. Severe depressive disorder presents with more intense manifestations, such as hopelessness, suicidal ideation, significant changes in sleep and appetite, and an inability to concentrate or perform daily activities.

The 2021 Global Mental Health Insights Report ^[2] indicates that over 300 million individuals globally are affected by depression, with the number of depression cases increasing by approximately 18% over the past decade. This suggests that about one in five individuals globally will experience depression at some point in their lives, with a lifetime prevalence of 15%–18%. The suicide rate associated with depression is estimated to be between 4.0% and 10.6%. According to the 2022 China Depression Blue Book ^[3] published by People's Daily, the lifetime prevalence of depressive disorders among adults in China is 6.8%, with approximately 280,000 suicides occurring annually in the country, of which 40% are linked to depression. The burden of mental illness worldwide has become more severe following the COVID-19 pandemic, with an additional 53 million cases of depression reported globally, representing a 27.6% increase. Additionally, instances of severe depression and anxiety have risen by 28% and 26%, respectively. Timely and effective detection of depression is not only a crucial step in improving public health but also a key measure in reducing the global mental health burden and preventing suicidal behavior. Advancing research and application in depression detection can enable early intervention, enhance treatment success rates, and ultimately improve the quality of life and mental well-being for millions of individuals worldwide.

In recent years, significant progress has been made in prediction tasks based on graph convolutional networks (GCNs). Researchers have extended GCNs to the field of disease detection. EEG signals are typically acquired from multiple electrodes, and the spatial structure between these electrodes exhibits strong dependencies. By representing EEG signals as graph structures, where electrodes are treated as nodes and spatial relationships between electrodes as edges, graph neural networks (GNNs) can effectively capture both local and global dependencies between electrodes through graph convolution operations. This approach is particularly effective for processing spatial information in EEG signals and modeling the complex relationships between brain regions ^[4].

Research has shown that spectral features perform well in speech signal recognition tasks ^[5]. Time-frequency representations reveal the frequency components of a signal that vary over time, making them especially effective for handling non-stationary signals. Traditional Fourier transforms provide global spectral information, but they ignore temporal dynamics. A continuous wavelet transform allows for multi-scale, multi-resolution time-frequency analysis. Smith et al. ^[6] used the Margenau-Hill transform to extract time-frequency domain features from EEG signals. The Margenau-Hill transform provides a localized representation of the signal in both time and frequency domains, making it more suitable for non-stationary signals compared to traditional Fourier transforms. However, in some cases, there may be a trade-off between time resolution and frequency resolution, which complicates the analysis. El-Sayed et al. ^[7] utilized recursive graphs to extract deep features from PPG signals, demonstrating that recursive graphs can visualize the recursive states of time series, helping to identify periodicities and patterns in the signals. However, recursive graphs are sensitive to noise and data quality, and noisy signals may lead to misleading patterns in the graphs. Siuly et al. ^[8] employed a wavelet scattering transform (WST) to capture time-frequency features of EEG signals, showing the superiority of time-frequency representations in capturing the characteristics of EEG signals. To further explore the advantages of time-frequency representations in physiological signal feature extraction, Smith et al. ^[9] compared several time-frequency methods, including the short-time Fourier transform, continuous wavelet transform, Zhao-Atlas-Marks distribution, and smoothed pseudo Wigner-Ville distribution (SPWVD). Recursive graphs can visualize the recursive state of time series, aiding in the identification of periodicity and patterns in the signal. However, recursive graphs are sensitive to noise and data quality, as noise can lead to misleading patterns in the graph. Compared to more complex time-frequency analysis methods, such as wavelet transforms or the Wigner-Ville distribution, the short-time Fourier transform (STFT) divides the signal into small windows, performing Fourier transforms within each window, thus preserving both time and frequency information while avoiding neglecting the time dimension. The STFT has lower computational cost and provides sufficient signal features while balancing time and frequency resolution. Therefore, we employ the short-time Fourier transform (STFT) to extract spectral features from speech signals, convert the frequency (y-axis) to a logarithmic scale, and use the color dimension to generate spectrograms. Subsequently, the y-axis is mapped to the mel scale to generate a mel spectrogram.

Vision transformer (ViT), a deep learning architecture based on the self-attention mechanism, has a powerful ability to model global dependencies. Traditional convolutional neural networks (CNNs) typically rely on local receptive fields to extract features, whereas a ViT leverages self-attention to model long-range dependencies between different positions, which is particularly important for time-frequency representations of EEG and speech signals. Time-frequency representations of EEG and speech signals often contain intricate interwoven frequency bands and complex time-frequency features. A ViT can effectively capture these complex spatiotemporal relationships, extracting deep features that are useful for tasks such as classification ^[10].

Based on this, the present study aims to combine GCNs and transformer models for multimodal depression detection based on EEG and speech singals. The main contributions of this study are as follows:

(1) Proposing a multimodal depression detection model (MHA-GCN_ViT): This study combines EEG and speech signals by utilizing GCNs and vision transformers to effectively extract and fuse the spatiotemporal, time-frequency features of the EEG and the time-frequency features of speech signals, thereby improving the accuracy of multimodal depression detection.

(2) Feature extraction using a discrete wavelet transform (DWT) and short-time Fourier transform (STFT): The study uses a DWT to extract discrete wavelet features from the EEG and construct a brain network structure, while a STFT is employed to extract time-frequency features from both EEG and speech signals, including mel spectrogram features.

(3) Introducing multi-head attention to enhance the brain network representation of the GCN: This model incorporates multi-head attention with GCNs to capture complex relationships between different EEG channels, thereby enhancing the GCN's ability to represent brain networks.

(4) Achieving significant performance improvement: The model was validated through five-fold cross-validation on the MODMA dataset. Experimental results demonstrate that the model achieves high accuracy, precision, recall, and F1 score, showing a significant improvement in depression detection performance. This confirms the model's effectiveness and potential for application in other multimodal detection tasks related to psychological and neurological disorders.

2.   Related work

Conventional approaches to diagnosing depression primarily rely on subjective evaluations. Clinicians engage in observation, active listening, and inquiry with patients, integrating these insights with standardized assessment scales to formulate comprehensive diagnosis. With the advancement of technology, researchers can now diagnose depression using biological information, magnetic resonance imaging (MRI), and physiological signals ^[11]. Current research on depression detection mainly focuses on using single modalities such as an EEG, speech, and text, as well as multimodal approaches that combine social media text, interview speech, and video. This paper will focus on multimodal depression detection by combining EEG and speech signals, summarizing the related research work.

2.1.   Depression detection based on EEG signals

Research has shown that there are distinct differences in electroencephalogram (EEG) signals between individuals with depression and healthy controls. For example, patients with depression exhibit different EEG signal characteristics within specific frequency bands ^[12]; there are also differences in the connectivity patterns of EEG signals between depressed individuals and healthy controls ^[13]. Additionally, the EEG responses of individuals with depression to stimuli or tasks differ, often showing weaker or slower responses compared to healthy individuals ^[14]. These responses are related to emotion regulation, cognitive control, and attention. However, EEG signals present certain challenges, such as temporal asymmetry, instability, low signal-to-noise ratio, and uncertainty regarding the specific brain regions involved in particular responses. In the review by Khare et al. ^[15], the methods for detecting mental disorders such as depression, autism, and obsessive-compulsive disorder using physiological signals are systematically discussed. A framework for the automatic detection of mental and developmental disorders using physiological signals is proposed. The review also explores the advantages of signal analysis, feature engineering, and decision-making, along with future development directions and challenges in this field. Therefore, depression detection based on EEG signals remains a challenging task.

The brain can be regarded as a complex network, where different brain regions are connected by neural fibers, forming an extensive interactive system. This network structure can be modeled as a graph, in which nodes represent EEG channels, and edges represent the connections between these channels. The graph structure is capable of capturing the intricate connectivity patterns between brain regions, which is beneficial for extracting the spatial features of EEG signals. Yang et al. ^[16] extracted nonlinear features, such as Lempel-Ziv complexity (LZC) and frequency domain power spectral density (PSD) features from EEG signals, analyzing the EEG during resting states with eyes closed and eyes open. They validated the effectiveness of multiple brain regions in detecting depression, identifying the temporal region as the most effective for depression detection with an accuracy rate of 87.4%. Considering the organizational structure of brain functional networks, Yao et al. ^[17] proposed the use of sparse group Lasso (sgLasso) to improve the construction of brain functional hyper-networks. They performed feature fusion and classification using multi-kernel learning on two sets of features with significant differences, selected through feature selection, achieving an accuracy of 87.88% after multi-feature fusion. Yang et al. ^[18] introduced a graph neural network-based method for depression recognition that utilizes data augmentation and model ensemble strategies. The method leverages graph neural networks to learn the features of brain networks and employs a model ensemble strategy to obtain predictions through majority voting on deep features. Experimental results demonstrated that graph neural networks possess strong learning capabilities for brain networks. Chen et al. ^[19] proposed a GNN-based multimodal fusion strategy for depression detection, exploring the heterogeneity and homogeneity among various physiological and psychological modalities and investigating potential relationships between subjects. Zhang et al. ^[20] developed a model based on graph convolutional networks (GCNs) with sub-attentional segmentation and an attention mechanism (SSPA-GCN). The model incorporates domain generalization through adversarial training, and experimental results showed that GCNs effectively capture the spatial features of EEG signals. Wu et al. ^[21] introduced a spatial-temporal graph convolutional network (ST-GCN) model for depression detection, creating an adjacency matrix for EEG signals using the phase-locking value (PLV). The ST-GCN network, constructed with spatial convolution blocks and standard temporal convolution blocks, improved the learning capacity for spatial-temporal features. Experimental results indicated that the ST-GCN combined with depression-related brain functional connectivity maps holds potential for clinical diagnosis. The attention mechanism provides an effective means to dynamically focus on the critical parts of the input information, capture long-range dependencies, enhance model interpretability, and thereby improve performance. Qin Jing et al. ^[22] proposed a probabilistic sparse self-attention neural network (PSANet) framework for depression diagnosis based on the EEG, integrating the EEG with the physiological parameters of patients for multidimensional diagnosis. The experimental results demonstrated that the fusion of physiological signals with other dimensions of signals achieved high classification accuracy. Jiang et al. ^[23] proposed a novel multi-graph learning neural network (MGLNN), which learns the optimal graph structure most suitable for GNN learning from multiple graph structures. The MGLNN demonstrates strong classification performance in multi-graph semi-supervised tasks. While depression detection based on EEG signals remains challenging, the application of graph structures and multimodal fusion plays a significant role in enhancing detection performance. Furthermore, depression detection based on speech signals is also of great importance.

2.2.   Depression detection based on speech signals

Individuals with depression exhibit abnormalities in behavioral signals, such as speech signals, compared to healthy individuals. Depression patients display certain vocal characteristics, including alterations in pitch, tone, speech rate, and volume, such as low, muffled, and weak voice quality ^[24]. The degree of speech clarity and fuzziness is also associated with depression, and analyzing and processing speech signals can help extract features relevant to depression. Kim et al. ^[25] employed a CNN model to analyze the mel-spectrograms of speech signals, learning the acoustic characteristics of individuals with depression. Their results indicated that deep learning methods outperformed traditional learning approaches, achieving a maximum accuracy of 78.14%. Yang et al. ^[26] proposed a joint learning framework based on speech signals, called the depression-aware learning framework (DALF), which includes the depression filter bank learning (DFBL) module and the multi-scale spectral attention (MSSA) module. On the DAIC-WOZ dataset, their approach achieved an F1 score of 78.4%, offering a promising new method for depression detection. Yin et al. ^[27] introduced the transformer-CNN-CNN (TCC) model for depression detection based on speech signals, utilizing parallel CNN modules to focus on local knowledge, while parallel transformer modules with linear attention mechanisms captured temporal sequence information. Experimental results on the DAIC-WOZ and MODMA datasets demonstrated that TCC performed well with relatively low computational complexity. However, depression detection based on a single modality still has certain limitations, such as insufficient robustness in specific contexts.

2.3.   Multimodal depression detection

Several researchers have adopted multimodal approaches to enhance the performance of depression diagnosis. Generally, multimodal fusion methods are categorized into early fusion, intermediate fusion, and late fusion ^[28]. Early fusion, also known as feature-level fusion, typically involves concatenating features from multiple modalities and then feeding them into a predictive model. Late fusion, also referred to as decision-level fusion, merges information from different modalities at the decision stage, facilitating the integration of multimodal information. Decision-level fusion preserves the decision results of each modality, avoiding potential feature information loss or blurring that may occur in feature-level fusion. It also considers the weight and importance of each modality, thereby fully integrating information from different modalities, which helps improve the model's understanding of multimodal data. In the field of image modality fusion, Liu et al. ^[29] proposed a novel adversarial learning-based multimodal fusion method for MR images. This method utilizes a segmentation network as the discriminator, enhancing the correlation of tumor pathological information by fusing contrast-enhanced T1-weighted images and fluid attenuated inversion recovery (FLAIR) MRI modalities. Zhu et al. ^[30] introduced a brain tumor segmentation approach based on deep semantic and edge information fusion. They used the swin transformer to extract semantic features and designed an edge detection module based on convolutional neural networks (CNNs). The proposed MFIB (multi-feature information blending) fusion method combines semantic and edge features, providing potential applications for multimodal fusion in disease detection. To further improve segmentation accuracy, Zhu et al. ^[31] proposed an end-to-end three-dimensional brain tumor segmentation model, which includes a modality information extraction (MIE) module, a spatial information enhancement (SIE) module, and a boundary shape correction (BSC) module. The output is then input into a deep convolutional neural network (DCNN) for learning, significantly improving segmentation accuracy. In recent studies, Liu et al. ^[32] proposed a statistical method to validate the effectiveness of objective metrics in multi-focus image fusion and introduced a convolutional neural network-based fusion measure. This measure quantifies the similarity between source images and fused images based on semantic features across multiple layers, providing a new approach for image-based multi-feature fusion. Bucur et al. ^[33] proposed a time-based multimodal transformer architecture that utilizes pre-trained models to extract image and text embeddings for detecting depression from social media posts. M. Roy et al. ^[34] proposed an improved version of the YOLOv4 algorithm, integrating DenseNet to optimize feature propagation and reuse. The modified path aggregation network (PANet) further enhances the fusion of multi-scale local and global feature information, providing an effective method for multi-feature fusion. To further improve fusion performance, M. Roy et al. ^[35] introduced a DenseNet and swin-transformer-based YOLOv5 model (DenseSPH-YOLOv5). By combining DenseNet and a Swin transformer, this model enhances feature extraction and fusion capabilities, incorporating a convolutional block attention module (CBAM) and a Swin transformer prediction head (SPH). This significantly improves the model's detection accuracy and efficiency in complex environments. Jamil et al. ^[36] proposed an efficient and robust phonocardiogram (PCG) signal classification framework based on a vision transformer (ViT). The framework extracts MFCC and LPCC features from 1D PCG signals, as well as various deep convolutional neural network (D-CNN) features from 2D PCG signals. Feature selection is performed using natural/biologically inspired algorithms (NIA/BIA), while a ViT is employed to implement a self-attention mechanism on the time-frequency representation (TFR) of 2D PCG signals. Experimental results demonstrate the effectiveness of the ViT in PCG signal classification. Fan et al. ^[37] introduced a transformer-based multimodal depression detection framework (TMFE) that integrates video, audio, and rPPG signals. This framework employs CNNs to extract video and audio features, uses an end-to-end framework to extract rPPG signal values, and finally inputs them into MLP layers for depression detection. The results showed that multimodal depression detection outperformed unimodal approaches, and the combination of physiological signals with behavioral signals demonstrated significant advantages. Ning et al. ^[38] proposed a depression detection framework that integrates linear and nonlinear features of EEG and speech signals, achieving an accuracy of 86.11% for depression patient recognition and 87.44% for healthy controls on the MODMA dataset. Abdul et al. ^[39] presented an end-to-end multimodal depression detection model based on speech and EEG modalities. This model uses a 1DCNN-LSTM to capture the temporal information of the EEG, while combining 2D time-frequency features of EEG signals and 2D mel-spectrogram features of speech signals, inputting them into a vision transformer model for depression detection. The experimental results demonstrated that the vision transformer effectively learned the spectral features of both EEG and speech signals.

Inspired by the above studies, this paper proposes a multimodal depression diagnosis method that combines physiological signals and speech signals, utilizing a graph convolutional network to model the relationships between brain channels and capture deep spatial and spectral features of EEG signals. The method also introduces decision-level fusion of multiple EEG features and speech spectral features, which more comprehensively integrates deep depression-related information from EEG and speech signals, significantly improving depression detection performance.

3.   Materials and methods

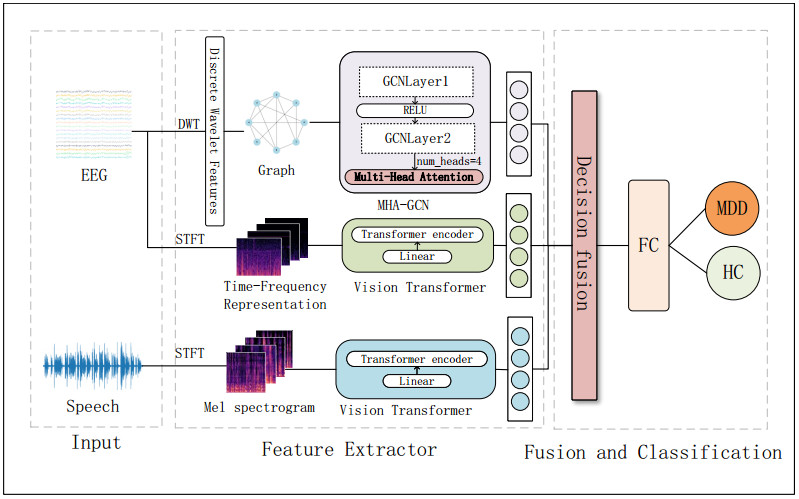
This section presents a multimodal model for the detection of depression, which integrates electroencephalogram (EEG) and speech signals. The model employs a multi-head attention graph convolutional network (MHA-GCN) and vision transformer (ViT) to extract deep spatiotemporal and spectral features from EEG signals, while utilizing the ViT model to extract deep spectral features from speech signals. The proposed model framework, illustrated in Figure 1, consists of three main components: the input layer, the feature extraction layer, and the decision fusion and classification layer.

Figure 1.  Model framework diagram.

DownLoad: Full-Size Img PowerPoint

3.1.   Discrete wavelet transform

Due to the complex time-frequency characteristics of EEG signals, which include varying frequency components and temporal waveform changes, traditional frequency-domain or time-domain analysis methods are insufficient for capturing comprehensive signal features. The discrete wavelet transform (DWT) allows for multi-scale decomposition of the signal, effectively capturing the feature information of EEG signals across different time scales and frequencies. By analyzing and processing the coefficients obtained from DWT decomposition, a more thorough understanding and description of the time-frequency characteristics of EEG signals can be achieved.

In this paper, after preprocessing the EEG signals (with details provided in Section 3.2.1), the DWT is used to extract wavelet features from each EEG channel as node features, which are then input into the GCN module. The formula for the wavelet transform is:

In Eq (3.1), $alpha$ represents the scale and $\tau$ represents the translation. The scale is inversely proportional to the frequency, while the translation corresponds to time. The scale controls the stretching or compression of the wavelet function, and the translation controls the shifting of the wavelet function. A window function is introduced as follows:

Based on this, the formula for the continuous wavelet transform (CWT) is given by:

Eq (3.3), $a$ represents the scale shift and $b$ represents the time shift. By restricting the two variables in the wavelet basis function to discrete points, the formula for the discrete wavelet transform (DWT) is obtained:

The discrete wavelet features of each channel are then stored as the node features of the MHA-GCN. The DWT process is illustrated in Figure 2.

Figure 2.  DWT extraction of discrete wavelet features from EEG channels.

DownLoad: Full-Size Img PowerPoint

3.2.   GCN module

Given that the spatial relationships between EEG channels are crucial for understanding brain function and pattern recognition, graph convolutional networks (GCNs) are capable of propagating information among neighboring nodes, capturing local spatial characteristics while considering global contextual relationships. Based on this, this paper constructs a graph convolutional network where each EEG channel is treated as a node. The Pearson correlation coefficient (PCC) between the features of each channel is calculated, and the adjacency matrix is obtained from the PCC matrix of the channels. The feature matrix, constructed with the DWT features extracted from each channel as node features, is then fed into the constructed graph convolutional network. The network, combined with the multi-head attention mechanism, extracts the deep correlation features between EEG channels.

In a graph convolutional network (GCN), a graph is defined as $G = (V, E, A)$, where $V$ represents the set of nodes, $E$ is the set of edges, and $A$ is the adjacency matrix of the graph $G$. $D$ is a diagonal matrix, $D_ii = \sum_j A_ij$, representing the degree of the node $v_i$. If there is an edge between node $i$ and node $j$, $A(i, j)$ denotes the weight of the edge; otherwise, $A(i, j) = 0$. For an unweighted graph, $A(i, j)$ is typically set to 1 if an edge exists and is 0 otherwise.

For all $V$, $H^{(l)}$ represents the feature matrix of all nodes at layer $l$, and $H^{(l+1)}$ represents the feature matrix after one graph convolution operation. The formula for a single graph convolution operation is given by:

In Eq (3.5), $I$ denotes the identity matrix. $\tilde{D}$ represents the degree matrix of $\tilde{A}$, which is computed as $\tilde{D} = \sum \tilde{A}_{ij}$. $\sigma$ denotes a nonlinear activation function, such as the ReLU function. $W^{(l)}$ represents the trainable parameter matrix for the graph convolution transformation at the current layer.

The GCN constructed in this paper comprises two layers of GCNLayer, with each layer's forward propagation including a linear layer and a convolution layer. The input data consists of the adjacency matrix and node features. Figure 3 illustrates the MHA-GCN model with four attention heads.

Figure 3.  MHA-GCN model.

DownLoad: Full-Size Img PowerPoint

3.3.   Multi-head attention module

To enhance the GCN's representation learning capability for the brain channel network graph and to improve its ability to understand and express relationships between nodes, a multi-head attention mechanism module is introduced. Given the query $q \in \mathbb{R}^{d_q}$, key $k \in \mathbb{R}^{d_k}$, and value $v \in \mathbb{R}^{d_v}$, the calculation formula for each attention head $h_i(i = 1, ..., n)$ is as follows:

In Eq (3.6), the learnable parameters are $W_i^{(q)} \in \mathbb{R}^{p_q\times{d_q}}$, $W_i^{(k)} \in \mathbb{R}^{p_k\times{d_k}}$, and $W_i^{(v)} \in \mathbb{R}^{p_v\times{d_v}}$. The function $f$ representing attention pooling can be either additive attention or scaled dot-product attention.

The output of the multi-head attention mechanism undergoes another linear transformation, corresponding to the concatenated results of the $h$ heads. Therefore, the learnable parameters are $W_o \in \mathbb{R}^{p_o\times{hp_v}}$, specifically defined as $W_o \begin{bmatrix} h_1 \\ \vdots \\ h_h \end{bmatrix} \in \mathbb{R}^{p_o}$. This allows each head to focus on different parts of the input. The multi-head attention mechanism is illustrated in Figure 4. In the proposed model, the multi-head attention mechanism is combined with the graph convolutional network (GCN). The node feature matrix output $X$ from the second GCN layer is used as input and is multiplied by the weight matrices $W^q$, $W^k$, and $W^v$ obtained during training, respectively, to derive the query $q$, key $k$, and value $v$ for the multi-head attention mechanism. The output represents the deep features for each node.

Figure 4.  Multi-head attention mechanism.

DownLoad: Full-Size Img PowerPoint

First, the node $i$ is linearly transformed with the nodes $j$ in its first-order neighborhood.

In Eq (3.7), $q_{c, i}$ represents the transformed feature vector of the central node $i$, $k_{c, j}$ represents the feature vector of a neighboring node $j$, $W_{c, q}$, $W_{c, k}$, $b_{c, q}$, and $b_{c, k}$ represent the learnable weights and biases, and $c$ represents the number of attention heads, which is set to 4 in this study.

Next, the multi-head attention coefficients between the central node and its neighboring node $j$ are calculated using scaled dot-product attention, as described in the following equation:

In Eq (3.8), $\alpha_{c, ij}$ represents the multi-head attention coefficient for each node, $[q, k] = exp(\frac{q^{T}k}{\sqrt{d}})$, respectively, and $d$ denotes the dimensionality of the node's hidden layer.

After obtaining the multi-head attention coefficients between each node and its neighboring nodes, we apply a linear transformation to the feature vectors of the neighboring nodes, $v_{c, j} = W_{c, v}h_j+b_{c, v}$. The feature vector of node $j$ after the linear transformation is denoted as $v_{c, j}$, where $W_{c, v}$ and $b_{c, v}$ represent the learnable weights and biases.

We then multiply the transformed feature vectors of the neighboring nodes by the corresponding multi-head attention coefficients and take the average to obtain the importance score of each node, as shown in the following equation:

In Eq (3.9), $Z = {z_1, z_2, ..., z_n}\in R^{n\times 1}$, $z_i$ represents the importance score of node $i$, and $C$ denotes the number of attention heads used in the attention mechanism.

By applying attention weighting to the feature matrix output by the GCN, the expressive power of the features can be enhanced, enabling the model to better learn the complex patterns and structures inherent in the graph data.

3.4.   Vision transformer module

In order to thoroughly analyze the time-frequency domain characteristics of electroencephalogram (EEG) and speech signals, these signals are transformed into two-dimensional (2D) EEG time-frequency spectrograms and 2D mel-spectrograms of speech using a short-time Fourier transform (STFT). The 2D EEG time-frequency spectrogram combines the time and frequency dimensions to display the frequency domain characteristics and temporal dynamics of EEG signals. This approach facilitates the investigation of brain frequency activity patterns, inter-regional brain coordination, and the dynamic changes in frequency components, which are crucial for understanding the spectral properties of EEG signals and conducting EEG signal analysis. The mel-spectrogram reflects the frequency distribution of speech signals, encompassing frequency components, pitch characteristics, resonance features, and acoustic traits, which highlight the acoustic differences between speech modalities in depressed patients and healthy subjects. The vision transformer effectively integrates global dependencies within the signals. Moreover, by applying the self-attention mechanism, the vision transformer assigns varying weights to signals at different time points, thereby addressing the non-stationary nature inherent in EEG and speech signals. Inspired by the work of Abdul et al. ^[39], this paper employs the vision transformer's positional encoding module and multi-head self-attention module to extract deep frequency domain features from EEG and speech signals. These features are then fused to classify depression by combining the multi-features of EEG signals with the frequency domain features of speech signals.

The structure of the vision transformer (ViT) model is illustrated in Figure 5. It includes a linear layer, a positional encoding module, and a multi-head self-attention module. The model parameters are configured as vit_base_patch16_224 ^[40], which defines the basic input size of the model. The 2D spectrograms are first divided into $16\times16$ patches, which then serve as the elements of the model's input sequence, with the resolution set to $224\times224$ pixels. In this study, the inputs to the ViT model are the 2D EEG time-frequency spectrograms and speech spectrograms, both in PNG format. The queries $q$, keys $k$, and values $v$ of the ViT are obtained by applying linear transformations to the input sequences, followed by multiplication with the weight matrices, $W^q$, $W^k$, and $W^v$, learned during the training process.

Figure 5.  Vision transformer model structure diagram.

DownLoad: Full-Size Img PowerPoint

3.5.   Decision-level weighted fusion

Traditional single-source or simple fusion methods may not meet the demands of complex tasks. To improve the accuracy and robustness of decision-making, decision-level weighted fusion assigns different weights to each information source, prioritizing decision cues with higher reliability or stronger relevance. This approach is better able to handle uncertainty and bias in the information. In this study, it is assumed that the outputs of classifiers based on EEG and speech signals are normalized and denoted as $[0, 1]$, where $m = [m_1, m_2]$, $n = [n_1, n_2]$, $v = [v_1, v_2]$, and $m_{i}$, $n_{i}$, and $v_{i}$ represent the probabilities predicted for normal and depressed states, respectively.

The validation accuracies of the EEG and speech models on the validation set are denoted as $\varepsilon = [\varepsilon_1, \varepsilon_2, \varepsilon_3]$, respectively. Then, the weighted sum of the probabilities is computed, denoted as $p_{i} = \varepsilon_1*m_{i}+\varepsilon_2*n_{i}+\varepsilon_3*v_{i}, i = 1, 2$, and the final predicted label $c$ is determined as follows:

4.   Dataset and data preprocessing

4.1.   Dataset

This study utilized the MODMA dataset ^[41], which is a multimodal depression dataset collected by the Key Laboratory of Wearable Computing, Gansu Province, Lanzhou University. The dataset primarily includes electroencephalogram (EEG) and speech data from clinical depression patients and matched healthy controls. The EEG data was collected using a traditional 128-channel electrode cap, involving 53 participants, including 24 outpatients with depression (13 males and 11 females; ages 16–56) and 29 healthy controls (20 males and 9 females; ages 18–55). The recordings include EEG signals in resting states and under stimulation. For the audio data collection, the dataset comprises 52 participants, including 23 outpatients with depression (16 males and 7 females; ages 16–56) and 29 healthy controls (20 males and 9 females; ages 18–55), with audio data recorded during interviews, reading tasks, and picture description tasks.

4.2.   Data preprocessing

4.2.1.   EEG data preprocessing

In this study, the preprocessing of EEG data was conducted utilizing the EEGLAB software. Initially, 29 channels were selected for each participant, namely [F7, F3, Fz, F4, F8, T7, C3, Cz, C4, T8, P7, P3, Pz, P4, P8, O1, O2, Fpz, F9, FT9, FT10, TP9, TP10, PO9, PO10, Iz, A1, A2, POz], with the EEG signal sampling frequency set to 250 Hz. All EEG signals underwent high-pass filtering with a cutoff frequency of 1 Hz and low-pass filtering with a cutoff frequency of 40 Hz. This filtering process preserved the EEG signal information while minimizing baseline drift and high-frequency electromyographic interference. Independent component analysis (ICA) was employed to eliminate artifacts associated with eye movements. Subsequently, discrete wavelet transform (DWT) was used to extract features from each channel, which were used as node features for constructing the brain channel network. Furthermore, a short-time Fourier transform (STFT) was applied to the artifact-free EEG data to extract two-dimensional time-frequency maps for the 29 channels, as illustrated in Figure 6.

Figure 6.  Time frequency maps of EEG signals in patients with depression (MDD) and healthy subjects (HC), with MDD on the left and HC on the right.

DownLoad: Full-Size Img PowerPoint

4.2.2.   Speech data preprocessing

Speech signals are temporal signals, and the preprocessing steps for speech signals include sampling and quantization, framing, windowing, and the short-time Fourier transform (STFT). The raw speech signal undergoes pre-emphasis, windowing, and framing. Pre-emphasis is a process that enhances the high-frequency components of the signal at the beginning of the transmission line to compensate for the excessive attenuation of high-frequency components during transmission. The mathematical representation of the pre-emphasis process is as follows:

where $\mu$ represents the pre-emphasis coefficient, typically set to 0.97, consistent with the parameter settings in reference ^[42].

Speech signals are also time-varying signals. It is generally assumed that speech signals are stable and time-invariant over short periods, referred to as frames, typically ranging from 10 to 30 milliseconds. In this study, frames are defined as 25 milliseconds, and framing is achieved using a weighted method with a finite-length movable window. A Hamming window is used as the window function, and the windowed speech signal is obtained by multiplying the window function with the signal:

In Eq (4.2), where $w(n)$ represents the Hamming window of length $N$:

Subsequently, each frame is subjected to the short-time Fourier transform (STFT), which facilitates the transformation of the time-domain signal into a frequency-domain representation. The energy spectrum of each frame is then computed by squaring the magnitude of each frequency spectrum point to obtain the power spectrum of the speech signal. A mel filter bank is designed to filter the power spectrum, with the frequency response of the filter defined as:

where $f(m)$ represents the center frequency. Finally, the mel spectrogram of the speech signal is obtained, as shown in Figure 7.

Figure 7.  Mel spectrogram of speech signals.

DownLoad: Full-Size Img PowerPoint

5.   Experimental results and analysis

5.1.   Experimental environment configuration

The experiments in this study were conducted using an NVIDIA GeForce GTX 3060 GPU, 16GB of RAM, with Python 3.9.0 and PyTorch 1.11.0 operating systems. To validate the effectiveness and generalization capability of the model, five-fold cross-validation was employed. The dataset was randomly divided into five subsets, with one subset used as the test set and the remaining four subsets used as the training set for each iteration of the cross-validation. The optimal parameters obtained from the training process are summarized in Table 1.

Table 1.  Model training parameters.

Parameters	Value
Learning rate	0.001
Batchsize	4
Epoch	400
Loss function	CrossEntropyLoss
Optimizer	Adam

---

 | Show Table

DownLoad: CSV

The original EEG signal has a dimension of $128 \times T$ where 128 represents the number of channels and T is the length of the signal. After applying a discrete wavelet transform (DWT), the output has a dimension of $29 \times 15 \times 180$, indicating 29 channels, 15 DWT features, and a time step of 180. Meanwhile, the EEG signal undergoes a short-time Fourier transform (STFT) to extract spectral features, resulting in a time-frequency representation with a dimension of $1 \times 512$. The speech signal, after being processed with a STFT to extract mel-frequency cepstral coefficients (MFCCs), is transformed into a mel spectrogram with a dimension of $3 \times 224 \times 224$. The model structure parameters are shown in Table 2.

Table 2.  The structure configuration of the MHA-GCN_ViT model.

Module	Network layer	Inputs	Outputs	Activation function	Parameters memory (MB)
MHA-GCN	GCNLayer1	(29, 15*180,180)	(29, 15*180,128)	RELU	5.578
	GCNLayer2	(29, 15*180,128)	(29,128,512)	-
	multihead_attn	(29,128,512)	(1,512)	Sigmoid
EEG_ViT	vit_base_patch16_224	(3,224,224)	(1,512)	Sigmoid	226.773
Speech_ViT	vit_base_patch16_224	(3,224,224)	(1,512)	Sigmoid	328.682
Decision-level weighted fusion	Weighted Sum and FC	(1,512)	(1, 2)	Sigmoid	2.64
		(1,512)
		(1,512)
Total					563.673

---

 | Show Table

DownLoad: CSV

5.2.   Evaluation metrics

To assess the performance and effectiveness of the proposed model, the evaluation metrics used in this study include accuracy, precision, recall, and F1 score. The calculation formulas are as follows:

In the formulas, TP (True Positive) denotes the number of true positive instances, TN (True Negative) denotes the number of true negative instances, FP (False Positive) denotes the number of false positive instances, and FN (False Negative) denotes the number of false negative instances.

5.3.   Experimental results

5.3.1.   Validation of the effectiveness of the MHA-GCN and decision-level fusion

To validate the effectiveness of the MHA-GCN and decision-level fusion, three models were designed for comparison:

(1) MHA-GCN + Feature Fusion: This model employs feature-level fusion in the fusion stage while keeping the other components unchanged.

(2) 1DCNN-LSTM + Decision Fusion: This model uses a 1DCNN-LSTM to extract deep features from the EEG discrete wavelet features, with the remaining components unchanged.

(3) MHA-GCN + Decision Fusion: This is the proposed model, denoted as MHA-GCN_ViT.

The performance of depression detection was compared across these models using the MODMA dataset, and the experimental results are presented in Table 3.

Table 3.  Results of comparative experiments for the MHA-GCN and decision-level fusion.

Model	MHA-GCN	Feature fusion	Decision fusion	Accuracy (%)	Precision (%)	Recall (%)	F1 Score (%)
MHA-GCN+Feature Fusion	$\checkmark$	$\checkmark$	-	75.42	75.33	75.41	75.32
1DCNN-LSTM+Desion Fusion	-	-	$\checkmark$	78.07	78.08	78.07	77.90
MHA-GCN+Decision Fusion	$\checkmark$	-	$\checkmark$	89.03	90.16	89.04	88.83

---

 | Show Table

DownLoad: CSV

A comparative analysis of models 1 and 3 reveals that the decision-level fusion achieved an accuracy of 89.03%, precision of 90.16%, recall of 89.04%, and an F1 score of 88.83%. These metrics represent improvements of 13.61%, 14.83%, 13.63%, and 13.51%, respectively, over feature-level fusion. This enhancement is attributed to the decision-level fusion's integration of different modalities at the decision stage, leveraging the complementarity and richness of multimodal information. It enhances the model's understanding and comprehensive judgment capabilities by reducing feature redundancy and avoiding repetition or conflicts between different modalities. This refinement leads to more precise and effective feature learning, improving the model's generalization ability, robustness, and reliability, thereby demonstrating the effectiveness and superiority of multimodal decision-level fusion.

In the comparison between models 2 and 3, the use of the MHA-GCN resulted in improvements of 10.96%, 12.08%, 10.97%, and 10.93% in accuracy, precision, recall, and F1 score, respectively, relative to the 1DCNN-LSTM model. This improvement is due to MHA-GCN's capability to effectively capture the global spatial features of EEG signals. The MHA-GCN offers greater flexibility and efficiency in modeling and feature learning for graph data, learning more representative feature representations, effectively reducing feature space dimensions, and enhancing the model's abstraction and expression of EEG signals. This, in turn, improves performance in classification tasks. The training and accuracy curves of the models are shown in Figure 8.

Figure 8.  Model training curve and accuracy curve.

DownLoad: Full-Size Img PowerPoint

5.3.2.   Ablation study of multimodal fusion

To validate the effectiveness of multimodal fusion, we designed ablation experiments utilizing four distinct models: the single-modal EEG_MHA-GCN, the single-modal EEG_ViT, the single-modal Audio_ViT, and the multimodal MHA-GCN_ViT.

(1) EEG_MHA-GCN: This model performs depression classification using single-modal EEG signals. After preprocessing, discrete wavelet features are extracted and combined with the MHA-GCN model.

(2) EEG_ViT: This model uses single-modal EEG signals. Time-frequency features are extracted from EEG signals and processed by the vision transformer for depression classification.

(3) Audio_ViT: This model utilizes single-modal audio signals. Mel-spectrogram features from the audio signals are processed by the vision transformer for depression classification.

(4) MHA-GCN_ViT: This multimodal model integrates both EEG and audio signals through decision-level fusion for depression classification. The experimental results are presented in Table 4.

Table 4.  Results of ablation experiments for single and multimodal modalities.

Model	Accuracy (%)	Precision (%)	Recall (%)	F1 Score (%)
EEG_MHA-GCN	66.45	78.56	66.46	68.55
EEG_ViT	74.05	73.84	75.28	67.38
Audio_ViT	62.30	60.83	62.57	63.30
MHA-GCN_ViT	89.03	90.16	89.04	88.83

---

 | Show Table

DownLoad: CSV

The results of the multimodal ablation experiments demonstrate that the MHA-GCN_ViT model achieved an accuracy of 89.03%, precision of 90.16%, recall of 89.04%, and F1 score of 88.83%. This performance can be attributed to the comprehensive integration of features from multiple modalities, which provides richer and more comprehensive information, enhancing both the data representation and the model's understanding capabilities. The effectiveness of multimodal fusion is thus confirmed. Furthermore, the MHA-GCN model, which combines multi-head attention and graph convolutional networks, effectively learns and represents the spatial features of EEG channels, capturing the inter-channel relationships and significance of EEG signals. This approach allows the model to better comprehend the structural characteristics of EEG signals, improving feature representation and the model's understanding capabilities. Decision-level fusion of EEG and audio signals at the decision layer leverages the complementarity and richness of multimodal information, enhancing the model's overall understanding and judgment capabilities. By integrating cross-modal information, the model can more comprehensively consider relationships between different modalities, thus improving the accuracy and reliability of depression detection.

5.3.3.   Comparison with other models

To evaluate the advanced nature of the proposed model, comparative experiments were conducted on the MODMA dataset with other models, and all results are sourced from the original papers.

MS2-GNN Model ^[19]: This model constructs intra-modal and inter-modal graph neural networks for EEG and speech signals after passing them through LSTM networks. The features are then fused and classified using attention mechanisms.

HD_ES Model ^[39]: This model extracts features from EEG signals using 1DCNN-LSTM and a vision transformer, and features from speech signals using a vision transformer. These features are then fused and classified.

Fully Connected Model ^[43]: Features from EEG and speech signals are extracted separately and then fused. Classification is performed using a deep neural network (DNN).

HD_ES ^[39]* is the experimental environment used in this study. The results were obtained under the same training and test datasets.

MultiEEG-GPT Model ^[44]: The MultiEEG-GPT model involves preprocessing EEG signals through filtering and constructing a topology graph. These EEG features, along with features extracted from speech signals (e.g., MFCCs, mel-spectrogram, chroma STFT), are fed into the GPT-4 API for feature learning and classification. MultiEEG-GPT-1 refers to the classification results under zero-shot prompting, while MultiEEG-GPT-2 refers to the classification results under few-shot prompting, as shown in Table 5. The results in the table indicate that the proposed model achieves improvements over the $MS^2-GNN$ model on the MODMA dataset, with increases of 2.54% in accuracy, 7.81% in precision, 1.54% in recall, and 3.98% in F1 score. Compared to the HD_ES* model, the proposed model shows improvements of 2.36% in accuracy, 2.95% in precision, 2.36% in recall, and 0.94% in F1 score. Compared to the Fully_Connected model, the proposed model achieves a notable enhancement of 12.72% in accuracy. These improvements are attributed to the proposed model's use of more comprehensive and effective feature representation methods, which better capture the inherent information and features of the data. This results in superior expressiveness and adaptability, thereby enhancing the model's performance and generalization capability. Consequently, the proposed model demonstrates better results in the experiments and outperforms the baseline models, confirming its effectiveness.

Table 5.  Comparative experimental results of different models.

Model	Accuracy (%)	Precision (%)	Recall (%)	F1 Score (%)
MS2-GNN [19]	86.49	82.35	87.50	84.85
HD_ES [39]	97.31	97.71	97.34	97.30
HD_ES [39]*	86.67	87.21	86.68	87.89
Fully_connected Model [43]	76.31	-	-	-
MultiEEG-GPT-1 [44]	73.54±2.03	-	-	-
MultiEEG-GPT-2 [44]	79.00±1.59	-	-	-
Ours	89.03	90.16	89.04	88.83

---

 | Show Table

DownLoad: CSV

6.   Conclusions

This paper proposes a multimodal depression detection model based on EEG and speech signals, utilizing a graph-based approach to model EEG channels and construct a brain channel network structure to capture the spatial features of EEG signals. To enhance depression detection performance, the model integrates speech signals for comprehensive assessment. Through comparative experiments and multimodal ablation studies, the effectiveness of the MHA-GCN and decision-level fusion have been demonstrated. The model's performance metrics have been shown to outperform those of baseline models in comparison with other advanced models.

Model advantages: The strength of our model lies in the MHA-GCN_ViT, which effectively extracts and integrates the time-frequency and spatiotemporal features of EEG signals, as well as the time-frequency features of speech signals. This enhances the model's ability to leverage information from different data sources. Additionally, the use of the GCN and vision transformer enables the model to capture the complex structures and dependencies within EEG and speech signals. Furthermore, MHA-GCN_ViT demonstrates strong performance and robustness in the task of depression detection.

Model limitations: Current issues include assessing whether the model is suitable for different degrees and types of depression, as well as understanding how individual differences such as age, gender, and cultural background might impact model performance. The MHA-GCN_ViT combines complex deep learning architectures such as the GCN and ViT, resulting in high computational complexity. In resource-constrained scenarios, such as on devices with limited computing power, the model may face significant computational burdens, potentially affecting real-time performance. Additionally, the model's generalization performance in other datasets or real clinical environments needs further validation to ensure its stability and reliability.

Future research directions: Based on the research by Khare et al. ^[45], we have identified that model interpretability and uncertainty quantification are of significant importance for emotion recognition, as well as for its application areas such as depression detection. Therefore, our future research direction will focus on investigating the individual differences that contribute to model variability, enhancing the model's generalization and robustness across different domains, such as anxiety, schizophrenia, and other diseases, as well as across various datasets. We also aim to improve the model's interpretability and uncertainty quantification. Furthermore, Singh et al. ^[46] developed a "Tinku" robot, which employs advanced deep learning models to assist in training children with autism, demonstrating the promising potential of these models in the field of disease treatment. Additionally, we will explore the application of our model in real-world clinical settings, developing corresponding tools or platforms to promote the practical application and dissemination of the model in depression detection and treatment ^[47].

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This work is supported by the Doctoral Research Start-up Fund of Shaanxi University of Science and Technology (2020BJ-30) and the National Natural Science Foundation of China (61806118).

Conflict of interest

The authors declare there is no conflict of interest.