Abbreviations: ABS: acrylonitrile butadiene styrene; AUT: Austria; DM: dry matter; DDT: dichlorodiphenyltrichloroethane; EU: European Union; FTIR: Fourier-transformation infrared spectroscopy; GC-MS: gas chromatography coupled with mass spectrometry; GER: Germany; HCH: hexachlorocyclohexane; HDPE: high-density polyethylene; LDPE: low-density polyethylene; MEPs: meso plastic; MP: micro plastic; NIR: near infrared; PA: polyamide; PAH: polycyclic aromatic hydrocarbons; PAN: polyacrylonitrile; PC: polycarbonate; PCB: polychlorinated biphenyl; PE: polyethylene; PES: polysulfone; PET: polyethylene terephthalate; PMMA: poly(methyl methacrylate); PP: polypropylene; PS: polystyrene; PS: polystyrene; PU: polyurethane; PVA: Poly(vinyl alcohol); PVC: polyvinyl chloride; SBR: styrene-butadiene rubber; TDS: thermal desorption; TED: thermal extraction desorption; TEM: Transmission Electronic Microscopy; TGA: thermogravimetric analysis; THF: tetrahydrofuran; UV: ultraviolet
1.
Introduction
Within a time span of 13 years (2004 to 2018) the production of plastics steadily increased–globally from 224 to 360 million tones and in Europe from 60 to 64 million tones [1,2]. This rise in plastic production is accompanied by a similarly increased amount of plastic waste. About 26 million tones plastic waste are produced each year in Europe and only 6% are collected for recycling, 31% are landfilled and 39% are incinerated. It has to be assumed that the residual 24% end up in the environment, where it accumulates in nearly all habitats [5] and causes severe damages [6]. If these current trends continue, a total of 12,000 megatons of plastic waste will have ended up on landfills and in the environment by the year 2050 [4,7].
1.1. Definition of microplastic
The term “microplastic” was used the first time in the year 2008. Until now it is just a rough orientation because it is based on physical properties, formal or pragmatic considerations, including e.g., shape, size, material, delimitation to nanoparticles and measuring techniques. [8].
Depending on the reference the definition of microplastic varies–which indicates the classification as an artificial system. In the past, the definition included any solid, water insoluble plastic particle in a size between 0.001 mm and 1 mm and is deriving from consumer products, but did not cover rubber and fibers [9].
A more recent definition includes rubber and synthetic fibers, since the term plastic (defined as synthesized, not metallic polymer with a high molecular weight, being assembled of recurring monomers) already covers rubber, elastomers as well as textile and technical fibers [10]. A further definition says that plastics are a subetaoup of polymers, which only include thermoplastics (e.g., polypropylene (PP), polyvinylchloride (PVC); can be softened and remolded) and thermosets (e.g., polyurethane (PU), epoxy and phenol resins, polystyrene (PS); sometimes also called duroplastics, cannot be softened by heat or pressure once they are formed). Nevertheless, recent research covers elastomers (e.g., rubber) and products based on synthetic polymers as well as modified natural polymers in the definition [11,12].
Other classifications are based on the particle sizes: usual ranges are 5–1 mm (large microplastic), 1–0.5 mm, 0.5–0.1 mm, 0.1–0.05 mm, 0.05–0.01 mm, 0.01–0.005 mm and 0.005–0.001 mm, which are linked to the numbers of particles that make up a total weight of 14.13 mg [11]. Frequently, microplastic particles are defined to be smaller than 5 mm or between 5 mm and 0.001 mm. Furthermore, the subdivision into big (5–1 mm) and small microplastic (1–0.001 mm) is often used. The term nanoplastic is used for particles smaller than 0.1 µm [13], being below the range of small microplastic. [10].
The definition of microplastic is not focused on environmental aspects, neither is it limited to substance groups with human-and ecotoxicological relevance, nor upper and lower limits exist [8].
1.2. Microplastic emission sources
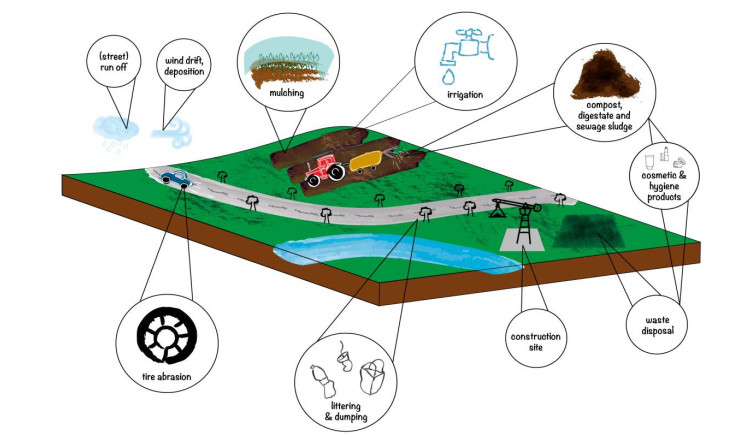
Microplastic can be categorized with regard to its origin into type A, type B and secondary microplastic. While type A is part of a product i.e., friction bodies in cosmetics or powder for laser sintering; type B arises during the utilization of products i.e., abrasion from tires or synthetic fibers released during washing of textiles. Secondary microplastic occurs through fragmentation of macroplastic, whose origins are, among others, mainly landfills, waste treatment, agricultural applications and littering. In the environment, plastic is fragmented into smaller pieces due to temperature changes and freezing, UV radiation, microorganisms, oxidation or mechanical stress [4]. The two ways, how plastic gets into the environment, can be summarized, from a personal point of view, as intended and unintended (Figure 1). Agricultural applications and additives in industrial products are examples for intended release [14], while unintended release includes littering, losses, dumping and tire abrasion, respectively. Often overlooked, packaged food waste which ends up in the organic waste bin contributes to the unintentional release of microplastic in soil [15].
Compost contains plastic due to incorrect disposal of plastic into the organic waste bin and since the removal through manual sorting and sieving before and after composting is insufficient. Digestate arises from anaerobic treatment of energy crops and agricultural residues but also of food waste, expired food, organic waste and residual or municipal waste. The packages are removed before the organic content enters the biogas plant, but plastic residues still remain and are then present in the digestate. A study focusing on organic fertilizers in Germany showed that 35 billion to 2.2 trillion microplastic particles larger than 1 mm are released into environment per year by organic waste treatment plants (composting plants, biogas plants). Digestate deriving from the treatment of municipal organic waste contains the highest number of particles (895 particles kg−1 DM), while high-quality compost shows the lowest numbers (25 particles kg−1 DM). The enrichment of non-digestible material and therewith of microplastic is much higher in anaerobic than in aerobic treatment. Reasons are the higher mass reduction in anaerobic systems [16] and maybe the fact that digestate is partly recirculated in the biogas plant. Additionally, accumulation and size distribution of microplastic may be affected by the way digestate is treated [17].
In wastewater treatment plants 90% of the microplastic–fibers of textiles, particles of cosmetic and hygiene products [13,18]–are transferred into sewage sludge [19] and remains there independent from the treatment procedures [18]. It mostly consists of nylon, polyester and acrylic fibers. Other sources in sewage sludge are water soluble, persistent polymers, which are for example used as transparent foils for dishwasher tabs [15]. In Europe, one third of the sewage sludge is used as fertilizer on agricultural land and 40% are landfilled [10]. While the first is a direct source of contamination, the second may leach microplastic in the environment in a slow and non-predictable way.
Especially in those locations where not enough water is available, treated sewage water is often used for irrigating field crops. Fibers from textiles and hygiene products are in such a case directly applied to the soil. On the other side, fields may be flooded by rivers, which transport and deposit plastic debris of all sizes on the soil [10]. The release of significant amounts of microplastic directly on the soil and the mechanical filtering effect are the main reasons for the 4-to 23-fold higher accumulation of microplastic in terrestrial compared to aquatic systems [8,13]. Besides floods, runoff and deposition from the atmosphere are important transport mechanism which may repeatedly lead to irregular pollution hotspots [13,19].
In Austria and in Germany, as in the whole EU mainly type B microplastic (89%) is emitted (Table 1), which primarily includes emissions from traffic, infrastructure and buildings (62%) followed by private consume and by commercial end-users (24%) and production industry (14%). Littering in Austria is estimated to account for just 0.5% of the total plastic waste, due to an efficient waste management system [8,10].
Independent from the way we classify microplastic, it would not accumulate in the environment if it would not had been released. While the unintended release is almost impossible to avoid as it requires drastic measures, the intentional release can be reduced more easily: Germany, for example, has introduced incentives to increase the collection of both, single-use and reusable PET bottles. Many other European countries have already released regulations to end production and distribution of single-use plastic products, following the EU single-use plastic directive (2018/852/EC) [4,8,15]. However, there is generally no refund system established for other types of plastic packaging and therefore motivation to reduce littering and illegal waste deposition remains is low for those.
1.3. Legislation regarding plastic release
The circular economy strategy of the EU aims on closing nutrient cycles and minimizing wastage of valuable resources. For this purpose, organic waste is used directly or preferably after aerobic or anaerobic degradation to compost or secondary fertilizer (digestate). [23]
In the EU [24] as well as in the US [25] the application of sewage sludge is regulated, depending on their content of pathogens, heavy metals and harmful substances. There are thresholds and limits for plastics among the other unwanted substances [19].
Current national legislation in Austria and Germany covers nutrient composition (e.g., nitrogen, phosphorus, potassium) and the related application limits for organic fertilizers in the same way as for mineral fertilizers. Upper limits of impurities, such as glass, metal and plastic apply as well. The limits concerning plastic particles aim towards those larger 1 mm, 2 mm and 20 mm, this means small microplastic and nanoplastic are not covered. The upper limits depend on the field of application as well as on the according regulation. In Austria the upper limits of plastic particles larger 2 mm and 20 mm for agriculture are 0.1–0.2% DM and 0.02% DM, respectively. The lower value (0.1%) is allocated to the fertilizer directive [26], while the larger values (0.2%) originates from the compost directive [27]. For landscaping, conservation and re-cultivation layers on landfills the upper limits of plastic particles larger 2 mm and 20 mm are 0.4% DM and 0.04% DM, respectively [27]. Currently only the province Vorarlberg sets upper soil limits and precautionary values by a regional regulation which is in force since 1 January 2019 [28]. The upper soil limits for plastic particles larger 1 mm are 200 mg kg−1 DM and 10 cm2 m−2 and include plastic as well as rubber and composite materials. The soil precautionary values for this particle size are 100 mg kg−1 DM and 5 cm2 m−2. Exceeding the soil precautionary values leads to limited application. More specifically, compost which is applied to soil must not contain plastic particles larger 25 mm, particles larger 2 mm are limited to 0.1% DM and 15 cm2 L−1. Reasons to issue this regulation were plastic particles in various sizes on fields after applying farm manure.
Plastic residues are considered to be unwanted compounds in solid and liquid waste such as digestate, compost and wastewater. Limits for the tolerable amounts exist for both, although identification and characterization is not mandatory. The category “filterable substances” does include plastic particles without explicit upper limits but counts towards the total amount of solids in industrial wastewaters. When industry wastewater is discharged into the sewer, no upper limits apply as long as the sewer function is not negatively affected [10,29].
In Germany the situation is similar: the upper limits for impurities, including plastic, are set at 0.4% DM for particles larger 1 mm for waste paper, cardboard, glass, metals and ductile non-deformable plastics and 0.1% DM for other not degradable materials. These limits are applied for fertilizer and manure, soil additives, growing media and plant growth stimulants [30]. For particles larger 2 mm the upper limit of 0.5% DM must not be exceeded, which includes glass, plastic and metal [31]. All these mentioned directives and regulations aim towards visual appearance by counting particle of a minimum size but do not cover microplastic nor do they consider possible effects on soil [15].
It is known for a long time that single use products make up the major share of plastic waste and litter [7]. For example, already in 1994 the European packaging regulation (94/62/EC) [32] clearly mentions measures to avoid waste by a priority list, which consist of prevention, re-use, recycling and recovery in descending order.
The most recent of the legal initiatives of the EU is the directive 2019/904/EC [33]. It prohibits placing single use plastic products and oxo-degradable plastics on the market. This directive includes the so called extended producer responsibility, which encourages member states to ensure that producers of single use plastic products cover the costs for cleaning up, transporting and treating litter resulting from those products. In addition to this directive the Austrian beverage industry has voluntarily undertaken several steps to reduce plastic waste. These steps include the wish to increase the market share of reusable packaging and campaigns to raise public awareness against littering [34].
2.
Microplastic in soil
2.1. Resilience of released plastic
Synthetic polymers were invented and designed to best possible withstand a re-integration into the biological cycle. The commonly communicated retention time of plastic (250–500 years) is just valid at laboratory conditions, where no energy and carbon source other than plastic is available for the degrading microorganisms. But in soil, in sediment and in sewage sludge many other organic substances are present that can be utilized more easily than the plastic polymers, making them the least attractive substrates in the habitat. Microorganisms always prefer to consume the most easily within all available nutrient sources (known as the principle of “diauxie” [35]) and step by step, substance by substance, they pass over to decompose the more hardly degradable substances. This means, persistent polymers will only then be degraded when no more organic substance like plant residues or humus is available [15].
2.2. Environmental impact of microplastic
All of the currently published impacts of plastic residues on physical, chemical and biological properties of soil are assumptions [15]. However, there is no evidence about a positive impact of plastic on soil: the polymers have no water holding capacity, no ion-exchange capacity, no soil particle binding, cannot act as carbon source to support microbial growth and do not contain mineral nutrients. Among the rare findings, polyacrylic fibers negatively impact water stable agammaegates and contribute to the formation of soil clumps; finally leading to erosion [13,36].
For that reason, microplastic is not beneficial for soil and is disparate to the benefits of organic carbon applied with compost [37].
With the fragmentation of (formerly) bigger pieces into microplastic, the probability to enter deeper soil layers increases. Further transport by wind and water may be reduced while biological transport (in the digestion tract of soil organisms) becomes an important factor. Longer dwell times of the microplastic particles result in longer exposure times for the various affected soil organisms [4,13,18,19].
The above mentioned changes in physical soil properties do indirectly affect all soil organisms. For example, a reduced water holding capacity increases water evaporation and reduces the available amount of water for plant growth. Reduced plant growth results in reduced amounts of root exudates and in reduced microorganism growth which results in reduced feed for grazing organisms. A small change of one soil characteristic may have big impact on the whole food web and may even become economically remarkable via reduced soil fertility [37,38].
Other effects are directly caused by chemicals, which are leaching from the plastic matrix or were adsorbed at their hydrophobic surfaces. Among the better known compounds are e.g., plasticizers like bisphenol A and phthalates, which are just loosely incorporated in the polymer structure and will leach out over time. Heavy metals and polychlorinated biphenyls (PCBs), polycyclic aromatic hydrocarbons (PAHs), organochlorine pesticides (e.g., DDT, HCH) and non-volatile organochlorines from PVC and other chlorinated substances can adsorb at the particles surface. [13,39]
Preferably animals and to a lesser extent also plants are affected by these compounds. Earthworms, nematodes, collembolan, isopods and mites directly ingest small microplastic particles [18] while plants can take up dissolved components, such as phthalates [19]. Hardly any information is available about the direct uptake of microplastic by plants. However, it is assumed that nanoplastics can pass the cell membrane (independent from plant or animal) due to their size, structure and properties and can be transported by the organisms flow systems (root, xylem, blood circulation) and can even reach and influence sub-cellular structures, such as transpiration, water and lipid fractions, plasma membrane potential, tonoplast potential, cytoplasm and vacuoles. [18].
Finally, nanoplastic, plastic additives and adsorbed substances not only influence the viability of microorganisms, animals and plants but also enter on this way the food chain and affect human health [13,18,19].
3.
Quantitative measurement of microplastic
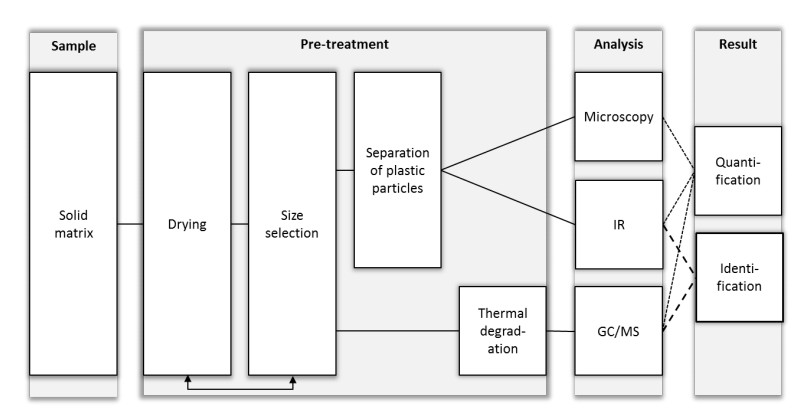
Until now, no standardized methods exist to detect, identify and quantify microplastic in soil. However, the need for comparable data, gained by standardized sampling, sample extraction and quantitative measurements is mandatory for any legislative work. Current methods are mainly categorized into thermo-analytical and spectroscopic measurements. Thermo-analytical methods include pyrolysis or thermal extraction desorption, which are combined with gaschromatography and mass spectrometry (Pyr-GC-MS, TED-GC-MS). Thermal extraction desorption (TED) is a combination of thermogravimetric analysis (TGA) and thermal desorption (TDS). Spectroscopic measurements include analysis via Raman or Fourier-transformation infrared spectroscopy (FT-IR), with different ranges of wavenumbers. The results of all the above methods are given in weight microplastic per sample weight (mg kg−1). Additionally, light microscopy methods are used, which result in particle numbers (per sample weight or per volume). Figure 2 gives an overview of analyzing principles and necessary sample preparation steps, which are currently used to identify microplastic in soil, compost, sewage sludge, digestate and other organic wastes [15]–a comprehensive overview with further details is provided in the supplementary materials.
3.1. General requirements for microplastic analysis
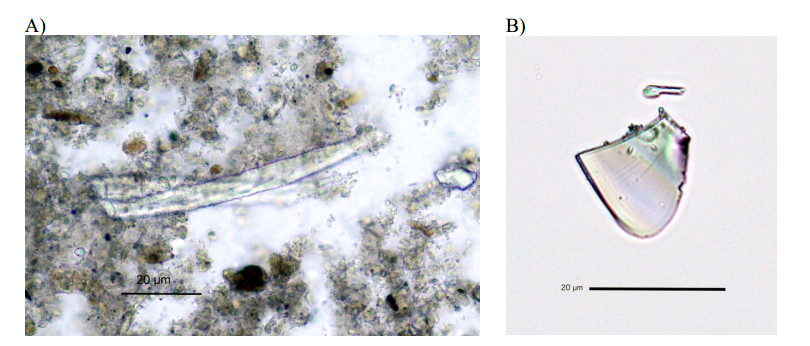
When analyzing microplastic, “plastic-free” conditions are mandatory during all steps (sampling, sample preparation, detection, etc.) to avoid contamination [11]. This is especially important for those sample types which contain only small numbers of plastic particles, such as river-or ground-water. Examining microplastic in solid matrices is challenging, due to their inhomogeneous nature (mixture of organic and inorganic materials of widely spread particle sizes, and layered structure) [40]. This makes the necessary separation of plastic from matrix particles (in case of spectroscopic measurements) difficult. Some materials have typical colors and shapes, while others look and behave similar. A visual differentiation between organic matrix and plastic components or degradation products therefore requires long training. Figure 3A shows how plastic and matrix particles are merged in a soil sample and gives an idea of the challenging task to visually distinguish between these particle types.
One of the first steps is to select the particle size of interest, independent from the quantification method. For this purpose samples are sieved, either before or after drying. This mainly depends on the water content of the sample.
Based on the requirements on the subsequently conducted analysis, it is often necessary to separate plastic from matrix; preferably based on densities. Subsequently, floating plastic is collected and washed [41]. Unfortunately, plastics with higher densities (e.g., PET, PVC) are lost. Another option is the chemical removal of organic matrix components by treatment with HNO3 or H2O2. In case of HNO3 particles of ABS, PA, and PET are also affected [11,42,43].
Samples need to be homogenized by either cutting or milling for some types of analyzes [40,44]. Especially when mills are used, the different characteristics of matrix and plastic particles need to be considered, since the later are often flexible and resist the grinding process [45].
Thermo-analytical methods are generally fast and simultaneously detect either all (Pyr-GC-MS) or selectively those components which can be absorbed and desorbed (TED-GC-MS). The determination limit is mostly below 1 µg kg−1. The methods require little sample preparation but have high prerequisites for a dust-free environment (TED-GC-MS). The procedures are destructive and not able to determine particle sizes and numbers. Furthermore, chemical interferences may occur and measuring times are sometimes long [11,40,44,46,47].
Spectroscopic measurements are fast, non-destructive and, in case of Raman, also contactless options. The determination limits for µ-Raman and FTIR are particles with a minimum size of 1 or 10 µm, respectively. The needed sample amount is in the range of µg to mg. These methods require a dust-free environment, complex sample preparation and are not able to quantify amounts or concentrations. Furthermore, in case of µ-Raman chemical and spectroscopic interferences may occur [11,46].
The advantages of microscopic methods are that they are simple, low-cost and that different shapes (fibers, fragments, films pellets) can be determined. The main disadvantages are that plastic contaminations cannot be quantified and their identification is difficult which can partly be overcome by comparing a sample with reference materials (Figure 3B) [15,41,48].
Method specific drawbacks can be avoided by combining microscopic, spectroscopic and thermo-analytical methods. For example, the combination of Pyr-GC‑MS and TEM (Transmission Electronic Microscopy) allows to identify and quantify microplastic in soil [47]. Another example is the examination and sorting of particles under the microscope and identification with Raman spectrometry, FTIR or thermo-chemical measurements [4], such as the examination of particles with a stereo microscope and subsequent analyses with µ-FTIR [41].
3.2. Methods used for investigating solid samples from Austria
We adapted sample pretreatment on the consistency (granular solid, pasty solid, liquid) and on the estimated content of organic and inorganic solids (mainly by color and sample type).
Soil and compost samples (granular, high content of inorganic solids) were sieved (<1 mm) and elutriated with deionized water in a weight based ratio of 1:10 (sample: water). Sewage sludge samples (high in filamentous organics) were diluted with deionized water to obtain a fluid consistency; a weight based ratio of 1:10 (sample: water) was aimed at. For practical reasons, all samples were weight into centrifuge tubes, the amount was recorded and tubes were balanced pairwise (for the later centrifugation) with water. This led to non-integer dilution ratios. None of the digestate samples required dilution with water or any other pretreatment.
Soil, compost and sewage sludge, all three are containing high amounts of disturbing matrix substances and had to be pretreated by heating at 95 ℃ for 4 hours in presence of 10 ml 30% H2O2 solution. Colored organics were oxidized and to filamentous agammaegates of sludge samples were disrupted by the procedure. Evaporated water was replaced on weight basis (after H2O2 addition, before heating). Compost and sewage sludge samples were ready for microscopy after this step.
Soil samples required a density separation with either saturated CaCl2 solution (1.35 g cm−3) or with saturated ZnCl2 solution (1.45 g cm−3). The solid salts (CaCl2, ZnCl2) were directly added to the H2O2 treated, suspended samples based on the calculated amount of water. The salts were fully dissolved and the tubes were then put into the ultra-sonic bath at 25 ℃ for 5 minutes to break up agammaegates. Centrifugation at ca. 3000 g for 15 minutes separated the mineral particles from the floating light fraction, which included all plastic. The upper half of the tube content was transferred into a new tube (via Pasteur pipette) and filled to the original volume with deionized water–therefore re-suspending the plastic without changing the dilution rate.
The amount of 15 to 20 µL treated sample suspension was inspected and counted in the light microscope at 100x and at 400x magnification (to cover big and small particles). Digital images were taken as backup for later revision–mainly to discuss uncertainties in the manual identification, which proved to be a valuable learning procedure.
We are aware of the high failure rate and subjective decisions, whether a certain particle is plastic or not [49]. To reduce the percentage of misjudged particles we started to create a reference database with microscopic images from natural and synthetic fibers and from mechanically broken pieces from the most common plastic types (LDPE, HDPE, PET, PP, PES, PC, PS, PVC, PA), from different types of hair and from typical silt and clay minerals. Additionally, we have been and we continue collecting published photos.
3.3. Method variants that did not improve the procedure nor the result quality
Variations of the microscopy technique were tested, such as dark field and phase contrast illumination, counting in the grid of a Thoma chamber with and without color staining of certain plastic types (such as polyester or polyethylene, etc).
Dyeing of plastics with commercially available products failed because of the specificity of those dyes and because of the comparably low color uptake of microplastic particles. The resulting coloring was pale and therefore not helpful for counting.
Exceptional high numbers of plastic particles were counted in all sample types when CaCl2 was used for density separation compared to ZnCl2 solution. We measured high plastic particle counts in pure CaCl2 solutions (without sample), independent from the brand and purity grade of the salt. This was not the case for ZnCl2. We will not use CaCl2 any longer and all analysis already done have been repeated with ZnCl2 separation.
Filtering the floating layers after density separation resulted in significant losses due to adhesion of the particles at the filter housing and due to formation of a stable foam in digestate and compost samples. For that reason, digestate and compost samples should not be density separated.
Counting attempts via Thoma chamber failed, since some particles or agglomerates were bigger than the chamber high and made the quantitative counting impossible.
Heating the sample on the glass slide after visual inspection (similar to Kofler melting point determination [48]) can improve the detection rate and the counting. At least the thermoplasts can clearly be differentiated from minerals based on their melting behavior. Knowing the melting point may lead to an identification of the plastic type as well. Although not error-free, this attempt is simple and cost effective. However, we did not evaluate the heating procedure and are currently not able to provide a deeper insight about appearance of certain plastic types in certain sample types.
3.4. Results from soil, compost, sludge and digestate samples
We investigated 16 compost, 11 soil, 12 digestate and 6 sewage sludge samples from different locations in Austria. Method development and treatment variations were tested and optimized with these samples. Table 2 provides an overview of the results obtained with the optimized treatment and analysis procedures. Some of the samples were analyzed in three replicates with the optimized procedure, others were analyzed only once per variation; failed procedures (classified as outliers according to ANOVA statistics) are not presented here.
The average number of plastic particles of 16 compost samples (a total of 22 analysis) was 15.4 Mil per kg sample, with 5.2 Mil minimum and 42.8 Mil maximum. The average of 11 soil samples (17 analysis in total) was 12.7 Mil plastic particles per kg sample, with 3.1 Mil minimum and 25.6 Mil maximum. The average of 12 digestate samples (a total of 18 analysis) was 7.1 Mil plastic particles per kg sample, with 0.6 Mil minimum and 38.7 Mil maximum. The average number of plastic particles found in 6 sewage sludge samples (12 analysis in total) was 3.0 Mil per kg sample, with 0.4 Mil minimum and 6.2 Mil maximum.
The total numbers of plastic particles found in those solid samples was surprisingly high. Deviations were much higher than those from other types of chemical measurements but were acceptable when considering that plastic particles will never be homogeneously distributed in solid (powdery or paste-like) samples.
Although, the methods cannot be considered to be final and quality parameters, such as repeatability and precision cannot be provided now, our results are a first data set for a comparably simple and rapid investigation procedure. The microscopic method does not need costly instrumentation and results can be obtained within 24 hours.
3.5. Outlook for upcoming method improvement
Reliable, simple and fast analyzing procedures are required for routine investigations. In contrast to many other authors, we are convinced that it is more important to quantify the amount of plastic than to identify the particle material. It is highly improbable to track back the contamination source from the finding of a certain microplastic particle. We doubt the necessity to know the origin of the plastic particle to estimate the effect of the contamination on a certain ecosystem.
A reliable routine method has to be applicable to various matrixes. For this purpose we use a light microscope (Olympus BX43,100x, 400x magnifications) connected to a camera (Canon 1100D) to detect microplastic in agricultural soil, in soil from public areas, in solid and liquid digestate, in sewage sludge and in compost. Our simple method allows the characterizing and counting of particles down to 5 µm. Possible disadvantages of the procedure are, it requires attention, training and some experience.
The next step in our approach is to improve the separation of plastic from matrix particles, in order to simplify their counting and analysis. An obvious option is the destructive removal of the organic matter with hot HNO3 and other oxidizing agents [41,43,50,51]. We will evaluate in how far plastic particles will still be detectable, how they keep their shapes and how the treatment will influence their micro-spectroscopic properties.
4.
Conclusions
We expect the plastic contaminations to have negative, at least no positive effects in soil. In accordance with the precautionary principle, action is urgently needed to avoid further accumulation of resilient plastic in the environment. Moreover, the effort to analyze solid environmental matrices is quite high and control samples or blanks are no longer available, as the contamination is ubiquitous.
We need to continue with the standardization attempt about definition of microplastic, taking all applications, plastic types like rubber, water soluble plastics and environmental effects into account. Standardized detection and quantification methods for microplastic in solid matrixes (soil, compost, sewage sludge, digestate) need to be developed and improved, at least to provide data for comparison with reports about plastic in marine samples. This would allow evaluation and comparison of contaminations and types of emissions on a global scale. Finally, legislation must be provided a database for upcoming regulations and for decision on measures to avoid further environmental pollution. It is now time for actions.
Acknowledgements
This work is freely financed by the University of Natural Resources and Life Sciences, Vienna. We gratefully thank Nina Hasselhahn of Hani Design, for creating the graphical overview. All authors declare no conflicts of interest in this paper.
Conflict of interest
The authors declare no conflict of interest.









 DownLoad:
DownLoad: