1.
Introduction
Cloud computing has revolutionized the IT industry, bringing benefits such as flexibility, scalability and cost-effectiveness. Virtualization is a crucial technique in cloud computing, enabling the transcendence of temporal and spatial boundaries. By dividing a physical computing resource into multiple same-function virtual machines (VMs), this technique enables the on-demand deployment of computing resources by VM migration [1]. Regrettably, virtualization has introduced new hidden dangers that are increasingly targeted by malware attacks [2]. These vulnerabilities can lead to significant harm to individuals and organizations, in addition to financial losses, and even pose a potential threat to human life [3]. Therefore, it is crucial to explore effective measures for safeguarding virtual environments against malware attacks in the cloud.
With the rapid development of cloud computing, the problem of malware propagation in cloud environments has become increasingly prominent [4]. Malware in cloud environments usually has the characteristics of large scale, fast propagation speed and being difficult to trace and control. To this end, researchers have proposed many related works for controlling the propagation of malware in cloud environments. These works mainly include malware detection, malware propagation path analysis and malware propagation control.
Malware detection is a crucial technology for controlling the spread of malware in cloud environments. Currently, researchers used feature-based and machine learning-based methods to detect malware [5]. By analyzing the code and behavior characteristics of malware, researchers can effectively detect it [6]. Malware propagation path analysis is another important aspect for understanding the propagation mechanism and rules of malware in cloud environments. Researchers mainly used graph theory-based and data mining-based methods to analyze the propagation path and rules by constructing a malware propagation graph [7,8,9]. Additionally, malware propagation control is a key technology for controlling the spread of malware in cloud environments. Researchers mainly used network security protocol-based methods for malware propagation control [10]. However, these methods can only play their maximum role after the emergence of malware, with significant lag in development and inability to predict malware propagation in cloud environments.
Noting the attractive analogies between malware and its biological counterparts, some epidemic dynamics of malware, which are devoted to capturing the way that malware spreads over a network so as to contain its diffusion, have been proposed, such as the SEIQR model [11], the SIR1R2 model [12], the SE1E2IQR model [13], the SIWQ model [14], the SIAR model [15,16], the SID model [17], the DDSEIR model [18], the SEIR model [19], the SEIRS-V model [20], the SEIRS-Q model [21], the SEIS model [22], the VCQPS model [23], the game model [24,25,26,27] and the multi-agent model [28]. However, these models are not specifically designed for cloud environments. On this basis, Abazari et al. [29] explored the effect of anti-malware with infectious nodes in cloud environments and proposed an SPI (susceptible-protected-infected) model, but they assumed that all the machines entering the cloud are susceptible, which does not fit the practical situations. In order to make up for the deficiency and based on the SPI model, a new dynamical model, the susceptible-infected-protected-susceptible (SIPS) model was proposed in [30], but this model cannot describe the cost and effectiveness of malware control.
In reality, it is necessary to consider the input cost and corresponding effects of malware control, and it is impossible to install anti-virus-software-like protection measures for every machine, though every machine must have the same level of protection. Therefore, in this paper, inspired by the above work and discussions, we propose a controlled dynamical model to explore how to effectively contain malware propagation in the cloud by means of optimal dynamic immunization. According to the control strategy and loss definition, we give the optimal control problem of the controlled dynamical model. The optimal analysis is examined theoretically and experimentally. Most importantly, the obtained results indicate the comprehensive effect of the optimal control strategy is the best.
The remaining material of our work is organized as follows: The preliminary knowledge is given in Section 2. Section 3 formulates the controlled dynamical model. The optimal control problem and theoretical analysis are presented in Section 4. Section 5 gives the experimental analysis. Section 6 summarizes this work.
2.
Preliminary knowledge
This section introduces several important lemmas, which are important support for subsequent research work.
Consider the following controlled differential dynamical system
where t0 is the initial time, tf is the terminal time, x is the system state vector, x0 is the state at the initial time of the system, g is the control vector, and G is the admissible control set.
Given the objective functional J(g)=∫tft0L(x,g)dt, the optimal control problem of the controlled differential dynamical system (2.1) can be denoted as:
where Ψ is a positive invariant for the system (2.1).
Now, let us introduce the following lemmas, which can be used to prove the solution existence and the optimality system.
Lemma 1. [31] Consider the optimal control problem (2.2). Then it has optimal control when these six conditions are met.
(i) There is g∈G such that system (2.1) is solvable,
(ii) G is convex,
(iii) G is closed,
(iv) f(x,g) is bounded by a linear function in x,
(v) L(x,g) is convex on G, and
(vi) L(x,g)≥c1‖g‖ρ2+c2 for some ρ>1, c1>0 and c2.
Lemma 2. [31] Suppose that g∈G is an optimal control of the optimal control problem (2.2), x is a solution of the controlled differential dynamical system (2.1). Then there is Φ so that
where H(x,g,Φ)=L(x,g)+ΦTf(x,g) is the Hamilton function of the optimal control problem (2.2).
The system composed of (2.1) and (2.3) is the "optimality system" of the optimal control problem (2.2). According to this system, we can get some candidate solutions of (2.2). This can narrow the search scope of the optimal solution, thereby accelerating the search effect.
3.
The controlled malware propagation model
This section mainly introduces the background and corresponding mathematical model of malware propagation control in cloud environments.
3.1. Background
With the rapid growth of cloud computing in recent years, security concerns surrounding cloud systems have become increasingly important. One of the most significant threats in cloud environments is the propagation of malware, which can be transmitted from one device to another, causing significant damage, data loss, and system downtime. To effectively mitigate the risk of malware propagation in cloud environments, the most effective and direct method is to develop corresponding antivirus software or patches to detect and kill malware. However, with the continuous development of technology, malware has become increasingly high-end and covert, and antivirus software or patches often lag behind the emergence of malware, making it difficult to predict the long-term evolution trend of malware. Therefore, inspired by biological infectious disease models, establishing a malware propagation model is a relatively effective attempt. However, currently available malware propagation models are generally copied from biological infectious disease models and do not take into account the unique conditions of the cloud environment, such as the cost and benefit of actual resource consumption when detecting and killing malware. It is necessary to develop optimized control strategies that can monitor and control the spread of malware [32]. Optimal control is a mathematical optimization technique that seeks to identify the optimal control inputs that can be applied to a system over time. By leveraging this mathematical technique, researchers can find solutions to monitor and control malware in the cloud environment, improving the security and reliability of cloud computing systems.
3.2. Model formulation
To solve the problem of malware propagation between virtual machines and study the key factors affecting the network propagation of malware, a dynamical propagation model was proposed in [30], whose mathematical expression is represented as:
where η1, η2, and η3 are the entering rate of infected, susceptible, and protected VMs, respectively; μ and γ are the shutdown rate and the migration rate of each VM, respectively; α and α0 are the installing rate and the expired rate of antivirus software, respectively; β and δ are the infected rate and the reinstalling system rate, respectively; At time t, S(t),I(t), and P(t) are the proportions of susceptible, infected, and protected VMs, respectively.
Obviously, this dynamical propagation model of malware does not consider dynamic control factors such as immunity. In the real world, immunizations (including treatment and vaccination) are dynamic, and several security controls can be implemented to protect computer systems from malware infections. These include antivirus software, firewalls, intrusion detection systems (IDS), security updates and patches, and user awareness training. To increase the reality of the developed model, let us take an example of the WannaCry ransomware attack that affected thousands of computers worldwide. This attack exploited a vulnerability in Microsoft Windows operating systems that had been previously patched. Organizations that had not applied the security update were vulnerable to this attack. To prevent such attacks, organizations should ensure that they regularly update their systems with the latest security patches. They should also implement a layered approach to security that includes antivirus software, firewalls, and IDS systems to provide comprehensive protection against malware infections. The scale of malware spread through the network can be controlled by changing the control strategy. To this end, we define two functions (vaccination function and treatment function) with respect to time t, α(t) and δ(t), to replace the constants α and δ in the model (3.1), respectively. Based on the model (3.1), we can obtain the mathematical representation of the corresponding controlled malware propagation model as follows.
with the initial condition (S(0),I(0),P(0))T∈Ψ, where
is a positive invariant for the system (3.2). S, I, P are the abbreviations of S(t),I(t),P(t), respectively, and the latter are the same if not specifically declared.
4.
Optimal control analysis of the model
In this section, we will perform an optimal control analysis of the controlled malware propagation model to determine the optimal control strategy. Firstly, the control strategy and loss definition will be presented. Next, we will formulate the optimal control problem. Finally, we will analyze the solution existence and optimality system.
4.1. Control strategy and loss definition
From the perspective of controlling the spread of malware, we hope to achieve the best control effect at the minimum control loss by the control strategy such as installing anti-malware software or patch.
Let g and L denote the control strategy and loss, respectively. From system (3.2), we can adjust vaccination function α(t) and treatment function δ(t) to implement control of malware propagation. The control loss is related to the control strategy. Specifically, the control loss mainly includes the cost of vaccination and treatment, as well as the losses caused by node infection. Then, the control strategy, at time t, can be described as g(t)=(α(t),δ(t))T, and the control loss can be represented as L(S(t),I(t),P(t),g(t)).
Let α_, ¯α and δ_, ¯δ denote the infimum and supremum of α(t) and δ(t), respectively. Furthermore, α_, ¯α, δ_, ¯δ are positive constants, and 0<α_<¯α<1, 0<δ_<¯δ<1. Let G represent the feasible control set of g, and then for t∈[0,T],
where L2[0,T] represents the Lebesgue square integrable function set.
4.2. Optimal control problem formulation
Let x(t)=(S(t),I(t),P(t))T. Then, L(S(t),I(t),P(t),g(t)) = L(x(t),g(t)), and system (3.2) can be represented by a matrix as follows.
where x(0)∈Ψ, g∈G.
During the time period [0,T], the goal is to find the control strategy g(⋅) that minimizes both the scale of malware spread and the total cost for treatment and vaccination. To achieve this goal, we need to solve the optimal control problem as follows.
subject to system (3.2) or (4.2), where
is the Lagrangian, and p,q>0 are tradeoff factors regarding the control goal of the treatment and vaccination.
Remark 1. Since the control loss mainly includes the cost of vaccination and treatment, as well as the losses caused by node infection, for convenience, we adopt α(t),δ(t) and I to represent the corresponding costs. In Eq (4.4), the control loss L(x(t),g(t)) is not limited to quadratic functions [33,34,35], and the power r (1<r≤2) of L(x(t),g(t)) may be more suitable for the actual situation. Therefore, we take Eq (4.4) for the control loss in this paper.
4.3. Solution existence of optimal control problem
From the preliminary knowledge and Lemma 1, we just need to prove that each condition in Lemma 1 is satisfied. Hence, we can derive the following results.
Lemma 3. There exists g∈G such that the system (3.2) or (4.2) is solvable.
Proof. By putting g≡ˉg:=(¯α,¯δ)T into the system (4.2), the following uncontrolled system can be obtained:
with the initial condition x(0)∈Ψ. Since f(x(t),ˉg) is continuously differentiable, and Ψ is a positive invariant, it is possible to derive the claim from the continuation theorem [36]. □
Lemma 4. The feasible control set G is convex.
Proof. Define
Since (L2[0,T])2 is a real vector space,
Furthermore,
Therefore, the proof is complete. □
Lemma 5. The feasible control set G is closed.
Proof. Let g=(α,δ)T be the limit of G, and gn=(αn,δn)T, n=1,2,⋯, which is a sequence of G. Then,
Based on the completeness of (L2[0,T])2, we can get
Note that
Hence, the closeness of G can be followed from the above observations, and the proof is complete. □
Lemma 6. f(x,g) is bounded by a linear function in x.
Proof. Since
Thus, from the above observations, the proof is complete. □
Lemma 7. L(x,g) is convex on G.
Proof. For g∈G, we can get the Hessian matrix of L(x,g) as follows.
For any t∈[0,T], we can obtain that Hg(L) is a real symmetric matrix with all positive eigenvalues. This implies that Hg(L) is a positive definite matrix. Therefore, from [37], the claimed result follows. □
Lemma 8. L(x,g)≥c1‖g‖ρ2+c2 for some ρ>1, c1>0 and c2.
Proof. Note that
Thus, the claimed result follows. □
According to Lemmas 3–8, we can derive the following important result.
Theorem 1. There exists an optimal control for the optimal control problem (4.2)+(4.3).
Proof. Based on Lemmas 3–8, it can be concluded that all six conditions in Lemma 1 are proven. Therefore, the claimed result can be derived from Lemma 1. □
Remark 2. Theorem 1 indicates there exists an optimal control strategy, which has important theoretical support and practical guidance for the actual control of malware propagation.
4.4. Optimality system of optimal control problem
Although we prove the existence of an optimal control strategy through Theorem 1, it is difficult to give an expression of the optimal strategy, which is not conducive to practical applications. Therefore, we are prepared to find an optimal system that meets the optimal solution, in order to narrow down the scope of searching for the optimal strategy, thereby achieving accelerated and practical results. Therefore, we can get the following theorem, which provides a way to find the optimal control of (4.2)+(4.3).
Theorem 2. Suppose that g∗(t) is an optimal control of the optimal control problem (4.2)+(4.3), and (S∗(t),I∗(t),P∗(t))T is a solution to the system (4.2). For t∈[0,T] and g(t)=g∗(t), then
where
In addition, we can get
Proof. According to the known conditions in the theorem, we can obtain the corresponding Hamiltonian as follows.
where θ1, θ2 and θ3 are undetermined, θ=(θ1,θ2,θ3)T.
From the Pontryagin Minimum Principle [38] and the Lemma 2, one can get that there exist θ∗1(t), θ∗2(t) and θ∗3(t), such that for t∈[0,T],
Therefore, by direct calculations, we can obtain the system (4.17).
The transversality conditions hold because the end cost is not specified, and the end state is free. Thus, noting that
one can obtain, (i)
or α∗(t)=α_ or α∗(t)=¯α, and (ii)
or δ∗(t)=δ_ or δ∗(t)=¯δ. Hence, the claimed result follows. □
From the preliminary knowledge and the above discussions, the following theorem about the optimality system of (4.2)+(4.3) can be derived.
Theorem 3. There exists an optimality system of the optimal control problem (4.2)+(4.3).
where t∈[0,T] and θ1(T)=θ2(T)=θ3(T)=0.
Remark 3. Theorems 2 and 3 show there exists an optimality system for (4.2)+(4.3), this is also a way to find the optimal control strategy. Through the optimality system, it is possible to accelerate the search for the optimal control strategy.
5.
Experiments
Theoretical analysis and results have been posed in the previous section. In this section, we mainly demonstrate the effectiveness of the optimal control strategy through some numerical simulations. It should be noted that all parameter values presented in the analysis are hypothetical, as real-world data is unavailable.
Firstly, let us introduce the system parameter settings as follows.
Example 1. Suppose that η1=0.05, η2=0.04, η3=0.01, μ=η1+η2+η3, α0=0.02, β=0.15, γ=0.5, α_=0.05, ¯α=0.8, δ_=0.05, ¯δ=0.9, p=0.0013, q=0.071, r=1.95, and T=80. The system of optimality equations (4.26) is numerically solved by calling the backward-forward Runge-Kutta fourth-order scheme, with the initial condition (S(0),I(0),P(0))=(0.5,0.3,0.2).
All subsequent experiments are conducted in Example 1, and the results are shown in Figures 1–4 and Table 1. Next, we will describe the experimental results in detail.
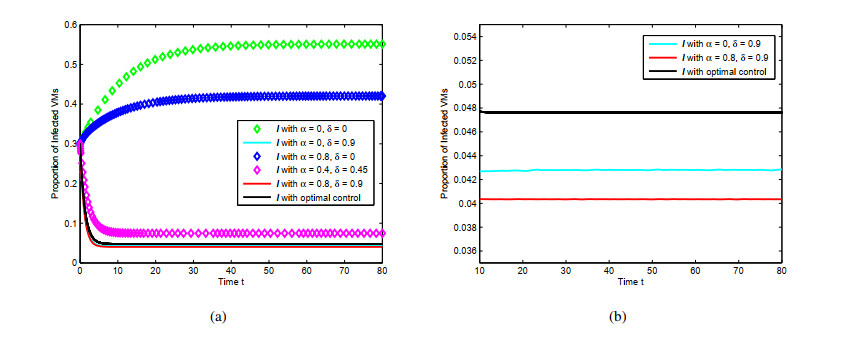
Figure 1(a) illustrates the changes in the proportion of infected VMs under different control strategies, showing the evolution of the system over time. As I with α=0,δ=0.9, I with α=0.8,δ=0.9, and I with optimal control cannot be distinguished, they are shown separately in Figure 1(b), which depicts the curves that are very close in Figure 1(a). From Figure 1(a), (b), one can see that there are apparent differences between different control strategies on the eventual scale of malware infection, which also shows the importance of studying control strategies. Specifically, I with α=0,δ=0 indicates that no control strategy is adopted, so the scale of malware infection is the largest. On the contrary, the optimal control strategy achieves much better results.
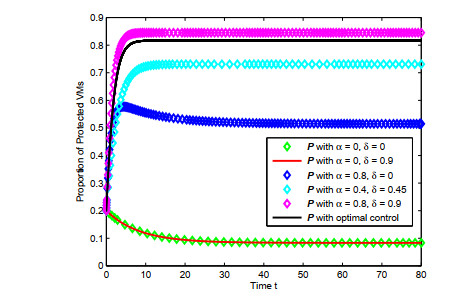
Figure 2 displays the changes in the proportion of protected VMs under different control strategies, showing the evolution of the system over time. Various control strategies also differ greatly in the final protected VMs scale. P with α=0,δ=0 represents that no control strategy is adopted, so the scale of protected VMs is the lowest. On the contrary, the optimal control strategy achieves the best results. This shows the importance of finding the optimal control strategy and also illustrates the significance of the existence of Theorems 4.2 and 4.3 from a lateral perspective.
Remark 4. From Figures 1 and 2, it can be seen that control functions α and δ impose main effects on proportions of protected, and infected VMs, which coincide with the meanings of α and δ, vaccination and treatment, respectively. In addition, it is evident that g∗ is highly effective in curbing the spread of malware. In the experiments, different values of α and δ correspond to different models, but these models are not optimization models, and their effectiveness is significantly inferior to our optimization model.
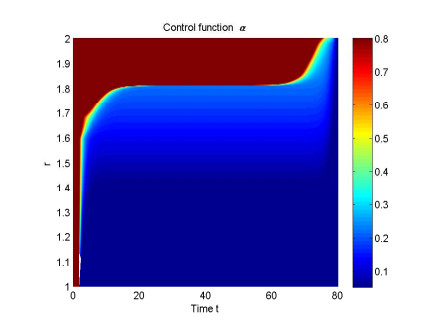
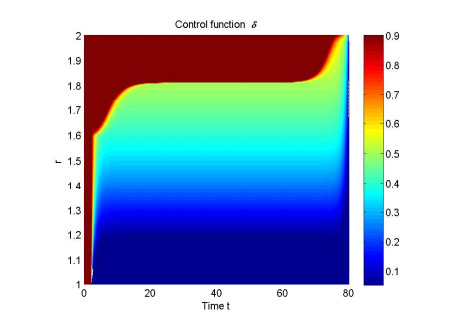
Figures 3 and 4 demonstrate the corresponding optimal control functions α and δ with varied r, respectively. It can be concluded that α and δ are both affected by r, and they increase as r increases. Although the trends of change are similar, δ increased faster, indicating that δ received a greater impact.
Table 1 summarizes the results of different control strategies in terms of the final proportion of infected VMs and their corresponding objective function J values. The table clearly indicates that the optimal control strategy g∗ is the most effective approach in minimizing the objective function J and reducing the prevalence of infected VMs to a significant extent. In addition, Table 1 also further demonstrates the results of the previous figures. It is not only necessary to look at the final control scale but also necessary to consider both the control scale and the control loss. Therefore, our study offers a fresh perspective on tackling the problem of malware diffusion in cloud computing environments.
6.
Summary
This paper has presented a novel controlled dynamical model for studying the propagation of malware in cloud computing environments, which integrates dynamic immunization strategies such as treatment and vaccination. The proposed model aims to provide a better understanding of the mechanisms underlying malware diffusion in the cloud. First, we introduce the control strategy and loss definition. Second, we define the optimal control problem. Next, we analyze the solution existence and optimality system of the optimal control problem. Finally, we provide numerical simulations to demonstrate how to determine an optimal immunization strategy. Notably, our results show that the proposed optimal immunization approach can effectively reduce the prevalence of infections at a low loss.
Use of AI tools declaration
The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.
Acknowledgments
The authors are grateful to the anonymous reviewers and the editor for their valuable comments and suggestions. This work was supported by the Chongqing Research Program of Basic Research and Frontier Technology (Nos. cstc2017jcyjAX0256 and cstc2021jcyj-msxmX0761), and the Natural Science Foundation of Chongqing, China (No. CSTB2022NSCQ-MSX1130).
Conflict of interest
The authors declare there is no conflict of interest.









 DownLoad:
DownLoad: