Neutral-type, leakage, and mixed delays in fractional-order neural networks: asymptotic synchronization analysis

1.   Introduction

The several methods for determining the differentiation and integration operators of real or complex orders are examined in fractional calculus. Although fractional calculus has been developed long time ago, problems in physics and engineering have only recently been satisfactorily solved using it. Engineers and scientists have therefore come to understand that the fractional derivative may be utilized to better define several phenomena, in the last years. Differential equations of fractional order have been proved more effective at describing a wide variety of systems in interdisciplinary fields like physics, heat transfer, mechanics, acoustics, electromagnetics, chemistry, biology, economy, and finance.

The infinite memory property has been proved for fractional-order systems. Given this, a neural network (NN) model would be significantly enhanced by the addition of a fractional derivative or integral, which represent the memory term. As a result, in ^[1], FONNs were developed. Stability and synchronization properties of different types for this sort of networks have been researched since then: asymptotic ^[2,3], Mittag-Leffler ^[4,5], or finite-time ^[6,7], and also other dynamic properties, such as dissipativity ^[8,9], bifurcation ^{[10,11,12,13,14,15,16,17]}, etc.

Time delays are present when NNs are implemented in electronics, because of the amplifiers' limited speed of switching. The NNs may become unstable and chaotic as a result of the temporal delays. As a consequence, NN models must include time delays. Time-delay NNs have grown into their own field of study, with hundreds of papers published each year. Fractional-order time-delayed NNs are one paradigm that has recently received more academic interest. We incorporate leakage delay and bounded time-varying delays into the proposed FONN model to account for these realities. Leakage delay appears in the negative feedback terms of the NN system, and was shown to have a destabilizing effect on the stability of NNs, which means that it cannot be ignored. It was considered in the context of FONNs in ^[18,19]. On the other hand, time-varying delays were very often incorporated into FONN models, most recently in ^[20,21].

On the other hand, dispersion propagation delays might be caused by a dispersion of conduction velocities along an NN's paths, necessitating the inclusion of continuously distributed delays into our model. Fractional-order network models with distributed delays were studied in ^[22,23].

It is also thought that past derivative knowledge affects the current state in neutral-type systems. These models are better at capturing the characteristics of brain response processes that take place in everyday life. The presence of the neutral-type delays complicates the analysis of these systems as opposed to traditional models with time-delay. Vibration masses connected to an elastic bar, population dynamics, and automatic control all require neutral-type time delays. Upon the implementation of NNs in VLSI circuits, neutral delays may appear, which encourages more research into neural systems with such delays. Rarely were neutral-type delays applied to FONNs. Among the papers using this type of delay are ^[6,24].

Due to its theoretical significance and practical implications in a variety of domains, including cryptography, modeling brain activity, and clock synchronization of sensor networks, the synchronization problem in NNs has attracted a lot of interest. Complete synchronization, phase synchronization, asymptotic synchronization, and projective synchronization are only a few of the several types of synchronization algorithms that have been described. Asymptotic synchronization is one of the most general and interesting types of synchronization.

In this paper, we propose a very general FONN model that takes into account all of the delays listed above: neutral-type, leakage, time-varying, and distributed delays. This is the first time, to our knowledge, that such a general model has been put forward in the literature.

Because the constant sign of a function's fractional derivative does not always ensure its monotonicity, the usual Lyapunov theory does not apply to fractional-order systems. As a result, to investigate the dynamic properties of FONNs, researchers must rely on a number of lemmas. Of the different types of lemmas, the Halanay-type lemmas are the most well-known and commonly used. Because of how they are used for FONNs, they produce fairly conservative sufficient criteria for their dynamic properties. In this paper, the Halanay-type lemma is used in a unique way, in order to build less conservative sufficient conditions, represented in terms of LMIs, for the proposed generic model.

As a consequence, three alternative and general Lyapunov-like functions are constructed, one of which is used for the first time, to our awareness, in the setting of delayed FONNs. On the basis of these functions, sufficient conditions in terms of LMIs and algebraic inequalities, respectively, are established in three theorems, which guarantee the asymptotic synchronization of FONNs, using a state feedback control scheme. Illustrating each theorem is one numerical example.

The following are the key contributions of the present research:

1) The neutral-type, leakage, time-varying, and distributed delays are all included in the FONN generic model put forward;

2) Three universal and different Lyapunov-like functions are constructed and employed in a novel way in the proposed model, one of which is used here for the first time in the domain of delayed FONNs, to our knowledge;

3) Three theorems based on these Lyapunov-like functions construct sufficient conditions for the asymptotic synchronization, using a state feedback control scheme, of the provided model, in terms of algebraic inequalities and LMIs, respectively;

4) The free weighting matrix technique is used among the first times in the setting of FONNs, to further minimize the conservativeness of the obtained criteria;

5) The findings may be applied to models with fewer types of delays, and the methodologies developed can be used to examine further dynamic properties of FONNs.

The rest of the research is structured as follows: Section 2 covers fundamental fractional calculus terminology, as well as the lemmas and assumptions that will serve as the foundation for the proofs of the three theorems provided in Section 3. Section 4 comprises three illustrative numerical examples for the theorems. In Section 5, the research's findings are summarized.

Notations: $A < 0$ – matrix $A$ is negative definite, $\lambda_{\min}(P)$ – smallest eigenvalue of matrix $P > 0$, $A^{T}$ – transpose of matrix $A$, $||\cdot||$ – $L_{2}$ norm, $|\cdot|$ – $L_{1}$ norm, $\mathbb{R}$ – real numbers, $\mathbb{R}^{+}$ – positive real numbers.

2.   Preliminaries

First, some definitions regarding fractional calculus will be presented.

Definition 1. (^[25]) The fractional integral of order $\alpha$ for an integrable function $x$: $[t_{0}, \infty)\to\mathbb{R}$ is defined as:

where $t\geq t_{0}$, $\alpha > 0$, and $\Gamma(\cdot)$ is the gamma function, defined by:

for $\text{Re}(\tau) > 0$, where $\text{Re}(\cdot)$ represents the real part.

Definition 2. (^[25]) The fractional Caputo derivative of order $\alpha$ for a function $x\in\mathcal{C}^{n}([t_{0}, \infty), \mathbb{R})$ is defined by:

where $t\geq t_{0}$ and $n$ is a positive integer, with $n-1 < \alpha < n$. Moreover, when $0 < \alpha < 1$, we have that:

The drive system is defined as:

$\forall i = 1, \ldots, N$, and $c_{i}\in\mathbb{R}^{+}$ – self-feedback weight, $a_{ij}\in\mathbb{R}$ – weight without time delay, $b_{ij}\in\mathbb{R}$ – weight with time delay, $g_{ij}\in\mathbb{R}$ – distributed delay weight, $h_{i}\in\mathbb{R}$ – neutral-type weight, $x_{i}(t)\in\mathbb{R}$ – state at time $t$, $\forall t > 0$, $I_{i}\in\mathbb{R}$ – external input, $f_{j}$: $\mathbb{R}\to\mathbb{R}$ – activation functions (nonlinear), $\forall j = 1, \ldots, N$, $\lambda\in\mathbb{R}^{+}$ – leakage delay, $\kappa$: $\mathbb{R}^{+}\to\mathbb{R}^{+}$ – time-varying delays, $\eta\in\mathbb{R}^{+}$ – distributed delay, and $\theta\in\mathbb{R}^{+}$ – neutral-type delay.

We will assume the continuity of the time-varying delays $\kappa$: $\mathbb{R}^{+}\to\mathbb{R}^{+}$, and that $\kappa(t) < \kappa$, $\forall t > 0$, where $\kappa > 0$. We also define $\omega$: $= \max\{\lambda, \kappa, \eta, \theta\}$.

For system (1), we formulate the initial conditions as:

and $\zeta_{i}\in\mathcal{C}([-\omega, 0], \mathbb{R})$, $\forall i = 1, \ldots, N$. For each $\zeta\in\mathcal{C}([-\omega, 0], \mathbb{R}^{N})$, its norm can be defined as:

The response system is given as:

$\forall i = 1, \ldots, N$, and $u_{i}(t)$ – control input, and $y_{i}(t)\in\mathbb{R}$ – state at time $t$, $\forall t > 0$.

For system (2), its initial conditions are:

and

By denoting

taking (1) and (2) into account, the error system has the expression:

$\forall i = 1, \ldots, N$, where

For system (3), the initial conditions are:

and

We can write system (3) in terms of matrices as:

The following assumption will be made about the activation functions:

Assumption 1. (^[6]) The activation functions $f_{j}$, $\forall j = 1, \ldots, N$, satisfy, $\forall x, \ x'\in\mathbb{R}$, the following Lipschitz conditions:

where $l_{j} > 0$, $\forall j = 1, 2, \ldots, N$, are the Lipschitz constants. We also denote $L: = {\text{diag}}(l_{1}, \ldots, l_{N})$.

The following lemmas will also be employed in our proofs:

Lemma 1. (^[26]) If $x\in\mathcal{C}^{1}([t_{0}, \infty), \mathbb{R}^{N})$ and $P\in\mathbb{R}^{N\times N}$ is a positive definite matrix, then

where $0 < \alpha < 1$.

Lemma 2. (^[27]) Let $V$: $[t_{0}-\rho, \infty)\to\mathbb{R}^{+}$ be bounded on $[t_{0}-\rho, t_{0}]$ and continuous on $[t_{0}, \infty)$. If there exist $\phi$, $v_{h}$, $\forall h = 1, \ldots, m$, such that

where $0 < \alpha < 1$, $v_{h} > 0$, $\phi > \sum_{h = 1}^{m}v_{h}$, $\rho = \max\{\rho_{1}, \ldots, \rho_{m}\}$, then $\lim_{t\to\infty}V(t) = 0$.

Lemma 3. (^[28]) For any vectors $X, Y\in\mathbb{R}^{N}$ and any positive definite matrix $Q\in\mathbb{R}^{N\times N}$, the following inequality holds:

Lemma 4. (^[29]) If $x\in\mathcal{C}^{1}([t_{0}, \infty), \mathbb{R}^{N})$ and $P\in\mathbb{R}^{N\times N}$ is a positive definite matrix, then

where $0 < \alpha < 1$, and $\odot$ represents the Hadamard product.

Lemma 5. (^[30]) If $x\in\mathcal{C}^{1}([t_{0}, \infty), \mathbb{R})$ and $p\geq1$, then

where $0 < \alpha < 1$.

Lemma 6. (Young's inequality) Let $u > 0$, $v > 0$, $r > 1$, $s > 1$ and $\frac{1}{r}+\frac{1}{s} = 1$, then the inequality

holds, with equality if $u^{r} = v^{s}$.

3.   Main results

Throughout the rest of the paper, the assumption that $0 < \alpha < 1$ is made.

To achieve asymptotic synchronization between the drive system (1) and response system (2), we shall employ the state feedback control technique. The controller, in this instance, is indicated by:

and $k_{i1}, \; k_{i2}, \; k_{i3}, \; k_{i4}, \; k_{i5}\in\mathbb{R}^{+}$, $\forall i = 1, \ldots, N$, are the control gains. System (3) is now recast as:

$\forall i = 1, \ldots, N$.

We can write now system (6) in terms of matrices as:

Theorem 1. Drive system (1) is asymptotically synchronized with response system (2) under control scheme (5) if Assumption 1 is true, and there exist positive definite (PD) matrix $P$, diagonal PD matrices $R_{1}$, $R_{2}$, any matrices $N_{1}$, $N_{2}$, $N_{3}$, $N_{4}$, $N_{5}$, $N_{6}$, $N_{7}$, and positive numbers $\phi$, $v_{1}$, $v_{2}$, $v_{3}$, $v_{4}$, such that $\phi > v_{1}+v_{2}+v_{3}+v_{4}$, and the following LMI holds:

where

$\Omega_{1, 1} = -PK_{1}-K_{1}P+(2+\phi)P+L^{T}R_{1}L,$ $\Omega_{1, 2} = -K_{1}N_{1}^{T},$ $\Omega_{1, 3} = -P(C+K_{2})-K_{1}N_{2}^{T},$ $\Omega_{1, 4} = -PK_{3},$ $\Omega_{1, 7} = PA+K_{1}N_{3}^{T},$ $\Omega_{1, 8} = PB+K_{1}N_{4}^{T},$ $\Omega_{1, 9} = -PK_{4}-K_{1}N_{5}^{T},$ $\Omega_{1, 10} = K_{1}N_{6}^{T},$ $\Omega_{1, 11} = K_{1}N_{7}^{T},$

$\Omega_{2, 2} = -N_{1}-N_{1}^{T},$ $\Omega_{2, 3} = -N_{1}(C+K_{2})-N_{2}^{T},$ $\Omega_{2, 4} = -N_{1}K_{3},$ $\Omega_{2, 7} = N_{1}A+N_{3}^{T},$ $\Omega_{2, 8} = N_{1}B+N_{4}^{T},$ $\Omega_{2, 9} = -N_{1}K_{4}-N_{5}^{T},$ $\Omega_{2, 10} = N_{1}G+N_{6}^{T},$ $\Omega_{2, 11} = N_{1}(H-K_{5})+N_{7}^{T},$

$\Omega_{3, 3} = -v_{1}P-N_{2}(C+K_{2})-(C+K_{2})N_{2}^{T},$ $\Omega_{3, 4} = -N_{2}K_{3},$ $\Omega_{3, 7} = N_{2}A+(C+K_{2})N_{3}^{T},$

$\Omega_{3, 8} = N_{2}B+(C+K_{2})N_{4}^{T},$ $\Omega_{3, 9} = -N_{2}K_{4}-(C+K_{2})N_{5}^{T},$ $\Omega_{3, 10} = N_{2}G+(C+K_{2})N_{6}^{T},$

$\Omega_{3, 11} = N_{2}(H-K_{5})+(C+K_{2})N_{7}^{T},$ $\Omega_{4, 4} = -v_{2}P+L^{T}R_{2}L,$ $\Omega_{4, 7} = K_{3}N_{3}^{T},$ $\Omega_{4, 8} = K_{3}N_{4}^{T},$ $\Omega_{4, 9} = -K_{3}N_{5}^{T},$

$\Omega_{4, 10} = K_{3}N_{6}^{T},$ $\Omega_{4, 11} = K_{3}N_{7}^{T},$ $\Omega_{5, 5} = -v_{3}P,$ $\Omega_{6, 6} = -v_{4}P,$ $\Omega_{7, 7} = -R_{1}-N_{3}A-A^{T}N_{3}^{T},$ $\Omega_{7, 8} = -N_{3}B-A^{T}N_{4}^{T},$ $\Omega_{7, 9} = N_{3}K_{4}+A^{T}N_{5}^{T},$ $\Omega_{7, 10} = -N_{3}G-A^{T}N_{6}^{T},$ $\Omega_{7, 11} = -N_{3}(H-K_{5})-A^{T}N_{7}^{T},$ $\Omega_{8, 8} = -R_{2}-N_{4}B-B^{T}N_{4}^{T},$ $\Omega_{8, 9} = N_{4}K_{4}+B^{T}N_{5}^{T},$ $\Omega_{8, 10} = -N_{4}G-B^{T}N_{6}^{T},$

$\Omega_{8, 11} = -N_{4}(H-K_{5})-B^{T}N_{7}^{T},$ $\Omega_{9, 9} = -N_{5}K_{4}-K_{4}N_{5}^{T},$ $\Omega_{9, 10} = N_{5}G+K_{4}N_{6}^{T},$

$\Omega_{9, 11} = N_{5}(H-K_{5})+K_{4}N_{7}^{T},$ $\Omega_{10, 10} = G^{T}PG-N_{6}G-G^{T}N_{6}^{T},$ $\Omega_{10, 11} = -N_{6}(H-K_{5})-G^{T}N_{7}^{T},$ $\Omega_{11, 11} = (H-K_{5})^{T}P(H-K_{5})-N_{7}(H-K_{5})-(H-K_{5})N_{7}^{T}.$

Proof. Define the following function:

By taking, along the trajectories of system (7), the fractional-order derivative of the above-defined function, and employing Lemma 1, we obtain:

Assumption 1 ensures the existence of PD diagonal matrices $R_{1}$ and $R_{2}$ which satisfy:

From Lemma 3, with $Q = P^{-1}$, we have that:

Now, using (10)–(13) together with (9), we obtain that:

For any matrices $N_{1}$, $N_{2}$, $N_{3}$, $N_{4}$, $N_{5}$, $N_{6}$, $N_{7}$, we have that the following identity holds:

By transposing identity (15), and adding both the original identity and its transpose to (14), we obtain:

where $\Omega$ is defined in (8), and

Because, by (8), $\Omega < 0$, we get that:

By applying Lemma 2, we deduce that $\lim_{t\to\infty}V(t) = 0$. Because

we get that drive system (1) is asymptotically synchronized with response system (2) based on controller (5), thus ending the proof of the theorem.□

For the next theorem, we consider system (1) with no neutral-type delay, meaning that system (1) now only has leakage and mixed delays. As a consequence, the controller will also not have the neutral-type term.

Theorem 2. Drive system (1) is asymptotically synchronized with response system (2) under control scheme (5) if Assumption 1 is true, and there exist positive numbers $\omega_{i}$, $i = 1, \ldots, N$, positive numbers $\phi$, $v_{1}$, $v_{2}$, $v_{3}$, such that $\phi > v_{1}+v_{2}+v_{3}$, and the following inequalities hold:

$\forall i = 1, \ldots, N$.

Proof. Define the following function:

By taking, along the trajectories of system (7), the fractional-order derivative of the above-defined function, and employing Lemma 5 and Assumption 1, we obtain:

By applying Lemma 6, we have that:

$\forall i, j = 1, \ldots, N$, $\forall t > 0$.

Now, (17) becomes:

Taking relations (16) into account, we get that:

By applying Lemma 2, we deduce that $\lim_{t\to\infty}V(t) = 0$. Because

we get that drive system (1) is asymptotically synchronized with response system (2) based on controller (5), thus ending the proof of the theorem.□

For the next theorem, we consider system (1) with no neutral-type and distributed delays, meaning that system (1) now only has leakage and time-varying delays. As a consequence, the controller will also not have the neutral-type and distributed delay terms.

Theorem 3. Drive system (1) is asymptotically synchronized with response system (2) under control scheme (5) if Assumption 1 is true, and there exist PD matrix $P$, diagonal PD matrices $R_{1}$, $R_{2}$, and positive numbers $\phi$, $v_{1}$, $v_{2}$, such that $\phi > v_{1}+v_{2}$, and the following LMI holds:

where

$\Omega_{1, 1} = -PK_{1}-K_{1}P+\phi P+L^{T}R_{1}L,$ $\Omega_{1, 2} = P(C+K_{2}),$ $\Omega_{1, 3} = PK_{3},$ $\Omega_{1, 4} = P|A|,$ $\Omega_{1, 5} = P|B|,$ $\Omega_{2, 2} = -v_{1}P,$ $\Omega_{3, 3} = L^{T}R_{2}L-v_{2}P,$ $\Omega_{4, 4} = -R_{1},$ $\Omega_{5, 5} = -R_{2}.$

Proof. Define the following function:

By taking, along the trajectories of system (7), the fractional-order derivative of the above-defined function, and employing Lemma 4, we obtain:

Assumption 1 ensures the existence of PD diagonal matrices $R_{1}$ and $R_{2}$ which satisfy:

Now, using (20) and (21) together with (19), we obtain that:

Relation (22) can now be recast in the following form:

where $\Omega$ is defined in (18), and

Because, by (18), $\Omega < 0$, we get that:

By applying Lemma 2, we deduce that $\lim_{t\to\infty}V(t) = 0$. Because

we get that drive system (1) is asimptotically synchronized with response system (2) based on controller (5), thus ending the proof of the theorem.□

4.   Numerical examples

This section will provide one example to illustrate each of Theorems 1–3. The fractional order will be $\alpha = 0.75$ for all the examples.

Let the following FONN be the drive system:

and the following FONN be the response system:

where $u(t)$ is the controller.

By denoting $\chi_{i}(t) = y_{i}(t)-x_{i}(t)$, $\forall t > 0$, $\forall i = 1, 2$, using the following state feedback scheme:

the error system is:

Example 1. In the first example, the parameters of the fractional-order systems are given as:

and the leakage delay $\lambda = 0.07$, the time-varying delays $\kappa(t) = 0.1|\cos t|$ (which implies that $\kappa = 0.1$), the distributed delay $\eta = 0.05$, and the neutral-type delay $\theta = 0.07$, so $\omega = \max\{\lambda, \kappa, \eta, \theta\} = 0.1$. From their definitions, we can see that the activation functions in Assumption 1 satisfy the Lipschitz criteria, and

The control gain matrices are designed as:

With these parameters, it can be verified that the conditions in Theorem 1 are satisfied for $\phi = 0.1$, $v_{1} = v_{2} = v_{3} = v_{4} = 0.022$, $R_{1} = \text{diag}(0.9212, 1.0136)$, $R_{2} = \text{diag}(0.0606, 0.1191)$ (the values of the other matrices are not given in order not to lengthen the paper). This implies that drive system (23) is asymptotically synchronized with response system (24) under the feedback control scheme given by (25), for the above-specified parameters.

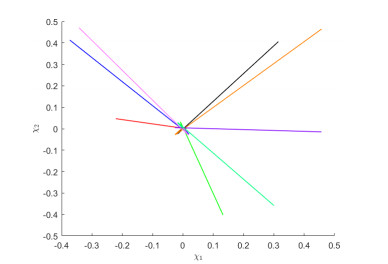
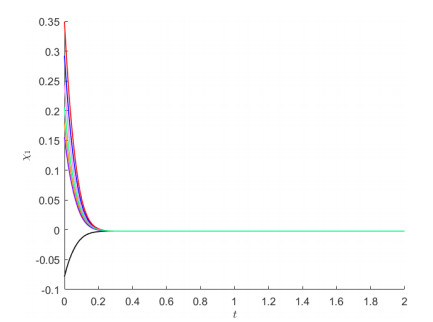
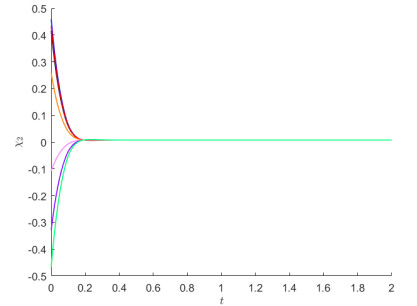
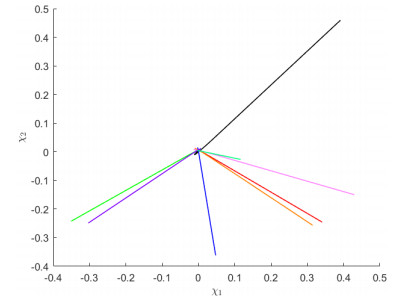
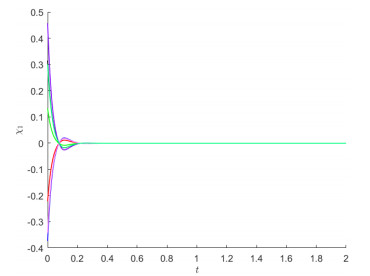
In Figures 1–3, starting from $8$ initial values, the state and phase trajectories for states $\chi_{1}$ and $\chi_{2}$ are presented.

Example 2. For the second example, the parameters are:

and the leakage delay $\lambda = 0.08$, the time-varying delays $\kappa(t) = 0.1|\sin t|$ (which implies that $\kappa = 0.1$), and the distributed delay $\eta = 0.05$, so $\omega = \max\{\lambda, \kappa, \eta\} = 0.1$. Again, we see that the activation functions satisfy the Lipschitz conditions in Assumption 1, from their definitions, and

The control gain matrices are designed as:

If $r = 1.5$, $\omega_{1} = \omega_{2} = 1$, $\phi = 1.6$, $v_{1} = v_{2} = v_{3} = 0.5$, it can be easily verified that the conditions of Theorem 2 are satisfied, meaning that, for the parameters given above, drive system (23) is asymptotically synchronized with response system (24) under the feedback control scheme given by (25).

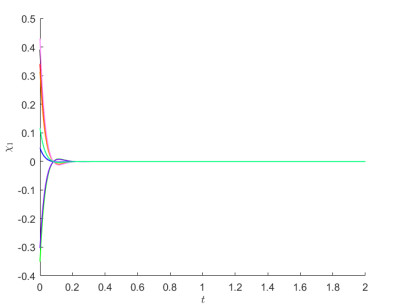
In Figures 4–6, starting from $8$ initial values, the state and phase trajectories for states $\chi_{1}$ and $\chi_{2}$ are presented.

Example 3. For the last experiment, we have the following parameters:

and the leakage delay $\lambda = 0.05$, and the time-varying delays $\kappa(t) = 0.1|\cos t|$ (which implies that $\kappa = 0.1$), so $\omega = \max\{\lambda, \kappa\} = 0.1$. The Lipschitz conditions in Assumption 1 are satisfied by the activation functions, and

The control gain matrices are designed as:

For

$R_{1} = \text{diag}(0.9663, 1.0031)$, $R_{2} = \text{diag}(0.0784, 0.1042)$, the conditions in Theorem 3 are satisfied. Thus, we deduce that drive system (23) is asymptotically synchronized with response system (24) under the feedback control scheme given by (25), for the above parameters.

In Figures 7–9, starting from $8$ initial values, the state and phase trajectories for states $\chi_{1}$ and $\chi_{2}$ are presented.

5.   Conclusions

To realize the asymptotic synchronization, using a state feedback control scheme of FONNs with neutral-type, leakage, time-varying, and distributed delays, three sufficient conditions described in terms of algebraic inequalities and LMIs were devised. To our knowledge, this is the first time such a broad model has been described in the literature. A novel form of Lyapunov-like function was also presented for the first time in the delayed FONNs context, and the free weighting matrix method for this sort of network was used among the first times. Both lead to an important reduction in the determined criteria's conservatism. The application of the Halanay-type lemma for fractional-order systems in a novel way is another factor that helps to reduce conservatism. Each of the three theorems was illustrated with a numerical example.

The techniques presented in this study are broad, and may be utilized to deduce sufficient conditions for the asymptotic synchronization of NN models with impulsive effects, Markov jump parameters, or reaction-diffusion terms, and also to address other dynamic properties, such as multistability, stabilization, dissipativity, or passivity. These advancements lead to intriguing future research avenues.

The results obtained in the paper regarding the asymptotic synchronization of FONNs can be used for the design of practical implementations of such networks in electronic circuits, benefiting applications in automatic control, criptography, image processing, etc.

Conflict of interest

The author declares that there is no conflict of interest.