1.
Introduction
In recent years, the incidence of allergic rhinitis in adults has ranged from 8.7% to 24.1%, and the incidence of allergic rhinitis in children is gradually increasing to 10.8% [1]. As a common chronic disease, rhinitis cannot be cured entirely. In addition to pharmacotherapy and immunotherapy [2], the mainstream medical treatment modalities can also be supplemented by physical therapy to relieve patients' symptoms, such as laser, microwave, radiofrequency, bio-resonance and other techniques [3]. Therefore, many rhinitis medical products available for home use have been introduced on the market. However, there is less research on the design of rhinitis medical products. Most of the commercially available household rhinitis therapy devices are technology-oriented and similar in design. The needs of users vary greatly, and the design of medical products also needs to consider medical attributes. For designers, the evaluation of various design elements in the product design decision-making process is serious and difficult.
The research shows that the AHP method can be used to quantitatively study qualitative problems and has been widely used in various topics. This method of obtaining the optimal solution by establishing mathematical models and calculations can solve many social problems. Wu et al. [4] solved the production transportation problem via a deterministic annealing neural network method. Wang et al. [5] developed an evaluation approach based on the Technique for Order Performance by Similarity to Ideal Solution (TOPSIS) to help the Air Force Academy in Taiwan choose optimal initial training aircraft in a fuzzy environment. Zhou et al. [6] used quality function deployment (QFD) and grey correlation analysis approach to calculate and sort user needs and technical information. Thus, the problems in the information construction and management of hydropower projects are solved. Fröhlingsdorf et al. [7] performed image processing by Hough transform and then mapped components by a decision tree method. This method optimizes the acoustic design of electric vehicles and improves work efficiency. Xiu et al. [8] established a mathematical model by simulating the driving environment and evaluated different seat structures, and then they obtained the optimal solution of the problem. Wang et al. [9] invited users to experience different driving scenarios and obtained the influencing factors of sound and vibration on driving comfort through subjective and objective scoring method. Irfan et al. [10] combined AHP and the G-TOPSIS method to evaluate and make decisions on industrial development obstacles and solved the problem of biomass industry development in India. In the design process of medical products, design elements need to be excavated from shallow to deep. The elements of all aspects of the product need to be selected according to different levels. Therefore, the AHP method obtains the optimal solution by sorting the weights of the elements at different levels, which is most suitable for the decision-making of the product design process. In this study, the analytic hierarchy process was used to weight the design elements of rhinitis physiotherapy instruments to support the evaluation process in product decision-making. The evaluation results are used for improved product conceptual design, providing solutions and practical basis for the development of family rhinitis treatment products and the application of the AHP method.
2.
Methodology
2.1. Current design situation of market
There is no authoritative and precise definition for household rhinitis therapy products. According to synonym search results and literature studies, household rhinitis therapy devices usually are medical aids that relieve symptoms such as nasal mucosal edema by dilating nasal blood vessels and accelerating blood circulation through physical techniques [11]. After researching, analyzing and screening the best-selling household rhinitis therapy devices in the online market, the representative products were briefly summarized in brand, technology, color and material, as shown in Table 1.
According to preliminary research results, most of the mainstream household rhinitis therapy devices in the current market are used to assist in the treatment of rhinitis using a laser light therapy technique. Although there are differences in the appearances of the above four representative products, such differences are insignificant. All of them are used to relieve various symptoms caused by rhinitis by irradiating the nasal cavity with a weak laser of about 630 nm at regular intervals [12]. In terms of product structure, they all contain a weak laser module, a communication module, an information display module and a power supply module. With the upgrading iteration of the product technology, patients can use the product through a wireless connection [13]. Such products also tend to be compact and portable in size and weight, but the size reduction usually also affects the range, functionality and efficiency of the product [14]. For household rhinitis therapy devices, whether designed based on users or scenarios, the trade-offs and considerations of various design elements require a more rational decision-making approach. The study applies the AHP method to propose design improvements and optimization solutions for household rhinitis therapy devices in order to promote the development of similar products in theory and practice.
2.2. Application of AHP in the design of household rhinitis therapy devices
2.2.1. AHP theory
AHP theory is a systematic and practical multi-criteria decision-making method proposed in the 1970s by American operations researcher Professor Saaty [15]. AHP allows the quantitative study of qualitative problems and has been widely used in the study of various topics. This theory usually starts with sorting out the influencing factors of the research subject and constructing reasonable indicators. Then, it determines the mutual importance of each category of indicators by expert scoring to build the corresponding judgment matrix [16]. Finally, the weight of each indicator is calculated to get the main influencing factors of the research subject.
2.2.2. Research procedure
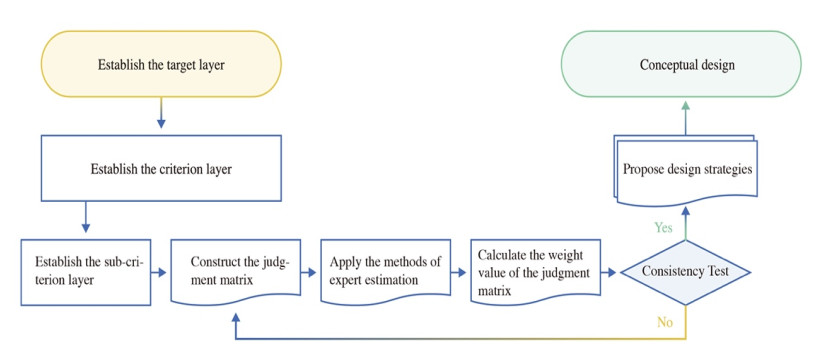
With the AHP theory, the research steps of this study are as follows (see Figure 1): 1) Establish a more reasonable and humanized solution for household rhinitis therapy devices as the target layer element. 2) Through research and semantic analysis, the factors that affect the product design of household rhinitis therapy devices are sorted out and used as elements of the criterion layer. 3) Expand the design attributes of the criterion layer into the corresponding sub-criterion layer design elements and construct a judgment matrix. 4) An expert group was established to compare and score the importance of directly related factors at each level. The weights of each design element are calculated according to the matrix, and then a consistency test is performed. 5) Propose conclusions based on the factor ranking results. Then, carry out a design practice and optimize it.
2.2.3. Extraction of design elements and model construction
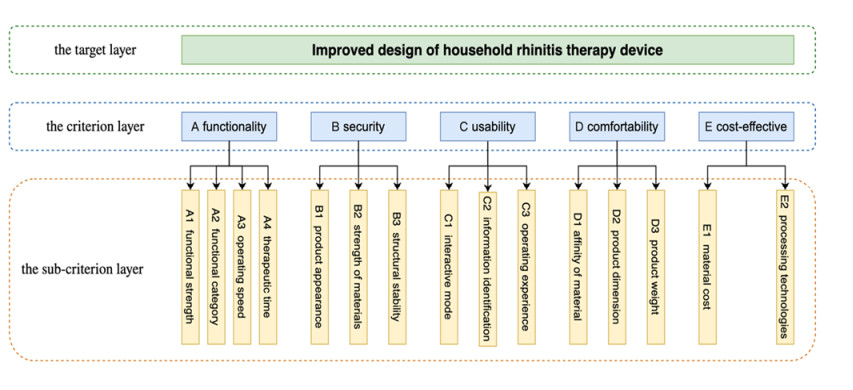
The target layer of this project is to propose a more reasonable and humanized improved design solution for household rhinitis therapy devices. Based on the preliminary interviews and research results, the elements are refined and classified to construct a guideline layer. We will extend the classification based on the criterion layer to derive more detailed design factors and build a sub-criterion layer. Laser treatment for rhinitis is a supplementary treatment [17]. Therefore, most patients have a neutral attitude toward such products, worrying that the promotion of the product will outweigh the actual effect and thus obsessing over the price, appearance, function, safety and other factors of the product. For home medical products, the user is the main focus of the product design [18]. Through reading rhinitis medical-related literature, combing rhinitis treatment data and interviewing and researching relevant users, this study summarizes five attributes that influence design of household rhinitis therapy devices: functionality, safety, usability, comfortability and cost-effectiveness, as shown in Table 2.
The factors affecting the product design of household rhinitis therapy devices were classified, and the criterion level evaluation indexes were established and mapped with numbers, as A functionality, B safety, C usability, D comfortability and E cost-effectiveness. Then, according to the AHP theory proposed by Prof. Saaty [19], the design attributes of the criterion layer are expanded into 15 design elements to establish sub-criterion layer evaluation indexes. Among them, functional strength is represented by A1, functional category is A2, operation speed is A3, therapeutic time is A4, and so on. The specific model is shown in Figure 2.
2.2.4. Matrix construction and weight calculation
In this study, a scale of 1–9 [20] was used to carry out the assignment, and the degree of importance between the two elements of the comparison was defined by numerical values. The specific scales and meanings are shown in Table 3. Meanwhile, to make the results of the study more generalizable, a total of 10 people were invited to form an expert group to score each index two by two, including five graduate students in the design direction, three patients with rhinitis and two experts in related product development and medical experts.
Using the geometric mean method [21], the weights of each evaluation index in the criterion layer and sub-criterion layer in the judgment matrix are calculated as follows: In the first step, the scalar product of each row is calculated by Eq (1), where bij is the evaluation index in the i-th row and j-th column. m is the number of evaluation indexes.
In the second step, the geometric mean of the product of the scalars of each row is calculated by Eq (2).
In the third step, the relative weights of each evaluation index are calculated by Eq (3).
The expert group members were invited to score the corresponding indicators in a two-by-two comparison according to the above steps. After calculating the geometric mean of each evaluation index, their weight values are calculated separately.
2.2.5. Consistency check
To avoid significant discrepancies between the index calculation results and the matrix logic, it is necessary to conduct consistency tests on the judgment matrix [22]. The specific calculation steps are as follows: In the first step, the maximum characteristic root is calculated by Eq (4), where Awi is the vector Aw i-th component, and n is the order.
In the second step, the consistency index (CI) of the judgment matrix is calculated by Eq (5), where n is the order corresponding to the evaluation index in the judgment matrix [23]. Generally, a smaller CI value resulted in a better consistency of the matrix.
In the third step, the consistency ratio (CR) was calculated by Eq (7), where the random index (RI) value is shown in Table 4. When CR ≤ 0.1, it indicates that the consistency test is passed. When CR > 0.1, it means that the consistency test is not passed, and the judgment matrix needs to be checked and corrected and then calculated and analyzed again [24].
3.
Results
According to the judgment matrix and weight calculation, the results of the criterion layer and sub-criterion layer are shown in Tables 5–10, respectively.
The consistency calculation of the judgment matrix above is shown in Table 11. All CR ≤ 0.1, the judgment matrix was proved to pass the consistency test, and the results are valid.
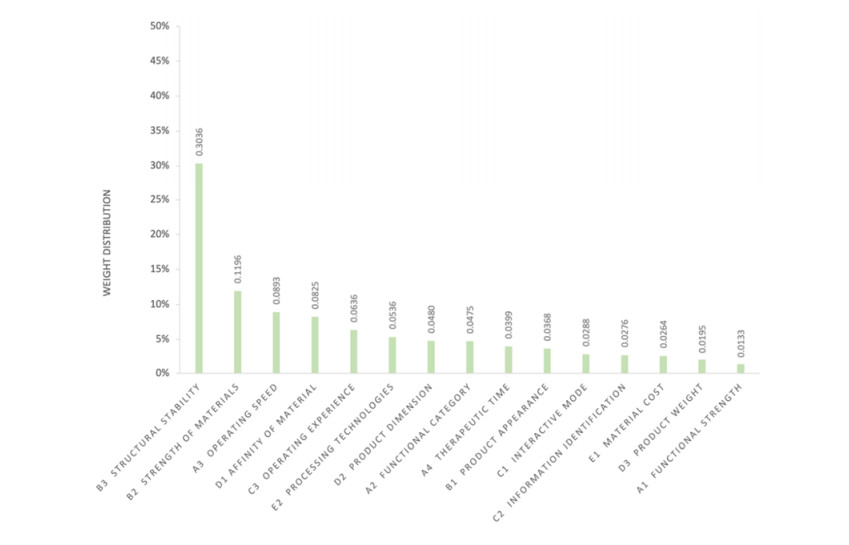
After completing the consistency test, the weight values of each evaluation index in the sub-criterion layer were normalized. To further clarify the importance of the design elements of the sub-criterion layer in influencing the design of household rhinitis therapy devices, the product of each design element of the sub-criterion layer and its corresponding design attribute of the criterion layer was calculated. The total weights of the 15 design factors of household rhinitis therapy devices were obtained, and the results were sorted and ranked as shown in Table 12 and Figure 3.
4.
Discussion
After graphical processing of the calculation results of the AHP method, the comprehensive weights and rankings of design factors can be clearly identified. The calculation results in the criterion layer show that B > A > D > C > E. The top three factors are safety, functionality and comfortability. The results are basically consistent with the existing product attributes on the market. Functionality and safety are the primary factors in the design of household rhinitis therapy devices. As a home medical product, effective functionality and reassuring safety are the prerequisites for consumer purchase [25]. This is followed by comfortability, usability and cost-effectiveness, which make the product more competitive in the market.
By further expanding the attributes of the criterion layer, it can be seen that the attribute ordering of the sub-criterion layer has undergone subtle changes. As shown in Figure 3, it can be seen that the product's structural stability, strength of materials, operating speed, affinity of material and operating experience are the most important factors. Therefore, the selection of materials is also crucial when designing products. The structural design of the product needs to avoid complexity. Many current household rhinitis therapy devices have complicated operation steps, requiring users to understand the settings and operational matters independently, which will inevitably cause errors and easy damage during use, resulting in poor medical results. Therefore, the user experience is also an aspect that cannot be ignored [26], and product design should minimize the obstacles that users may encounter when using it.
Through the application of the AHP method, product design decision-making can dig out easily overlooked details from a deeper level. For household medical products exposed to rhinitis patients, the appearance and straightforward function of medical treatment lead to almost the same product. With the user-centered design concept deeply rooted in the hearts of the people, solving the real pain points of users has always been a headache for designers. As a mathematical tool to obtain the optimal solution, the AHP method solves this problem well.
4.1. Design strategy
4.1.1. Simple and stable structure
Current household rhinitis therapy devices on the market usually use 630 ± 20 nm red light to irradiate the nasal cavity at high frequencies, thus relieving symptoms. Users need to wear a separate laser emission module to use. The structure of the wired connection between the central unit and the laser module is inconvenient for storage and easily an obstacle and safety hazard in use. The problems of low battery, easy loss and uncomfortable wearing usually accompany the structure of the wireless connection [27]. According to the weighting results of the AHP theory in this study, user experience elements are given priority.
4.1.2. Comfortable and durable material
Depending on the physical and mechanical properties, chemical resistance, molding and processing properties and other elements, plastic, metal, polymer materials, etc. can be considered in product design [28]. Since the laser module of the household rhinitis therapy devices needs to transmit light to irradiate the nasal cavity, this part must be made of light-transmitting materials. Although glass has sound light transmission and texture, as part of the intimate contact with the nasal cavity, the use of glass will cause shattering and form a safety hazard. This part of the material can be chosen from transparent plastic, through the surface treatment to enhance the comfort of the product, with a replacement silicone cover. Frosted plastic or silicone enhances user comfort but affects the light transmission rate of the parts and affects product function, treatment time, etc. When such contradictions occur, user comfort is prioritized according to the weighting order of the AHP theory. In the choice of the primary material and color of the product, the household rhinitis therapy devices on the market are usually based on white plastic, with additional colors to embellish. Different colors will give users different feelings [29]. For example, cold colors will provide people with tranquility, calm and rationality, and warm colors will give people a sense of mildness, nature and friendliness [30]. To avoid too emotionally strong reactions from users, too bright colors also need to be excluded.
4.1.3. Easy interaction and simple operation
Household rhinitis therapy devices must be designed to avoid overly complex functions and operations because of the limited technology required [31]. During the process of product design, the tasks required for treatment can be automated and one-buttoned. Simple and intuitive operation logic for patients of all ages can minimize barriers to use and thus increase user satisfaction.
4.1.4. Medical appearance and better universality
As a home medical product, the product's appearance must conform to the medical properties to increase the user's trust in the product's function and safety. The product's shape also needs to avoid overlapping with the inherent form of other products and causing cognitive bias [32]. Some household rhinitis therapy devices look like wireless headphones, while others are unrecognizable at first glance. The design can be combined with function and usage to make the form more recognizable, and the color tends to be neutral or universal.
4.1.5. Comfortable and portable
Since household rhinitis therapy devices are worn, they need to be as light and compact as possible to reduce the user's use burden. The design can be based on ergonomics [33], using an organic structure to fit the human body and enhance the user experience [34].
4.2. Design scheme
According to the above design strategies of structure, material, usage, appearance and size, the design was developed and rendered by RHINO and KEYSHOT software.
Figure 4a shows the overall effect of the product. The innovation of the design lies in the wearable integrated structure [35]. Household rhinitis therapy devices usually have the controller, power supply and laser module separated or connected by wires. In contrast, the integrated system is more stable and convenient in terms of use and storage. In terms of material, the main shell of the product is made of frosted textured white plastic, and the lower half of the body is made of glossy gray plastic to distinguish between the modules. The upper part of the product is a fixed structure that fits the shape of the human face through the organic form. The ventilation grid in the middle can reduce the user's resistance to breathing when using the product ventilation grid under the power indicator, as shown in Figure 4b. Figure 4c shows the details of the laser module. When the user wears the product and turns it on, two infrared laser heads provide physical phototherapy. Figure 4d is the power switch. Figure 4e is the function key switch. Users can turn on or off the power and use one key to open the physiotherapy mode without complicated settings and operations.
5.
Conclusions
This topic studied the user pain points and constructed a judgment matrix for the design elements of the rhinitis physiotherapy instrument. Then, the relative weight of each element is calculated by the AHP method to clarify the design points of rhinitis physiotherapy instrument. Through the application of the AHP method, the problem of factor decision-making in the process of rhinitis medical product design is solved. This study also combined the calculation results of the AHP method to carry out the design practice. This work improved the scientificity and rigor of the product design decision-making process, and it also provided a theoretical basis for the design of rhinitis medical products. Still, due to shortcomings in many aspects such as research steps and schemes, it is hoped that it can be improved in future work.
Conflict of interest
All authors declare no conflicts of interest in this paper.













 DownLoad:
DownLoad: