1.
Introduction
Cirrhosis is a chronic liver disease that causes irreversible destruction of liver cells. It is characterized by areas of fibrosis (scarring) and death of hepatocytes. Its main consequences are failure in liver function and increased blood pressure in the portal vein [1]. Cirrhosis ranks 11th in the world's leading causes of death, with approximately one million deaths per year [2] and its main causes are alcohol intake, fatty liver and viral hepatitis [3,4]. Most of the treatments have been oriented to the suppression or inactivation of the damaging agent. However, in some cases this is not achieved and the disease progresses. To this day, there is no effective treatment for this disease [5]. Therefore, it is pertinent to study medicinal plants as an alternative to solve this health problem. In this sense, both ethnobotany and popular medicine have reported a variety of medicinal plants used in gastrointestinal diseases with a hepatoprotective effect [6,7,8]. For example, silybum marianum l., commonly known as silymarin, has a hepatoprotective effect due to the presence of flavolignans. This organic compound is perhaps the most used by complementary alternative medicine (CAM) in the treatment of liver diseases [6,9].
Based on common knowledge on the use of medicinal plants by the Mexican population [10,11,12], our laboratory formulated a mixture of seven plants called EHAM7. This mixture was prepared using the substances:
● bidens odorata cav. l., with diuretic and antidiarrheal activity
● tecoma stans l., with anti-inflammatory effect
● linum usitatissimum l., with protective effects against a variety of chronic diseases and risk factors, including breast and colon carcinogenesis
● cynara scolymus l., with antimicrobial and antioxidant activity (also reduces lipid levels in plasma)
● equisetum hyemale l., with antioxidant, antimicrobial and diuretic activity
● peumus boldus l., with choleretic, cholagogue, diuretic, antioxidant and antiatherosclerotic effects
● rosmarinus officinalis l., with anti-inflammatory, antioxidant, hepatoprotective and neuroprotective activity
For more details on these substances and their properties, we refer the reader to [13] and the references therein.
On the other hand, it is well known that mathematical modeling can be an effective tool to take decisions in all areas, and health care is no exception. This is particularly the case when direct experiments are not possible due to ethical and financial issues. Regarding liver diseases, the role of mathematical modeling for nonalcoholic fatty liver disease is discussed in [14]. There are models based on Cox regression for predicting survival for individual patients with primary biliary cirrhosis [15,16]. A spatial-temporal study of chronic hepatitis B virus and liver fibrosis has been carried out using partial differential equations [17], while other works analyze liver injury through single-cell-based models [18,19] or via ordinary differential equation systems (ODEs) [20,21,22,23,24]. However, to the best of our knowledge, there are no previous works considering mathematical modeling of liver injury and the corresponding protective effect of medicinal plants.
It is important to point out that, in general, there are many studies in the specialized literature, in which mathematical models are proposed to approximate experimental data. For example, there are models for decision-making related to prognosis in primary biliary cirrhosis [15,16], models for the optimal control strategies for preventing hepatitis B infection and reducing chronic liver cirrhosis incidence [25], mathematical models for the diagnosis of liver diseases [26], natural history models of primary biliary cirrhosis [27], Mayo primary biliary cirrhosis survival models applied to Mayo liver transplant patients [28], models describing the relationship between activation of the sympathetic nervous system and renal blood flow autoregulation in cirrhosis [29] and multilevel mathematical models to study hepatic perfusion characteristics in case of liver cirrhosis [30], among many other reports in the field. However, we must mention that the literature lacks reports on the mathematical modeling of the effect of plant extracts (and chemical substances in general) as treatment against cirrhosis. The present work is one of the first works in this area.
The aim of this paper is to propose a mathematical model based on ODEs that describes liver damage evolution, the protective effect produced by the administration of EHAM7, and the dynamics of the concentrations of the two main indicator enzymes of liver functionality, namely, alanine aminotransferase (ALT) and aspartate aminotransferase (AST). The model is tested on a group of rats with induced cirrhosis via carbon tetrachloride (CCl4), which received administrations of EHAM7, an extract made with a mixture of plants commonly used in popular Mexican medicine. Model predictions related to liver recovery are performed in this study. More precisely, the present manuscript is organized as follows. The biological background used to construct the mathematical model is described in Section 2. In Section 3, the model based on ODEs is presented. Fittings to experimental data, numerical results and some simulations are shown in Section 4. In Section 5, the results obtained in this work are discussed. Finally, a brief conclusion is provided in Section 6.
2.
Background
The mathematical model is based on the biological processes and mechanisms observed from experiments reported in [13]. In those experiments, groups of control and cirrhotic rats with and without treatment were conformed. The hepatic damage was induced by means of a mixture of carbon tetrachloride (CCl4) and mineral oil (MO) supplied intraperitoneally. Out of the two groups of cirrhotic rats, one of them received a mixture of seven plants, i.e., bidens odorata cav. l., tecoma stans l., equisetum hyemale l., rosmarinus officinalis l., cynaya scolymus l., peumus boldus l. and linum usitatissimum l. (EHAM7), in order to demonstrate its hepatoprotective properties. The induced cirrhosis scheme consisted of supplying 0.2 ml of CCl4/MO mixture intraperitoneally every third day for eight weeks with the following volume proportions:
● 1:6 first week
● 1:5 second week
● 1:4 third week
● 1:3 from the fourth to the eighth week
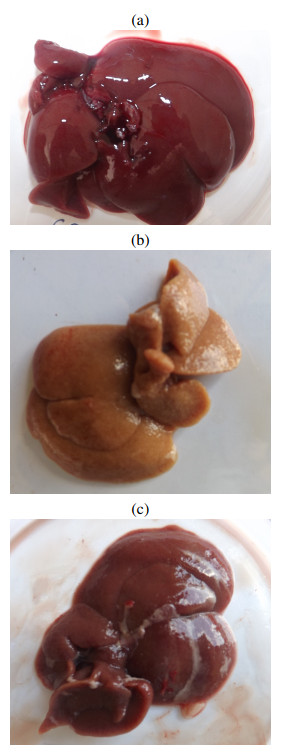
The application scheme consisted of oral administrations of 200 mg/kg of EHAM7, diluted in saline solution (SS), during the week previous to damage induction and then every third day during eight weeks, that is, the CCl4/MO mixture and the EHAM7/SS are supplied simultaneously for the cirrhotic treated rats during these eight weeks. This simultaneous procedure is important because the EHAM7 has protective effects against CCl4, but there is no effect if it is administered separately. At the end of damage induction the control rats, the cirrhotic with and without EHAM7/SS applications were sacrificed and the AST and ALT levels were measured and registered in Table 1. We have paid more attention to these levels because they are directly related to liver damage. In addition, livers for each group were extracted in order to determine visually the level of liver damage. From that visual examinations, we established the following reasonable quantitative assumptions:
● for control group, 100% of liver functionality remains,
● for cirrhotic group without treatment, 30% of the group survived until sacrifice, and
● for cirrhotic group with treatment, 80% of the group survived until sacrifice.
We refer to Fig. 1 for photos showing samples of the states of the livers for each group. More details on this experiment can be consulted in [13].
3.
Mathematical model
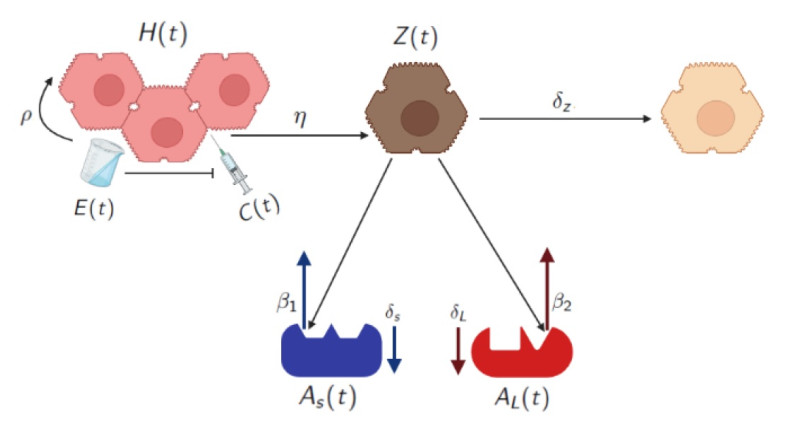
To describe mathematically the hepatic behavior of each rat in the different groups, we propose the following set of time-dependent variables. Let H(t) represent the percentage of healthy hepatocytes, Z(t) is the percentage of damaged hepatocytes, AS(t) is the concentration of AST, AL(t) is the concentration of ALT, C(t) is the concentration of CCl4, and E(t) denotes the concentration of the extract EHAM7. The parameters associated to each biological process, interactions and dynamics between variables are shown in Fig. 2. Thus, the mathematical model that describes the evolution of all dependent variables is given by the following system of ODEs:
The first equation describes the evolution of healthy hepatocytes H(t). The regenerative capacity of the liver is taken into account in the first term and corresponds to a logistic growth. The second term is a decrease by action of the CCl4 against the healthy hepatocytes. Note that the effect of this term is reduced when the concentration of extract E(t) is increased by means of the factor η1+κE. The percentage of damaged hepatocytes Z(t) is described by the equation (3.2), where the first term results from the healthy hepatocytes damaged by CCl4, and they died at rate δZ. Equations (3.3) and (3.4) express the levels of AST and ALT which increase proportionally with the damaged cells Z(t), and they tend to be stabilized by a natural process of the body at the normal levels AS0 and AL0, respectively. The stabilization occurs for AST at a rate δS and, for ALT, at a rate δL. Finally, Equations (3.5) and (3.6) are, respectively, the exponential eliminations of CCl4 and EHAM7 concentrations. Table 2 shows the biologically accepted values for the model parameters, except for κ, β1 and β2. For those parameters, it was not possible to find a study from which to estimate their values, so they will be estimated from the best fit to the experimental data.
The following conditions establish the change of variable values when the corresponding doses of CCl4 and EHAM7 are supplied according to the scheme described in Section 2:
Here, we define f(t−j)=limt→t−jf(t). The values C∗ and E∗ are, respectively, the CCl4 and EHAM7 concentrations reaching liver tissue, which can be consulted in Table 3.
4.
Numerical results
In order to obtain the values of the non-fixed parameters, we fit the model to the experimental data described in Section 2. More explicitly, for the group of cirrhotic rats without treatment, the final percentages of healthy hepatocytes was 30%, and 70% of damaged ones. For each rat, the possible parameter values were restricted —as mentioned in Section 3— to the intervals shown in Table 2. We define the final value levels of AST and ALT as ASTID and ALTID, respectively. For each rat, these values are obtained from Table 1(b). In addition, H(0)=100% and Z(0)=0 because, at the beginning of the experiments, rats are completely healthy. As it can be seen in Table 1, not all the rats have the same value of healthy levels of AST and ALT, so AS(0)=AS0 and AL(0)=AL0. We obtain the best fit for each rat of this group by minimizing the error function
For the group of cirrhotic rats with treatment, the final percentage of healthy hepatocytes was 80%, and 20% of damaged ones. The procedure is similar to the previous one, and we calculate the best fit for each rat of this group minimizing the function
The resulting parameter values for the best fit are shown in Table 4. Note that there is practically no dispersion of parameter values for all cases.
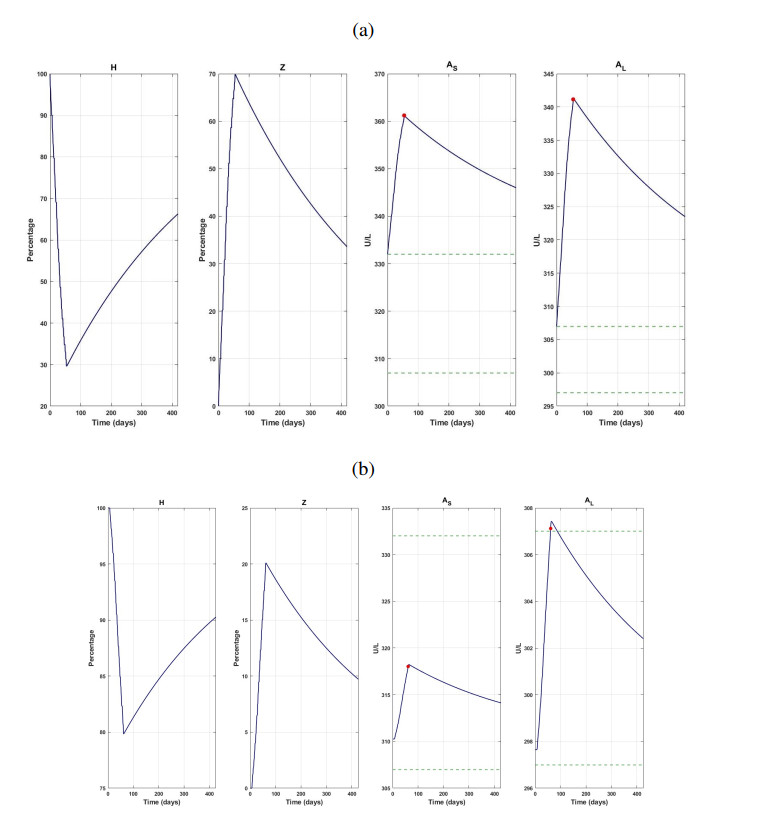
After the fits to the experimental data, we let each rat evolve for a year without any damage or treatment, as if they had not been sacrificed. We show the result for rats IDs 3 and 1 of the cirrhotic and cirrhotic treated groups, in Figs. 3(a) and (b), respectively. Similar results were obtained for the other rats. Finally, we perform a simulation for a rat with only cirrhotic damage regime for the first 28 days and, after that, EHAM7 is added. Simulation ends after 84 days. Here, we use the parameter values obtained from the fit, and aleatory values of AS0 and AS0 are assigned according to the control group (see Table 2). The results are shown in Fig. 4.
Before closing this section, it is important to point out that the simulations were carried out the standard function ODE45 provided by MATLAB R2021a on a HP Pavillion laptop Intel(R) Core(TM) i5-8265U CPU, at 1.60GHz and 1.80 GHz. The function ODE45 provides an improved implementation of the Runge–Kutta method of order 4, to solve systems of ordinary differential equations. This Runge–Kutta method is stable, and has order of consistency and convergence at least equal to 4. We chose this approach in view of the fact that the simulations can be reproduced in this way by any researcher interested in reproducing our results. Also, since it is a standard implementation, little knowledge is required to produce simulations. Indeed, most scientists with limited knowledge of mathematics and computational tools are able to easily solve systems of ordinary differential equations using this standard function from MATLAB. Notice that there are other approaches in the literature [35,36,37,38,39,40,41], but we believe that the current approach has much more pros than cons.
5.
Discussion
From Table 4, it is clear that there is no substantial variation in the values of each parameter of the model. That means that there is no difference between individual rats as long as the same species and breed is used. The only difference occurs in the AST and ALT initial values, where we propose an interval according to the control group. Our model reproduces the data observed in the experiment described in Section 2 where, for the cirrhotic group, we assumed 30% of healthy hepatocytes and 70% of damaged ones at the end of the experiment, as well as the final concentrations of AST and ALT for each rat. We can see that if we let the model evolve without CCl4, the rats would start to recover though not fast enough. On the other hand, for the cirrhotic group with treatment, the model reproduces the assumption of 80% of healthy hepatocytes and 20% of damaged ones. Also, it reproduces the final levels of AST and ALT at the end of the experiment.
Similarly, if we let evolve the model without any damage or treatment, the recovery is also slow. However, it is enough to reach 90% of healthy hepatocytes and normal values of AST and ALT. It occurs in view that the hepatoprotective effect of EHAM7 helps in reducing the CCl4 action on the liver, so a better recovery is obtained. In the simulation shown in Fig. 4, we can see that, after 28 days of damage, approximately 60% of healthy hepatocytes remained. When EHAM7 is applied (along with CCl4), it is possible to reduce the damage velocity though the damage is not entirely avoided. It is important to mention that the goal of the experiments in [13] was to evaluate the protective properties of EHAM7 extract. Additional studies are needed to determine if the EHAM7 extract also has curative features.
It is worthwhile to notice that the figures presented in the previous section were all results from fitting the mathematical model to the experimental data obtained from the laboratory. To that end, appropriate treatments were given to each of the rats in their respective groups, as mentioned in the previous section. As a result, we considered two groups for the experiments, namely, cirrhotic and treated groups. The cirrhotic dynamics for rats with IDs 3 and 1 for these two groups are depicted in Figs. 3(a) and (b), respectively. The graphs show model fitting results for (a) the rat ID 3 of the CCl4 group adding a year of free-evolution. CCl4 is applied until day 54, and (b) the rat ID 1 of the CCl4 + EHAM7 group adding a year of free-evolution. CCl4 + EHAM7 is applied until day 61. The red points correspond to the AST/ALT measured level values when the rat was sacrificed. Horizontal dashed green lines correspond to minimum and maximum concentrations of AST and ALT measured in the control group. The results show that the progression of cirrhosis is controlled more when the plant extract is used as treatment.
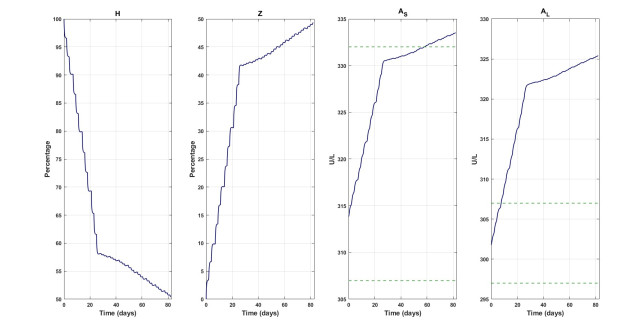
Finally, Fig. 4 shows simulation for a virtual rat with CCl4 the first 28 days and CCl4 + EHAM7 the next 56 days. Horizontal dashed green lines correspond to minimum and maximum concentrations of AST and ALT measured in the control group. As pointed out before, the simulation was performed for a rat with only cirrhotic damage regime for the first 28 days. After that, EHAM7 is added. Simulation ends after 84 days. Here, we use the parameter values obtained from the fit, and aleatory values of AS0 and AS0 are assigned according to the control group (see Table 2). As with Fig. 3, the results show that the progression of cirrhosis is controlled when the plant extract is used as treatment.
6.
Conclusion
We have formulated a mathematical model that reproduces the results of the experiments performed in [13], where a group of rats were damaged with CCl4 in order to induce cirrhosis and another group was also damaged with CCl4 but was also simultaneously administered the extract EHAM7 as hepatoprotective agent. The model could be used to define more precise schemes of cirrhosis induction with CCl4, that is, whether it is needed to reach a concrete level of liver damage to carry out a specific biological experiment. The model can be used to compute the number of CCl4 administrations and the time interval between them. Also, it could be used to continue studying the biochemical properties of EHAM7 extract in future reports.
Before closing this work, it is important to mention that some avenues for future research still remain open after the conclusion of this work. As an example, it is worth noticing that the experiments which motivated this work were carried out using rats. In that sense, the results are relatively limited to this species. Perhaps the most interesting route of research could be to try to verify experimentally and analytically the validity of our model for the human species. From the scientific point of view, this problem has an important relevance since cirrhosis is a fatal disease among humans. The authors would like to confirm that the plant extract under investigation in this work is a means to protect mankind against cirrhosis. On the other hand, experiments with humans require more licenses, and many obstacles lie ahead when human individuals are part of scientific experiments. However, we hope that the results reported in this work will support future experiments to determine whether the plant extract is helpful for people.
Use of AI tools declaration
The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.
Acknowledgments
The authors L.E.A-H and C.G.R-M wish to thank CONACYT for the financial support granted through scholarships 779584 and 511479 respectively. Also, the corresponding author, J.E.M.-D., was funded by the National Council for Science and Technology of Mexico (CONACYT) through grant A1-S-45928. All the authors acknowledge the support from the University of Guadalajara through the program PROINPEP. The authors would like to thank the anonymous reviewers and the editor in charge of handling this submission. Their suggestions were all taken into account, and they resulted in a substantial improvement of our work.
Conflict of interest
The authors declare that there is no conflict of interest.
Data statement
The data that support the findings of this study are available from the corresponding author, J.E.M.-D., upon reasonable request.








 DownLoad:
DownLoad: