1. Introduction
In the last few years, colon cancer research groups have retrospectively reviewed data from large phase three trials in advanced disease, and made the observation that primary tumour location has an important impact on overall survival. The key finding is that patients with left sided colon cancers (LCC) (from splenic flexure to distal rectum) live considerably longer than patients with right sided colon cancers (RCC) (caecum to splenic flexure). In the CALGB/SWOG 80405 phase 3 trial, median overall survival for LCC of 32.9 months versus 19.6 months for RCC (p < 0.0001) was recorded. Furthermore, retrospective analysis of this study demonstrated that primary tumour location had a significant impact on the response to anti-EGFR targeted therapy in RAS wildtype tumours. The addition to chemotherapy of Cetuximab compared to Bevacizumab significantly prolonged median OS in LCC (39.3 v 32.6 months, HR = 0.77, 95% CI, 0.59-0.99, p < 0.05), but not in RCC (13.7 v 29.2 months, HR = 1.36, 95% CI, 0.93-1.99, p = 0.11, see Table 1) [1]. Although not used prospectively as a means to stratify patients in such clinical trials, the impact of primary tumour location on patient outcomes has been corroborated across the retrospective analysis of several trials (see Table 1). The aetiology of this observation is currently uncertain and under investigation. Furthermore, primary tumour location (PTL) appears to differentially affect the response to therapies such as targeted agents, raising the prospect that PTL could be used as predictive biomarker. The evidence for this will be scrutinised in this review. The current position on this topic is that PTL might actually be a convenient surrogate for another molecular biomarker, and that such knowledge might help to build a new understanding of colon cancer being a cluster of diseases, with divergent clinical outcomes and different responses to therapies.
Table 1. Overall survival in 1st line metastatic RAS-WT colorectal randomised trials investigating anti-EGFR therapies in according to LCC v RCC.
| Trial |
Left colon cancer
OS (months) |
HR, 95% CI
p value |
Right colon cancer
OS (months) |
HR, 95% CI
p value |
| CALGB 80405 |
Overall pop = 32.9 |
|
Overall pop = 19.6 (p < 0.0001) |
|
| Chemo + Cet |
Chemo + Bev |
|
Chemo + Cet |
Chemo + Bev |
|
| 39.3 |
32.6 |
0.77 (0.59-0.99)
p = 0.05 |
13.7 |
29.2 |
1.36 (0.93-1.99)
p = 0.11 |
| FIRE-3 |
38.3 |
28.0 |
0.63 (0.48-0.85)
p = 0.002 |
18.3 |
23.0 |
1.31 (0.81-2.11)
p = 0.27 |
|
FOLFIRI + Cet |
FOLFIRI only |
|
FOLFIRI + Cet |
FOLFIRI only |
|
| CRYSTAL |
28.7 |
21.7 |
0.65 (0.50-0.86)
p = 0.002 |
18.5 |
15.0 |
1.08 (0.65-1.81)
p = 0.77 |
|
FOLFOX + Pani |
FOLFOX only |
|
FOLFOX + Pani |
FOLFOX only |
|
| PRIME |
30.3 |
23.6 |
0.73 (0.57-0.93)
p = 0.012 |
11.1 |
15.4 |
0.87 (0.55-1.37)
p = 0.55 |
|
FOLFOX + Pani |
FOLFOX + Bev |
|
FOLFOX + Pani |
FOLFOX + Bev |
|
| PEAK |
43.4 |
32.0 |
0.77 (0.46-1.28)
p = 0.31 |
17.4 |
21.0 |
0.67 (0.30-1.50)
p = 0.32 |
| Cet: Cetuximab; Pani: Panitumumab; Bev: Bevacizumab; OS: Overall survival; HR: Hazard ratio. |
2. Definitions of right versus left-sided colon cancer
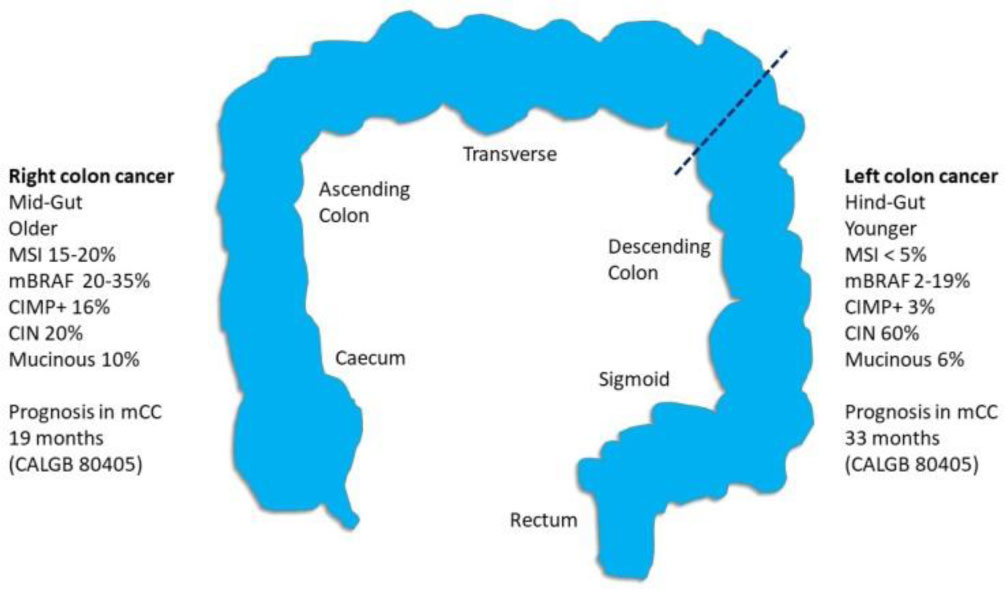
Right-sided colon cancers (RCC) comprise primary tumours located anywhere between the caecum and the distal part of the transverse colon (see Figure 1). For most authors, Left-sided colon cancers (LCC) comprise primary tumours located anywhere between the splenic flexure and the distal rectum. However, some studies have treated rectal cancers as a separate entity, largely because the surgical approach and use of radiotherapy/chemoradiotherapy differs for rectal cancer as compared to colon cancers. Such categorisation follows differences in embryological origin, with the right colon (caecum to two thirds of the transverse colon) deriving from the midgut, and the left colon (splenic flexure to distal rectum) deriving from the hind-gut. Furthermore, the allocation of the transverse colon to either right or left side is not consistent, some studies considering it wholly part of the right side of the colon, whilst others have excluded data relating to the transverse colon [2], acknowledging that its features (blood supply, histology, molecular traits) lie somewhere on a continuum between right and left. In addition, there is recognition by many authors that the correct attribution of tumours to the transverse colon is missing from many studies, owing either to the lack of natural landmarks available during diagnostic endoscopy or to the lack of precise surgical or pathological reporting.
3. Actuarial differences between right and left colon cancer
The publication of several large case-series and databases has raised awareness that prognosis was different between patients with right-sided colon cancer (RCC) versus left-sided colon cancer (LCC) (see Table 2) [3,4].
Table 2. Large datasets of colorectal cancers demonstrating different prognoses between LCC and RCC.
| Author |
Number of patients |
Year of pub. |
5 yr OS (R v L) |
Median OS (R v L) in months |
Risk of death as HR (95% CI) |
| Benedix |
17,000 |
2010 |
67% v 71% (p < 0.01) |
|
|
| Meguid |
78,000 |
2008 |
56% v 60% (p < 0.001) |
78 v 89 (p < 0.001) |
0.96 (0.93-0.99) |
| Price |
2,900 |
2015 |
|
9.6 v 20.3 (p < 0.0001) |
|
| Petrelli |
1.4 Million |
2017 |
|
|
0.82 (0.79-0.84) |
Differences in histological characteristics, patient age and stage at diagnosis explain some of the observed differences. A large prospective German study in the early 2000s collected data on over 17,000 new colon cancer diagnoses (excluding rectal cancers), which included early and advanced cancer. Patients with RCC were 3 years older than patients with LCC (71 v 68.5 years, p < 0.01), had higher rates of poorly differentiated tumours (Odds Ratio of 1.53, 95% 1.42-1.66, p < 0.01), and in those patients who underwent curative intent primary bowel resection (11,500 patients), higher proportions of American Joint Committee on Cancer (AJCC) stage II (43.1% v 37.8%, p < 0.01%) and stage III (36.1% v 33.6%, p < 0.01%) were seen in RCC compared to LCC. Five-year survival was significantly higher in LCC (71%) compared to RCC (67%) (p < 0.01) [4]. In an analysis of the American Surveillance, Epidemiology and End Results program (SEER) database in the early 2000s comprising nearly 78,000 patients who had undergone colon cancer resections, when controlled for confounders such as age, stage and histological grade, patients with RCC had shorter 5-year OS than LCC (56% v 60%, p < 0.001), with a HR for death of 1.04 (95% CI, 1.02-1.07) [3]. Recent analysis of the South Australian Registry for metastatic colorectal cancer, which includes over 2900 patients, found a statistically different OS between RCC and LCC (9.6 v 20.3 months, p < 0.001). Furthermore, multivariate analysis confirmed that PTL was an independent prognostic marker [5]. A large systematic review and meta-analysis encompassing data from 66 studies and over 1.4 million patients with early and advanced colon cancer found that LCC carried a 19% lower risk of death compared to RCC, with a HR in favour of LCC of 0.82 (95% CI, 0.79-0.84, p < 0.001). Furthermore, PTL was an independent prognostic factor, independent of race, stage (II, III and IV), publication year and type of study (prospective versus retrospective) [6].
These epidemiological findings have also been observed in randomised clinical trials. In 2001, O'Dwyer published randomised evidence of a 5 month difference in survival in patients with advanced colon cancer treated with 5FU favouring left-side as primary tumour location compared to right side, with median OS of 15.8 months for LCC versus 10.9 months for RCC (p < 0.001) [7].
4. Differences in histological and molecular traits between RCC and LCC
Genetic differences were proposed to exist between RCC and LCC as a consequence of distinct embryology, vascular supply (superior versus inferior mesenteric artery), and microenvironment [8], see Figure 1. Histological subtypes of adenocarcinoma usually associated with poorer prognosis are more common in RCC than LCC, e.g. mucinous (10.6% v 6.3%, p < 0.01%), signet-ring (0.9% v 0.3%, p < 0.01%), and undifferentiated (0.7% v 0.2%, p < 0.01%) [4].
There is a wealth of literature concerning molecular differences between RCC and LCC. Three broad molecular pathways leading to CRC have been described in the literature, including their relationship to primary tumour location: Chromosomal instability (CIN), microsatellite instability (MSI), and CpG island methylator phenotype (CIMP). CIN is more common in LCC than in RCC, with rates of 60% v 20% reported [9]. Microsatellite instability (MSI), which leads to defects in DNA mismatch repair is more prominent in RCC, representing 15-50% of RCC depending on case series [10], compared to LCC, where it arises in less than 5% of cases. In a comprehensive clinicopathological analysis of 734 colorectal cancer specimens from South Korea, the CpG island (hypermethylator) phenotype (CIMP or CIMP+), a condition characterised by the methylation of multiple CpG islands in the promoter region of genes, was found in higher proportions in RCC than LCC, with significant differences in incidence of 16% in RCC, 3% in distal colon, and 2.5% in the rectum (p = 0.001). In the same study, MSI-High status was also more prevalent in RCC v LCC, with significant differences in incidence of 19% in RCC, 7.2% in distal colon, and 2.5% in rectum (p < 0.001) [11,12]. There is a strong correlation between CIMP+ and sporadic colorectal cancers with MSI-High by virtue of the methylation of hMLH1 [13], and the CIMP+ phenotype accounts for almost all cases of BRAF mutated CRC [14], which are far more common in RCC (20-35%) compared to LCC (2-19%) [12]. These molecular traits vary in a linear fashion with frequencies of MSI-High, CIMP+, and BRAF mutations gradually increasing from rectum to ascending colon [12].
More recently, colon cancers have been classified according to molecular subtypes using RNA expression profiling. Various methodologies have been used to formulate different categorizations: The Colorectal Cancer Assigner (CRCA) subtypes (5 subgroups), the Colorectal Cancer Subtypes (CCS, 3 subgroups), and the Consensus Molecular Subtypes (CMS, 4 subgroups) [15,16,17,18,19,20]. The CMS group proposed four subtypes that are labelled CMS1 (called MSI Immune, representing 14% of colorectal cancer cases, mostly MSI tumours, more common in females and in RCC), CMS2 (called Canonical, 37%, mostly LCC with better survival after relapse), CMS3 (called Metabolic, 13%), and CMS4 (called Mesenchymal, 23%, usually diagnosed at higher stage with worse prognosis) [17]. The relationship between these CMS profiles and somatic mutations is not so clear: Although CMS1 tumours were enriched in BRAF mutations and CMS3 tumours were enriched in KRAS mutations, single genomic mutations did not define any of the CMS groups [17]. A correlative study was performed in another series of 608 patients with colorectal cancer between PTL, CMS groups, and mutations in genes such as RAS, BRAF, PIK3CA, and PTEN. CMS profiles showed a decline in CMS1 and CMS3, and a rise CMS2 prevalence moving distally [21]. A similar investigation was performed in an early cancer setting. An analysis of the NSABP/NRG C-07 adjuvant trial demonstrated the benefit of the addition of oxaliplatin to 5FU [22]. In this scenario, neither PTL or CMS were found to be prognostic or predictive of response to oxaliplatin [23]. In a separate study of the same samples, a CRCA subset called stem-like (equivalent to CCS3 or CMS4 in the other classification systems) was found to carry poor prognosis and was not correlated with benefit from oxaliplatin chemotherapy [24]. In patients with RAS-WT metastatic disease, a retrospective analysis of the CALGB/SWOG 80405 data found that patients with CMS1 (mostly RCC patients) benefitted significantly more if they had been randomised to Bevacizumab compared to Cetuximab, whereas a trend towards better outcomes was observed for CMS2 patients if they had been randomised to Cetuximab [25]. Further work is needed to determine if these molecular signatures are predictive of benefit to specific treatments, and also to definitively answer the question as to whether these molecularly-defined subtypes cluster according to sidedness, especially given the real-life advantages of having a cheap and easy predictive biomarker (PTL) versus an expensive and still cumbersome method (RNA expression profiling).
5. Primary tumour location and adjuvant chemotherapy
The benefit of adjuvant chemotherapy in stage III colorectal cancer is considered to be independent of location of primary tumour. However, the majority of large randomised trials in this setting have not addressed this question. An appraisal of the SEER database suggests that the benefit of adjuvant chemotherapy is not driven by PTL, with 5-year OS advantage from chemotherapy established for both RCC (HR = 0.64, p < 0.001) and LCC (HR = 0.61, p < 0.001). Retrospective analyses at single institutions suggest that the benefit from adjuvant chemotherapy might be more pronounced for RCC compared to LCC [26]. Microsatellite instability (MSI) or defects in the mismatch repair pathway (dMMR), found in approximately 15% of colorectal cancers, more commonly in RCC v LCC (80% v 20%) [27], contributes to these observations. In the NO147 trial investigating the benefit of Cetuximab added to oxaliplatin-based chemotherapy in the adjuvant treatment of 2,680 patients with stage III colon cancer, proximal dMMR cancers had better DFS compared to proximal proficient MMR tumours (HR = 0.71, 95% CI, 0.53-0.94), whereas for distal cancers, the DFS of deficient versus proficient MMR cases was no different (HR = 1.71, 95% CI, 0.99-2.95) [28]. This raised the question of whether proximal dMMR had better intrinsic prognosis compared to matched proficient MMR tumours or whether they benefited differently from chemotherapy. Retrospective analysis of the QUASAR trial data suggests that early (stage II) dMMR tumours have a good prognosis regardless of adjuvant chemotherapy and indeed, in these cases, the benefit of adjuvant chemotherapy has been called into question [29]. A larger study that included clinicopathological data from several North-American and European adjuvant 5FU-based chemotherapy trials, totalling 2141 patients with stage II and III colon cancer, determined that dMMR was present in 16.1% tumours, and significantly more likely to occur in RCC v LCC (p < 0.001). dMMR was associated with reduced 5-year recurrence compared to pMMR (22% v 33%, p < 0.001), and was independently associated with improved DFS (HR = 0.80, 95% CI, 0.64-0.99, p = 0.035) and OS (HR = 0.79, 95% CI, 0.64-0.99, p = 0.031) [27]. Therefore, it appears that in early colon cancers (Stage II, or Stage III N1 disease), it is not so much the PTL that is prognostic but rather certain molecular makers—in this case dMMR, which happens to occur more frequently in RCC—that determine prognosis.
6. Impact of primary tumour location on effectiveness of 1st line chemotherapy
The key recent finding was that primary tumour location was found to be an independent prognostic marker (independent from Age, Gender, CMS, MSI, BRAF) in a retrospective analysis of patients with advanced colon cancer treated within the large Phase III CALGB/SWOG 80405 trial which compared the efficacy of Cetuximab v Bevacizumab when added to standard 1st line chemotherapy [2,30]. LCC had a median prognosis of 33.3 months versus 19.4 months for patients with RCC (HR = 1.55, 95% CI [1.32-1.82], p < 0.0001).
7. Primary tumour location and anti-EGFR therapy
A retrospective analysis of the phase 2 AIO KRK-1014 trial, in which 400 patients with metastatic colon cancer were randomised to CAPIRI + Cetuximab v CAPOX + Cetuximab indicated the prognostic significance of PTL in patients with KRAS-WT tumours [31]. In the KRAS WT subgroup median OS for LCC was 29 months v 13 months for RCC (HR = 0.42, p < 0.001). Conversely, in patients with KRAS mutations, no significant difference in OS was found between LCC and RCC. Based on these observations, the authors proposed that LCC might be a predictor of Cetuximab efficacy [31]. A similar observation was made in the FIRE-3 trial that randomised 592 patients to FOLFIRI with either Cetuximab or Bevacizumab [32]. In KRAS-WT patients treated with cetuximab, significantly greater efficacy was observed in LCC compared to RCC, with better OS (HR = 0.26), PFS (HR = 0.35), and overall response rate (ORR, HR = 2.7) recorded. The same treatment effect according to PTL was observed in PEAK [33]. In CALCB/SWOG80405, FIRE-3 and PEAK trials, a statistically significant advantage in OS was observed in favour of LCC over RCC across treatment groups (see Table 1).
In all three trials, for LCC, PTL was predictive of benefit to anti-EGFR versus anti-VEGF therapy, with statistically superior OS observed ranging between 6-11 months (apart from PEAK, where the advantage of Panitumumab over Bevacizumab was non-significant). For RCC, in each case, a non-statistically superior advantage of 3-15 months was observed in favour of Bevacizumab therapy (see Table 1). Based on these findings, data was pooled in meta-analyses, where outcomes of patients treated with chemotherapy with Cetuximab versus chemotherapy alone or with Bevacizumab could be analysed according to RCC v LCC. One analysis included six clinical trials (CRYSTAL, FIRE-3, CALGB 80405, PRIME, PEAK and 20050181) [34] where data of 2159 out of 5760 patients is complete for both RAS-WT status and PTL. In LCC, OS analysis showed a statistically significant benefit in favour of the addition of anti-EGFR to chemotherapy (HR 0.75, 95% CI: 0.67-0.84). Crucially, no OS benefit was observed for anti-EGFR in RCC (HR = 1.12, 95% CI: 0.87-1.44). In a separate meta-analysis of the PRIME and CRYSTAL trials [35], an OS advantage was observed for the addition of anti-EGFR MAb in LCC cancers (HR = 0.69, p < 0.0001), but not RCC (HR = 0.96, p = 0.8). The same authors performed a meta-analysis of CALGB/SWOG 80405, FIRE-3, and PEAK, 3 trials that compared anti-EGFR against anti-VEGF when added to chemotherapy, totalling 1011 patients, and found a significant OS advantage in favour of anti-EGFR therapy for LCC (HR = 0.71, p = 0.0003), and a non-significant OS favouring anti-VEGF (HR = 1.3, p = 0.081) for RCC [35].
8. Primary tumour location and 2nd line metastatic setting
Retrospective analysis was performed on the efficacy of second line chemotherapy for 70% of patients (n = 411) treated within the FIRE-3 trial who progressed after first line therapy, in whom PTL was known. Comparable frequencies of oxaliplatin, fluoropyrimidines and other respective other antibody (-class) were used in both arms of FIRE-3. For both LCC and RCC, rates of uptake of second line therapy were similar. It was found that efficacy of second line therapy was significantly superior for LCC than for RCC, with longer PFS (6 v 3.8 months, HR = 0.61, 95% CI 0.47-0.78), as well as longer OS for LCC (15.9 v 11.0 months, HR = 0.64, 95% CI 0.49-0.84, p = 0.001). The choice of targeted first-line therapy influenced the PFS and OS of second-line therapy only for LCC, favouring a Cetuximab-Bevacizumab rather than a Bevacizumab-Cetuximab sequence (LCC OS 17.6 v 14.1 months, HR = 0.65, 95% CI 0.49-0.85, p = 0.002; RCC OS 11.0 v 12.4 months, HR = 1.02, 95% CI 0.64-1.61, p = 0.94). The survival differences observed between LCC and RCC and sequencing of biologic agent in this retrospective study were not thought to be due to a cross-over effect, but to be a result of different tumour biology. Furthermore, based on the different survival outcomes of second line therapy observed in this study, as well as the different survival outcomes noted in first-line setting of FIRE-3, the authors have proposed for RAS-WT advanced colorectal cancer an ideal sequencing of targeted therapy favouring anti-EGFR followed by Bevacizumab for LCC versus Bevacizumab followed by anti-EGFR for RCC [36].
9. Primary tumour location and 3rd line metastatic setting
Differences in outcomes between RCC and LCC were also observed in the setting of chemotherapy-refractory cancers within the Phase III CO.17 trial. In this trial, patients who had progressed on standard chemotherapy were randomised to Cetuximab or best supportive care (BSC), with overall survival significantly longer in the treatment versus the control arm (6.1 v 4.6 months, HR = 0.77, p = 0.005) [37]. Retrospective survival analysis found that PTL was not a predictor of prognosis (the survival of the BSC group was unaffected by PTL). However, analysis of the Ras-WT subgroup found that PTL was a predictive of a survival advantage from treatment with Cetuximab. For patients with LCC, the cetuximab group had a median overall survival of 10.1 months compared to 4.8 months for the BSC group (p = 0.002). For patients with RCC, a non-significant OS of 6.2 months v 3.5 months (p = 18) was observed [38].
10. Primary tumour location and anti-angiogenic therapy
There is limited published data surrounding the predictive impact of PTL on response to bevacizumab. PTL as a predictive marker of benefit from bevacizumab therapy in the setting of first line chemotherapy for metastatic colon cancer has been studied retrospectively in two randomised trials, AVF2107g (Irinotecan-based chemotherapy + Bevacizumab or Placebo) [39], and NO16966 (Oxaliplatin-based chemotherapy + Bevacizumab or placebo) [40], and one prospective pharmacogenetic study (PROVETTA), totalling over 2000 patients, and reported by Loupakis and co-authors [41]. In both randomized studies, PTL was a strong prognostic marker with LCC having better PFS and OS than RCC, but Bevacizumab efficacy was independent of PTL. The effect of PTL on outcomes of patients treated with Bevacizumab was also retrospectively assessed in the randomised Phase III MAX trial, which investigated capecitabine +/− Bevacizumab as 1st line treatment of metastatic colorectal cancer [42]. Data from this trial according to PTL was presented at the ESMO 2014 conference and suggested no difference in benefit between RCC and LCC [43]. The predictive value of PTL was assessed in relation to the benefit of the anti-VEGF inhibitor Aflibercept, when added to second-line FOLFIRI chemotherapy in the VELOUR study, and found not to be predictive of preferential outcomes for either RCC or LCC [44]. Therefore, it appears that based on the published evidence benefit from anti-angiogenic therapy does not depend on PTL.
11. Impact on primary tumour location on response to immunotherapy
Immunotherapy is rapidly increasingly important therapy for cancer and is at the forefront of research. This has particularly been the case for Melanoma and Lung Cancer, but evidence for its effectiveness in CRC is still trailing. A potential role for immunotherapy was envisaged for microsatellite unstable (MSI) colon cancers, with increased frequency of mutated cancer epitopes providing a milieu for heightened immunogenicity was put forward as an explanation [45]. Given that MSI CRC is more prominently found in RCC compared to LLC, one expects that successful immunotherapy in CRC might be the preserve of some subtypes (MSI) of metastatic RCC. Phase II data has recently been published demonstrating high response rates (40%) of MSI metastatic colon cancer to treatment with pembrolizumab compared to very low response rates (0%) in MSS colon cancers [46]. Phase III data is awaited to assess the magnitude of therapeutic benefit and also to ascertain whether dMMR will form the basis of a strong predictive biomarker to immunotherapy in colon cancer, and what place PTL might play in this regard. Currently, more mature Phase II data from the same authors, including the use of Pembrolizumab in tumour sites other than colon cancer, suggests that dMMR is a very strong predictive biomarker of response to Pembrolizumab [47]. Concerning the use of such treatment in colon cancers, PTL could not be considered a good predictive biomarker of response to Pembrolizumab, but at best be an incomplete surrogate marker of dMMR.
12. Effectiveness of metastatectomy according to PTL
The question of the prognostic impact of PTL on surgical outcomes of liver metastasectomies has been addressed in several retrospective series [48,49]. The consensus from these publications is that metastatic RCC has worse overall prognosis (worse OS), but that recurrence in the liver following hepatic resection is independent of PTL, whilst extra-hepatic recurrence is more common in rectal cancers. The same question has been posed in the case of pulmonary metastasectomy in a case series involving 698 patients, where lung metastases from rectal cancer were associated with worse 5 year disease-free survival (60.1%) compared to that of patients with lung metastases from colon cancer (67.2%, p = 0.004), even though overall survival was not different (p = 0.545). Owing to small numbers, the colon group was not further subdivided in RCC and LCC. In those patients with rectal cancer who recurred following pulmonary metastasectomy, the most common site of recurrence was lung, whereas for patients with colon cancer it was the liver (p = 0.0001) [50]. These retrospective case series highlight the different preferential locations of metastatic behaviour previously described between RCC and LCC. Although the differences in outcomes observed are insufficient to inform differential management, they identify questions to be tested in clinical trials.
13. Effectiveness of SIRT according to PTL
The impact of PTL has also been retrospectively investigated in relation to the effectiveness of selective Internal radiation therapy using yttrium-90 resin microspheres in patients with liver-predominant metastases from colorectal cancer [51]. SIRT did not result in improved survival when combined with chemotherapy in patients with liver-predominant metastatic disease [52]. In the combined analysis of three randomised trials (FOXFIRE, SIRLFOX and FOXFIRE-GLOBAL) that tested the use of mFOLFOX6 chemotherapy +/− SIRT therapy in a total of 1103 patients, no benefit in either median PFS (HR = 0.90; 95% CI 0.79-1.02, p = 0.108) or OS (HR = 1.04, CI 0.90-1.19, p = 0.609, 24.3 months with SIRT v 24.6 months without SIRT, p = 0.24) was found for the addition of SIRT in the overall population. However, when combined data from the SIRFLOX and FOXFIRE-GLOBAL was split according to PTL, a small but significant benefit in OS emerged for RCC as opposed to LCC (22.0 v 17.1 months, HR = 0.67 [0.48-0.92], p = 0.007) [51,53]. This data must be interpreted with caution given relative small numbers of patients and the retrospective nature of the analysis. The biology underpinning this observation is unknown. However this raises the possibility that liver metastases from RCC might respond better to radiotherapy than that those of LCC. Further clinical trials are warranted in this field, either for sole inclusion of RCC, or where PTL forms the basis of an integral pre-specified subgroup analysis.
14. Conclusions and discussion
Primary tumour location has emerged as an interesting prognostic and predictive marker in the therapeutic paradigm of colorectal cancer, particularly for metastatic disease. It has to be noted that the majority of data has been obtained through retrospective analysis of clinical trials and case series where PTL was neither part of the stratification, nor pre-planned subgroup analysis. Despite the caution in interpretation because of risk of recall bias the analyses are consistent in observing the same prognostic effect, with several studies establishing PTL as an independent prognostic marker. Furthermore, the predictive power of Left side in determining extra therapeutic benefit from anti-EGFR treatment is very strong whereas the data presented in this review questions any therapeutic benefit of these drugs in RCC. Our view is that clinicians and patients should carefully discuss the merits of adding anti-EGFR therapy to chemotherapy in metastatic RCC. The prognostic and predictive attributes of PTL add weight to the fact that RCC and LCC have different behaviours and are therefore distinct entities. The question currently is whether LCC and RCC are truly different diseases by virtue of their distinct embryological origins, or whether left and right are surrogate variables for an as yet to be determined molecular signature that predicts different disease behaviour and response to treatment. It is most likely the case that further research and discoveries in molecular subtyping will enable further refinement in the segregation of patients at a prognostic level but also eventually into responders and non-responders to novel therapies. It is also likely that there will be some overlap between this molecular stratification and primary tumour location according to a RCC v LCC dichotomy. Short of possessing a robust molecular stratification system to guide choice of therapy for patients undergoing systemic treatment, segregating patients according to RCC v LCC is a useful and pragmatic approach to guide decision-making regarding biological agents and should be adopted by oncologists in clinical practice. Future clinical trials will benefit from PTL data being prospectively collected and some clinical trials should in our view stratify participants according to PTL. This is particularly the case for clinical trials investigating drugs targeting the EGFR pathway, given the very strong benefit in RAS-WT LCC compared to RCC treated with these agents.
Acknowledgements
The authors declare no conflict of interest.
Conflict of interest
PJR has received grant funding from Sanofi, speakers fees from Amgen, Merck-Serono, Servier and Sirtex.









 DownLoad:
DownLoad: