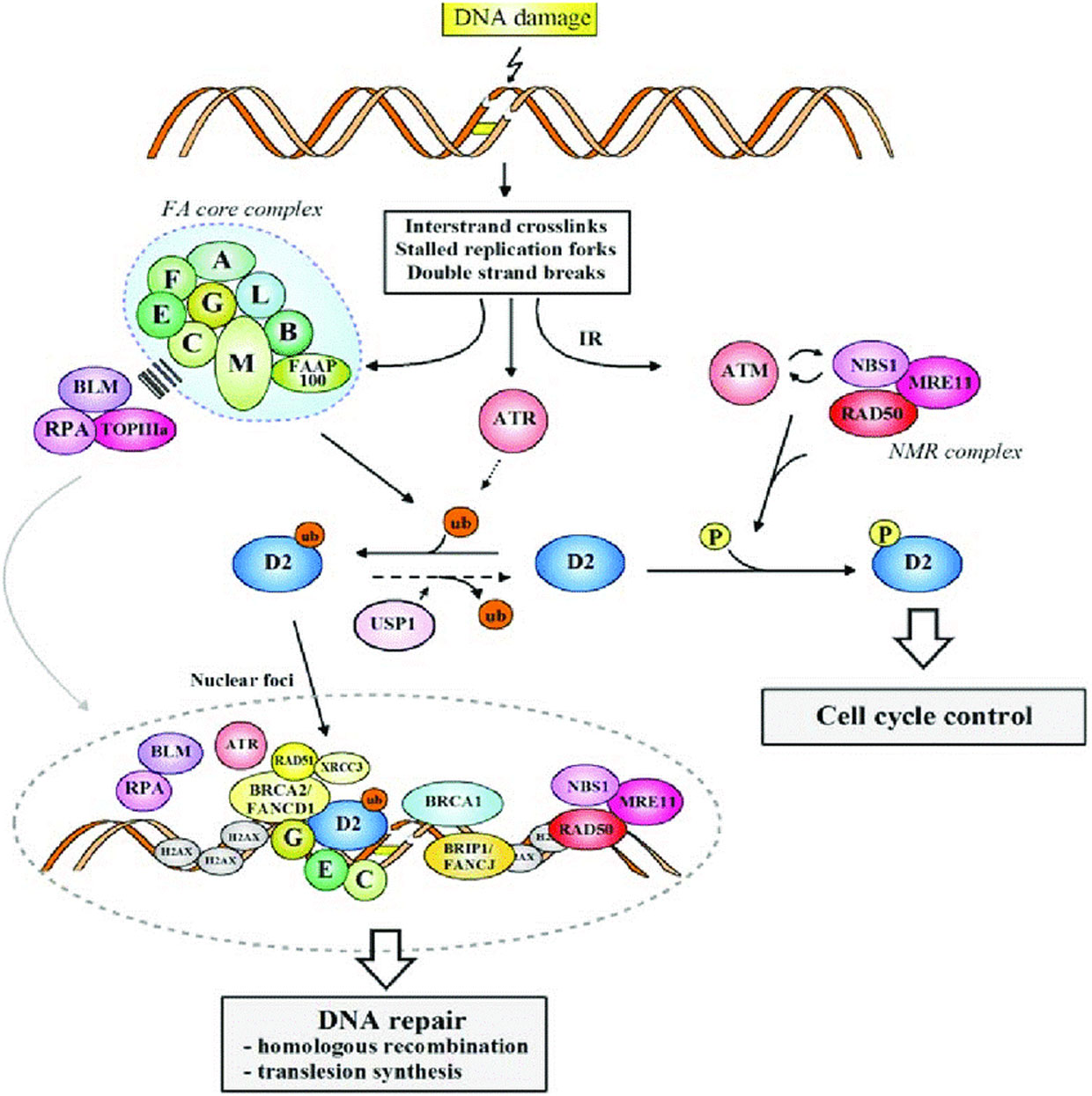
Fanconi anemia (FA) is a rare genetic disorder characterized by multiple congenital malformations, progressive bone marrow failure, and susceptibility to cancer. The FA-D1 subtype is associated with biallelic mutations in the breast cancer 2 genes also known as FANCD1. Patients with this mutation display severe disease phenotype. In addition, different types of cancer other than breast cancer are associated with this mutation, such as leukemia, solid tumors of the central nervous system, etc. In this review, we have surveyed the literature on FA, FA genes, their biological roles, and specifically discussed the current information available on the FA-D1 disease subtype. The observations show that the timing of biallelic loss of BRCA2 can establish the specific cancer spectrum. The knowledge about effects of the FANCD1/BRCA2 mutation on FA and cancer pathogenesis can be used for further understanding the FA-D1 subtype of the disease.
1.
Introduction
Since the pioneering works of Lorentz [1] and Oseen [2], the use of fundamental solutions has become a common and widely applied approach (referred to as the method of hydrodynamic singularities) for solving incompressible Stokes flows [3,4,5]. Important theoretical results in low-Reynolds number hydrodynamics have been obtained in this way, for instance, in quantifying the resistance of an arbitrarily shaped particle in a confined fluid [6], in constructing exact solutions for simple flows [7,8], in expressing the Generalized Faxén theorem [9] for generic immersed bodies. Furthermore, hydrodynamic singularities represent also one of the principal tools in numerical methods, such as Stokesian dynamics [10] or the Method of Fundamental Solutions [11].
Depending on the presence of a solid boundary at finite distance from the pole of the singularity, a distinction can be made between unbounded and bounded singularities [4]. In dealing with bounded singularities we consider, throughout this article, exclusively no-slip conditions at the boundaries.
In the unbounded case, all the hydrodynamic singularities can be constructed starting from the Green function for the Stokes flow, representing the lowest-order singularity, referred to as the Stokeslet [12], the Oseen tensor [3] or the Lorentzlet [13], see also [14] for a gradient-gauge approach, by applying to it a differential operator at the pole or at the source point. The relative simplicity in constructing hydrodynamic fields as a linear superposition of a collection of unbounded singularities has made the use of singular solutions extremely popular in the analytical description of velocity fields originated by the motion of solid bodies with different geometries in a Stokes fluid, thus simplifying considerably their representation with respect to those obtained by means of other approaches involving polar coordinates or multipole expansions [3]. Some well-known examples of solutions of hydrodynamic problems expressed in the singular representation refer to the motion of solid spheres [15], ellipsoids [7,8,9,16], tori [17] or slender bodies [12,18,19,20] in unbounded Stokes fluids. Moreover, the singular representation of the solutions of the Stokes flow has been used for characterizing the locomotion of microorganisms [12,21], and the rheological behavior of suspensions and complex fluids [22,23].
In the overwhelming majority of these works, the singularity functions are represented in a Cartesian reference system, since either the flow domain is unbounded, or, in the bounded case, the singularities lie on a flat manifold (mainly points and lines). In point of fact, a general theory of the Stokes singularities, should take into account any possible system configuration, that can, in principle, be constituted by curved boundaries (such as cylindrical channels, spheroidal capsules, wavy surfaces etc.), and immersed curved objects (helical flagellae, biconcave disk shaped cells etc.), for which it is convenient to associate singularities lying on curved manifolds due to their symmetries. Therefore, it may happen that the appropriate coordinate system for specific hydrodynamic problems is curvilinear. As well known, Navier-Stokes fields are invariant under coordinate transformations and, it easy to show, that hydrodynamic singularities are invariant also at the pole.
Tensor calculus [24] is the natural geometric framework for addressing invariance with respect to coordinate systems. In dealing with the singularity approach to Stokes flows, the singular fields depend at least on two points (and in principle, are multi-point functions), the source (at the pole of the singularity) and the field point (at the fluid element position). Consequently, a generalization of tensor calculus is required, represented by the bitensorial formalism [25,26,27], specifically developed for handling the Green functions in field theoretical developments within the theory of general relativity. The bitensor calculus, developed originally by Ruse [25], and further extended by Synge [26] and De Witt [27] for describing multi-point dependent fields in general relativity, is an extension of the tensor calculus that allows us to distinguish between the components of two-point dependent tensors (such as the Stokes singularities) and to make operations between them by means of the so called parallel propagator. A thorough analysis of bitensor calculus can be found in [28], while Appendix A succintly reviews the main concepts used in this article.
One goal of the present article is to develop a bitensorial formalism that ensures and preserves in a simple way invariant relations for the hydrodynamic singularity functions both at the source and the field points. In a broader perspective, the aim of this work is not only to transfer the bitensor formalism to the analysis of the hydrodynamic Green functions, which is a useful task in itself, as it makes the Stokesian formalism clear and unambiguous, but also to derive out of this formalism new hydrodynamic properties and operators. A significant example involves the generalization of the Faxén operator associated with an immersed body. In the hydrodynamic literature [3,4], the Faxén operator associated with an immersed body is defined as the integro-differential operator that, once applied to the ambient velocity field, provides the force acting on the body. Specifically, we derive the analytic expression for the generalized $ n $-th order Faxén operator that, starting from the fundamental Green function (e.g., a Stokeslet), provides the disturbance field associated with an $ n $-th order ambient flow (see Section 5 for details).
The article is organized as follows. Section 2 introduce the tensor algebra within the framework of the Stokes equations. In Section 3, we show how bitensor calculus eliminates the formal ambiguities (related to the meaning of the tensorial indices, and to the action of linear operators on tensorial singularities) occurring in the current formulation of Stokesian hydrodynamics [3,4] and it allows us to obtain a clear definition of singular solutions of Stokes flow (bounded and unbounded), specifying the associated homogeneous equations and boundary conditions.
Since the Stokes singularities can be viewed as generalized functions (or distributions), the generalized function theory [29] and its connections with the theory of moments [30] are applied to bitensorial quantities of hydrodynamic interest in Section 4. Specifically, we show that the linear operator providing the singularity system of a bounded flow is uniquely specified by the system of moments associated with the forces acting on the obstacle. Although the present definition of moments is altogether different from that proposed in [31], where, assuming no-slip boundary conditions, the moments are defined by surface integrals of the stress tensor, the two approaches yield the same final result as regard the expression of the disturbance field, showing that the no-slip boundary condition assumption is unnecessary. This represents the only intersection point between the present theory and the one developed by Ichiki [31] in the particular case of no-slip spheres in a Stokes flow. In Section 5, we introduce the $ n $-th order Faxén operator, and we derive an $ n $-th order Faxén theorem, by expressing a generic disturbance field as a series expansion involving the $ n $-th order Faxén operators.
In Section 6, the operator yielding the disturbance field associated with a Stokeslet is considered showing that it is directly related to the reflection operator [32,33] of the geometry considered. This result is applied in Section 7 to the singularities near a plane wall. The characterization of the singularities bounded by a no-slip planar wall has been analyzed in the literature either as a reflection problem [1,34,35] or using a system of image singularities [36,37]. These two approaches are reviewed in [3]. We show in Section 7 that the present formalism highlights the equivalence between these two approches. In fact, the same differential operator furnishes directly either the Lorentz's mirror form of the solution, if applied at the field point, or the Blakes' singularity solution form, if applied at the source point of the Stokeslet. Moreover, since the position of the pole enters as a variable in the reflection operator, this formalism overcomes the original shortcomings in obtaining the higher order bounded singularities by differentiating the Green's function at the pole, due to the fact that, in the Blake's solutions, the distance of the pole from the plane enters as a parameter. In this way, we obtain unknown (Source Dipole and Stresslet) and known (Rotlet and Sourcelet) bounded singularities, the latter ones already derived in [37] by means of a more elaborate Fourier-Hankel transform.
2.
The Stokes flow equations
If a Newtonian fluid, possessing viscosity $ \mu $, is subjected to a volume force field $ {\bf f}({\bf x}) $, the controvariant components of the stress field $ {\pmb \sigma}({\bf x}) $, the velocity $ {\bf v} ({\bf x}) $ and the scalar pressure field $ p({\bf x}) $ are solution, for vanishing Reynolds number, and under steady conditions, of the Stokes equations [38]
$ a = 1, 2, 3 $ where $ V_f $ is the fluid domain. Throughout this article, the Einstein summation convention is adopted. The operators $ \nabla_a $ and $ \nabla^a $ in Eq (2.1) represent the covariant and controvariant derivatives, respectively, related by the transformation $ \nabla_a = g_{a b} \nabla^b $, where $ g_{a b} = g_{a b}({\bf x}) $ is the metric tensor [39] and $ \Delta_{x} = g^{ab}\nabla_a\nabla_b $ is the Laplacian operator at the point $ {\bf x} $. For a rank-2 tensor $ T^a_{\ b} $ in mixed representation, its covariant derivative reads
where $ T^a_{\ b; c} $ is an alternative and more compact notation for the covariant derivative of $ T^a_{\ b} $, and $ \Gamma_{m c}^{a} $ are the Christoffel symbols
Henceforth, we will use both the notations $ \nabla_c T^a_{\ b} $ and $ T^{a}_{\ b; c} $ for the covariant derivatives.
The component of the associated stress tensor for a Newtonian incompressible fluid are therefore expressed by [38]
As well known, the controvariant components of the generic tensorial field $ {\bf f} ({\bf x}) = (f^a({\bf x})) $ change from the coordinate system $ \{ x^a \} $ to a new system $ \{ \tilde{x}^a \} $ via a linear transformation defined by the matrix $ \left(\frac{\partial \tilde{x}^b}{\partial x^a}\right) $
whereas the inverse matrix at the point $ {\bf x} $ yields the transformation of the covariant components
3.
Bitensorial fundamental solutions of the Stokes flow
In this section we extend the tensorial notation to the case of the fundamental solutions of the Stokes flow, with the aim of obtaining a clear definition of its singular solutions From the theory of distributions, we can write the fields entering Eq (2.1) equipped with homogeneous Dirichlet boundary condition at $ \partial V_f $ as volume potentials [40], with a kernel $ \mathrm{G}_{\ \alpha}^a({\bf x}, {\pmb \xi}) $ for the velocity field
and a kernel $ \mathrm{P}_{\alpha}({\bf x}, {\pmb \xi}) $ for the pressure field
where $ f^{\alpha}({\pmb \xi}) $ are the controvariant components of the force field at a source point $ {\pmb \xi} $, $ g({\pmb \xi}) = \det(g^{ab}({\pmb \xi})) $ and $ d^3\xi = d\xi^1d\xi^2d\xi^3 $. Observe that the coordinate representation of the source point $ {\pmb \xi} $ could in principle be different from that of the field point $ {\bf x} $. This fact is notationally highlighted throughout the article, by using greek letters instead of latin ones for any index $ \alpha = 1, 2, 3 $ referred to the entries of tensorial entities evaluated at the source point. Therefore, the transformations for the controvariant and covariant components of $ {\bf f}({\pmb \xi}) $ at the source point read
where $ \xi^{\beta'} $ are the components of $ {\pmb \xi}' $. This notation, with primed indices to indicate the transformed coordinated, will be used throughout the article.
The kernels $ \mathrm{G}_{\ \alpha}^a({\bf x}, {\pmb \xi}) $ and $ \mathrm{P}_{\alpha}({\bf x}, {\pmb \xi}) $ are two-point dependent distributions, with tensorial character both at $ {\bf x} $ and $ {\pmb \xi} $, thus corresponding to bitensorial quantities [25,26,27,28]. This is a common feature of any fundamental solutions (or Green functions) in mathematical physics. Further details on the theory of bitensors are succintly reviewed in Appendix A. Specifically, the kernel entries $ \mathrm{G}_{\ \alpha}^a({\bf x}, {\pmb \xi}) $ are the components of a bitensor with vectorial character both at the source and the field point, and consequently their transformation in new coordinate systems both at the source and the field points takes the form
whereas the transformation rule for the pressure bitensor, with scalar character at the field point $ {\bf x} $ and vectorial at the source point $ {\pmb \xi} $, is given by
Finally, using the invariance properties of the Dirac delta function [28] and the parallel transport of tensorial quantities, it is possible to express the force field entering Eq (2.1) as
where $ g_{\ \alpha}^{a} ({\bf x}, {\pmb \xi}) $ is the parallel propagator bitensor, which propagates in a parallel way a vector along the unique geodesics connecting $ {\bf x} $ to $ {\pmb \xi} $. In a distributional meaning, it follows that $ g^a_{\alpha}({\bf x}, {\pmb \xi}) \delta({\bf x}, {\pmb \xi}) = \delta^a_{\ \alpha}\delta({\bf x}, {\pmb \xi}) $ being $ {\bf x} $ and $ {\pmb \xi} $ coincident.
By substituting Eqs (3.1), (3.2) and (3.6) in Eq (2.1), we obtain the bitensorial Green function equations of the Stokes flow, yielding the velocity and pressure at the field point $ {\bf x} $ due to an impulsive force acting at the source point $ {\pmb \xi} $
From Eq (2.4), the stress field $ \mathrm{\Sigma}^{a b}_{\alpha}({\bf x}, {\pmb \xi}) $ associated with the Green function is defined by
In the case the source point is kept fixed, bitensors become simple tensors depending only on the field point. Therefore, by choosing the force field $ {\bf f} ({\pmb \xi}) = {\bf f}_0 \delta({\pmb \xi} - {\pmb \xi}_0) $, from Eqs (3.1) and (3.2), we obtain the velocity/pressure fields due to an impulsive force with intensity $ {\bf f}_0 $ placed at a singular point $ {\pmb \xi}_0 $
for which the stress tensor $ \sigma^{ab}({\bf x}) $ takes the form
The reciprocity relation [3,4] for the Green function in bitensorial notation becomes
By exchanging $ {\bf x} \leftrightarrow {\pmb \xi} $, and thus $ a \leftrightarrow \alpha $, and enforcing the reciprocity relation (3.12), it follows that $ \mathrm{G}^a_{\ \alpha}({\bf x}, {\pmb \xi}) $ is also the solution of the system
where $ \Delta_{\xi} = g^{\alpha \beta}({\pmb \xi})\nabla_\alpha \nabla_\beta $ is the Laplacian at point $ {\pmb \xi} $. In this case, the associated stress field becomes
Since the Green function vanishes at $ {\pmb \xi} \in \partial V_f $ for any $ {\bf x} $, $ \mathrm{P}_{\alpha}({\bf x}, {\pmb \xi}) $ must be constant for $ {\pmb \xi} \in \partial V_f $ due to Eq (3.7), and therefore can be set equal to zero. Furthermore, the pressure scalar-vector $ \mathrm{P}_{\alpha}({\bf x}, {\pmb \xi}) $ is a potential scalar field at $ {\bf x} $ possessing the following properties
The first relation stems from Eq (3.7), by taking the divergence with respect to $ {\bf x} $, while the second relation follows by taking the divergence with respect to $ {\pmb \xi} $, enforcing the second relation in Eq (3.13). In a similar way, $ \mathrm{P}^a({\pmb \xi}, {\bf x}) $ fulfills the relations
Observe that Eq (3.15) for $ \mathrm{P}_{\alpha}({\bf x}, {\pmb \xi}) $, and likewise Eq (3.16) for $ \mathrm{P}^a({\pmb \xi}, {\bf x}) $ do not constitute a boundary value problem for the pressure variable, as the boundary condition is assigned for a variable ($ {\pmb \xi} $ in Eq (3.15)) different from that involved in the differential equation ($ {\bf x} $ in Eq (3.15)), thus representing a collection of properties fulfilled by the pressure field.
To obtain the higher order singularities, the Green function should be differentiated at the pole $ {\pmb \xi} $ maintaining homogeneous Dirichlet conditions at the field point. The first derivative at the pole yields the Stokesian dipole, the second derivative the Stokesian quadrupole and so on.
The Stokesian dipole $ \mathrm{G}^a_{\ \alpha; \beta}({\bf x}, {\pmb \xi}) $ can also be expressed as superposition of two other singular solutions of the Stokes equations: a symmetric and an antisymmetric tensor field at the source points
where
is the field due to a singular strain of the fluid at the source point, and
where $ \varepsilon_{\alpha \beta \gamma} $ is the Levi-Civita symbol (in the italian mathematical literature also called the Ricci tensor [38]), is the field due to a singular rotation of the fluid at the source point.
The symmetric strain component is the solution of the Stokes system of equations
which can be also computed directly from Eqs (3.13), (3.14) by exchanging source and field points in the pressure and stress fields related to the solution of the Green function
The antisymmetric part of the Stokes dipole corresponds to the solution of the Stokes system
A further differentiation at the pole defines the Stokes quadrupole. Specifically, by applying the Laplacian operator $ \Delta_{\xi}/2 $ to the Green function, we obtain the so called Source Dipole
Also the solution of this system can be obtained by exchanging source and field points in the gradient of the pressure field associated with the Green function. In point of fact, from the first relation in Eq (3.13), we have
3.1. Unbounded singularities
In this paragraph, unbounded singularities are briefly analyzed. Due to translational invariance, the singularities in $ \mathbb{R}^3 $, depend solely on the vector $ {\bf x}-{\pmb \xi} $. Henceforth, the unbounded singular functions will be indicated by sans-serif capital letters. The Green function $ \mathsf{S}_{\ \alpha}^a({\bf x}-{\pmb \xi}) $, usually referred to as the Stokeslet, is the solution of the Stokes problem
Since the Laplacian is invariant under translation (and, more generally, under Euclidean transformations [41]), we have for a generic function $ f({\bf x}-{\pmb \xi}) $, $ \Delta_{x-\xi} f({\bf x}-{\pmb \xi}) = \Delta_{x} f({\bf x}-{\pmb \xi}) = \Delta_{\xi} f({\bf x}-{\pmb \xi}) $. Therefore, it is possible to express the pressure in Eq (3.15) as the solution of the harmonic problem
thus
while that the associated velocity and stress-tensor fields are given by [4,14]
As $ \mathsf{P}_{\alpha; \beta}({\bf x}-{\pmb \xi}) = \mathsf{P}_{\beta; \alpha}({\bf x}-{\pmb \xi}) $, the symmetric part of the Stokes dipole corresponds to the solution of the problem
and due to Eq (3.21) it takes the expression
This field can be viewed as the superposition of two terms: the contribution $ \mathsf{M}^a({\bf x}-{\pmb \xi}) = -\mathsf{P}^a({\pmb \xi}-{\bf x})/2 $, which is the solution of a Stokes problem everywhere but at the pole
Strictly speaking, the field $ \mathsf{M}^a({\bf x}-{\pmb \xi}) $, usually called the Sourcelet [4,37], is not a Stokesian singular solution, since its divergence does not vanish at the pole and, thus, it does not satisfy the overall mass balance over the fluid. It can be physically interpreted as the velocity field stemming from a pointwise fluid source (or sink, if the sign is reversed) at the pole. Its bounded counterpart can be defined solely for external problems, so that it could match the regularity condition and the overall mass balance at infinity. However, it cannot be generally neither obtained from the Green function (as the Green function is divergence-free), nor it is related to the Green function pressure field, as in the unbounded case.
Similarly, also the second term is not a singular Stokesian solution. In fact, the field $ \mathsf{T}^a_{\alpha \beta}({\bf x}-{\pmb \xi}) = \mathsf{\Sigma}^a_{\alpha \beta}({\pmb \xi}-{\bf x})/2 $, called the Stresslet, is the solution of the problem
possessing non vanishing divergence. Therefore, the symmetric Strainlet Eq (3.31) can be expressed as
Next consider the antisymmetric term defined by Eq (3.19). In unbounded flows $ \mathsf{\Omega}^{a \gamma}({\bf x} - {\pmb \xi}) $ is referred to as the Rotlet. Since $ \varepsilon^{\gamma \epsilon \eta}\mathsf{P}_{\epsilon; \eta}({\bf x}-{\pmb \xi}) = 0 $, the Rotlet is a constant pressure solution of the Stokes system
the analytic expression of which is
Another low order irrotational singularity of the Stokes problem is the solution of Eq (3.23) in unbounded domain, namely
This solution, referred to as the Source Doublet, can be obtained from Eq (3.25) and from the definition of $ \mathsf{M}^a({\bf x}-{\pmb \xi}) $
4.
Singular representation of bounded flows
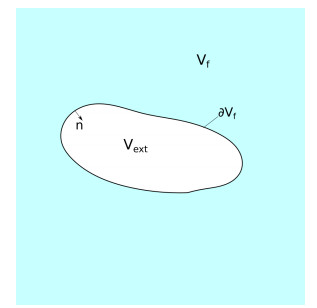
In the previous section we have discussed how all the singularities of bounded flows can be obtained by differentiating the Stokeslet at its pole. In this Section, we develop a method to obtain the singular representation of a Stokes flow in a given domain $ V_f $ containing solid boundaries by means of a linear operator applied to the Stokeslet in the external domain $ V_{ext} \equiv \mathbb{R}^3/V_f $, and yielding the disturbance field in $ V_f $. More precisely, consider a given solution $ {\bf u}({\bf x}) $ of the Stokes equation in $ V_f $, attaining arbitrary values at the boundaries $ \partial V_f $ (at which, the Stokes problem dictates no-slip boundary conditions). The velocity field $ {\bf u}({\bf x}) $ is referred to as the ambient flow. In order to match the no-slip boundary condition, a disturbance flow $ {\bf w}({\bf x}) $ should be added so that $ {\bf v}({\bf x}) = {\bf w}({\bf x})+{\bf u}({\bf x}) $ is the Stokes solution within $ V_f $ satisfying the no-slip conditions on $ \partial V_f $. Thus, the disturbance flow is a solution of the equations
where $ q({\bf x}) $ is the associated pressure field. It is convenient to extend this problem over the whole physical space $ \mathbb{R}^3 $ in order to obtain its singular representation. To this purpose, we can formulate the problem defined by Eq (4.1) in the form of the non-homogeneous unbounded Stokes equations in $ {\mathbb R}^3 $ as
with the condition that $ f^a({\bf x}) $ are distributions defined on a compact support in $ V_{ext} $, and satisfying the integral equation
Let us introduce the $ n $-th order tensorial moments of the function $ {\bf f}({\bf x}) $, extending the scalar moment theory [30], as
or, using the scalar-product notation on the external domain
where $ \langle \cdot, \cdot \rangle $ indicates the scalar product in $ V_{ext} \equiv {\mathbb R}^3/V_f $, $ {\bf a}_n = (a_1, \dots, a_n) $ is a multi-index, $ g_{{\pmb \alpha}_n}^{\ {\bf a}_n}({\pmb \xi}, {\bf x}) = g_{\alpha_1}^{\ a_1}({\pmb \xi}, {\bf x})... g_{\alpha_n}^{\ a_n}({\pmb \xi}, {\bf x}) $ and $ ({\bf x} -{\pmb \xi})_{{\bf a}_n} = ({\bf x} -{\pmb \xi})_{a_1}... ({\bf x} -{\pmb \xi})_{a_n} $. It is shown in Appendix B that the moments $ M^a_{\ {\bf a}_n}({\pmb \xi}) $ can be reduced to the Ichiki's surface integrals [31] in the case that the no-slip boundary conditions are assumed, thus
where $ {\pmb \sigma}({\bf x}) $ is the stress tensor related to the total velocity field $ {\bf v}({\bf x}) $, and $ n_b({\bf x}) $ the covariant components of the outwardly oriented normal unit vector at points $ {\bf x} $ of $ \partial V_{f} $ as shown in Figure 1. Therefore, given a reference point $ {\pmb \xi} $, all the moments on the volume $ V_{ext} $ are uniquely determined by the stress field at the surface, since Eq (4.6) does not depend on the chosen function $ {\bf f}({\bf x}) $.
Consider the tensorial Taylor expansion [42] of the components of the vectorial test function $ {\pmb \phi}({\bf x}) $ around a given point $ {\pmb \xi} \in V_{ext} $
where $ \nabla_{{\pmb \alpha}_n} = \nabla_{\alpha_1} \cdots \nabla_{\alpha_n} $. Owing to the bitensorial notation, there is no ambiguity in the definition of $ \nabla_{{\pmb \alpha}_n} $ as greek indices refer to the source point.
Applying the test function to the momentum balance equation entering Eq (4.2) we have
where we have made use of the relations $ g_a^{\ \alpha}({\bf x}, {\pmb \xi}) = g_{\ a}^{\alpha}({\pmb \xi}, {\bf x}) $ and $ ({\bf x}-{\pmb \xi})^{{\pmb \alpha}_n} = (-1)^n ({\pmb \xi}-{\bf x})^{{\pmb \alpha}_n} = ({\bf x}-{\pmb \xi})^{{\bf a}_n} g_{{\bf a}_n}^{\ {\pmb \alpha}_n}({\pmb \xi}, \bf x) $ see Appendix A.
Since the derivatives of the test functions can be formulated in scalar-product notation as
substituting Eq (4.9) into Eq (4.8), the function $ {\bf f}({\bf x}) $ can be finally expressed as
Although the moments depend on the reference points $ {\pmb \xi} $, the summation in Eq (4.10) does not depend on $ {\pmb \xi} $. Therefore, Eq (4.10) can be generalized by considering $ {\pmb \xi} $ as a point of an arbitrary $ k $-dimensional ($ k \leq 3 $) set of points $ \Omega $, averaging Eq (4.10) over $ \Omega $,
where $ d\Omega({\pmb \xi}) $ is the measure element and
is the Lebesgue measure of $ \Omega $. Depending on the symmetries of the flow geometry, the set $ \Omega $ can be chosen in some particular cases as to reduce the infinite summation entering Eq (4.11) to a finite number of terms.
From the structure of Eq (4.10) we can introduce a differential operator
that in Eq (4.10) acts on the Dirac delta function. In a similar way, if Eq (4.10) is generalized by Eq (4.11), the operator $ \mathcal{D}^{*\alpha} $ attains an integro-differential representation
so that $ f^a = \mathcal{D}^{*\alpha}g^a_{\ \alpha}({\bf x}, {\pmb \xi}) \delta({\bf x}, {\pmb \xi}) $. Its adjoint $ \mathcal{D} $, $ \langle {\mathcal D}^{* a} f, g \rangle = \langle f, \mathcal{D} g \rangle $, is expressed by
Therefore, the problem defined by Eq (4.2) can be reformulated as
and the singular representation of the velocity field $ {\bf w}({\bf x}) $ follows from Eqs (3.1) and (3.2), namely
and
where the scalar products in Eqs (4.16), (4.17) correspond to an integration over $ {\pmb \xi}' $. Thus the operator $ \boldsymbol{ \mathcal{D}} $ defined by the (4.14) provides the singular expansion, of the flow at the source point $ {\pmb \xi} $.
The existence of an integro-differential operator yielding the disturbance field once applied to the Stokeslet is hypothesized in Stokesian hydrodynamics for solid bodies [9,43] and, more generally, in developing the singularity method [4]. The procedure outlined above, based on the generalized function theory, provides an explicit expression for this operator in the form of a series expansion the coefficients of which are the moments. The main advantages of this explicit representation are: (i) for a specific flow problem the terms in the series expansion of the operator can be obtained numerically with arbitrary precision, (ii) it is possible to manipulate its formal structure in order to obtain new relations as will be shown in the next Sections.
5.
Representation of the $ n $-th order Faxén operators
In this section we focus on the Stokes flow around an object with no-slip boundary condition, thus considering the external volume $ V_{ext} \equiv V_B $, where $ V_B $ is the domain occupied by the object, bounded by the closed surface $ \partial V_B $. In this case $ V_f = {\mathbb R}^3 / V_B $. For this class of hydrodynamic problems, the Faxén operator, and its generalizations, play an important role. In fact, as shown by Kim [9], the linear operator that, applied at the pole of the Stokeslet gives the velocity field due to a particle translating into the fluid, coincides with the operator that, applied to an ambient flow, returns the force onto the particle immersed in the flow. This operator takes its name from Faxén (see [23]), who derived its expression for the first time providing the force on a sphere from the values of the field and its Laplacian at the center of a spherical object. A corresponding theorem holds also for rotations and strains of the body.
Faxén operators for objects with geometry different from the sphere can be expressed in infinite series involving the derivatives of any order of the field evaluated at points within the domain corresponding to the object [44]. Exploiting the symmetry of particular objects, such as spheroids [7,8], ellipsoids [3], tori [17], etc., it is possible to express the same operator by means of a finite system of derivatives of the field evaluated on a manifold $ \Omega \subset V_B $, such as the focal axis, the focal ellipse, the symmetry circle, etc..
Making use of the concepts and the formalism developed in Sections 3 and 4, and considering the Stokes flow around an object, below we derive the properties and the analytical representation of a generalization of the Faxén operator, referred to as the $ n $-th order Faxén operator. To this aim, let us consider the disturbance field $ {\bf w}_{(n)}({\bf x}; {\pmb \xi}') $ of a purely $ n $-th order unbounded ambient flow centered at the point $ {\pmb \xi}' $,
with pressure
and stress field
i.e., the solution $ ({\bf w}_{(n)}({\bf x}), {\pmb \tau}_{(n)}({\bf x})) $ of the following Stokes problem
where the subscript "$ (n) $" is not a tensorial index, but simply indicates that an $ n $-order ambient flow is considered. As in Section 4, let us introduce the $ m $-th order moments, associated with the stress tensor $ {\pmb \sigma}_{(n)}({\bf x}; {\pmb \xi}') = {\pmb \tau}_{(n)}({\bf x}; {\pmb \xi}')+{\pmb \pi}_{(n)}({\bf x}; {\pmb \xi}') $
From the definition and the linearity of the problem, the moments in Eq (5.5) can be rewritten as,
where the latter equation can be viewed as the definition of the geometric moments $ m^{\alpha \ \ \beta}_{\ {\pmb \alpha}_m\ {\pmb \beta}_n}({\pmb \xi}; {\pmb \xi}') $. In fact, enforcing linearity, i.e., $ \sigma^{ac}({\bf x}; {\pmb \xi}') = A^{\ {\bf b}_n}_b \hat{\sigma}_{{\bf b}_n}^{acb}({\bf x}; {\pmb \xi}') $, one obtains for the geometric moments the following expression
Geometric moments possess the following symmetry
that can be proved by applying the Lorentz reciprocal theorem
Componentwise Eq (5.9) reads
from which Eq (5.8) follows.
Let us define the following integro-differential operator
the adjoint of which is given by
and introduce also its contracted form
From the analysis developed in Section 4, the Stokes problem (5.2) can be extended in $ \mathbb{R}^3 $ in the singular form as
and from Eqs. (4.13)–(4.16), the velocity field solution of Eq (5.14) is given by
Since it is possible to express the ambient velocity field $ {\bf u}_{(n)}({\pmb \xi}) $, $ {\pmb \xi} \in V_B $, within the domain of the body in the surface integral form [4,40]
by applying the operator $ \mathcal{F}_{\alpha}^{(n)} $ to the above ambient flow we obtain
which, due to Eq (4.6), implies
Therefore, the integro-differential operator defined by Eq (5.11) returns either the $ n $-th order disturbance flow, once applied to the Stokeslet according to Eq (5.15), or the $ n $-th order moment (4.6) once applied to the ambient flow according to Eq (5.18). In virtue of these properties, we can refer to $ \mathcal{F}_{\ \ \ {\pmb \alpha}_n}^{\beta \alpha} $ as the generalized $ n $-th order Faxén operator.
We can now express the disturbance velocity field entering Eq (4.16), in the presence of generic Dirichlet boundary condition on the surface of the body, as
Expliciting the Faxén operator, and making use of the symmetries of the geometric moments entering Eq (5.8), we obtain
and since
the disturbance velocity field can be expressed as a series expansion involving the generalized Faxén operators
Equation (5.22) can be rewritten in a more compact form as
where $ \mathcal{F}^{\alpha }_{(m)} = 8\pi\mu A_\beta^{\ {\pmb \beta}_m}\mathcal{F}^{\alpha \beta }_{\ \ \ {\pmb \beta}_m} $, as in the definition Eq (5.13), and the expansion coefficients $ A_\beta^{\ {\pmb \beta}_m} $ are given by
Equation (5.23) provides a compact and elegant way to decompose the disturbance field due to a body immersed in an ambient flow in elementary motions associated with the different $ n $-order velocity fields defined at the boundary of the object.
6.
Reflection operator
In hydrodynamics problems involving bounded flows and confined geometries, the Green function $ \mathrm{G}_{\ \alpha'}^a({\bf x}, {\pmb \zeta}) $, solution of the equations
(referred for short to as the bounded Green function) plays a central role as it provides the volume potential in the fluid domain $ V_f $, starting from which any flow with no-slip boundary conditions at $ \partial V_f $, can be constructed.
Bounded Green function are available in the literature for a handful of simple geometries, as reviewed in [4]. In special cases, such as for the Green function of a fluid bounded by a plane [36] or outside a sphere [45,46] (see also [3]), a representation of the bounded Green function in terms of unbounded singularities placed outside the fluid domain is available. This representation is referred to as the image system [3], which is particularly handy for analytical and numerical calculations whenever the set of singularities is either finite or localized on simple manifolds. The latter property characterizes flows with suitable and simple symmetries while, for generic bounded flows, an image system of singularities is not available.
Based on the theory developed in Section 4, this Section addresses the properties of the operator providing the image system for a generic bounded Green function. To this aim, let us to consider as the ambient field the unbounded flow due to a Stokeslet centered at the point $ {\pmb \zeta} \in V_f $ and let us use the primed indices, say $ \alpha', \beta', ... $, for referring to this point
As a consequence, the boundary condition for the disturbance field is given by
Owing to linearity, let us define the field $ \mathrm{W}^a_{\ \alpha'}({\bf x}, {\pmb \zeta}) $, depending on $ {\pmb \zeta} $, but regular at this point, such that
The theory developed in Section 4 can be applied, and enforcing Eq (4.16) the field $ \mathrm{W}^a_{\ \alpha'} $ is given by
where
Therefore, the Green function solution of Eq (6.1) can be expressed as the sum of two contributions: a singular part, due to the Stokeslet centered in the point $ {\pmb \zeta} $, and a regular part due to the integro-differential operator $ \mathcal{D}^\alpha_{\ \alpha'} $ acting on the poles of the Stokeslet outside the domain of the fluid
Owing to the properties of the Green functions, the same result can be obtained by applying the operator $ \mathcal{D}^\alpha_{\ \alpha'} $ at the field point. In point of fact, making use of the reciprocal identities for the Green functions, $ \mathrm{G}^{a}_{\ \alpha'}({\bf x}, {\pmb \zeta}) = \mathrm{G}^{\ a}_{\alpha'}({\pmb \zeta}, {\bf x}) $ and $ \mathsf{S}^{a}_{\ \alpha'}({\bf x}, {\pmb \zeta}) = \mathsf{S}^{\ a}_{\alpha'}({\pmb \zeta}, {\bf x}) $, it follows that
where, due to the reciprocity, the point $ {\pmb \xi} $ (corresponding in Eq (6.5) to a source point) has been transformed into a field point outside the domain. By changing the dummy variable $ ({\pmb \xi} \rightarrow {\bf y})\in V_B $ and the index $ \alpha, \beta, ... \rightarrow a', b', ... $ in order to keep the convention that field points are associated with latin lettering, the Green function can be expressed as
where now
Although Eqs (6.7) and (6.10) are equivalent, their physical meaning in slightly different. In Eq (6.7), the Green function is expressed as a combination of singular solutions of the unbounded Stokes equation, with poles in $ \Omega $, weighted by the moments that, in turn, depend on the pole $ {\pmb \zeta} $ entering the original problem Eq (6.1). Conversely, in Eq (6.10) the field variable enters in the expression of the operator $ \mathcal{D}_{a'}^{\ a} $ through the moments, and the regular part, solution of the Stokes equations as a whole, is a combination of terms each of which individually is not a solution of the Stokes equation.
The operators $ \mathcal{D}^\alpha_{\ \alpha'} $ defined by Eq (6.6), depend on the pole $ {\pmb \zeta} $ via the moments, and consequently, for each $ {\pmb \zeta} $, a new system of moments is defined, determining a different operator $ \mathcal{D}^\alpha_{\ \alpha'} $. For this reason, it is convenient to introduce a new operator, independent of the position of the pole, and such that, its action on the Stokeslet outside the domain of the fluid furnishes the Green function. To this purpose, let us assume that the geometry of the problem is such that there exists a bijective correspondence between points inside $ {\pmb \zeta} $ and outside $ {\pmb \xi} $ the domain of the fluid, defined by a smooth and invertible function $ r $,
As addressed in Appendix A, and following the Ruse approach to bitensor calculus [25], Eq (6.11) enables us to view $ {\pmb \xi} $ and $ {\pmb \zeta} $ as conjugate points in two different metric spaces, such that tensorial quantities defined at a point in one of the two spaces can be transported to the conjugate point of the other space via the parallel propagator
where the parallel propagator is given by
It follows from Eq (6.12) and from the above bitensorial interpretation of the bijective correspondence Eq (6.11) between point in the flow domain and image points outside it, that the stress tensor $ \mathrm{\Sigma}_{\alpha'}^{ab}({\bf x}, { \pmb \zeta }) $ can be parallel transported from the point $ {\pmb \zeta} $ to the point $ {\pmb \xi} $
Substituting Eq (6.14) into Eq (6.6) one obtains
where
Enforcing Eq (6.15), it is possible to express the operator $ \mathcal{D}^\alpha_{\ \alpha'} $ in terms of a reflection operator independent of the pole $ {\pmb \zeta} $, and such that the functional dependence on $ {\pmb \zeta} $ is encompassed in the parallel propagator. For highlighting this delicate issue, let us consider the simplest case where $ \Omega $ reduces to a point $ r({\pmb \zeta}) $. In this case, it follows from Eq (6.15) that the operator $ \mathcal{D}^\alpha_{\ \alpha'} $ attains the form
The operator $ \mathcal{R}^\alpha_{\beta} $ furnishes the regular part of the Green function starting from the Stokeslet, independently on the source point $ {\pmb \zeta} $ and, for the reasons discussed below, it can be referred to as the reflection operator of the bounded flow problem.
By Eqs (6.7) and (6.9), the operator $ \mathcal{R}^\alpha_{\beta} $ can be applied on equal footing either at the source or at the field point. In the first case, the Green function reads
In the second case, i.e., by applying the operator at the field point, an alternative representation of the Green function follows
where $ {\bf y} = r^{-1}({\bf x}) $ and $ {\bf x} = r({\bf y}) $. The latter expression permits to interpret the regular part of the Green function as a "reflected field" of the ambient flow, that in the present case is given by a Stokeslet centered at the point $ {\pmb \zeta} $. In fact, the operator $ \mathcal{R}^{\ b}_{a'} $ furnishes a continuation of the Stokes solution with homogeneous Dirichlet boundary conditions in the external domain, usually referred as a reflection principle [32,33]. To show this, consider the integral form of a generic solution vanishing at the boundary $ \partial V_f $ [40]
and its continuation in $ \mathbb{R}^3/V_f $,
Since, by the definition of the disturbed field
by using the reciprocal identity $ \mathsf{S}^a_{\ \alpha'}({\bf x}-{\pmb \zeta}) = \mathsf{S}^{\ a}_{\alpha'}({\pmb \zeta}-{\bf x}) $ and exchanging latin and greek letters, it easy to verify that
Therefore, by applying the operator $ \mathcal{R}^{b'}_{a'} $ at the field in (6.21) we obtain at the r.h.s of Eq (6.21) the field defined by Eq (6.20) and the reflection formula can be derived
The reflection formula in Eq (6.24) requires in principle the estimate of infinite terms as the operator $ \mathcal{R}^{b'}_{a'} $ admits in general a series expansion in terms of the countable system of moments. It is known from harmonic function theory, that if the reflection operator (e.g., associated with an electrostatic problem) possesses a finite number of non-vanishing terms, then the boundary is either a plane or a sphere [47] and the relation equivalent to Eq (6.24) is referred as a point-to-point reflection principle. In the case of the solutions of the Stokes problem, that involves biharmonic functions, it is known that a point-to-point reflection principle does not hold even for spherical boundaries, and a weaker point-to-set principle [34,47,48] should be considered, where a bijective relation occurs between a point $ {\bf x} $ in the fluid domain and a set parameterized by its conjugate point $ {\bf y} = r(\bf{x}) $ in the complementary domain.
Equation (6.17) and the analysis developed in the previous Section indicate the close relation (duality) between the image system of singularities of a bounded flow problem and the formulation of a reflection principle, as the two problems are governed by essentially the same operators $ \mathcal{D}^\alpha_{\ \alpha'} $ and $ {\mathcal R}_\beta^\alpha $, parallel transported between a source point and its conjugate image. The duality between image system and reflection principle has been practically neglected in Stokesian hydrodynamics. Several works have investigated the image system of singularities near a plane [36,37] or near spherical boundaries [46], and, almost independently, parallel works on reflected fields near a planar [35] and spherical boundaries [34] has been published. In our opinion, the main difficulty in recognizing a common formal structure underlying image systems and reflection principle in Stokesian hydrodynamics stems from the tensorial nature of the operators involved, and by the need of a parallel transport between conjugate points. The introduction of the bitensorial formalism for hydrodynamic Green functions has made possible to highlight this issue.
The duality between the image system of singularities and the existence of a reflection principle make it possible to transfer and apply methods and techniques developed for solving one of these two problems to the other one. The next Section provides an application of this principle in connection with the problem of singularities bounded by planar boundaries.
7.
Singular fields bounded by a single plane
Below, the results found in Section 6 are applied to the problem of the singularities of a flow bounded by a rigid plane. In this case, the function $ r $ transforming points $ {\bf x} \in V_f $ into conjugate points $ {\bf y} \in \mathbb{R}^3 /V_f $ is given by the mirror operator $ {\bf J} = {\bf I} - 2 \, {\bf n} \otimes {\bf n} $, $ {\bf I} $ being the identity matrix, and $ {\bf n} $ the unit normal to the plane, so that $ {\bf y} = {\bf J}\cdot {\bf x} $ and $ {\bf x} = {\bf J}\cdot {\bf y} $, since $ {\bf J}^2 = {\bf I} $.
Consider a Cartesian coordinate system ($ X_1 $, $ X_2 $, $ X_3 $) with the origin on the plane and such that the flow domain corresponds to $ X_3 > 0 $. Let $ {\bf x} \in V_f $ with coordinates ($ x_1 $, $ x_2 $, $ x_3 $), and its mirror point $ {\bf y} \in \mathbb{R}^3/V_f $ with coordinates $ y_{a'} = J_{a' a} x_a $.
The parallel propagator (see Appendix A) between these conjugate points is given by
The reflection operator acting at the point $ {\bf y} $, corresponding to Eq (6.24) is the so called Lorentz mirror operator [1,34]
The Green function of the Stokes flow centered at the source point $ {\pmb \zeta} \in V_f $ can be obtained either by applying the reflection operator at the field point, according to Eq (6.19), or at the source point, according to Eq (6.18). In the first case we have
while the application at the source point provides
with the expression for the pressure
and for the stress tensor
Since the pole is fixed at $ {\pmb \xi} = {\bf J} \cdot {\pmb \zeta} = (0, 0, -h) $, we obtain the singular form
and
The singular representation of the Green function Eq (7.7), here obtained simply by applying the Lorentz reflection operator at the source point, coincides with the result obtained by Blake using a much more elaborate approach involving the Fourier-Hankel transforms [36,37].
Blake and Chwang in [36,37] have obtained the singular reflection systems related to bounded Stokeslet, Sourcelet and Rotlet by applying the Fourier-Hankel transforms to separate and distict problems specified by the boundary conditions adopted. In point of fact, the operator formalism developed in Section 6 permits to obtain any higher-order singularity in a unitary way, by simply differentiating the Green's function at the pole, Eqs (7.4)–(7.6).
To begin with, consider the bounded Source Dipole $ \mathrm{D}_{a\alpha'}({\bf x}, {\pmb \zeta}) $ defined by (3.24), applying the Laplacian operator $ -\Delta_{\zeta}/2 $ to the expression (7.4). Being the Laplacian operator invariant with respect to any Euclidean transformation, and thus under the reflection transformation $ {\pmb \zeta} = {\bf J}\cdot {\pmb \xi} $, we have $ \Delta_{\xi} = \Delta_{\zeta} $, and therefore
where, enforcing the identity,
the third term at the r.h.s of Eq (7.10) reads
The fourth term in Eq (7.10) can be simplified as
so that the singular representation of the Source Dipole reads
and since $ \xi_3 = -h $, Eq (7.14) becomes
The associated pressure field can obtained by applying the same operator $ -\Delta_{\zeta}/2 = -\Delta_{\xi}/2 $ to the pressure Green function Eq (7.5). Since the unbounded pressure field is a potential vector field with respect to the source point coordinates, the only non vanishing contribution is given by the third term at the r.h.s of Eq (7.5), and therefore
Figure 2 provides the schematic representation of the unbounded singularities at the image pole necessary to cancel the velocity field at the plane due to the unbounded Source Doubled at the pole in the fluid domain. Panel (a) refers to $ \mathrm{D}_{a1} = D_{a2} $, panel (b) to $ D_{a3} $. The vector plot of the bounded Source Dipole defined by Eq (7.15) is depicted in Figure 3.
In the far field, $ |{\bf x}| > > h $, we have
To obtain the Stokes Doublet Eq (3.16), we can apply the covariant derivative at the pole of the Green function. The bounded solution of the Rotlet (3.22) giving the antisymmetric part of the Stokes doublet can be found, according to Eq (3.19), by applying the curl at the pole of the Green function to obtain
and the associated pressure reads
In the far field we have the asymptotic scaling
The vector plot of the Rotlet is depicted in Figure 4.
To obtain the bounded Strainlet Eq (3.20), i.e., the symmetric part of the Stokes Doublet, we could evaluate $ (\nabla_{\beta'} \mathrm{G}_{a\alpha'} +\nabla_{\alpha'}\mathrm{G}_{a\beta'})/2 $. Alternatively, it is more convenient to use Eq (3.21), substituting in it Eq (7.5) for the pressure, and Eq (7.6) for the stress tensor of the bounded Green function
where
and
Since $ \Delta_{\xi} = \Delta_{\zeta} = \Delta_{x} = \Delta_{y} $, in this particular case, where the boundary of the fluid is a plane, it is possible to define the bounded Source $ \mathrm{M}_{a}({\bf x}, {\pmb \zeta}) = -\mathrm{P}_{a}({\pmb \zeta}, {\bf x}) /2 $ and the bounded Stresslet $ \mathrm{T}_{a \alpha' \beta'}({\bf x}, {\pmb \zeta}) = -\mathrm{\Sigma}_{\alpha' \beta' a }({\pmb \zeta}, {\bf x})/2 $, that are the bounded counterparts of the Sourcelet defined in Eq (3.32) and the Stresslet in Eq (3.33). Therefore, the Strainlet can be expressed as
By making the following transformation
we obtain for $ \mathrm{M}_{a}({\bf x}, {\pmb \zeta}) $ and $ \mathrm{T}_{a \alpha' \beta'}({\bf x}, {\pmb \zeta}) $ the following expressions
which possess the following far-field asymptotics
Gathering Eqs (7.26) and (7.27) and substituting them into Eq (7.24), the analytic expression for the bounded Strainlet follows
and putting $ \xi_3 = -h $, one obtains
The vector plot of the bounded Strainlet is depicted in Figure 5.
8.
Conclusions
In this article we have applied the bitensor calculus to the singularity method in Stokes flow. The nature of the bitensorial formalism, that distinguishes between source and field points of singular fields, allows us to manipulate mathematically singularities without ambiguity, resulting useful even if the fluid domain is regarded as a flat space.
We have provided a clear definition of the singularities in Stokes flow, specifying the associated non-homogeneous equations and boundary conditions, obtaining the most common unbounded singularities as a particular case of the more general bounded counterparts. Although this topic can be found in any monograph on Stokesian hydrodynamics [3,4], the detailed description of some of the most common Stokesian singularities has never been, to the best of our knowledge, addressed in the hydrodynamic literature.
Moreover, an explicit formulation of the singular method, providing a way for expressing bounded flows in terms of unbounded singularities, has been derived. To this aim, we have defined the moments as volume integrals in the domain of the obstacle, and we have used a tensorial moment theory to obtain the integro-differential operator yielding the disturbance flow once applied at the pole of the Stokeslet in term of a countable set of moments. As shown in Appendix B, this definition is coincident whit the surface moments defined by Ichiki [31] for no-slip spheres immersed in a Stokes flow. To evaluate the moments of a specific flow problem, we developed a method based on geometrical moments related to the obstacle immersed in purely $ n $-th order ambient flow. This method is useful either in numerical applications or in theoretical analysis. We have shown that starting from the geometrical moments it is possible to define a $ n $-th order Faxén operator, i.e., an operator satisfying a generalized Faxén theorem. In addition, we found that a generic disturbance flow can be developed in a series of Faxén operators applied at the Stokeslet's pole, thus expressing a generic field as a series of simpler disturbance flows associated with purely $ n $-th order ambient flows.
Enforcing the reciprocal symmetry of the Green function, we have shown that it is possible to apply the operator both to the source and and to the field point of the Stokeslet, in order to obtain the disturbance contribution to the flow field. The main consequence of the latter result is that, whenever it is possible to define a reflection operator, this operator coincides with the operator derived from moment theory furnishing the image system of singularity. This result, applied to the Green function bounded by a plane provides an alternative way for expressing the hydrodynamic singularities which is simpler than the method used by Blake [36] involving Fourier-Hankel transforms, and it has been used to derive other singularities, such as the Source Dipole and the Strainlet.
The practical application of the theory to specific bounded Stokes problem will be addressed in forthcoming works.
Conflict of interest
The authors declare no conflict of interest.
Appendix
A. Bitensor calculus
The development of bitensor calculus has followed two parallel pathways: an algebraic [25] and purely geometric approach [26,27]. As the algebraic approach is particularly relevant in the present hydrodynamic theory of bounded Green functions, and moreover it is scarsely mentioned in the literature, this brief review on bitensor calculus is mainly focused on this formulation, addressing its connection with the geometric theory at the end of this Appendix.
In [25], Ruse defines bitensors as follows: Let $ {\bf x} = (x^1, ..., x^n) $ and $ {\pmb \xi} = (\xi^1, ..., \xi^m) $ be two set of independent variables and let $ f^{a'}({\bf x}) $, $ a' = 1, \dots, n $ be $ n $ functions dependent on $ {\bf x} $ and $ \phi^{\alpha'}({\pmb \xi}) $, $ \alpha' = 1, \dots, m $, $ m $ functions dependent on $ {\pmb \xi} $, such that we can define the new variables
Let $ T^{a \alpha}({\bf x}, {\pmb \xi}) $ denote the array of $ n \times m $ functions depending on both $ {x}^a $ and $ {\xi}^\alpha $
Moreover, let $ T^{a' \alpha}(\bf x', {\pmb \xi}) $ be a set of functions depending on the variables $ {\bf x}' $ and $ {\pmb \xi} $, $ T^{a \alpha'}({\bf x}, {\pmb \xi}') $ a set of functions depending on the variables $ {\bf x} $ and $ {\pmb \xi}' $, $ T^{a' \alpha'}({\bf x}', {\pmb \xi}') $ a set of functions depending on the variables $ {\bf x}' $ and $ {\pmb \xi}' $. If these functions are related by the equations
then they are the components of the bivector $ {\bf T} $ expressed in the systems of coordinates $ ({\bf x}, {\pmb \xi}) $, $ ({\bf x}', {\pmb \xi}) $, $ ({\bf x}, {\pmb \xi}') $, $ ({\bf x}', {\pmb \xi}') $, respectively. More generally a set of $ n^{r+s} \times m^{p+q} $ functions are the components of a bitensor $ {\bf T} $, if they are related by the equations
If $ {\pmb \xi} $ is kept fixed, then $ T^{a 1}... T^{a m} $ are the components ($ a = 1, \dots, n $) of $ m $ ordinary vectors at $ {\bf x} $, whereas if $ {\bf x} $ is kept fixed $ T^{1 \alpha}... T^{n \alpha} $ are the components ($ \alpha = 1, \dots, m $) of $ n $ vectors at $ {\pmb \xi} $. The bitensor $ T^{a \alpha} $ is, then, named vector-vector bitensor and, more generally, the bitensor $ {T}^{a_1... a_r \alpha_1... \alpha_q}_{b_1... b_s \beta_1... \beta_p} $ is named $ (r+s) $tensor-$ (p+q) $tensor.
Next consider two symmetric scalar-$ (2) $tensor $ g_{a b}({\bf x}, {\pmb \xi}) $ and $ \gamma_{\alpha \beta}({\bf x}, {\pmb \xi}) $, and suppose that $ {\bf x} $ and $ {\pmb \xi} $ are two systems of coordinates of two distinct Riemannian spaces defined respectively by the two metric forms
Equations (A.8)–(A.9) define a multiple-infinite set of Riemannian spaces. In fact, fixed the set of variables $ {\pmb \xi} $, Eq (A.8) determines a Riemannian space, while fixing $ {\bf x} $, a Riemannian space is determined by Eq (A.9). In the case that $ n = m $, it is possible to define a vector-vector bitensor $ k^a_{\ \alpha}({\bf x}, {\pmb \xi}) $, belonging to both spaces, so that
which represents a system of $ n(n+1)/2 $ equations for the $ n^2 $ unknown components of $ k^a_{\ \alpha} $ (due to the symmetry of $ g_{ab} $ and $ \gamma_{\alpha \beta} $).
Note that, keeping either $ {\bf x} $ or $ {\pmb \xi} $ fixed, the $ n $ ordinary vectors $ k^1_{\ \alpha}... k^n_{\ \alpha} $ and $ k^a_{\ 1}... k^a_{\ n} $ are orthogonal to each other
and similarly
A particular case occurs when $ g_{a b}({\bf x}, {\pmb \xi}) = g_{a b}({\bf x}) $ does not depend on $ {\pmb \xi} $ and moreover $ \gamma_{\alpha, \beta}({\bf x}, {\pmb \xi}) = g_{\alpha \beta}({\pmb \xi}) $. In this case, the two metric spaces defined by Eqs (A.8)–(A.9) represent the same metric space at two different points, and Eq (A.10) becomes
In Euclidean spaces, it is always possible to express the component of the metric tensors $ g_{a b}({\bf x}) $, $ g_{\alpha \beta}({\pmb \xi}) $ in the same Cartesian coordinate system $ X_{(i)} = (X_{(1)}, X_{(2)}, X_{(3)}) $, $ (i) = 1, 2, 3 $ being the indices for the Cartesian components. Thus, from Eq (A.13) one has
where $ I_{(ij)} = \rm{diag}(1, 1, 1) $ from which it follows that
that reduces to $ k_a^{\ \alpha}({\bf x}, {\pmb \xi}) = \delta^a_\alpha $ if we choose the same coordinate system at both points.
If the coordinates of the two points are related by a bijective transformation
we can consider $ \xi^\alpha $ and $ x^a $ as two set of coordinates of the same point and, by classical tensor calculus, we have
Comparing Eq (A.17) with Eq (A.13), we find
therefore, an ordinary transformation in the classical tensor calculus, can be viewed as a transformation between two metric spaces
If the two points belong to a generic Riemannian space, it is not always possible to express the components in the same Cartesian coordinate system. However, we can define, at one point, say $ {\bf x} $, a triad of vector $ e_{(i)}^a({{\bf x}}) $, forming locally an orthonormal basis, so that [38,39]
Parallel transporting the vectors $ e_{(i)}^a({\bf x}) $ from the point $ {\bf x} $ to the point $ {\pmb \xi} $, i.e., integrating the differential equation
along the geodetics connecting the point $ {\bf x} $ to $ {\pmb \xi} $, $ {\bf z}(u) $ being a generic point on the geodetics identified by the parameter $ u $ and such that $ {\bf z}(0) = {\bf x} $, we obtain the triad of vectors at the point $ {\pmb \xi} $, that is still orthonormal. Thus,
Using Eq (A.21) and (A.23), it is possible to express both the metric tensors $ g_{ab}({\bf x}) $ and $ g_{\alpha \beta}({\pmb \xi}) $ in a common orthonormal basis. Equation (A.14) thus, becomes
obtaining the more general expression for the parallel propagator
In the case the two points $ {\bf x} $ and $ {\pmb \xi} $ become coincident, we have
where $ [ \cdot ] $ indicate the whole tensorial entity. Consequently,
Therefore, it is customary to use the same symbol for indicating either the parallel propagator or the metric tensor
To make an example, consider a unit vector $ p^a({\bf x}) $ at $ {\bf x} $,
Using the definition of the parallel propagator Eq (A.13)
we have
that represents the unit vector parallel-transported from the point $ {\bf x} $ to the point $ {\pmb \xi} $. In fact, since
we have in the triad basis
and thus the components of the vector $ p^\alpha({\pmb \xi}) $ in the common triad basis coincide with those of $ p^a({\bf x}) $. From this result, and from the property
it follows that any vector $ v^a({\bf x}) $ can be the parallel transported from $ {\bf x} $ to $ {\pmb \xi}' $ via the relation
To conclude, an important bitensor is the so called Synge's world function [26], that is a measure of the geodetic distance between the points $ {\bf x} $ and $ {\pmb \xi} $, defined as
In Euclidean spaces, it can be explicited as as
$ x^{(i)} $ and $ \xi^{(i)} $ being the Cartesian coordinates of the two points. Its derivative at $ {\bf x} $ is
while the corresponding derivative at $ {\pmb \xi} $ reads
Let $ ({\bf x}-{\pmb \xi})_\alpha = g^{\ a}_{\alpha}({\pmb \xi}, {\bf x})({\bf x}-{\pmb \xi})_a $ and $ ({\pmb \xi}-{\bf x})_a = g^{\ \alpha}_{a}({\bf x}, {\pmb \xi}) ({\pmb \xi}-{\bf x})_\alpha $. From Eq (A.38) we have
that is a useful relation in moment analysis.
B. Moment surface integrals
In this Appendix we show that, owing to the property of the Stokes flow, the moments defined in Section 4 can be reduced to surface integrals of the stress tensor, in the case no-slip boundary conditions are assumed.
To this purpose, consider the following Stokes problems: Ⅰ) a flow with no-slip conditions at the boundaries of the fluid, $ {\bf v}({\bf x}) = {\bf w}({\bf x}) + {\bf u}({\bf x}) $, where $ {\bf u}({\bf x}) $ is the ambient and $ {\bf w}({\bf x}) $ the disturbance flow. Thus, $ {\bf v}({\bf x}) $ is solution of the system
II) a purely n-th order velocity field $ {\bf u}_{(n)}({\bf x}) $ defined as in Section 5
where $ A_a^{\ {\bf a}_n} $ are the components of a constant (n+1)-rank matrix, and the associated pressure $ p_{(n)}({\bf x}) $ and stress tensor $ {\pmb \pi}_{(n)}({\bf x}) $ are given by the Eqs (5.2) and (5.3).
Appling to the fields $ {\bf v}({\bf x}) $ an $ {\bf u}_{(n)}({\bf x}) $ the Lorentz reciprocal theorem [4]
Since these fields are defined in the whole space $ \mathbb{R}^3 $, we can integrate Eq (B.3) over the domain of the obstacle $ V_{ext} $
Since $ \nabla_b\sigma^{ab}_{(n)}({\bf x}) = 0 $, using Eqs (B.1), (B.2) and the definition of moments $ M_{\ {\pmb \alpha}_n}^\alpha({\pmb \xi}) $ in (4.4), the term at l.h.s in Eq (B.4) provides
whereas, using Gauss divergence theorem the r.h.s, further considering that $ {\bf v}({\bf x}) = 0 $ and $ u^{(n)}_a({\bf x}) = A_a^{\ {\bf a}_n}({\bf x}-{\pmb \xi}) _{{\bf a}_n} $ on the boundaries $ \partial V_{ext} $, one obtains
Gathering Eqs (B.5) and (B.6), we have
which provides the expression of the moments in terms of surface integrals of the stress tensor.









 DownLoad:
DownLoad: