Spectral theory for nonconservative transmission line networks

1.   Introduction

Fractional calculus is a branch of mathematics that investigates the properties of arbitrary-order differential and integral operators to address various problems. Fractional differential equations provide a more appropriate model for describing diffusion processes, wave phenomena, and memory effects ^[1,2,3,4] and possess a diverse array of applications across numerous fields, encompassing stochastic equations, fluid flow, dynamical systems theory, biological and chemical engineering, and other domains^[5,6,7,8,9].

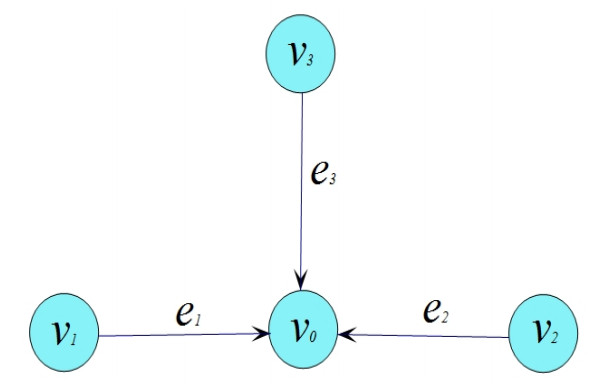
Star graph $ G = (V, E) $ consists of a finite set of nodes or vertices $ V(G) = \{v_{0}, v_{1}, ..., v_{k}\} $ and a set of edges $ E(G) = \{e_{1} = \overrightarrow{v_{1}v_{0}}, e_{2} = \overrightarrow{v_{2}v_{0}}, ..., e_{k} = \overrightarrow{v_{k}v_{0}}\} $ connecting these nodes, where $ v_{0} $ is the joint point and $ e_{i} $ is the length of $ l_{i} $ the edge connecting the nodes $ v_{i} $ and $ v_{0} $, i.e., $ l_{i} = |\overrightarrow{v_{i}v_{0}}| $.

Graph theory is a mathematical discipline that investigates graphs and networks. It is frequently regarded as a branch of combinatorial mathematics. Graph theory has become widely applied in sociology, traffic management, telecommunications, and other fields^[10,11,12].

Differential equations on star graphs can be applied to different fields, such as chemistry, bioengineering, and so on^[13,14]. Mehandiratta et al. ^[15] explored the fractional differential system on star graphs with $ n+1 $ nodes and $ n $ edges,

where $ {}^{C}D^{\alpha}_{0, x}, \; {}^{C}D^{\beta}_{0, x} $ are the Caputo fractional derivative operator, $ 1 < \alpha\leq2 $, $ 0 < \beta\leq\alpha-1 $, $ \mathfrak{f}_{i}, i = 1, 2, ..., k $ are continuous functions on $ C([0, 1]\times\mathbb R\times\mathbb R) $. By a transformation, the equivalent fractional differential system defined on $ [0, 1] $ is obtained. The author studied a nonlinear Caputo fractional boundary value problem on star graphs and established the existence and uniqueness results by fixed point theory.

Zhang et al. ^[16] added a function $ \lambda_{i}(x) $ on the basis of the reference ^[15]. In addition, Wang et al. ^[17] discussed the existence and stability of a fractional differential equation with Hadamard derivative. For more papers on the existence of solutions to fractional differential equations, refer to ^{[18,19,20,21]}. By numerically simulating the solution of fractional differential systems, we are able to solve problems more clearly and accurately. However, numerical simulation has been rarely used to describe the solutions of fractional differential systems on graphs ^[22,23].

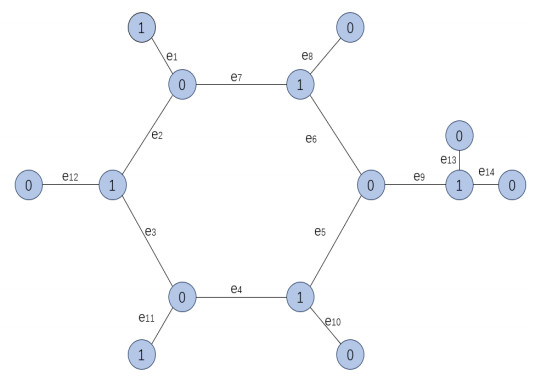
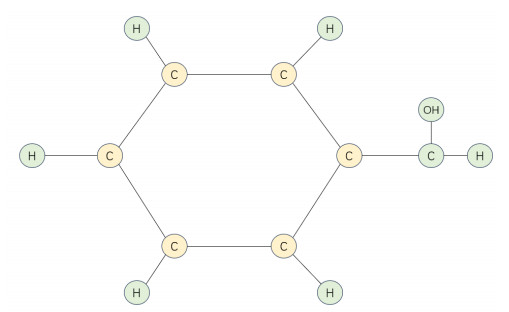
The word chemical is used to distinguish chemical graph theory from traditional graph theory, where rigorous mathematical proofs are often preferred to the intuitive grasp of key ideas and theorems. However, graph theory is used to represent the structural features of chemical substances. Here, we introduce a novel modeling of fractional boundary value problems on the benzoic acid graph (Figure 1). The molecular structure of the benzoic acid seven carbon atoms, seven hydrogen atoms, and one oxygen atom. Benzoic acid is mainly used in the preparation of sodium benzoate preservatives, as well as in the synthesis of drugs and dyes. It is also used in the production of mordants, fungicides, and fragrances. Therefore, a thorough understanding of its properties is of utmost importance.

By this structure, we consider atoms of carbon, hydrogen, and oxygen as the vertices of the graph and also the existing chemical bonds between atoms are considered as edges of the graph. To investigate the existence of solutions for our fractional boundary value problems, we label vertices of the benzoic acid graph in the form of labeled vertices by two values, 0 or 1, and the length of each edge is fixed at $ e $ ($ |\overrightarrow{e_{i}}| = e, \; i = 1, 2, ..., 14 $) (Figure 2). In this case, we construct a local coordinate system on the benzoic acid graph, and the orientation of each vertex is determined by the orientation of its corresponding edge. The labels of the beginning and ending vertices are taken into account as values 0 and 1, respectively, as we move along any edge.

Motivated by the above work and relevant literature^{[15,16,17,18,19,20,21,22,23]}, we discuss a boundary value problem consisting of nonlinear fractional differential equations defined on $ |\overrightarrow{e_{i}}| = e, \; i = 1, 2, \cdots, 14 $ by

and the boundary conditions defined at boundary nodes $ e_{1}, e_{2}, \cdots, e_{14} $, and

together with conditions of conjunctions at 0 or 1 with

Overall, we consider the existence and stability of solutions to the following nonlinear boundary value problem on benzoic acid graphs:

where $ {}^{H}D^{\alpha}_{1^{+}}, {}^{H}D^{\beta}_{1^{+}} $ represent the Hadamard fractional derivative, $ \alpha\in (1, 2], \; \beta\in (0, 1], \; f_{i}\in C([1, e]\times\mathbb R \times\mathbb R) $, $ \varrho_{i} $ is a real constant, and $ \phi_{p}(s) = sgn(s)\cdot |s|^{p-1} $. The existence and Hyers-Ulam stability of the solutions to the system (1.1) are discussed. Moreover, the approximate graphs of the solution are obtained.

It is also noteworthy that solutions obtained from the problem (1.1) can be depicted in various rational applications of organic chemistry. More precisely, any solution on an arbitrary edge can be described as the amount of bond polarity, bond power, bond energy, etc. This paper lies in the integration of fractional differential equations with graph theory, utilizing the formaldehyde graph as a specific case for numerical simulation, and providing an approximate solution graph after iterations.

2.   Preliminaries

In this section, for conveniently researching the problem, several properties and lemmas of fractional calculus are given, forming the indispensable premises for obtaining the main conclusions.

Definition 2.1. ^[2,20] The Hadamard fractional integral of order $ \alpha $, for a function $ g\in L^{p}[a, b] $, $ 0\leq a\leq t\leq b \leq \infty $, is defined as

and the Hadamard fractional integral is a particular case of the generalized Hattaf fractional integral introduced in ^[24].

Definition 2.2. ^[2,20] Let $ [a, b]\subset\mathbb R $, $ \delta = t\frac{d}{dt} $ and $ AC^{n}_{\delta}[a, b] = \{g:[a, b]\rightarrow \mathbb R:\delta^{n-1}(g(t))\in AC[a, b]\}. $ The Hadamard derivative of fractional order $ \alpha $ for a function $ g\in AC^{n}_{\delta} [a, b] $ is defined as

where $ n-1 < \alpha < n $, $ n = [\alpha]+1 $, and $ [\alpha] $ denotes the integer part of the real number $ \alpha $ and $ log(\cdot) = log_{e}(\cdot) $.

Definition 2.3. ^[25] Completely continuous operator: A bounded linear operator $ f $, acting from a Banach space $ X $ into another space $ Y $, that transforms weakly-convergent sequences in $ X $ to norm-convergent sequences in $ Y $. Equivalently, an operator $ f $ is completely-continuous if it maps every relatively weakly compact subset of $ X $ into a relatively compact subset of $ Y $.

Compact operator: An operator $ A $ defined on a subset $ M $ of a topological vector space $ X $, with values in a topological vector space $ Y $, such that every bounded subset of $ M $ is mapped by it into a pre-compact subset of $ Y $. If, in addition, the operator $ A $ is continuous on $ M $, then it is called completely continuous on this set. In the case when $ X $ and $ Y $ are Banach or, more generally, bornological spaces and the operator $ A:X\rightarrow Y $ is linear, the concepts of a compact operator and of a completely-continuous operator are the same.

Lemma 2.4. ^[20] For $ y\in AC^{n}_{\delta}[a, b] $, the following result hold

where $ c_{i}\in \mathbb{\mathbb{R}}, \; i = 0, 1, \cdots, n-1 $.

Lemma 2.5. ^[21] For $ p > 2 $, $ \mid x\mid, \; \mid y\mid\leq M $, we have

Lemma 2.6. ^[4] Let $ M $ be a closed convex and nonempty subset of a Banach space $ X $. Let $ T, S $ be the operators $ T-S:M\rightarrow X $ such that

(ⅰ) $ Tx+Sy\in M $ whenever $ x, y\in M $;

(ⅱ) $ T $ is contraction mapping;

(ⅲ) $ S $ is completely continuous in $ M $.

Then $ T+S $ has at least one fixed point in $ M $.

Proof. For every $ Z\in S(M) $, we have $ T(x)+z:M\rightarrow M $. According to (ⅱ) and the Banach contraction mapping principle, $ Tx+z = x $ or $ z-x = Tx $ has only one solution in $ M $. For any $ z, \tilde{z}\in S(M) $, we have

So we have

Thus, $ |t(z)-t(\tilde{z})|\leq \frac{1}{1-\nu}|z-\tilde{z}| $. It indicates that $ t\in C(S(M)) $. Because of $ S $ is completely continuous in $ M $, $ tS $ is completely continuous. According to the Schauder fixed point theorem, there exists $ x^{\ast}\in M $, such that $ tS(x^{\ast}) = x $. So we have

□

Lemma 2.7. Let $ h_{i}(t)\in AC([1, e], \mathbb R), \; i = 1, 2, \cdots, 14 $; then the solution of the fractional differential equations

is given by

Proof. By Lemma 2.4, we have

where $ c_{i}^{(1)}, \; c_{i}^{(2)} $ are constants. The boundary condition $ r_{i}(1) = 0 $ gives $ c_{i}^{(1)} = 0, $ for $ i = 1, 2, \cdots, 14. $

Hence,

Also

Now, the boundary conditions $ r_{i}(e) = r_{j}(e) $ and $ \sum\limits_{i = 1}^{k}\varrho_{i}^{-1}r'_{i}(e) = 0 $ implies that $ c_{i}^{(2)} $ must satisfy

On solving above Eqs (2.4) and (2.5), we have

which implies

Hence, we get

Hence, inserting the values of $ c_{i}^{(2)} $, we get the solution (2.2). This completes the proof. □

3.   Main results

In this section, we discuss the existence and uniqueness of solutions of system (1.1) by using fixed point theory.

We define the space $ X = \{r:r\in C([1, e], \mathbb R), {}^{H}D^{\beta}_{1^{+}}r\in C([1, e], \mathbb R)\} $ with the norm

Then, $ (X, \|.\|_{X}) $ is a Banach space, and accordingly, the product space $ \big(X^{k} = X_{1}\times X_{2}\cdots\times X_{14}, \; \|.\|_{X^{k}}\big) $ is a Banach space with norm

In view of Lemma 2.7, we define the operator $ T:X^{k}\rightarrow X^{k} $ by

where

where $ \phi_{p}\left(\frac{f_{i}\big(s, r_{i}(s), {}^{H}D^{\beta}_{1^{+}}r_{i}(s)\big)}{s}\right) = \phi_{p}\left(g_{i}\big(s, r_{i}(s), {}^{H}D^{\beta}_{1^{+}}r_{i}(s)\big)\right) $.

Assume that the following conditions hold:

$ (H_{1}) $ $ g_{i}:[1, e]\times\mathbb R\times\mathbb R\rightarrow \mathbb R, i = 1, 2, \cdots, 14 $ be continuous functions, and there exists nonnegative functions $ l_{i}(t)\in C[1, e] $ such that

where $ t\in[1, e], (x, y), (x_{1}, y_{1})\in\mathbb R^{2}; $

$ (H_{2}) $ $ \iota_{i} = \sup\limits_{t\in [1, e]}|u_{i}(t)|, \; i = 1, 2, \cdots, 14; $

$ (H_{3}) $ There exists $ Q_{i} > 0 $, such that

$ (H_{4})\; \sup\limits_{1\leq t\leq e}\mid g_{i}(t, 0, 0)\mid = \kappa < \infty, \; i = 1, 2, ..., 14 $.

For computational convenience, we also set the following quantities:

Theorem 3.1. Assume that $ (H_{1}) $ and $ (H_{2}) $ hold; then the fractional differential system (1.1) has a unique solution on $ [1, e] $ if

where $ \chi_{i}, \; i = 1, 2, \cdots, 14 $ are given by Eq (3.2).

Proof. Let $ u = (r_{1}, r_{2}, \cdots, r_{14}), \; v = (v_{1}, v_{2}, \cdots, v_{14})\in X^{k}, \; t\in [1, e] $, we have

Using Lemma 2.5, $ (H_{1}) $ and $ (H_{2}) $, $ t\in [1, e] $ and $ \Big(\frac{\varrho_{j}^{-1}}{\sum_{j = 1}^{k}\varrho_{j}^{-1}}\Big) < 1 $ for $ j = 1, 2, \cdots, k $, we obtain

Hence,

By the formula in reference^[3],

we have

Using Lemma 2.5, $ (H_{1}) $ and $ (H_{2}) $, $ \Gamma(2-\beta)\leq1 $ and $ \Big(\frac{\varrho_{j}^{-1}}{\sum_{j = 1}^{k}\varrho_{j}^{-1}}\Big) < 1 $ for $ j = 1, 2, \cdots, k $, we obtain

Hence,

From (3.4) and (3.5), we have

Hence,

where $ \chi_{i}, \; i = 1, 2, \cdots, k $ are given by (3.2).

From the above Eq (3.6), it follows that

Since

we obtain that $ T $ is a contraction map. According to Banach's contraction principle, the original system (1.1) has a unique solution on $ [1, e] $. □

Theorem 3.2. Assume that $ (H_{1}) $ and $ (H_{2}) $ hold; then system (2.1) has at least one solution on $ [1, e] $ if

where $ \Upsilon_{i}, \; i = 1, 2, \cdots, 14 $ are given by Eq (3.3).

By Theorem 3.1, $ T $ is defined under the consideration of Krasnoselskii's fixed point theorem as follows:

where

Proof. For any $ \delta = (\delta_{1}, \delta_{2}, \cdots, \delta_{14})(t) $, $ \mu = (\mu_{1}, \mu_{2}, \cdots, \mu_{14})(t)\in X^{k} $, we have

which implies that

In a similar way, we get

Then,

Hence,

It follows from $ \Bigg(\sum\limits_{i = 1}^{k}\Upsilon_{i}\Bigg)\Bigg(\sum\limits_{i = 1}^{k}\iota_{i}\Bigg) < 1 $ that $ \varpi_{2} $ is a contraction operator. In addition, we shall prove that $ \varpi_{1} $ is continuous and compact. For any $ \delta = (\delta_{1}, \delta_{2}, \cdots, \delta_{14})(t)\in X^{k} $, we have

Then,

which implies

Hence,

This shows that $ \varpi_{1} $ is bounded. In addition, we will prove that $ \varpi_{1} $ is equi-continuous. Let $ t_{1} $, $ t_{2}\in[1, e] $; we have

and

Therefore, from (3.10) and (3.12), we obtain

This indicates that $ \|\varpi_{1}\delta(t_{2})-\varpi_{1}\delta(t_{1})\|_{X}\rightarrow0 $, as $ t_{2}\rightarrow t_{1} $.Thus, $ \|\varpi_{1}\delta(t_{2})-\varpi_{1}\delta(t_{1})\|_{X^{^{k}}}\rightarrow0 $, as $ t_{2}\rightarrow t_{1} $. By the Arzela-Ascoli theorem, we obtain that $ \omega_{1} $ is completely continuous. According to Lemma 2.6, system (2.1) has at least one solution on $ [1, e] $, which denotes that the original system (1.1) has at least one solution on $ [1, e] $. □

4.   Hyers-Ulam stability

Let $ \varepsilon_{i} > 0 $. Consider the following inequality

Definition 4.1. ^[16] The fractional differential system (1.1) is called Hyers-Ulam stable if there is a constant $ c_{f_{1}, f_{2}, ..., f_{k}} > 0 $ such that for each $ \varepsilon = \varepsilon(\varepsilon_{1}, \varepsilon_{2}, ..., \varepsilon_{k}) > 0 $ and for each solution $ r = (r_{1}, r_{2}, ..., r_{k})\in X^{k} $ of the inequality (4.1), there exists a solution $ \bar{r} = (\bar{r}_{1}, \bar{r}_{2}, ..., \bar{r}_{k})\in X^{k} $ of (1.1) with

Definition 4.2. ^[16] The fractional differential system (1.1) is called generalized Hyers-Ulam stable if there exists-function $ \psi_{f_{1}, f_{2}, ..., f_{k}}\in \mathbb C(\mathbb R^{+}, \mathbb R^{+}) $ with $ \psi_{f_{1}, f_{2}, ..., f_{k}}(0) = 0 $ such that for each $ \varepsilon = \varepsilon(\varepsilon_{1}, \varepsilon_{2}, ..., \varepsilon_{k}) > 0 $, and for each solution $ r = (r_{1}, r_{2}, ..., r_{k})\in X^{k} $ of the inequality (4.1), there exists a solution $ \bar{r} = (\bar{r}_{1}, \bar{r}_{2}, ..., \bar{r}_{k})\in X^{k} $ of (1.1) with

Remark 4.3. Let function $ r = (r_{1}, r_{2}, \cdots, r_{k})\in X^k, \; k = 1, 2, \cdots, 14 $, be the solution of system (4.1). If there are functions $ \varphi_{i}:[1, e]\rightarrow \mathbb R^+ $ dependent on $ u_{i} $ respectively, then

(ⅰ) $ |\varphi_{i}(t)|\leq\varepsilon_{i} $, $ t\in [1, e] $, $ i = 1, 2, \cdots, 14; $

(ⅱ) $ ^{H}D^{\alpha}_{1^+}r_{i}(t) = \varrho_{i}^{\alpha}\phi_{p}\left({f}_{i}\big(t, r_{i}(t), ^{H}D^{\beta}_{1^+}r_{i}(t)\big)\right) +\varphi_{i}(t), t\in [1, e], i = 1, 2, ..., 14. $

Remark 4.4. It is worth noting that Hyers-Ulam stability is different from asymptotic stability, which means that the system can gradually return to equilibrium after being disturbed. If the Lyapunov function satisfies certain conditions, the system is asymptotically stable. This stability emphasizes the behavior of the system over a long period of time, that is, as time goes on, the state of the system will return to the equilibrium state, while the error of Hyers-Ulam stability is bounded (proportional to the size of the disturbance).

Lemma 4.5. Suppose $ r = (r_{1}, r_{2}, ..., r_{k})\in X^k $ is the solution of inequality (4.1). Then, the following inequality holds:

where

and here

Proof. From Remark 4.3, we have

By Lemma 2.7, the solution of (4.2) can be given in the following form:

and

Then, we deduce that

and

□

Theorem 4.6. Assume that Theorem 3.1 hold; then the fractional differential system (1.1) is Hyers-Ulam stable if the eigenvalues of matrix $ A $ are in the open unit disc. There exists $ |\lambda| < 1 $ for $ \lambda\in \mathbb C $ with $ det(\lambda I-A) = 0 $, where

Proof. Let $ r = (r_{1}, r_{2}, ..., r_{14})\in X^k, \; k = 1, 2, \cdots14, $ be the solution of the inequality given by

and $ \bar{r} = (\bar{r}_{1}, \bar{r}_{2}, ..., \bar{r}_{14})\in X^k $ be the solution of the following system:

By Lemma 2.7, the solution of (4.3) can be given in the following form:

Now, by Lemma 4.5, for $ t\in[1, e] $, we can get

and

Hence, we have

where

Then we have

where

Then, we can get

Let

Obviously, $ h_{i, j} > 0, \; i, j = 1, 2, \cdots, 14 $. Set $ \varepsilon = max\{\varepsilon_{1}, \varepsilon_{2}, ..., \varepsilon_{14} \} $, then we can get

Thus, we have derived that system (1.1) is Hyers-Ulam stable. □

Remark 4.7. Making $ \psi_{f_{1}, f_{2}, ..., f_{k}}(\varepsilon) $ in (4.4). We have $ \psi_{f_{1}, f_{2}, ..., f_{k}}(0) = 0 $. Then by Definition 4.2, we deduce that the fractional differential system (1.1) is generalized Hyers-Ulam stable.

5.   Example

The benzoic acid graph we studied in the system (1.1) can be extended to other types of graphs. For example, star graphs and chord bipartite graphs provide a theoretical basis for physics, computer networks, and other fields. Here we only discuss the fractional differential system on the star graphs (i = 1, 2, 3). We discuss the solution of a fractional differential equation on a formaldehyde graph, and the approximate graphs of solutions are presented by using iterative methods and numerical simulation.

Example 5.1. Consider the following fractional differential equation:

corresponding to the system (1.1), we obtain

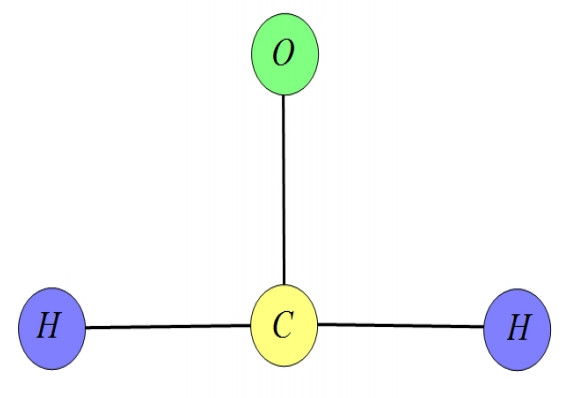
Figure 3 (The structure of formaldehyde) is from reference^[22]. Coordinate systems with $ r_{1}, \; r_{2}, $ and $ r_{3} $ are established, respectively, on the formaldehyde graph with 3 edges (Figure 4).

For$ t\in [1, e], $

For any $ x, \; y, \; x_{1}, \; y_{1} $, it is clear that

So we get

and

Therefore, by Theorem 3.1, system (5.1) has a unique solution on $ [1, e] $.

Meanwhile,

Let

so we have

It follows from Theorem 4.6 that system (5.1) is Hyer-Ulams stable, and by Remark 4.4, it will be generalized Hyer-Ulams stable.

Ultimately, the iterative process curve and approximate solution to the fractional differential system (5.1) are carried out by using the iterative method and numerical simulation. Let $ u_{i, 0} = 0 $, the iteration sequence is as follows:

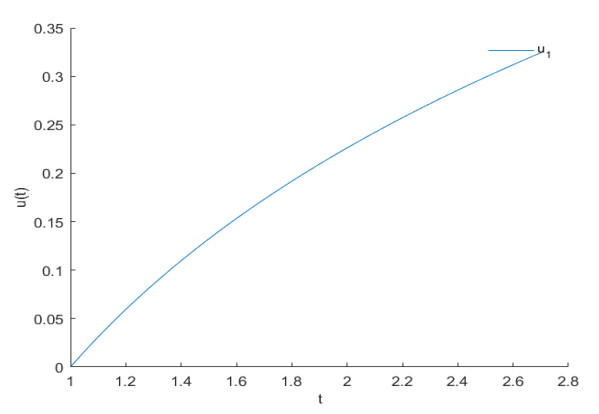
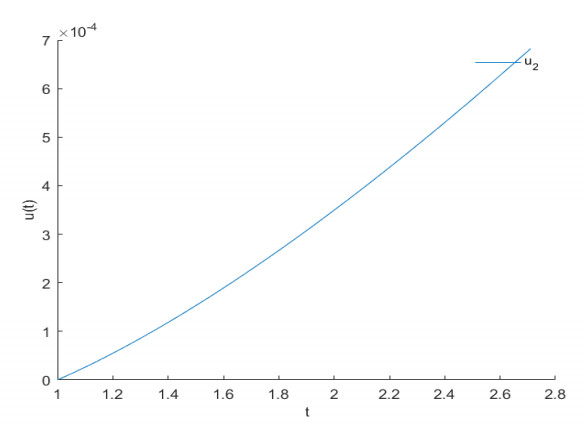
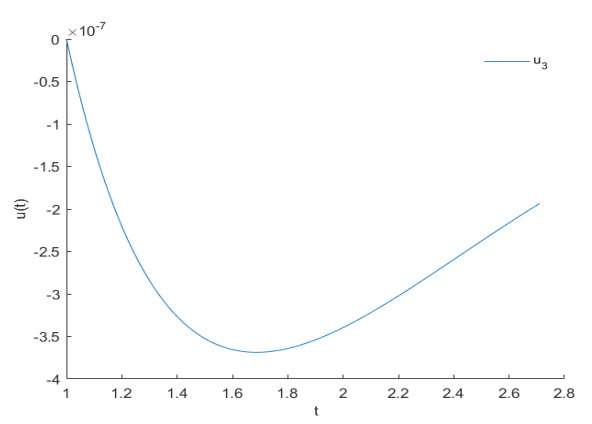
The iterative sequence of $ r_{2, n+1} $ and $ r_{3, n+1} $ is similar to $ r_{1, n+1} $. After several iterations, the approximate solution of fractional differential system (5.1) can be obtained by using the numerical simulation. Figure 5 is the approximate graph of the solution of $ \overrightarrow{r_{1}r_{0}} $ after iterations. Figure 6 is the approximate graph of the solution of $ \overrightarrow{r_{2}r_{0}} $ after iterations. Figure 7 is the approximate graph of the solution of $ \overrightarrow{r_{3}r_{0}} $ after iterations.

6.   Conclusions and prospects

Using the idea of star graphs, several scholars have studied the solutions of fractional differential equations. They chose to utilize star graphs since their method required a central node connected to nearby vertices through interconnections, but there are no edges between the nodes.

The purpose of this study was to extend the technique's applicability by introducing the concept of a benzoic acid graph, a fundamental molecule in chemistry with the formula $ C_{7}H_{6}O_{2} $. In this manner, we explored a network in which the vertices were either labeled with 0 or 1, and the structure of the chemical molecule benzoic acid was shown to have an effect on this network. To study whether or not there were solutions to the offered boundary value problems within the context of the Caputo fractional derivative with $ p $-Laplacian operators, we used the fixed-point theorems developed by Krasnoselskii. Meanwhile, the Hyers-Ulam stability has been considered. In conclusion, an example was given to illustrate the significance of the findings obtained from this research line.

The following open problems are presented for the consideration of readers interested in this topic: At present, the research prospects of fractional boundary value problems and their numerical solutions on graphs are very broad, which can be extended to other graphs, such as chord bipartite graphs. The follow-up research process, especially the research on chemical graph theory, has a certain practical significance. This is because such research does not need chemical reagents and experimental equipment. In the absence of experimental conditions and reagents, the molecular structure is studied, and the same results are obtained under experimental conditions. Although the differential equation on the benzoic acid graph is studied in this paper, the molecular structure is not studied by the topological index in the research process. It can be tried later to provide a theoretical basis for the study of reverse engineering and provide new ideas for the study of mathematics, chemistry, and other fields.

Author contributions

Yunzhe Zhang: Writing-original draft, formal analysis, investigation; Youhui Su: Supervision, writing-review, editing and project administration; Yongzhen Yu: Resources, editing. All authors have read and approved the final version of the manuscript for publication.

Use of Generative-AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This work is supported by the Xuzhou Science and Technology Plan Project (KC23058) and the Natural Science Research Project of Jiangsu Colleges and Universities (22KJB110026).

Conflict of interest

The author declares no conflicts of interest.