1.
Introduction
Calcific aortic valve stenosis (CAVS) is a continuous global progressive disease that causes stenosis and contraction of the left ventricular outflow tract in the later stage of the disease, causing destructive damage to the heart that affects hemodynamics [1]. Several epidemiological studies have shown that 2.8% of the elderly (over 75 years old) have varying degrees of CAVS, and as many as 25% of the community population over 65 years old have risk factors for valve sclerosis. Older men, high triglyceride levels, smoking time limit, and early aortic valve replacement have been determined to be associated with the progression of CAVS [2]. A calcified aortic valve often leads to aortic valve stenosis. Inflammatory cell infiltration, lipid accumulation, and tissue fibrosis play a leading role in the initial stage of the mechanism of CAVS [3]. Therefore, exploring the pathophysiological process of CAVS is essential for the diagnosis and treatment of this complex disease with a poor prognosis.
The immune and inflammatory response is a key link in the pathological process of CAVS [4]. A variety of inflammatory markers such as Toll-like receptor (TLR), interleukin-37, interleukin-6, transforming growth factor-β1 are closely related to aortic valve stenosis caused by calcified aortic valve Related [5,6]. Amyloid P Component Serum (APCS), Heat Shock Protein 90 (HSP90), Protein Disulfide Isomerase Family A Member 3 (PDIA3), Annexin A2 (ANXA2), Toll Like Receptor 7 (TLR7) and other immune-related genes (IRGs) also suggest that they have therapeutic effects in the process of CAVS fibrosis [7,8]. Immune cell infiltration is also closely related to CAVS. CD8 T lymphocytes, macrophages, and regulatory T lymphocytes (Tregs) appear in the pathophysiological process of CAVS [9,10,11]. In addition, statin anti-inflammatory therapy affects CAVS and maybe a drug target for the prevention of related diseases [12,13].
This study conducted bioinformatics and machine learning analysis of IRGs in CAVS and explored potential regulatory methods and functional differences related to IRGs. Compared with traditional models, machine learning models show superior performance in disease classification and prediction [14]. The use of machine learning models is a novel method for disease diagnosis and prediction [15,16,17]. We use Single-sample GSEA (ssGSEA) and CIBERSORT to explore the relationship between differential immunity-related genes (DEIRGs) and the level of immune infiltration of cell subsets. In addition, to better understand the immune mechanism of CAVS, the potential connection between key immune signals and immune cell subsets was studied. The flow chart of this research analysis is shown in Supplementary Figure 1.
2.
Materials and methods
2.1. Patient sample collecting and data preprocessing
Download the micro data set from Gene Expression Omnibus (GEO) (https://www.ncbi.nlm.nih.gov/geo/). The following are the screening criteria: 1) Select tissue samples including CAVS patients and normal controls; 2) Exclude samples from mitral and tricuspid valves; 3) No other organic diseases. The data set GSE12644 and GSE51472 of the GPL570 platform ([HG-U133_Plus_2] Affymetrix Human Genome U133 Plus 2.0 Array) were selected as the training data set, and the data set GSE83453 of the GPL10558 platform (Illumina HumanHT-12 V4.0 expression beadchip) was selected as the verification. GSE12644 includes 10 calcified aortic valve samples and 10 normal controls (10 CAVS vs 10 NC). GSE51472 includes 5 calcified aortic valve tissues and 5 normal controls (5 CAVS vs 5 NC). GSE83453 includes 9 aortic valve tissues with stenosis and calcification and 8 normal controls (9 CAVS vs 8 NC). All tissue sample data undergoes background correction and de-batch effect.
2.2. Gene set variation analysis (GSVA) pathway analysis and identification of DEIRGs
Use GSVA to analyze the data set to find pathways with significant differences between samples, analyzing genes more biologically meaningful [18]. The Benjamini & Hochberg method was used for multiple testing calibrations. The score value > 0.5 and adjust P-value < 0.05 is the cutoff value of pathway enrichment. The Limma package [19] (Version 3.44.3) in the R software (Version 4.0.2; https://www.r-project.org/) is used to screen differentially expressed genes (DEGs). The screening criteria for significant differences are P-value < 0.05, | log2 (Fold Change) | ≥ 1. A total of 2483 IRGs were obtained from the ImmPort (https://www.immport.org/) database, and DEIRGs were identified by matching IRGs and DEGs. The ggplot2 package [20] (Version 3.3.5) draws bar graphs of GSVA and volcano graphs of DEIRGs.
2.3. Pathway enrichment analysis of DEIRGs
Enrichment analysis of pathways and functions of DEIRGs to discover possible immune pathways and functions. Gene Ontology (GO) and Disease Ontology (DO) enrichment analysis are sorted by adjust P-value < 0.05 and Count value. We use the ggplot2 package (Version 3.3.5) of R software to visualize the plot. The Molecular Signatures Database (MSigDB) library is a collection of annotated gene sets. We can perform a series of analyses on the predefined gene set in the MSigDB library. Gene Set Enrichment Analysis (GSEA) uses "c2.cp.kegg.v7.2.symbols.gmt" under MSigDB (https://www.gsea-msigdb.org/gsea/msigdb/) [21] as the reference gene set, and the cutoff value is set to adjust P-value < 0.05.
2.4. Key immune signal screening and external verification
The obtained DEIRGs were further screened using machine learning methods to obtain key immune signals. Two machine learning methods—Least Absolute Shrinkage Selection Operator (LASSO) [22] and Support Vector Machine Recursive Feature Elimination (SVM-RFE) [23] perform feature screening for differences in gene expression values to obtain more accurate screening predictions. LASSO is an analysis method that can perform feature selection on research models. After screening, it aims to enhance the prediction accuracy and reliability of the model. SVM-RFE adopts the risk minimization principle and the experience error minimization principle. It can be used to improve learning performance to filter models. We use the glmnet package [24] (Version 4.1) and e1071 package [25] (Version 1.7) of the R software to execute the LASSO and SVM-RFE algorithms. Afterward, the external verification data set GSE83453 was verified against the selected key immune signals.
2.5. Evaluation of tissue-infiltrating immune cells
ssGSEA [26] and CIBERSORT [27] are two tools for analyzing immune infiltrating cell subtypes. CIBERSORT analyzes the infiltration of immune cells between CAVS and normal controls. Subsequently, the relationship between the DEIRGs of CAVS and the subtypes of immune infiltrating cells was established. At the same time, the key immune signals obtained by machine learning screening are correlated with the immune infiltrating cells obtained by two analysis methods. Finally, in the MSigDB library "c5.all.v7.4.symbols.gmt" uses "IMMUNITY" as the keyword to find the immune pathway of interest, calculate the pathway enrichment score and analyze the key immune signals found and their correlation. Spearman correlation analysis was used for the correlation. We used the corrplot package [28] (Version 0.9) of R software to make a related heat map. The pheatmap [29] package (Version 1.0.12) constructs a heat map of immune cells. The vioplot package [30] (Version 0.3.7) is used to compare the levels of immune cells between the two groups.
2.6. Potential drug analysis of immune-related genes
The Connectivity Map (CMap) (https://www.broadinstitute.org/connectivity-map-cmap) [31] is a database that analyzes the relationship between genes and their possible targeted drugs. Use CLUE (https://clue.io/) to predict the targeted drugs for CAVS immunotherapy on the 150 most significant up-and down-regulated immune genes in the data set. At the same time, use the Touchstone module to analyze the mechanism of actions (MoA) of the drug of interest and explore potential modes of action.
2.7. Statistical analysis
All statistical analysis uses R software (Version 4.0.2). Use Student's t test for normally distributed variables and Mann-Whitney U test for abnormally distributed variables to compare the differences between the two groups.
3.
Results
3.1. GSVA results and DEIRGs
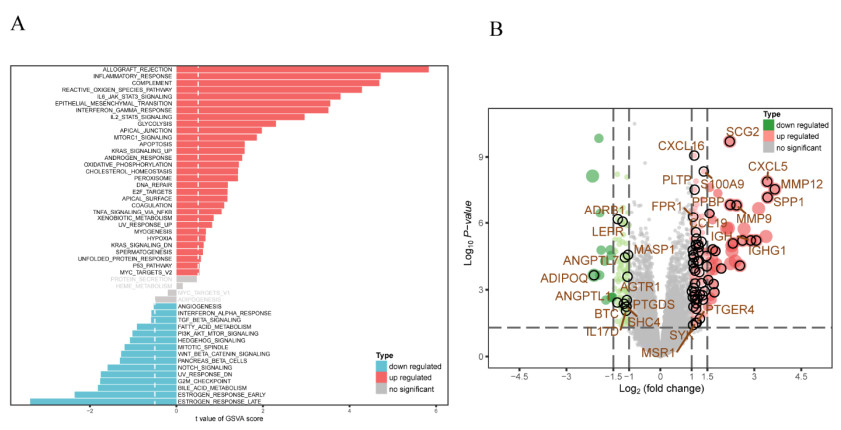
Use non-parametric unsupervised GSVA for gene sets to find the difference between the gene set in CAVS and normal control in the enrichment pathway, suggesting that it has a greater correlation with multiple immune pathways (Figure 1A). After the integration of GSE12644 and GSE51472 microarray matrix standardization and removal of batch effects, 266 DEGs (164 up-regulated genes, 102 down-regulated genes) were obtained, and 71 significant DEIRGs were obtained through integration with immune genes (60 up-regulated genes and 11 down-regulated genes). The volcano map shows the differences in genes. The DEIRGs related to immunity are marked by black circles. The names of some DEIRGs of interest are also marked (Figure 1B).
3.2. Pathway and function enrichment analysis
GO enrichment found that the biological processes (BP) mainly focused on reactive oxygen species, oxidative stress, cellular response to oxidative stress, and decreased oxygen levels. Cell component (CC) is mainly related to various components of the synaptic membrane. Molecular function (MF) is mainly related to receptor activity and enzyme binding (Figure 2A). DO found that cardiovascular diseases such as arteriosclerotic cardiovascular disease, arteriosclerosis, atherosclerosis, coronary artery disease, and myocardial infarction were significantly enriched. In addition, it includes lung disease, obstructive lung disease, kidney disease, and so on (Figure 2B). GSEA found that two immune-related pathways, Cytokine-cytokine receptor interaction and Chemokine signaling pathway were significantly enriched. It may be related to the immune-related pathways of CAVS (Figure 2C).
3.3. Machine learning to screen key immune signals
According to the LASSO method, the optimal lambda.min is set as 0.007915132 based on the amount of gene expression. The 6 immune signals screened out are Angiotensin II Receptor Type 1(AGTR1), C-X-C Motif Chemokine Ligand 16 (CXCL16), Leptin Receptor (LEPR), Phospholipid Transfer Protein (PLTP), Secretogranin II (SCG2), Secretory Leukocyte Peptidase Inhibitor (SLPI) (Figure 3A). After screening using SVM-RFE, the first 50 variables were screened by 5x cross-check, and the first 4 immune signals were Angiotensin II Receptor Type 1(AGTR1), Phospholipid Transfer Protein (PLTP), Secretogranin II (SCG2), and Tenascin C (TNC) (Figure 3B). Integrating the two results, AGTR1, PLTP, and SCG2 are considered by us to be the key immune signals of CAVS (Figure 3C). The external validation data set GSE83453 verified it and found that the three key immune signals distinguished well between CAVS and normal control (Figure 3D). The areas under the ROC curve were AGTR1 (AUC = 0.917), PLTP (AUC = 0.875), and SCG2 (AUC = 0.917), with high diagnostic value (Figure 3E).
3.4. CIBERSORT and ssGSEA immune infiltration analysis
Two methods of CIBERSORT and ssGSEA were used to analyze the immune infiltration of CAVS and normal controls. The relative percentages of the 22 immune cells evaluated by CIBERSORT are displayed in a bar graph (Figure 4A). Correlation analysis between immune cells found that NK cells resting and T cells regulatory (Tregs) were positively correlated, and the correlation reached 0.81. The highest negative correlation between Mast cells resting and Mast cells activated, T cells gamma delta and T cells regulatory (Tregs) reached 0.77(Figure 4B). The violin chart shows that B cells naïve (P < 0.01), Macrophages M0 (P < 0.01), Macrophages M2 (P < 0.01) have a higher degree of discrimination between CAVS and normal controls. B cells naïve and Macrophages M2 are less in CAVS, while Macrophages M0 is more in CAVS (Figure 4C). The PCA chart also shows that CAVS is well distinguished from normal controls (Figure 4D). The correlation results between immune-related differential genes (DEIRGs) and immune infiltrating cells produced by the two methods are represented by heat maps (Figure 5A, B). ssGSEA found that most DEIRGs are positively correlated with more immune cells, while CIBERSORT shows that B cells memory, Macrophages.M2, and NK cells activated are negatively correlated with DEIRGs.
3.5. The connection of key immune signals with specific immune pathways and immune infiltrating sub-cells
Among the three key immune signals of CAVS, AGTR1 is negatively correlated with the immune pathway of interest in MSigDB, while PLTP and SCG2 are positively correlated (Figure 6A–C). There is a high degree of positive correlation between most immune pathways. Among the 28 immune cells analyzed by ssGSEA, AGTR1 was negatively correlated with most, while PLTP and SCG2 were positively correlated with most (Figure 6D–F). The correlation among 28 kinds of immune cells is shown in the correlation heat map. Among the 22 immune cells analyzed by CIBERSORT, the most significant is that AGTR1 is positively correlated with NK cells activated (r = 0.83, P = 1.32E-08), and NK cells resting is negatively correlated (r = -0.63, P = 0.000194) (Figure 6G). PLTP had the most significant positive correlation with Neutrophils (r = 0.69, P = 3.89E-05), and the most significant negative correlation with B cells naive (r = -0.36, P = 0.045151) (Figure 6H). SCG2 had the most significant positive correlation with Macrophages.M0 (r = 0.68, P = 2.63E-05), and the most significant negative correlation with Macrophages.M2 (r = -0.56, P = 0.001529) (Figure 6I).
3.6. Analysis of potential drug effects of CMap
CMap analysis found that isoliquiritigenin, parthenolide, pyrrolidine-dithiocarbamate, radicicol, RITA, roscovitine, securinine, midazolam, mitomycin-c, and colforsin are the top ten targeted drugs related to CAVS immunity (Figure 7A). The scores of isoliquiritigenin, parthenolide, and pyrrolidine-dithiocarbamate were 92.40, 88.23, and 84.24. The first three drugs isoliquiritigenin, parthenolide, and pyrrolidine-dithiocarbamate were analyzed by the drug MoA and found to be related to the NFkB pathway inhibitor, Immunostimulant, etc (Figure 7B–D).
4.
Discussion
Calcific aortic valve stenosis is the most prevalent valve disease in the world. It exists in large numbers in the elderly, and the disease has caused severe damage to the patients [32]. Once the clinical symptoms of severe CAVS appear, the prognosis is poor without intervention. Although there is still a lack of precise molecular insights into the pathophysiological process of CAVS, early intervention of the disease has become more realistic. More evidence shows that aortic valve calcification is closely related to immune inflammation [33,34]. Therefore, we tried to find DEIRGs and explore the possible role of immune cell infiltration in CAVS. 71 DEIRGs (60 up-regulated genes, 11 down-regulated genes) were identified as biomarkers of CAVS, and the potential enrichment function of DEIRGs was further studied. GO enrichment revealed that DEIRGs are associated with the immune inflammatory response. DO enrichment analysis found that DEIRGs are mainly closely related to cardiovascular diseases. GSEA enrichment revealed that two immune-related pathways, Cytokine-cytokine receptor interaction and Chemokine signaling pathway were significantly enriched. Two machine learning methods, LASSO and SVM-RFE, are used to confirm that AGTR1, PLTP, and SCG2 are the key immune signals of CAVS.
The protein encoded by AGTR1 is part of the renin-angiotensin system and is used to regulate the balance of blood and body fluids. This gene may play a role in the production of arrhythmia after reperfusion after ischemia or infarcted myocardial blood flow is restored. A study showed that the AGTR1 gene has a moderate level of evidence that may be related to the risk of CAVS [35]. At the same time, the pathogenesis of some cardiovascular diseases is also related to AGTR1 [36,37]. PLTP is one of the lipid transfer proteins, which binds to Apolipoprotein A1(ApoA) [38]. Several studies have shown that ApoA is related to calcification and stenosis of the aortic valve. It is mostly located in its fibrous tissue and co-localizes with the calcified area [39,40,41]. In addition, studies in mice have shown that PLTP deficiency can reduce plasma total cholesterol and triglycerides and prevent the progression of arterial calcification [42]. SCG2 is a member of the granulin family. Studies have found that SCG2 is present in mouse myocardium [43]. In addition, a study also found that SCG2 plays a key role in the development of aortic valve calcification [44]. However, the specific mechanism of SCG2 and CAVS remains to be studied.
CIBERSORT and ssGSEA analyzed the subtypes of CAVS immune infiltrating cells and found that B cells naïve (P < 0.01) and Macrophages M2 (P < 0.01) were less in CAVS, while Macrophages M0 (P < 0.01) were more in CAVS. ssGSEA and CIBERSORT found that most DEIRGs are positively correlated with immune cells, and DEIRGs are more negatively correlated with B cells memory, Macrophages.M2, and NK cells activated. Among the three key immune signals of CAVS, AGTR1 is negatively correlated with the immune pathway of interest in MSigDB, while PLTP and SCG2 are positively correlated. Analysis of the key immune signals and immune cell subtypes of the three CAVS showed that among the 28 immune cells obtained from ssGSEA, AGTR1 was negatively correlated with the majority, while PLTP and SCG2 were positively correlated with the majority. Among the 22 immune cells analyzed by CIBERSORT, the most significant is that AGTR1 is positively correlated with NK cells activated, and NK cells resting is negatively correlated. PLTP is positively correlated with Neutrophils and negatively correlated with B cells naive. SCG2 is positively correlated with Macrophages.M0 and negatively correlated with Macrophages.M2.
Finally, we performed CMap analysis on immune genes in the dataset to find possible related drugs. Isoliquiritigenin, parthenolide, pyrrolidine-dithiocarbamate, radicicol, RITA, roscovitine, securinine, midazolam, mitomycin-c, and colforsin are the top ten targeted drugs related to the immune mechanism of CAVS. At the same time, it was found that the top three drugs isoliquiritigenin, parthenolide, and pyrrolidine-dithiocarbamate are related to NFkB pathway inhibitor and Immunostimulant. Based on these results, AGTR1, PLTP, and SCG2 seem to play a key role in CSVA by regulating immune infiltration.
5.
Conclusions
In this study, we obtained 266 DEGs in CAVS and normal controls, and 71 DEIRGs were obtained through integration with immune genes. Enrichment analysis found that DEIRGs are related to oxidative stress, synaptic membrane components, receptor activity, and a variety of cardiovascular diseases and immune pathways. Two machine learning algorithms identified AGTR1, PLTP, and SCG2 as the key immune signals of CAVS. Immune infiltration found that B cells naïve and Macrophages M2 are less in CAVS, while Macrophages M0 is more in CAVS. At the same time, AGTR1, PLTP, SCG2 are highly correlated with a variety of immune cell subtypes. CMap analysis found that isoliquiritigenin, parthenolide, and pyrrolidine-dithiocarbamate are the top three targeted drugs related to CAVS immunity. Our findings will help improve the understanding of CAVS disease and explain new molecular mechanisms and potential targets.
Acknowledgments
We acknowledge GEO database for providing their platforms and contributors for uploading their meaningful datasets.
Conflict of interest
The authors declare that they have no conflict of interest.









 DownLoad:
DownLoad: