Prioritizing COVID-19 vaccination. Part 1: Final size comparison between a single dose and double dose

1.   Introduction

Modeling of activity represents, manipulates and communicates real-world objects of daily life ^[11]. One of the basic tools in mathematical models for representing the biological processes of the human brain are neural networks. These are also commonly referred to as parallel distributed processing models or simply neural nets. The first mathematical model of a neural network is attributed to McCulloch and Pitts ^[17] who in 1943 showed that any logical function could be configured by a parallel distributed processing system of interconnected digital neurons. A very concise summary of the foundations of neural networks was provided in the book ^[4]. Various models of neural networks are used to consider specific tasks and in order to specify a particular neural network model it suffices to define its architectural, computational, and adaptive dynamics. The computational dynamics specifies the network initial state and a rule for its up­dates in time, providing that the network topology and configuration are fixed. At the beginning of the computational mode, the states of input neurons are assigned to the network input and the remaining neurons find themselves in the initial state. All potential network inputs and states form the input and state space of neural network, respectively. In dynamic (recurrent, feedback) systems, the current output signals depend, in general, on current and past input signals. There are two equivalent classes of dynamic systems: continuous-time and discrete-time systems. Continuous-time dynamic systems operate with signals which are functions of a continuous variable, that is continuous functions of time and they are described by means of differential equations.

The main objective of this paper is to study stability of continuous-time neural networks without assuming the smoothness, monotonicity and unboundedness of the activation function. The model introduced is a generalization of some additive neural networks. These type of models can simulate biological neural networks and artificial intelligence systems, from the view point of reality, and it should also naturally take into account evolutionary processes of the biological systems as well as disturbances of external influence.

In controlling nonlinear systems, the Lyapunov second method provides a way to analyze the stability of the system without explicitly solving the differential equations. Stability results concerning neural networks can be found in ^[10,15]. One type of stability, very useful in real world problems, is the so called Lipschitz stability. Dannan and Elaydi ^[5] introduced the notion of Lipschitz stability for ordinary differential equations and as noted in ^[5] this type of stability is important only for nonlinear problems, since it coincides with uniform stability in linear systems.

Sometimes neural networks are subjected to certain impulsive state displacements at fixed moments of time. Stability problems of neural networks under the presence of instantaneous impulses was considered in ^[2,3,6]. Finite-time stability of systems with instantaneous impulses was studied in ^[16] and for delays see ^[13,14]. In the case when the time acting of these state displacements is not negligibly small, this phenomenon is modeled by so called non-instantaneous impulses.

In ^[19] the speed of the neural impulse is discussed and the reason why modeling with instantaneous impulses is not adequate is considered. As a result, we will consider non-instantaneous impulses in modeling neural impulses.

In this paper, we study stability properties of neural networks with non-instantaneous impulses, i.e. perturbations which start their actions abruptly at some points and then continue on given finite intervals. We study the general case when

$-$ the self-regulating parameters of all units are variable in time;

$-$ the functions of the connection between two neurons in the network are variable in time bounded functions;

$-$ the activation functions are non-Lipschitz (usually in the literature only the case of Lipschitz activation functions is studied).

In this paper, the investigation is based on the Lyapunov method. Some Lipschitz stability sufficient criteria are provided by using Lyapunov functions (not only quadratic ones). The results are illustrated on several particular neural networks.

2.   System description

We will consider the model proposed by Hopfield ^[7] and known as Hopfield's graded response neural network in the case when the neurons are subject to a certain impulsive state displacement at fixed moments and the duration of this displacement is not negligible small (they are known as non-instantaneous impulses). The model is based on an analog circuit consisting of capacitors, resistors and amplifiers. The input-output characteristics of the amplifiers in the circuit are modeled by some functions known as activation functions. In the literature these functions are assumed to satisfy a wide variety of assumptions, mainly they are Lipschitz functions. A neuron in the circuit is modeled by an elementary sub-circuit composed of an amplifier, a reverse amplifier, a capacitor and a resistor. The neural network is itself constructed from such elementary neurons interconnected by resistors which are analogous to biological synapses. The biological counterpart of inhibitory synapses is realized by reverse amplifiers. Usually there are two sets of inputs to the neurons. The first set of inputs are the currents $I_1, I_2, \dots, I_n$ which are external inputs and often in the literature are considered as constants. The second set consists of those arising from feedback connections from other op-amps including possible self-connections. Resistances are always positive and a negative resistance to a neuron can be implemented by choosing an inverted output from certain amplifiers.

In this paper, we will assume two increasing sequences of points $\{t_i\}_{i = 1}^\infty$ and $\{s_i\}_{i = 1}^\infty$ are given such that $0 < s_i\leq t_i < s_{i+1}$, $i = 1, 2, \dots$, and $\lim_{k\to \infty}s_k = \infty$.

Let $t_0 \in \mathbb{R}_+ = [0, \infty)$ be a given arbitrary point. Without loss of generality we will assume that $0\leq t_0 < s_1$.

Remark 1. In the case $t_k = s_{k}, \ k = 1, 2, \dots$ we obtain the case of instantaneous impulses and the so called fixed points of impulses (see, for example ^[8,12]).

If for the natural number $k:\ t_k\not = s_k$ then the interval $(s_k, t_{k}]$ is called the interval of non-instantaneous impulses (see ^[1]).

Consider the general model of Hopfield's graded response neural network with non-instantaneous impulses (NNNI)

where $n$ represents the number of neurons in the network, $x_i(t)$ corresponds to the membrane potential of $i$-th neuron at time $t$, $x(t) = (x_1(t), x_2(t), \dots, x_n(t))^T\in \mathbb{R}^n$, $x_i(s_{k}-0) = \lim_{t\uparrow s_k} x_i(t), \ k = 1, 2, \dots, i = 1, 2, \dots, n$, $c_i(t) > 0, i = 1, 2, \dots, n,$ is the rate with which the unit self-regulates or resets its potential when isolated from other units and inputs of the $i$-th unit at time $t$, $a_{ij}(t), \ i, j = 1, 2, \dots, n,$ correspond to the synaptic connection weights of the $i$-th neuron to the $j$-th neuron at time $t$, $f_j(x_j)$ denotes a measure of response or activation of $j$-th neuron to its membrane potential, $f(x) = (f_1(x_1), f_2(x_2), \dots, f_n(x_n))^T$ and $I = (I_1, I_2, \dots, I_n)^T$ is an external bias vector, the intervals $(s_k, t_k), k = 1, 2, \dots,$ are intervals of acting the state displacements which are impulsive activated at fixed moments $s_k$, the functions $\Phi_{k, i}(t, x_i), \ k = 1, 2, \dots$ are the impulsive functions giving the impulsive perturbation of the $i$-th neuron on the interval $(s_k, t_k]$.

In applications, when Hopfield-type neural networks are used for associative memories, the equilibrium states of the network serve as stored patterns and their stability implies that the stored patterns can be retrieved in the presence of perturbations of the network which can be non-instantaneous impulsive state displacements. When Hopfield networks are used for the solution of optimization problems, the equilibrium states denote the possible optimal solutions and their stability will guarantee the convergence to the solutions beginning from an appropriate initial state.

Definition 1. A vector $x^*\in \mathbb{R}^n, \ x^* = (x_1^*, x_2^*, \dots, x_n^*)^T$ is an equilibrium of NNNI (2.1), iff the equalities

and

hold.

Remark 2. The problem (2.1) is studied in ^[6] in the special case of constant self-regulating parameters $c_i(t)\equiv c_i$, constant connection of the $i$-th neuron to the $j$-th neuron, i.e. $a_{ij}(t)\equiv a_{ij}, \ i, j = 1, 2, \dots, n$, constant external bias vectors $I(t)\equiv I$, instantaneous impulses $t_k = s_{k}$ and Lipschitz activation functions. Several types of sufficient conditions for existence of a constant vector satisfying equality (2.2) for $t\geq t_0$ are given in ^[6].

We assume the following:

Assumption A1. The NNNI (2.1) has an equilibrium $x^*\in \mathbb{R}^n$.

If assumption A1 is satisfied, then we can shift the equilibrium point $x^*$ of system (2.1) to the origin. The transformation $y(t) = x(t)- x^*$ is used to put system (2.1) in the following form:

where $F_j(u) = f_j(u+x_ j^*)-f_j(x_ j^*), j = 1, 2, \dots, n$ and $\phi_{k, i}(t, u) = \Phi_{k, i}(t, u+x_i^*)-\Phi_{k, i}(t, x_i^*), \ i = 1, 2, \dots, n, \ k = 1, 2, \dots$, $y_i^0 = x_i^0-x_i^*$ with $u\in\mathbb{R}$.

Note that $F_i(0)\equiv 0$ and $\Phi_{j, i}(t, 0) = 0$ for $j = 1, 2, \dots, \ i = 1, 2, \dots, n,$ and $t\in[s_j, t_j]$ and if the point $x^*\in \mathbb{R}^n$ is an equilibrium of NNNI (2.1), then the point $y^* = 0$ is an equilibrium of NNNI (2.4). This allows us to study the stability properties of the zero equilibrium of NNNI (2.4). Also, without loss of generality we can assume $t_0 = 0$.

We will discuss the equilibrium of some NNNI with various activation functions. It will be useful for stability analysis.

EXAMPLE 1. Let $n = 1$, $\Phi_k\in C([s_k, t_k]\times \mathbb{R}, \mathbb{R})$, $k = 1, 2, \dots$, $f\in C(\mathbb{R}, \mathbb{R})$ and consider the scalar NNNI

where $c\in C(\cup_{k = 0}^\infty (t_k, s_{k+1}], (0, \infty))$, $I\in C(\cup_{k = 0}^\infty (t_k, s_{k+1}], \mathbb{R})$.

Case 1.. Let $I(t) = 0.5\pi c(t)$, $\Phi_k(t, u) = \frac{t}{k}u+(1-\frac{t}{k})\frac{\pi}{2}, t\in [s_k, t_k]$, and the activation function be the cosine function $f(u) = \cos (u)$ (see ^[18]).

The point $x^* = 0.5\pi$ is an equilibrium point of NNNI(2.5) because

and $0.5\pi = \Phi_k(t, 0.5\pi), t\in [s_k, t_k], k = 1, 2, \dots$.

The transformation $y(t) = x(t)-0.5\pi$ will shift the model (2.5) to the following model with zero equilibrium:

with $y_0 = x_0-\frac{\pi}{2}$.

Case 2. Let $I(t) = 0.5c(t)$, $\Phi_k(t, u) = \frac{t}{k}u+0.5-\frac{t}{2k}, t\in [s_k, t_k],$ and the activation function be the Probit function $f(u) = \sqrt{2}\ {\mbox{erf}}^{-1}(2u-1)$ with ${\mbox{erf}}(u) = \frac{2}{\sqrt{\pi}}\int_0^u e^{-t^2}dt$ is the error function or the activation function be the Logit function $f(u) = \log \Big(\frac{u}{1-u}\Big).$

The point $x^* = 0.5$ is an equilibrium point of NNNI(2.5) because $-c(t)0.5+a(t)f(0.5) +0.5c(t) = 0$ for all $t\in \cup_{k = 0}^\infty [t_k, s_{k+1}]$ and $\Phi_k(t, 0.5) = 0.5$ for $t\in [s_k, t_k]$.

The transformation $y(t) = x(t)-0.5$ will shift the model (2.5) to the following model with zero equilibrium:

with $y_0 = x_0-0.5$.

Case 3. If $I(t) = 0$, $\Phi_k(t, u) = \xi_k(t)u$ for $t\in [s_k, t_k], u\in\mathbb{R}$ with $\xi_k\in C([s_k, t_k], \mathbb{R})$ and any activation function such that $f(0) = 0$ then the point $x^* = 0$ is an equilibrium point of NNNI(2.5).

3.   Lipschitz stability for non-instantaneous impulsive differential equations

First we give some results for Lipschitz stability of the general type of nonlinear non-instantaneous impulsive differential equations (NIDE).

Consider the general type of initial value problem (IVP) for NIDE:

where $x, x_0 \in \mathbb{R}^n, H:\cup_{k = 0}^\infty[t_k, s_{k+1}]\times \mathbb{R}^n \rightarrow \mathbb{R}^n, \Psi_k:[s_k, t_{k}] \times \mathbb{R}^n \rightarrow \mathbb{R}^n, (k = 1, 2, 3, \ldots).$

Remark 3. The model MNNI (2.1) is a special case of NIDE (3.1).

A detailed description of the solutions of IVP for NIDE (3.1) and some qualitative properties of the solutions of (3.1) are given in the book ^[1].

Let $J \subset \mathbb{R}^+$ be a given interval. We introduce the following classes of functions

Remark 4. According to the above description any solution of (3.1) might have a discontinuity at any point $s_k, k = 1, 2, \ldots.$

Let $J\subset \mathbb{R}_+, \ 0\in J$, $\rho > 0$. We introduce the following sets:

Remark 5. The function $a(u) = K_1u$, $K_1 > 0$ is from the class $\mathcal{K}(\mathbb{R}_+)$ with $K_a = K_1$.

The function $a(u) = K_2 \sqrt{u}, \ K_2\geq 1$ is from the class $\mathcal{M}([0, 1])$ with $q_a(\alpha) = \alpha^2$.

The function $a(u) = K_3 u, \ K_3\geq 1$ is from the class $\mathcal{M}(\mathbb{R}_+)$ with $q_a(\alpha) = K_3\alpha$.

We will use the class $\Lambda$ of Lyapunov-like functions, defined and used for impulsive differential equations in ^[12].

Definition 2. Let $J \subset \mathbb{R}_+$ be a given interval, and $\Delta \subset \mathbb{R}^n$ be a given set. We will say that the function $V(t, x):J \times \Delta \rightarrow \mathbb{R}_+,$ belongs to the class $\Lambda (J, \Delta)$ if

$-$ The function $V(t, x)$ is a continuous on $J/\{s_k \in J\}\times \Delta$ and it is locally Lipschitz with respect to its second argument;

$-$ For each $s_k \in J$ and $x \in \Delta$ there exist finite limits

Lipschitz stability of systems of differential equations with non-instantaneous impulses is defined and studied in ^[9]:

Definition 3. (Lipschitz Stability) ^[9] The equilibrium $x^*$ of NNNI (2.1) is said to be

$-$ uniformly Lipschitz stable if there exists $M \geq 1$ and $\delta > 0$ such that for any $t_0\geq 0$ and $x_0 \in \mathbb{R}^n$ the inequality $|x_0-x^*| < \delta$ implies $|x(t; t_0, x_0)-x^*| \leq M|x_0-x^*|$ for $t \geq t_0;$

$-$ globally uniformly Lipschitz stable if there exists $M \geq 1$ such that for any $t_0 \geq 0$ and $x_0 \in \mathbb{R}^n$ the inequality $|x_0-x^*| < \infty$ implies $|x(t; t_0, x_0)-x^*| \leq M|x_0-x^*|$ for $t \geq t_0.$

Remark 6. In Definitions 1.1-1.4 ^[5] for Lipschitz stability the constants $M > 0$. Note we use the constant $M \geq 1$ in Definition 3 since our inequality has to hold at $t = t_0$.

Remark 7. Note the Lipschitz stability property of the equilibrium of NNNI (2.1) implies the corresponding stability property of the zero solution of (2.4) and vice versa.

We will use the following scalar comparison differential equation with non-instantaneous impulses:

where $u, u_0 \in \mathbb{R}, g:\cup_{k = 0}^\infty[t_k, s_{k}]\times \mathbb{R} \rightarrow \mathbb{R}, \psi_k:[s_k, t_{k+1}] \times \mathbb{R} \rightarrow \mathbb{R} \ (k = 0, 1, 2, 3, \ldots).$

Note the Lipschitz stability of the scalar non-instantaneous impulsive equation (3.2) is similarly defined as in Definition 3.

We introduce the following conditions:

(H1). The function $H\in C([0, s_1]\bigcup_{k = 1}^{\infty}[t_k, s_{k+1}] \times \mathbb{R}^n, \mathbb{R}^n)$, $H(t, 0) = 0$, and for any $k = 1, 2, \dots$ the functions $\Psi_k\in C([s_k, t_{k}] \times \mathbb{R}^n, \mathbb{R}^n), \ \Psi_k(t, 0) = 0$.

(H2). The function $g\in C([0, s_1]\bigcup_{k = 1}^{\infty}[t_k, s_{k+1}] \times \mathbb{R}_+, \mathbb{R}),$ $g(t, 0) = 0$, and for any $k = 1, 2, \dots$ the functions $\psi_k \in C([s_k, t_{k}] \times \mathbb{R}_+, \mathbb{R}_+)$ are nondecreasing with respect to their second argument and $\psi_k(t, 0) = 0$.

EXAMPLE 2. Consider the scalar ordinary differential equation

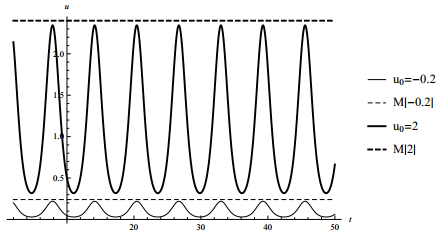
with a solution $u(t) = u_0 e^{\sin(t)-\sin(t_0) }$ for $t\geq t_0$. Therefore, $|u(t)|\leq |u_0| e^{2}$ for $t\geq t_0$, i.e. the solution is globally uniformly Lipschitz stable. (see Figure 1 for the graph of the solution with initial value $u_0 = -0.2$ and the graph of the solution with initial value $u_0 = 2$ and $M = 1.1$).

Now consider the scalar differential equation with non-instantaneous impulses:

where $t_k = 2k+1, k = 0, 1, 2, \dots, \ s_k = 2k, k = 1, 2, \dots$.

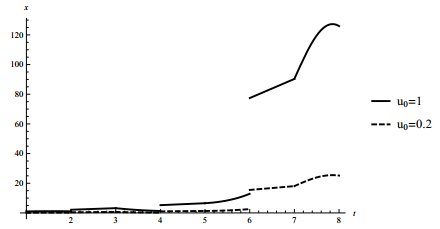
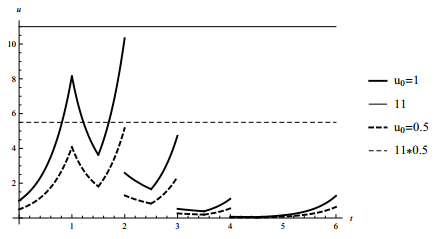
Case 1. Let $\psi_k(t, u) = t u$. The solution is a nondecreasing function approaching infinity and the zero solution is not globally uniformly Lipschitz stable (see Figure 2 for the graph of the solution with initial value $u_0 = 1$ and the graph of the solution with initial $u_0 = 0.2$).

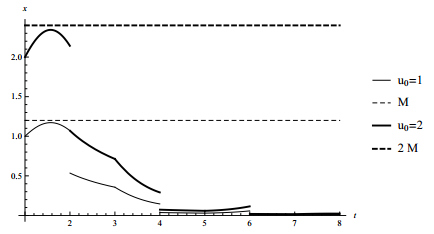
Case 2. Let $\psi_k(t, u) = \frac{u}{t}$. The zero solution is uniformly Lipschitz stable with $M = 1.2$ and $\delta = 2$ (see Figure 3) but it is not globally uniformly Lipschitz stable.

Theorem 1. ^[9] Let the following conditions be satisfied:

1. Conditions (H1), (H2) are fulfilled.

2. There exists a function $V(t, x) \in \Lambda (\mathbb{R}_+, \mathbb{R}^n)$ and

($i$) the inequalities

hold, where $b\in K([0, \rho])$, $a\in M([0, \rho])$, $\rho > 0$;

($ii$) the inequality $D^+V(t, x) \leq g(t, V(t, x)), t \in [0, s_1]\bigcup_{k = 1}^{\infty}(t_k, s_{k}), x \in S_\rho$ holds where $D^+V(t, x) = \lim\sup_{h\to0^+} \frac{1}{h}\{V(t, x)-V(t-h, x-hH(t, x))\}$;

($iii$) for any $k = 1, 2, \ldots$ the inequality

holds.

3. The zero solution of (3.2) is uniformly Lipschitz stable (globally uniformly Lipschitz stable).

Then the zero solution of (3.1) is uniformly Lipschitz stable (globally uniformly Lipschitz stable).

Corollary 1. Let (H1) be satisfied and the inequalities

and

hold.

Then the zero solution of (3.1) is globally uniformly Lipschitz stable.

Proof. For $V(t, x) = 0.5 \sum_{i = 1}^n x_i^2, \ x = (x_1, x_2, \dots, x_n)^T$ from (3.5) it follows that condition 2(ⅱ) of Theorem 1 is satisfied with $g(t, u)\equiv 0$ and from (3.6) it follows that 2(ⅲ) of Theorem 1 is fulfilled with $\psi_k(t, u) = u$. Then the comparison scalar equation is the following equation:

The solution of the IVP (3.7) is $u(t) = u_0$ for $t\geq t_0$ and therefore the zero solution of (3.7) is globally uniformly Lipschitz stable with $M = 1$. According to Theorem 1 the zero solution of (3.1) is globally uniformly Lipschitz stable.

4.   Stability analysis of neural networks with non-instantaneous impulses

We will study stability properties of several different types of NNNI (2.1).

4.1.   Lipschitz activation functions.

We will introduce the following assumptions:

Assumption A2. The neuron activation functions are locally Lipschitz, i.e. there exist positive numbers $L_i, \ i = 1, 2, \dots, n$ and $\lambda > 0$ such that $|f_i(u)-f_i(v)|\leq L_i|u-v|, \ i = 1, 2, \dots, n$ for $u, v\in \mathbb{R}:\ |u-x_i^*|\leq \lambda, |v-x_i^*|\leq \lambda$ where the point $x^*\in \mathbb{R}^n$ is the equilibrium from assumption A1.

Assumption A3. There exist positive numbers $M_{i, j}, \ i, j = 1, 2, \dots, n$ such that $|a_{i, j}(t)|\leq M_{i, j}$ for $t\in[0, s_1]\bigcup\cup_{k = 1}^\infty (t_k, s_{k+1}]$.

Assumption A4. There exists a number $B > 0$ such that $c_{i}(t)\geq B$ for $t\in[0, s_1]\bigcup\cup_{k = 1}^\infty (t_k, s_{k+1}], \ i = 1, 2, \dots, n$ and the inequality

holds.

Assumption A5. For any $k = 1, 2, \dots$ and $x\in \mathbb{R}^n:\ ||x-x^*||\leq \lambda$ the inequalities

hold where $x^*$ is the equilibrium point from assumption A1 and $\lambda$ is the number defined in A2.

Remark 8. Assumption A5 and the inequality (4.1) are connected with the strength of the self-regulating negative feedback of each neuron which dominates its own contribution to the entire network. Such phenomena are observed in Lotka-Volterra systems modeling interacting population systems.

Theorem 2. Let assumptions A1 - A5 be satisfied. Then the equilibrium $x^*$ of NNNI (2.1) is globally uniformly Lipschitz stable.

Proof. From the definition of the functions $F_j$, assumption A2 and the inequality $2ab\leq a^2+b^2, \ a, b\in\mathbb{R}$ we get the inequalities

From assumption A5 it follows that the inequality (3.5) holds.

From assumption A5 it follows that the inequality (3.6) holds for $\Psi_{k, i}(t, y_i) = \Phi_{k, i}(t, y_i+x_i^*)-\Phi_{k, i}(t, x_i^*)$.

According to Corollary 1 the zero solution of (2.1) globally uniformly Lipschitz stable. This proves the claim.

EXAMPLE 3. Let $n = 3$, $t_0 = 0, \ s_k = (k-0.5^k)\pi, \ t_k = k\pi, k = 1, 2, \dots$. Consider the NNNI

with $\Phi_{k, i}(t, u) = \sin kt\ u+(1-\sin kt)0.5 \pi$ and $A = a_{ij}(t)$ is given by

The point $x^* = (0.5 \pi, 0.5 \pi, 0.5 \pi)$ is the equilibrium point of NNNI (4.3).

Note assumptions A2, A4 are satisfied with $L = 1$ and $B = 0.9$. Next assumption A5 is fulfilled because

Also, $|a_{ij}|\leq M_{ij}, \ i, j = 1, 2, 3, \ t\geq 0$ where $M = \{M_{ij}\},$ is given by

and $\sum_{i = 1}^3 \max_jM_{ij} +\max_i\sum_{j = 1}^3 M_{ij} = (0.4+0.3+0.2)+\max(0.4, 0.9, 0.6) = 0.9+0.9 = 1.8$, i.e. inequality (4.1) holds. Therefore, according to Theorem 2 the equilibrium of NNNI(4.3) is globally uniformly Lipschitz stable.

Consider the system (4.3) without any impulses. The right side part is not defined for all $t\geq t_0$ because of the function $csc(t)$. The appropriate perturbing of the model by non-instantaneous impulses can induce existence of the solution and stability properties of the equilibrium.

4.2.   Non-Lipschitz activation functions.

There are many types of activation functions which are not Lipschitz. In this case, we assume:

Assumption A6. There exists a function $\xi\in C([0, s_1]\bigcup\cup_{k = 1}^\infty (t_k, s_{k+1}], \mathbb{R})$ such that for any point $x:\ x-x^*\in S(\lambda)$ and $t\in[0, s_1]\bigcup\cup_{k = 1}^\infty (t_k, s_{k+1}]$ the inequality

holds where $x^*$ is the equilibrium from condition A1.

Theorem 3. Let the following conditions be satisfied:

1. Assumptions A1 and A6 are satisfied.

2. The functions $c_{i}\in C(\cup_{k = 0}^\infty (t_k, s_{k+1}], \mathit{\mathbb{R}} _+)$, $i = 1, ,\dots, n$.

3. The impulsive functions $\Phi_{k, i}\in C([s_k, t_k]\times \mathit{\mathbb{R}}, \mathit{\mathbb{R}})$ and there exists a positive number $\lambda$ such that for $k = 1, 2, \dots$ and $x\in \mathit{\mathbb{R}} ^n: x-x^*\in S(\lambda)$ the inequality

holds where $x^*$ is the equilibrium from condition 1.

4. There exists a function $p\in C^1([0, \infty), \mathit{\mathbb{R}} _+): 0 < \alpha\leq p(t)\leq \beta, t\geq 0$ such that $p(t)\leq p(s_k)$ for $t\in [s_k, t_k]$ and the zero solution of the scalar non-instantaneous impulsive equation (3.2) with $g(t, u) = 2\gamma(t)u$ and $\psi_k(t, u) = \mu_k(t)u$ is uniformly Lipschitz stable (globally uniformly Lipschitz stable) where

Then the equilibrium $x^*$ of NNNI (2.1) is uniformly Lipschitz stable (globally uniformly Lipschitz stable).

Proof. Consider the Lyapunov function $V(t, x) = p(t)\sum_{i = 1}^nx_i^2, \ x = (x_1, x_2, \dots, x_n)$. Then condition 2(ⅰ) of Theorem 1 is satisfied with $b(u) = \alpha \sqrt{u}$ and $a(u) = K \sqrt{u}, \ K = \max\{1, \beta\}$. From Remark 5 it follows that $b\in \mathcal{K}([0, \lambda])$ and $a\in \mathcal{M}([0, \lambda])$. From assumption A6 it follows that the function $F$ in NNNI (2.4) satisfies the inequality

From inequality (4.5) with $u_i = y_i-x_i^*\in S(\lambda)$ we obtain for the Dini derivative among the system (2.4):

Therefore, Condition 2(ⅱ) of Theorem 1 is satisfied with $g(t, u) = 2\gamma(t)u$.

Then for $t \in (s_k, t_{k}], \ y \in S_\lambda$ the Lyapunov function satisfies

Therefore, Condition 2(ⅲ) of Theorem 1 is satisfied with $\psi_k(t, u) = \mu_k(t)u$.

According to Theorem 1 the zero solution of NNNI (2.4) is uniformly Lipschitz stable (globally uniformly Lipschitz stable)

This proves the claim of Theorem 3.

Remark 9. The conditions in Theorem 2 and Theorem 3 differ. The inequality for the impulsive functions in condition 3 of Theorem 3 is weaker than Assumption A5. At the same time if Assumption A2 is satisfied then Assumption A6 follows. However the inequality in condition 4 of Theorem 3 is more restrictive than the inequality in Assumption A3. Both Theorems are applicable in different cases.

We will illustrate the difference between the applications of Theorem 2 and Theorem 3 on an example.

EXAMPLE 4. To simplify the calculations we consider the simplest neural network of two units, i.e. $n = 2$. Let $t_0\in [0, 1)$, $s_k = k, \ t_k = k+0.5, \ k = 1, 2, \dots$ and consider the nonlinear NNNI

where the activation functions are the Probit function $f_1(u) = \sqrt{2} \ erf^{-1}(2u-1)$ and the cosine function $f_2(u) = \cos (u)$, $c_1(t) = e^{-t}$, $c_2(t) = \frac{1}{t+1},$ $I_1(t) = 0.5 e^{-t}-\frac{1}{t+1}$, $I_2(t) = \frac{1}{t+1}$, $\Phi_{1, k}(t, u) = \frac{1}{t}u-0.5\frac{t-1}{t}$, $\Phi_{2, k}(t, u) = \frac{u}{t}$ and

Then the equilibrium is $x^*_1 = 0.5, x^*_2 = 0$.

Theorem 3 is not applicable because assumptions A4 and A2 for $c_1(t), c_2(t)$ and $f_1(u)$ are not satisfied.

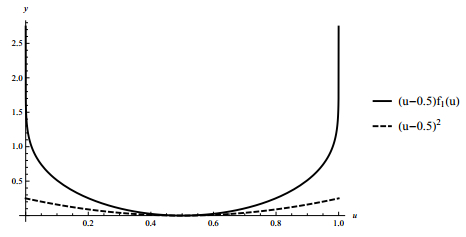
Now using $(u -0.5)f_1(u)\geq (u-0.5)^2, \ u\in \mathbb{R}$ (see Figure 4) it follows that

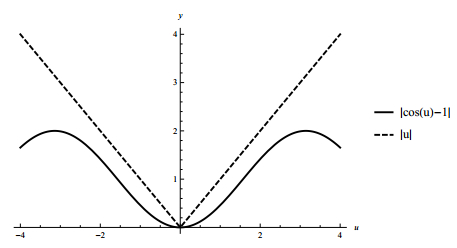
According to inequalities (4.8) and $|cos(u)-1|\leq |u|, \ u\in\mathbb{R}$ (see Figure 5) we obtain

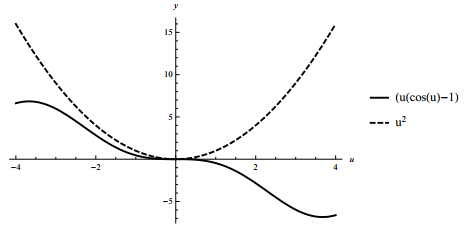
From inequality $u(\cos (u)-1)\leq u^2$ (see Figure 6) it follows that

Therefore, assumption A6 is satisfied with $\xi(t) = \frac{1}{t+1}.$

Consider the function $p(t) = 1.1 +\cos(t), \ 0.1 < p(t)\leq 1.1$ for $t\geq 0$. The inequality $p(t)\leq p(s_k)$ holds for $t\in [s_k, t_k]$.

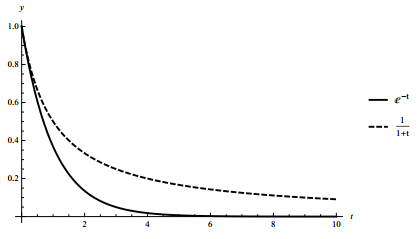
Also, applying the inequality $e^{-t}\leq \frac{1}{1+t}$ (see Figure 7) we obtain the inequality

Condition 3 of Theorem 3 is satisfied with $\mu_k(t) = \frac{1}{t^2}$ because $\sum_{i = 1}^2 \Big(\Phi_{k, i}(t, x_i)-\Phi_{k, i}(t, x_i^*)\Big)^2 = \frac{1}{t^2}\Big((x_1-0.5)^2+x_2^2\Big), \ \ \ \ t\in[s_k, t_k]$.

Then the scalar non-instantaneous impulsive equation (3.2) will be reduced to

The zero solution of (4.12) is uniformly Lipschitz stable (see Figure 8) with $M = 11$ and $\delta = 1$. According to Theorem 3 the equilibrium of (4.7) is uniformly Lipschitz stable.

5.   Conclusions

Several sufficient conditions are given for stability of the equilibrium point of neural networks with non-instantaneous impulses. We study the general case when

$-$ the self-regulating parameters of all units are variable in time;

$-$ the functions of the connection between two neurons in the network are variable in time bounded functions;

$-$ the activation functions are non-Lipschitz (usually in the literature only the case of Lipschitz activation functions is studied).

The investigation is based on applying the Lyapunov approach and various types of Lyapunov functions are used. These piecewise continuous Lyapunov functions are used as an apparatus to study stability properties of neural networks with non-instantaneous for different types of activation functions. Many examples with different types of activation functions such as cos function, Logit function, continuous Tan-Sigmoid function, are provided to illustrate the practical application of our results.

Conflict of interest

All authors declare no conflicts of interest in this paper.