Error correction of semantic mathematical expressions based on bayesian algorithm

1.   Introduction

1.1.   Primary background

A hybrid optical system combines traditional optical elements like lenses and mirrors with modern digital components such as sensors or holographic displays. This integration aims to leverage the strengths of both technologies to achieve enhanced imaging capabilities, improved adaptability, and multifunctional applications. By merging optics with digital technology, these systems can offer superior performance in areas such as medical imaging, surveillance, aerospace, and entertainment. Challenges in design complexity and calibration need to be carefully addressed for optimal functionality. Overall, hybrid optical systems represent a versatile and powerful solution, capitalizing on the synergies between traditional and advanced optical technologies ^[1].

Fractional calculus is a field within mathematical analysis that extends the principles of differentiation and integration to non-integer orders. In contrast to classical calculus, which focuses on integer-order derivatives and integrals, fractional calculus encompasses operations involving derivatives and integrals with non-integer orders ^[2,3].

A fractional-order (FO)-modified hybrid optical system integrates traditional optical components with fractional calculus principles, allowing for enhanced control over system dynamics. This innovation, leveraging non-integer derivatives or integrals, provides increased adaptability in light propagation, signal processing, and image manipulation. The system shows promise in applications such as signal processing, offering improved performance over integer-order systems. However, its implementation requires careful consideration of both optical and fractional calculus principles, adding complexity to system design and analysis ^[4,5].

Controlling a FO-modified hybrid optical system comes with its fair share of challenges. These systems have complex dynamics that are tough to predict because they involve memory effects and long-range dependencies, which can make them harder to manage than traditional systems. Stability is a big concern, as the unique properties of FO systems can lead to unexpected behavior or sluggish responses. Plus, these systems are sensitive to changes in parameters, meaning that getting the control settings just right is crucial. The hybrid nature of optical systems, which combines various technologies, also adds another layer of complexity by introducing potential noise and disturbances that can affect performance.

However, there are compelling reasons to tackle these challenges. FO controllers can offer a higher level of precision and robustness, better capturing real-world processes with their memory-dependent characteristics. This means improved system performance and stability, even in the face of uncertainties or parameter changes. Working on control strategies for FO systems not only pushes the boundaries of current technology but also opens doors to advancements in fields like telecommunications, medical imaging, and sensors, where precise and reliable control is essential.

Over the past twenty years, there has been a noticeable rise in the number of scientists and engineers exploring FO systems for modeling a wide range of phenomena. The extensive documentation of the role of FO systems extends across various fields, including quantum systems ^[6], aerospace UAV systems ^[7], economical mechanisms ^[8], body health systems ^[9], power systems ^[10], artificial networks ^[11], and more. This arises from their oscillatory characteristics and heightened susceptibility to initial values. Numerous studies have asserted that a significant portion of fractional-order systems (FOs) exhibits unpredictability owing to their oscillatory traits and pronounced sensitivity to initial conditions. Consequently, scholars have directed their attention toward formulating alternative approaches for synchronizing and sustaining chaotic FOs ^[12]. In this context, diverse control methodologies have been suggested, encompassing the adaptive control method ^[13,14], the observer controller ^[15], the robust control method ^[16], the fuzzy control method ^[17], the sliding mode control method ^[18], the multi-switching based method ^[19], and the PID control method ^[20], all aimed at governing and stabilizing chaotic FOs.

For the purpose of coordinating and controlling nonlinear FOs, the TS-fuzzy methodology has emerged as a widely used method, and it has found favor in both theoretical research and practical application ^[21]. When it comes to effectively converting nonlinear systems into linear counterparts, the TS-fuzzy technique makes use of fuzzy weight and cost functions as tools. Benefits can be attributed to the TS-fuzzy flexibility method such as robust theoretical analysis, practical applicability, and enduring resilience.

In recent decades, the sliding mode control (SMC) technique has gained rapid acclaim as one of the most preferred control strategies, gaining recognition in both theoretical frameworks and practical scenarios ^[22,23]. In a broad sense, the SMC can be dissected into two fundamental components, as delineated below ^[24]:

Ⅰ. The formulation of an appropriate and stable sliding surface.

Ⅱ. The generation of control signals designed to suppress chaotic trajectories of FO systems, ensuring their conformity to the specified sliding surface.

TS-fuzzy sliding mode controllers provide a means to represent and control complex nonlinear relationships, ensuring adaptability to changing system dynamics. The incorporation of fuzzy logic allows for smooth transitions between control modes and reduces the chattering phenomenon associated with traditional sliding mode control. TS-fuzzy sliding mode controllers demonstrate improved robustness by operating on a designated sliding surface, effectively mitigating the impact of external disturbances. Their versatility extends across various applications, including robotics and industrial processes, and they strike a balance between complexity and ease of implementation. The integration of human expertise into the control system, stability, and convergence further enhances their practical usability, making them a valuable tool for addressing control challenges in diverse domains ^[25].

1.2.   An exploration of the pertinent literature

Many scholars have embraced the TS-fuzzy method as a valuable tool for stabilizing and synchronizing FO nonlinear systems. This is notably demonstrated, for example, in ^[26], where a proposed adaptive TS-fuzzy method, utilizing Lyapunov functions and fractional-order adaptation laws, stabilized the model, ensuring convergence and bounded signals. In ^[27], Zhang and Wang addressed the stabilization of TS-fuzzy singular FOs while considering the impact of actuator saturation. In ^[28], a novel observer for TS-fuzzy singular Fos was established, enabling the simultaneous assessment of immeasurable or partly detectable states and defects. An adaptive control scheme was then suggested to estimate actuator faults in these systems, with conditions for admissibility established through linear matrix inequalities (LMIs). In ^[29], Zhang and Jin proposed state and output feedback-control methods for TS-fuzzy singular FOs. In ^[30], an adaptive TS-fuzzy variable structure control method was suggested for chaotic FOs, handling challenges like saturated input and control variations. Using the fuzzy Lyapunov function approach, stability analysis and stabilization for FO TS-fuzzy systems were investigated in ^[31]. In contrast to the conventional nonlinear Lyapunov functions, fuzzy Lyapunov functions contain the product of three-term functions when compared to the typical Lyapunov functions. Through the use of a TS-fuzzy model technique, the researchers of ^[32] examined the positivity and stability of fractional-order delayed systems. In ^[33], the development of an adaptive SMC observer for a distinct type of TS-fuzzy descriptor FOs was discussed. An investigation was conducted into an observer-based controller for polynomials fuzzy FOs that makes use of the Lyapunov approach ^[34]. In ^[35], two fuzzy switching sliding surfaces were introduced using an event-triggered method for TS-fuzzy systems. Unlike traditional approaches, it leveraged fuzzy membership functions and their derivatives to develop a fuzzy integral switching function. In ^[36], adaptive sliding mode control with a radial basis function (RBF) neural network was used for uncertain fractional-order nonlinear systems. The RBF network handles nonlinearities and disturbances, while a proportional-integral control term reduces chattering. In ^[37], Fan and Wang tackled asynchronous event–triggered fuzzy sliding mode control for fractional-order fuzzy systems. They used asynchronous premise variables, creating a different term involving both continuous and triggering states. In ^[38], Zhang and Huang proposed an integral sliding mode control scheme for uncertain nonlinear singular fractional-order systems with actuator faults, modeled using the interval type-2 Takagi-Sugeno approach. In ^[39], authors addressed fractional-order adaptive neuro-fuzzy sliding mode control for fuzzy singularly perturbed systems with uncertainties and disturbances. They introduced a new sliding mode surface and used an ε-dependent Lyapunov function to ensure robust stability and ${H}_{\infty }$ performance. Giap ^[40] introduced a secure communication system for text messages based on FO chaotic systems, incorporating a TS-fuzzy disturbance observer and SMC method. In ^[41], the stabilization of delayed FO chaotic TS-fuzzy systems, addressing input saturations and system uncertainties, was investigated. Yan et al. ^[42] explored the SMC method utilizing reinforcement learning for a TS-fuzzy delayed FO multiagent system. In ^[43], an adaptive sliding mode control based on the radial basis function (RBF) neural network for TS-fuzzy fractional order systems was designed. The RBF neural network was used to approximate nonlinearities and external disturbances. Wan and Zeng ^[44] explored the stability and stabilization of TS-fuzzy second-FO linear networks using a non-reduced order methodology.

Typically, the cited research works exhibit one or more of the following limitations:

1) The use of the Caputo FO derivative in existing research has been criticized, as some scholars argue that it inadequately accounts for pseudo-state space developments. The incapacity of a FOS to take into account the physical behavior of systems is the source of this constraint. A FOS requires the inclusion of its complete history in order to determine its prospective, even when time is equal to zero ^[45].

2) Existing research often relies heavily on either linear or nonlinear components in the suggested control techniques, limiting the comprehensiveness of the approaches.

3) In many instances, the utilization of SMC control methods is accompanied by the occurrence of chattering phenomena that are not acceptable.

4) The majority of these works simplify system definitions by neglecting uncertainties, external distributions, and input saturations, which are essential aspects of real-world systems.

Hence, the identified limitations prompt us to integrate the non-integer version of the Lyapunov stability theory with linear matrix inequality and TS-fuzzy theorem. This integration aims to develop a resilient SMC technique for TS-fuzzy systems that is free from chattering, dynamic-free, and can effectively handle uncertainties and input saturation. Furthermore, this approach relies on a reliable definition of the FO derivative.

1.3.   Contribution and motivation

In light of the preceding discussions, it becomes imperative to devise and propose an anti-chattering TS-fuzzy SMC mechanism tailored for intricate FO chaotic modified hybrid optical system (MHOS) amidst the challenges posed by system uncertainty, external disturbances, and input saturation. Notably, the exploration of a no-chatter TS-fuzzy SMC method for stabilizing FO chaotic MHOS has not been extensively addressed to date, emphasizing the primary objective of this research. Furthermore, the consideration of input saturation is pivotal in constructing practical controllers, as it imposes an upper limit on control energy, curbing energy wastage in the control system. Additionally, the employment of a novel definition for the non-integer derivative provides assurance regarding the reliability of the outcomes.

As a result, this study proposes that developing a no-chatter TS-fuzzy sliding mode control (SMC) mechanism is an effective solution for addressing the stabilization challenges present in fractional-order (FO) chaotic modified hybrid optical systems (MHOS). These challenges often arise due to system uncertainties, external disturbances, and issues related to input saturation. The approach begins by introducing a user-friendly and straightforward sliding surface design, grounded in the concept of FO integration. Following this, the study employs a non-integer version of Lyapunov stability theory to create a dynamic-free TS-fuzzy SMC method, ensuring that sliding occurs effectively without introducing unwanted chattering.

The proposed TS-fuzzy SMC approach is carefully designed to avoid relying on both linear and nonlinear factors associated with the dynamic elements of FO chaotic MHOS, aiming for a more stable and reliable control mechanism. To showcase the practicality and effectiveness of this dynamic-free TS-fuzzy SMC technique, the study includes two demonstration scenarios. These examples illustrate how the proposed method can be applied in real-world situations, highlighting its potential benefits and efficacy in improving system stability and performance.

In summary, this study presents key motivations and contributions, encapsulating the following significant points:

• The study pioneers the creation of a no-chatter TS-fuzzy SMC approach. The primary objective is to stabilize a vast array of intricate and disordered FO chaotic MHOS. This is achieved through the incorporation of a novel description of non-integer calculus, leveraging the efficiency of a continuous function.

• The proposed TS-fuzzy SMC technique demonstrates resilience, effectively mitigating the effects of uncertainty and input saturation in the FO chaotic MHOS.

• To achieve trustworthy conclusions about the overall and asymptotical robustness of the coordinating closed-loop FO MHOS, the study utilizes LMI and the fractional-order version of the LST.

• In real-world applications, the proposed TS-fuzzy SMC technique demonstrates superior performance compared to alternative methods, emphasizing its efficacy in practical problem-solving.

1.4.   The overview of the paper's organization

The paper's organization unfolds as follows. Section 2 delves into foundational concepts related to FO calculus and systems. Section 3 articulates the problem description, specifically focusing on the synchronization of FO chaotic MHOS. The development of a dynamic-free TS-fuzzy SMC technique to address the stabilization challenge is detailed in Section 4. Moving forward, Section 5 provides applied examples that serve to illustrate the practical efficacy and efficiency of the proposed TS-fuzzy SMC method. Finally, Section 6 comprehensively covers the obtained results and their implications and outlines future plans.

2.   Basic principles

Definition 1. The gamma function, expressed by $\mathrm{\Gamma }\left(v\right)$, is a complex-valued function defined for complex numbers $v$ with real part greater than zero, or equivalently, for $v$ in the complex plane excluding negative real numbers and zero. The gamma function is defined by the following integral:

Here, $v$ is a complex number, ${t}_{0}$ shows the initial condition of time, and the integral is taken over the positive real numbers.

Definition 2. ^[46] The Riemann-Liouville definition of the $k$-order FO integral for a continuous/smooth function $Q\left(t\right)$ is presented as follows:

Definition 3. ^[47] Consider a function Q(t) introduced on the interval $\left[0, \infty \right)$ in the real numbers space ($\mathbb{R}$). In this context, we define the conformable fractional derivative of order f as follows:

where $t > 0$, and $k\in \left(\mathrm{0, 1}\right)$.

Feature 1. ^[47] For any point with $t > 0$, if $0 < k\le 1$, and both n and m are differentiable functions, then the $k$th derivative of their product, $n\left(t\right).m\left(t\right),$ can be expressed as:

Feature 2. ^[47] For any constant value function $r$ in the real numbers $(r\in R)$, the $k$th derivative with respect to any variable is equal to 0, i.e., ${D}^{k}r = 0$.

Definition 4. ^[48] If $H$ is an $n\times n$ matrix and $I$ is the identity matrix, the matrix sign function is defined as follows:

in which $m$ shows the order of the approximation and ${sgn}_{\left(m\right)}\left(H\right)\in \left[-\mathrm{1, 1}\right].$

Moreover, in the case of a sliding surface such as $\sigma \left(t\right)\in {R}^{3}$

Lemma 1. ^[49] For regular matrices $L$ and $R$ and a symmetric matrix $W$ of allowable dimensions, the following condition holds:

if and only if for any $\mathrm{\epsilon } > 0$

wherein $L$ fulfills ${\mathrm{L}}^{T}L\le I$.

Lemma 2. ^[50] For any three matrices $A, B,$ and $C$ with suitable dimensions, provided that $C$ is a positive-definite matrix, the following results hold:

Theorem 1. ^[51] Let $k$ be a value within the range (0, 1), and let us assume that the Lipschitz condition is met for the fractional order (FO) system described as ${D}^{k}\gamma \left(t\right) = g(\gamma, t)$, where there exists an equilibrium point at $\gamma = 0$. Additionally, we consider the existence of a Lyapunov function $V(t, \gamma (t\left)\right)$ and class-K functions ${l}_{1}, {l}_{2}$ and ${l}_{3}$, subject to the following inequalities holding:

where $\beta \in \left(\mathrm{0, 1}\right)$. Subsequently, the equilibrium point of the system ${D}^{\beta }\gamma \left(t\right) = g(\gamma, t)$ will attain asymptotical stability.

3.   Problem description and TS-fuzzy analysis

This section expresses the problem statement's characterization. Following that, the systems' TS-fuzzy formulation will be addressed.

3.1.   Problem description

Recently, a novel 3D FO MHOS was developed in ^[52], with the system equations presented as follows:

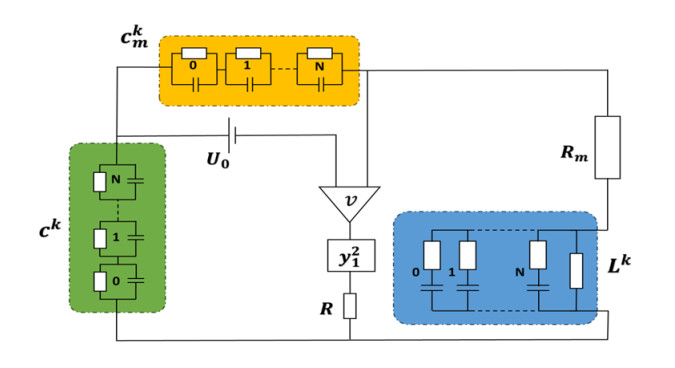
here, ${y}_{1}, {y}_{2},$and ${y}_{3}$ represent the states of the FO chaotic MHOS, and $k$ is a non-integer order of derivative. A circuit diagram of the FO chaotic MHOS (3.1) is presented in Figure 1 ^[53]. In ^[54], it has been shown that when $\alpha = 0.35$, $\beta = 0.6$, and $k$ is in the range $(0.7, 1.03)$, the FO system (3.1) displays unpredictable chaotic dynamics.

Figure 2 illustrates the unpredictable chaotic performance of the FO system (3.1) with initial values ${y}_{1}\left(0\right) = 2, {y}_{2}\left(0\right) = 1,$and ${y}_{3}\left(0\right) = 2.$and $k = 0.98$.

Now, consider the following result of 3-dimensional uncertain chaotic FO nonlinear system (3.1):

where $k\in \left(\mathrm{0, 1}\right)$, and $Y\left(t\right) = {\left[{y}_{1}\left(t\right), {y}_{2}\left(t\right), {y}_{3}\left(t\right)\right]}^{T}$ is in ${R}^{3\times 1}$ denotes the vectors representing the system's states, whereas $G$ denotes the matrices of constants. Furthermore, $\Delta G$ specifies the external disturbance and uncertainty elements.

Furthermore, $\psi \left(u\left(t\right)\right)$ is the controller's vector, and the actuator-saturation is indicated by:

where

for this case, the intervals of the actuator-saturation function are denoted by ${u}^{+},$ ${u}_{+}\in {R}^{+}$, and ${u}^{-},$ ${u}_{-}\in {R}^{-}$-, respectively, while the slope of the actuator-saturation equation is denoted by $\theta \in {R}^{+}$.

3.2.   Generalization of TS-fuzzy model for FO chaotic MHOS

This part presents the modeling of the stabilization issue for the TS-fuzzy uncertain FO chaotic MHOS (3.1). With saturation inputs, the nonlinear FO chaotic MHOS (3.1) may be modeled as plant pattern j: IF ${\zeta }_{1}$ be ${\xi }_{j1}$, ${\zeta }_{2}$ be ${\xi }_{j2}$, … and ${\zeta }_{l}$ be ${\xi }_{jl}$, THEN

here, ${\zeta }_{1}, {\zeta }_{2}, \dots, {\zeta }_{l}$ represent known premise variables, ${\xi }_{jl}$for $j = 1, \mathrm{2, 3}, l = 1, 2, 3$ denote fuzzy sets, and n represents the plant rules. ${G}_{j}$ is the matrix of known constants, ${\Delta G}_{j}$ is the matrix of unknown uncertainties of external disturbance, and $\psi \left(u\left(t\right)\right)$ represents input saturation. The ultimate outcome of the fuzzy FOS is expressed as follows:

where

and ${\rho }_{ji}\left({\vartheta }_{i}\right(t\left)\right)$ shows the $j$th fuzzy set of membership of ${\zeta }_{i}\left(t\right)$ in ${\xi }_{ji}.$ Also, it is considered that ${\beta }_{j}\left(\zeta \left(t\right)\right)\ge 0$, therefore, $\sum _{j = 1}^{3}{\beta }_{j}\left(\zeta \left(t\right)\right)\ge 0$; additionally, for $j = 1, \mathrm{2, 3}$, ${\alpha }_{j}\left(\zeta \left(t\right)\right)\ge 0,$ and $\sum _{j = 1}^{3}{\alpha }_{j}\left(\zeta \right(t\left)\right) = 1$, for all $t\ge 0$.

Remark 1. In relations (3.7), $Y\left(t\right)$ is a vector of state trajectories as $Y\left(t\right) = {\left[{y}_{1}\left(t\right), {y}_{2}\left(t\right), {y}_{3}\left(t\right)\right]}^{T}$, where all of these components are dependent to the parameter $t.$ Also, the term $\left({G}_{j}+{\Delta G}_{j}\right)\left(Y, t\right)$ is a function containing the FO MHOS function ${G}_{j}\left(Y, t\right)$ and the external disturbance and uncertainty elements ${\Delta G}_{j}\left(Y, t\right)$, where both of these functions are dependent to the state trajectories $Y\left(t\right)$ and the parameter $t$.

Remark 2. In TS-fuzzy modeling, several key assumptions are made to effectively describe and manage nonlinear system dynamics. First, the system is represented using a set of fuzzy IF-THEN rules, each corresponding to a local linear model within a specific fuzzy region. The fuzzy membership functions, which define the degree of belonging to each fuzzy set, are assumed to be well-defined and normalized to ensure proper weighting of the local models. The model assumes that the nonlinear system dynamics can be sufficiently approximated by these linear local models and that uncertainties can be managed within this framework. The stability of the linear models and convergence of the system states to desired trajectories are crucial, relying on a proper design of fuzzy rules and membership functions. Additionally, the fuzzy system and its membership functions are assumed to be continuous, ensuring smooth transitions and avoiding abrupt control actions. These assumptions enable the TS-fuzzy model to apply linear control techniques within a fuzzy logic framework, facilitating effective control of nonlinear systems. Moreover, in TS-fuzzy modeling and control, several critical constraints and perturbation sources must be considered to ensure effective system performance. The rule base must comprehensively cover the entire input space to avoid inaccuracies in regions not addressed by the fuzzy rules. Each fuzzy rule relies on local linear models, assuming that these models can accurately approximate the nonlinear system dynamics within their fuzzy regions; thus, the linearization must be precise. Fuzzy membership functions should be well-defined, normalized, and continuous to ensure proper weighting and smooth transitions, preventing implementation issues. The stability of each local linear model is essential for the overall system stability. Perturbations such as modeling errors from linear approximations, external disturbances, parameter variations, and limitations in actuators and sensors can impact control effectiveness. Additionally, quantization and computational constraints in digital implementations can lead to deviations from the ideal model. Addressing these constraints and perturbations is crucial for maintaining robustness and accuracy in TS-fuzzy control applications. However, TS-fuzzy SMC can address various constraints and perturbations by leveraging the strengths of both fuzzy logic and sliding mode control techniques. To overcome constraints, TS-fuzzy SMC improves rule base completeness by integrating fuzzy logic to generate and refine rules that cover the entire input space, while using adaptive algorithms to continuously update local linear models for better accuracy. It optimizes membership functions to ensure proper weighting and smooth transitions between fuzzy rules, thereby enhancing the system's response to changes in inputs. For handling perturbations, TS-fuzzy SMC incorporates the robustness of sliding mode control, which inherently deals with system uncertainties and external disturbances through high-gain control actions that drive the system state onto a predefined sliding surface. This approach also adapts to parameter variations using adaptive sliding mode techniques and addresses actuator and sensor limitations by employing robust design principles. Furthermore, TS-fuzzy SMC mitigates quantization and computational constraints by optimizing control algorithms and using filtering techniques to ensure effective digital implementation. Together, these strategies ensure that TS-fuzzy SMC maintains robust performance and accurate control even in the presence of various challenges.

4.   Principal outcome

Within this section, the explanation of the sliding surface will take place depending on the TS-fuzzy technique as well as the LMI strategy. Following that, the design of the control technique will be undertaken, and the presentation of analytical results will follow.

Let $W$ be a full rank matrix and let ${W}_{i}$ be a submatrix with a rank of $r$, and given the presence of an orthogonal transformation matrix E in a certain configuration,

in which $E = col\left\{{\mathrm{\Psi }}_{1}^{T}{\mathrm{\Psi }}_{2}^{T}\right\}$, ${\mathrm{\Psi }}_{1}\in {R}^{3\times r}$ and ${\mathrm{\Psi }}_{2}\in {R}^{3\times (3-r)}$ show unitary matrices, $r < 3$, and $\mathrm{\Psi } = \left[{\mathrm{\Psi }}_{1}{\mathrm{\Psi }}_{2}\right]$. Also, $\stackrel{-}{W}\in {R}^{r\times r}$ is a nonsingular matrix; also, suppose that $\stackrel{-}{W}$ has been divided into the singular valued subsets: $\stackrel{-}{W} = \mathrm{\Psi }\left[\begin{array}{c}{\mathrm{\rho }}_{r\times r}\\ {0}_{\left(3-r\right)\times r}\end{array}\right]{H}^{T}$ such that ${\mathrm{\rho }}_{r\times r}$ is a positive diagonal matrix.

By defining $\delta \left(t\right) = EY\left(t\right) = \left[\begin{array}{c}{\delta }_{1}\left(t\right)\\ {\delta }_{2}\left(t\right)\end{array}\right]$, the following equations can be deduced from Eq (3.7).

where ${\delta }_{1}\left(t\right)\in {R}^{3-r}$, ${\delta }_{2}\left(t\right)\in {R}^{r}$,

According to (4.2) and (4.3), a sliding surface will be defined as follows:

It is known that the condition $\sigma \left(t\right) = 0$ is true when the sliding motion happens, therefore,

Hence, from (4.5) and (4.2) we obtain

Theorem 2. The asymptotic stability of the sliding-mode dynamic motion, as defined in Eq (4.6), is guaranteed by the sliding surface (4.4) if, for any constant $\beta > 0$, there are positive definite symmetric matrices $\stackrel{-}{F}$ and $P$ that satisfy the specified LMI:

Such that, ${\stackrel{-}{\beta }}_{j} = {\beta }_{j}^{2}$, $P = \mathrm{\Xi }\stackrel{-}{F}$,

Also, the symbol * indicates the symmetric terms of the symmetric matrix.

Proof. Using Theorem 1, the following $\mathrm{V}\left(\mathrm{t}\right)$ is a proposed Lyapunov function:

Utilizing (2.4) in Feature 1 and (4.8), one gets

Now, based on (4.6)

Thus,

Therefore,

such that

To show ${D}^{k}\mathrm{V}\left(\mathrm{t}\right) < 0,$for each nonzero ${\delta }_{1}\left(t\right),$ the condition $\lambda < 0$ should be satisfied. Therefore, by multiplying both sides of $\lambda$ by ${F}^{-1}$, and denoting $\stackrel{-}{F} = {F}^{-1}F{F}^{-1}$, one can derive,

Drawing from Lemma 1, the satisfaction of the LMI (4.17) for all ${N}_{j}\left(t\right)$ subject to ${N}_{j}^{T}\left(t\right){N}_{j}\left(t\right)\le I$, is established if and only if there exists a positive constant ${\mu }_{j}^{-1}$:

Here, if $\sigma = \left({\stackrel{-}{\mathrm{G}}}_{11j}-{\stackrel{-}{\mathrm{G}}}_{12j}\mathrm{\Xi }\right)\stackrel{-}{F}+\stackrel{-}{F}{\left({\stackrel{-}{\mathrm{G}}}_{11j}-{\stackrel{-}{\mathrm{G}}}_{12j}\mathrm{\Xi }\right)}^{T}, E = {\mathrm{\Psi }}_{2}^{T}{M}_{j}$ and ${\left[{{\left(\stackrel{-}{F}{\mathrm{\Psi }}_{2}^{T}-{{P}^{T}\mathrm{\Psi }}_{1}^{T}\right)O}_{j}}^{T}\right]}^{T}$.

Subsequently, the condition outlined in Lemma 1 is met. Upon applying the Schur-complement to (4.18), the derived result is (4.7). Then, the proof is completed.

After establishing the sliding surface to ensure suitable responses in sliding dynamic systems, the next step in the SMC design process entails developing a control mechanism that enables a smooth transition to the specified sliding dynamic (4.4). At this point, the following conditions are articulated:

Now, let us unveil the TS-fuzzy SMC rule as follows:

such that

Let $D > 0$ and $\mathcal{q} > 0$, and ${C}_{min}$ and ${C}_{max}$ represent the smallest and largest number of eigenvalues of ${D}_{i}$, respectively. Furthermore, let

Remark 3. The use of a sliding surface (4.4) in control systems enhances stability and robustness by guiding the system's state (3.7) toward a desired trajectory. Once the system (3.7) reaches the sliding surface (4.4), it ensures that the system converges quickly to the desired state, even in the presence of disturbances or uncertainties. Additionally, the well-designed sliding surface (4.4) can minimize chattering, resulting in smoother control actions and improved overall system performance.

Theorem 3. In the context of the TS-fuzzy chaotic optical systems (3.7), assuming the feasibility of LMIs (4.7) and the existence of the sliding surface (4.4) determined by $\Xi$ through (4.7), it can be concluded that the closed-loop TS-fuzzy FOS, which is governed by the control law (4.21), will exhibit asymptotic stability for all of its FOS states.

Proof. Drawing on ${\sigma }^{T}\left(t\right){D}^{k}\sigma \left(t\right)$, and the sliding surface (4.4), the ensuing results can be derived:

such that,

in which $D > 0$and $\mathcal{q} > 0$.

Additionally, the following conditions can be considered:

we have

By leveraging Lemmas 1 and 2, it becomes evident that ${\mathrm{Q}}_{2}\le {\stackrel{~}{\mathrm{Q}}}_{4}$, and consequently, one acquires:

Hence, upon the implementation of the control law (4.21), the FO chaotic MHOS (3.1) is expected to converge toward the sliding surface (4.4).

Given the preceding results (4.35), (4.36), and Theorem 2, it can be established that the FO chaotic MHOS (3.1) is asymptotically stable. Consequently, considering $\delta \left(t\right) = EY\left(t\right)$, if $\delta \left(t\right)\to 0$, then $Y\left(t\right)$ will asymptotically converge to zero.

Remark 4. The Lyapunov function is crucial for ensuring stability in the proof of Theorems 2 and 3. The Lyapunov function is selected to be positive definite and is tailored to account for the fractional-order nature of the system. It typically includes terms that reflect both the system's fractional dynamics and the fuzzy control strategy. The derivative of this function is analyzed to ensure it is negative definite or negative semi-definite, which demonstrates that the system will converge to a stable equilibrium over time. This approach helps in proving that the TS-fuzzy sliding mode control effectively stabilizes the system. It also guides the design of the control laws by ensuring that the control parameters are set to make the Lyapunov function decrease, thereby stabilizing the system. Additionally, the function addresses the unique fractional-order dynamics, ensuring robust performance under various conditions.

Remark 5. The proposed TS-fuzzy sliding mode control strategy with input nonlinearities offers several advantages:

• Greater robustness: It effectively deals with input nonlinearities, ensuring that the system remains stable and performs well even when faced with these challenges.

• Improved stability: By combining sliding mode control with Takagi-Sugeno fuzzy logic, the controller enhances the overall stability of the system, making it more resilient to disturbances and variations.

• Better nonlinearity management: The fuzzy logic component helps in addressing and compensating for nonlinear behaviors in the input, leading to more precise and reliable control.

• Less chattering: The strategy is designed to reduce chattering, which helps in smoothing out control actions and improving the system's performance and durability.

In essence, this controller provides a more stable, robust, and adaptable solution for handling complex and nonlinear inputs, leading to more reliable system operation.

5.   Simulation results

In this context, we have explored two illustrative scenarios to show the efficacy of the suggested chattering-free TS-fuzzy SMC scheme. Additionally, in order to highlight the enhanced performance of the TS-fuzzy SMC method, the controller is activated after a 15-s delay. The numerical simulations were conducted using MATLAB software, incorporating a specialized adaptation of the Adams-Bashforth-Moulton pattern as detailed in ^[55,56].

5.1.   Problem description

Setting $k = 0.95$ induces chaotic behavior in the FO chaotic MHOS (3.1). To exert control over this system, specific parameter adjustments have been made. Furthermore, the system's initial values are defined as ${y}_{1}\left(0\right) = -1.5, {y}_{2}\left(0\right) = 1.5$, and ${y}_{3}\left(0\right) = -1$.

If ${y}_{1}\left(t\right)$ belongs to $(-d, d)$ with $d = 8$, the subsequent relations are employed to ascertain the membership functions within the fuzzy model aimed at stabilizing the FO chaotic MHOS (3.1):

Subsequently, the following TS-fuzzy relations will be established:

• Plant rule 1: If ${y}_{1}\left(t\right)$ is ${\gimel }_{1}\left({y}_{1}\left(t\right)\right)$, then ${D}^{k}Y\left(t\right) = \left({G}_{1}+\Delta {G}_{1}\right)\left(Y, t\right)+\psi \left(u\left(t\right)\right)$;

• Plant rule 2: If ${y}_{1}\left(t\right)$ is ${\gimel }_{2}\left({y}_{1}\left(t\right)\right)$, then ${D}^{k}Y\left(t\right) = \left({G}_{2}+\Delta {G}_{2}\right)\left(Y, t\right)+\psi \left(u\left(t\right)\right)$,

where $Y\left(t\right) = {[{y}_{1}\left(t\right), {y}_{2}\left(t\right), {y}_{3}\left(t\right)]}^{T}$, $u\left(t\right)$ is the single input controller, and

Furthermore, ${G}_{1},$and ${G}_{2}$ serve to clarify the undisclosed parameters and characteristics inherent in the system. Moreover, for $i = 1,$ and $2$, the terms ${\Delta \mathrm{G}}_{i} = {M}_{i}{N}_{i}\left(t\right){O}_{i}$ denote the uncertainties of the systems, introduced as outlined below:

To illustrate the feasibility of the proposed TS-fuzzy SMC method and verify the accuracy of the stabilization condition, the system parameters are deliberately chosen as

Also, for LMI (4.7), $\stackrel{-}{F} = 4.5$ and $\mathrm{\Xi } = 7.8$. In addition, it should be mentioned that the control input commences operation at t = 15 s.

Figure 3 is included to visually portray the controlled dynamics of the TS-fuzzy FO chaotic MHOS (3.1). The evident stabilization of the FO chaotic MHOS (3.1) is discernible from the graphical representations within the article. Additionally, Figure 4 offers insight into the saturated single input control signal (4.21), while Figure 5 provides a visualization of the sliding surface (4.4). Notably, Figure 4 attests to the absence of chattering occurrences in the controller impulses.

Moreover, as illustrated in Figure 4, the saturation condition modulates the single input control signal (4.21) as it approaches saturation limits, resulting in distinctive leap occurrences. This implies the facile application of transitioning and leaping states, especially when leveraging switches and predefined saturation conditions. Examining Figure 5, one can discern the sliding surface (4.4) converging toward its origin. This signifies the efficacy of the proposed TS-fuzzy SMC in governing the TS-fuzzy FO chaotic MHOS (3.1).

Furthermore, as showcased in Figure 4, the saturation condition limits the single input control signal as it nears saturation limits, leading to discernible leap occurrences. Consequently, the application of transitioning and leaping states becomes seamless, particularly with the integration of switches and predefined saturation conditions. Figure 5 reinforces the observation that the sliding surface (4.4) converges toward its origin, underscoring the successful stabilization achieved by the proposed TS-fuzzy SMC for the TS-fuzzy FO chaotic MHOS (3.1).

5.2.   Scenario 2

Now, setting $k = 0.98$ initiates chaotic behavior in the FO MHOS (3.1). To govern this system, precise parameter adjustments have been implemented. Moreover, the initial values for the system are specified as ${y}_{1}\left(0\right) = -1.5, {y}_{2}\left(0\right) = 1.5$, and ${y}_{3}\left(0\right) = -1$.

In the event that ${y}_{1}\left(t\right)$ belongs to $(-d, d)$ with $d = 10$, the subsequent relations are employed to figure out the membership functions within the fuzzy model, with the objective of stabilizing the FO chaotic MHOS (3.1):

Following this, the fuzzy relations will be established in the following manner:

• Plant rule 1: If ${y}_{1}\left(t\right)$ is ${\gimel }_{1}\left({y}_{1}\left(t\right)\right)$, then ${D}^{k}Y\left(t\right) = \left({G}_{1}+\Delta {G}_{1}\right)\left(Y, t\right)+\psi \left(u\left(t\right)\right)$;

• Plant rule 2: If ${y}_{1}\left(t\right)$ is ${\gimel }_{2}\left({y}_{1}\left(t\right)\right)$, then ${D}^{k}Y\left(t\right) = \left({G}_{2}+\Delta {G}_{2}\right)\left(Y, t\right)+\psi \left(u\left(t\right)\right),$

where

Moreover, ${G}_{1},$and ${G}_{2}$ serve to elucidate the undisclosed parameters and characteristics inherent in the system. Additionally, for $i = 1,$ and $2$, the terms ${\Delta \mathrm{G}}_{i} = {M}_{i}{N}_{i}\left(t\right){O}_{i}$ denote the uncertainties of the systems, introduced as detailed below.

To showcase the feasibility and the accuracy of the designed control condition and assess the effectiveness of the suggested TS-fuzzy SMC strategy, the system parameters are intentionally selected as

Moreover, for LMI (4.7), $\stackrel{-}{F} = 3.5$ and $\mathrm{\Xi } = 4.6$.

Figure 6 is incorporated to visually depict the controlled dynamic trajectories of the TS-fuzzy FO chaotic MHOS (3.1) for $k = 0.98$. The evident stabilization of the FO chaotic MHOS (3.1) is perceivable from the graphical representations within the article. Additionally, Figure 7 provides insight into the saturated single input control signal (4.21), while Figure 8 visualizes the sliding surface (4.4). Notably, Figure 7 affirms the absence of chattering occurrences in the TS-fuzzy SMC controller impulses.

Furthermore, as demonstrated in Figure 7, the saturation condition modulates the single input control signal (4.21), for $k = 0.98$, as it approaches saturation limits, resulting in distinctive leap occurrences. This implies the facile application of transitioning and leaping states, especially when utilizing switches and predefined saturation conditions. Examining Figure 8, one can observe the sliding surface (4.4) converging toward its origin. This signifies the effectiveness of the proposed TS-fuzzy SMC in governing the TS-fuzzy FO chaotic MHOS (3.1).

Moreover, as illustrated in Figure 7, the saturation condition limits the single input control signal as it nears saturation limits, leading to discernible leap occurrences. Consequently, the application of transitioning and leaping states becomes seamless, particularly with the integration of switches and predefined saturation conditions. Figure 8 reinforces the observation that the sliding surface (4.4) converges toward its origin, underscoring the successful stabilization.

Remark 6. The controller parameters were fine-tuned through a trial-and-error process, where we made adjustments and closely monitored the system's behavior to find the best settings. This hands-on approach helped us achieve the stability, performance, and robustness needed for the TS-fuzzy SMC system. In future work, we aim to use deep learning methods to automate this tuning process. We believe this could greatly improve the efficiency and precision of the tuning, resulting in even better system performance and reliability.

Remark 7. Chattering is a phenomenon where a system undergoes rapid, small oscillations or fluctuations, often caused by high-frequency switching or control actions, leading to instability or noise. Here, at the beginning of the controller's operation, both the sliding surface and controllers must expend energy to counteract the system's undesirable behavior and stabilize it. Once the system is stabilized, this energy expenditure gradually converges to zero. Therefore, the abrupt changes in energy observed in Figures 3, 4, 7, and 8 represent the initial efforts to control the system.

Now, we employ an adaptive fuzzy control (AFC) approach to stabilize the FO chaotic MHOS (3.1) for $\kappa = 0.98$, aiming to establish a comparison with the designed TS-fuzzy SMC method (4.21) and other existing methods. A recent publication ^[57] introduced an adaptive fuzzy controller specifically designed for stabilizing fractional-order systems. The description of this controller is as follows:

A compared depiction of the trajectories of controlled states for the FO chaotic MHOS is presented in Figure 9. These trajectories are governed by Eqs (3.1) and (3.2). To control this system, both the AFC technique (5.7) and the proposed TS-fuzzy SMC method (4.21) are employed. While both approaches effectively return the states to their initial positions, it is evident that the recommended TS-fuzzy SMC method demonstrates a superior level of convergence compared to the AFC technique (5.7). It is abundantly clear that the TS-fuzzy SMC (4.21) surpasses the AFC approach (5.7) in terms of both convergency and robustness. Moreover, one can see the undesired chattering phenomenon in the results of the AFC approach (5.7). Table 1 provides a comprehensive analysis, highlighting key aspects and detailed comparisons.

Remark 8. The proposed TS-fuzzy SMC controller provides several advantages over existing algorithms:

Ⅰ. Enhanced robustness: Effectively handles system uncertainties and external disturbances, ensuring stable performance.

Ⅱ. Reduced chattering: Incorporates fuzzy logic to smooth control actions and minimize chattering, improving system longevity.

Ⅲ. Better handling of nonlinearities: Adapts to complex nonlinear behaviors with fuzzy logic, enhancing control effectiveness.

Ⅳ. Flexible control design: Offers an intuitive design process with easily adjustable fuzzy rules, making it versatile for various applications.

Ⅴ. Improved system performance: Achieves faster response times, better stability, and improved tracking accuracy compared to traditional control methods.

Remark 9. In a fractional-order hybrid optical system, maintaining robust control is crucial due to the system's inherent complexities, including nonlinearity, external disturbances, and uncertainties in the model. The TS-fuzzy SMC is designed to handle these challenges by combining the strengths of fuzzy logic and sliding mode control. However, a more detailed discussion is needed to highlight how this controller manages to maintain stability and performance under varying conditions. We plan to explore how the controller's robustness is tested against parameter variations, unexpected disturbances, and the fractional-order dynamics that often complicate the control process. This will help clarify the extent to which the TS-fuzzy SMC can reliably ensure system stability and performance in real-world scenarios. Furthermore, in FO hybrid optical systems, convergence speed refers to how quickly the system's state reaches and maintains its desired position after a disturbance or control action. The unique characteristics of fractional-order systems, such as their non-integer order dynamics, often lead to slower responses compared to integer-order systems. The following factors have a direct impact on the convergence speed of TS-Fuzzy SMC:

• Fuzzy logic component: The fuzzy logic controller provides a more flexible and adaptive approach by approximating the system's nonlinear behavior. This adaptability can lead to smoother control actions and, consequently, faster convergence to the desired state by reducing abrupt changes that might slow down the system's response.

• Sliding mode control: Sliding mode control aims to drive the system's state to a predefined sliding surface where the system behavior is robust and predictable. The effectiveness of this approach in reaching and maintaining the sliding mode can significantly impact convergence speed. Properly designed sliding surfaces and carefully tuned gains are crucial to ensuring that the system converges quickly and reliably.

• Parameter tuning: The convergence speed is sensitive to the controller parameters, including the gains used in the TS-fuzzy SMC. Higher gains generally lead to faster convergence but may introduce issues like chattering or instability. Hence, fine-tuning these parameters is essential for achieving an optimal balance between fast convergence and system stability.

• System dynamics: The fractional-order nature of the system introduces additional complexity, which can affect convergence speed. Understanding the specific dynamics of the hybrid optical system allows for better tuning of the controller parameters, improving convergence performance.

In future work, we plan to delve deeper into analyzing and optimizing the convergence speed by conducting comprehensive simulations and applying advanced optimization techniques. This will help us better understand how the TS-fuzzy SMC performs and ensure it meets the desired performance standards for fractional-order hybrid optical systems.

6.   Discussion and conclusions

The present work introduces a dynamic-free TS-fuzzy sliding mode control (SMC) technique that effectively addresses input saturation challenges and stabilizes a fractional-order chaotic modified hybrid optical system. By incorporating a novel definition of fractional calculus, fractional iteration of Lyapunov stability theory, and linear matrix inequality concepts, the proposed method successfully suppresses undesirable behaviors in fractional-order chaotic systems and avoids chattering phenomena. Beyond summarizing these findings, this study has significant broader implications. The proposed control scheme demonstrates potential applications in various fields requiring robust control under uncertainties, external disturbances, and input saturation, such as advanced manufacturing, aerospace systems, and robotics. Its capability to manage complex and unpredictable dynamics is particularly valuable for industries where maintaining stability is crucial.

For future work, several key directions are suggested. Analyzing the convergence speed of the proposed control method could provide insights into its efficiency and responsiveness under different conditions. Additionally, exploring parameter tuning using deep learning techniques could enhance the adaptability and performance of the control scheme, allowing for more precise adjustments and optimization. Investigating these areas, along with practical implementation studies and applications to other chaotic and nonlinear systems, will help validate the theoretical results and extend the method's applicability, ultimately advancing the field of nonlinear control.

Author contributions

Majid Roohi: Methodology, Software, formal analysis, visualization, writing original draft preparation, supervision; Saeed Mirzajani: Methodology, writing original draft preparation; Ahmad Reza Haghighi: Conceptualization, validation, writing review and editing original draft preparation; Andreas Basse-O'Connor: validation, Conceptualization, writing review and editing, investigation, resources, project administration, supervision. All authors have read and approved the final version of the manuscript for publication.

Conflict of interest

The authors state that the publishing of this work does not include any conflicts of interest for them.