1.
Introduction
Most of the information hiding methods embed secret information into the complex texture area of the cover [1] by slight modification of the content and structure (digital image, video [2] and audio). Although these steganography techniques can implement covert communication, the information of the cover is modified. It is inevitable to leave a trace of modification on the stego cover. Therefore, the stego cover is difficult to resist the detection of existing steganalysis algorithms. In order to resist the detection of steganalysis algorithms, experts from China proposed a new concept of "coverless information hiding" in May 2014.
"Coverless" does not mean that no cover is needed. The secret information is used to generate/acquire the stego cover directly instead of embedding them into the cover, and the cover is not modified. The secret information is transmitted by the natural normal cover, so it can resist all existing steganalysis algorithms based on anomaly detection. For text, when the secret information is character, the natural text may contain some of the information that needs to be transmitted. If the text containing the secret information can be found in some way, and the location of the secret information in the text and the length of the secret information are determined by a certain labeling protocol, the secret information can be transmitted by transmitting the natural text; for the image, it contains a lot of feature information, such as pixel brightness value, color, texture, edge, contour and high-level semantics. With proper feature description, it is possible to have some mapping relationship between the feature information and the secret information. If you can obtain a series of natural images with such a mapping relationship, secret information can be transmitted by these images. They can resist the detection of various types of image steganalysis methods effectively.
The existing CIS methods have low hidden capacity, and as the secret bits increases in each image, the number of images which we need in the image database grows exponentially. Besides, there may be case where we cannot find the images that meet the condition. This paper proposes a high-capacity CIS technology. In this framework, firstly, we divide the original image into several image blocks and obtain the hash value of the image. Secondly, the secret information is converted into a secret binary sequence. The secret binary sequence is matched with the hash sequence of the original image one by one. If the same location has the same value, the original image block remains unchanged. If not, the similar natural image block is retrieved in the image block database for replacement, so that the hash value of original image block is flipped. Finally we synthesize these image blocks and get the stego image. When the receiver receives the image, the secret information is extracted by using the same hash method.
The main contributions of this paper can be concluded as follows:
(1) The hidden capacity reaches 10000 bits with a 3 × 3 block size of the proposed method, which is far more than state-of-art CIS method that can hide 384 bits secret information;
(2) Experiment results show that the visual quality of the stego image is very good of the proposed method, which solves the boring mosaic effect;
(3) The proposed method can hide all secret data. In other word, the success rate of data information hiding is 100%;
(4) The hidden secret information can be extracted correctly.
The rest of the paper is organized as follows: Related work is described in Section 2. The framework of CIS is introduced in Section 3. Experimental results and analysis are provided in Section 4. Finally, conclusions are drawn in Section 5.
2.
Related work
Recently, many CIS algorithms have been proposed, which can be divided into two classifications: the text CIS and the image CIS.
In the text field, the algorithm proposed by Chen et al. [3] can only hide one Chinese character in one text. Later, in order to improve the hidden capacity, Zhou et al.
[4] proposed a multi-keyword information hiding algorithm based on text, in which they decompose the secret information into keywords and calculate the length of the secret information. Then they retrieve all of natural texts containing the keywords and its length in text database.
Although the algorithm [4] improves the capacity of information hiding, it is difficult to find the stego-text because it requires the text containing the secret information and its length at the same time, which results in a low success rate. Later, Zhou et al. [5] proposed a CIS algorithm based on "tag + keyword". It divides the text into keywords and uses the Chinese character mathematical expression to divide the Chinese characters into part sets which will be selected as the information location tag, and then the text containing the "tag + keyword" combination is retrieved in the database. Xia et al. [6] proposed a CIS method based on the least significant bit (LSB) of Chinese character Unicode encoding. The method which uses the component decomposed by the Chinese character mathematical expression as a tag has a bad result on security and text retrieval success rate.
In order to solve above problem, Chen et al. [7] proposed a text CIS method based on Chinese character encoding, in which, the LSB of Chinese character Unicode is selected as the tag selects, which improved security and retrieval success rate because of its more uniform distribution. In order to take advantage of the common advantages of various tags, Sun et al. [8] proposed a text CIS algorithm based on hybrid tags. It uses both Chinese character encoding and Chinese character mathematical expression as labels. The text with a larger embedded capacity is selected as the cover text. Chen et al. [9] proposed a text CIS algorithm based on keyword combination and selection, which converts Chinese characters into binary numbers, and then forms a combined word according to the word frequency in the text.
Fu et al. [10] proposed a text CIS algorithm based on the label model, in which they use each tag to locate as many keywords as possible and adds a file header to hide the number of keywords. In [11], the binary-labeled protocol is used to study the CIS algorithm based on English text.
It can be seen that the traditional text CIS method also has its own defects from the above, and this method does not modify the cover text, so as long as the text itself has not been changed, the transmitted secret information will not be affected. Even some modifications to the text itself may not affect the extraction of hidden information. This is also an important reason why CIS method will be widely concerned and supported after being proposed.
In the image field, since the digital image itself contains a large amount of redundant information, and has been widely used in various fields. It is often used as an ideal cover for information hiding. Similarly, if the unmodified image is used as a cover to deliver secret information using some methods, the CIS of the image is achieved. Compared to text, images contain a lot of feature information, such as pixel brightness values, colors, textures, edges, outlines, and high-level semantics. This is why we focus on studying the coverless image information hiding method. By describing the feature of the image in a special way, it is possible to make this seemingly unrelated image information into regular information that can be utilized. If the mapping relationship between the image and the secret information can be found, the secret information can be transmitted through the natural images, thereby the CIS method that can transmit the secret information without modifying the cover can be obtained which can resist the detection of various types of image steganalysis methods effectively.
In the field of images, binary bit streams, text, images, etc. can be delivered by images. Researchers have proposed many algorithms for different secret information type. In [12], the secret information transmitted is a binary bit stream. For each image in the database, its hash sequence is obtained by comparing the relationship of adjacent pixel values, and then they retrieve the image which hash sequence is the same as the secret information sequence as a stego image. The capacity of the algorithm proposed in this paper is 8 bits.
In order to improve the hidden capacity, Zheng et al. [13] improved the hash algorithm of [12] and increased the length of the secret information. The capacity is 18 bits. The hash sequence is obtained based on SIFT features. The gradient direction of the sampling point is used to determine the hash value of the image block. Yuan et al. [14] proposed the CIS based on SIFT and BOF. This method converts the secret information into binary. The image hash sequence is obtained through feature extraction and clustering and the image which hash sequence is the same as the secret information sequence is transmitted as a stego image to the recipient. Zhou et al. [15] uses partial-duplicate visual retrieval to realize CIS and the transmitted secret information is image. The algorithm is inspired by the find that some parts of the two images are similar. Some image blocks which are similar with secret image blocks can be obtained. However, the secret information cannot be completely extracted correctly. As shown in the Figure 1, the recovered image has a clear mosaic effect. The visual quality of the image is very bad. The CIS algorithm proposed in the paper [16] is combined with natural language processing. The NER system is used to mark the location of hidden information through an algorithm based on active learning of named entities (NER). The algorithm proposed in [17,18] combines the CIS with machine learning, and uses the generated model to generate images related to secret information for transmission. Liu et al. [17] uses ACGAN to generate digital according to the secret information. After much iteration, digital images with high visual quality are obtained. Duan et al.
[18] uses WGAN to generate a meaning-normal and independent image different from the secret image. However, the model in [18] is not universal and every secret image needs to create a new model. Peng et al. [19] generated the feature sequence through the relation between Direct Current coefficients in the adjacent blocks. The max length of the feature sequence is 15 that the hidden capacity is very low.
In order to solve the fore-mentioned problems in CIS, a high-capacity CIS algorithm is proposed in this paper.
3.
The proposed coverless steganography method
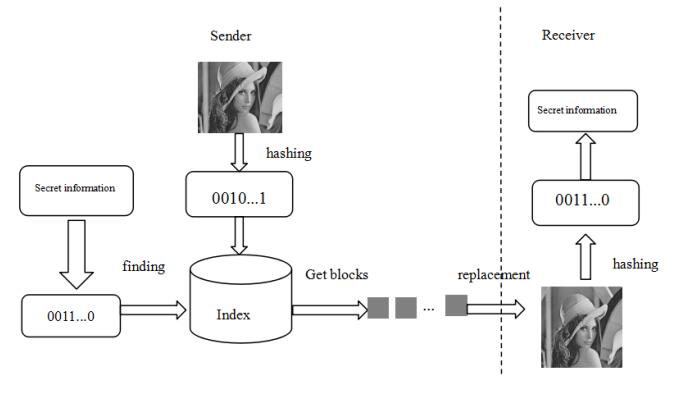
In this section, we will illustrate the secret information hiding and extracting procedures. Figure 2 shows the framework of the proposed CIS method.
Firstly, we select an original natural image as the cover image from the image database randomly, then divide it into a number of non-overlapping blocks with same size, and obtain the binary hash value of image block with hash algorithm.
Secondly, we convert secret information into the binary sequence. Then we match the binary sequence with the hash sequence of the original image one by one. If the value in the same position is the same, the original image block in that position remains unchanged. If not, the similar natural image block is retrieved in the image block database for replacement, so that the binary hash value of original image block in that position is flipped. Finally we can get the stego image.
At the receiver end, the receiver can also divide the stego image into the same number of image blocks, and then obtain the binary hash value with the same hash algorithm, and the secret information can be extracted.
3.1. Hash sequence generation
In this section, we introduce the generation of binary hash value of every image block. Then we can get the hash sequence of the image, which can be mapped to secret information. Every image block can be represented by 0 or 1 according the hash algorithm. For a given image I, suppose the size of the image is Nw×Nh, then, the process is described in the following.
Step1. Divide I into non-overlapping image blocks with sized l×l, then the number of image blocks BN = [(Nw×Nh)/(l×l)]. For simplify, we set l = 3 in the paper, but the method is still reasonable under the other value. So, the blocks Bi with raster scan order are Bi = {b1, b2, …, bBN}, 1≤i≤BN.
Step2. Calculate the mean value of all non-center pixels, denote the mean value is mi = {m1, m2, …, mBN}, 1≤i≤BN.
Step3. For all image blocks, denote the center pixel value is Pi = {P1, P2, …, PBN}, 1≤i≤BN Calculate the binary hash value of every image block by comparing Pi and mi. Then, we can get the hash sequence hi of every image block by the following formula. We can get the hash sequence of the image by sequentially connecting the binary hash value of the image block.
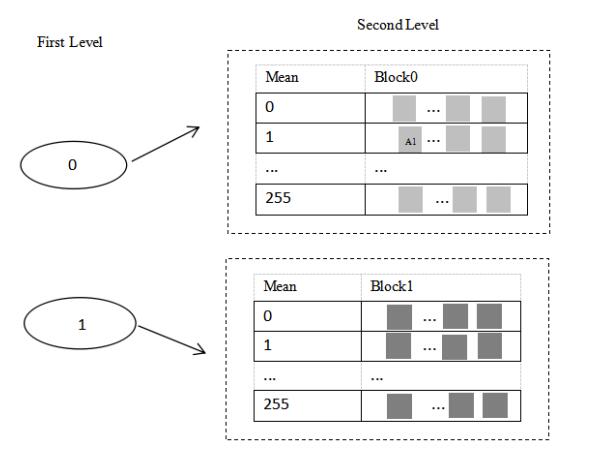
3.2. Construction of the double-level index
The index is used to store the binary hash value and the image blocks corresponding to it. We collect a large number of images to construct a large-scale database and divide the images into blocks to get the image block database. The index can be established according to the binary hash value of the image block. However, it will cost much time to find a proper image block which matches the requirement of secret information because every image block in the index should be compared with cover image block that needs to be replaced.
So we establish double-level index to speed up the retrieval efficiency.
In the first level index, the image blocks are divided into two categories, class 0 and class 1. The hash value of image block is 0 and 1 for the class 0 and class 1, respectively.
In the second level index, the image blocks are divided into 256 classes according to the mean value of 8 non-center pixels of an image block. For example, A1 represents an image block with a hash value of 0 and a mean value of 1. The diagram of the double-level index is shown in Figure 3.
3.3. Image block matching using double-level index
For given secret information, this section introduces how to find the image blocks for matching.
To transmit the secret information, the sender matches the sequence of the secret information with the hash sequence of the original image one by one. If the corresponding location has the same value, the image block remains unchanged. Otherwise, we should retrieve the image block from the database according to secret information sequence for matching to achieve the flip of hash value of the original image block.
In order to ensure the high visual quality of the stego image, we designed an efficient block matching scheme according to the mean square error (MSE), the processing can be described as follows.
Firstly, we determine the correct category in the first-level index according to the binary hash value of the secret information, if the value is 0, we select the image blocks in class 0, and else we select the image blocks in class 1. Secondly, we target the class in the second-level according to the mean value of all non-center pixels of the image block which needed to be replaced, and then we calculate the mean square error MSE of all image blocks in the second level index and the original image block which needed to be replaced according to the formula 2, and find the image block which has the smallest MSE for replacement. The smaller the value of MSE, the more similar the image block found is to the image block that needs to be replaced, so the visual quality of the image will be higher.
Where Oi and Bi are the pixel value of the original image block and the second level index image block, respectively.
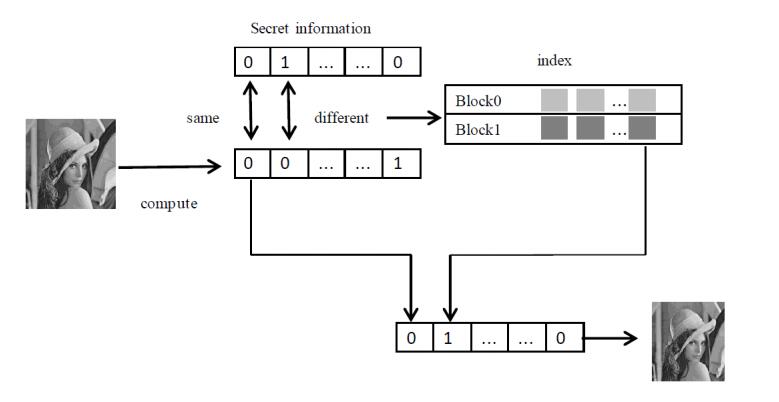
3.4. The communication of secret information
When the image blocks that best match the original image blocks are found, we can synthesize them into stego image. We will detail the process of information transfer.
For the sender, as shown in the following Figure 4, we obtain the hash sequence of the original image according to the hash algorithm introduced above, and then match the secret information sequence with the hash sequence of the original image one by one. If the same location has the same value, the corresponding image block remains unchanged. If the value is not the same, then the natural image block that is most similar to the original image block is found for replacement in the index. The process is as described in Section 3.3, so that the hash value at the corresponding position is flipped. Therefore, the hash sequence of the stego image is the same as the secret information sequence. Finally, the stego image is sent to the receiving end.
For the receiving end, the image is segmented according to the same rule to obtain the hash value of the image block, and then get the hash sequence of the stego image by sequentially connecting the binary hash value of the image block. Since the stego image is replaced according to the secret information. The hash sequence of the stego image is the secret information sequence.
4.
Experiments
We conduct our experiments on a standard computer with E5-2650 2.60GHz CPU and 24GB memory, and the ImageNet database is selected as the test set. The experimental results show that when the number of images exceeds 5000, performance of the proposed method is not significantly improved, but the efficiency is seriously consumed. Therefore, a total of 5, 000 images are chosen as the candidate image set which is used to provide the replaceable block for the test image.
4.1. Capacity of steganography
In our approach, the capacity is defined as the number of bits hidden in a stego image. Because every image block can embed 1 bit secret information, the number of the image block is the capacity. Therefore, we assume that the size of original image is Iw×Ih and the size of image block is l×l. For simplify, we set l=3 and Iw×Ih=300×300 in the paper, but the method is still reasonable for the other setting. The size of the stego image is the same as original image. The embedding capacity (EC) is calculated using as follows.
We compare our embedding capacity with four existing CIS methods. Their approaches are coverless image steganography using partial-duplicate visual retrieval [15], denoted as CIS-PDVR, coverless image steganography method based on bag-of-words [20], denoted as CIS-BOW, coverless image steganography based on SIFT and BOF [14], denoted as CIS-BOF and robust coverless image steganography based on DCT and LDA [19], denoted as CIS-DCT.
So far, the largest capacity is provided by the method of CIS-PDVR, in which the secret information transmitted is an image. The fewer images required, the larger the hidden capacity in each image, but the worse the quality of the recovered image. Compared with the method in CIS-DCT, the length of secret information hidden in each image is variable but the maximum length of secret information is much higher than the length 15 in CIS-DCT, and the longer the length of the secret information, the more images are needed in CIS-DCT. This problem does not exist in our method that we just need one image to transmit information. The length of the hash sequence of the image is constant in CIS-BOW and CIS-BOF, so only 16-bits and 8-bits secret information can be hidden, respectively. As shown in the Table 1, the hidden capacity of the proposed method is higher than other methods.
4.2. Visual quality of the stego image
We use the peak signal-to-noise ratio (PSNR) to measure the quality of stego image. In general, PSNR higher than 40 dB indicates that the image quality is excellent (it is very close to the original image), and 30–40 dB PSNR usually indicates that the image quality is good (That is, the distortion can be perceived but acceptable). The image quality is poor at 20–30 dB, and the image is unacceptable when PSNR is less than 20 dB [21].
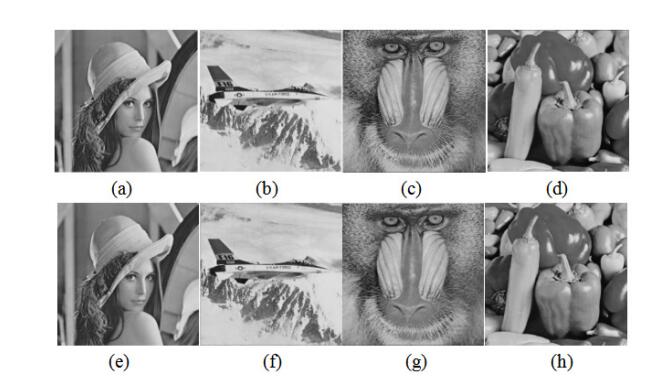
Figure 5(a–d) give some examples about the test images and (e–h) are the stego images correspondingly with the maximum length of secret information 1000 bits. The image database, which is used to provide the replace blocks include 5000 natural images. From the Figure 5, we can see that there is no obvious mosaic effect, basically the same as the original image.
During the experiment, we find that the size of the image database affects the quality of the stego image. The Table 2 below shows the PSNR for the stego images (Lena, Airplane, Baboon and Peppers) under different number of image database. As can be seen from the Table 2, the larger the image database, the better the visual quality of the stego image.
For a steady test results, we also select 100 images as test images from the ImageNet database, than calculate the average PSNR value in the case of different number of image database, and the results are shown in Table 3, we can see the PSNR values are more than 38dB, which indicates that the image quality is very good.
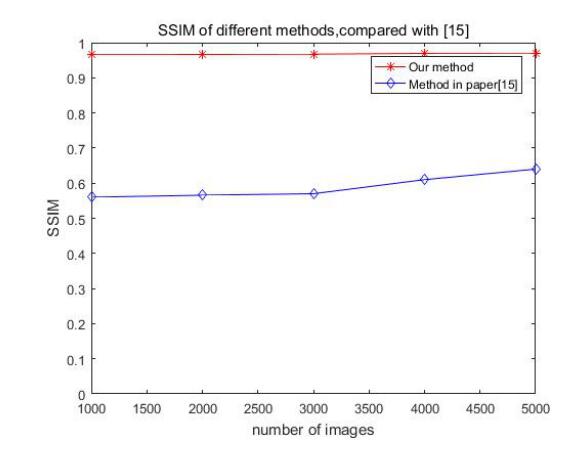
Besides, we compare the SSIM (Structure Similarity Index) of proposed method with the method of [15] under different number of image database. The SSIM is an image quality evaluation method that the evaluate result seems more consistent with the subjective sensation, which is in the range of [0, 1] and when it equals to one, the two images are identical. Figure 6 shows the average SSIM of 100 images and the average SSIM in [15]. We can see the SSIM of the proposed method is higher than that in [15]. The experimental results show that the quality of the image in the proposed method is better than [15].
4.3. The resistance to steganalysis algorithm
Steganalysis is an attack technique that is opposed to steganography. The purpose of this technique is to detect secret information and even obtain information content, which is mainly used to supervise the illegal use of steganography. Because all kinds of digital carriers are rich in source and content, and there are many hidden algorithms, it is difficult to analyze the specific hidden information size and content. Therefore, the main purpose of the steganalysis is to judge whether there is hidden information in the cover. The steganalysis algorithms include special steganalysis algorithm and general steganalysis algorithm. We choose one typical algorithm respectively for experiment, which are RS steganalysis algorithm and steganalysis algorithm based on extended DCT statistical features. Let's take the Lena image as an example.
(1) RS steganalysis algorithm
RS is mainly a method for the steganography using a pseudo-random LSB embedding algorithm [22]. The RS steganography analysis algorithm considers that there is a certain nonlinear correlation between the bit planes of the image. When the LSB steganography algorithm is used to hide the secret information, the correlation will be destroyed. The theory of the RS steganography analysis method is: any image that has been changed by LSB, the lowest bit distribution satisfies the randomness, that is, the probability of 0 and 1 is 1/2, and the image that has not been changed does not have this feature.
For an image that does not contain hidden information, it has the following rules (4):
But when secret information is embedded in the image, the following formula (5) is established:
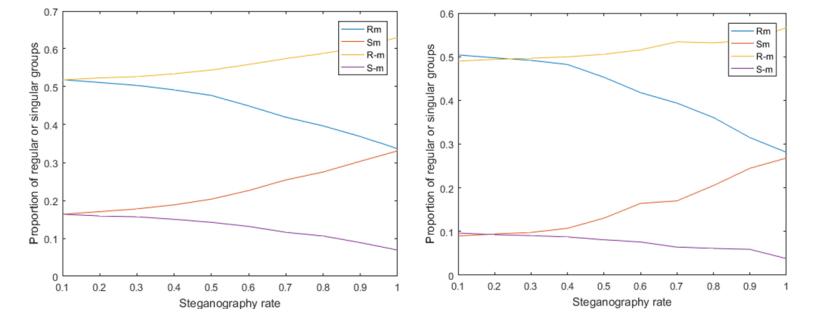
That is to say, for a cover to be detected, only the above statistics are needed, and then by comparing the relationship between the four statistical parameters, it can be determined whether the cover contains secret information. Where RM is the ratio of the regular group to the total of the pixel groups under the action of the exchange function F1, and R-M is the ratio of the regular group to the total of the pixel groups under the action of the offset function F-1, and SM is the ratio of the singular groups to all the pixel groups under the action of the exchange function F1, and S-M is the ratio of the singular groups to all the pixel groups under the action of the offset function F-1. We perform LSB matching on the Lena image, and then analyze the stego image, as shown in the following Figure 7. The left side is the graph of the original image. When the steganography rate is close to zero, RM is about equal to R-M, and SM is equal to S-M. The right side is the stego image. It is obvious that RM is not equal to R-M, SM is not equal to S-M when the steganography rate is close to zero.
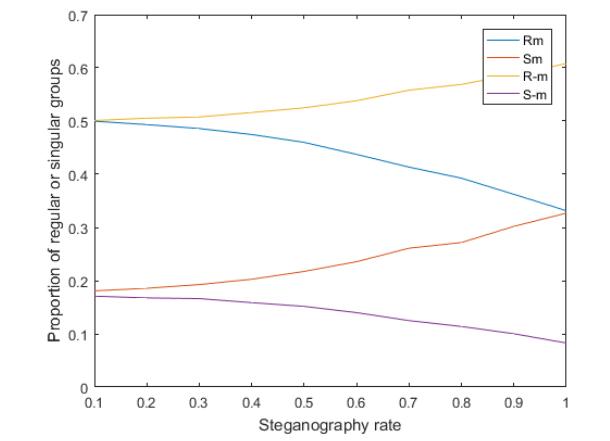
Then, we test the stego image obtained by the algorithm proposed in this paper. The results are as follows. From Figure 8, it can be found that when the steganography rate is close to zero, RM is equal to R-M, SM is about equal to S-M, and RM > SM, R-M > S-M, so our algorithm is very resistant to the RS steganalysis algorithm.
(2) Steganalysis algorithm based on extended DCT statistical features.
In the steganalysis algorithm with DCT coefficient statistics, Fridrich [23] first proposed the concept of "calibration" and the calculation principle for steganalysis.
The principle of adopting such a calculation method is as follows: the image's statistical characteristics are also similar to the original image after cropping it. However, this process is very sensitive to the image which has secret information, making the features very different after cropping it.
We extract the features of the stego image and obtain the partial feature difference in Table 4. We can find that the feature difference between the cropped image and the original image is small, indicating that the algorithm can also resist steganalysis algorithm based on extended DCT coefficient statistics.
5.
Conclusion
This paper proposes a high-capacity image coverless steganography method. By matching the secret information and the hash sequence of the image one by one, the similar natural image block is found in the image block database for replacement, then the hash value is inverted. Since the stego image block which obtained from the natural image is the image block most similar to the original image block, the visual quality of the stego image is still high. And our method can still resist the steganalysis. However, only one kind of feature is discussed in this article, the next work will focus on the selection of features describing the cover image and the similarity between cover image block and replacement image block to obtain stego images with higher visual quality. With the continuous development of deep learning, the production method is more and more mature, and future work will be devoted to generating more natural images based on secret information through machine learning, which can achieve better results than artificial synthesis.
Acknowledgments
This work is supported by the National Key R & D Program of China under grant 2018YFB1003205; by the National Natural Science Foundation of China under grant U1836208, U1536206, U1836110, 61602253, 61672294; by the Jiangsu Basic Research Programs-Natural Science Foundation under grant numbers BK20181407; by the Priority Academic Program Development of Jiangsu Higher Education Institutions (PAPD) fund; by the Collaborative Innovation Center of Atmospheric Environment and Equipment Technology (CICAEET) fund, China.
Conflict of interest
The authors declare that they have no conflict of interest.










 DownLoad:
DownLoad: