1. Introduction
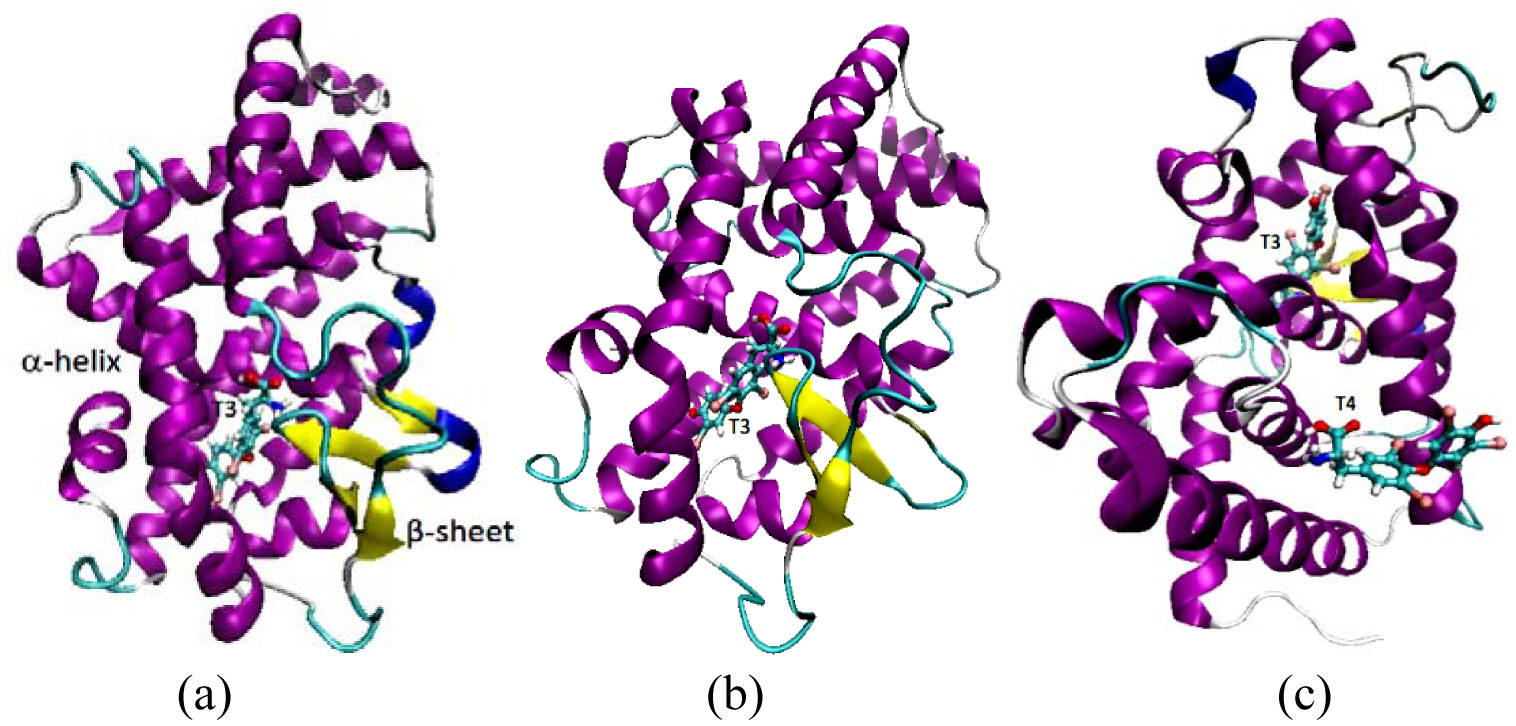
Thyroid signaling defects broadly depend on the action of thyroid hormone receptors (THRs), local ligands, thyroid hormone (TH) carrier proteins, coactivators, corepressors, neural development and metabolism [1]. There are two THR subtypes (THR-α and THR-β) consisting of ligand binding domain (LBD) and homogeneous DNA-binding domain (DBD). The LBDs of these subtypes differ only by a single amino acid residue: Ser277 in THR-α and Asn331 in THR-β [2]. THR isoforms differ in chain length by amino as well as carbxy termini. THR-α1 (triiodothyronine: T3-binding splice product of THR-α) is expressed in skeletal muscle, heart and brain. THR-β has three T3-binding splice products: THR-β1 is expressed in wide regions of body tissues; THR-β2 is in retina, brain and inner ear; and THR-β3 is predominant in liver, kidney and lung [1]. THs interact with different signalling pathways and their fuction is based on iodine and nutritional status. The TH-liganded isoforms: THR-β, THR-β1 and THR-α in cartoon view of globular forms are shown in Figure 1. The mutational evidances found in THR isoforms indicate thyroid disorders with resistance to THs (RTH) [1,3]. THR isoform selective agonists interfere with the carboxyterminal helix 12. Helix 12 dynamics is responsible for the interaction of THR with corepressors and coactivators. T3 has higher binding affinity than thyroxine (T4) in THR and the T3 bounded isoforms regulate gene expressions under DNA transcription. The unliganded THR represses basal transcription which is known as transcriptional silencing. The abnormal changes in serum TH concentrations are the indicators of hypothyroidism or hyperthyroidism with subacute thyroiditis which are directly or indirectly associated with T3 regulated gene expressions [4].
Biologically active molecules are responsible for the heat conduction after the sudden increase in temperature by means of chemical or photochemical reactions. Heat energy transfers through the vibrational states and the residues of globular proteins giving rise to anisotropic flow of energy. It is central to understantand the protein function including ligand binding and dissociation [5]. Heat capacity of a protein-hormone system at a particular temperature depends on folding and unfolding states, polar and non-polar groups in solution, hydration states, and protein-ligand interactions [6]. The heat capacity of a native globular protein is close to the value found from the heat capacities of individual amino acid residues in an extended polypeptide chain [7]. Moreover, T3-liganded and unliganded THRs have the different heat capacities. Anharmonicity enhances thermal conductivity of proteins by the energy flow through localized normal modes of vibration [8]. Heat capacity and thermal conductivity being the temperature dependent quantities, thermal diffusivity also depends on temperature. The temperature gradient differs from chemically active cites to LBDs providing microscopic basis for the signal transduction. The energy fluctuation and dissipation or the temperature dependent changes in internal energy during molecular dynamics simulations (MDS) support to calculate heat capacity of the biomolecular system. The mean energy contributing heat capacity of such complex system is calculated from the ensemble averages of individual terms in potential function describing the system [6]. The temperature relaxation across protein-water interface is the basis of finding thermal diffusivity and then thermal conductivity [9,10]. This process relies on the principles of transient non-equilibrium thermodynamics.
2. Methodology
2.1. Theory
Enthalpy or mean energy (E) is expressed in terms of ensemble averages of energy terms (Ui) describing a complex molecular system [6], i.e.
| E=〈U〉=∑Ni=1〈Ui〉=∑Ni=1Ei |
(1) |
where i refers to the energy related to bond angle, bond length, dihedral, van der Waal, electrostatic, improper and cross-terms giving rise to Hamiltonian or net potential function (U). Each of these terms contributes heat capacity of the system. The terms 〈Ui〉 differ in case of any perturbation, or mutation, or liganded and unliganded THR so that the total energy obtained is used to compute Boltzmann weight. The heat capacity, using the method of energy fluctuation in canonical ensemble [6,11], is defined by:
| CV=dEdT=d〈U〉dT=〈δU2〉KBT2=〈U2〉−〈U〉2KBT2=mcV |
(2) |
where m is mass and cV is specific heat capacity of the system, KB = 0.00198657 kcal mol−1K−1 is Boltzmann constant, and T is absolute temperature.
The possible sources of change in heat capacity are protein folding and unfolding including polar and apolar hydration contributions, equilibrium effect, electrostatics, vibrational terms, van der Waal interactions, H-bonding and protein conformational entropy. For the protein in solution, the heat capacity changes due to protein-protein interactions as well as hydration effect. After solvating the globular form of protein in a neutral water-ion solution providing the cellular environment, one can determine the heat capacity of the solvated protein by method of mixture or mole fraction [12,13]. Under thermal equilibrium, McV=MPcpV+MWcwV where the suffix “p” refers to protein-ligands and “w” refers to water-ions. Then, the heat capacity of the protein-hormone system in solution is given by:
Knowing the relative masses and the specific heat capacities of mixture and solution, we can determine the specific heat capacity of the protein-hormone system under ideal condition. For this purpose, we perform MDS approach separately for the solvated system or mixture and for the water-ion solution at constant temperature.
The properties of the biological macromolecules explain their functional impact on the living organisms in response to an external perturbation such as thermal gradient. The linear response theory describes the small perturbation relating non-equilibrium transport to equilibrium thermodynamic properties of the system. The complex biomolecular system is solvated under non-periodic boundary conditions forming a spherical droplet. The local temperature T(r,t) of the system depends on position (r) and time (t) which is governed by the heat diffusion equation:
where D is thermal diffusivity. For the radius R of the solvated protein-ligand in a globular form, the boundary conditions are: T(r,0)=Tifor r<R,and T(r,t)=Tffor r>R where Ti is initial temperature of the system and Tf is final temperature of the surrounding fluid-shell of thickness Δr. Using these boundary conditions, solution of the Eq 4 ,14] in the form of mean temperature of the protein-ligand system is written as:
| 〈T(t)〉=Tf+6Ti−Tfπ2∑∞n=11n2exp[−(nπR)2Dt] |
(5) |
Knowing the thermal diffusivity (D) by fitting the simulated data with Eq 5, and using density (ρ) and specific heat (cv), we can determine thermal conductivity (k) of the protein-hormone system in solution from the relation:
2.2. Molecular dynamics simulation
Crystal structures of three THR isoforms consisting of TH-ligands (T3 and/or T4): THRT3-β, THRT3-β1 and THRT3T4-α were obtained from the protein data bank (pdb) codes 3GWS [15], 1XZX [16] and 4LNX [17], respectively. CHARMM-force field topologies and parameters [18,19,20] were implemented to prepare the simulation packages for solvation, energy minimization, equilibration and production runs by using visual molecular dynamics (VMD) [21] and nanoscale molecular dynamics (NAMD) [22] interfaces. The ligands T3 and T4 were parameterized suitably [20] for the NAMD runs.
The separate THR isoforms: THR-β, THRT3-β, THRT3-β1 and THRT3T4-α were solvated fully in an explicit solvent of neutral water-ions providing the cellular environment. Here, THRT3T4-α was truncated in size by omitting initial residue IDs from 145 to 156 of almost free strand. At first, THR-β as well as THRT3-β was solvated under periodic boundary conditions in TIP3P-water box of cell basis vectors 50.36, 60.92 and 74.78 Å, neutrallized by adding Na+ and Cl− ions in the concentration of 0.15 mol/L, performed energy minimization up to 3000 conjugate gradient (CG) steps and then separate equilibration runs were performed up to 2 ns at five different constant temperatures 300, 305, 310, 315 and 320 K. The Langevin constant temperature and pressure (1 atm) controls were used with damping coefficient of 1 ps−1 and integrator papameter of 2 fs/step by keeping rigid bonds of H-atoms. The force field related switching, cut-off and pair list distances were 10, 12 and 14 Å, repectively with 1-4 scaling 1.0. The mean energy, 〈U〉 of THR-β and that of THRT3-β at the five different temperatures were noted down from the last 0.5 ns runs. The slope of straight line fit in 〈U〉 vs. T plot provides the heat capacity (CV) of a mixture of solvating T3-liganded or unliganded THR at the body scale temperature 310 K. The same procedure with identical terms and conditions was implemented to a neutral water-ion box of cell basis vectors 30, 45 and 60 Å to find the heat capacity (CwV) of the solvent only. It is to be noted that CwV found for the solvent (water) by keeping rigid bonds of H-atoms with 2 fs/step is contributed by the non-bond (electrostatic and van der Waal) energies only. Then, from Eq 3, specific heat capacities (cpV) of THR-β and THRT3-β were obtained and compared.
Each of the THR isoforms was solvated in a water-sphere (TIP3P water model) neutralized with Na+ and Cl− ions in the concentration of 0.15 mol/L to study their heat conduction properties such as heat capacity (CpV), thermal diffusivity (D) and thermal conductivity (k). During the solvation under non-periodic boundary conditions, the radii of THRT3-β, THRT3-β1 and THRT3T4-α related water-droplets were 37.48, 36.99 and 31.29 Å, respectively. The force-filed and integrator parameters, and Langevin dynamics for constant temperature control were fixed as mentioned in the periodic boundary conditions. Each of the systems was geometrically optimized up to the sufficient (2000-5000) CG steps and equilibrated up to 20 ns. Conformational stability of the system was monitored by plotting graphs for root mean square deviation (RMSD) and/or radius of gyration (RG) during equilibration as well as production runs. The systems were also subjected to the additional production runs of 2 ns each in NVT ensemble at 310 K to find the heat capacity (CV) by using energy fluctuations (Eq 2). Putting CV of protein-ligand solvated sphere, cwV of water-ion solvent, and the related masses in Eq 3, the specific heat cpV of a THR isoform was obtained. The specific heat found from d〈U〉/dT by fitting straight line in the periodic boundary conditions as stated above and the specific heat found from energy fluctuation method in non-periodic boundary conditions were compared taking the cases of THR-β and THRT3-β.
The final coordinates of each equilibrated droplet consisting of a THR isoform were taken after its 20 ns run at 310 K. The inner sphere (r < R) was kept at initial temperature, Ti = 310 K and the outer shell (r > R) was fixed at the final temperature, Tf = 200 K where R = 33 Å and Δr = 4.48 Å for THRT3-β; R = 33 Å and Δr = 3.99 Å for THRT3-β; and R = 27 Å and Δr = 4.29 Å for THRT3T4-α. Then, NAMD simulations of temperature relaxation were performed without any constraint imposed into the atomic vibrations to monitor the change in system's temperature. The cooling process was done up to 20 ps each. By fitting the temperature data with the theoretical expression in Eq 5, the thermal diffusivity of each isoform was obatined and compared. Finally, the system's thermal conductivity was obtatined using Eq 6.
3. Results and discussion
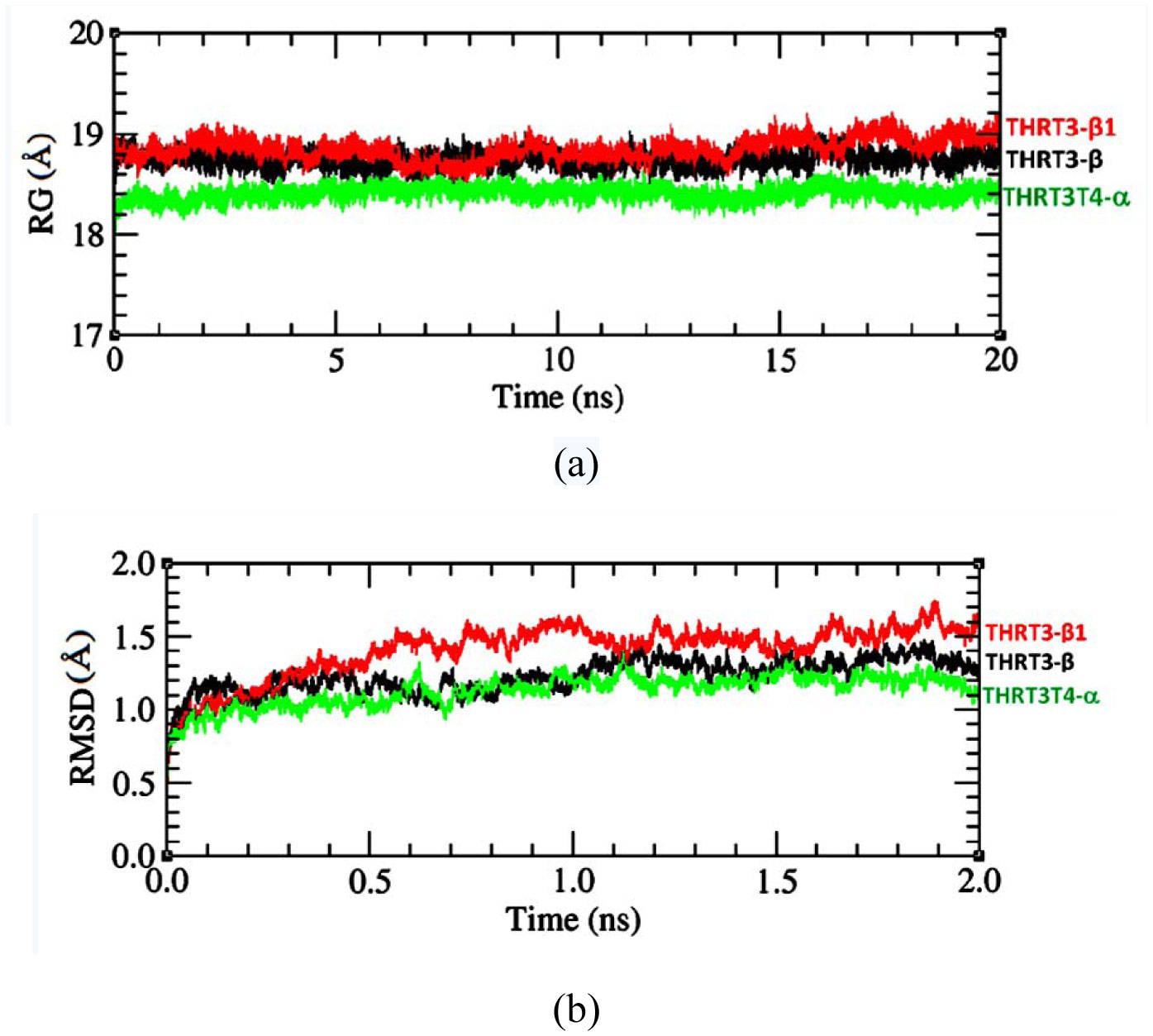
The separately performed 20 ns equilibration runs at 310 K of THR-isoforms solvated in water-droplets result mean ± SD of protein's RMSD: 2.13 ± 0.38 Å for THRT3-β, 1.98 ± 0.21 Å for THRT3-β1, and 2.24 ± 0.31 Å for THRT3T4-α; and the related RGs are 18.74 ± 0.07, 18.84 ± 0.11, and 18.41 ± 0.06 Å, respectively. In case of unliganded THR-β, RG is 18.70 ± 0.09 Å and RMSD is 2.61 ± 0.50 Å during its 20 ns long equilibration. Almost constant values of RG with small SD indicate that the protein-hormone systems are conformationally stable during their equilibration runs as plotted as shown in Figure 2a. The small fluctuations seen in RMSD plots (Figure 2b) are due to formation and breaking of H-bonds among the more stable residues, α-helix and β-sheets of the protein systems while searching for their conformational stability during the course of simulations. The additional production runs up to 2 ns in canonical (NVT) ensemble yield more small values of RMSD: 1.23 ± 0.11, 1.41 ± 0.18 and 1.13 ± 0.11 Å for THRT3-β, THRT3-β1 and THRT3T4-α proteins, respectively.
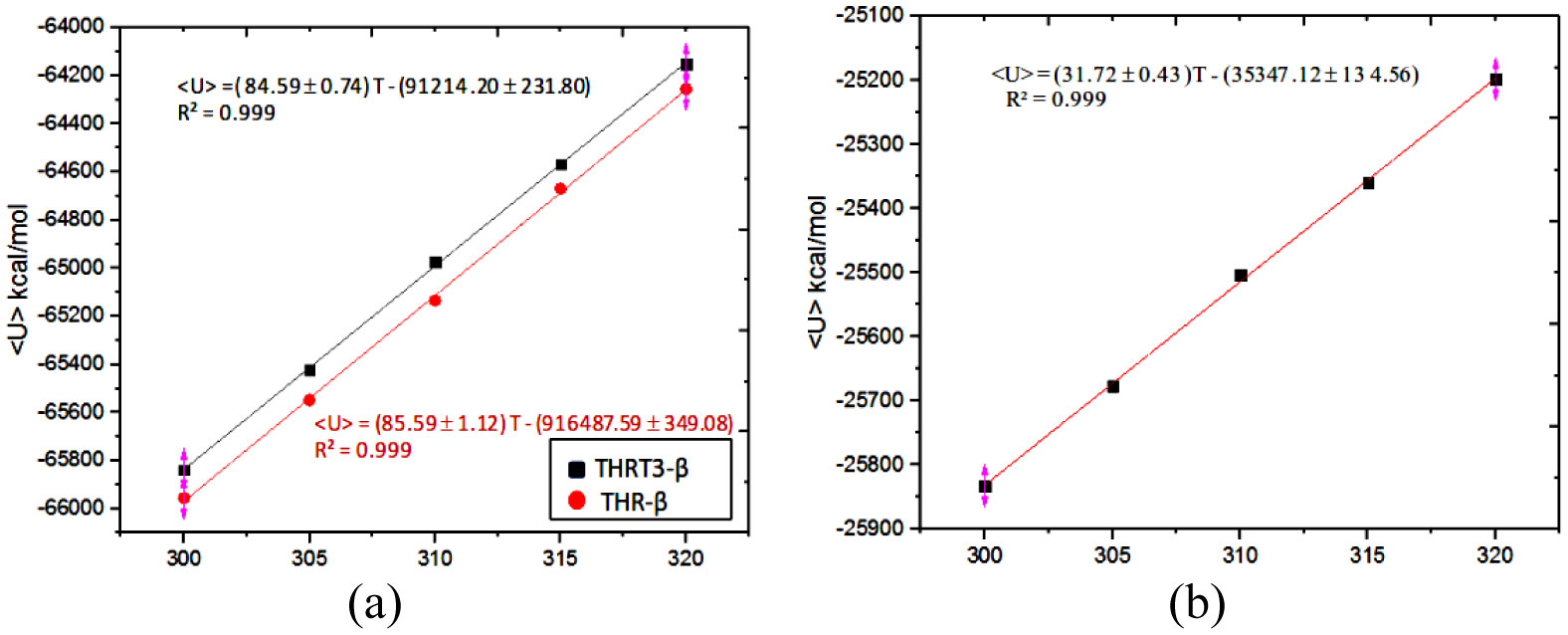
Five NVT simulations up to 2 ns each at temperature difference of 5 K about the body scale temperature 310 K result the values of <U> for liganded and unliganded THR-β under the periodic boundary conditions. The slope of linear fit in <U> vs. T plot (Figure 3a) obtains the heat capacity, CV of the entire THRT3-β solvated water-box which is 84.59 ± 0.74 kcal mol−1K−1 at about 310 K. Since the total mass of THRT3-β solvated water-box is 131765 amu, the related specific heat, cV is 2688.52 ± 23.52 Jkg−1K−1. Similarly, CV of THR-β solvated water-box (mass = 131186 amu) is 85.59 ± 1.12 kcal mol−1K−1 and the related cV is 2732.31 ± 35.75 Jkg−1K−1. Upon implementing the same procedure with identical terms and conditions for the simulations of a neutral water-ion box with 2 fs/step and rigid bonds of H-atoms, its heat capacity, CwV contributed by electrostatic and van der Waal energy terms is 31.72 ± 0.43 kcal mol−1K−1. Since mass of the modelled water-ion box is 45357 amu, the related specific heat, cwV = 2928.75 ± 39.70 Jkg−1K−1. Figure 3b shows the best linear fit of <U> vs. T for the water-box where the slope of straight line gives CwV. The mass of THR-β is 27640 amu and that of THRT3-β is 28291 amu. By using Eq 3, the specific heat capacities, cpV of THR-β and THRT3-β in water-ion solution are 1996.25 ± 20.95 Jkg−1K−1 and 1809.88 ± 35.66 Jkg−1K−1, respectively. This difference in heat capacity is due to the presence of ligand (T3) in LBD of THR and the T3-receptor interactions as explained in [23,24]. Hydrophobic, vibrational and conformational contributions to the heat capacity changes are involved in the protein-ligand interactions.
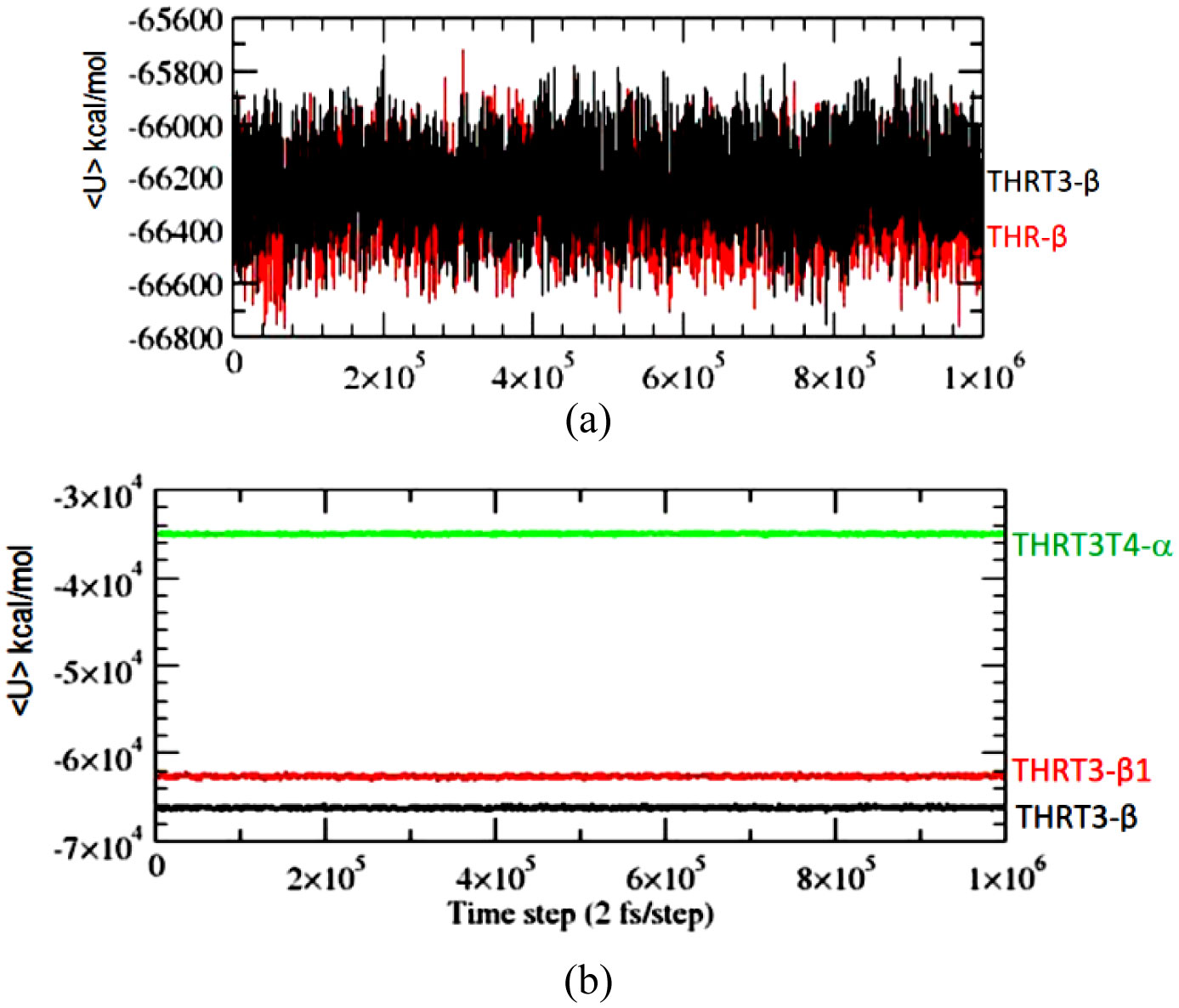
The heat capacities of the systems are also determined from the mean energy fluctuations in their canonical ensembles (Eq 2). The specific heat capacities of the globular protein-hormone systems found from this technique (see cpV of THR-β and THRT3-β in Table 2) are in close agreement with their values found from the method of linear fit for 〈U〉 vs. T (Figure 3a). The flutuations in mean energy of THR-β and THRT3-β solvated droplets are shown in Figure 4a where the values of 〈U〉 at 310 K are −66286.35 ± 128.43 and −66218.22 ± 128.76 kcal/mol, respectively. Figure 4b demonstrates the fluctutating energy levels of THR-isoform solvated droplets. The obtained values of mean square fluctuations of energy, masses of THR-isoform slovated droplets and the related heat capacities are depicted in Table 1. We use cwV = 2928.75 ± 39.70 Jkg−1K−1 and cV from Table 1 to find the specific heats cPV of THRs (Table 2) in solution with the help of Eq 3. cPV of the protein-hormone system, determined in this study (e.g. 2030.62 ± 105.32 Jkg−1K−1 for THRT3-β) at 310 K, lies within the experimental range: 1200 to 2300 Jkg−1K−1 for the native state globular proteins at 25 °C as given by Privalov et al. 1986 [25]. The heat capacity changes of proteins at different temperatures representing folding and unfolding states are explained by Privalov et al. 2007 [26]. The values of cPV for THRs, in this technique, are a bit higher than the heat capacities: 6.5 ± 2.1 kJmol−1K−1 for myoglobin and 180 ± 35 kJmol−1K−1 for Ca2+ ATP-ase (ISU4) in water calculated by Lervik et al. 2010 using MDS method [9]. In the previous studies [8,13,27,28], the average heat capaacity of a native globular protein in solution is about 1500 Jkg−1K−1 at 300 K. In a computational work of antifreeze protein performed by Pandey et al. 2017 [29], the hydration states of the protein depending on protein-water H-bonds make influence on its partial heat capacity so that cPV ranges from 0.494 cal g−1K−1 for the dry state protein to 0.606 cal g−1K−1 for the fully hydrated protein at about 300 K. Our results of cPV for THRs lie in the range of specific heat for the proteins in the hydration limit given by Pandey's study.
Table 1. Heat capacity of THRs solvated droplets (THR-protein + T3/T4 ligand + water + ions) at T = (310 ± 1) K in the NVT ensemble having average poteintial energy 〈U〉 where KB = 0.00198657 kcal mol−1K−1.
| Molecule in water sphere |
No. of atoms in mixture |
Total mass, M (amu) |
〈U2〉
(k cal mol−1)2 |
〈U〉2
(k cal mol−1)2 |
CV=〈U2〉−〈U〉2KBT2
(k cal mol−1K−1) |
cV
(J kg−1K−1) |
| THR-β |
21157 |
132213 |
4393896241.65 |
4393879748.25 |
86.39 ± 0.28@ |
2736.42 ± 8.87 |
| THRT3-β |
21192 |
132864 |
4384867565.23 |
4384850985.47 |
86.85 ± 0.28 |
2737.51 ± 8.82 |
| THRT3-β1 |
20266 |
127468 |
3925226341.90 |
3925210205.54 |
84.52 ± 0.27 |
2776.85 ± 8.87 |
| THRT3T4-a |
12249 |
79395.7 |
1225218557.93 |
1225208975.47 |
50.19 ± 0.16 |
2647.36 ± 8.44 |
| @ The error has been calculated from CV=CV(U,T),i.e.ΔCV=CV√(ΔUU)2+(ΔTT)2 where ΔU and ΔT are standard errors in potential energy and temperature, respectively. |
Table 2. Specific heat capacity (cPV), thermal diffusivity (D) corresponding to temperature relaxation between 310 to 200 K and thermal conductivity (k) of THRs in solution where the specific heat contributed by solvent (water + ions) in the droplet is 2928.75 ± 39.70 Jkg−1K−1 and density of the protein-hormone system in solution is (950 ± 50) kgm−3 at 310 K.
| Molecule |
No. of atoms |
Mass, mp(amu) |
cPV (Jkg−1K−1)a |
D (m2/s)b |
k (Wm−1K−1)c |
| THR-β |
3895 |
27640 |
2008.75 ± 107.77 |
(1.56 ± 0.02) × 10−7 |
0.30 ± 0.023@@ |
| THRT3-β |
3930 |
28291 |
2030.62 ± 105.32 |
(1.57 ± 0.03) × 10−7 |
0.30 ± 0.023 |
| THRT3-β1 |
4014 |
29069 |
2244.53 ± 95.73 |
(1.35 ± 0.05) × 10−7 |
0.29 ± 0.022 |
| THRT3T4-α |
3986 |
28853 |
2154.44 ± 46.32 |
(1.28 ± 0.04) × 10−7 |
0.26 ± 0.017 |
@@ The error has been calculated from k=k(CV,D,ρ),i.e.Δk=k√(ΔCVCV)2+(ΔDD)2+(Δρρ)2 where ΔCV, ΔD and Δρ are standard errors in specific heat, thermal diffusivity and density, respectively.
a From the calorimetric measurements by Privalov et al. 1986 [25], cPV of native globular proteins ranges from 1200 to 2300 Jkg−1K−1 at 300 K.
b D (water) = 14.6 Å2/ps, D (protein) = 21.1 Å2/ps for green fluoroscent protein (GFP), 18.7 Å2/ps for myoglobin [8]; and D (protein) = 4-18 Å2/ps at the temperature relaxation from 350 to 250 K [9].
c k (water) = 0.64 Wm−1K−1 & k (protein) = 0.13-0.28 Wm−1K−1 at 300 K [8,9]. |
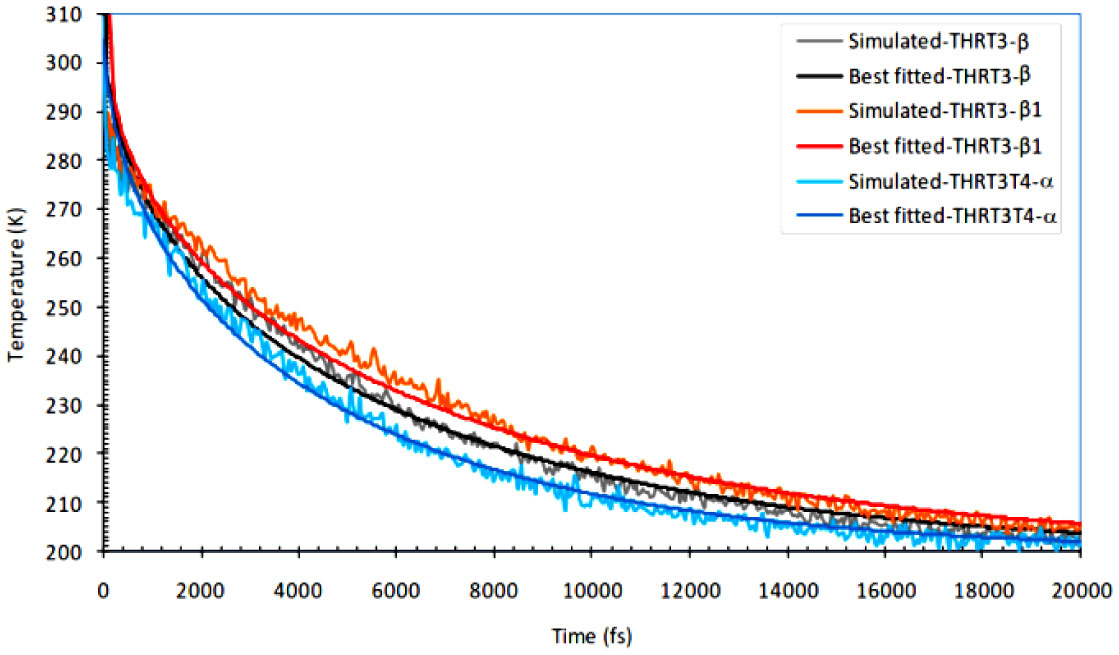
Thermal diffusivity of THRs ranges from 1.28 × 10−7 to 1.57 × 10−7 m2/s at the temperature relaxation from 310 to 200 K that is calculated from the best fitting of theoretical expression (Eq 5) with the simulated data (Figure 5). This result is near to the thermal diffusivity of water (Dw = 1.46 × 10−7 m2/s) and proteins (Dp = 2.11 × 10−7 m2/s for GFP and 1.87 × 10−7 m2/s for myoglobin) reported by Yu et al. 2005 [8]. According to Lervik et al. 2010 [9], Dp ranges from 0.4 × 10−7 m2/s to 1.8 × 10−7 m2/s for the different proteins at the temperature relaxation from 350 to 250 K. We observed a little bit higher thermal diffusivity for THRT3-β than that for THRT3-β1 and THRT3T4-α while cooling them by using the principle of thermal relaxation through the protein-water boundary. The slightly different heat transfer properties observed in THR isoforms (Figure 5) are associated with their structural evidences for the inter-residue H-bonding, energy transport channels and thermal boundary conductance between protein and water [30]. The H-bonding between protein and water facilitate vibrational energy and thermal transport across the interface.
Thermal conductivity of THR proteins, as depicted in Table 2, ranges from 0.26-0.30 Wm−1K−1 provided with the standard error of about 0.02 Wm−1K−1. This result shows that the protein-hormone systems are bad conductors of heat in comparision to water (kw = 0.64 Wm−1K−1). As reported by Yu et al. 2005 [8], thermal conductivity of both GFP and myoglobin is kp = 0.27 Wm−1K−1. The value of kp ranges from 0.13-0.23 Wm−1K−1 for the different proteins according to Lervik et al. 2010 [9]. The slightly higher value of kp has been observed for THRT3-β than that for THRT3-β1 and THRT3T4-α. Such change in heat conduction property is related to the effect of protein surface curvature, hydrophilic and hydrophobic patches and H-bonding between protein residues and protein-water interface [9,30]. According to the theory of non-equilibrium thermodynamics, the development of temperature gradient across THRs-water interface and the related thermal conduction are important biophysical phenomena linked with the functions of the protein-hormone systems towards the regulation of body temperature. The result of lower values of thermal conductivity of proteins than that of water is supporting the principle of body temperature regulation.
4. Conclusion
We have performed molecular dynamics simulations to find heat transfer coefficients of THRs. Heat capcity has been determined by using formula of mole fraction to the constituents of THR solvated periodic-box as well as nano-droplet of water. Numerical differentiation or slope of the best fitted straight line in mean potential function vs. temperature of the periodic box yields the same heat capacity as obtained from the method of mean energy fluctuations of the nano-droplet in canonical ensemble. The heat capacity of THR isoforms in solution ranges from 2000 to 2200 Jkg−1K−1 with the standard error limit of about 100 Jkg−1K−1 at 310 K. This result lies within the range of 1200 to 2300 Jkg−1K−1 as reported by Privalov et al. 1986 and a bit higher than 1500 Jkg−1K−1 as given by Yu et al. 2005 for the native globular proteins at 300 K. Our results for the specific heats of the protein-hormone systems are also in the close agreement with that of antifreeze protein in the hydration limit ranging from 2065 Jkg−1K−1 for dry state to 2533 Jkg−1K−1 for fully hydrated protein at about 300 K as studied by Pandey et al. 2017. In overt hypothyroid disorder, THRs become free of T3. The heat capaity values of T3-liganded and unliganded THR-β are different in some extent due to the change in degrees of freedom, protein-ligand interactions, H-bonding, and hydrophobic, vibrational and conformational changes in presence and absence of T3-hormone in LBD of the receptor. Thermal properties of THRs are directly associated with gene expressions and regulation of body temperature. Thermal diffusivity of THRs has been found to be ranging from 1.28 × 10−7 to 1.57 × 10−7 m2/s near to 1.46 × 10−7 m2/s of water at body scale temperature 310 K. A little bit higher value of thermal diffusion coefficient for THRT3-β than that of THRT3-β1 and THRT3T4-α is associated with the effect of inter-residue and protein-water H-bonding, thermal transport channels and boundary conductance in the protein-water interface. Thermal conductivity of THRs ranges from 0.26-0.30 Wm−1K−1 with the higher value for THRT3-β in the standard error limit of about 0.02 Wm−1K−1 which is about half the value, 0.64 Wm−1K−1 for water at 310 K. Our result for the thermal conductivity is also consistent with 0.27 Wm−1K−1 as reported by Yu et al. 2005 for GFP and myoglobin. The slightly different values of the heat transfer coefficients for THR-isoforms are related to H-bonding in protein-water interface, surface curvature, and hydrophobic and hydrophillic patches. In conclusion, specific heat, thermal diffusivity and thermal conductivity of THRs are consistent with that of other proteins as published in the previous literatures supporting the theory and the methodology implemented for their calculations.
Acknowledgements
The authors are thankful to Prof. Dr. Raju Khanal, Central Department of Physics, Tribhuvan University, Kathmandu, Nepal for providing the computing facilities. This work has been partially supported by Nepal Academy of Science and Technology (NAST) through a grant of PhD fellowship to the first author.
Conflict of interest
The authors declare that they have no conflict of interest.









 DownLoad:
DownLoad: