Immune classification of osteosarcoma

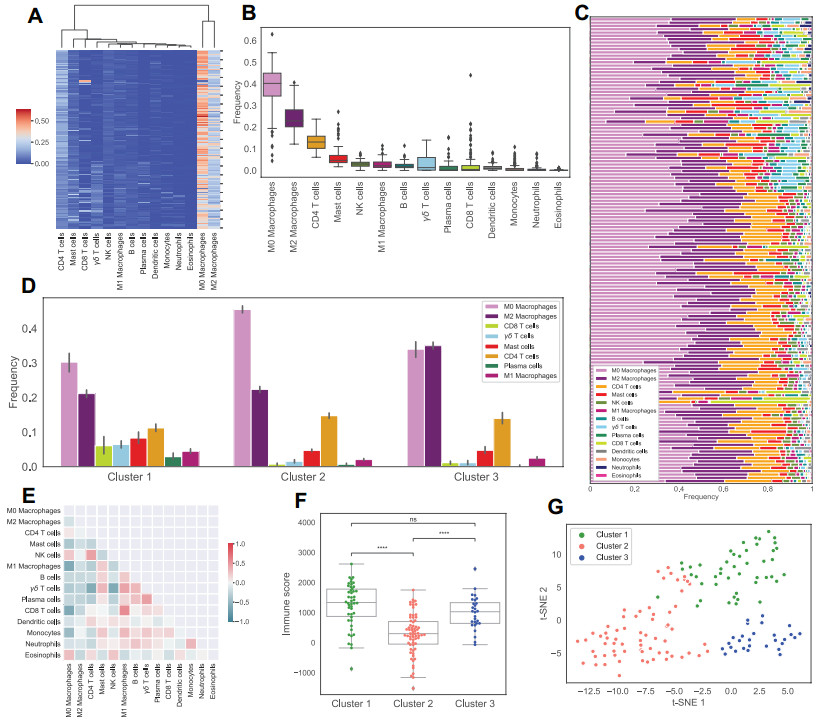
1.   Introduction

Research on single machine scheduling problems with location-based learning effects has long been the focus of scholars. Early pioneering research can be found in Biskup ^[1] and Moshiov ^[2]. In their research, they assumed that the processing time of the job was constant and a decreasing function of its position respectively. Moshiov ^[3] described the parallel machine case. Mosheiov and Sidney ^[4] introduced job-dependent learning effects and thought that the problem could be transformed into an allocation problem. Since then, many scholars have studied similar or improved models. There are many related achievements, and the research perspective is becoming more and more open. Mosheiov and Sidney ^[5] studied the case that all tasks have a common due date, and proved that the model is polynomial solvable. Bachman and Janiak ^[6] provided a method of proof using diagrams. Lee, Wu and Sung ^[7] discussed the two-criteria problem, and put forward the skills of searching for the optimal solution. The authors followed the methods of the non-increasing order of ${{\omega }_{j}}$ and the shortest processing time sequence achieves the optimal solution. Lee and Wu ^[8] solved a flow shop scheduling problem with two machines using a heuristic algorithm. Janiak and Rudek ^[9] discussed the complexity results of a single machine scheduling problem that minimizes the number of delayed jobs. Zhao, Zhang and Tang ^[10] investigated the polynomial solutions of some single machine problems, parallel machine problems, and flow shop problems in environments with learning effects. Cheng, Sun and Yu ^[11] considered some permutation flow shop scheduling problems with a learning effect on no-idle dominant machines. Eren and Ertan ^[12] studied the problem of minimizing the total delay in the case of learning effects, and used the 0-1 integer programming model to solve this problem. Zhang and Yan ^[13], Zhang et al. ^[14], Liu and Pan ^[15] and Liu, Bao and Zheng ^[16] have all studied scheduling problems based on learning effects from the perspective of problem model innovation or improvement.

With the deepening of research, many scholars found that p is not always a constant and there will be different processing times in different environments, different machines or different workers. Therefore, some scholars put forward the stochastic scheduling problem. Pinedo and Rammouz ^[17], Frenk ^[18] and Zhang, Wu and Zhou ^[19] have done a lot of pioneering work. Based on research results of the above scholars, Zhang, Wu and Zhou ^[20] studied the single machine stochastic scheduling problem based on the learning effect of location, and studied the optimal scheduling strategy for stochastic scheduling problems with and without machine failures. Ji et al. ^[21] considered the parallel machine scheduling caused by job degradation and the learning effect of DeJong. They proved that the proposed problem is polynomial solvable, and provided a fully polynomial time approximation solution. A labor scheduling model with learning effect is proposed by Qin, Liu and Kuang ^[22]. By piecewise linearizing the curve, the mixed 0-1 nonlinear programming model (MNLP) was transformed into the mixed 0-1 linear programming model (MLP) for solution. Zhang, Wang and Bai ^[23] proposed a group scheduling model with both degradation and learning effects. Xu et al. ^[24] proposed a multi machine order scheduling problem with learning effect, and use simulated annealing and particle swarm optimization to obtain a near optimal solution. Wu and Wang ^[25] consider a single machine scheduling problem with learning effects based on processing time and truncation of job delivery times related to past sequences. Vile et al. ^[26], Souiss, Benmansour and Artiba ^[27], Liu et al. ^[28] and Liu et al. ^[29] applied scheduling models separately to emergency medical services, supply chain, manufacturing management and graph theory. Li ^[30] studied the processing time of the job as random and uses a job-based learning rate. At the same time, he provided a method to deal with problems by using the difference between EVPI and EVwPI. Toksari and Atalay ^[31] studied four problems of the coexistence of learning effect and homework refusal. In order to reduce production costs, Chen et al. ^[32] focused on multi-project scheduling and multi-skilled labor allocation. Shi et al. ^[33] applied a machine learning model to medical treatment, estimate service level and its probability distribution, and used various optimization models to solve scheduling programs. Wang et al. ^[34] improved and studied several existing problems.

Ham, Hitomi and Yoshida ^[35] first proposed the "group technology" (GT). According to type or characteristics, jobs are divided into different groups. Each group of jobs is produced by the same means and, once the jobs are put into production, they cannot be stopped. Lee and Wu ^[36] proposed a group scheduling learning model where the learning effect not only depends on the work location, but also on the group location. We have demonstrated that the problem is polynomial solvable under the proposed model. Yang and Chand ^[37] studied a single machine group scheduling problem with learning and forgetting effects to minimize the total completion time of tasks. Zhang and Yan ^[38] proposes a group scheduling model with deterioration and learning effects. Under the proposed model, the completion time and total completion time problems are polynomial optimal solvable. Similarly, Ma et al. ^[39], Sun et al. ^[40] and Liu et al. ^[41] provided appropriate improvements to the model. Li and Zhao ^[42] considered the group scheduling problem on a single machine with multiple expiration window assignments. They also divided the homework into several groups to improve production efficiency and save resources. However, this work is only an improvement on some problems or solutions and has not achieved groundbreaking results. Liang ^[43] inquired into the model with deteriorating jobs under GT to minimize the weighted sum of manufacturing time and resource allocation costs. Wang et al. ^[44] considered the issue of maturity allocation and group technology at the same time. They determined the best sequence and the best deadline allocation of the group and intra-group jobs by minimizing the weighted sum of the absolute values of the lateness and deadline allocation costs. Wang and Ye ^[45] established a stochastic grouping scheduling model. Based on SDST and preventive maintenance, Jain ^[46] proposed a method based on a genetic algorithm to minimize the performance measurement of completion time.

The above literature provides assistance in establishing problem models and solving methods for classical sorting and random sorting with learning effects. In the learning effect, the learning factor is a very important quantity which often affects the actual processing time of the job. There are many factors that affect learning factors, which can be internal or external and often have randomness. In this case, the learning factor is no longer a constant–it is variable–and sometimes the probability density can be calculated. These aspects were not considered in previous works. Therefore, the discussion of the randomness of learning factors in this study has practical significance. Based on the above ideas, this study establishes a new stochastic scheduling model. In the model, workers participate in production, the processing of jobs has a position based learning effect and the learning index is random. The method to solve the problem is to use heuristic algorithms to find the optimal seqencing of the problems.

2.   Scheduling problem with stochastic learning rate: single machine

$n$ independent jobs are processed on one machine. The job can be processed at any time and cannot be stopped during processing.

First model is

where $f\left({{C}_{j}} \right)$ is function of processing time of job ${{J}_{j}}$.

First, we give some lemmas.

Lemma 2.1. ^[16] X is a random variable, continuous on the definition field, and ${{f}_{X}}\left(x \right)$ is density function, $Y = g\left(X \right)$, there is $E\left(Y \right) = E\left[g\left(X \right) \right] = \int_{-\infty }^{+\infty }{g\left(x \right)}{{f}_{X}}\left(x \right)dx$.

Lemma 2.2. ^[16] The meaning of X is the same as Lemma 2.1, function $g\left(x \right)$ is everywhere derivable and monotonous, $Y = g\left(X \right)$, then,

in which $\alpha, \; \beta$ is the minimum and maximum value of $g\left(-\infty \right), g\left(+\infty \right)$ respectively, $h\left(y \right) = {{g}^{-1}}\left(x \right)$.

Lemma 2.3. When $x > 1$, $y\left(x \right) = \frac{1}{\ln x}\left(1-\frac{1}{x} \right)$ is monotonic and does not increase, $z\left(x \right) = 1-\frac{1}{\ln x}\left(1-\frac{1}{x} \right)$ is a monotone increasing function, and $z\left(x \right) > 0$.

It is easy to prove the conclusion by using the method of derivation and function limit.

Lemma 2.4. If the random variable $a\sim U\left(0, \lambda \right)$, $X = p{{r}^{-a}}$, where $p$ is constant, then ${{f}_{X}}\left(x \right) = \frac{1}{\lambda }\cdot \frac{1}{x\ln r}$.

Proof. From (2.1), when $a\sim U\left(0, \lambda \right)$, we can get $X\in \left(p{{r}^{-\lambda }}, p \right)$, and

□

Second, we give the symbols and their meanings in the theorems (see Table 1).

Theorem 2.1. For $1\left| p_{j}^{r} = {{p}_{j}}{{r}^{-{{a}_{j}}}}, {{a}_{j}}\sim U\left(0, {{\lambda }_{j}} \right) \right|E\left({{C}_{\max }} \right)$, if p is consistent with the parameters $\lambda$, that is, for all$\ {{J}_{i}}, {{J}_{j}}$, if there is ${{p}_{i}}\le {{p}_{j}}\Rightarrow {{\lambda }_{i}}\le {{\lambda }_{j}}$, if the $\lambda$ is large, arrange it first, we can obtain the optimal ranking of the problem.

Proof. (1) There is the first job in the exchanged jobs, the job in the first and second positions is exchanged.

According to hypothesis and Lemma 2.1, we have

Note that ${{p}_{1}}\le {{p}_{2}}\Rightarrow {{\lambda }_{1}}\le {{\lambda }_{2}}$, ${{2}^{{{\lambda }_{2}}}} > {{2}^{{{\lambda }_{1}}}} > 1$, from Lemma 2.3, we can get

From (2.3)–(2.5), it can be obtained that

(2) When there is no first job in the exchanged jobs, that is $r\ge 2$. We compare $E\left[{{C}_{j}}\left(S \right) \right]$ of ${{J}_{j}}$ in $S$ with $E\left[{{C}_{i}}\left({{S}'} \right) \right]$ of ${{J}_{i}}$ in ${S}'$.

From hypothesis and Lemma 2.1, we get

Notice the hypothesis of the Theorem 2.1, for all $\ {{J}_{i}}, {{J}_{j}}$, if there is ${{p}_{i}}\le {{p}_{j}}\Rightarrow {{\lambda }_{i}}\le {{\lambda }_{j}}$, and when $r\ge 2$, ${{r}^{{{\lambda }_{i}}}} > 1$. From Lemmas 2.2, 2.3 and (2.6), (2.7), we get

Proof complete. □

Theorem 2.2. For model $1\left| p_{j}^{r} = {{p}_{j}}{{r}^{-{{a}_{j}}}}, {{a}_{j}}\sim U\left(0, {{\lambda }_{j}} \right) \right|E\left(\sum{{{\omega }_{j}}{{C}_{j}}} \right)$, if p and its weight meet $\frac{{{p}_{i}}}{{{p}_{j}}}\le \min \left\{ 1, \frac{{{\omega }_{i}}}{{{\omega }_{j}}} \right\}$, the optimal order is obtained by the larger ${{\lambda }_{j}}{{\omega }_{j}}$ first.

Proof. Suppose ${{p}_{i}}\le {{p}_{j}}$, according to the previous assumptions, we have

Notice $\frac{{{p}_{i}}}{{{p}_{j}}}\le \min \left\{ 1, \frac{{{\omega }_{i}}}{{{\omega }_{j}}} \right\}$, ${{\omega }_{j}}{{\lambda }_{j}}\ge {{\omega }_{i}}{{\lambda }_{i}}$ and (2.8)–(2.11), we can get

Theorem 2.2 is proved. □

Theorem 2.3. When ${{\lambda }_{i}}\le {{\lambda }_{j}}\Rightarrow {{d}_{i}}\le {{d}_{j}}$ for ${{J}_{i}}, {{J}_{j}}$, the EDD rule, that is non-decreasing of ${{d}_{j}}$ is the optimal algorithm of problem $1\left| p_{j}^{r} = {{p}_{j}}{{r}^{a}}, {{p}_{j}}\sim U\left(0, {{\lambda }_{j}} \right) \right|E\left({{L}_{\max }} \right)$.

Proof. First, we consider ${{\lambda }_{i}}\le {{\lambda }_{j}}$. The parameters of ${{J}_{i}}, {{J}_{j}}$ in ${S}'$ satisfy the relationship ${{\lambda }_{i}}\le {{\lambda }_{j}}\Rightarrow {{d}_{i}}\le {{d}_{j}}$, but they violate the EDD rule, that is, ${{J}_{j}}$ is processed before ${{J}_{i}}$. In fact, ${{J}_{i}}$ is processed before ${{J}_{j}}$ in $S$. Then we prove that the sequence ${S}'$ can be transformed into a non-decreasing of ${{d}_{j}}$ sequence $S$ and this transformation makes the maximum delay non-increasing. Further more, we suppose the last job in ${{\pi }_{1}}$ is on the $\left(r-1 \right)$-th position and the expected completion time of it is $E\left({{t}_{0}} \right)$. From (2.8)–(2.11), we get the expected delays of ${{J}_{i}}, {{J}_{j}}$ in sequence $S$ are

Similarly, the expected delays of ${{J}_{i}}, {{J}_{j}}$ in sequence ${S}'$ are

Because ${{\lambda }_{i}}\le {{\lambda }_{j}}$, ${{d}_{i}}\le {{d}_{j}}$ and (2.12)–(2.15), so

Then from (2.16) and (2.17), we have

Thus, exchanging the position of ${{J}_{i}}$ and ${{J}_{j}}$ does not cause an increase in the maximum delay. After a limited number of similar processing, the optimal sequence can be transformed into the order of non-decreasing of due time ${{d}_{j}}$ and the expected maximum delay will not increase. □

Theorem 2.4. For $1\left| p_{j}^{r} = {{p}_{j}}{{r}^{a}}, {{p}_{j}}\sim U\left[0, {{\lambda }_{j}} \right] \right|E\left(\sum{{{T}_{j}}} \right)$, when ${{\lambda }_{i}}\le {{\lambda }_{j}}\Rightarrow {{d}_{i}}\le {{d}_{j}}$, we have the optimal algorithm by non-decreasing order of ${{d}_{j}}$.

Proof. First we assume ${{d}_{i}}\le {{d}_{j}}$. The necessary condition for the theorem proof is the same as that of Theorem 2.3. Now we show that exchanging the position of ${{J}_{i}}$ and ${{J}_{j}}$ does not increase the objective function value. Then we repeat the exchange of adjacent jobs to get the optimal sequence of problem.

We discuss it in two cases:

Case 1. $E\left[{{C}_{j}}\left({{S}'} \right) \right]\le {{d}_{j}}$, in which $E\left[{{T}_{i}}\left(S \right) \right]\neq 0$, $E\left[{{T}_{j}}\left(S \right) \right]\neq 0$. If one of them is zero, the conclusion is obviously true.

From Theorem 2.3 and ${{d}_{i}}\le {{d}_{j}}$, we have

Case 2. $E\left[{{C}_{j}}\left({{S}'} \right) \right] > {{d}_{j}}$. Notice ${{d}_{i}}\le {{d}_{j}}$, ${{\lambda }_{i}}\le {{\lambda }_{j}}$, we have

From (2.19) and (2.20), we get $E\left[{{T}_{i}}\left(S \right) \right]\text{+}E\left[{{T}_{j}}\left(S \right) \right]\le E\left[{{T}_{i}}\left({{S}'} \right) \right]\text{+}E\left[{{T}_{j}}\left({{S}'} \right) \right].$ □

In the following discussion, we assume that ${{d}_{j}} = d, j = 1, 2, \cdots, n$.

Theorem 2.5. For $1\left| p_{j}^{r} = {{p}_{j}}{{r}^{a}}, {{p}_{j}}\sim U\left(0, {{\lambda }_{j}}, \right){{d}_{i}} = d \right|E\left(\sum{{{\omega }_{j}}{{U}_{j}}} \right)$, there are the following results:

(1) When $d-t > \min \left({{\lambda }_{1}}, {{\lambda }_{2}} \right)$, according to the non-decreasing order of ${{\lambda }_{j}}$, we can get the smaller number of expected weighted tardy jobs;

(2) When $d-t < {{\lambda }_{1}}$, $d-t < {{\lambda }_{2}}$, ${{\omega }_{1}}\le {{\omega }_{2}}\Rightarrow d-t\ge \frac{2\left({{\lambda }_{2}}-{{\lambda }_{1}} \right)}{{{\left(r+1 \right)}^{a}}}\cdot \frac{{{\omega }_{1}}\mathit{\text{+}}{{\omega }_{2}}}{{{\omega }_{1}}-{{\omega }_{2}}}+\frac{{{\omega }_{1}}{{\lambda }_{1}}-{{\omega }_{2}}{{\lambda }_{2}}}{{{\omega }_{1}}-{{\omega }_{2}}}$, we can get the minimum expected value of the objective function according to the non-decreasing rules of job weight.

Proof. (1) First we assume the machine is idle at time $t$ and then there are two jobs ${{J}_{1}}, {{J}_{2}}$ without processing. Suppose processing times of ${{J}_{1}}, {{J}_{2}}$ are ${{p}_{1}}$ and ${{p}_{2}}$, ${{J}_{1}}, {{J}_{2}}$ are processed at the $r$-th position and $\left(r\text{+}1 \right)$-th position respectively. The weights of ${{J}_{1}}, {{J}_{2}}$ are ${{\omega }_{1}}$ and ${{\omega }_{2}}$. When $d-t > \min \left({{\lambda }_{1}}, {{\lambda }_{2}} \right)$, we should process the job for which $\lambda {}_{j}$ is smaller first, so that we can guarantee the target value is smaller.

(2) In the following we assume ${{\omega }_{1}}\le {{\omega }_{2}}$, $d-t < {{\lambda }_{1}}$ and $d-t < {{\lambda }_{2}}$.

Let $E\left[\sum{\omega U\left(1, 2 \right)} \right]$ denotes the expected weighted number of tardy jobs when we process ${{J}_{1}}$ first and then process ${{J}_{2}}$, then

The meaning of $E\left[\sum{\omega U\left(2, 1 \right)} \right]$ is similar to $E\left[\sum{\omega U\left(1, 2 \right)} \right]$, then

According to (2.21) and (2.22), we obtain

When condition (2) of the theorem is satisfied we can get $E\left[\sum{\omega U\left(1, 2 \right)} \right] < E\left[\sum{\omega U\left(2, 1 \right)} \right].$ The proof of Theorem 2.5 is completed. □

3.   The case of GT with random learning rate of job

Now, we will discuss the case of group scheduling. All jobs in the model can be processed at zero time. In a group, the job can be worked continuously. The machine must have preparation time before entering the next group, and it is subject to the classical learning effect hypothesis. p is a random with learning effect based on the position in the group, and the learning rate follows a uniform distribution.

Our model is expressed as

The assumptions and symbols of the model (see Table 2) are as follows:

Theorem 3.1. For $1\left| p_{ij}^{k} = {{p}_{ij}}{{k}^{-{{a}_{ij}}}}, {{a}_{ij}}\sim U\left(0, {{\lambda }_{ij}} \right), G, s_{i}^{r} = {{s}_{i}}{{r}^{-a}} \right|E\left({{C}_{\max }} \right)$, when the jobs in the group satisfy: For all ${{J}_{ik}}, {{J}_{il}}$, ${{p}_{ik}}\le {{p}_{il}}\Rightarrow {{\lambda }_{ik}}\le {{\lambda }_{il}}$, the internal parts of the group are in accordance with ${{\lambda }_{ik}}$ large rule, the group is on the basis of the non-decreasing order of ${{s}_{i}}$, we can get the optimal solution.

Proof. Suppose ${{s}_{i}}\le {{s}_{j}}$, and $a > 0$. We can get

Then, we can get the sorting rules of the group by repeating the exchange operation.

The scheduling problem of jobs in a group can be summed up as

Theorem 2.1 has been proved.

We have completed the proof of Theorem 3.1. □

Theorem 3.2. For $1\left| p_{ij}^{k} = {{p}_{ij}}{{k}^{-{{a}_{ij}}}}, {{a}_{ij}}\sim U\left(0, {{\lambda }_{ij}} \right), G, s_{i}^{r} = {{s}_{i}}{{r}^{-a}} \right|E\left(\sum{{{C}_{j}}} \right)$, if $\frac{{{s}_{i}}}{{{n}_{i}}}\le \frac{{{s}_{j}}}{{{n}_{j}}}$, the larger ${{\lambda }_{ij}}$ of the job in the group, the better the arrangement. The group is arranged by the non-decreasing order of $\frac{\sum\limits_{l, k = 1}^{{{n}_{i}}}{\frac{{{p}_{ik}}}{\ln \left({{k}^{{{\lambda }_{ij}}}} \right)}\cdot \left(1-\frac{1}{{{k}^{{{\lambda }_{ij}}}}} \right)}}{{{n}_{i}}}$, we can get the optimal sort.

Proof. Assumptions are the same as Theorem 3.1.

And $\frac{{{s}_{i}}}{{{n}_{i}}}\le \frac{{{s}_{j}}}{{{n}_{j}}}$, $\frac{\sum\limits_{l, k = 1}^{{{n}_{i}}}{\frac{{{p}_{ik}}}{\ln \left({{k}^{{{\lambda }_{ik}}}} \right)}\cdot \left(1-\frac{1}{{{k}^{{{\lambda }_{ik}}}}} \right)}}{{{n}_{i}}}\le \frac{\sum\limits_{l, k = 1}^{{{n}_{j}}}{\frac{{{p}_{jk}}}{\ln \left({{k}^{{{\lambda }_{jk}}}} \right)}\cdot \left(1-\frac{1}{{{k}^{{{\lambda }_{jk}}}}} \right)}}{{{n}_{j}}}$, then

Then, we just need to repeat the previous method to complete the proof of the group order rule.

Secondly, for the scheduling problem of jobs in a group, we can reduce it to problem $1\left| p_{j}^{r} = {{p}_{j}}{{r}^{-{{a}_{ij}}}}, {{a}_{ij}}\sim U\left(0, {{\lambda }_{ij}} \right) \right|E\left(\sum{{{\omega }_{j}}{{C}_{j}}} \right)$, and ${{\omega }_{j}} = 1$, Theorem 2.2 has been proved.

Therefore, we have completed the proof. □

4.   Algorithms and examples

The following are heuristic algorithms and examples for Theorems 3.1 and 3.2.

Algorithm 1

Step 1: When ${{p}_{ik}}\le {{p}_{il}}\Rightarrow {{\lambda }_{ik}}\le {{\lambda }_{il}}$, the priority principle shall be followed ${{\lambda }_{ij}}$ in group;

Step 2: Priority arrangement for groups with small ${{s}_{i}}$.

The group ${{G}_{i}}$ time complexity is $O\left({{n}_{i}}\log {{n}_{i}} \right)$, the total time complexity of step 1 is $\sum\limits_{i = 1}^{m}{O\left({{n}_{i}}\log {{n}_{i}} \right)}$; the optimal order time complexity of step 2 is $O\left(m\log m \right)$. The time complexity of Algorithm 1 is $O\left(n\log n \right)$.

An example of Algorithm 1:

Example 1. $m = 2$, ${{G}_{1}} = \left\{ {{J}_{11}}, {{J}_{12}}, {{J}_{13}} \right\}$, ${{G}_{2}} = \left\{ {{J}_{21}}, {{J}_{22}} \right\}$, ${{s}_{1}} = 2$, ${{s}_{2}} = 3$, $a = 2$, ${{a}_{11}}\sim U\left(0, 2 \right)$, ${{a}_{12}}\sim U\left(0, 4 \right)$, ${{a}_{13}}\sim U\left(0, 3 \right)$, ${{a}_{21}}\sim U\left(0, 2 \right)$, ${{a}_{22}}\sim U\left(0, 4 \right)$, ${p}_{11} = 1$, ${p}_{12} = 3$, ${p}_{13} = 2$, $p_{21} = 4$, $p_{22} = 5$.

solution. Step 1: In ${{G}_{1}}$, because ${{\lambda }_{11}} = 2 < {{\lambda }_{13}} = 3 < {{\lambda }_{12}} = 4$, $p_{11} = 1 < p_{13} = 2 < p_{12} = 3$; ${{\lambda }_{21}} = 2 < {{\lambda }_{22}} = 4$, ${{p}_{21}} = 4 < {{p}_{22}} = 5$, satisfy the consistency assumption, the order is ${{J}_{12}}\to {{J}_{13}}\to {{J}_{11}}$, ${{J}_{22}}\to {{J}_{21}}$;

Step 2: Because ${{s}_{1}} = 2 < {{s}_{2}} = 3$, so ${{G}_{1}}\to {{G}_{2}}$.

The solution of this example is $E\left({{C}_{\max }} \right) = 13.07$.

Algorithm 2

Step 1: Arrange the production of jobs in the group by the priority of ${{\lambda }_{ij}}$;

Step 2: When the requirements are met $\frac{{{s}_{i}}}{{{n}_{i}}}\le \frac{{{s}_{j}}}{{{n}_{j}}}$ in the group, the group processing shall be arranged according to the non-decreasing order of $\frac{\sum\limits_{l, k = 1}^{{{n}_{i}}}{\frac{{{p}_{ik}}}{\ln \left({{k}^{{{\lambda }_{ik}}}} \right)}\cdot \left(1-\frac{1}{{{k}^{{{\lambda }_{ik}}}}} \right)}}{{{n}_{i}}}$.

The complexity analysis of Algorithm 2 is the same as Algorithm 1.

We give an example of Algorithm 2.

Example 2. Same as Example 1.

solution. Step 1: Compare the values of ${{\lambda }_{ij}}$, we can get ${{J}_{12}}\to {{J}_{13}}\to {{J}_{11}}$, ${{J}_{22}}\to {{J}_{21}}$;

Step 2: Because $\frac{{{s}_{1}}}{{{n}_{1}}} = \frac{2}{3} < \frac{{{s}_{2}}}{{{n}_{2}}} = \frac{3}{2}$, $\quad \frac{\sum{\frac{{{p}_{1j}}}{\ln \left({{k}^{{{\lambda }_{1j}}}} \right)}}\cdot \left(1-\frac{1}{{{k}^{\lambda j}}} \right)}{{{n}_{1}}} = 0.866 < \frac{\sum{\frac{{{p}_{2j}}}{\ln \left({{k}^{{{\lambda }_{2j}}}} \right)}}\cdot \left(1-\frac{1}{{{k}^{\lambda j}}} \right)}{{{n}_{2}}} = 2.844$. The group order is ${{G}_{1}}\to {{G}_{2}}$.

After calculation, we have $E\left({{C}_{\max }} \right) = 50.15.$

5.   Conclusions

For the single machine stochastic scheduling and group stochastic scheduling problems established in this paper, we consider that the learning rate is a random variable, which is not available in previous literature. We find that such problems are very general, and we can also find examples in real life. For example, if workers participate in learning a new project training, their mastery time of new technology may be random, which can be expressed by random variables. After transforming the problem, we give corresponding theoretical assumptions for the proposed problem, and then give the solution of the optimal order. For the case of group technology, we give a numerical example to verify the theoretical results.

Next, we can combine it with intelligent algorithms to solve the problems of large number of jobs, machine maintenance, waiting time for job processing, and multi-stage processing of jobs.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This research was funded by Shanghai Philosophy and Social Sciences General Project (2022BGL010); the Post-funded Project of the National Social Science Fund Project of China (22FGLB109); Laboratory of Philosophy and Social Sciences for Data lntelligence and Rural Revitalization of Dabie Mountains, Lu'an, Anhui 237012, China; Key projects of Humanities and Social Sciences in Colleges and Universities of Anhui Province (SK2018A0397).

Conflict of interest

The authors declare no conflicts of interest.