Teaching learning-based whale optimization algorithm for multi-layer perceptron neural network training

Yongquan Zhou; Yanbiao Niu; Qifang Luo; Ming Jiang; Yongquan Zhou; Yanbiao Niu; Qifang Luo; Ming Jiang

doi:10.3934/mbe.2020319

Mathematical Biosciences and Engineering

2020, Volume 17, Issue 5: 5987-6025. doi: 10.3934/mbe.2020319

Previous Article Next Article

Research article Special Issues

Teaching learning-based whale optimization algorithm for multi-layer perceptron neural network training

1.
College of Artificial Intelligence, Guangxi University for Nationalities, Nanning 530006, China
2.
Key Laboratory of Guangxi High Schools Complex System and Computational Intelligence, Nanning 530006, China
3.
Guangxi Key Laboratories of Hybrid Computation and IC Design Analysis, Nanning 530006, China
4.
Guangxi Institute of Digital Technology, Nanning 530000, China

Received: 29 May 2020 Accepted: 24 August 2020 Published: 10 September 2020

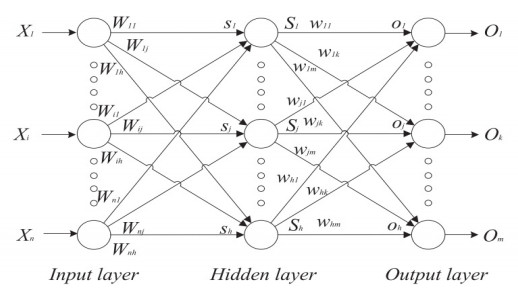
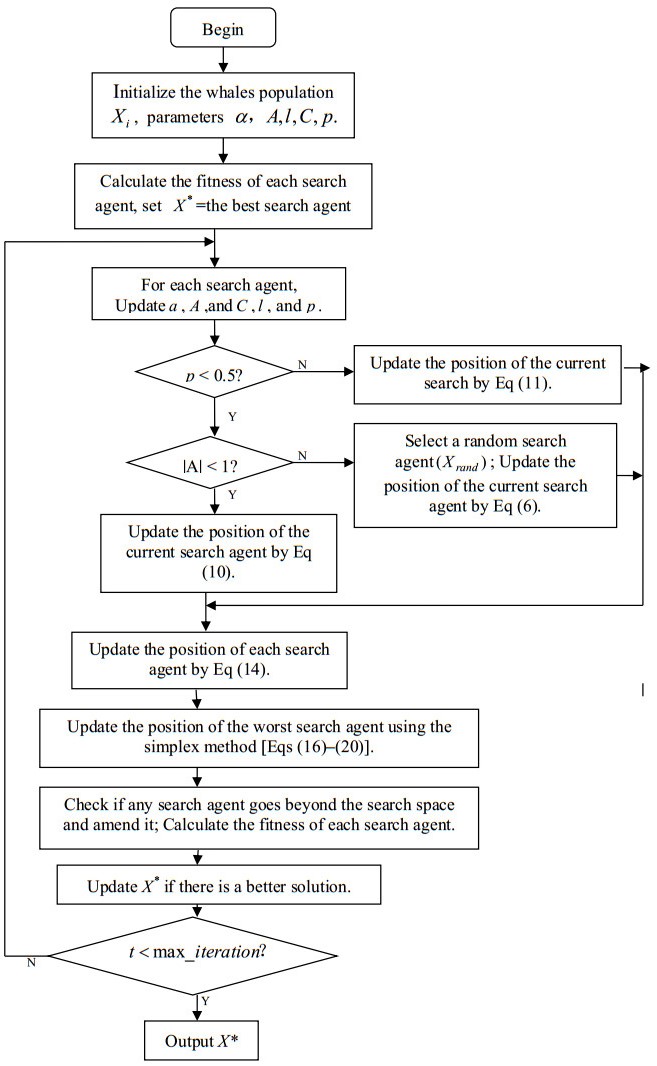
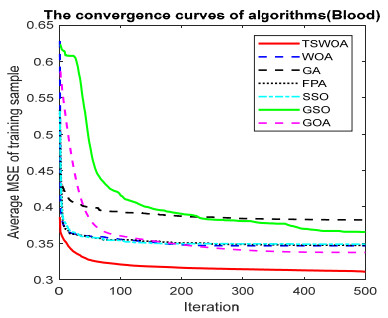
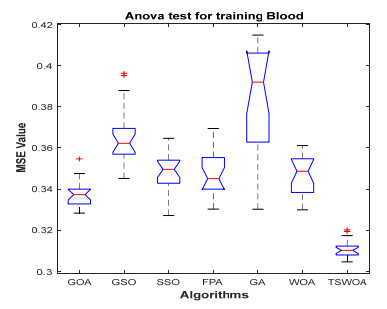
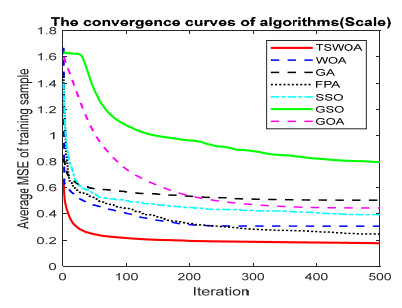
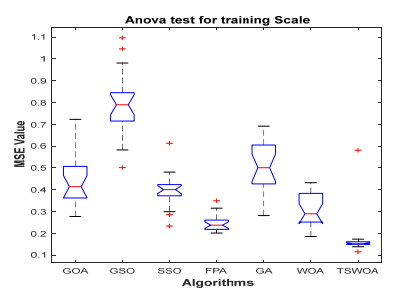
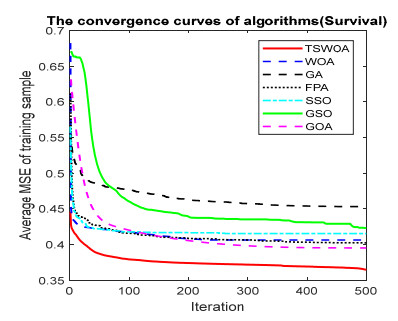
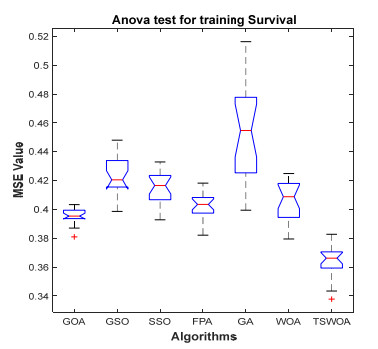
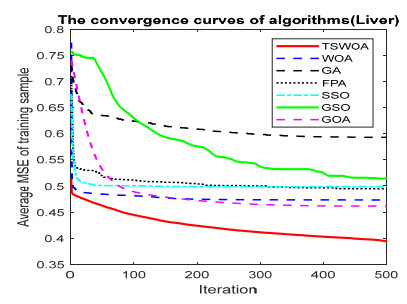
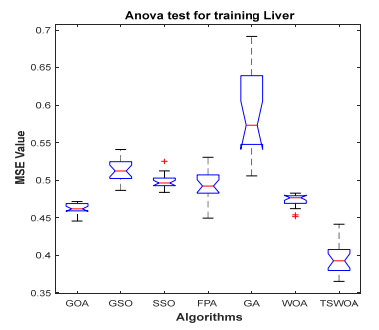
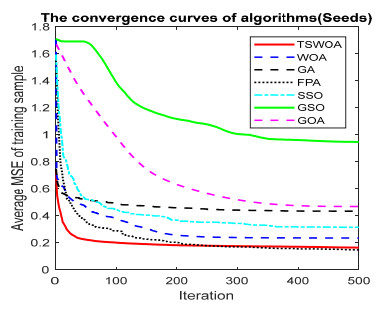
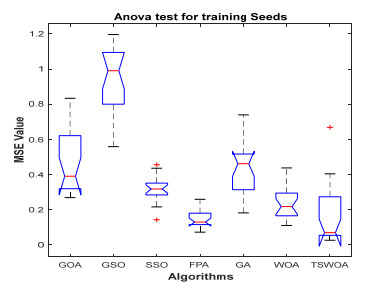
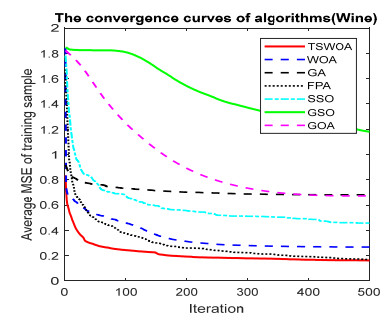
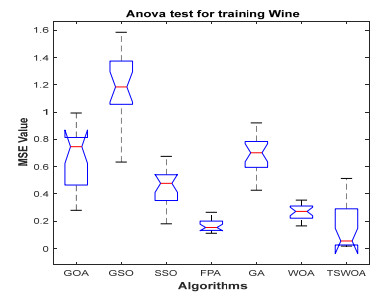
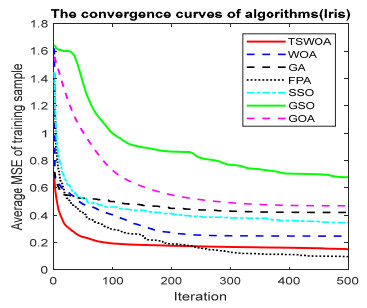
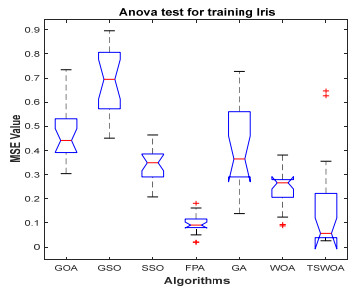
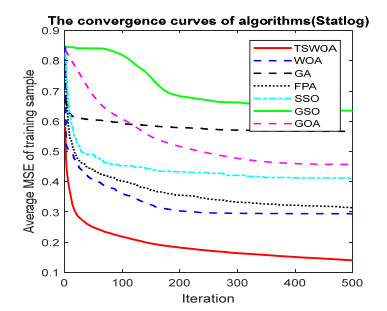
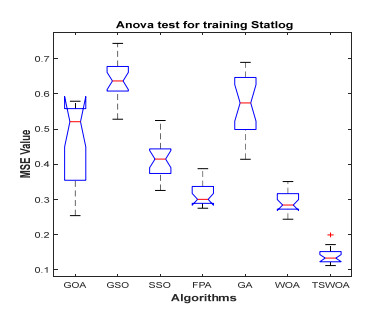
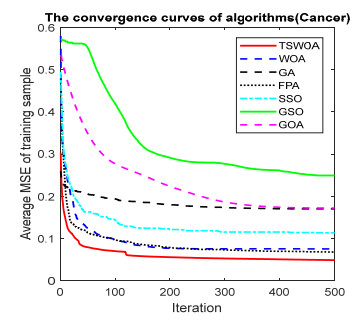
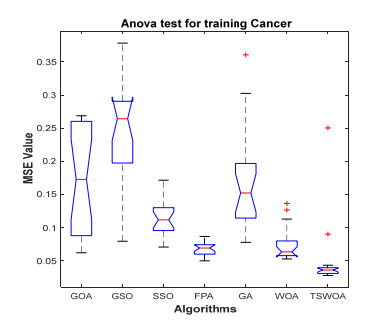
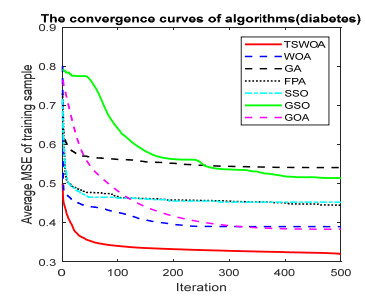
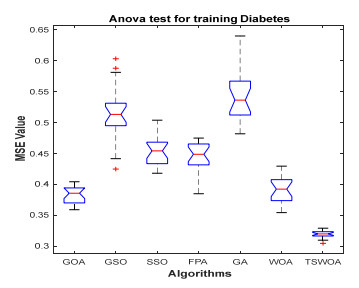
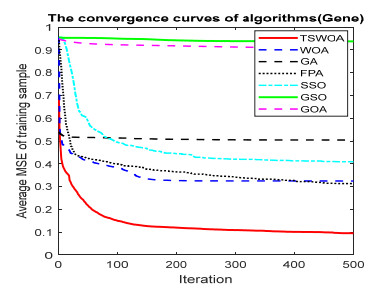
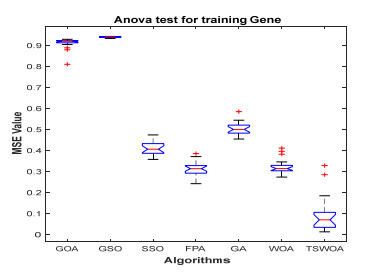
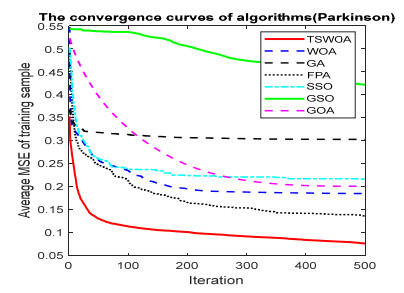
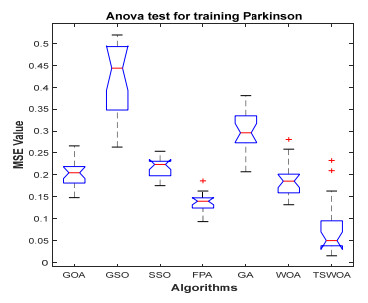
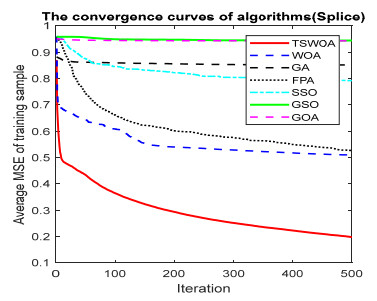
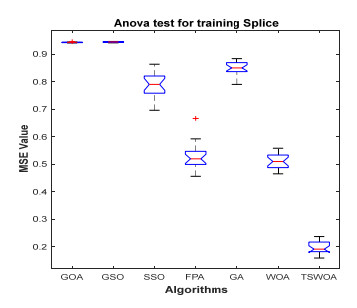
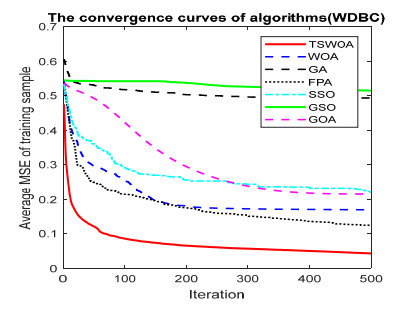
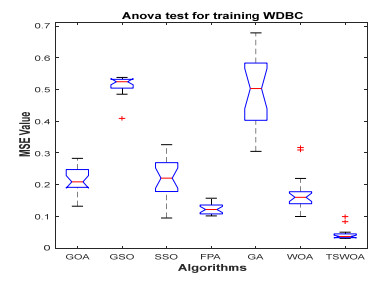
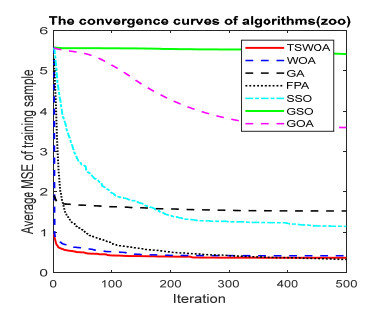
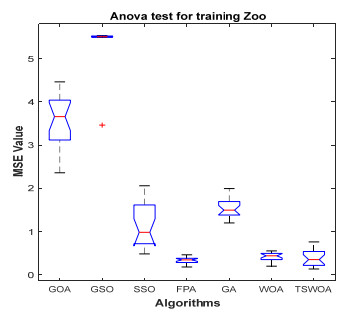
This paper presents an improved teaching learning-based whale optimization algorithm (TSWOA) used the simplex method. First of all, the combination of WOA algorithm and teaching learning-based algorithm not only achieves a better balance between exploration and exploitation of WOA, but also makes whales have self-learning ability from the biological background, and greatly enriches the theory of the original WOA algorithm. Secondly, the WOA algorithm adds the simplex method to optimize the current worst unit, averting the agents to search at the boundary, and increasing the convergence accuracy and speed of the algorithm. To evaluate the performance of the improved algorithm, the TSWOA algorithm is employed to train the multi-layer perceptron (MLP) neural network. It is a difficult thing to propose a well-pleasing and valid algorithm to optimize the multi-layer perceptron neural network. Fifteen different data sets were selected from the UCI machine learning knowledge and the statistical results were compared with GOA, GSO, SSO, FPA, GA and WOA, severally. The statistical results display that better performance of TSWOA compared to WOA and several well-established algorithms for training multi-layer perceptron neural networks.

Keywords:

teaching learning-based,
whale optimization algorithm,
multi-layer perceptron (MLP) neural network,
metaheuristic algorithm

Citation: Yongquan Zhou, Yanbiao Niu, Qifang Luo, Ming Jiang. Teaching learning-based whale optimization algorithm for multi-layer perceptron neural network training[J]. Mathematical Biosciences and Engineering, 2020, 17(5): 5987-6025. doi: 10.3934/mbe.2020319

Related Papers:

[1]	Juan Wang, Chunyang Qin, Yuming Chen, Xia Wang . Hopf bifurcation in a CTL-inclusive HIV-1 infection model with two time delays. Mathematical Biosciences and Engineering, 2019, 16(4): 2587-2612. doi: 10.3934/mbe.2019130
[2]	Bing Li, Yuming Chen, Xuejuan Lu, Shengqiang Liu . A delayed HIV-1 model with virus waning term. Mathematical Biosciences and Engineering, 2016, 13(1): 135-157. doi: 10.3934/mbe.2016.13.135
[3]	Xiaohong Tian, Rui Xu, Jiazhe Lin . Mathematical analysis of an age-structured HIV-1 infection model with CTL immune response. Mathematical Biosciences and Engineering, 2019, 16(6): 7850-7882. doi: 10.3934/mbe.2019395
[4]	A. M. Elaiw, N. H. AlShamrani . Stability of HTLV/HIV dual infection model with mitosis and latency. Mathematical Biosciences and Engineering, 2021, 18(2): 1077-1120. doi: 10.3934/mbe.2021059
[5]	Jinhu Xu, Yicang Zhou . Bifurcation analysis of HIV-1 infection model with cell-to-cell transmission and immune response delay. Mathematical Biosciences and Engineering, 2016, 13(2): 343-367. doi: 10.3934/mbe.2015006
[6]	Haitao Song, Weihua Jiang, Shengqiang Liu . Virus dynamics model with intracellular delays and immune response. Mathematical Biosciences and Engineering, 2015, 12(1): 185-208. doi: 10.3934/mbe.2015.12.185
[7]	Patrick W. Nelson, Michael A. Gilchrist, Daniel Coombs, James M. Hyman, Alan S. Perelson . An Age-Structured Model of HIV Infection that Allows for Variations in the Production Rate of Viral Particles and the Death Rate of Productively Infected Cells. Mathematical Biosciences and Engineering, 2004, 1(2): 267-288. doi: 10.3934/mbe.2004.1.267
[8]	Shingo Iwami, Shinji Nakaoka, Yasuhiro Takeuchi . Mathematical analysis of a HIV model with frequency dependence and viral diversity. Mathematical Biosciences and Engineering, 2008, 5(3): 457-476. doi: 10.3934/mbe.2008.5.457
[9]	Yu Yang, Gang Huang, Yueping Dong . Stability and Hopf bifurcation of an HIV infection model with two time delays. Mathematical Biosciences and Engineering, 2023, 20(2): 1938-1959. doi: 10.3934/mbe.2023089
[10]	Urszula Foryś, Jan Poleszczuk . A delay-differential equation model of HIV related cancer--immune system dynamics. Mathematical Biosciences and Engineering, 2011, 8(2): 627-641. doi: 10.3934/mbe.2011.8.627

Abstract

1. Introduction

Ultrasonography of peripheral nerves has become an increasingly popular method for the diagnosis of peripheral entrapment neuropathy. Electrophysiological examination is the gold standard for the diagnosis of this type of disease ^[1], and mainly reflects the functional changes of the nerve ^[2]. Studies have shown that changes in patient symptoms are associated with morphological changes of the nerve ^[3,4,5,6,7], thus the nerve image information is essential in disease diagnosis. The shortcomings of electrophysiological examination primarily include two aspects: it is an invasive procedure and it does not reflect the morphological changes of the nerve. Ultrasound examination in medical applications and researches is widely implemented ^[8,9,10], especially real-time three-dimensional ultrasound method ^[11,12]. Ultrasound examination can avoid these two shortcomings of electrophysiological examination and has become an important approach to diagnose peripheral entrapment neuropathy ^[13].

Ultrasound examination faces significant challenges in determining a specific diagnostic protocol and criteria, because the obtained ultrasound images do not provide complete morphological information. The main parameters for diagnosis include the following: (1) cross-sectional area (CSA) of the diseased nerve segment ^[14,15,16], (2) CSA ratio, difference or mean to that of the adjacent segment ^[15,17], (3) CSA ratio to that of the adjacent nerves in the same level ^[18], (4) ultrasound findings of increased blood flow within the nerve ^[19,20], and (5) shear wave elastography image ^[21,22]. Currently, the major shortcoming of ultrasound diagnosis for peripheral entrapment neuropathy is the presence of individual variation ^{[23,24,25,26]}. The examination site is limited to a certain point or a segment within the lesion range but does not reflect the overall condition or change trend of the diseased nerve. The range of neuropathy cannot be defined before treatment.

Therefore, to eliminate the shortcomings of the current diagnostic methods, a multilevel side-to-side image contrast ultrasound technique was proposed for the diagnosis of unilateral peripheral entrapment neuropathy in this study. This method will maximally eliminate individual variation, explore the full course of the lesion segment of the nerve, reflect the trend of neuromorphic changes, and identify the sites as well as the range of neuropathy before treatment.

2. Materials and methods

2.1. Workflow of determination of diagnostic and therapeutic threshold by multilevel side-to-side image contrast ultrasonography

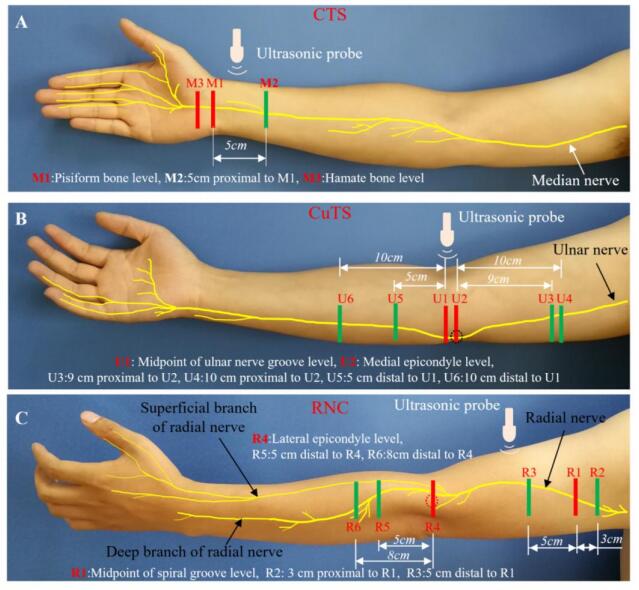
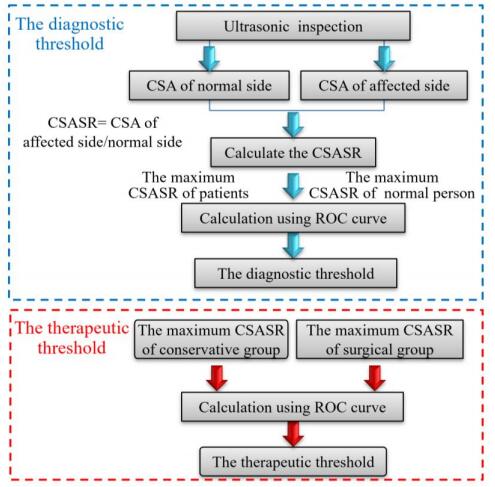
The three most common types of peripheral entrapment neuropathy, namely, carpal tunnel syndrome (CTS), cubital tunnel syndrome (CuTS) and radial nerve compression (RNC), were selected as the study targets. The diagnostic and therapeutic thresholds were determined by multilevel side-to-side image contrast ultrasonography. The flow chart of the study is shown in Figure 1.

Figure 1. Flowchart for determining the diagnostic and therapeutic thresholds by multilevel side-to-side image contrast ultrasonography.

DownLoad: Full-Size Img PowerPoint

First, ultrasonography was performed to measure the CSA at multiple corresponding levels of the affected and contralateral nerve. Next, the cross-sectional area swelling ratio (CSASR) was calculated, i.e., the degree of swelling of the affected side relative to that of the contralateral side-CSASR = CSA of the affected nerve / CSA of the corresponding site of the contralateral nerve.

Second, the diagnostic threshold was obtained using the receiver operation characteristic (ROC) curve. The diagnostic threshold was calculated using the maximal CSASR of the patient and the maximal CSASR of the normal controls.

Third, the ROC curve was used to calculate the therapeutic threshold. The therapeutic threshold was calculated by using the maximal CSASR of the surgical treatment group and the maximal CSASR of the conservative treatment group.

Finally, the segment of the diseased nerve was identified. The most severe point of the diseased nerve was identified according to the location presenting the maximal CSASR. The nerve segment with a CSASR greater than the diagnostic threshold was identified as the diseased nerve segment.

2.2. Multilevel side-to-side image contrast ultrasound examination

A Philips iU22 ultrasound system (Philips Electronics, Amsterdam, Netherlands) was used to perform a longitudinal ultrasound scan of the upper limbs of the patients to observe the general morphological characteristics of the nerves and to measure the CSA of multiple corresponding levels of the affected and the contralateral nerve. A longitudinal scan is used to scan the nerve longitudinally along the direction of nerve travel and determines changes in the diameter of the nerve along the longitudinal direction. It can observe whether the surrounding tissue produces exogenous compression to the nerve and can observe echo changes in the inside and outer membrane of the nerve. The measured cross sections were determined according to the three types of neuropathy, as stated below.

CTS: The diseased nerve segment is approximately only 5 cm in length. Therefore, it is necessary to scan in three levels only: M1, M2 and M3. M1 represents the level of the pisiform bone (carpal tunnel entrance), M2 represents the level 5 cm proximal to pisiform bone level, and M3 represents the level of the hamate bone (the midpoint of the carpal tunnel) (Figure 2A).

Figure 2. Ultrasonic measurements of the cross section. (A) CTS. (B) CuTS. (C) RNC.

DownLoad: Full-Size Img PowerPoint

CuTS: The nerve lesion is located in the range from U1 to U6 regions. The measurement was performed at six levels, from U1 to U6. U1 is located at the midpoint of ulnar nerve groove, U2 is located in the level of the medial epicondyle, U3 is located at the level 9 cm proximal to the medial epicondyle, U4 is located at the level 10 cm proximal to the medial epicondyle, U5 is located at the level 5 cm distal to the midpoint of ulnar nerve groove, and U6 is located at the level 10 cm distal to the midpoint of the ulnar nerve groove (Figure 2B).

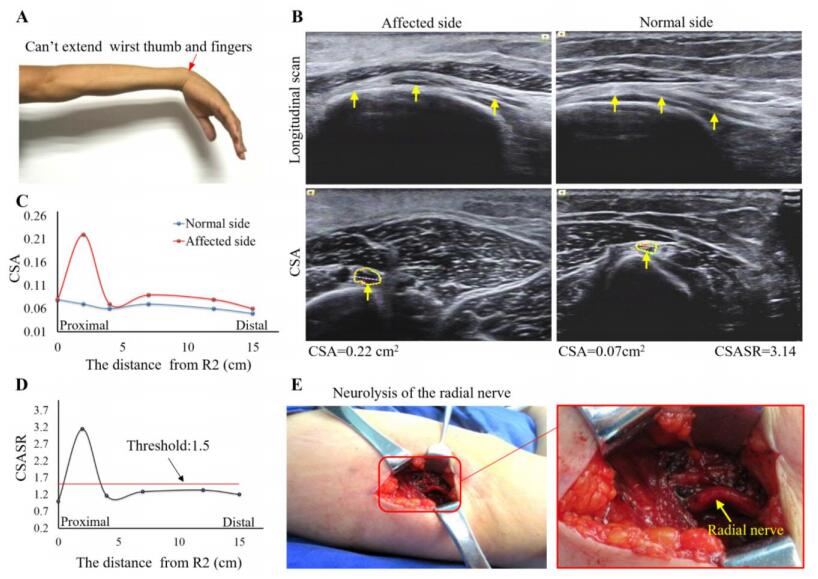
RNC: The nerve lesion is located in the range from R1 to R6 regions. The measurement was performed at six levels, from R1 to R6. R1 is located at the level of the midpoint of the spiral groove, R2 is located at the level 3 cm proximal to the midpoint of the spiral groove, R3 is located at the level 5 cm distal to the midpoint of the spiral groove, R4 is at the level of the lateral epicondyle, R5 is located at the level 5 cm distal to the lateral epicondyle, and R6 is located at the level 8 cm distal to the lateral epicondyle (Figure 2C).

2.3. The diagnostic and therapeutic thresholds of multilevel side-to-side image contrast ultrasonography for peripheral entrapment neuropathy

The SPSS statistical software 19.0 (IBM, Armonk, USA) was used for statistical analysis. Spearman's rank correlation coefficient was used to analyse the correlation between the ultrasound morphological index and the electrophysiological index. The ROC curve was used to obtain diagnostic and therapeutic thresholds. P < 0.05 was considered to be statistically significant.

The mean of the maximal CSA of the affected and the normal side were calculated, and the t-test was used to analyse the significant difference between the two groups. The mean of the maximal CSASR was then calculated. In electrophysiological examination, motor nerve conduction velocity (MNCV), motor nerve amplitude (MNAP), sensory nerve conduction velocity (SNCV) and sensory nerve amplitude (SNAP) reflect the extent of motor demyelinating lesions, motor axonal lesions, sensory nerve lesions, and sensory axonal lesions, respectively. The correlation analysis between the maximal CSASR and MNCV, MNAP, SNCV, and SNAP were performed to determine the reliability of CSASR to reflect the extent of the four types of lesions. According to the maximal CSASRs of the patients and normal controls, the ROC curve was used to calculate the diagnostic threshold and its sensitivity, specificity, area under the ROC curve (AUC) and P value. According to the maximal CSASRs of patients who underwent conservative treatment and patients who underwent surgical treatment, the ROC curve was used to calculate the therapeutic threshold and its sensitivity, specificity, AUC and P values. The location and distribution of the maximal CSASR was determined.

2.4. Patients

A total of 62 patients with CTS, CuTS or RNC who were treated in China from March 2016 to July 2018 and 30 subjects in the normal control group were included in this study (Table 1). The patient data was provided by the following 5 hospitals: Ningbo No. 6 Hospital, Cixi Traditional Chinese Medicine Hospital, Kyer Hospital, Hu Fangdou Orthopedic Hospital and Lin'an Orthopedic Hospital.

Table 1. General data.

	Number of people(n)	Age (y)(mean±SD)	M/F (n)	Left/right (n)	Mean duration of disease (m)(mean±SD)	Conservative/surgical treatment (n)
CTS	15	52.2 ± 12.8	6/9	9/6	17.3 ± 10.2	4/11
CuTS	34	50.7 ± 14.3	28/6	16/18	14.9 ± 7.4	9/25
RNC	13	39.8 ± 18.5	10/3	8/5	1.9 ± 1.0	8/5
Control group	30	45.4 ± 15.1	17/13	30/30	0	-

| Show Table

DownLoad: CSV

The neurophysiological examination of the patients was performed using a Haishen NDI-092 electrophysiological/evoked potential meter (Haishen Medical Electronic Instrument Co., Ltd., Shanghai, China). The bipolar transdermal stimulator and the surface recording electrode were used during the examination, and the temperature of the distal limb was controlled at approximately 32 ℃.

3. Results

The diagnostic and therapeutic thresholds for CTS, CuTS and RNC were obtained by statistical analysis, and then the thresholds were used to retrospectively validate the data in 62 patients undergoing ultrasound examination. The diagnostic accuracy rate was 92.9%, and the accuracy for selecting the treatment method was 87.1%. All preoperative ultrasound findings were consistent with the intraoperative findings. All patients had varying degrees of symptom improvement after treatment, and rare lesion sites were not missed.

3.1. Mean

The mean of the maximal CSA and CSASR in patients with CTS, CuTS or RNC are shown in Table 2. The paired t-tests showed that there was a statistically significant difference in the maximal CSA values between the affected side and the normal side.

Table 2. Mean and significant differences of maximal CSA and mean of CSASR.

	Mean of maximal CSA (cm²) (mean ± S D)		Side-to-side CSA significant difference (P value)	Mean of maximal CSASR (mean ± SD)
	Affected side	Normal side	Side-to-side CSA significant difference (P value)	Mean of maximal CSASR (mean ± SD)
CTS	0.148 ± 0.046	0.105 ± 0.021	= 0.001	1.53 ± 0.35
CuTS	0.168 ± 0.071	0.092 ± 0.028	< 0.001	2.99 ± 0.99
RNC	0.093 ± 0.042	0.060 ± 0.018	< 0.001	2.98 ± 1.40

| Show Table

DownLoad: CSV

3.2. Correlation analysis

Correlation analyses between the maximal CSASR and MNCV, MNAP, SNCV and SNAP in patients with CTS, CuTS or RNC were performed, and the correlation coefficients are given in Table 3. The maximal CSASR of the median nerve was negatively correlated with MNCV, and significantly negatively correlated with SNCV and SNAP. The maximal CSASR of the ulnar nerve was negatively correlated with MNAP and significantly negatively correlated with MNCV, SNCV and SNAP. There was no significant correlation between the maximal CSASR of the radial nerve and MNCV, MNAP, SNCV or SNAP.

Table 3. Correlation analysis between ultrasonography and electrophysiology.

		MNCV	MNAP	SNCV	SNAP
Maximal CSASR of the median nerve	correlation coefficient	−0.610*	−0.059	−0.659**	−0.745**
	n	15	15	15	15
	P	0.016	0.834	0.008	0.001
Maximal CSASR of the ulnar nerve	correlation coefficient	−0.515**	−0.433*	−0.651**	−0.636**
	n	34	34	32^△	33^△△
	P	0.002	0.011	< 0.001	< 0.001
Maximal CSASR of the radial nerve	correlation coefficient	−0.177	−0.221	0.146	−0.271
	n	13	13	10^△△△	13
	P	0.563	0.468	0.688	0.370
* The correlation is significant when the confidence coefficient is 0.05. **The correlation is significant when the confidence coefficient is 0.01. △ SNCV was not recorded during electrophysiological examination in 2 patients with CuTS. △△ SNAP was not recorded during electrophysiological examination in a patient with CuTS. △△△ SNCV was not recorded during electrophysiological examination in 3 patients with RNC.

| Show Table

DownLoad: CSV

3.3. Diagnostic threshold and therapeutic threshold

The calculated diagnostic thresholds for patients with CTS, CuTS or RNC are shown in Table 4. The diagnostic thresholds for CTS, CuTS, and RNC were 1.22, 1.51, and 1.50, respectively. That is, if the maximal CSASR value of CTS, CuTS and RNC was greater than or equal to the diagnostic threshold of 1.22, 1.51 and 1.50, respectively, the entrapment neuropathy could be confirmed. If they were less than the diagnostic threshold, entrapment neuropathy could be ruled out. At the same time, the sensitivity, specificity, AUC and P value were calculated, and they were statistically significant.

Table 4. Diagnostic threshold.

	Diagnostic Threshold	Sensitivity (%)	Specificity (%)	AUC	P
CTS	1.22	86.7	83.3	0.862	< 0.001
CuTS	1.51	91.2	93.3	0.928	< 0.001
RNC	1.50	100	86.7	0.982	< 0.001

| Show Table

DownLoad: CSV

The CSASR thresholds for the conservative treatment group and the surgical treatment group were statistically calculated (Table 5). Independent sample t-test analysis showed that the mean maximal CSASR value in the surgical treatment group were significantly higher than in the conservative treatment group. The surgical therapeutic thresholds of the CSASR for CTS, CuTS and RNC were 1.48, 1.67 and 3.04, respectively. That is, conservative treatment should be chosen when the maximal CSASR of the diseased nerve was less than the therapeutic threshold. Surgical treatment should be selected when the maximal CSASR of the diseased nerve is greater than or equal to the therapeutic threshold.

Table 5. Therapeutic threshold.

	Mean of maximal CSASR(mean ± SD)		Differences between conservative and surgical treatment groups(P)	Therapeutic threshold	Sensitivi-ty (%)	Specifici-ty (%)	AUC	P
	Conservative treatment group	Surgical treatment group		Therapeutic threshold	Sensitivi-ty (%)	Specifici-ty (%)	AUC	P
CTS	1.23 ± 0.23	1.64 ± 0.33	0.043	1.48	63.6	100	0.846	0.01
CuTS	1.48 ± 0.35	2.58 ± 0.99	0.003	1.67	100	79.4	0.95	< 0.001
RNC	2.21 ± 0.55	4.17 ± 1.54	0.045	3.04	80	100	0.90	0.001

| Show Table

DownLoad: CSV

3.4. Determination of lesion sites of the nerve

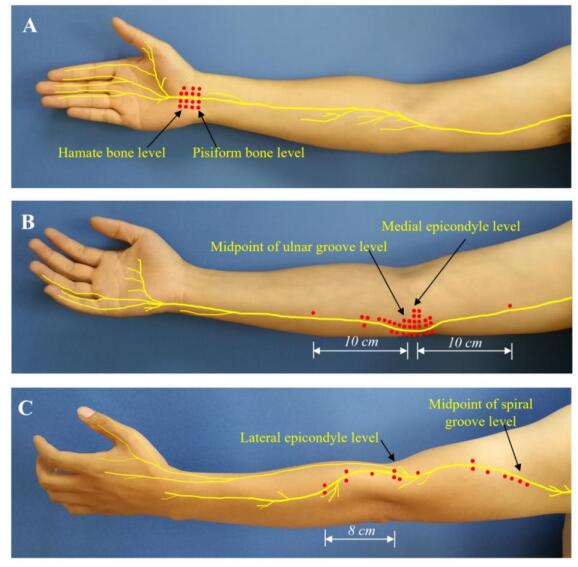
The sites with maximal CSASR in patients are presented in Table 6. The maximal CSASR in CTS patients is mainly located at the entrance of the carpal tunnel and mostly located near the elbow joint in the patients with CuTS. The distribution of the maximal CSASR values in RNC patients was random. The sites of each maximal CSASR were marked with red dots (Figure 3).

Table 6. Determination of lesion sites of the nerve (determinated by the maximal CSASR).

	Sites where maximal CSASR was obtained (%)	Ratio (%)
CTS	Carpal tunnel entrance	53.3
CuTS	The site between 1 cm proximal to U2 and U5	94.1
RNC	Scattered distribution	-

| Show Table

DownLoad: CSV

Figure 3. Distribution of the sites with maximal CSASR. (A) CTS. (B) CuTS. (C) RNC.

DownLoad: Full-Size Img PowerPoint

3.5. Typical cases

3.5.1. Typical case of CTS

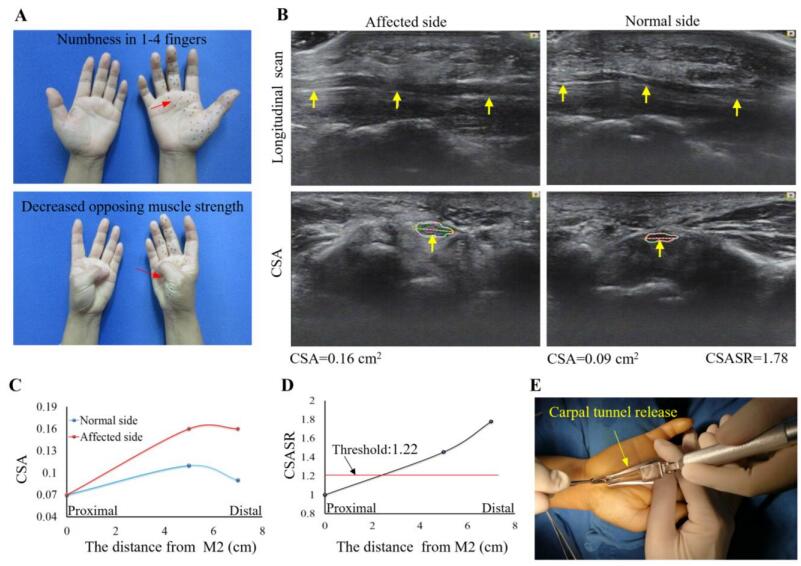
A case of right carpal tunnel syndrome is displayed in Figure 4. The patient was admitted due to right hand numbness and weak thumb movement for 1 year. Ultrasound examination revealed that the median nerve within the right carpal tunnel was significantly swollen compared to that in the left side. The maximal CSASR was 1.78 and was obtained at the midpoint of the carpal tunnel, i.e., the level of hamate bone. Surgical treatment was chosen because the CSASR was greater than the therapeutic threshold. The intraoperative findings confirmed that the affected nerve segment was confined to the nerve within the carpal tunnel, particular at the level of the midpoint of the carpal tunnel, with congested epineurium. The Swiss pushing knife was used to release the carpal tunnel during surgery. At the 10-week follow-up visit, the patient's symptom of numbness had subsided, and the thenar muscle strength increased from grade M3 to M4.

Figure 4. Typical case of CTS. (A) Patient with radial palmar numbness and decreased thenar muscle strength. (B) Comparison of longitude and cross section of the nerve at the level of the midpoint of the carpal tunnel between the affected and the normal side (Yellow arrows show median nerves). (C) Comparison of CSA at each ultrasound scanning section between the affected and the normal side. (D) CSASR at each ultrasound scanning section. (E) Carpal tunnel release by using a Swiss pushing knife.

DownLoad: Full-Size Img PowerPoint

3.5.2. Typical case of CuTS

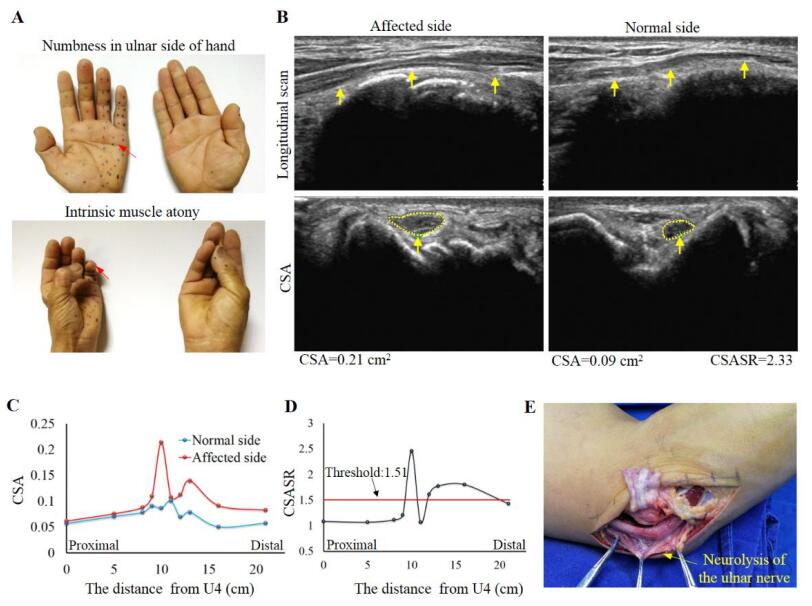
A case of left cubital tunnel syndrome is illustrated in Figure 5. The patient was admitted due to ulnar numbness of the left hand and weak fine movement for 4 months. An ultrasound examination showed that the left ulnar nerve at the elbow level was significantly swollen compared to that in the right side. The maximal CSASR was 2.33 and was obtained at the level of medial epicondyle. Surgical treatment was selected. Intraoperative findings showed that the ulnar nerve at the elbow level was swollen, particularly at the level of the medial epicondyle in which the nerve segment tissue was harder than the adjacent site. During the operation, ulnar nerve release was performed with the anterior transposition of the ulnar nerve under the fascia. The patient's symptom of hand numbness was immediately relieved after the postoperative anaesthetic effect subsided. At the follow-up visit 3 months after treatment, the patient's symptom of hand numbness was partially improved, and the strength of the intrinsic muscles of the hand increased from the grade M2 to M3.

Figure 5. Typical case of CuTS. (A) Patient with ulnar numbness of the left hand and decreased muscle strength of the intrinsic muscles of the hand. (B) Comparison of longitude and cross section of the nerve at the level of the medial epicondyle between the affected and the normalside (Yellow arrows show ulnar nerves). (C) Comparison of CSA at each ultrasound scans section between the affected and the normal side. (D) CSASR at each ultrasound scanning section. (E) The ulnar nerve release and preparation of performing the anterior transposition of the ulnar nerve under the fascia.

DownLoad: Full-Size Img PowerPoint

3.5.3. Typical case of RNC

A patient with right radial nerve compression is presented in Figure 6. The patient was admitted due to numbness of the first web of hand and disability of wrist, finger and thumb extension for 3 months. An ultrasound examination revealed that the radial nerve in the right spiral groove was significantly swollen compared to that in the left side. The maximal CSASR was 3.14 and was obtained at the level of the midpoint of the spiral groove. The CSASR was greater than the therapeutic threshold, and the diagnosis was confirmed. Surgical treatment was selected. The intraoperative findings showed that the middle segment of the upper arm of the radial nerve was swollen, particular at the level of the midpoint of the spiral groove in which the nerve segment tissue was harder than that in the adjacent site. Radial nerve release was performed. At the 4-month follow-up visit, the strength of the extensor carpi muscle and the extensor pollicis muscle increased from grade M0 to M2.

Figure 6. Typical case of RNC. (A) Patient with disability of extension of the right wrist, finger and thumb. (B) Comparison of longitude and cross section of the nerve at the level of the midpoint of the spiral groove between the affected and the normal side (Yellow arrows show radial nerves). (C) Comparison of CSA at each ultrasound scanning section between the affected and the normal side. (D) CSASR at each ultrasonic scanning section. (E) Radial nerve release.

DownLoad: Full-Size Img PowerPoint

4. Discussion

The establishment of a uniform standard for ultrasound examination of the peripheral nerve remains a challenge. This study has verified that there is a statistically significant difference in the CSA of the nerves between the affected and normal sides and demonstrated that the nerve in the patient's healthy limb can be used as a control for diagnosis ^[27,28,29]. According to the statistical analysis of 62 patients with entrapment neuropathy, the CSASR diagnostic and therapeutic thresholds for CTS, CuTS and RNC were determined. In terms of diagnosis, entrapment neuropathy can be diagnosed when the maximal CSASR of the nerve is greater than or equal to the diagnostic threshold, otherwise entrapment neuropathy is excluded. In terms of treatment, conservative treatment should be selected when the maximal CSASR of the nerve is less than the therapeutic threshold, otherwise surgical treatment is selected. The novel multilevel side-to-side image contrast ultrasonography proposed in this study can greatly reduce the impact of individual variation and can explore the full course of the diseased nerve. It is a novel approach for the diagnosis, treatment selection, and determination of treatment sites in patients with unilateral peripheral entrapment neuropathy.

Previous studies ^[26,30,31] have shown that inter-individual variation, intra-neural variation, and inter-neural variation exist. In normal subjects, the CSA at the same level of the median nerve, ulnar nerve, and radial nerve between the left and right sides is not significantly different, indicating a symmetry CSA of the bilateral nerves ^[27,32,33]. There was a statistically significant difference in CSA between the affected limb of patients with CuTS and the limb in normal control group ^[27]. But there was a statistically significant difference of CSA in the ulnar nerve between the normal side limb of patients and limb in normal control group; thus, it is controversial to use the patient's contralateral ulnar nerve as a control. The patient's normal side limb can be considered as a special part of asymptomatic limbs that tend to develop disease ^[28]. We verified that there was a statistically significant difference in CSA between the bilateral nerves of the patient and eliminated the controversy. Therefore the CSA of the normal side of patients could be used as a control for diagnosis.

The novel multilevel side-to-side image contrast ultrasound technique proposed in this study provides a series of continuous data that reflected the trend of nerve shape and could accurately locate and identify the sites of the lesion those were the sites to be treated. The range of ultrasound examination in this study can cover all common sites of entrapment neuropathy and will not miss the rare lesion sites, especially in patients with CuTS and RNC who have more variable nerve compression sites. Typical cases are shown in Figures 4–6. The CSASR data of all levels were calculated to plot the curve, the apex of which represents the site with the most severe lesion. Moreover, the segment of the compressed nerve that is greater than the diagnostic threshold can be determined by CSASR and is treated accordingly.

During the treatment, the accuracy of the ultrasound examination proposed in this study for localization of the lesion segment was comparable to that by using X-ray or CT examination before bone and joint surgery, though X-ray or CT techniques ^[34] are in some detections and diagnoses. In future, the three-dimensional reconstruction technology would be helpful for aiding diagnosis of peripheral entrapment neuropathy ^[35]. In this study, the diagnostic accuracy rate in the 62 patients was 92.9%, and the accuracy rate for selecting the treatment method was 87.1%. This indicates the relatively high accuracy of this method for determining treatment sites. In previous surgical treatments, the diseased nerve segment was approximately localized by electrophysiological examination or segmentary ultrasound examination. This may cause deviation of the surgical incision site. Before surgical treatment, the site of the surgical incision can be strictly localized by ultrasound guidance to reduce the trauma caused by the operation itself and to shorten the operative time. When using this technique for steroid injection, the steroid agent can be accurately delivered to the diseased region to improve its efficiency and reduce the amount of steroid agent injected into the ineffective treatment area.

Acknowledgements

This work was supported by Natural Science Foundation of China (NSFC) project grant (No. 81671928) and Australian National Health and Medical Research Council (NHMRC) Fellowship (No. 1158402).

Conflicts of interest

The authors declare no conflict of interest.

References

[1]	W. S. McCulloch, W. Pitts, A logical calculus of the ideas immanent in nervous activity, Bull. Math. Biophys., 5 (1943), 115-133.
[2]	A. Krogh, What are artificial neural networks?, Nat. Biotechnol., 26 (2008), 195-197.
[3]	A. Leśnia, M. Juszczyk, Prediction of site overhead costs with the use of artificial neural network based model, Arch. Civil. Mech. Eng., 18 (2018), 973-982.
[4]	S. Kaymak, A. Helwan, D. Uzun, Breast cancer image classification using artificial neural networks, Proc. Comput. Sci., 120 (2017), 126-131.
[5]	J. D. Sitton, Y. Zeinali, B. A. Story, Rapid soil classification using artificial neural networks for use in constructing compressed earth blocks, Constr. Build. Mater., 138 (2017), 214-221.
[6]	D. Valero, D. B. Bung, Artificial Neural Networks and pattern recognition for air-water flow velocity estimation using a single-tip optical fibre probe, J. Hydro. Environ. Res., 19 (2018), 150-159.
[7]	C. C. Lai, K. L. Su, Development of an intelligent mobile robot localization system using Kinect RGB-D mapping and neural network, Comput. Electr. Eng., 67 (2018), 620-628.
[8]	O. Erkaymaz, M. Ozer, M. Perc, Performance of small-world feedforward neural networks for the diagnosis of diabetes, Appl. Math. Comput., 311 (2017), 22-28.
[9]	N. Wan, W. X. Shi, S. S. Fan, S. X. Liu, PSO-FNNbased vertical handoff decision algorithm in heterogeneous wireless networks, Proc. Environ. Sci., 11 (2011), 55-62.
[10]	A. A. Hameed, B. Karlik, M. S. Salman, Back-propagation algorithm with variable adaptive momentum, Knowl. Based Syst., 114 (2016), 79-87.
[11]	D. J. Montana, L. Davis, Training feedforward neural networks using genetic algorithms, Proceedings of the 11th International Joint Conference on Artificial Intelligence, 1989. Available from: https://www.ijcai.org.
[12]	C. Reale, K. Gavin, L. Librić, D. Jurić-Kaćunić, Automatic classification of fine-grained soils using CPT measurements and Artificial Neural Networks, Adv. Eng. Inf., 36 (2018),207-215.
[13]	W. Li, Improving particle swarm optimization based on neighborhood and historical memory for training multi-layer perceptron, Information, 9 (2018), 16.
[14]	S. Gambhir, S. K. Malik, Y. Kumar, PSO-ANN based diagnostic model for the earl detection of dengue disease, New Horiz. Trans. Med., 4 (2017, 1-8.
[15]	S. Z. Mirjalili, S. Saremi, S. M. Mirjalili, Designing evolutionary feedforward neural networks using social spider optimization algorithm, Neural Comput. Appl., 26 (2015),1919-1928.
[16]	E. Uzlu, M. Kankal, A. Akpınar, T. Dede, Estimates of energy consumption in Turkey using neural networks with the teaching-learning-based optimization algorithm, Energy, 75 (2014), 295-303.
[17]	I. Aljarah, H. Faris, S. Mirjalili, Optimizing connection weights in neural networks using the whale optimization algorithm, Soft Comput., 22 (2016), 1-15.
[18]	P. A. Kowalski, S. Łukasik, Training neural networks with Krill Herd algorithm, Neural Process. Lett., 44 (2016), 5-17.
[19]	D. A. Alboaneen, H. Tianfield, Y. Zhang, Glowworm swarm optimization for training multi-layer perceptrons, Proceedings of the Fourth IEEE/ACM International Conference on Big Data Computing, Applications and Technologies, 2017. Available from: https://dl.acm.org/doi/abs/10.1145/3148055.3148075.
[20]	A. A. Heidari, H Faris, I Aljarah, S Mirjalili, An efficient hybrid multilayer perceptron neural network with grasshopper optimization, Soft. Comput., 23 (2019), 7941-7958.
[21]	E. Valian, S. Mohanna, S. Tavakoli, Improved cuckoo search algorithm for feedforward neural network training, Int. J. Artif. Intell. Appl., 2 (2011), 36-43.
[22]	C. Blum, K. Socha, Training feed-forward neural networks with ant colony optimization: an application to pattern classifcation, Fifth International Conference on Hybrid Intelligent Systems (HIS'05), 2005. Available from: https://ieeexplore.ieee.org/abstract/document/1587754.
[23]	K. Socha, C. Blum, An ant colony optimization algorithm for continuous optimization: Application to feed-forward neural network training, Neural Comput. Appl., 16 (2007), 235-247.
[24]	D. Karaboga, B. Akay, C. Ozturk, Artifcial Bee Colony(ABC) optimization algorithm for training feed-forward neural networks, Proceedings of the International Conference on Modeling Decisions for Artifcial Intelligence (MDAI '07), 2007. Available from: https://link.springer.com/chapter/10.1007/978-3-540-73729-2_30.
[25]	S. Mirjalili, How effective is the Grey Wolf optimizer in training multi-layer perceptions, Appl. Intell., 43 (2015),150-161.
[26]	M Branch, A multi-layer perceptron neural network trained by invasive weed optimization for potato color image segmentation, Trends Appl. Sci. Res., 7 (2012), 445-455.
[27]	D. H. Wolpert, W. G. Macready, No free lunch theorems for optimization, IEEE Trans. Evol. Comput., 1 (1997), 67-82.
[28]	S. Mirjalili, A. Lewis. The whale optimization algorithm, Adv. Eng. Soft., 95 (2016), 51-67.
[29]	M. Abdel-Basset, A. N. Hessin, L. Abdel-Fatah, A comprehensive study of cuckoo-inspired algorithms, Neural Comput. Appl., 29 (2018), 345-361.
[30]	A. A. Heidari, P. Pahlavani, An efficient modified grey wolf optimizer with Lévy flight for optimization tasks, Appl. Soft. Comput., 60 (2017), 115-134.
[31]	S. W. Lin, Z. J. Lee, K. C. Ying, C. Y. Lee, Applying hybrid metaheuristics for capacitated vehicle routing problem, Expert. Syst. Appl., 36 (2009), 1505-1512.
[32]	J. Chen, B. Xin, Z. Peng, L. Dou, J. Zhang, Optimal contraction theorem for exploration-exploitation tradeoff in search and optimization, IEEE Trans. Syst. Man Cybern. Part A Syst. Hum., 39 (2009), 680-691.
[33]	R. Li, S. Hu, Y. Wang, M. Yin, A local search algorithm with tabu strategy and perturbation mechanism for generalized vertex cover problem, Neural Comput. Appl., 28 (2017), 1775-1785.
[34]	N. H. Awad, M. Z. Ali, P. N. Suganthan, R. G. Reynolds, CADE: a hybridization of cultural algorithm and differential evolution for numerical optimization, Inf. Sci., 378 (2017), 215-241.
[35]	M. El-Abd, M. Kamel, A taxonomy of cooperative search algorithms, Int. Workshop Hybrid Metaheuristics, 36 (2005), 32-41.
[36]	V. K. Ojha, A. Abraham, V. Snášel, Metaheuristic design of feedforward neural networks: a review of two decades of research, Eng. Appl. Artif. Int., 60 (2017), 97-116.
[37]	P. Sarkar, N. M. Laskar, S. Nath, K. L. Baishnab, S. Chanda, Offset voltage minimization based circuit sizing of CMOS operational amplifier using whale optimization algorithm, J. Inf. Optim. Sci., 39 (2017), 1-17.
[38]	R. V. Rao, V. J. Savsani, D. P. Vakharia, Teaching-learning-based optimization: A novel method for constrained mechanical design optimization problems, Comput. Aided Des., 43 (2011), 303-315.
[39]	W. Spendley, G. R. Hext, F. R. Himsworth, Sequential application of simplex designs in optimisation and evolutionary operation, Technometrics, 4 (1962), 441-461.
[40]	A. A. Heidari, P. Pahlavani, An efficient modified grey wolf optimizer with lexvy flight for optimization tasks, Appl. Soft. Comput., 60 (2017),115-134.
[41]	J. Villanueva, Kolmogorov theorem revisited, J. Differ. Equations, 244 (2008), 2251-2276.
[42]	H. Samet, F. Hashemi, T. Ghanbari, Minimum non detection zone for islanding detection using an optimal Artificial Neural Network algorithm based on PSO, Renewable Sustainable Energy Rev., 52 (2015), 1-18.
[43]	D. A. Alboaneen, H. Tianfield, Y. Zhang, Glowworm swarm optimisation for training multi-layer perceptrons, Proceedings of the Fourth IEEE/ACM International Conference on Big Data Computing, Applications and Technologies, 2017. Available from: https://dl.acm.org/doi/abs/10.1145/3148055.3148075.
[44]	S. Z. Mirjalili, S. Saremi, S. M. Mirjalili, Designing evolutionary feedforward neural networks using social spider optimization algorithm, Neural Comput. Appli., 26 (2015), 1919-1928.
[45]	I. Aljarah, H. Faris, S. Mirjalili, Optimizing connection weights in neural networks using the whale optimization algorithm, Soft Comput., 22 (2016), 1-15.
[46]	H. Wu, Y. Zhou, Q. Luo, M. A. Basset, Training feedforward neural networks using symbiotic organisms search algorithm, Comput. Intell. Neurosci., 2016 (2016).
[47]	J. Derrac, S. García, D. Molina, F. Herrera, A practical tutorial on the use of nonparametric statistical tests as a methodology for comparing evolutionary and swarm intelligence algorithms, Swarm Evol. Comput., 1 (2011), 3-18.
[48]	J. Li, Q. Luo, L. Liao, Y. Zhou, Using spotted hyena optimizer for training feedforward neural networks, International Conference on Intelligent Computing, 2018. Available from: https://link.springer.com/chapter/10.1007/978-3-319-95957-3_88.

This article has been cited by:

1.	Mansoureh Mamarabadi, John A. Morren, Steven J. Shook, Enhancing diagnostic accuracy using a side‐to‐side cross‐sectional area ratio for the diagnosis of unilateral ulnar mononeuropathy at the elbow, 2021, 0148-639X, 10.1002/mus.27178
2.	Jonelle M. Thomas, Eric Y. Chang, Alice S. Ha, Roger J. Bartolotta, Matthew D. Bucknor, Jamie T. Caracciolo, Karen C. Chen, Jonathan Flug, Manickam Kumaravel, Noah M. Raizman, Andrew B. Ross, Matthew L. Silvis, Devaki Shilpa Surasi, Francesca D. Beaman, ACR Appropriateness Criteria® Chronic Elbow Pain, 2022, 19, 15461440, S256, 10.1016/j.jacr.2022.09.022
3.	James E. Gardner, Hannah Jones, Eric R. Wagner, Robert L. Bowers, Ultrasound Diagnosis of Upper Extremity Peripheral Entrapment Neuropathies, 2024, 12, 2329-9185, 10.2106/JBJS.RVW.24.00099
4.	Miao Yu, Wenquan Ding, Guoqing Shao, Miaozhong Li, Xiaoling Zhou, Linhai Liu, Xueyuan Li, Application of a nerve stereoscopic reconstruction technique based on ultrasonic images in the diagnosis of neuralgic amyotrophy, 2023, 14, 1664-042X, 10.3389/fphys.2023.1201275
5.	Miao Yu, Wenquan Ding, Guoqing Shao, Miaozhong Li, Xiaoling Zhou, Linhai Liu, Xueyuan Li, Ultrasound‐Based Multi‐Planar Bilateral Comparisons as a Diagnostic and Treatment‐Definition Method for Unilateral Peripheral Nerve Entrapment, 2024, 43, 0278-4297, 1883, 10.1002/jum.16521

Reader Comments

Your name:*

Email:*
© 2020 the Author(s), licensee AIMS Press. This is an open access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0)