This study proposes a multi-objective mixed integer linear programming (MOMILP) model for assigning a set of flights to different runways and determining their actual arrival and departure times. The proposed model envisages unique operation model of each runway (i.e., takeoff, landing, or mixed takeoff and landing). Further, interference in two flights between adjacent runways are also fully considered in this model. The work aims at reveal the optimal relationship between traffic stream characteristics, operation mode of each runway and flight scheduling to simultaneously minimizing flight delays and maximizing runway utilization. Since the problem of interest has a non-deterministic polynomial (NP-hard) complexity, a heuristic-based non-dominated sorting genetic algorithm (NSGA-Ⅱ) is also presented to find Pareto-optimal solutions in a reasonable amount of time, where coding structure and heuristic algorithm for producing initial population are defined. Finally, a real-world example is provided to compare the difference in quality between the proposed and traditional models, and reveal changes in trends between delay time of flights and idle time of the runways, which can verify the correctness of the model.
1.
Introduction
Aircraft arrival and departure scheduling (AADS) aims at assigning a set of flights to different runways and determining their actual arrival or departure times to improve operational efficiency. Due to different starting and occupation time of each flight, related with aircraft type (i.e., light, medium and heavy plane) and flight type (i.e., takeoff, landing), an unreasonable assignment of trips to runway may lead to idle runway and its queues for flights to take off or land at the same time [1]. Further, as the number of flights arriving exceeds the capacity of the airport's runway, it would cause an increase in delays. It is important to find optimal relation between the flight delay and improve runway utilization by reasonably scheduling flights of multiple runways [2,3]. Therefore, it has attracted wide attention from domestic and foreign scholars.
At present, most of the small airports have only one runway because of their low traffic flow, all planes of flights take off or land on the same runway [4]. Due to the origin or destination of each flight being different, some conflicts between their paths from the airport to in-out waypoints are existing, resulting in not only safety problems, but also efficiency problems. When the traffic flow increases, such problems of single-runway airport become more and more serious. Hence, some airports with large traffic flow have built and operated multiple runways for the landing and take-off of aircraft. In multiple runways of an airport, some runways are only used to taking off aircraft, part of them are dedicated to landing aircraft, to avoid the above phenomenon. According to the arrival rate of arrival and departure flights, how to determine the operation mode of each runway and its aircraft arrival and departure scheduling is a new research problem, which is much more complicated than traditional problems. However, few existing studies address this issue [2,3,4,5].
Another motivation for this paper is to study AADS with consideration of conflict between two aircrafts on adjacent runways. If the distance between two runways is short, they are not independent operation. When an aircraft takes off or lands on a runway, it makes some vortexes in aircraft wakes, which not only affects the takeoff or landing of the rear aircraft of the same runway, but also restricts the takeoff or landing of the aircraft of short-distance adjacent runway at same time. Compared with the traditional model, the study will reduce the capacity of the runway, but the operation is safe and practical. At present, domestic and foreign scholars also pay little attention to this issue [3,6,7].
The major contribution of this study is to propose a MOMILP model for AADS in order to reveal optimal relation between flight delays and runway utilization. The main contents in the paper are as follows: (1) Coordination of assignment of flights to runways and their arrival or departure time guidance process by considering type of each flight matching unique operation model of each runway and interference in two flights between adjacent runways; (2) a heuristic-based NSGA-Ⅱ algorithm is developed by defining coding structure and heuristic algorithm for producing initial population to efficiently find a set of Pareto-optimal solutions. Finally, a numerical example is provided to illustrate the effectiveness of proposed model.
The rest of this study is described as follows. Section 2 introduces the latest literatures at home and abroad and summarizes their shortcomings. The research framework is described and the mathematical model is given in section 3. The detail of NSGA-Ⅱ to resolving proposed model is given in section 4. A real numerical example is given to prove the applicability of this study in section 5. Some conclusions of my work, some critical remarks and possible future developments are discussed in section 6.
2.
Review of literature
In the last decades, the AADS is a well-established and significant study problem of assigning all flights to different runways in the landing and taking-off procedures [5]. There are many variants of the AADS, involving different objectives and constraints, include: cost, delay and fairness. However, those differences in variants of the AADS don’t usually change the properties of the AADS, which lead to the use of existing formulations and solution methods to study them. Bianco et al. [6] has proved that the AADS with consideration of delay penalty costs being aircraft-dependent is a NP-hard problem. Further, Briskorn and Stolletz [7] has also proved that the problem is polynomial in the number of runway operations but exponential in the number of runways and operation classes under these assumptions of delay penalty costs being operation class-dependent.
In the early days, most airports had only one runway. The AADS with single runway (AADS-SR) was proposed by Dear [8] and Psaraftis [9], where few factors lead to that the research has been relatively mature. With the popularity of multi-runway airports in recent years, AADS-SR was then extended by Hansen [10], Pinol and Beasley [11], Salehipour et al. [12], and Liu [13] to consider multiple runways (AADS-MR). In AADS-MR, most of them has assumed independent runways to neglect runway-dependent earliest operation times, and few of them has considered interdependent runways by repeating some operation times for all separated pairs of runways [14,15,16]. However, none of the studies have considered interdependent runways in their numerical studies. These models were the static or the dynamic ones. In the static AADS, landing/departing flights are assigned to different runways, and sequenced by their start times in advance. In general, some mixed-integer models were developed for dealing with two cases of AADS-SR and AADS-MR, and their solutions were then solved using exact and heuristic algorithms [10,17,18]. In the dynamic AADS, an uncompleted set of landing/departing flights must be reassigned and sequenced using the First in First Out (FIFO) rule when a future incoming aircraft enter the system at every time [6,17,18]. All above studies adopted one of accurate formulations of the AADS, i.e., job shop scheduling model [16,21,22] and the alternative graph model [6]. When the AADS is generally viewed as a job shop scheduling plus additional constraints, each runway represents a machine and each flight denotes a job. Differently from AADS based on job shop scheduling, the microscopic representation of the alternative graph has taken air traffic regulations into account [3].
Their solution methods could be fallen into three categories, i.e., mixed-integer programming (MIP), dynamic programming (DP), and branch- & -price (BP). The MIP approaches aims at building a mathematical optimization model for the AADS, which can be solved by using a standard solver, such as CPLEX. The most cited MIP model was proposed by Beasley et al. [18], and reformulated by, e.g., Farhadi et al. [21] and Ghoniem and Farhadi [23,24] to tighten these models. However, this method cannot yield the solutions for big problem instances quickly. DP approaches have been used by, e.g., Balakrishnan and Chandran [25], Harikiopoulo and Neogi [26], Furini et al. [22], Lieder et al. [27] to deal with the AADS in fast computation times. All of them only study a DP approach for the time-indexed AADS-SR, except for AADS-MR of Lieder et al. [27]. However, they must follow some additional assumptions which is done to simplify the underlying models. In BP approaches, the underlying problem is divided into several subproblems which use single-runway problems as subproblems to generate columns [24]. Hence, this approach cannot be used to solve AADS with interdependent runways. Compared with BP approaches, DP approaches can offer a better chance for generalization of AADS with more new constraints such as general runway configurations.
A review of literature on AADS revealed the following critical issues, which deserve further investigations:
(1) Most studies have assumed that all operations of aircraft take-off or landing can be executed on all runways. From the safety perspective of aircraft entry and exit procedures in AADS-MR, some runways can be specially used for aircraft taking off or landing, and some runways can be used for both taking off and landing [2,3].
(2) Most studies have neglected heterogeneous or interdependent runways in AADS-MR [10,11,12,13,28]. In this case, there are at least a minimum diagonal separation delay between adjacent aircrafts on two-runway systems with interdependent runways.
(3) In AADS, flight delays minimization and runway utilization maximization are two favorable objectives. Since AADS is known as an NP-hard problem, a multiple-objective heuristic algorithm should be used to efficiently find a set of Pareto solutions to reveal optimal relation between them [29,30].
3.
Methodology
3.1. Research framework
An airport has multiple runways, where operation model of each runway is unique, i.e., one of three operation models, including takeoff, landing, or mixed takeoff and landing runway. There are some arrival and departure flights assigned to these different runways. Obviously, arrival flights must be assigned to one of landing and mixed runway, while departure flights should only be assigned to takeoff or mixed runway. Each flight has a planned starting and ending time occupying the runway, depending on the type of aircraft and the type of flight. If two adjacent flights are served by the same runway, the ending time of the previous flight plus wake vortex time of the front aircraft is less than the starting time of the next flight. Wake vortex time is decided by aircraft type of each flight and the type of takeoff or landing for these two flights. Further, if two flights from these runways take off or land at the same time, they affect each other, when the distance between adjacent runways is small. In this case, headway time between two aircraft must be greater than interval for the interference in these two runways. The main aim of this study is to assign a set of flights to different runways, route each runway to allow each flight to take off or land in sequence, and determining their actual arrival and departure times. A MOMILP model for this study is presented to simultaneously minimize flight delays and maximize runway utilization. To deal with real-life situations, this study will follow some assumptions:
(1) Each flight must be only assigned to a runway, and all of them cannot be modified.
(2) The wake time affected by the front plane to the rear plane can be estimated.
(3) The difference in arrival and departure flights only lies in their maximum delay time.
(4) The effect of the capacity of the approach point on arrival and departure flight scheduling is neglected.
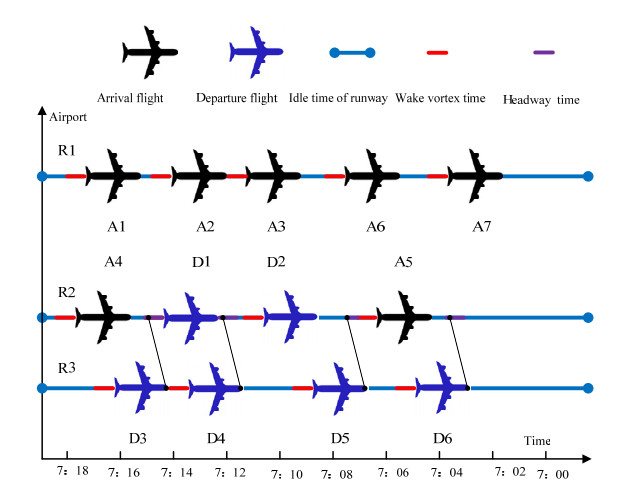
To clearly explain the underlying principles of the proposed model, a small example consisting of three runways (R1-R3), seven arrival flights (A1-A7), and six departure flights (D1-D6) is shown in Figure 1. The runway R1 is only used for landing of an aircraft, the runway R2 is used for both of takeoff and landing of an aircraft, and the runway R3 is only used for takeoff of an aircraft. There are three generated flight tasks that takes off or lands on their runways in the optimization process, i.e., [A7-A6-A3-A2-A1], [A5-D2-D1-A4], and [D6-D5-D4-D3]. For example, flight A5 is completed on runway R2 at 7:06. After one-minute wake cortex and idle time of the preceding aircraft (A5) on the same runway and one-minute headway time of another aircraft (D5) on an affected runway (R3), flight D2 is started at 7:09. Similarly, the starting times of two flights D1 and A4 are 7:12 and 7:16, and their ending times are 7:17 and 7:18. In this case, each objective function of all runway tasks can be calculated easily.
3.2. Model formulation
3.2.1. Notations
To facilitate model presentation, all definitions and notations used hereafter are summarized in Table 2.
3.2.2. Formulation
The proposed problem can be formulated as the following MOMILP model, which requires minimization of:
which is subject to:
In this formulation, the objective function (1) aims at minimizing total delay time for all flights. The objective functions (2) aim at minimizing total idle time for all runways. Constraint (3) guarantees that each arrival flight would be assigned landing to or mixed runway. Constraint (4) is used to assign each departure flight to takeoff to or mixed runway. Constraint (5) guarantees that the actual arrival or departure time of a flight does not exceed the maximum delay time. Constraint (6) and (7) set all flights (except virtual flight) being served by each runway to have the same incoming and outgoing arcs. Constraint (8) is used for the sub-tour elimination of flight tasks in the runway. Constraints (9) guarantees ending time of the previous flight plus the minimum safety interval time is not earlier than starting time of next flight. Constraint (10) is used for calculating wake cortex time of adjacent flights. Constraints (11) is used for avoiding flight conflicts between adjacent runways.
4.
Heuristic-based NSGA-Ⅱ
Since this study is an NP-hard problem with two conflicting objectives, many evolutionary algorithms and metaheuristics [31,32,33,34,35,36] could be used to find a set of Pareto-optimal solutions in a short time, due to the exact algorithm not solving the large-scale problem quickly. The NSGA-Ⅱ, as one of the most popular evolutionary multi-objective optimization algorithms, is a fast non dominated sorting algorithms based on the NSGA, by introducing crowding of solutions for different targets, which improve the computational efficiency and robustness of the algorithm [29,30,36,37,38]. In this study, a hybrid intelligent algorithm based on NSGA-Ⅱ is designed to solve proposed model, which defines chromosome code, heuristic algorithm for generating initial population, etc. The details are described as follows.
4.1. Chromosome coding
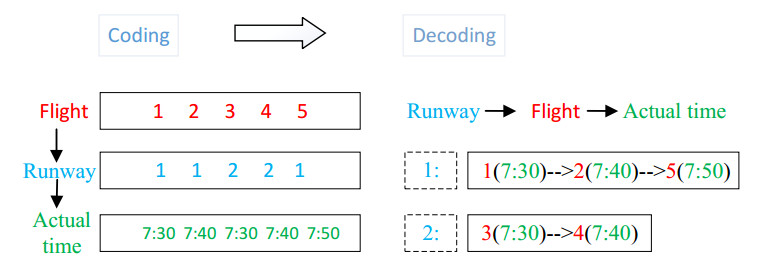
As above mentioned, the core of solving the problem lies in three variables xri、zrij and tai, where xri and tai determines zrij. Using integer encoding, the two-dimensional vector U=(U1,U2) is used to represent each solution of the problem, where the element ui of U1=(u1,u2,…,uF) denotes assigned runway of flight i, ranging from 1 to R, the element ui of U2=(uF+1,uF+2,…,u2F) denotes actual arrival or departure time of flight i. For example, seen from Figure 3, one chromosome X = {11221 7:30 7:40 7:30 7:40 7:50} of five flights and two runways can be decoded as: flights 1, 2 and 5 are assigned to runway 1 and their times are 7:30, 7:40 and 7:50; flights 3 and 4 are assigned to runway 2 and their times are 7:30 and 7:40.
4.2. Heuristic algorithm for generating initial population
The quality of the initial population determines the solution quality. Due to the overlap of the time window of any two adjacent flights assigned to a runway, the probability of generating a feasible solution is low. Therefore, the heuristic algorithm is used to generate the feasible solution to create the initial population. The specific steps are as follows:
Step 1: All flights ∀i∈F are sorted according to tpi, and let the result be F"′={F"1,F"2,…,F"|F|}′.
Step 2: Set the set of runways that could complete all flights F". Let i=1.
Step 3: Find set vR of feasible runways to complete flight F"i. If vR≠∅, randomly select a runway∀r∈vR to run flight F"i, and turn to step4; otherwise, turn to step2.
Step 3.1: Let vR=∅.
Step 3.2: Find any runway ∀r∈R that matches the flight type, and obtain its last flight lF(r).
Step 3.3: Check whether the runway can continue to run flight F"i after the completion of the flight lF(r). If one of the following conditions is met: ①lF(r)=∅, ②talF(r)+thlF(r)+max(T1lF(r)F"i,T2lF(r)F"i)≤taF"i, let vR=vR∪{r}.
Step 4: Let i=i+1, if i≤|F|, turn to step3; otherwise, output the result and the algorithm is terminated.
4.3. Non-dominated sorting
4.3.1. Non-dominated sorting
Step 1: Let the set and quantity of dominated individuals for a solution ∃x∈P be Sx=∅ and nx=0, respectively. For any solution∀q∈P, if q≻x, Sx=Sx∪{q}; otherwise, nx=nx+1.
Step 2: Let Q=∅,xrank=1 and i=1, F1={x|nx=0,∀x∈P}.
Step 3: For ∀q∈Sx of ∀x∈Fi, nq=nq−1. If nq=0, qrank=i+1 and Q=Q∪{q}.
Step 4: If Q≠∅, i=i+1 and Fi=Q, turn to step 3;otherwise, output the result and the algorithm is terminated.
4.3.2. Crowding distance
For each objective function, the average edge length εm(xi) of individual xi between adjacent individualsxi−1andxi+1is calculated, according to the order of the objective value of all individuals. Crowded distance of individualxiis calculated by using Distance(xi)=∑Mm=1εm(xi) to depict the intensity of surrounding other individuals, where M is the number of target functions.
4.3.3. Selection operator
The aims of selecting individuals is to distribute Pareto solutions evenly by following two rules: ① If and only if irank<jrank and i≻nj, ② irank=jrank and Distance(xi)>Distance(xj). For any two individuals, if their non-dominant order is different, take the individuals with low order, otherwise an individual with a small crowding distance would be selected.
4.4. Algorithm process
The detail steps of NSGA-Ⅱ are shown as follows:
Step 1: Set the algorithm parameters, including: chromosome number N, maximum number of iterations Niter, crossover and mutation rate.
Step 2: Let t = 0, and randomly generate an initial population P0.
Step 3: Selection, variation and crossover operations of populationRt are carried out to produce the descendant population Qt. Let Rt=Pt∪Qt, turn to the step 4.
Step 4: Calculate the nondominant order and crowding distance of 2N individuals of Rt, and a total of N individuals would be selected to generate a new population Pt+1 according to their ranks.
Step 5: t=t+1. If t≥Niter, output the result and the algorithm is terminated; otherwise, turn to Step3.
5.
Numerical example
5.1. Example description
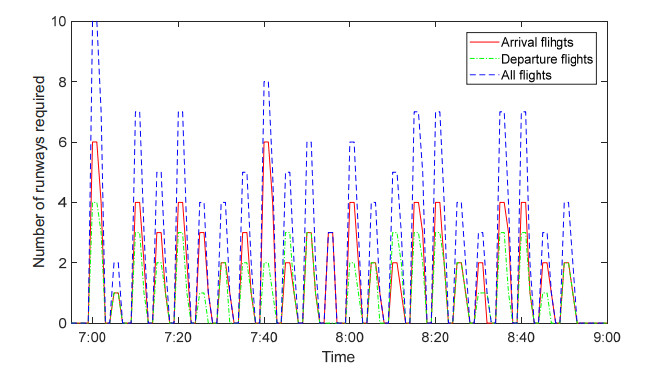
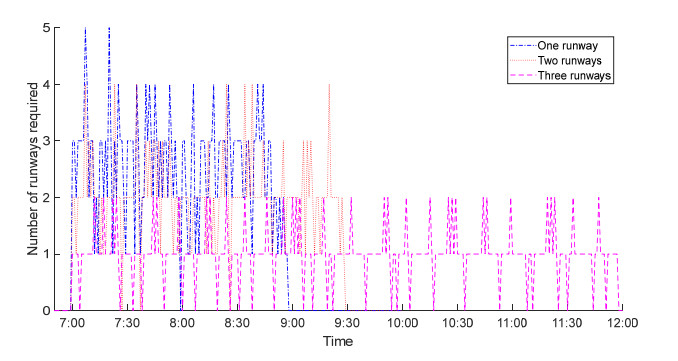
In this section, a real-word example of flight scheduling in an airport in China during 7:00 and 9:00 is described to prove the applicability of the proposed model. There are 72 arrival flights and 51 departure flights during 7:00 and 9:00 in a day. Their aircraft types mainly involve light and medium - sized planes. According to the planned take-off or landing time of all flights, the number of runways required by these flights in different time periods is shown in Figure 3. Because the number of runways required in most of the time is greater than the actual number of runways at the airport, most flights must queue for takeoff or landing, which causes these flights to be delayed widely. In order to reduce the large area of flight delay, the aim of this study is to balance flight delays and runway utilization, by coordinating optimization process of the operation mode of each runway, assignment of flights to runways and their arrival and departure times. The solutions are obtained using NSGA-Ⅱ. The key parameters used in the case study are given as follows:
● Maximum delay time of each flight:di = 480min.
● Wake cortex time of adjacent flights:T1ij = 1min (∀i,j∈F)
● Safe span time of adjacent flights covered by a controller:T2ij = 2min (∀i,j∈F)
● Affected time between two flights on adjacent runways:T12= 1min, T13=T23= 0min.
● Related parameters of NSGA-Ⅱ: maximum number of iterations 500, number of chromosomes 500, crossover probability 0.8, mutation probability 0.05 and shared radius 0.05.
5.2. Results and discussion
One of the aims of the study is to reveal influence of different combination of runways operation modes on result. We analyze the difference between the traditional model and the present model under different number of runways. The results are shown in Table 3, from which it can be seen that:
(1) With the increase in the number of runways, the delay time of flights is gradually decreased and the idle time of runways is also increased. When the number of runways is 1, the idle time of runways is 0 because the number of runways required in all time periods is less than the actual value. Similarly, when the number of runways is more than 1, it is greater than the number of runways required in some periods, resulting in runway idle phenomenon in some time periods.
(2) For the same number of runways, as the number of arrival flights is greater than the number of departure flights, the more the number of mixed and special landing runways, the less the delay time of the flight and the idle time of the runway (i.e., the runway utilization efficiency is high). Therefore, the operation mode of each runway should be reasonably determined by flight type and arrival rate of all flights to reduce their delays, excepting for considering flights conflicts. According to the flight type and space distribution of the airport, the operation mode of the runway should be reasonably determined to reduce the flight delay.
Another aim of this study is to reveal influence of flight conflicts between adjacent runways on result. The difference in model performance between the traditional model and the present model is also analyzed under different number of runways. The results are shown in Table 4, from which it can be seen that:
(1) When there is only one runway, the results of these two models are consistent because there is no interference between adjacent runways.
(2) As the number of runways more than two increases, since the landing and taking-off procedures of all flights in a runway are not interfered with by other runways, the runway idle time of the traditional model is always kept at zero. Meanwhile, the increase in the number of runways has led to fewer queues for flights to take off or land, so delays of the traditional model have been gradually reduced.
(3) As the number of runways more than two increases, since the runway idle time of the improved model contains interference time, it is not zero. In addition, an increase in the number of runways has led to a decrease in the number of flights allocated to the runways, which resulted in a gradual decrease in the runway idle time of the proposed model.
(4) When adjacent runways are close to each other, in order to ensure the safe operation of each aircraft, disturbed runways require more idle time to avoid aircraft interference, which takes more time to complete the takeoff or landing of all flights, resulting in increased flight delays. Although the delay time of proposed model is more than traditional one, it is more in line with the actual control operation process.
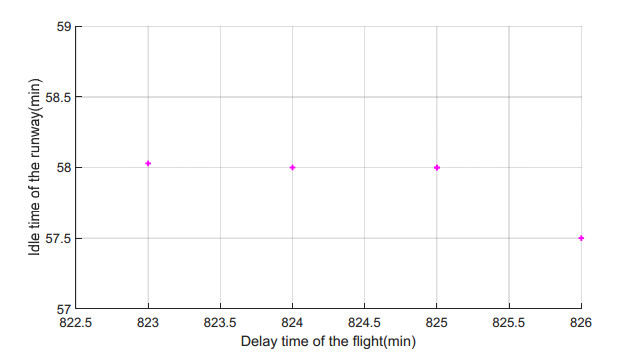
As above mentioned, the total delay times of all flights are the least, when all the runways are mixed takeoff and landing mode. Taking three mixed runways as an example, four Pareto solution is sought to reveal the trends in change relationship between flight delay time and runway idle time. As shown in Figure 4, the upper and lower limits of flight delay time are 823 min and 826 min, and the upper and lower limits of runway idle time are 57.5 min and 58.2 min. The reduced idle time of the runways will gradually increase the delay time of the flights. This is because the runway's idle time will be reduced due to the further shortage of runway resources. In this case, there may be more flights queuing for takeoff or landing. The calculation results are in line with the intuitive analysis.
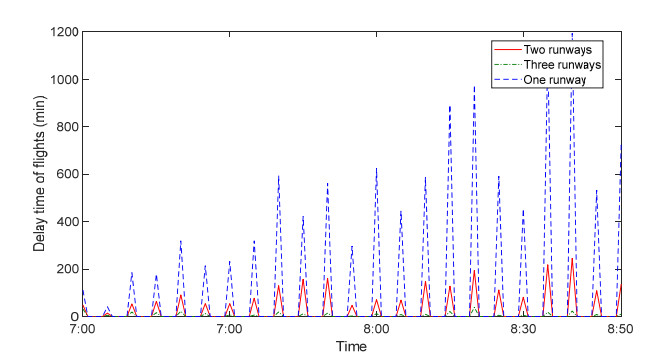
Figures 5 and 6 shows a comparative analysis of the number of runways occupied and delay time of all flights under different number of runways, respectively. The result shows:
(1) The number of runways required at different time periods is different. They are insufficient in some time periods, but wasted in other time periods. It is necessary to comprehensively optimize the flight schedule to make them take off or land evenly in each time period to reduce the delays.
(2) As the number of runways increases, the number of flights queuing for takeoff or landing decreases, so the total delay time of all flights is reduced;
(3) If the number of runways required is always greater than the actual number of runways at any time, the total delay time of flights will gradually spread as time goes on.
6.
Conclusions
In this paper, a novel MOMILP model is proposed for aircraft arrival and departure scheduling to reveal optimal relation between flight delays and runway utilization. Proposed model has features in different operating modes of multiple runways and flight conflicts between adjacent runways. Furthermore, wake cortex time and safe span time of a controller are incorporated into the proposed model in order to represent real-world conditions. Our model is infinitely close to reality, and the generated scheduling scheme can be applied in practice. A heuristic-based NSGA-Ⅱ is also designed to find a set of the meta-optimal solutions in a short time. The main findings can be summarized as follows:
(1) For the same number of runways, the reduction in total idle time of the runways will lead to an increase in total delay time of the flights.
(2) As the number of runways increases, the number of flights queuing for takeoff or landing decreases, which lead to increase of total idle time of runways and reduction in the total delay time of flights.
(3) If the operation modes of multiples runways should not match the spatial and temporal distribution of arrival and departure flights, the demand for some arrival or departure flights requesting for runways for taking off or landing aircrafts has not been met.
(4) When some flight conflicts between adjacent runways are considered, runway capacity would be decreased and flight delays would be also increased.
It can be seen from the above that our conclusion is in line with the value analysis, which is of great help to improve the operation efficiency of the runway. Note that the premise of this study is to a given fixed route from the runway to the airway point/gate, and ignores the influence of their route design on model performance. On the one hand, route design from the gate to a runway determines time of the plane arriving at the runway, which may cause planes to line up on the runway for takeoff or landing; on the other hand, route design from the runway to the airway point determines time of the plane passing through the airway point, which may cause the aircraft to hover in the air waiting for takeoff or landing. In this sense, the integrated operation of this study and routes design pay an important role in reducing flight delays and improving airport capacity. As a result, extending this model to simultaneously select routes from the runway to the airway point/gate is worth further study.
Acknowledgements
This study was financially supported by the Humanities and Social Sciences Foundation of the Ministry of Education of China (20YJCZH176); the Central College Basic Scientific Research Operating Expenses Fund of the Civil Aviation University of China (3122020079).
Conflict of interests
The authors declared that they have no conflicts of interest to this work.









 DownLoad:
DownLoad: