Search Advanced

AIMS Energy

2020, Volume 8, Issue 4: 686-700. doi: 10.3934/energy.2020.4.686
Previous Article Next Article
Research article Special Issues

Defining a new method to set certainty factors to improve power systems prognosis with fuzzy petri nets

  • 1.
    Department of Electrical Power Engineering, Tishreen University, Lattakia, Syria
  • 2.
    Department of Medical Engineering, Al Andalus University, Tartus, Syria
  • In power systems, faults are unavoidable events. They can cause disastrous problems to operations. In this study, we aim to reduce the bad effects resulting from these faults in order to raise the operation performance. Fuzzy petri nets (FPN) are very important tools used to diagnose and prognosis issues. However, they take constant certainty factors (CFs) and depend upon long-term statistical average values to describe initial places. A new method is introduced here to determine CFs and initial truth degrees in FPN, so they can reflect different operating states and adapt to any changes in conditions in order to improve the prognosis. For this purpose, we define new kinds of CFs in order to take various conditions into account and represent a wide range of their effects on the system. The main purpose of this study is to analyze the system operation at different states under different conditions to determine the state that may cause problems, and take convenient procedures to prevent them. The proposed method is applied on a reliability test system to show its ability to make the FPN model more flexible and cover a wide range of operation cases.

    Citation: R. S. Solaiman, T. G. Kherbek, A. S. Ahmad. Defining a new method to set certainty factors to improve power systems prognosis with fuzzy petri nets[J]. AIMS Energy, 2020, 8(4): 686-700. doi: 10.3934/energy.2020.4.686

    Related Papers:

    [1] Jun Gao, Qian Jiang, Bo Zhou, Daozheng Chen . Convolutional neural networks for computer-aided detection or diagnosis in medical image analysis: An overview. Mathematical Biosciences and Engineering, 2019, 16(6): 6536-6561. doi: 10.3934/mbe.2019326
    [2] Haiyan Song, Cuihong Liu, Shengnan Li, Peixiao Zhang . TS-GCN: A novel tumor segmentation method integrating transformer and GCN. Mathematical Biosciences and Engineering, 2023, 20(10): 18173-18190. doi: 10.3934/mbe.2023807
    [3] Tongping Shen, Fangliang Huang, Xusong Zhang . CT medical image segmentation algorithm based on deep learning technology. Mathematical Biosciences and Engineering, 2023, 20(6): 10954-10976. doi: 10.3934/mbe.2023485
    [4] Jinyun Jiang, Jianchen Cai, Qile Zhang, Kun Lan, Xiaoliang Jiang, Jun Wu . Group theoretic particle swarm optimization for gray-level medical image enhancement. Mathematical Biosciences and Engineering, 2023, 20(6): 10479-10494. doi: 10.3934/mbe.2023462
    [5] Tong Shan, Jiayong Yan, Xiaoyao Cui, Lijian Xie . DSCA-Net: A depthwise separable convolutional neural network with attention mechanism for medical image segmentation. Mathematical Biosciences and Engineering, 2023, 20(1): 365-382. doi: 10.3934/mbe.2023017
    [6] Mei-Ling Huang, Zong-Bin Huang . An ensemble-acute lymphoblastic leukemia model for acute lymphoblastic leukemia image classification. Mathematical Biosciences and Engineering, 2024, 21(2): 1959-1978. doi: 10.3934/mbe.2024087
    [7] Binju Saju, Neethu Tressa, Rajesh Kumar Dhanaraj, Sumegh Tharewal, Jincy Chundamannil Mathew, Danilo Pelusi . Effective multi-class lungdisease classification using the hybridfeature engineering mechanism. Mathematical Biosciences and Engineering, 2023, 20(11): 20245-20273. doi: 10.3934/mbe.2023896
    [8] Tingxi Wen, Hanxiao Wu, Yu Du, Chuanbo Huang . Faster R-CNN with improved anchor box for cell recognition. Mathematical Biosciences and Engineering, 2020, 17(6): 7772-7786. doi: 10.3934/mbe.2020395
    [9] Vasileios E. Papageorgiou, Georgios Petmezas, Pantelis Dogoulis, Maxime Cordy, Nicos Maglaveras . Uncertainty CNNs: A path to enhanced medical image classification performance. Mathematical Biosciences and Engineering, 2025, 22(3): 528-553. doi: 10.3934/mbe.2025020
    [10] Shen Jiang, Jinjiang Li, Zhen Hua . Transformer with progressive sampling for medical cellular image segmentation. Mathematical Biosciences and Engineering, 2022, 19(12): 12104-12126. doi: 10.3934/mbe.2022563
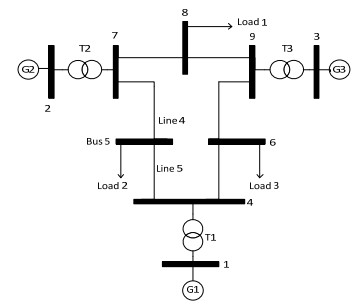
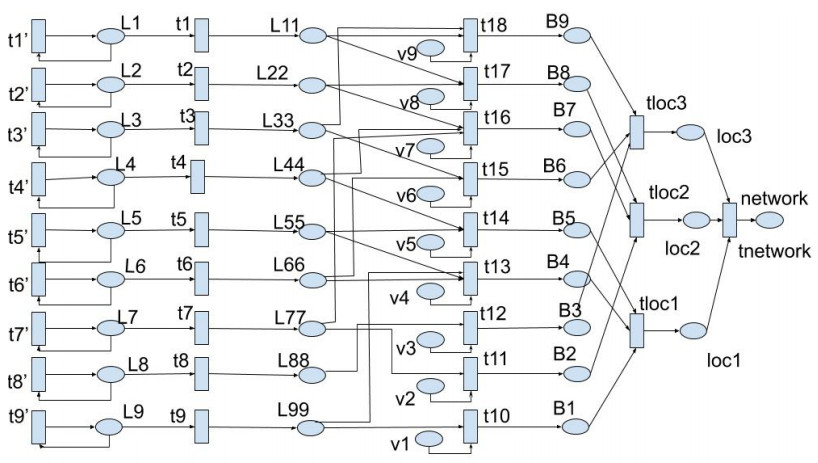
  • In power systems, faults are unavoidable events. They can cause disastrous problems to operations. In this study, we aim to reduce the bad effects resulting from these faults in order to raise the operation performance. Fuzzy petri nets (FPN) are very important tools used to diagnose and prognosis issues. However, they take constant certainty factors (CFs) and depend upon long-term statistical average values to describe initial places. A new method is introduced here to determine CFs and initial truth degrees in FPN, so they can reflect different operating states and adapt to any changes in conditions in order to improve the prognosis. For this purpose, we define new kinds of CFs in order to take various conditions into account and represent a wide range of their effects on the system. The main purpose of this study is to analyze the system operation at different states under different conditions to determine the state that may cause problems, and take convenient procedures to prevent them. The proposed method is applied on a reliability test system to show its ability to make the FPN model more flexible and cover a wide range of operation cases.


    1.   Introduction

    Breast cancer is one of the most common malignant tumors in women. In 2013, there were about 180 million new cases of female breast cancer in the world [1,2]. In China, the incidence rate of breast cancer in 2013 was 42.02/10 million, ranking the first place in the incidence of cancer in women, and the mortality rate was 9.74/10 million, ranking fifth in the female cancer death cause [3,4,5]. Breast cancer seriously endangers women's life and health, and brings huge economic burden to the family and society [6].

    At present, the traditional statistical methods to analyze the medical expenses and influencing factors of breast cancer include multiple linear regression, logistic regression analysis and so on [7,8,9,10]. Back propagation (BP) neural network is an artificial neural network model based on error back propagation [11]. Compared with traditional statistical methods, it has no special requirements for the type and distribution of data, and has some fault tolerance, so it has more advantages [12,13,14,15]. In recent years, BP neural network model and other data mining methods have also been applied to analyze the medical expenses of cancer patients such as gastric cancer, lung cancer, liver cancer, gynecological cancer and so on [16,17,18].

    In this study, the medical expenses of female breast cancer patients in rural areas of Anhui Province were selected as the research object. After the BP neural network model was constructed, the results were compared with the multiple linear model. The aim was to verify the effectiveness and predictive power of the two models for the influencing factors of medical expenses of breast cancer patients, so as to provide scientific theoretical basis for reasonable control of medical expenses of breast cancer.

    2.   Materials and methods

    2.1.   General data

    According to the data of cancer registration report in Anhui Province, the medical records of all female breast cancer patients diagnosed from 2017 to 2019 and coded as C50 according to ICD-10 disease code were collected from four county people's hospitals (Feidong, Feixi, Changfeng, and Lujiang) in Anhui Province, including hospitalization number, medical insurance number, medical payment method, operation, chemotherapy and radiotherapy; Medical insurance number, name, date of birth, disease diagnosis, total cost of hospitalization, hospital and other information were collected from social security department. A total of 846 samples were collected. All research variables were assigned values (Table 1). After the samples with missing values and illogicality were excluded, 795 cases were included in the study, and the effective rate was 93.97%.

    Table 1.  Study variable and its assignment table.
    Variable Code Value
    Region X1 1 = Feidong; 2 = Feixi; 3 = Changfeng; 4 = Lujiang
    Diagnosis year X2 1 = 2017; 2 = 2018; 3 = 2019
    Medical payment X3 1 = Rural insurance; 2 = Urban workers; 3 = Urban residents; 4 = Others
    Operation X4 1 = Yes; 2 = No
    Chemotherapy X5 1 = Yes; 2 = No
    Radiotherapy X6 1 = Yes; 2 = No
    Clinical stages X7 1 = Ⅰ; 2 = Ⅱ; 3 = Ⅲ; 4 = Ⅳ; 5 = Unknown
    Age (years) X8 1 = < 45; 2 = 45~59; 3 = 60~4; 4 = ≥ 75
    Length of stay (days) X9 Logarithm of the actual value
    Medical expenses Y1 Logarithm of the actual value
     | Show Table
    DownLoad: CSV

    2.2.   Back propagation neural network

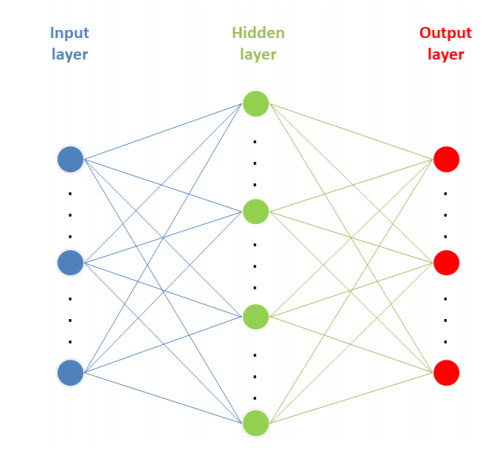
    BP neural network is the abbreviation of error back propagation neural network. It is a multilayer feedforward network trained by error back propagation algorithm. It is one of the most widely used neural network models at present. It is composed of an input layer, one or more hidden layers and an output layer. Each layer is composed of a certain number of neurons. Its structure is shown in Figure 1. First, the number of neurons in each layer is determined. The number of neurons in the input layer and the output layer is determined by the independent and dependent variables of the actual research. There is no unified calculation method for the number of neurons in the hidden layer. In this study, the formula (M represents the number of neurons in the hidden layer, n represents the number of neurons in the input layer, m represents the number of neurons in the output layer, and represents any value from 1 to 10) is used to calculate the number of neurons in the hidden layer. Secondly, network training. Through SSPS Clementine 12.0 software to simulate the training set, different BP neural network models are obtained. Finally, the network test is carried out. The test set is substituted into each model, and the model with the highest accuracy is the optimal model.

    Figure 1.  Structure of back propagation neural network model.
    DownLoad: Full-Size Img PowerPoint

    2.3.   Multiple linear regression

    Multiple linear regression is a regression analysis based on the given values of multiple explanatory variables. It is a method to study the linear relationship between a dependent variable and multiple independent variables [19]. The general form of multiple linear regression model is:

    Y=β0+β1x1+β2x2+β3x3+I+βixi+e (1)

    Where β0 is a constant term, I is the number of independent variables, βi (i = 1, 2… i) is partial regression coefficient, e is random error. The meaning of partial regression coefficient is the average change of dependent variable Y when the independent variable changes one unit while other independent variables remain unchanged. After the multiple linear regression parameters are obtained, it is necessary to carry out statistical tests to determine the reliability of the model performance, including the fitting test (coefficient of determination), the significance test of the overall linear equation (F test), the significance test of variables (t test), etc. [20].

    2.4.   Model evaluation method

    The performance of the two models is evaluated by the following indicators, where R2 is the coefficient of determination, which can explain the percentage of the independent variable explaining the change of the dependent variable. The value range is between 0 and 1. The closer the value is to 1, the better the fitting degree of the model to the sample is [21]. The absolute mean error (MAE) reflects the actual error of the model, and the root mean square error (RMSE) is the arithmetic square root of the mean square error (MSE). The calculation formula of each index is as follows.

    R2=1−∑ni=1(yi−^yl)2∑ni=1(yi−¯yl)2 (2)
    MAE=1n∑ni=1|∧yl−yi| (3)
    MSE=1n∑ni=1wi(yi−∧yi)2 (4)
    RMSE=√1n∑ni=1wi(yi−∧yi)2 (5)

    The predicted data of all patients were test by the normality test. The data both in back propagation neural network model and multiple linear regression model were consistent with normal distribution. After passing the homogeneity test, the difference between the two models were compared by t test.

    3.   Result

    3.1.   Basic information of patients

    The median medical expenses of breast cancer patients were (24576 ± 4792) RMB, and the hospitalization days was (31.4 ± 6.7) d. The composition ratio of other variables is shown in Table 2.

    Table 2.  Basic information of hospitalized patients with breast cancer.
    Variable Case Composition ratio (%) Variable Case Composition ratio (%)
    Region Age
     Feidong 196 24.7 < 45 159 20.0
     Feixi 258 32.5 45–59 378 47.5
     Changfeng 164 20.6 60–74 214 26.9
     Lujiang 177 22.3 ≥ 75 44 5.5
    Diagnosis year Clinical stages
     2017 262 33.0 Ⅰ 76 9.6
     2018 254 31.9 Ⅱ 348 47.8
     2019 279 35.1 Ⅲ 94 11.8
    Medical payment Ⅳ 26 3.3
     Rural insurance 570 71.7 Unknown 251 31.6
     Urban workers 64 8.1 Chemotherapy
     Urban residents 135 17.0 Yes 679 85.4
     Others 26 3.3 No 116 14.6
    Operation Radiotherapy
     Yes 712 89.6 Yes 42 5.3
     No 83 10.4 No 753 94.7
     | Show Table
    DownLoad: CSV

    3.2.   Modeling results

    The SPSS Clementine 12.0 data mining platform was used to construct BP neural network model and multiple linear regression model for medical expenses of female breast cancer patients. BP neural network model takes nine indicators such as region, year of diagnosis and medical payment mode as input and logarithm of medical expenses as output. It adopts random sampling method and takes 70% samples as training set and 30% samples as test set. After repeated verification, a three-layer BP neural network model is finally constructed, with 9 neurons in the input layer, 10 neurons in the hidden layer and 1 neuron in the output layer, and the accuracy is 95.97%. The model results are shown in Table 3.

    Table 3.  Summary of Back propagation neural network model results.
    Data set Number of samples Minimum error Maximum error Average error Absolute mean error Standard deviation Linear correlation
    Training set 557 −0.669 0.668 −0.003 0.127 0.167 0.889
    Test set 238 −1.151 0.852 −0.004 0.149 0.221 0.863
     | Show Table
    DownLoad: CSV

    In the multiple linear regression model, 9 indicators such as region, year of diagnosis and medical payment mode were taken as independent variables, and the logarithm of medical expenses was taken as dependent variable. The multiple correlation coefficient was 0.841, which indicated that the model fitted well. The probability of F statistic of the model population linear test (P < 0.001) indicates that there is a significant linear relationship between independent variables and dependent variables. The model results are shown in Table 4.

    Table 4.  Summary of multiple linear regression models.
    R R2 Adjust R2 Error of standard estimation F P
    0.838 0.696 0.689 0.202 126.647 < 0.001
     | Show Table
    DownLoad: CSV

    3.3.   Comparative analysis of influencing factors of medical expenses of breast cancer patients

    BP neural network model gives the sensitivity of each variable, that is, the influence of each variable change on medical expenses. The analysis and comparison results of the two models are shown in Table 5. It can be seen that the top two influencing factors for medical expenses of breast cancer patients are length of stay and region; whether radiotherapy, surgery, age and chemotherapy also have a greater impact on medical expenses; medical payment method, diagnosis year and clinical stage have a smaller impact on medical expenses.

    Table 5.  Comparative analysis of influencing factors of medical expenses in patients with breast cancer.
    Variable Code BP neural network model Multiple linear regression model
    Sensibility Sort Regression coefficient sort
    Length of stay X9 0.552 1 0.731 1
    Region X1 0.161 2 0.259 2
    Radiotherapy X6 0.064 3 0.008 9
    Operation X4 0.057 4 0.082 3
    Age X8 0.045 5 0.038 6
    Chemotherapy X5 0.041 6 0.074 4
    Medical payment X3 0.035 7 0.051 5
    Diagnosis year X2 0.033 8 0.029 7
    Clinical stages X7 0.022 9 0.021 8
     | Show Table
    DownLoad: CSV

    3.4.   Comparison between back propagation neural network model and multiple linear regression model

    All samples were substituted into the established BP neural network model and multiple linear regression model to evaluate the performance of the two models. The results are shown in Table 6. The coefficient of determination (R2) of BP neural network model was larger than that of multiple linear regression model, so the fitting degree of BP neural network model was better than that of multiple linear regression model. The MAE, MSE and RMSE values of BP neural network model were less than those of multiple linear regression model, so the prediction ability of BP neural network model was better than that of multiple linear regression model.

    Table 6.  Comparison between back propagation neural network model and multiple linear regression model.
    Evaluation criteria R2 MAE MSE RMSE
    BP neural network 0.771 ± 0.152 0.131 ± 0.028 0.034 ± 0.004 0.186 ± 0.034
    Multiple linear regression 0.662 ± 0.117 0.168 ± 0.031 0.045 ± 0.005 0.221 ± 0.025
    t/P value 8.767/ < 0.001 13.664/ < 0.001 26.503/ < 0.001 12.795/ < 0.001
     | Show Table
    DownLoad: CSV

    4.   Discussion

    In this study, the median medical expenses and length of stay of breast cancer patients were (24576 ± 4792) RBM and (31.4 ± 6.7) d. The high cost of hospitalization not only affects the delay of treatment, but also hinders the choice of treatment [22,23]. At the same time, breast cancer brings huge disease burden to patients. Therefore, it is suggested to strengthen cancer screening for women, so as to achieve early detection, early diagnosis and early treatment, so as to reduce the economic burden and disease burden for individuals, families and society.

    The results show that BP neural network model and multiple linear regression model can fit the data well. Through the comparative analysis of the influencing factors of medical expenses of breast cancer patients, it can be seen that the hospitalization days and regions are consistent in the two models, whether surgery, age of diagnosis, chemotherapy, medical payment method, year of diagnosis and clinical stage are basically consistent in the two models, but whether radiotherapy is inconsistent in the two models. The length of stay has the greatest impact on the cost of hospitalization, which is consistent with the existing research. Therefore, on the premise of ensuring the level of medical services, shortening the length of stay is an effective measure to reduce the medical expenses of breast cancer patients. There are also great differences in the medical expenses of breast cancer among regions, mainly due to the different economic development and medical technology levels. It is suggested that medical service providers can standardize the clinical pathway and provide efficient and affordable treatment for patients. Medical insurance is the main means to reduce the economic burden of rural patients. In this study, it has little impact on medical expenses. It is suggested that medical insurance policy makers should strengthen the compensation for rural cancer patients and reduce their economic risks.

    In recent years, BP neural network model has been widely used in the field of medicine, and achieved good results [24,25]. Although BP neural network model has some disadvantages, such as over training, slow convergence speed, easy to fall into local optimum, it has no requirements for data type and distribution, has certain fault tolerance, and can correct errors repeatedly in the process of self-learning [26,27]. These advantages have great advantages in dealing with medical data with the characteristics of complexity and diversity. The results show that the determination coefficient of BP neural network model is greater than that of multiple linear regression model, and the values of MAE, RMSE and MSE are less than the corresponding values of multiple linear regression model, so its prediction ability is higher than that of multiple linear regression model.

    5.   Conclusions

    Compared with multiple linear regression model, BP neural network model is more suitable for the analysis of medical expenses in patients with breast cancer. However, the model itself has no advantages or disadvantages, only the applicable conditions of each model are different.

    Acknowledgements

    The authors would like to acknowledge the all the breast cancer patients for their participation and support.

    Conflict of interest

    The authors declared that there was no conflict of interests.



    [1] Chang L, Wu Z (2011) Performance and reliability of electrical power grids under cascading failures. Int J Electr Power Energy Syst 33: 1410-1419. doi: 10.1016/j.ijepes.2011.06.021
    [2] Innal F (2008) Contribution to modelling safety instrumented systems and to assessing their performance-critical analysis of IEC 61508 standard. PhD thesis, University of Bordeaux.
    [3] Cardoso G, Rolim JG, Zurn HH (2004) Application of neural network modules to electric power system fault section estimation. IEEE Trans Power Del 19: 1034-41. doi: 10.1109/TPWRD.2004.829911
    [4] Leao FB, Pereira RAF, Mantovani JRS (2014) Fast fault section estimation in distribution control centers using adaptive genetic algorithm. Int J Electr Power Energy Syst 63: 787-805. doi: 10.1016/j.ijepes.2014.06.052
    [5] Sang-Won M, Jin-Man S, Jong-Keun P, et al. (2004) Adaptive fault section estimation using matrix representation with fuzzy relations. IEEE Trans Power Syst 19: 842-848. doi: 10.1109/TPWRS.2003.821036
    [6] Liu HC, Lin QL, Ren ML (2013) Fault diagnosis and cause analysis using fuzzy evidential reasoning approach and dynamic adaptive fuzzy Petri nets. Comput Ind Eng 66: 899-908. doi: 10.1016/j.cie.2013.09.004
    [7] Yang JW, HeZheng Y, Tan XJ, et al. (2010) A distributed fault diagnosis approach in power system based on fuzzy reasoning Petri net. IEEE Fund project: Project Supported by National Science Foundation of China.
    [8] Yan Z, Yong Z, Fushuan W, et al. (2016) A fuzzy Petri net based approach for fault diagnosis in power systems considering temporal constraints. Electr Power Energy Syst J 78: 215-224. doi: 10.1016/j.ijepes.2015.11.095
    [9] Yang J, He Z (2011) Power system fault diagnosis approach based on time sequence fuzzy Petri net. Autom Electr Power Syst 35: 46-51.
    [10] Jagabondhu H, Sinha AK (2006) Prognosis of catastrophic failures in electric power systems. IEEE international conference on industrial technology ICIT.
    [11] David L, Zhaoyin C, Oliver S, et al. (2019) A neural network evolutionary computational framework for remaining useful life estimation of mechanical systems. Neural Netw 116: 178-187. doi: 10.1016/j.neunet.2019.04.016
    [12] Malhi A, Yan R, Gao RX (2011) Prognosis of defect propagation based on recurrent neural networks. IEEE Trans Instrum Meas 60: 703-711. doi: 10.1109/TIM.2010.2078296
    [13] Jun Z, Nan C, Weiwen P (2019) Estimation of bearing remaining useful life based on multiscale convolutional neural network. IEEE Trans Ind Electr 66: 3208-3216. doi: 10.1109/TIE.2018.2844856
    [14] Yun SL, Goran S (2002) Analytical approach to probabilistic prediction of voltage sags on transmission networks. IEE Proc-gener Transm Distrib 149: 7-14. doi: 10.1049/ip-gtd:20020008
    [15] Mojtaba K, Amir Z, Marcos O, et al. (2019) A modular fault diagnosis and prognosis method for hydro-control valve system based on redundancy in multisensor data information. IEEE Trans 68: 330-341.
    [16] Ammour R, Leclercq E, Sanlaville E, et al. (2016) Faults prognosis using partially observed stochastic Petri nets. Proceedings of the 13th International Workshop on Discrete Event Systems, Xi'an, China.
    [17] Balaje T, Miles F, Jagannathan S (2014) A model-based fault detection and prognostics scheme for Takagi-Sugeno fuzzy systems. IEEE Trans Fuzzy Syst 22: 736-748. doi: 10.1109/TFUZZ.2013.2272584
    [18] Wang Z, Hu C, Wang W, et al. (2012) An off-online fuzzy modelling method for fault prognosis with an application. Proceedings of the IEEE 2012 Prognostics and System Health Management Conference (PHM-2012 Beijing), 1-7.
    [19] Panita P, Poj T, Kanokchai N (2007) Evaluation of road traffic congestion using fuzzy techniques. TENCON, IEEE Region 10 International Conference.
    [20] Mojtaba K, Foad S, Mehrdad S (2020) A new hybrid fault prognosis method for MFS systems based on distributed neural networks and recursive bayesian algorithm. IEEE Syst J.
    [21] Mariana D (2013) Combined Fuzzy-Petri nets hybrid model for power system performability analysis. Computing Science and Automatic Control (CCE) Mexico City, Mexico.
    [22] Chen SM (2000) Fuzzy backward reasoning using fuzzy Petri nets. IEEE Trans Syst Ma Cybern Part B: Cybern 30: 846-856. doi: 10.1109/3477.891146
    [23] Mojtaba K, Mehrdad S, Marcos O, et al. (2019) Failure prognosis and applications-A survey of recent literature. IEEE Trans Reliab.
    [24] Zhao XL, Zhou JZ, Liu H (2008) Research of fault diagnostic model based on probability Petri nets. Comput Eng 24: 7-224.
    [25] Hongbo C, Zhengyou H, Qi W, et al. (2015) Fault diagnosis method based on Petri nets considering service feature of information source devices. Comput Electr Eng 46:1-13. doi: 10.1016/j.compeleceng.2015.06.016
    [26] Iman K, Saeed L (2020) Fault section identification in smart distribution systems using Multi-Source data based on fuzzy Petri nets. IEEE Trans Smart Grid.
    [27] Dhananjay K, Shivam P, Akash T, et al. (2018) Identification of weak bus using load variation. Int Res J Eng Technol 5: 841-847.
    [28] Vdokuments khnowledge project. Available from: https://vdocuments.mx/fuzzy-logic-toolbox-users-guide.html. Accessed on 13-Jan-2017.
    [29] Vdokuments khnowledge project. Available from: https://vdocuments.mx/psat-eecswsuedu-ee521material20120927psat-psat-power-system-analysis.html. Accessed on 19-Jul-2018.

  • This article has been cited by:

    1. Li Wu, Zhijie Lv, Linjing Lai, Penglei Zhou, Assessment of influencing factors of hospitalization expenses for Crohn's disease patients: Based on LASSO and linear mixed model, 2022, 10, 2296-2565, 10.3389/fpubh.2022.925616
    2. Cheng-Wei Liu, Fu-Hsing Wu, Yu-Lun Hu, Ren-Hao Pan, Chuen-Horng Lin, Yung-Fu Chen, Guo-Shiang Tseng, Yung-Kuan Chan, Ching-Lin Wang, Left ventricular hypertrophy detection using electrocardiographic signal, 2023, 13, 2045-2322, 10.1038/s41598-023-28325-5
    3. Wei Guo, Guoyun Gao, Jun Dai, Qiming Sun, Kelvin Wong, Prediction of Lung Infection during Palliative Chemotherapy of Lung Cancer Based on Artificial Neural Network, 2022, 2022, 1748-6718, 1, 10.1155/2022/4312117
    4. Yihao Zhu, Xiaojing Yang, Yao Zu, Integrated analysis of WGCNA and machine learning identified diagnostic biomarkers in dilated cardiomyopathy with heart failure, 2022, 10, 2296-634X, 10.3389/fcell.2022.1089915
    5. Yuanhong Che, Zhangdong Wei, Jing Wen, Hangjun Che, Construction of Surface Water Pollution Prediction Model Based on Machine Learning, 2022, 2022, 1875-919X, 1, 10.1155/2022/7211094
    6. Hong Jiang, Sinuo Ren, Shengbo Zhang, Xudan Luo, Rui He, ShuaiFei Wang, JianDong Yan, Shan Zhou, Chengliang Yin, Ying Xiao, Zhihuan Li, Analyzing factors influencing hospitalization costs for five common cancers in China using neural network models, 2025, 1369-6998, 1, 10.1080/13696998.2025.2494459
  • Reader Comments
  • © 2020 the Author(s), licensee AIMS Press. This is an open access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0)
通讯作者: 陈斌, bchen63@163.com
  • 1. 

    沈阳化工大学材料科学与工程学院 沈阳 110142

  1. 本站搜索
  2. 百度学术搜索
  3. 万方数据库搜索
  4. CNKI搜索
AIMS Energy
1.8 3.7

Metrics

Article views(3701) PDF downloads(136) Cited by(2)

Preview PDF
Download XML
Export Citation
Article outline
Abstract
   Introduction
   Materials and methods
   Result
   Discussion
   Conclusions
Acknowledgements
Conflict of interest
References

Figures and Tables

Figures(5)  /  Tables(9)

Other Articles By Authors

Related pages

Tools

Copyright © AIMS Press

/

DownLoad:  Full-Size Img  PowerPoint
Return
Return

Catalog