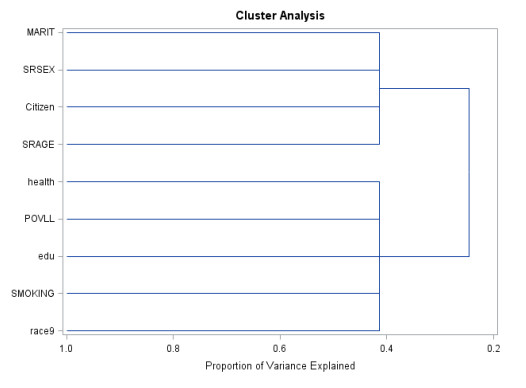
This study aimed to estimate the prevalence of uninsurance among California adults and Asian Americans, and to examine the associations of social-behavioral variables with uninsurance. A total of 24,136 adults (aged 18-64) including 2,060 Asian Americans were selected from the combined 2013-2014 California Health Interview Survey. Weighted univariate and multivariate logistic regression analyses were used to estimate the associations of potential factors with uninsurance. To evaluate the relationship of independent variables, the oblique principal component cluster analysis (OPCCA) was used to classify 9 variables into disjoint clusters. For Whites, African Americans, Latinos, and Asians, the prevalence of uninsurance was 8.5%, 10.3%, 24.7%, and 12.6%, respectively. Among Asians, the prevalence of uninsurance was 15.5%, 9.2%, 6.2%, 20.8% and 12.1% for Chinese, Filipinos, Japanese, Koreans, and Vietnamese, respectively. In the whole sample, multivariate logistic regression analysis revealed that being male, non-citizen, lower education, higher poverty, and current smoking were associated with uninsurance. Among Asians, compared to Koreans, being Filipinos and Vietnamese were associated with lower odds of being uninsured; meanwhile being male, non-citizen, lower education, and higher poverty were significantly associated with increased odds of uninsurance. Elder age groups and current smoking were significantly associated with increased odds of uninsurance in bivariate analysis; however, such associations disappeared after adjusting for other factors. Nine independent variables were divided into 2 clusters, where the variables in the same cluster were strongly correlated but had weak correlations with the variables in the other cluster. In conclusion, there are differences in the prevalence of uninsurance between Asians and Whites, and among Asian subgroups. Being male, non-citizen, lower education, higher poverty and current smoking were positively significantly associated with uninsurance.
1.
Introduction
In the reliability and life testing experiments, censored samples are common way to save time and reduce the number of failed experimental items. Type-Ⅰ and Type-Ⅱ censoring schemes are the most common censoring schemes used in the life-testing and reliability studies. The mixture of these two schemes is called the hybrid censoring scheme. For more details about the hybrid censoring schemes, see Balakrishnan and Kundu [1]. The main disadvantage of the conventional Type-Ⅰ and Type-Ⅱ and the hybrid censoring schemes is that they do not allow the experimenter to remove the experimental items at any time point other than the terminal point. For this reason, one may use a general censoring scheme which called progressive Type-Ⅱ censoring. In this censoring scheme n items are placed on a test and the number of items to be failed, denoted by m, and the number of items that are removed at each failure time, denoted Ri, are determined in advance. At the time of the first failure x1:m:n, R1 items are randomly removed from the remaining n−1 surviving items. Similarly, at the time of the second failure x2:m:n, R2 items of the remaining n−2−R1 items are randomly removed and so on. At the time xm:m:n, all the remaining n−m−R1−R2−⋅⋅⋅−Rm−1 items are removed. For more information see Balakrishnan and Aggarwala [2] and Balakrishnan [3].
Kundu and Joarder [4] introduced the Type-Ⅰ progressive hybrid censoring scheme by combining the concepts of progressive and hybrid censoring schemes. In this scheme, n items are placed on a test with the progressive censoring scheme R1,R2,⋅⋅⋅,Rm and the experiment is terminated at T∗=min(xm:m:n,T), where T is a predetermined time. The drawback of this scheme is that the statistical inference methods will have low efficiency or may not be applicable. Since the number of failures is random and it can be zero or a very small number. To overcome this disadvantage and increase the efficiency of the statistical inference, Ng et al. [5] proposed an adaptive Type-Ⅱ progressive hybrid censoring scheme (A-II PHCS). In the A-II PHCS, the number of failures m and the progressive censoring scheme R1,R2,⋅⋅⋅,Rm are predetermined and the experimental time is allowed to run over the predetermined time T with the flexibility of changing some values of Ri during the experiment. When Xm:m:m<T, then the experiment stops at this time and we will have the conventional progressive Type-Ⅱ censoring scheme. On the other hand, if XJ:m:n<T<XJ+1:m:n, where XJ:m:n is the Jth failure time occur before the predetermined time T and J+1<m, then we adjust the progressive censoring scheme by resetting RJ+1,RJ+2,⋅⋅⋅,Rm−1=0 and Rm=n−m−∑Ji=1Ri. This adaption assures us to terminate the experiment when m is occurred, and guarantee that the total test time will not be too long away from the time T.
Recently, many authors have studied different distributions based on A-II PHCS. For example, Lin et al. [6], discussed the estimation problem of Weibull distribution. Hemmati et al. [7], discussed the maximum likelihood and approximate maximum likelihood estimation for the log-normal distribution. Mahmoud et al. [8], studied the Bayes estimation of Pareto distribution. Ismail [9], investigated the estimation of Weibull distribution and the acceleration factor under step-stress partially accelerated life test model. AL Sobhi and Soliman [10], studied the estimation of parameters, reliability and hazard functions of the exponentiated Weibull distribution. Nassar and Abu-Kasem [11] and Nassar et al. [12] investigated the estimation problems of inverse Weibull and Weibull distributions, respectively.
Burr [13] introduced the Burr type-XII distribution as a member of a 12 types of cumulative distribution functions. The Burr type-XII distribution has many applications in various fields including probability theory, reliability, failure time modeling and household income. A random variable X is said to have two-parameters Burr type-XII distribution, denoted by Burr(a,b), if its probability density and reliability functions are given, respectively, by
and
where a and b are shape parameters. The Lomax distribution can be obtained as a special case from Burr(a,b) distribution by stting a=1. Also, when b=1, the Burr(a,b) distribution reduces to the Champernowne distribution. Evans and Ragab [14] discussed the Bayesian inferences from Burr type-XII distribution based on Type-Ⅱ censored scheme. Moore and Papadopoulos [15] used the Bayesian estimation method to estimate the Burr type-XII distribution parameters using three different loss functions. Mousa and Jaheen [16] obtained the Bayesian estimators of the Burr type-XII distribution parameters under progressive Type-Ⅱ censored scheme. Jaheen and Okasha [17] discussed the estimation problem of the Burr type-XII distribution using Bayesian and E-Bayesian estimation using Type-Ⅱ censored scheme. Hanieh and Abdolreza [18] presented the statistical inference and prediction of the Burr type-XII distribution under unified hybrid scheme. See also, Montaser [19], Jia et al. [20] and Arabi and Noori [21].
To the best of our knowledge, the E-Bayesian estimation of the Burr(a,b) distribution under A-II PHCS has not yet been studied. The main aim of this paper is to investigate the E-Bayesian estimation of the parameter b and the reliability function of the Burr(a,b) distribution under A-II PHCS with the assumption that the parameter a is known. The maximum likelihood method, Bayesian and E-Bayesian estimations are considered using three different prior distributions. The Bayesian and E-Bayesian estimations are discussed based on squared error (SE) and LINEX loss functions. The E-Bayesian properties are studied and the E-Posterior risk is also obtained. A simulation study is conducted to compare the performance of the different estimators of the parameter b and the reliability function. Application to a real data shows that the E-Bayesian estimators perform better than the maximum likelihood and Bayesian estimators.
The rest of this paper is organized as follows: In Section (2), we obtain the maximum likelihood and Bayesian estimations of the parameter b and the reliability function of Burr(a,b). The E-Bayesian estimation is considered in Section (3). In Section (4), we study the properties of the E-Bayesian estimation. The E-posterior risk of the E-Bayesian estimation is obtained in Section (5). A simulation study is performed in Section (6). A real data is analyzed in Section (7). Finally, the paper is concluded in Section (8).
2.
Bayesian estimation
Based on adaptive Type-Ⅱ progressive hybrid censoring sample of size m obtained from a life test experiment of n items from the Burr(a,b) distribution, we can write the likelihood function as follows
where
where R∗=n−m−∑Ji=1Ri, and xi=xi:m:n for simplicity of notation. Assuming that the parameter a is known, then the maximum likelihood estimate (MLE) of the parameter b is obtained as follows
From (2.2) and the invariance property of the maximum likelihood, we can obtain the MLE of the reliability function R(x) by replacing b by its MLE in (1.2).
In the Bayesian estimation, we assume that the parameter a is known and the parameter b follows the gamma conjugate prior distribution as proposed by Papadopoulos [15] in the following form
where α>0 and θ>0. From (2.1) and (2.3), the posterior density of b given x_ can be written as
where
To obtain the Bayes estimate of b, we consider two types of loss functions. The first loss function is the SE loss function and the Bayes estimate in this case is the posterior mean. The second one is the LINEX loss function with the Bayes estimate obtained as
Based on the SE loss function, we can obtain the Bayes estimate of b as follows
while the Bayes estimate of b using the LINEX loss function can be obtained from (2.4) and (2.6) by
Under the SE loss function, the Bayes estimate of the reliability function can be obtained from (1.2) and (2.4) as
where
Similarly, from (1.2), (2.4) and (2.6), the Bayes estimate of the reliability function under LINEX loss function can be obtained as follows
3.
E-Bayesian estimation
Han [22] introduced the E-Bayesian (Expected Bayesian) estimation to obtain the estimate of the scale parameter of the exponential distribution based on SE loss function. He also derived the properties of the E-Bayesian estimation. For more relevant research about the E-Bayesian estimation, see Han [22,23], Okasha and Wang [24], Azimi et al. [25], Okasha [26,27,28], and Abdallah and Junping [29]. Han [22] stated that the prior distribution of α and θ should be determined to ensure that the prior distribution g(b) is a decreasing function in b. To make sure this condition is satisfied, we obtain the first derivative of g(b) with respect to b as
where α,θ,b>0. It is noted that when 0<α<1 and θ>0 the function dg(b)b<0, and therefore g(b) is a decreasing function of b. Suppose that α and θ are independent and have the bivariate density function
then, according to Han [30] the E-Bayesian estimate of the parameter b (expectation of the Bayesian estimate of b) can be obtained as follows
where ˆbEB(α,θ) is the Bayes estimate of b under any loss function. For more details about E-Bayesian estimation, see Han [22], Jaheen and Okasha [17] and Okasha [26,27,28].
3.1. E-Bayesian estimation under SE loss function
Here, we obtain the E-Bayesian estimates of the parameter b by considering three different prior distributions of the hyper-parameters α and θ. These prior distributions are selected to show the effect of the different prior distributions on the E-Bayesian estimation of the parameter b. The selected priors distributions are given by
where B(u,v) is the beta function. These prior distributions are used by Zeinhum and Okasha [17] to guarantee that g(b) is a decreasing function in b. Now, the E-Bayesian estimates of the parameter b under SE loss function can be obtained from (2.7), (3.1) and (3.2). Using the prior distribution π1(α,θ), the E-Bayesian estimate of b under SE loss function is given by
Using the same approach, the E-Bayesian estimates of b based on π2(α,θ) and π3(α,θ) are given, respectively, by
and
3.2. E-Bayesian estimation under LINEX loss function
The E-Bayesian estimation of b under LINEX loss function can be obtained by using the different prior distributions of the hyperparameters given in (3.2). For the prior distribution π1(α,θ) and based on (2.8) and (3.1), the E-Bayesian estimate of b is obtained as
Similarly, the E-Bayesian estimates of b using π2(α,θ) and π3(α,θ) are given, respectively, by
and
3.3. E-Bayesian estimation of the reliability function under SE and LINEX loss functions
Based on the SE loss function, the E-Bayesian estimates of the reliability function can be derived by using the three different prior distributions of the hyper-parameters given by (3.2). For the first prior distribution π1(α,θ), the E-Bayesian estimate of the reliability function is obtained from (2.9) and (3.1) as
where F1:1(.,.;.) is the generalized hypergeometric function. See for more details Gradshteyn and Ryzhik [31]. Similarly, the E-Bayesian estimates of the reliability function based on the prior distributions 2 and 3 are given, respectively, by
and
The integrals in (3.9), (3.10) and (3.11) can not be computed in a simple closed forms. Therefore, a numerical techniques should be used to obtain the E-Bayesian estimates of the reliability functions based on the SE loss function using the different prior distributions.
Under LINEX loss function, the E-Bayesian estimates of the reliability function using the prior distribution πi(α,θ),i=1,2,3, can be obtained from (2.10) and (3.1) as
The integrals in (3.12) are very complicated to obtain, so a numerical computations are used to obtain the E-Bayesian estimates of the reliability function under LINEX loss function.
4.
Properties of Bayesian estimation
In this section, we investigate the relations among the different E-Bayesian estimates of the parameter b and the reliability function based on the SE loss function in terms of biases Bi(bEBSi) and Bi(REBSi), i=1,2,3. Moreover, we discuss the relations between the different E-Bayesian estimates of b and the reliability function under the LINEX loss function through the relations between biases, Bi(bEBli) and Bi(REBLi).
The relations between Bi(bEBSi), Bi(bEBli), Bi(REBSi) and Bi(REBli), i=1,2,3 are described in the following theorems:
Theorem 1. Let y=cP, c>0, 0<cP<1, and bEBSi are given by (3.3), (3.4) and (3.5).Then we have the following conclusions:
(i) Bi(bEBS2)<Bi(bEBS1)<Bi(bEBS3),
(ii) limy→0Bi(bEBS1)=limy→0Bi(bEBS2)=limy→0Bi(bEBS3).
Proof. (i) From (3.3), (3.4) and (3.5), we have
For −1<x<1, we have: ln(1+x)=x−x22+x33−x44+…=∑∞k=1(−1)k−1xkk. Let y=cP, when c>0, 0<cP<1, we have:
From (4.1) and (4.2), we have
that is
(ii) From (4.1) and (4.2), we get
That is, limy→0Bi(bEBS1)=limy→0Bi(bEBS2)=limy→0Bi(bEBS3).
Theorem 2. Let c>0, 0<cP<1, and bEBLi are given by (3.6), (3.7) and (3.8).Then we have the following conclusions:
(i) Bi(bEBL2)<Bi(bEBL1)<Bi(bEBL3),
(ii) limP→∞Bi(bEBL1)=limP→∞Bi(bEBL2)=limP→∞Bi(bEBL3),
Proof. (i) From (3.6), (3.7) and (3.8), we have
Since,
From (4.3) and (4.4), when c>0, 0<cP<1, we have:
that is
(ii) From (4.3) and (4.4) we get
That is, limP→∞Bi(bEBL1)=limP→∞Bi(bEBL2)=limP→∞Bi(bEBL3).
Theorem 3. Let c>0, 0<cP<1, and REBSi are given by (3.9), (3.10) and (3.11).Then we have the following conclusions:
(i) Bi(REBS2)<Bi(REBS1)<Bi(REBS3),
(ii) limP→∞Bi(REBS1)=limP→∞Bi(REBS2)=limP→∞Bi(REBS3)
Proof. (i) From (3.9), (3.10) and (3.11), we have
For α∈(0,1), θ∈(0,c), (2θ−c)(θ+Pθ+P+P∗)m+α and αu−1(1−α)v−1c2B(u,v) are continuous functions and αu−1(1−α)v−1c2B(u,v)>0, by the generalized mean value theorem for definite integrals, there is at least one number α0∈(0,1) and θ0∈(0,c) such that
Therefore, we obtain that
that is
(ii) From (4.6) we get
That is, limP→∞Bi(REBS1)=limP→∞Bi(REBS2)=limP→∞Bi(REBS3).
Theorem 4. Let c>0, 0<cP<1, and REBLi are given by (3.12). Then we have the following conclusions:
(i) Bi(REBL3)<Bi(REBL2)<Bi(REBL1).
(ii) limP→∞Bi(REBL1)=limP→∞Bi(REBL2)=limP→∞Bi(REBL3)
Proof. (i) From (3.2) and (3.12), we have
For α∈(0,1), θ∈(0,c), (2θ−c)ln(∑∞i=0(−δ)iΓ(i)(θ+Pθ+P+iP∗)m+α) and αu−1(1−α)v−1c2B(u,v) are continuous functions and αu−1(1−α)v−1c2B(u,v)>0, by the generalized mean value theorem for definite integrals, there is at least one number α1∈(0,1) and θ1∈(0,c) such that
Therefore, we obtain that
that is
(ii) From (4.9) we get
That is, limP→∞Bi(REBL1)=limP→∞Bi(REBL2)=limP→∞Bi(REBL3).
5.
E-posterior risk
In this section, we derive the E-posterior risk of the E-Bayesian estimations of the parameter b using the three different prior distributions in (3.2) under SE and LINEX loss functions.
5.1. E-posterior risk under SE loss function
Let ℓ(ˆμ,μ) be any loss function where ˆμ is the Bayes estimator of μ, and q(μ|x_) is the posterior distribution of μ, then the posterior risk (PR) for the Bayesian estimation is
Under SE loss function the PR of the Bayes estimation is the posterior variance. From the posterior distribution in (2.4) we can obtain the PR of Bayesian estimation of b as follows
According to Han [23] the E-posterior risk of the E-Bayesian estimation can be obtained as
where PRBS is the posterior risk defined in (5.2) and π(α,θ) is the prior distribution. Now, from (3.2), (5.2) and (5.3) we can obtain the E-posterior risk of the E-Bayesian estimation under SE loss function as follow
(i) The E-posterior risk of the E-Bayesian estimation of ˆbEBS1 is
(ii) The E-posterior risk of the E-Bayesian estimation of ˆbEBS2 is
(iii) The E-posterior risk of the E-Bayesian estimation of ˆbEBS3 is
5.2. E-posterior risk under LINEX loss function
Using the same approach in the previous subsection we can obtain the posterior risk of the Bayes estimate of b under LINEX loss function as follows
From (3.2), (5.3) and (5.4), the E-posterior risk of the E-Bayesian estimation of b under LINEX loss function can be obtained as follow
(i) The E-posterior risk of the E-Bayesian estimation of ˆbEBL1 is
(ii) The E-posterior risk of the E-Bayesian estimation of ˆbEBL2 is
(iii) The E-posterior risk of the E-Bayesian estimation of ˆbEBL3 is
6.
Simulation study
In this section we compare the different estimators of the parameter a and the reliability function by conducting a simulation study. We compare the performance of the different estimators in terms of their biases and mean square errors (MSE). We consider different values of n, m, T and the following three censoring schemes (Sch)
● Sch 1: R1=⋅⋅⋅=Rm−1=0andRm=n−m.
● Sch 2: R1=⋅⋅⋅=Rm−1=1andRm=n−2m+1.
● Sch 3: R1=⋅⋅⋅=Rm=n−mm.
In all the setting we choose the parameter a to be one and consider b=(0.5,1.5). The simulation is conducted according to the following steps:
(i) Determine n,m,R′is,T and the value of the parameter b.
(ii) Generate the conventional progressive Type-Ⅱ censored sample from Burr type-XII model acording to the method proposed by Balakrishnan and Sandhu [32], by using X=[(1−U)−1/b−1]1/a, where U is uniform (0,1).
(iii) Determine the value of J, and withdraw all the observations greater than the J−th observation.
(iv) Generate (m−J−1) Type-Ⅱ censored sample from f(x)/[1−F(xJ+1)] and stop the experiment at xm. Therefore, X={[1−U(1+xaJ+1)b]−1/b−1}1/a.
(v) Obtain the the different estimates of the parameter b and the reliability function at time x=0.75.
(vi) Repeat steps 2–5, 1000 times.
(vii) Obtain the average values of biases and MSEs (for the reliability function we obtain the MSE only).
To obtain the Bayesian and E-Bayesian estimates of the parameter b, we choose the hyperparameters values to be α=0.5 and θ=1 for b=0.5 and α=0.75 and θ=0.5 for b=1.5. These values are selected to make the prior means are same as the original means. The Bayesian and and E-Bayesian estimates using the LINEX loss function are obtained by setting z=−3 in all the cases. The values of average biases and average MSEs for the parameter b=0.5 are shown in Table 1 and in Table 3 for b=1.5. The average values of MSEs for the different estimates of the reliability function are displayed in Table 2 for b=0.5 and in Table 4 for b=1.5.
From Tables 1–4 we have the following observations:
(i) The average biases decrease as m increases in all the cases, which indicates that the different estimators used to estimate the parameter b are asymptotically unbiased.
(ii) The average MSEs decrease and tend to zero as m increases in all the cases. Thus the different estimators used to estimate the parameter b and the reliability function are consistent.
(iii) The Bayesian and E-Bayesian estimates of the parameter b perform better than MLE in all the cases in terms of minimum average biases and MSEs.
(iv) Under SE loss function, the E-Bayesian estimates of the parameter b have less average biases and MSEs than the Bayes estimate.
(v) Under LINEX loss function, the E-Bayesian estimates of the parameter b have less average biases and MSEs than the Bayes estimate.
(vi) The performance order of E-Bayesian estimates under SE and LINEX loss functions in terms of minimum average biases and MSEs are the estimates using prior distribution 2, then the estimates using prior distribution 1 and then the estimates using prior distribution 3.
(vii) The E-Bayesian estimate of the parameter b under LINEX loss function using prior distribution 2 has the smallest average biases and MSEs among all other different estimates in all the cases.
(viii) The E-Bayesian estimate of reliability function under LINEX loss function using prior distribution 3 perform better than the other estimates in terms of minimum average biases and MSEs.
(ix) Comparing the three censoring schemes, we observed that Sch 3 has the smallest average biases and MSEs in all the cases followed by Sch 2 and then 1.
(x) The E-Bayesian estimate of the parameter b under LINEX loss function using prior distribution 2 has the minimum average biases and MSEs among all the other estimates.
It is observed that the E-Bayesian estimates under the two loss functions using prior distribution 2 perform better than other estimates. It is known that the density of the prior distribution 2 is a decreasing function in the hyper-parameter θ and the density of the prior 3 is an increasing function. From this comparison, we can conclude that when the prior distribution of the hyper-parameter θ is decreasing the E-Bayesian estimates perform better than other estimates based on the other priors. Moreover, we obtain E-posterior risk of the parameter b under SE and LINEX loss functions. Here, we only display the case of b=0.5, n=60, m=(10,20) and T=0.3 using the three censoring schemes in Figure 1. From Figure 1, it is observed that the E-Bayesian risk decreases as the number of failure m increases in all the cases. Also, it is to be noted that under SE loss function the E-Bayesian risk using prior distribution 3 perform better than other prior distributions. Similarly, under LINEX loss function the E-Bayesian risk using prior distribution 3 have the smallest E-posterior risk among all other prior distributions. Finally, the ordering of performance of E-Bayesian risks under SE and LINEX loss functions are the E-Bayesian risk using prior distribution 3, then prior distribution 1, then prior distribution 2.
7.
Real data analysis
In this section we anlayze a real data set given by Lawless [33]. These data represent the time to breakdown of an insulating fluid between electrodes at a voltage of 34 k.v. Zimmer et al.[34], showed that the Burr type-XII distribution is suitable to fit these data. The original data set consists of 19 observations. We used the maximum likelihood method to obtain the estimates of the parameters a and b from the complete data set. The MLEs of a and b are 1.7379 and 0.2936, respectively. Mahmoud et al.[8], used these data to generate two adaptive progressively censored samples by considering m=10, T=6,9 and R={3,0,0,0,3,0,0,0,0}. The generated samples are
These data are also analyzed by Nassar et al. [12]. Here, we assume that the parameter a is known and equal to 1.7379 and use the two adaptive progressively hybrid censored samples to estimate the unknown parameter b. To compute the Bayesian and E-Bayesian estimates, we consider the case of noninformative priors by choosing the hyperparamters to be b∼gamma(0.01,0.01).
The MLE, Bayesian and E-Bayesian estimates of the parameter b are obtained and displayed in Table 5. The Bayesian and E-Bayeian risk are also obtained and presented in Table 5. From the observation matrix we obtain the variance of the MLE of b. From Table 5, it is observed that the ˆbEBS2 under SE and ˆbEBL2 under LINEX loss function are closer to the true value of b more than the other estimates. Also, the E-Bayesian risk using the prior distribution 3 under SE and LINEX loss functions has the minimum risk among all the other priors. These results coincide with the results discussed before in the simulation section. Table 6 shows the different estimates of the reliability function by considering different values of x. Comparing the different estimates of the reliability function given in Table 6, we can conclude that the estimates based on prior distribution 2 under SE and LINEX loss function are closer to the true value of the reliability function that is based on the parameter values obtained from the complete sample.
8.
Conclusions
In this paper we have investigated the E-Bayesian estimation of the parameter and the reliability function of the Burr type-XII distribution based on A-II PHCS. The E-Bayesian estimation is considered by using three different prior distributions under two loss functions, namely the SE and LINEX loss functions. The properties of the E-Bayesian estimation as well as the E-posterior risk are also derived. We compared the performance of the E-Bayesian estimation with the maximum likelihood and Bayesian estimators via an extensive simulation study. The simulation results revealed that the E-Bayesian estimation perform better than the maximum likelihood and Bayesian estimators in terms of minimum biases and MSEs. Moreover, we analyzed one real data set for illustration purpose and the results are coincide with those in the simulation section. As a future work, the E-Bayesian estimation for the Burr type-XII distribution under A-II PHCS is still an open problem when the two parameters are unknown. Another future work is to obtain the E-Bayesian estimates for the parameters of the Burr type-XII distribution under A-II PHCS using different prior distributions for the hyper-parameters.
Acknowledgments
The authors would like to express their thanks to the editor and anonymous referees for useful suggestions and comments. This project was funded by the Deanship Scientific Research (DSR), King Abdulaziz University, Jeddah under grant no. (G: 537-130-1441). The authors, therefore, acknowledge with thanks DSR for technical and Financial support.
Conflict of interest
The authors declare there is no conflicts of interest in this paper.









 DownLoad:
DownLoad: