Mathematical modeling of tumor growth: the MCF-7 breast cancer cell line

Hsiu-Chuan Wei; Hsiu-Chuan Wei

doi:10.3934/mbe.2019325

Mathematical Biosciences and Engineering

2019, Volume 16, Issue 6: 6512-6535. doi: 10.3934/mbe.2019325

Previous Article Next Article

Research article Special Issues

Mathematical modeling of tumor growth: the MCF-7 breast cancer cell line

Hsiu-Chuan Wei ^,

Department of Applied Mathematics, Feng Chia University, Seatwen, Taichung 40724, Taiwan

Received: 31 December 2018 Accepted: 04 July 2019 Published: 15 July 2019

Breast cancer is the second most commonly diagnosed cancer in women worldwide. MCF-7 cell line is an extensively studied human breast cancer cell line. This cell line expresses estrogen receptors, and the growth of MCF-7 cells is hormone dependent. In this study, a mathematical model, which governs MCF-7 cell growth with interaction among tumor cells, estradiol, natural killer (NK) cells, cytotoxic T lymphocytes (CTLs) or CD8+ T cells, and white blood cells (WBCs), is proposed. Experimental data are used to determine functional forms and parameter values. Breast tumor growth is then studied using the mathematical model. The results obtained from numerical simulation are compared with those from clinical and experimental studies. The system has three coexisting stable equilibria representing the tumor free state, a microscopic tumor, and a large tumor. Numerical simulation shows that an immune system is able to eliminate or control a tumor with a restricted initial size. A healthy immune system is able to effectively eliminate a small tumor or produces long-term dormancy. An immune system with WBC count at the low parts of the normal ranges or with temporary low NK cell count is able to eliminate a smaller tumor. The cytotoxicity of CTLs plays an important role in immune surveillance. The association between the circulating estradiol level and cancer risk is not significant.

Keywords:

Citation: Hsiu-Chuan Wei. Mathematical modeling of tumor growth: the MCF-7 breast cancer cell line[J]. Mathematical Biosciences and Engineering, 2019, 16(6): 6512-6535. doi: 10.3934/mbe.2019325

Related Papers:

[1]	Ekaterina Kldiashvili, Archil Burduli, Gocha Ghortlishvili . Application of Digital Imaging for Cytopathology under Conditions of Georgia. AIMS Medical Science, 2015, 2(3): 186-199. doi: 10.3934/medsci.2015.3.186
[2]	Anuj A. Shukla, Shreya Podder, Sana R. Chaudry, Bryan S. Benn, Jonathan S. Kurman . Non-small cell lung cancer: epidemiology, screening, diagnosis, and treatment. AIMS Medical Science, 2022, 9(2): 348-361. doi: 10.3934/medsci.2022016
[3]	Nicole Lavender, David W. Hein, Guy Brock, La Creis R. Kidd . Evaluation of Oxidative Stress Response Related Genetic Variants, Pro-oxidants, Antioxidants and Prostate Cancer. AIMS Medical Science, 2015, 2(4): 271-294. doi: 10.3934/medsci.2015.4.271
[4]	Masahiro Yasunaga, Shino Manabe, Masaru Furuta, Koretsugu Ogata, Yoshikatsu Koga, Hiroki Takashima, Toshirou Nishida, Yasuhiro Matsumura . Mass spectrometry imaging for early discovery and development of cancer drugs. AIMS Medical Science, 2018, 5(2): 162-180. doi: 10.3934/medsci.2018.2.162
[5]	Sherven Sharma, Pournima Kadam, Ram P Singh, Michael Davoodi, Maie St John, Jay M Lee . CCL21-DC tumor antigen vaccine augments anti-PD-1 therapy in lung cancer. AIMS Medical Science, 2021, 8(4): 269-275. doi: 10.3934/medsci.2021022
[6]	Ayomide Abe, Mpumelelo Nyathi, Akintunde Okunade . Lung cancer diagnosis from computed tomography scans using convolutional neural network architecture with Mavage pooling technique. AIMS Medical Science, 2025, 12(1): 13-27. doi: 10.3934/medsci.2025002
[7]	Timothy Hamerly, Margaret H. Butler, Steve T. Fisher, Jonathan K. Hilmer, Garth A. James, Brian Bothner . Mass Spectrometry Imaging of Chlorhexidine and Bacteria in a Model Wound. AIMS Medical Science, 2015, 2(3): 150-161. doi: 10.3934/medsci.2015.3.150
[8]	Prarthana Shrestha, Rik Kneepkens, Gijs van Elswijk, Jeroen Vrijnsen, Roxana Ion, Dirk Verhagen, Esther Abels, Dirk Vossen, and Bas Hulsken . Objective and Subjective Assessment of Digital Pathology Image Quality. AIMS Medical Science, 2015, 2(1): 65-78. doi: 10.3934/medsci.2015.1.65
[9]	Anne A. Adeyanju, Wonderful B. Adebagbo, Olorunfemi R. Molehin, Omolola R. Oyenihi . Exploring the multi-drug resistance (MDR) inhibition property of Sildenafil: phosphodiesterase 5 as a therapeutic target and a potential player in reversing MDR for a successful breast cancer treatment. AIMS Medical Science, 2025, 12(2): 145-170. doi: 10.3934/medsci.2025010
[10]	Salma M. AlDallal . Quick glance at Fanconi anemia and BRCA2/FANCD1. AIMS Medical Science, 2019, 6(4): 326-336. doi: 10.3934/medsci.2019.4.326

Abstract

1. Introduction

In mathematical modelling, the term diffusion is used to describe the motion of species from one region to another. Influenced by various natural factors, such as geographic, hydrological or climatic conditions and human activities, migrations occur between patches, which affects the population dynamics, for example the persistence and extinction of species ^{[1,2,3,4,5,6,7,8]}. The growth of species population is also affected by competition caused by disputing food, resources, territories and spouses, including intraspecific and interspecific competitions among populations. To see the effects of the diffusion and competition on population dynamics, we propose the following mathematical model with $n$ species, for $\;i, j = 1, 2, \ldots, n,$

$\begin{eqnarray} {\rm d}x_{i}(t)& = &x_{i}(t)\bigg[r_{i}-a_{ii}x_{i}(t)-\sum\limits_{j = 1, j\neq i}^{n}a_{ij}x_{j}(t)+\sum\limits_{j = 1, j\neq i}^{n}D_{ij}x_{j}(t)\\ &&-\sum\limits_{j = 1, j\neq i}^{n}D_{ij}\alpha_{ij}x_{i}(t)\bigg] {\rm d}t, \end{eqnarray}$

(1)

where $x_{i}(t)$ is the population size at time $t$ of the $i$ th species, positive constants $r_{i}$ , $a_{ii}$ are the growth rate and the interspecific competition rate of the $i$ th species respectively, $a_{ij}>0\;(j\neq i)$ is the competition rate between species $i$ and $j$ , $D_{ij}\geq 0$ is the diffusion coefficient from species $j$ to species $i$ , $\alpha_{ij}\geq 0$ indicates the diffusion boundary condition.

Recently, time delays have been widely used in biological and ecological models in order to get more realistic mathematical models, for example ^{[9,10,11,12,13,14,15,16]}. In this paper, we also consider the time delay, which is accounted for the diffusion. For example, birds cannot migrate immediately after they were born, so the time delay here is the time it takes for them to learn to fly before they can migrate, and death can also occur in the process. Then, from (1) we have the model with time delays as follows

$\begin{eqnarray} {\rm d}x_{i}(t)& = &x_{i}(t)\bigg[r_{i}-a_{ii}x_{i}(t)-\sum\limits_{j = 1, j\neq i}^{n}a_{ij}x_{j}(t)+\sum\limits_{j = 1, j\neq i}^{n}D_{ij}e^{-d_{j}\tau_{ij}}x_{j}(t-\tau_{ij})\\ &&-\sum\limits_{j = 1, j\neq i}^{n}D_{ij}\alpha_{ij}x_{i}(t)\bigg] {\rm d}t, \;i, j = 1, 2, \ldots, n, \end{eqnarray}$

(2)

where $\tau_{ij}\geq 0$ is the time delay and $d_{j}$ is the death rate of the $j$ th species. Let $\tau = \max_{i, j = 1, \ldots, n}\{\tau_{ij}\}$ and $C([-\tau, 0];R_{+}^{n})$ denote the family of all bounded and continuous functions from $[-\tau, 0]$ to $R_{+}^{n}$ . We assume model (2) is subject to the following initial condition

$\begin{equation} x(\theta) = \left(x_{1}(\theta), \ldots, x_{n}(\theta)\right)^{T} = \left(\phi_{1}(\theta), \ldots, \phi_{n}(\theta)\right)^{T} = \phi(\theta)\in C\left([-\tau, 0];R_{+}^{n}\right). \end{equation}$

(3)

Reference ^[17] suggests that the growth rate of organisms is generally affected by environmental fluctuations accounted for the disturbance of ecological environment in nature, consequently parameters in biologic models will exhibit random perturbations ^[18]. Thus, the deterministic models, like (2) are not applicable to capture the essential characters. In the past years, researchers have suggested the use of white noises to capture the main characters of these stochastic fluctuations, see ^{[18,19,20,21,22,23,24,25,26,27]} for example. Denote by $\{B_{i}(t)\}_{t\geq 0}, (i = 1, 2, \ldots, n)$ the independent standard Brownian motions defined on a complete probability space $(\Omega, \{F_{t}\}_{t\in R_{+}}, P)$ with $\sigma_{i}^{2}$ represents the intensity of the environment noises. Then, the growth rate subject to random perturbation can be described by

$r_{i}\rightarrow r_{i}+\sigma_{i} {\rm d}B_{i}(t),$

with which the model (2) reads

(4)

We further consider the optimal harvesting problem of model (4). The research on the optimal harvesting of the population is of great significance to the utilization and development of resources, and can also help mankind to get the optimal strategy of harvesting in order to obtain the most long-term benefits ^{[28,29,30,31,32,33,34,35]}. Then, we reach the following model accounted for harvesting:

(5)

where $h_{i}\geq 0$ denotes the harvesting effort of the species $i$ .

In the rest of the paper, we will devote ourselves to explore the dynamics and the optimal harvesting strategy of model (5). More precisely, in Section 2, we establish necessary conditions for persistence of species in mean and extinction of the species. In Section 3, we investigate conditions of stability, and prove asymptotic stability in distribution of the model, namely, there is a unique probability measure $\rho(\cdot)$ such that for each $\phi \in C([-\tau, 0];R_{+}^{n})$ , the transition probability $p(t, \phi, \cdot)$ of $x(t)$ converges weekly to $\rho(\cdot)$ when $t\rightarrow\infty$ . In Section 4, by the use of the Hessian matrix and theorems of optimal harvesting due to ^[36], we investigate the optimal harvesting effort and gain the maximum of expectation of sustainable yield (ESY). In Section 5, we numerically illustrate our theoretical results obtained in previous sections, and then conclude our study in Section 6.

2. Persistence and extinction

For the convenience of the following discussion, we define some notations as follows

$b_{i} = r_{i}-h_{i}-0.5\sigma_{i}^{2}, \;q_{i j} = a_{ii}+\sum\limits_{j = 1, j\neq i}^{n}D_{ij}\alpha_{ij}, \;c_{i} = b_{i}-\sum\limits_{j = 1, j\neq i}^{n}\frac{a_{ij}}{q_{ji}}b_{j}, \;i, j = 1, \ldots, n,$

and assume that $\sum_{j = 1, j\neq i}^{n}a_{ij}\geq \sum_{j = 1, j\neq i}^{n}D_{ij}e^{-d_{j}\tau_{ij}}$ holds in the rest of the paper.

Following the same argument as in ^[37], we can prove the existence of the positive solution.

Lemma 2.1. Given initial value (3), model (5) admits a unique global positive solution $x(t) = \left(x_{1}(t), \ldots, x_{n}(t)\right)^{T}$ almost surely. Furthermore, for each $p>1$ , there exists a positive constant $K = K(p)$ such that

$\begin{equation} \limsup\limits_{t\rightarrow+\infty}\mathbb{E}\bigg|x(t)\bigg|^{p}\leq K. \end{equation}$

(6)

To show our main result of this section, we consider the following auxiliary equations

$\begin{equation} {\rm d}\Phi_{i}(t) = \Phi_{i}(t)\bigg(r_{i}-h_{i}-a_{ii}\Phi_{i}(t)-\sum\limits_{j = 1, j\neq i}^{n}D_{ij}\alpha_{i j}\Phi_{i}(t)\bigg) {\rm d}t+\sigma_{i}\Phi_{i}(t) {\rm d}B_{i}(t), \end{equation}$

(7)

$\begin{eqnarray} {\rm d}\Psi_{i}(t)& = &\Psi_{i}(t)\bigg(r_{i}-h_{i}-a_{ii}\Psi_{i}(t)-\sum\limits_{j = 1, j\neq i}^{n}a_{i j}\Phi_{j}(t)+\sum\limits_{j = 1, j\neq i}^{n}D_{ij}e^{-d_{j}\tau_{i j}}\Phi_{j}(t-\tau_{i j})\\ &&-\sum\limits_{j = 1, j\neq i}^{n}D_{i j}\alpha_{ij}\Psi_{i}(t)\bigg) {\rm d}t+\sigma_{i}\Psi_{i}(t) {\rm d}B_{i}(t), \end{eqnarray}$

(8)

with initial value

$\Phi_{i}(\theta) = \Psi_{i}(\theta) = x_{i}(\theta), \;\theta\in[-\tau, 0], \;i = 1, 2, \ldots, n.$

By [38,Stochastic Comparison Theorem], we know that for $t\geq -\tau$ ,

$\begin{equation} \Psi_{i}(\theta)\leq x_{i}(\theta)\leq \Phi_{i}(\theta)\;a.s., \;i = 1, 2, \ldots, n. \end{equation}$

(9)

Remark 1. It is easy to see from ^[39] that the explicit solution of (7) is

$\begin{equation} \Phi_{i}(t) = \frac{\exp\{b_{i}t+\sigma_{i}B_{i}(t)\}}{\Phi_{i}^{-1}(0)+(a_{ii}+\sum\limits_{j = 1, j\neq i}^{n}D_{ij}\alpha_{i j})\int_{0}^{t}\exp\{b_{i}s+\sigma_{i}B_{i}(s)\} {\rm d}s}, \;i = 1, 2, \ldots, n. \end{equation}$

(10)

Similar calculation gives

$\begin{eqnarray} \Psi_{i}(t)& = &\exp\bigg\{b_{i}t-\sum\limits_{j = 1, j\neq i}^{n}a_{i j}\int_{0}^{t}\Phi_{j}(s) {\rm d}s+\sum\limits_{j = 1, j\neq i} ^{n}D_{i j}e^{-d_{j}\tau_{i j}}\int_{0}^{t}\Phi_{j}(s-\tau_{i j}) {\rm d}s+\sigma_{i} {\rm d}B_{i}(t)\bigg\}\\ &&\times\bigg\{ \Psi_{i}^{-1}(0)+\bigg(a_{ii}+\sum\limits_{j = 1, j\neq i}^{n}D_{i j}\alpha_{i j}\bigg)\int_{0}^{t}\exp\bigg\{b_{i}s-\sum\limits_{j = 1, j\neq i}^{n} a_{i j}\int_{0}^{s}\Phi_{j}(u) {\rm d}u\\ &&+\sum\limits_{j = 1, j\neq i}^{n}D_{i j}e^{-d_{j}\tau_{i j}}\int_{0}^{s}\Phi_{j}(u- \tau_{i j}) {\rm d}u+\sigma_{i}B_{i}(s)\bigg\} {\rm d}s\bigg\}^{-1}, \;i = 1, 2, \ldots, n. \end{eqnarray}$

(11)

Then, by using ^[40], we obtain the following.

Lemma 2.2. Let $b_{i}>0$ . Then, from (7) we have

$\begin{equation} \lim\limits_{t\rightarrow+\infty}t^{-1}\ln\Phi_{i}(t) = 0, \;\lim\limits_{t\rightarrow+\infty}t^{-1}\int_{0}^{t}\Phi_{i}(s) {\rm d}s = \frac{b_{i}}{q_{ij}}, \;a.s., \;i = 1, 2, \ldots, n. \end{equation}$

(12)

Based on Lemma 2, we assume:

Assumption 2.1. $b_{i}>0, \;c_{i}>0, \;i = 1, 2, \ldots, n.$

Remark 2. A result due to Golpalsamy ^[10] and Assumption 2.1 imply that there exists a unique positive solution $(\det(A_{1})/\det (A), \ldots, \det(A_{n})/\det (A))^{T}$ for the following system

$\begin{equation} \left\{\begin{array}{l} {(a_{11}+\sum\limits_{j = 2}^{n}D_{1j}\alpha_{1j})x_{1}+(a_{12}-D_{12}e^{-d_{2}\tau_{12}})x_{2}+\ldots+(a_{1n}- D_{1n}e^{-d_{n}\tau_{1 n}})x_{n} = b_{1}\triangleq r_{1}-h_{1}-\frac{1}{2}\sigma_{1}^{2}, }\\ {(a_{21}-D_{21}e^{-d_{1}\tau_{21}})x_{1}+(a_{22}+\sum\limits_{j = 1, j\neq 2}^{n}D_{2j}\alpha_{2j})x_{2}+\ldots+(a_{2 n}-D_{2 n}e^{-d_{n}\tau_{2n}})x_{n} = b_{2}\triangleq r_{2}-h_{2}-\frac{1}{2}\sigma_{2}^{2}, }\\ {\ldots\ldots\ldots\ldots\ldots\ldots\ldots\ldots\ldots\ldots\ldots\ldots\ldots\ldots\ldots\ldots\ldots \ldots\ldots\ldots\ldots\ldots\ldots\ldots\ldots\ldots\ldots\ldots}, \\ {(a_{n1}-D_{n1}e^{-d_{1}\tau_{n1}})x_{1}+(a_{n2}-D_{n2}e^{-d_{2}\tau_{n 2}})x_{2}+\ldots+ (a_{nn}+\sum\limits_{j = 1}^{n-1}D_{nj}\alpha_{nj})x_{n} = b_{n}\triangleq r_{n}-h_{n}-\frac{1}{2}\sigma_{n}^{2}}, \end{array} \right. \end{equation}$

(13)

in which

$A = \left( \begin{array}{cccc} a_{11}+\sum_{j = 2}^{n}D_{1j}\alpha_{1j} & a_{12}-D_{12}e^{-d_{2}\tau_{12}} & \cdots & a_{1n}-D_{1n}e^{-d_{n}\tau_{1 n}} \\ a_{21}-D_{21}e^{-d_{1}\tau_{21}} & a_{22}+\sum\limits_{j = 1, j\neq 2}^{n}D_{2j}\alpha_{2j} & \cdots & a_{2 n}-D_{2 n}e^{-d_{n}\tau_{2n}} \\ \vdots & \vdots & \ddots & \vdots \\ a_{n1}-D_{n1}e^{-d_{1}\tau_{n1}} & a_{n2}-D_{n2}e^{-d_{2}\tau_{n 2}} & \cdots &a_{nn}+\sum_{j = 1}^{n-1}D_{nj}\alpha_{nj} \end{array} \right)$

and $A_{i}$ is the matrix given by using the $(b_{1}, b_{2}, \ldots, b_{n})^{T}$ to replace the $i$ th column of matrix $A$ .

Now we are in the position to show our main results.

Theorem 2.1. All species in system (5) are persistent in mean $a.s.$ , $i.e.$ ,

$\begin{equation} \lim\limits_{t\rightarrow+\infty}t^{-1}\int_{0}^{t}x_{i}(s) {\rm d}s = \det(A_{i})/\det(A) \gt 0\;\;a.s., \;i = 1, 2, \ldots, n. \end{equation}$

(14)

when Assumption 2.1 is satisfied.

Proof. Let $b_{i}>0$ , according to (12) that for $i, j = 1, 2, \ldots, n, \;j\neq i$ , one has

$\begin{equation} \lim\limits_{t\rightarrow+\infty}t^{-1}\int_{t-\tau_{ij}}^{t}\Phi_{j}(s) {\rm d}s = \lim\limits_{t\rightarrow+\infty}\bigg(t^{-1}\int_{0} ^{t}\Phi_{j}(s) {\rm d}s-t^{-1}\int_{0}^{t-\tau_{ij}}\Phi_{j}(s) {\rm d}s\bigg) = 0, \end{equation}$

(15)

which together with (9) yields

$\begin{equation} \lim\limits_{t\rightarrow+\infty}t^{-1}\int_{t-\tau_{i j}}^{t}x_{j}(s) {\rm d}s = 0, \;i, j = 1, 2, \ldots, n, \;j\neq i. \end{equation}$

(16)

By using Itô's formula to (5), one can see that

$\begin{align} &t^{-1}\ln x_{i}(t)-t^{-1}\ln x_{i}(0)\\ = &b_{i}- a_{ii}t^{-1}\int_{0}^{t}x_{i}(s) {\rm d}s- \sum\limits_{j = 1, j\neq i}^{n}a_{ij}t^{-1}\int_{0}^{t}x_{j}(s) {\rm d}s +\sum\limits_{j = 1, j\neq i}^{n}D_{ij}e^{-d_{j}\tau_{ij}}t^{-1}\int_{0}^{t}x_{j}(s-\tau_{ij}) {\rm d}s\\ &-\sum\limits_{j = 1, j\neq i}^{n}D_{ij}\alpha_{ij}t^{-1}\int_{0}^{t}x_{j}(s) {\rm d}s+\sigma_{i}t^{-1}B_{i}(t)\\ = &b_{i}-\bigg[a_{ii}t^{-1}\int_{0}^{t}x_{i}(s) {\rm d}s+ \sum\limits_{j = 1, j\neq i}^{n}a_{ij}t^{-1}\int_{0}^{t}x_{j}(s) {\rm d}s- \sum\limits_{j = 1, j\neq i}^{n}D_{ij}e^{-d_{j}\tau_{ij}}t^{-1}\int_{0}^{t}x_{j}(s) {\rm d}s\\ &+\sum\limits_{j = 1, j\neq i}^{n}D_{ij}\alpha_{ij}t^{-1}\int_{0}^{t}x_{i}(s) {\rm d}s\bigg]+\sum\limits_{j = 1, j\neq i}^{n}D_{ij}e^{-d_{j}\tau_{ij}}t^{-1}\bigg[\int_{-\tau_{ij}}^{0}x_{j}(s) {\rm d}s\ -\int_{t-\tau_{i j}}^{t}x_{j}(s) {\rm d}s\bigg]\\ &+\sigma_{i}t^{-1}B_{i}(t), \;\;\;i, j = 1, 2\ldots, n, \;i\neq j. \end{align}$

(17)

According to (16) together with the property of Brownian motion, we obtain

$\lim\limits_{t\rightarrow+\infty}t^{-1}\bigg[\int_{-\tau_{i j}}^{0}x_{j}(s) {\rm d}s-\int_{t-\tau_{i j}}^{t}x_{j}(s) {\rm d}s\bigg] = 0,$

$\lim\limits_{t\rightarrow+\infty}t^{-1}B_{i}(t) = 0, \;\;\lim\limits_{t\rightarrow+\infty}t^{-1}\ln x_{i}(0) = 0, \;a.s.$

We next to show that

$\lim\limits_{t\rightarrow+\infty}t^{-1}\ln x_{i}(t) = 0, \;i = 1, 2, \ldots, n.$

In view of (9) and (12), we have

$\liminf\limits_{t\rightarrow+\infty}t^{-1}\ln \Psi_{i}(t)\leq \liminf\limits_{t\rightarrow+\infty}t^{-1}\ln x_{i}(t)\leq \limsup\limits_{t\rightarrow+\infty}t^{-1}\ln x_{i}(t)\leq \limsup\limits_{t\rightarrow+\infty}t^{-1}\ln \Phi_{i}(t) = 0.$

Therefore we obtain

$\begin{equation} \liminf\limits_{t\rightarrow+\infty}t^{-1}\ln \Psi_{i}(t)\geq 0\;a.s., \;i = 1, 2, \ldots, n. \end{equation}$

(18)

From (15) and (12), we get

$\begin{align} &\lim\limits_{t\rightarrow+\infty}t^{-1}\int_{0}^{t}\Phi_{j}(s-\tau_{i j}) {\rm d}s\\ & = \lim\limits_{t\rightarrow+\infty}t^{-1}\bigg(\int_{0}^{t}\Phi_{j}(s) {\rm d}s-\int_{t-\tau_{i j}}^{t}\Phi_{j}(s) {\rm d}s +\int_{\tau_{i j}}^{0}\Phi_{j}(s) {\rm d}s\bigg)\\ & = \frac{b_{j}}{q_{ji}}, \;\;a.s., \;\;i, j = 1, 2\ldots, n, \;i\neq j. \end{align}$

By using $\lim_{t\rightarrow+\infty}t^{-1}B_{i}(t) = 0$ together with what we have just obtained, yields that for any given $\varepsilon>0$ , there exists a $T = T(\omega)$ thus for $t\geq T, \;i, j = 1, 2\ldots, n, \;i\neq j,$

$b_{j}/q_{ji}-\varepsilon\leq t^{-1}\int_{0}^{t}\Phi_{j}(s-\tau_{ij}) {\rm d}s\leq b_{j}/q_{ji}+\varepsilon, \;\;-\varepsilon\leq t^{-1}\sigma_{i}B_{i}(t)\leq \varepsilon.$

Applying these inequalities to (11), we have

$\begin{align} &\frac{1}{\Psi_{i}(t)}\\ = &\exp\bigg\{-b_{i}t+\sum\limits_{j = 1, j\neq i}^{n}a_{ij}\int_{0}^{t}\Phi_{j}(s) {\rm d}s- \sum\limits_{j = 1, j\neq i}^{n}D_{ij}e^{-d_{j}\tau_{ij}}\int_{0}^{t}\Phi_{j}(s-\tau_{ij}) {\rm d}s- \sigma_{i}B_{i}(t)\bigg\}\\ &\times \bigg\{\Psi_{i}^{-1}(0)+\left(a_{ii}+\sum\limits_{j = 1, j\neq i}^{n}D_{ij}\alpha_{ij}\right) \int_{0}^{t}\exp\bigg\{b_{i}s-\sum\limits_{j = 1, j\neq i}^{n}a_{ij}\int_{0}^{s}\Phi_{j}(u) {\rm d}u\\ &+\sum\limits_{j = 1, j\neq i}^{n}D_{ij}e^{-d_{j}\tau_{ij}}\int_{0}^{s}\Phi_{j}(u-\tau_{ij}) {\rm d}u+ \sigma_{i}B_{i}(s)\bigg\} {\rm d}s\bigg\} \\ = &\exp\bigg\{-b_{i}t+\sum\limits_{j = 1, j\neq i}^{n}a_{ij}\int_{0}^{t}\Phi_{j}(s) {\rm d}s- \sum\limits_{j = 1, j\neq i}^{n}D_{ij}e^{-d_{j}\tau_{ij}}\int_{0}^{t}\Phi_{j}(s-\tau_{ij}) {\rm d}s- \sigma_{i}B_{i}(t)\bigg\}\\ &\times \bigg\{\Psi_{i}^{-1}(0)+\left(a_{ii}+\sum\limits_{j = 1, j\neq i}^{n}D_{ij}\alpha_{ij}\right) \int_{0}^{T}\exp\bigg\{b_{i}s-\sum\limits_{j = 1, j\neq i}^{n}a_{ij}\int_{0}^{s}\Phi_{j}(u) {\rm d}u\\ &+\sum\limits_{j = 1, j\neq i}^{n}D_{ij}e^{-d_{j}\tau_{ij}}\int_{0}^{s}\Phi_{j}(u-\tau_{ij}) {\rm d}u+ \sigma_{i}B_{i}(s)\bigg\} {\rm d}s\\ &+\bigg(a_{ii}+\sum\limits_{j = 1, j\neq i}^{n}D_{ij}\alpha_{ij}\bigg) \int_{T}^{t}\exp\bigg\{b_{i}s-\sum\limits_{j = 1, j\neq i}^{n}a_{ij}\int_{0}^{s}\Phi_{j}(u) {\rm d}u\\ &+\sum\limits_{j = 1, j\neq i}^{n}D_{ij}e^{-d_{j}\tau_{ij}}\int_{0}^{s}\Phi_{j}(u-\tau_{ij}) {\rm d}u+ \sigma_{i}B_{i}(s)\bigg\} {\rm d}s\bigg\} \\ \leq& \exp\bigg\{t\bigg[-b_{i}+\sum\limits_{j = 1, j\neq i}^{n}a_{ij}\bigg(\frac{b_{j}}{q_{ji}}+\varepsilon\bigg)- \sum\limits_{j = 1, j\neq i}^{n}D_{ij}e^{-d_{j}\tau_{ij}}\bigg(\frac{b_{j}}{q_{ji}}-\varepsilon\bigg)+ \varepsilon\bigg]\bigg\}\\ &\times \bigg\{\Psi_{i}^{-1}(0)+M_{ij}+\bigg(a_{ii}+\sum\limits_{j = 1, j\neq i}^{n}D_{ij}\alpha_{ij}\bigg) \int_{T}^{t}\exp\bigg\{s\bigg[b_{i}-\sum\limits_{j = 1, j\neq i}^{n}a_{ij}\bigg(\frac{b_{j}}{q_{ji}}-\varepsilon\bigg)\\ &+\sum\limits_{j = 1, j\neq i}^{n}D_{ij}e^{-d_{j}\tau_{ij}}\bigg(\frac{b_{j}}{q_{ji}}+\varepsilon\bigg) +\varepsilon\bigg]\bigg\} {\rm d}s\bigg\}, \;i, j = 1, \ldots, n, \end{align}$

in which $M_{ij}>0$ is a constant. Note that $c_{i} = b_{i}-\sum_{j = 1, j\neq i}^{n}\frac{a_{ij}}{q_{ji}}b_{j}>0$ , thereby for large enough $t$ , one has that

$\begin{align} &\Psi_{i}^{-1}(0)+M_{ij}\\ &\leq \bigg(a_{ii}+\sum\limits_{j = 1, j\neq i}^{n}D_{ij}\alpha_{ij}\bigg) \int_{T}^{t}\exp\bigg\{s\bigg[b_{i}-\sum\limits_{j = 1, j\neq i}^{n}a_{ij}\bigg(\frac{b_{j}}{q_{ji}}-\varepsilon\bigg)+ \sum\limits_{j = 1, j\neq i}^{n}D_{ij}e^{-d_{j}\tau_{ij}}\bigg(\frac{b_{j}}{q_{ji}}+\varepsilon\bigg) +\varepsilon\bigg]\bigg\} {\rm d}s. \end{align}$

Hence for sufficiently large $t$ , we obtain

$\begin{align} &\frac{1}{\Psi_{i}(t)}\\ \leq&\exp\bigg\{t\bigg[-b_{i}+\sum\limits_{j = 1, j\neq i}^{n}a_{i j}\bigg(\frac{b_{j}}{q_{ji}}+\varepsilon\bigg)- \sum\limits_{j = 1, j\neq i}^{n}D_{i j}e^{-d_{j}\tau_{i j}}\bigg(\frac{b_{j}}{q_{ji}}-\varepsilon\bigg)+ \varepsilon\bigg]\bigg\}\\ &\times 2\bigg(a_{ii}+\sum\limits_{j = 1, j\neq i}^{n}D_{i j}\alpha_{i j}\bigg) \int_{T}^{t}\exp\bigg\{s\bigg[b_{i}-\sum\limits_{j = 1, j\neq i}^{n}a_{ij}\bigg(\frac{b_{j}}{q_{ji}}-\varepsilon\bigg)\\ &+\sum\limits_{j = 1, j\neq i}^{n}D_{i j}e^{-d_{j}\tau_{i j}}\bigg(\frac{b_{j}}{q_{ji}}+\varepsilon\bigg) +\varepsilon\bigg]\bigg\} {\rm d}s \\ = &\frac{2\bigg(a_{ii}+\sum_{j = 1, j\neq i}^{n}D_{i j}\alpha_{i j}\bigg)} {b_{i}-\sum_{j = 1, j\neq i}^{n}a_{i j}\bigg(\frac{b_{j}}{q_{ji}}-\varepsilon\bigg)+ \sum_{j = 1, j\neq i}^{n}D_{i j}e^{-d_{j}\tau_{i j}}\bigg(\frac{b_{j}}{q_{ji}}+\varepsilon\bigg) +\varepsilon}\\ &\times \exp\bigg\{t\bigg[-b_{i}+\sum\limits_{j = 1, j\neq i}^{n}a_{i j}\bigg(\frac{b_{j}}{q_{ji}}+\varepsilon\bigg)- \sum\limits_{j = 1, j\neq i}^{n}D_{i j}e^{-d_{j}\tau_{i j}}\bigg(\frac{b_{j}}{q_{ji}}-\varepsilon\bigg)+ \varepsilon\bigg]\bigg\}\\ &\times \exp\bigg\{\bigg[b_{i}-\sum\limits_{j = 1, j\neq i}^{n}a_{i j}\bigg(\frac{b_{j}}{q_{ji}}-\varepsilon\bigg)+ \sum\limits_{j = 1, j\neq i}^{n}D_{i j}e^{-d_{j}\tau_{i j}}\bigg(\frac{b_{j}}{q_{ji}}+\varepsilon\bigg)+ \varepsilon\bigg](t-T)\bigg\}. \end{align}$

Rearranging this inequality shows that

$\begin{eqnarray} t^{-1}\ln \Psi_{i}(t)&\geq& t^{-1}\ln \frac{b_{i}-\sum_{j = 1, j\neq i}^{n}a_{i j}\bigg(\frac{b_{j}}{q_{ji}}-\varepsilon\bigg)+ \sum_{j = 1, j\neq i}^{n}D_{i j}e^{-d_{j}\tau_{i j}}\bigg(\frac{b_{j}}{q_{ji}}+\varepsilon\bigg)+ \varepsilon}{2\bigg(a_{ii}+\sum_{j = 1, j\neq i}^{n}D_{i j}\alpha_{i j}\bigg)}\\ &&-2\varepsilon \bigg(\sum\limits_{j = 1, j\neq i}^{n}a_{i j}+\sum\limits_{j = 1, j\neq i}^{n}D_{i j}e^{-d_{j}\tau_{i j}}+1\bigg)+ \bigg[b_{i}-\sum\limits_{j = 1, j\neq i}^{n}a_{i j}\bigg(\frac{b_{j}}{q_{ji}}-\varepsilon\bigg)\\ &&+\sum\limits_{j = 1, j\neq i}^{n}D_{i j}e^{-d_{j}\tau_{i j}}\bigg(\frac{b_{j}}{q_{ji}}+\varepsilon\bigg)+ \varepsilon\bigg]\frac{T}{t}. \end{eqnarray}$

Since $t$ is large enough and $\varepsilon$ is arbitrary, we get (14). This completes the proof of Theorem 2.1.

Corollary 2.1. If there is a $b_{i}<0$ , then according to (17), one has $\limsup_{t\rightarrow+\infty}t^{-1}\ln x_{i}(t)\leq b_{i}<0, \;a.s.$ It is to say $\lim_{t\rightarrow+\infty}x_{i}(t) = 0, \;a.s.$ , which means that the $i$ th species in system (5) will die out.

3. Stability in distribution

In this section, we study the stability of the model. To this end, we suppose the following holds:

Assumption 3.1. $a_{ii}+\sum_{j = 1, j\neq i}^{n}D_{ij}\alpha_{ij}\geq \sum_{j = 1, j\neq i}^{n}a_{ji}+\sum_{j = 1, j\neq i}^{n}D_{ji}e^{-d_{i}\tau_{ji}}, \;i = 1, 2, \ldots, n.$

Then, we can prove the following.

Theorem 3.1. The system (5) is asymptotically stable in distribution if Assumption 3.1 holds.

Proof. Given two initial values $\phi(\theta), \psi(\theta) \in C\left([-\tau, 0];R_{+}^{n}\right)$ of model (5), the corresponding solutions are $x^{\phi}(t) = (x_{1}^{\phi_{1}}(t), \ldots, x_{n}^{\phi_{n}}(t))^{T}$ and $x^{\psi}(t) = (x_{1}^{\psi_{1}}(t), \ldots, x_{n}^{\psi_{n}}(t))^{T}$ respectively. Let

$V(t) = \sum\limits_{i = 1}^{n}\bigg|\ln x_{i}^{\phi_{i}}(t)-\ln x_{i}^{\psi_{i}}(t)\bigg|+ \sum\limits_{i = 1}^{n}\sum\limits_{j = 1, j\neq i}^{n}D_{i j}e^{-d_{j}\tau_{i j}} \int_{t-\tau_{i j}}^{t}\bigg|x_{j}^{\phi_{j}}(s)-x_{j}^{\psi_{j}}(s)\bigg| {\rm d}s.$

Applying Itô's formula yields

$\begin{align} & {\rm d}^{+}V(t)\\ = &\sum\limits_{i = 1}^{n} {\rm sgn}\bigg(x_{i}^{\phi_{i}}(t)-x_{i}^{\psi_{i}}(t)\bigg) {\rm d}\bigg(\ln x_{i}^{\phi_{i}}(t)-\ln x_{i}^{\psi_{i}}(t)\bigg) +\sum\limits_{i = 1}^{n}\sum\limits_{j = 1, j\neq i}^{n}D_{ij}e^{-d_{j}\tau_{ij}}\bigg|x_{j}^{\phi_{j}}(t)-x_{j}^{\psi_{j}}(t)\bigg| {\rm d}t\\ &-\sum\limits_{i = 1}^{n}\sum\limits_{j = 1, j\neq i}^{n}D_{i j}e^{-d_{j}\tau_{i j}}\bigg|x_{j}^{\phi_{j}}(t-\tau_{i j})- x_{j}^{\psi_{j}}(t-\tau_{i j})\bigg| {\rm d}t\\ = &\sum\limits_{i = 1}^{n} {\rm sgn}\bigg(x_{i}^{\phi_{i}}(t)-x_{i}^{\psi_{i}}(t)\bigg) \bigg[-a_{ii}\bigg(x_{i}^{\phi_{i}}(t)-x_{i}^{\psi_{i}}(t)\bigg) -\sum\limits_{j = 1, j\neq i}^{n}a_{i j}\bigg(x_{j}^{\phi_{j}}(t)-x_{j}^{\psi_{j}}(t)\bigg)\\ &+\sum\limits_{j = 1, j\neq i}^{n}D_{i j}e^{-d_{j}\tau_{i j}}\bigg(x_{j}^{\phi_{j}}(t-\tau_{i j})-x_{j}^{\psi_{j}}(t-\tau_{i j})\bigg) -\sum\limits_{j = 1, j\neq i}^{n}D_{i j}\alpha_{i j}\bigg(x_{i}^{\phi_{i}}(t)-x_{i}^{\psi_{i}}(t)\bigg)\bigg] {\rm d}t\\ &+\sum\limits_{i = 1}^{n}\sum\limits_{j = 1, j\neq i}^{n}D_{i j}e^{-d_{j}\tau_{i j}}\bigg|x_{j}^{\phi_{j}}(t)-x_{j}^{\psi_{j}}(t)\bigg| {\rm d}t -\sum\limits_{i = 1}^{n}\sum\limits_{j = 1, j\neq i}^{n}D_{i j}e^{-d_{j}\tau_{i j}}\bigg|x_{j}^{\phi_{j}}(t-\tau_{i j})- x_{j}^{\psi_{j}}(t-\tau_{i j})\bigg| {\rm d}t\\ \leq& -\sum\limits_{i = 1}^{n}a_{ii}\bigg|x_{i}^{\phi_{i}}(t)-x_{i}^{\psi_{i}}(t)\bigg| {\rm d}t +\sum\limits_{i = 1}^{n}\sum\limits_{j = 1, j\neq i}^{n}a_{i j}\bigg|x_{j}^{\phi_{j}}(t)-x_{j}^{\psi_{j}}(t)\bigg| {\rm d}t\\ &+\sum\limits_{i = 1}^{n}\sum\limits_{j = 1, j\neq i}^{n}D_{i j}e^{-d_{j}\tau_{i j}}\bigg|x_{j}^{\phi_{j}}(t-\tau_{i j}) -x_{j}^{\psi_{j}}(t-\tau_{i j})\bigg| {\rm d}t +\sum\limits_{i = 1}^{n}\sum\limits_{j = 1, j\neq i}^{n}D_{i j}\alpha_{i j}\bigg|x_{i}^{\phi_{i}}(t)-x_{i}^{\psi_{i}}(t)\bigg| {\rm d}t\\ &+\sum\limits_{i = 1}^{n}\sum\limits_{j = 1, j\neq i}^{n}D_{i j}e^{-d_{j}\tau_{i j}}\bigg|x_{j}^{\phi_{j}}(t)-x_{j}^{\psi_{j}}(t)\bigg| {\rm d}t -\sum\limits_{i = 1}^{n}\sum\limits_{j = 1, j\neq i}^{n}D_{i j}e^{-d_{j}\tau_{i j}}\bigg|x_{j}^{\phi_{j}}(t-\tau_{i j}) -x_{j}^{\psi_{j}}(t-\tau_{i j})\bigg| {\rm d}t\\ = &-\sum\limits_{i = 1}^{n}\bigg(a_{ii}-\sum\limits_{j = 1, j\neq i}^{n}a_{ji}+\sum\limits_{j = 1, j\neq i}^{n}D_{i j}\alpha_{i j} -\sum\limits_{j = 1, j\neq i}^{n}D_{ji}e^{-d_{i}\tau_{ji}}\bigg)\bigg|x_{i}^{\phi_{i}}(t)-x_{i}^{\psi_{i}}(t)\bigg| {\rm d}t. \end{align}$

Therefore

$\mathbb{E}(V(t))\leq V(0)-\sum\limits_{i = 1}^{n}\bigg(a_{ii}-\sum\limits_{j = 1, j\neq i}^{n}a_{ji}+\sum\limits_{j = 1, j\neq i}^{n}D_{i j}\alpha_{i j} -\sum\limits_{j = 1, j\neq i}^{n}D_{ji}e^{-d_{i}\tau_{ji}}\bigg)\int_{0}^{t}\mathbb{E} \bigg|x_{i}^{\phi_{i}}(s)-x_{i}^{\psi_{i}}(s)\bigg| {\rm d}s.$

Together with $\mathbb{E}(V(t))\geq 0$ , one has

$\sum\limits_{i = 1}^{n}\bigg(a_{ii}-\sum\limits_{j = 1, j\neq i}^{n}a_{ji}+\sum\limits_{j = 1, j\neq i}^{n}D_{i j}\alpha_{i j} -\sum\limits_{j = 1, j\neq i}^{n}D_{ji}e^{-d_{i}\tau_{ji}}\bigg)\int_{0}^{t}\mathbb{E} \bigg|x_{i}^{\phi_{i}}(s)-x_{i}^{\psi_{i}}(s)\bigg| {\rm d}s\leq V(0) \lt \infty.$

Hence we have $\mathbb{E}\bigg|x_{i}^{\phi_{i}}(s)-x_{i}^{\psi_{i}}(s)\bigg|\in L^{1}[0, \infty), \;i = 1, 2, \ldots, n.$ At the same time, by using (5) we obtain that

$\begin{align} &\mathbb{E}(x_{i}(t))\\ = &x_{i}(0)+\int_{0}^{t}\bigg[\mathbb{E}(x_{i}(s))(r_{i}-h_{i})-a_{ii}\mathbb{E}(x_{i}(s))^{2}- \sum\limits_{j = 1, j\neq i}^{n}a_{i j}\mathbb{E}(x_{i}(s)x_{j}(s))\\ &+\sum\limits_{j = 1, j\neq i}^{n}D_{i j}e^{-d_{j}\tau_{i j}}\mathbb{E}(x_{i}(s)x_{j}(s-\tau_{i j})) -\sum\limits_{j = 1, j\neq i}^{n}D_{i j}\alpha_{i j}\mathbb{E}(x_{i}(s))^{2}\bigg] {\rm d}s \\ = &x_{i}(0)+\int_{0}^{t}\bigg[\mathbb{E}(x_{i}(s))(r_{i}-h_{i})-a_{ii}\mathbb{E}(x_{i}(s))^{2}- \sum\limits_{j = 1, j\neq i}^{n}a_{i j}\mathbb{E}(x_{i}(s)x_{j}(s))\\ &-\sum\limits_{j = 1, j\neq i}^{n}D_{i j}\alpha_{i j}\mathbb{E}(x_{i}(s))^{2}\bigg] {\rm d}s +\sum\limits_{j = 1, j\neq i}^{n}D_{i j}e^{-d_{j}\tau_{i j}}\bigg[\int_{-\tau_{ij}}^{0}\mathbb{E}(x_{i}(s)x_{j}(s)) {\rm d}s\\ &+\int_{0}^{t}\mathbb{E}(x_{i}(s)x_{j}(s)) {\rm d}s- \int_{t-\tau_{ij}}^{t}\mathbb{E}(x_{i}(s)x_{j}(s)) {\rm d}s\bigg]\\ \leq& x_{i}(0)+\int_{0}^{t}\bigg[\mathbb{E}x_{i}(s)(r_{i}-h_{i})-a_{ii}\mathbb{E}(x_{i}(s))^{2}- \sum\limits_{j = 1, j\neq i}^{n}a_{i j}\mathbb{E}(x_{i}(s)x_{j}(s))\\ &-\sum\limits_{j = 1, j\neq i}^{n}D_{i j}\alpha_{i j}\mathbb{E}(x_{i}(s))^{2}\bigg] {\rm d}s +\sum\limits_{j = 1, j\neq i}^{n}D_{i j}e^{-d_{j}\tau_{i j}}\bigg[\int_{-\tau_{ij}}^{0}\mathbb{E}(x_{i}(s)x_{j}(s)) {\rm d}s\\ &+\int_{0}^{t}\mathbb{E}(x_{i}(s)x_{j}(s)) {\rm d}s\bigg]. \end{align}$

That is to say $\mathbb{E}(x_{i}(t))$ is continuously differentiable with respect of $t$ . Computing by (5) leads to

$\begin{align} &\frac{ {\rm d}\mathbb{E}(x_{i}(t))}{ {\rm d}t}\\ \leq& \mathbb{E}(x_{i}(t))(r_{i}-h_{i})-\bigg(a_{ii}+\sum\limits_{j = 1, j\neq i}^{n}D_{i j}\alpha_{i j}\bigg)\mathbb{E}(x_{i}(t))^{2} -\sum\limits_{j = 1, j\neq i}^{n}a_{i j}\mathbb{E}(x_{i}(t)x_{j}(t))\\ &+\sum\limits_{j = 1, j\neq i}^{n}D_{i j}e^{-d_{j}\tau_{i j}}\mathbb{E}(x_{i}(t)x_{j}(t))\\ \leq& \mathbb{E}(x_{i}(t))r_{i}\leq r_{i}K, \end{align}$

in which $K>0$ is a constant. It implies that $\mathbb{E}(x_{i}(t))$ is uniformly continuous. Using ^[41], we get

$\begin{equation} \lim\limits_{t\rightarrow+\infty}\mathbb{E}|x_{i}^{\phi_{i}}(t)-x_{i}^{\psi_{i}}(t)| = 0, \;a.s., \;i = 1, 2, \ldots, n. \end{equation}$

(19)

Denote $p(t, \phi, {\rm d} y)$ as the transition probability density of the process $x(t)$ and $P(t, \phi, A)$ represents the probability of event $x(t)\in A$ . By (6) and [42,Chebyshev's inequality], we can obtain that the family of $p(t, \phi, {\rm d} y)$ is tight. Now define $\Gamma\left(C\left([-\tau, 0];R^n_+\right)\right)$ as the probability measures on $C\left([-\tau, 0];R^n_+\right)$ . For arbitrary two measures $P_1, P_2\in \Gamma$ , we define the metric

$\begin{equation*} d_\mathbb{L}(P_1, P_2) = \sup\limits_{v\in \mathbb{L}}\bigg|\int_{R^n_+}v(x)P_1(\mathrm{d}x)-\int_{R^n_+}v(x)P_2(\mathrm{d}x)\bigg|, \end{equation*}$

where

$\begin{equation*} \mathbb{L} = \left\{v:C\left([-\tau, 0];R^3_+\right)\rightarrow R:||v(x)-v(y)||\leq\parallel x-y\parallel, | v(\cdot)|\leq1\right\}. \end{equation*}$

Since $\{p(t, \phi, {\rm d} y)\}$ is tight, then according to (19) we know that for any $\varepsilon>0$ , there is a $T>0$ satisfies that for $t\geq T, s>0$ ,

$\begin{equation*} \sup\limits_{v\in \mathbb{L}}\bigg|\mathbb{E}v(x(t+s))-\mathbb{E}v(x(t))\bigg|\leq\varepsilon. \end{equation*}$

Therefore $\{p(t, \xi, \cdot)\}$ is Cauchy in $\Gamma$ with metric $d_\mathbb{L}$ , in which $\xi\in C\left([-\tau, 0];R^n_+\right)$ is arbitrary given. Hence there exists a unique $\kappa(\cdot)\in \Gamma(C([-\tau, 0];R^n_+))$ such that $\lim\limits_{t\rightarrow\infty}d_\mathbb{L}(p(t, \xi, \cdot), \kappa(\cdot)) = 0$ . At the same time, it follows from (19) that

$\begin{equation*} \lim\limits_{t\rightarrow\infty}d_\mathbb{L}(p(t, \phi, \cdot), p(t, \xi, \cdot)) = 0. \end{equation*}$

Consequently,

$\begin{equation*} \lim\limits_{t\rightarrow\infty}d_\mathbb{L}(p(t, \phi, \cdot), \kappa(\cdot))\leq\lim\limits_{t\rightarrow \infty}d_\mathbb{L}(p(t, \phi, \cdot), p(t, \xi, \cdot))+\lim\limits_{t\rightarrow\infty}d_\mathbb{L} (p(t, \xi, \cdot), \kappa(\cdot)) = 0. \end{equation*}$

This completes the proof of Theorem 3.1.

4. Optimal harvesting

In this section, we consider the optimal harvesting problem of system (5). Our purpose is to find the optimal harvesting effort $H^{*} = (h_{1}^{*}, \ldots, h_{n}^{*})$ such that:

(ⅰ) $Y(H) = \lim_{t\rightarrow+\infty}\sum_{i = 1}^{n}\mathbb{E}(h_{i}x_{i}(t))$ is maximum;

(ⅱ) Every $x_{i}(i = 1, 2, \ldots, n)$ is persistent in the mean.

Before we give our main results, we define

$\begin{equation} \Theta = (\theta_{1}, \theta_{2}, \ldots, \theta_{n})^{T} = [A(A^{-1})^{T}+I]^{-1}G, \end{equation}$

(20)

in which $G = (r_{1}-0.5\sigma_{1}^{2}, r_{2}-0.5\sigma_{2}^{2}, \ldots, r_{n}-0.5\sigma_{n}^{2})^{T}$ and $I$ is the unit matrix, and make an assumption:

Assumption 4.1. $A^{-1}+(A^{-1})^{T}$ is positive definite,

Theorem 4.1. Suppose Assumptions 3.1 and 4.1 hold, and If these following inequalities

$\begin{equation} \theta_{i}\geq 0, \;b_{i}\mid_{h_{i} = \theta_{i}} \gt 0, \;c_{i}\mid_{h_{m} = \theta_{m}, \;m = 1, 2, \ldots, n} \gt 0, i = 1, \cdots, n \end{equation}$

(21)

are satisfied. Then, for system (5) the optimal harvesting effort is

$\begin{equation*} H^{*} = \Theta = [A(A^{-1})^{T}+I]^{-1}G \end{equation*}$

and the maximum of ESY is

$\begin{equation} Y^{*} = \Theta^{T}A^{-1}(G-\Theta). \end{equation}$

(22)

Proof. Denote $W = \{H = (h_{1}, \ldots, h_{n})^{T}\in R^{n}\mid b_{i}>0, \;c_{i}>0, \;h_{i}>0, \;i = 1, \ldots, n\}$ . Easily we can see that for any $H\in W$ , (14) is satisfied. Note that $\Theta\in W$ , then $W$ is not empty. According to (14), we have that for every $H\in W$ ,

$\begin{equation} \lim\limits_{t\to+\infty} t^{-1}\int_0^tH^\mathrm{T}x(s)\mathrm{d}s = \sum\limits_{i = 1}^n h_i\lim\limits_{t\to+\infty} t^{-1}\int_0^tx_{i}(s)\mathrm{d}s = H^\mathrm{T}A^{-1}(G-H). \end{equation}$

(23)

Applying Theorem 4.1, there is a unique invariant measure $\rho(\cdot)$ for model (5). By [43,Corollary 3.4.3], we obtain that $\rho(\cdot)$ is strong mixing. Meanwhile, it is ergodic according to [43,Theorem 3.2.6]. It means

$\begin{equation} \lim\limits_{t\to+\infty} t^{-1}\int_0^tH^\mathrm{T}x(s)\mathrm{d}s = \int_{R^n_+}H^\mathrm{T}x\rho(\mathrm{d}x). \end{equation}$

(24)

Let $\mu(x)$ represent the stationary probability density of system (5), then we have

$\begin{equation} Y(H) = \lim\limits_{t\to+\infty}\sum\limits_{i = 1}^n\mathbb{E}(h_ix_{i}(t)) = \lim\limits_{t\to+\infty}\mathbb{E}(H^\mathrm{T}x(t)) = \int_{R^n_+}H^\mathrm{T}x\mu(x)\mathrm{d}x. \end{equation}$

(25)

Since the invariant measure of model (9) is unique, one has

$\begin{equation} \int_{R^n_+}H^\mathrm{T}x\mu(x)\mathrm{d}x = \int_{R^n_+}H^\mathrm{T}x\rho(\mathrm{d}x). \end{equation}$

(26)

In other words,

$\begin{equation} Y(H) = H^\mathrm{T}A^{-1}(G-H). \end{equation}$

(27)

Assume that $\Theta = (\theta_{1}, \theta_{2}, \ldots, \theta_{n})^{T}$ is the solution of the following equation

$\begin{equation} \begin{aligned} \frac{\mathrm{d}Y(H)}{\mathrm{d}H}& = \frac{\mathrm{d}H^\mathrm{T}}{\mathrm{d}H}A^{-1}(G-H)+ \frac{\mathrm{d}}{\mathrm{d}H}\left[(G-H)^\mathrm{T}(A^{-1})^\mathrm{T}\right]H\\ & = A^{-1}G-\left[A^{-1}+(A^{-1})^\mathrm{T}\right]H\\ & = 0. \end{aligned} \end{equation}$

(28)

Thus, $\Theta = [A(A^{-1})^\mathrm{T}+I]^{-1}G$ . By using of the Hessian matrix (see ^[44,45]),

$\begin{equation*} \begin{aligned} \frac{\mathrm{d}}{\mathrm{d}H^\mathrm{T}}\left[\frac{\mathrm{d}Y(H)}{\mathrm{d}H}\right] & = \left(\frac{\mathrm{d}}{\mathrm{d}H}\left[\left(\frac{\mathrm{d}Y(H)}{\mathrm{d}H}\right)^\mathrm{T}\right]\right) ^\mathrm{T} \\ & = \left(\frac{\mathrm{d}}{\mathrm{d}H}\left[G^\mathrm{T}(A^{-1})^\mathrm{T}-H^\mathrm{T}[A^{-1}+(A^{-1})^\mathrm {\mathrm{T}}]\right]\right)^\mathrm{T}\\ & = -A^{-1}-(A^{-1})^\mathrm{T} \end{aligned} \end{equation*}$

is negative defined, then $\Theta$ is the unique extreme point of $Y(H)$ . That is to say, if $\Theta\in W$ and under the condition of (21), the optimal harvesting effort is $H^* = \Theta$ and $Y^*$ is the maximum value of ESY. This completes the proof of Theorem 4.1.

5. Numerical simulations

To see our analytical results more clearly, we shall give some numerical simulations in this section. Without loss of generality, we consider the following system

$\begin{equation} \left\{\begin{aligned} {\rm d}x_{1}(t) = &x_{1}(t)\bigg[r_{1}-h_{1}-a_{11}x_{1}(t)-a_{12}x_{2}(t)+ D_{12}e^{-d_{2}\tau_{12}}x_{2}(t-\tau_{12})-D_{12}\alpha_{12}x_{1}(t)\bigg] {\rm d}t\\ &+\sigma_{1}x_{1}(t) {\rm d}B_{1}(t), \\ {\rm d}x_{2}(t)& = x_{2}(t)\bigg[r_{2}-h_{2}-a_{22}x_{2}(t)-a_{21}x_{1}(t)+ D_{21}e^{-d_{1}\tau_{21}}x_{1}(t-\tau_{21})-D_{21}\alpha_{21}x_{2}(t)\bigg] {\rm d}t\\ &+\sigma_{2}x_{2}(t) {\rm d}B_{2}(t), \end{aligned} \right. \end{equation}$

(29)

which is the case when $n = 2$ in (5), with initial value

$x(\theta) = \phi(\theta)\in C\left([-\tau, 0];R_{+}^{2}\right), \;\tau = \max\{\tau_{1}, \tau_{2}\},$

where $r_{i}>0, \;a_{ij}>0, \;\tau_{i}\geq 0, \;i, j = 1, 2$ .

Firstly, we discuss the persistence in mean of $x_{1}$ and $x_{2}$ . For that, we take the parameter values as follows:

Table 1. Parameter Values for Figure 1–3.

Parameter	Value	Parameter	Value	Parameter	Value
$r_{1}$	0.9	$h_{1}$	0.1	$\alpha_{12}$	0.6
$r_{2}$	0.8	$h_{2}$	0.05	$\alpha_{21}$	0.3
$a_{11}$	0.6	$a_{12}$	0.2	$a_{21}$	0.35
$a_{22}$	0.23	$\sigma_{1}$	0.05	$\sigma_{2}$	0.05
$d_{1}$	1	$d_{2}$	1	$D_{12}$	4
$D_{21}$	3	$\tau_{12}$	8	$\tau_{21}$	5

| Show Table

DownLoad: CSV

The initial values are $x_{1}(\theta) = 0.5+0.01\sin\theta$ , $x_{2}(\theta) = 0.5+0.02\sin\theta$ , $\theta\in[-\tau, 0]$ . Simple calculations show that $b_{1} = 0.7988>0, \;b_{2} = 0.7488>0, \;c_{1} = 0.6662>0, \;c_{2} = 0.6556>0$ implying Assumption 2.1 is satisfied. Then by Theorem 2.1, we can obtain that in (29)

Figure 1. Time series of species

$x_{1}$ and

$x_{2}$ of system (29) with initial values

$x_{1}(\theta) = 0.5+0.01\sin\theta$ ,

$x_{2}(\theta) = 0.5+0.02\sin\theta$ ,

$\theta\in[-\tau, 0]$ and parameter values in Table 1.

DownLoad: Full-Size Img PowerPoint

$\lim\limits_{t\rightarrow+\infty}t^{-1}\int_{0}^{t}x_{1}(s) {\rm d}s = \det(A_{1})/\det(A) = 0.2268 \gt 0\;\;a.s.,$

$\lim\limits_{t\rightarrow+\infty}t^{-1}\int_{0}^{t}x_{2}(s) {\rm d}s = \det(A_{2})/\det(A) = 0.5964 \gt 0\;\;a.s..$

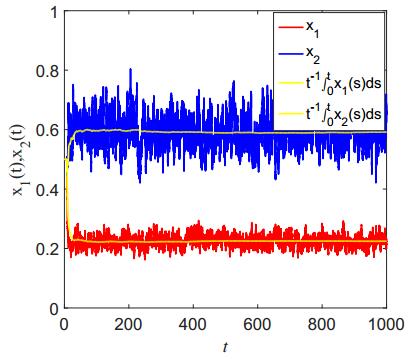
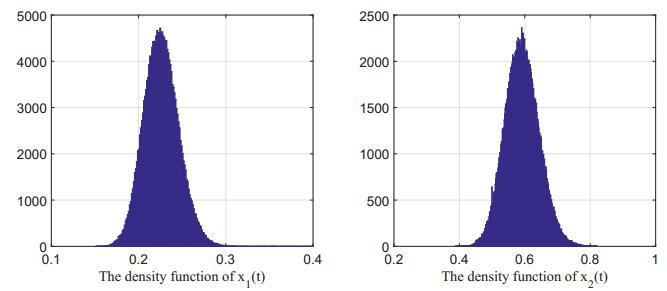
Applying the Milstein numerical method in ^[47], we then obtained the numerical solution of system (29), see Figure 1. It shows that $x_{1}$ and $x_{2}$ respectively asymptotical approach to 0.2268 and 0.5964 time averagely. And this agrees well with our results in Theorem 2.1. Then we research the distributions of $x_{1}$ and $x_{2}$ under the same conditions. Obviously, we have $a_{11}+D_{12}\alpha_{12}\geq a_{21}+D_{21}e^{-d_{1}\tau_{21}}, \;a_{22}+D_{21}\alpha_{21}\geq a_{12}+D_{12}e^{-d_{2}\tau_{12}}$ , it is to say Assumption 3.1 is satisfied. Thus by Theorem 3.1, system (29) is asymptotically stable in distribution as suggested by Figure 2.

Figure 2. Distributions of species

$x_{1}$ and

$x_{2}$ of system (29) with initial values

$x_{1}(\theta) = 0.5+0.01\sin\theta$ ,

$x_{2}(\theta) = 0.5+0.02\sin\theta$ ,

$\theta\in[-\tau, 0]$ and parameter values in Table 1.

DownLoad: Full-Size Img PowerPoint

Lastly, we consider the optimal harvesting strategy of system (29). It is easy to see that the Assumption 2.1 and Assumption 3.1 are satisfied. Furthermore, we have

$\Theta = (\theta_{1}, \theta_{2})^{T} = [A(A^{-1})^{T}+I]^{-1}(r_{1}-0.5\sigma_{1}^{2}, r_{2} -0.5\sigma_{2}^{2})^{T} = (0.4817, 0.3820)^{T},$

in which $I = \left( \begin{array}{cc} 1 & 0 \\ 0 & 1 \end{array} \right)$ . Since condition (21) is satisfied, by Theorem 4.1, the optimal harvesting effort is

$H^{*} = \Theta = (\theta_{1}, \theta_{2})^{T} = [A(A^{-1})^{T}+I]^{-1}(r_{1}-0.5\sigma_{1}^{2}, r_{2} -0.5\sigma_{2}^{2})^{T} = (0.4817, 0.3820)^{T},$

on the other hand, the maximum of ESY is

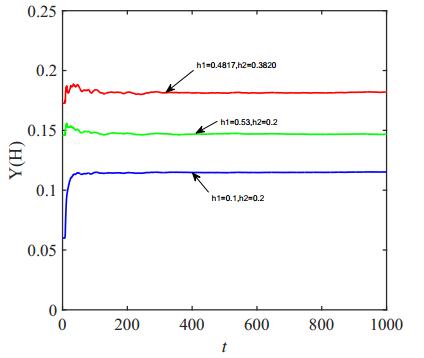
$Y^{*} = \Theta^{T}A^{-1}(r_{1}-0.5\sigma_{1}^{2}-\theta_{1}, r_{2}- 0.5\sigma_{2}^{2}-\theta_{2})^{T} = 0.1789.$

By using the Monte Carlo method (see ^[48]) and the parameters in Table 1, we can obtain Figure 3, showing our results in Theorem 4.1.

Figure 3. The harvesting policies

$E[h_{1}x_{1}(t)+h_{2}x_{2}(t)]$ of system (29) with initial values

$x_{1}(\theta) = 0.5+0.01\sin\theta$ ,

$x_{2}(\theta) = 0.5+0.02\sin\theta$ ,

$\theta\in[-\tau, 0]$ and parameter values in Table 1. The red line is with

$h_{1} = h_{1}^{*} = 0.4817, \;h_{2} = h_{2}^{*} = 0.3820$ , the green line is with

$h_{1} = 0.53, \;h_{2} = 0.2$ , the blue line is with

$h_{1} = 0.1, \;h_{2} = 0.2$ .

DownLoad: Full-Size Img PowerPoint

Table 2. Parameter Values for Figure 4-6.

Parameter	Value	Parameter	Value	Parameter	Value
$r_{1}$	2	$h_{1}$	0.4452	$\alpha_{12}$	0.8
$r_{2}$	1.12	$h_{2}$	0.3307	$\alpha_{13}$	0.67
$r_{3}$	0.6	$h_{3}$	0.3307	$\alpha_{21}$	0.56
$\alpha_{23}$	0.8	$\alpha_{31}$	0.6	$\alpha_{32}$	0.77
$a_{11}$	0.18	$a_{12}$	0.35	$a_{13}$	0.3
$a_{21}$	0.45	$a_{22}$	0.22	$a_{23}$	0.6
$a_{31}$	0.4	$a_{32}$	0.3	$a_{33}$	0.2
$\sigma_{1}$	0.05	$\sigma_{2}$	0.05	$\sigma_{3}$	0.05
$d_{1}$	0.39	$d_{2}$	0.57	$d_{3}$	0.37
$\tau_{12}$	3	$\tau_{13}$	3	$\tau_{21}$	5
$\tau_{22}$	5	$\tau_{31}$	4	$\tau_{32}$	5.5
$D_{12}$	4	$D_{13}$	5	$D_{21}$	2.4
$D_{23}$	4	$D_{31}$	2	$D_{32}$	2.5

| Show Table

DownLoad: CSV

Next, we consider a case of three species.

$\begin{equation} \left\{\begin{aligned} {\rm d}x_{1}(t) = &x_{1}(t)\bigg[r_{1}-h_{1}-a_{11}x_{1}(t)-\bigg(a_{12}x_{2}(t)+a_{13}x_{3}(t)\bigg)+ \bigg(D_{12}e^{-d_{2}\tau_{12}}x_{2}(t-\tau_{12})\\ &+D_{13}e^{-d_{3}\tau_{13}}x_{3}(t-\tau_{13})\bigg) -\bigg(D_{12}\alpha_{12}x_{1}(t)+D_{13}\alpha_{13}x_{1}(t)\bigg)\bigg] {\rm d}t\\ &+\sigma_{1}x_{1}(t) {\rm d}B_{1}(t), \\ {\rm d}x_{2}(t) = &x_{2}(t)\bigg[r_{2}-h_{2}-a_{22}x_{2}(t)-\bigg(a_{21}x_{1}(t)+a_{23}x_{3}(t)\bigg)+ \bigg(D_{21}e^{-d_{1}\tau_{21}}x_{1}(t-\tau_{21})\\ &+D_{23}e^{-d_{3}\tau_{23}}x_{3}(t-\tau_{23})\bigg) -\bigg(D_{21}\alpha_{21}x_{2}(t)+D_{23}\alpha_{23}x_{2}(t)\bigg)\bigg] {\rm d}t\\ &+\sigma_{2}x_{2}(t) {\rm d}B_{2}(t), \\ {\rm d}x_{3}(t) = &x_{3}(t)\bigg[r_{3}-h_{3}-a_{33}x_{3}(t)-\bigg(a_{31}x_{1}(t)+a_{32}x_{2}(t)\bigg)+ \bigg(D_{31}e^{-d_{1}\tau_{31}}x_{1}(t-\tau_{31})\\ &+D_{32}e^{-d_{2}\tau_{32}}x_{2}(t-\tau_{32})\bigg) -\bigg(D_{31}\alpha_{31}x_{3}(t)+D_{32}\alpha_{32}x_{3}(t)\bigg)\bigg] {\rm d}t\\ &+\sigma_{3}x_{3}(t) {\rm d}B_{3}(t). \end{aligned} \right. \end{equation}$

(30)

We use the following parameter values:

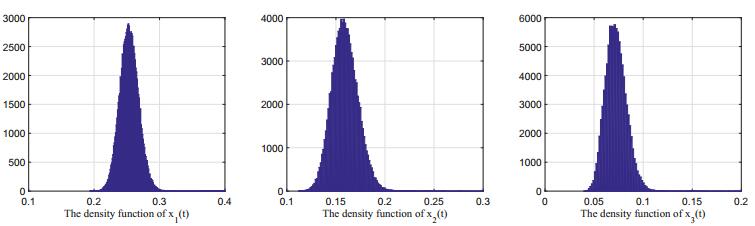
The initial values are $x_{1}(\theta) = 0.5+0.01\sin\theta$ , $x_{2}(\theta) = 0.5+0.02\sin\theta$ , $x_{3}(\theta) = 0.5+0.001\sin\theta$ , $\theta\in[-\tau, 0]$ . Easily we get that $b_{1} = 0.1.5536>0, \;b_{2} = 0.7881>0, \;b_{3} = 0.2681>0, \;c_{1} = 1.4502>0, \;c_{2} = 0.0552>0, \;c_{3} = 0.0229>0.$ Thus Assumption 2.1 is hold. By Theorem 2.1, we have for (30)

$\lim\limits_{t\rightarrow+\infty}t^{-1}\int_{0}^{t}x_{1}(s) {\rm d}s = \det(A_{1})/\det(A) = 0.2543 \gt 0\;\;a.s.,$

$\lim\limits_{t\rightarrow+\infty}t^{-1}\int_{0}^{t}x_{2}(s) {\rm d}s = \det(A_{2})/\det(A) = 0.1601 \gt 0\;\;a.s.,$

$\lim\limits_{t\rightarrow+\infty}t^{-1}\int_{0}^{t}x_{3}(s) {\rm d}s = \det(A_{3})/\det(A) = 0.0730 \gt 0\;\;a.s..$

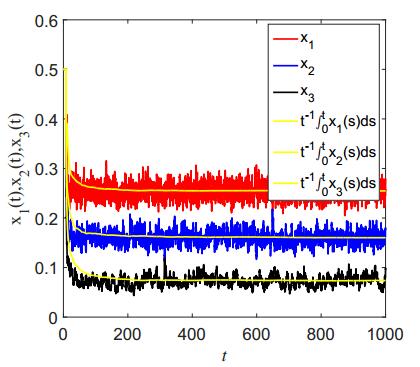
The numerical results of Theorem 2.1 when $n = 3$ are shown in Figure 4.

Figure 4. Time series of species

$x_{1}$ ,

$x_{2}$ and

$x_{3}$ of system (30) with initial values

$x_{1}(\theta) = 0.5+0.01\sin\theta$ ,

$x_{2}(\theta) = 0.5+0.02\sin\theta$ ,

$x_{3}(\theta) = 0.5+0.001\sin\theta$ ,

$\theta\in[-\tau, 0]$ and parameter values in Table 2.

DownLoad: Full-Size Img PowerPoint

The stable distribution for $n = 3$ are shown in Figure 5.

Figure 5. Distributions of species

$x_{1}, \;x_{2}$ and

$x_{3}$ of system (30) with initial values

$x_{1}(\theta) = 0.5+0.01\sin\theta$ ,

$x_{2}(\theta) = 0.5+0.02\sin\theta$ ,

$x_{3}(\theta) = 0.5+0.001\sin\theta$ and parameter values in Table 2.

DownLoad: Full-Size Img PowerPoint

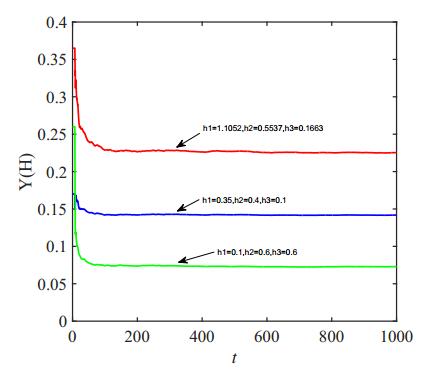
To numerical illustrate the optimal harvesting effort of (30), we set

$\Theta = (\theta_{1}, \theta_{2}, \theta_{3})^{T} = [A(A^{-1})^{T}+I]^{-1}(r_{1}-0.5\sigma_{1}^{2}, r_{2} -0.5\sigma_{2}^{2}, r_{3}-0.5\sigma_{3}^{2})^{T} = (1.1052, 0.5537, 0.1663)^{T},$

which yield $H^{*} = \Theta = (1.1052, 0.5537, 0.1663)^{T}$ , and the maximum of ESY is $Y^{*} = 0.2263$ , see Figure-6.

Figure 6. The harvesting policies

$E[h_{1}x_{1}(t)+h_{2}x_{2}(t)+h_{3}x_{3}(t)]$ of system (29) with initial values

$x_{1}(\theta) = 0.5+0.01\sin\theta$ ,

$x_{2}(\theta) = 0.5+0.02\sin\theta$ ,

$x_{3}(\theta) = 0.5+0.001\sin\theta$ and parameter values in Table 2. The red line is with

$h_{1} = h_{1}^{*} = 1.1052, \;h_{2} = h_{2}^{*} = 0.5537, \;h_{3} = h_{3}^{*} = 0.1663$ , the green line is with

$h_{1} = 0.1, \;h_{2} = 0.6, \;h_{3} = 0.6$ , the blue line is with

$h_{1} = 0.35, \;h_{2} = 0.4, \;h_{3} = 0.1$ .

DownLoad: Full-Size Img PowerPoint

6. Conclusions and discussions

In this paper, a stochastic n-species competitive model with delayed diffusions and harvesting has been considered. We studied the persistence in mean of every population, which is biologically significant because it shows that all populations can coexist in the community. Since the model (5) does not have a positive equilibrium point and its solution can not approach a positive value, we considered its asymptotically stable distribution. By using ergodic method, we obtained the optimal harvesting policy and the maximum harvesting yield of system (5). We have also done some numerical simulations of the situations for $n = 2$ and $n = 3$ in model (5) to illustrate our theoretical results as it is very useful whether in terms of mathematics or biology to visualize our conclusions.

Our studies showed some interesting results

(a) Both environmental disturbance and diffused time delay can effect the persistence and optimal harvesting effort of system (5)..

(b) Environmental noises have no effect on asymptotic stability in distribution of system (5), but the time delays have.

There are other meaningful aspects that can be studied further since our paper only consider the effects of white noises on population growth rate. In future, for example, we can consider the situation when white noises also have influences over harvesting (see ^[45]) and non-autonomous system (see ^[46]); the time delay will also be reflected in competition (see ^[49]). Furthermore, we can consider something more complex models such as the ones with regime-switching (see ^[50,51]) or Lévy jumps (see ^[14,42]).

Acknowledgments

This work was supported by the Research Fund for the Taishan Scholar Project of Shandong Province of China, and the SDUST Research Fund (2014TDJH102).

Conflict of interest

The authors declare that there is no conflict of interest regarding the publication of this paper.

References

[1]	D. R. Jutagir, B. B. Blomberg, C. S. Carver, et al., Social well-being is associated with less pro-inflammatory and pro-metastatic leukocyte gene expression in women after surgery for breast cancer, Breast Cancer Res. Treat., 165 (2017), 169–180.
[2]	S. Katkuri and M. Gorantla, Awareness about breast cancer among women aged 15 years and above in urban slums: a cross sectional study, Int. J. Community Med. Public Health, 5 (2018), 929–932.
[3]	A. Pawlik, M. Slomi´ nska-Wojewódzka and A. Herman-Antosiewicz, Sensitization of estrogen receptor-positive breast cancer cell lines to 4-hydroxytamoxifen by isothiocyanates present in cruciferous plants, Eur. J. Nutr., 55 (2016), 1165–1180.
[4]	D. L. Holliday and V. Speirs, Choosing the right cell line for breast cancer research, Breast Cancer Res., 13 (2011), 215–215.
[5]	R. L. Sutherland, R. E. Hall and I. W. Taylor, Cell proliferation kinetics of MCF-7 human mammary carcinoma cells in culture and effects of tamoxifen on exponentially growing and plateau-phase cells, Cancer Res., 43 (1983), 3998–4006.
[6]	B. S. Katzenellenbogen, K. L. Kendra, M. J. Norman, et al., Proliferation, hormonal responsiveness, and estrogen receptor content of MCF-7 human breast cancer cells grown in the short-term and long-term absence of estrogens, Cancer Res., 47(1987), 4355–4360.
[7]	A. Maton, Human biology and health, 1^st edition, Prentice Hall, New Jersey, 1997.
[8]	L. V. Rao, B. A. Ekberg, D. Connor, et al., Evaluation of a new point of care automated complete blood count (CBC) analyzer in various clinical settings, Clin. Chim. Acta., 389 (2008), 120–125.
[9]	S. Bernard, E. Abdelsamad, P. Johnson, et al., Pediatric leukemia: diagnosis to treatment a review, J. Cancer Clin. Trials, 2(2017), 131.
[10]	A. Shankar, J. J. Wang, E. Rochtchina, et al., Association between circulating white blood cell count and cancer mortality: a population-based cohort study, Arch. Intern. Med., 166 (2006), 188–194.
[11]	K. Kim, J. Lee, N. J. Heo, et al., Differential white blood cell count and all-cause mortality in the Korean elderly, Exp. Gerontol., 48 (2013), 103–108.
[12]	C. Ruggiero, E. J. Metter, A. Cherubini, et al., White blood cell count and mortality in the Baltimore Longitudinal Study of Aging, J. Am. Coll. Cardiol., 49 (2007), 1841–1850.
[13]	D. S. Bell and J. H. O'Keefe, White cell count, mortality, and metabolic syndrome in the Baltimore longitudinal study of aging, J. Am. Coll. Cardiol., 50(2007), 1810.
[14]	G. D. Friedman and B. H. Fireman, The leukocyte count and cancer mortality, Am. J. Epidemiol., 133 (1991), 376–380.
[15]	M. H. Andersen, D. Schrama, P. thor Straten, et al., Cytotoxic T cells, J. Invest. Dermatol., 126 (2006), 32–41.
[16]	J. Folkman and R. Kalluri, Cancer without disease, Nature, 427 (2004), 787.
[17]	T. Fehm, V. Mueller, R. Marches, et al., Tumor cell dormancy: implications for the biology and treatment of breast cancer, Apmis, 116 (2008), 742–753.
[18]	N. Almog, Molecular mechanisms underlying tumor dormancy, Cancer Lett., 294 (2010), 139–146.
[19]	A. Friedman, Cancer as multifaceted disease, Math. Model. Nat. Pheno., 7(2012), 3–28.
[20]	R. Eftimie, J. L. Bramson and D. J. Earn, Interactions between the immune system and cancer: a brief review of non-spatial mathematical models, Bull. Math. Biol., 73 (2011), 2–32.
[21]	S. Banerjee and R. R. Sarkar, Delay-induced model for tumor–immune interaction and control of malignant tumor growth, Biosystems, 91 (2008), 268–288.
[22]	H. Moore and N. K. Li, A mathematical model for chronic myelogenous leukemia (CML) and T cell interaction, J. Theor. Biol., 227 (2004), 513–523.
[23]	L. Anderson, S. Jang and J. Yu, Qualitative behavior of systems of tumor-CD4⁺-cytokine interactions with treatments, Math. Method. Appl. Sci., 38 (2015), 4330–4344.
[24]	A. d'Onofrio, Metamodeling tumor–immune system interaction, tumor evasion and immunotherapy, Math. Comput. Model., 47 (2008), 614–637.
[25]	A. Khar, Mechanisms involved in natural killer cell mediated target cell death leading to spontaneous tumour regression, J. Biosci., 22 (1997), 23–31.
[26]	T. Boon and P. van der Bruggen, Human tumor antigens recognized by T lymphocytes, J. Exp. Med., 183 (1996), 725–729.
[27]	D. Kirschner and J. C. Panetta, Modeling immunotherapy of the tumor–immune interaction, J. Math. Biol., 37 (1998), 235–252.
[28]	L. G. de Pillis, W. Gu and A. E. Radunskaya, Mixed immunotherapy and chemotherapy of tumors: modeling, applications and biological interpretations, J. Theor. Biol., 238 (2006), 841–862.
[29]	H. P. de Vladar and J. A. González, Dynamic response of cancer under the influence of immunological activity and therapy, J. Theor. Biol., 227 (2004), 335–348.
[30]	U. Fory´ s, J. Waniewski and P. Zhivkov, Anti-tumor immunity and tumor anti-immunity in a mathematical model of tumor immunotherapy, J. Biol. Syst., 14 (2006), 13–30.
[31]	R. W. De Boer, J. M. Karemaker and J. Strackee, Relationships between short-term blood-pressure fluctuations and heart-rate variability in resting subjects I: a spectral analysis approach, Med. Biol. Eng. Comput., 23 (1985), 352–358.
[32]	A. Cappuccio, M. Elishmereni and Z. Agur, Cancer immunotherapy by interleukin-21: potential treatment strategies evaluated in a mathematical model, Cancer Res., 66 (2006), 7293–7300.
[33]	N. Kronik, Y. Kogan, V. Vainstein, et al., Improving alloreactive CTL immunotherapy for malignant gliomas using a simulation model of their interactive dynamics, Cancer Immunol. Immunother., 57 (2008), 425–439.
[34]	A. M. Jarrett, J. M. Bloom, W. Godfrey, et al., Mathematical modelling of trastuzumab-induced immune response in an in vivo murine model of HER2+ breast cancer, Math. Med. Biol., (2018), dqy014.
[35]	K. Annan, M. Nagel and H. A. Brock, A mathematical model of breast cancer and mediated immune system interactions, J. Math. Syst. Sci., 2(2012), 430–446.
[36]	R. Roe-Dale, D. Isaacson and M. Kupferschmid, A mathematical model of breast cancer treatment with CMF and doxorubicin, Bull. Math. Biol., 73 (2011), 585–608.
[37]	B. Ribba, N. H. Holford, P. Magni, et al., A review of mixed-effects models of tumor growth and effects of anticancer drug treatment used in population analysis, CPT Pharmacometrics Syst. Pharmacol., 3(2014), 1–10.
[38]	R. Bhat and C. Watzl, Serial killing of tumor cells by human natural killer cells–enhancement by therapeutic antibodies, PloS One, 2 (2007), e326.
[39]	T. Sutlu and E. Alici, Natural killer cell-based immunotherapy in cancer: current insights and future prospects, J. Intern. Med., 266 (2009), 154–181.
[40]	T. R. Stravitz, T. Lisman, V. A. Luketic, et al., Minimal effects of acute liver injury/acute liver failure on hemostasis as assessed by thromboelastography, J. Hepatol., 56 (2012), 129–136.
[41]	Y. Zhang, D. L. Wallace, C. M. De Lara, et al., In vivo kinetics of human natural killer cells: the effects of ageing and acute and chronic viral infection, Immunotherapy, 121(2007), 258–265.
[42]	P. Wilding, L. J. Kricka, J. Cheng, et al., Integrated cell isolation and polymerase chain reaction analysis using silicon microfilter chambers, Anal. Biochem., 257(1998), 95–100.
[43]	V. Pascal, N. Schleinitz, C. Brunet, et al., Comparative analysis of NK cell subset distribution in normal and lymphoproliferative disease of granular lymphocyte conditions, Eur. J. Immunol., 34(2004), 2930–2940.
[44]	L. de Pillis, T. Caldwell, E. Sarapata, et al., Mathematical modeling of the regulatory T cell effects on renal cell carcinoma treatment, Discrete Continuous Dyn. Syst. Ser. B, 18(2013), 915–943.
[45]	T. D. To, A. T. T. Truong, A. T. Nguyen, et al., Filtration of circulating tumour cells MCF-7 in whole blood using non-modified and modified silicon nitride microsieves, Int. J. Nanotechnol., 15(2018), 39–52.
[46]	C. Chen, Y. Chen, D. Yao, et al., Centrifugalfilter device for detection of rare cells with immuno-binding, IEEE T. Nanobiosci., 14(2015), 864–869.
[47]	P. Dua, V. Dua and E. N. Pistikopoulos, Optimal delivery of chemotherapeutic agents in cancer, Comput. Chem. Eng., 32(2008), 99–107.
[48]	A. G. López, J. M. Seoane and M. A. Sanjuán, A validated mathematical model of tumor growth including tumor–host interaction, cell-mediated immune response and chemotherap, Bull. Math. Biol., 76(2014), 2884–2906.
[49]	K. Liao, X. Bai and A. Friedman, The role of CD200–CD200R in tumor immune evasion, J. Theor. Biol., 328(2013), 65–76.
[50]	M. C. Martins, A. M. A. Rocha, M. F. P. Costa, et al., Comparing immune-tumor growth models with drug therapy using optimal control, AIP Conf. Proc., 1738(2016), 300005.
[51]	M. Fernandez, M. Zhou and L. Soto-Ortiz, A computational assessment of the robustness of cancer treatments with respect to immune response strength, tumor size and resistance, Int. J. Tumor Ther., 7(2018), 1–26.
[52]	D. F. Tough and J. Sprent, Life span of naive and memory T cells, Stem Cells, 13(1995), 242–249.
[53]	C. M. Rollings, L. V. Sinclair, H. J. M. Brady, et al., Interleukin-2 shapes the cytotoxic T cell proteome and immune environment–sensing programs, Sci. Signal., 11(2018), eaap8112.
[54]	E. M. Janssen, E. E. Lemmens, T. Wolfe, et al., CD4+ T cells are required for secondary expansion and memory in CD8+ T lymphocytes, Nature, 421(2003), 852.
[55]	I. Gruber, N. Landenberger, A. Staebler, et al., Relationship between circulating tumor cells and peripheral T-cells in patients with primary breast cancer, Anticancer Res., 33(2013), 2233–2238.
[56]	D. Homann, L. Teyton and M. B. Oldstone, Differential regulation of antiviral T-cell immunity results in stable CD8+ but declining CD4+ T-cell memory, Nat. Med., 7(2001), 913–919.
[57]	R. J. De Boer, D. Homann and A. S. Perelson, Different dynamics of CD4+ and CD8+ T cell responses during and after acute lymphocytic choriomeningitis virus infection, J. Immunol., 171(2003), 3928–3935.
[58]	G. T. Skalski and J. F. Gilliam, Functional responses with predator interference: viable alternatives to the Holling type II model, Ecology, 82(2001), 3083–3092.
[59]	H. Nawata, M. T. Chong, D. Bronzert, et al., Estradiol-independent growth of a subline of MCF-7 human breast cancer cells in culture, J. Biol. Chem., 256(1981), 6895–6902.
[60]	R. Clarke, N. Brünner, B. S. Katzenellenbogen, et al., Progression of human breast cancer cells from hormone-dependent to hormone-independent growth both in vitro and in vivo, Proc. Natl. Acad. Sci. USA, 86(1989), 3649–3653.
[61]	N. T. Telang, G. Li, M. Katdare, et al., The nutritional herb Epimedium grandiflorum inhibits the growth in a model for the Luminal A molecular subtype of breast cancer, Oncol. Lett., 13 (2017), 2477–2482.
[62]	T. A. Caragine, M. Imai, A. B. Frey, et al., Expression of rat complement control protein Crry on tumor cells inhibits rat natural killer cell–mediated cytotoxicity, Blood, 100 (2002), 3304–3310.
[63]	M. R. Müller, F. Grünebach, A. Nencioni, et al., Transfection of dendritic cells with RNA induces CD4-and CD8-mediated T cell immunity against breast carcinomas and reveals the immunodominance of presented T cell epitopes, J. Immunol., 170 (2003), 5892–5896.
[64]	J. Chen, E. Hui, T. Ip, et al., Dietary flaxseed enhances the inhibitory effect of tamoxifen on the growth of estrogen-dependent human breast cancer (mcf-7) in nude mice, Clin. Cancer Res., 10(2004), 7703–7711.
[65]	P. V. Sivakumar, R. Garcia, K. S. Waggie, et al., Comparison of vascular leak syndrome in mice treated with IL21 or IL2, Comparative Med., 63 (2013), 13–21.
[66]	C.Wu, T.Motosha, H.A.Abdel-Rahman, etal., Freeandprotein-boundplasmaestradiol-17during the menstrual cycle, J. Clin. Endocrinol. Metab., 43(1976), 436–445.
[67]	E. Nikolopoulou, L. R. Johnson, D. Harris, et al., Tumour-immune dynamics with an immune checkpoint inhibitor, Lett. Biomath., 5(2018), S137–S159.
[68]	P. Vacca, E. Munari, N. Tumino, et al., Human natural killer cells and other innate lymphoid cells in cancer: friends or foes? Immunol. Lett., 201(2018), 14–19.
[69]	A. Cerwenka, J. Kopitz, P. Schirmacher, et al., HMGB1: the metabolic weapon in the arsenal of NK cells, Mol. Cell. Oncol., 3(2016), e1175538.
[70]	I. J. Fidler, Metastasis: quantitative analysis of distribution and fate of tumor emboli labeled with 125i-5-iodo-2'-deoxyuridine, J. Natl. Cancer Inst., 4(1970), 773–782.
[71]	G. G. Page and S. Ben-Eliyahu, A role for NK cells in greater susceptibility of young rats to metastatic formation, Dev. Comp. Immunol., 23(1999), 87–96.
[72]	O. E. Franco, A. K. Shaw, D. W. Strand, et al., Cancer associated fibroblasts in cancer pathogenesis, Semin. Cell Dev. Bio., 21(2010), 33–39.
[73]	G. P. Dunn, A. T. Bruce, H. Ikeda, et al., Cancer immunoediting: from immunosurveillance to tumor escape, Nat. Immunol., 3(2002), 991.
[74]	D. Mittal, M. M. Gubin, R. D. Schreiber, et al., New insights into cancer immunoediting and its three component phases-elimination, equilibrium and escape, Curr. Opin. Immunol., 27(2014), 16–25.
[75]	J. Nowak, P. Juszczynski and K. Warzocha, The role of major histocompatibility complex polymorphisms in the incidence and outcome of non-Hodgkin lymphoma, Curr. Immunol. Rev., 5(2009), 300–310.
[76]	J. G. B. Alvarez, M. González-Cao, N. Karachaliou, et al., Advances in immunotherapy for treatment of lung cancer, Cancer Biol. Med., 12(2015), 209–222.
[77]	M. E. Dudley and S. A. Rosenberg, Adoptive-cell-transfer therapy for the treatment of patients with cancer, Nat. Rev. Cancer, 3(2003), 666–675.
[78]	M. Su, C. Huang and A. Dai, Immune checkpoint inhibitors: therapeutic tools for breast cancer, Asian Pac. J. Cancer Prev., 17 (2016), 905–910.
[79]	M. Ebbo, L. Gérard, S. Carpentier, et al., Low circulating natural killer cell counts are associated with severe disease in patients with common variable immunodeficiency, EBioMedicine., 6(2016), 222–230.
[80]	S. H. Jee, J. Y. Park, H. Kim, et al., White blood cell count and risk for all-cause, cardiovascular, and cancer mortality in a cohort of Koreans, Am. J. Epidemiol., 162 (2005), 1062–1069.
[81]	W. B. Kannel, K. Anderson and T. W. Wilson, White blood cell count and cardiovascular disease: insights from the Framingham Study, Jama, 267 (1992), 1253–1256.
[82]	K. L. Margolis, J. E. Manson, P. Greenland, et al., Leukocyte count as a predictor of cardiovascular events and mortality in postmenopausal women: the Women's Health Initiative Observational Study, Arch. Intern. Med., 165(2005), 500–508.
[83]	B. K. Duffy, H. S. Gurm, V. Rajagopal, et al., Usefulness of an elevated neutrophil to lymphocyte ratio in predicting long-term mortality after percutaneous coronary intervention, Am. J. Cardiol., 97 (2006), 993–996.
[84]	B. D. Horne, J. L. Anderson, J. M. John, et al., Which white blood cell subtypes predict increased cardiovascular risk? J. Am. Coll. Cardiol., 45(2005), 1638–1643.
[85]	R. N. O. Cobucci, H. Saconato, P. H. Lima, et al., Comparative incidence of cancer in HIV-AIDS patients and transplant recipients, Cancer Epidemiol., 36(2012), e69–e73.
[86]	C. Bodelon, M. M. Madeleine, L. F. Voigt, et al., Is the incidence of invasive vulvar cancer increasing in the United States? Cancer Causes Control, 20(2009), 1779–1782.
[87]	M. R. Shurin, Cancer as an immune-mediated disease, Immunotargets Ther., 1 (2012), 1–6.
[88]	J. S. Lawrence, Leukopenia: its mechanism and therapy, J. Chronic. Dis., 6(1957), 351–364.
[89]	P. Venigalla, B. Motwani, A. Nallari, et al., A patient on hydroxyurea for sickle cell disease who developed an opportunistic infection, Blood, 100(2002), 363–364.
[90]	M. Iwamuro, S. Tanaka, A. Bessho, et al., Two cases of primary small cell carcinoma of the stomach, Acta. Med. Okayama, 63(2009), 293–298.
[91]	A. O. O. Chan, I. O. L. Ng, C. M. Lam, et al., Cholestatic jaundice caused by sequential carbimazole and propylthiouracil treatment for thyrotoxicosis, Hong Kong Med. J., 9(2003), 377–380.
[92]	J. H. Goodchild and M. Glick, A different approach to medical risk assessment, Endod. Topics, 4(2003), 1–8.
[93]	S. E. Hankinson, Endogenous hormones and risk of breast cancer in postmenopausal women, Breast Dis., 24(2006), 3–15.
[94]	R. Kaaks, S. Rinaldi, T. J. Key, et al., Postmenopausal serum androgens, oestrogens and breast cancer risk: the European prospective investigation into cancer and nutrition, Endocr. Relat. Cancer, 12(2005), 1071–1082.
[95]	S. A. Missmer, A. H. Eliassen, R. L. Barbieri, et al., Endogenous estrogen, androgen, and progesterone concentrations and breast cancer risk among postmenopausal women, J. Natl. Cancer Inst., 96(2004), 1856–1865.
[96]	A. A. Arslan, R. E. Shore, Y. Afanasyeva, et al., Circulating estrogen metabolites and risk for breast cancer in premenopausal women, Cancer Epidemiol. Biomarkers Prev., 18(2009), 2273–2279.
[97]	S. B. Brown and S. E. Hankinson, Endogenous estrogens and the risk of breast, endometrial, and ovarian cancers, Steroids, 99(2015), 8–10.
[98]	L. C. Houghton, D. Ganmaa, P. S. Rosenberg, et al., Associations of breast cancer risk factors with premenopausal sex hormones in women with very low breast cancer risk, Int. J. Environ. Res. Public Health, 13(2016), 1066.
[99]	R. Kaaks, K. Tikk, D. Sookthai, et al., Premenopausal serum sex hormone levels in relation to breast cancer risk, overall and by hormone receptor status-results from the EPIC cohortk, Int. J. cancer, 134(2014), 1947–1957.
[100]	A. Diefenbach, E. R. Jensen, A. M. Jamieson, et al., Rae1 and H60 ligands of the NKG2D receptor stimulate tumour immunity, Nature, 413(2001), 165.
[101]	A. Iannello and D. H. Raulet, Cold Spring Harbor symposia on quantitative biology, 1^st edition, Cold Spring Harbor Laboratory Press, New York, 2013.
[102]	M. B. Pampena and E. M. Levy, Natural killer cells as helper cells in dendritic cell cancer vaccines, Front. Immunol., 6 (2015), 1–8.
[103]	E. Vivier, S. Ugolini, D. Blaise, et al., Targeting natural killer cells and natural killer T cells in cancer, Nat. Rev. Immunol., 12(2012), 239–252.
[104]	G. Liu, X. Fan, Y. Cai, et al., Efficacy of dendritic cell-based immunotherapy produced from cord blood in vitro and in a humanized NSG mouse cancer model, Immunotherapy, 11(2019), 599–616.
[105]	M. Schnekenburger, M. Dicato and M. F. Diederich, Anticancer potential of naturally occurring immunoepigenetic modulators: A promising avenue? Cancer, 125(2019), 1612–1628.
[106]	X. Feng, L. Lu, K. Wang, et al., Low expression of CD80 predicts for poor prognosis in patients with gastric adenocarcinoma, Future Oncol., 15 (2019), 473–483.
[107]	X. Lai and A. Friedman, Combination therapy of cancer with cancer vaccine and immune checkpoint inhibitors: a mathematical model, PloS One, 12 (2017), e0178479.

Reader Comments

Your name:*

Email:*
© 2019 the Author(s), licensee AIMS Press. This is an open access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0)